Using CFD Modeling to Investigate the Non-Uniform Circumferential Distribution of Heat Transfer Characteristics in a Single-Phase Helical Coiled Tube

Abstract

Helical coiled tube (HCT) heat exchangers (HXs) are used in the nuclear industry, particularly in the residual heat removal systems of nuclear power plants (NPPs) and steam generators for small modular reactors. In this study, a single-phase CFD model was developed to investigate non-uniform circumferential distributions in the local wall heat transfer characteristics of a vertical HCT to obtain localized information critical for the safety of NPPs. In a comparison, the predicted circumferential heat transfer characteristics agreed well with the measured data. Governed by centrifugal/gravitational forces, these non-uniform distributions are clearly visible in the results, explaining the test data. We performed additional simulations of the conjugated heat transfer from the hot fluid of the shell side to the cold fluid of the tube side, confirming that the inhomogeneity of circumferential distributions in HCTs is due to the assumption of a constant heat flux boundary condition.

1. Introduction

Due to its special shape and curvature, a helical coiled tube (HCT) can withstand more thermal expansion stress than a spring. It also has a larger heat exchange area within its given volume and a higher capacity for heat transfer due to the stronger secondary flow caused by centrifugal force [1,2,3,4]. For these reasons, HCTs have been extensively applied in industrial components, particularly in heat exchangers. In nuclear power plants (NPPs), HCT heat exchangers (HCTHXs) are incorporated into the Residual Heat Removal Systems (RHRSs) and Steam Generators (SGs) of Small Modular Reactors (SMRs), such as IRIS [5], CAREM-25 [6], HTR-PM [7] and NuScale [8]. Most previous works on HCT heat exchangers (HCTHXs) focused on their overall heat transfer capability and performance. However, localized information (for example, regarding hot spots or inferior heat transfer points) is needed for NPPs to operate safely. In this work, CFD simulations were performed to investigate the localized heat transfer characteristics of single-phase convection in an HCT. The results of this study can support the safe operation and maintenance of nuclear power plants.

Numerical studies related to the single-phase convective heat transfer of HCTHXs were reviewed. Ferng et al. [3] developed a 3D single-phase CFD model to investigate the effects of the Dean (De) number and pitch size on the thermal–hydraulic characteristics of an HCTHX. The average Nussel (Nu) number versus the tube length were presented and compared with measured data and appropriate correlations. Based on their simulation results, the overall state of the HCTHX was reasonably captured, including flow acceleration and separation in the shell side, the secondary flow within the tube, and the behaviors developing near the entrance of the coiled tube. Through single-phase numerical simulations, Lin et al. [4] investigated the effects of different turbulence models on the flow and heat transfer characteristics of an HCTHX. Three turbulence models were considered, including the realizable k–ε turbulence model (RKE), low-Reynolds k–ε turbulence model (LKE), and Reynolds stress model (RSM). They reported that, compared to the other two models and experimental data, the LKE turbulence model over-predicted the heat exchanger’s performance. Alimoradi and Veysi [9] numerically and experimentally studied the heat transfer of an HCTHX under various parameters, including the physical properties of the fluid, operational parameters, and geometrical parameters. Their results showed that the shell-side Nu number increased with increasing pitch and decreased as the height and diameter of the shell increased. In addition, two correlations were developed to predict the Nu numbers of the coil and shell sides for wide ranges of Reynolds (Re) and Prandtl (Pr) numbers. Sepehr et al. [10] numerically studied heat transfer, pressure drop, and entropy generation in shell and helical coiled finned tube heat exchangers. The effects of the fin height and number were considered. Their model was validated by comparing the overall Nu of both sides and the average friction factor of the coil side with the appropriate empirical correlations.

Elattara et al. [11] numerically investigated the thermal and hydraulic performance of an MTTHC (Multi-Tubes in Tube Helical Coiled) heat exchanger for the turbulent flow. They also considered the effects of the operating and geometrical parameters of the coil on the Nu number, pumping power, and effectiveness, etc. Their results showed that the largest heat transfer coefficient and greatest effectiveness were predicted for inner tube = 3 and coil inclination angle = 0° and 90°. Mirgolbabaei [12] performed a thermal performance assessment of a vertical HCTHX at various mass flow rate, coil-to-tube diameter ratio, and coil pitch values. A conjugate thermal boundary condition for the tube wall fluid-to-fluid heat transfer mechanism was considered. Based on the simulation results, the effectiveness of the heat exchanger decreased with increasing coil pitch and was not influenced by variations in the tube diameter. Using a single-phase CFD approach, Tuncer et al. [13] compared the performance of a modified shell and helical coiled heat exchanger (SHCHX) with a conventional one. The modified SHCHX was designed with a hollow tube integrated into the shell side, which offered advantages of regulating the fluid flow in the shell side and improving the heat transfer. The corresponding modified SHCHX was experimentally tested to determine its effectiveness, and the authors reported an average difference between the predicted and measured results of 8%.

Güngor et al. [14] attached rings and discs to the helical coiled tubes to modify a conventional HCTHX. According to their simulation results, the average heat transfer rate of the modified heat exchanger increased to 7.1% compared to the conventional heat exchanger. The modified HX was fabricated and experimentally tested under the same conditions in a laboratory to verify the simulation results. A comparison revealed that the simulation results were close to the experimental data, with a difference of 2.4% in the average heat transfer rate. Xu et al. [15] performed numerical simulations to study the effects of various grooving methods and depths on the overall heat transfer characteristics of HCTHXs. Their results implied that grooving on the plain tube could enhance the comprehensive heat transfer performance and simultaneously increase the fluid pressure drop. They concluded that the maximum performance evaluation criterion (PEC) was satisfied for a helical coiled spiral grooved tube (HCSGT) HX with a 0.5 mm groove depth. Yuan et al. [16] numerically and experimentally studied the performance of a double-shell pass multi-layer helical coiled tube heat exchanger (DSMHCTHX). Their results confirmed that both the heat transfer rate and thermal effectiveness of the DSMHCTHX increased from 5.1% to 12.9%, when compared with a traditional multi-layer helical tube heat exchanger. However, the shell-side pressure drop increased from 60.7 % to 83.4%.

Duan et al. [17] developed a tube–shell coupled model for a helical coiled corrugated tube heat exchanger. The effects of the Re number, corrugation height, and corrugation length on flow and heat transfer performance were also considered. They concluded that the Nu number for both sides and the PEC significantly increased with an increasing corrugation height and decreasing length. Although, the corrugation height enhanced the friction factor, its length had a little impact. Cao et al. [18] numerically studied the heat transfer and flow resistance characteristics of an internally finned helical coiled tube heat exchanger. They also performed corresponding tests. The empirical correlations used to calculate the Nu number and friction factor of the internally finned helical coiled tube were summarized and validated using the measurements and predictions, and they reported that the internally finned helical coiled tube heat exchanger performed better than smooth HCTHXs. Through CFD simulations, Missaoui [19] investigated the influence of different helical coil structure designs on the heat exchanger’s heat transfer characteristics, including a constant-diameter coil, variable-diameter coil, and variable-pitch coil. This CFD model was validated with experimental measurements, and the author reported that higher Nu number values for the helical coil with variable pitch than the other configurations.

The above literature review shows that most CFD studies related to HCTs or HCTHXs focused on the overall heat transfer behavior and performance under various parameters, such as HCT shape, De number, pitch size, and inlet flowrate. Few CFD simulations have been conducted to study localized heat transfer characteristics (especially the circumferential distribution of heat transfer parameters) in detail or compared the predicted localized results against measured test data. Most previous CFD works were directly validated using overall heat transfer performance data for the HCT or HCTHX but not local measured results, revealing a deficiency in this research area. Obtaining localized information is a challenge for the safe design and operation of NPPs with HCTHXs. In this work, a single-phase CFD model is developed based on the Best Practice Guidelines (BPGs) [20] to capture the localized heat transfer characteristics of an HCT. The results of this CFD methodology were validated with localized test data of the non-uniform circumferential distribution of wall temperature and the heat transfer coefficient [21] in an HCT. These CFD results can also help explain the measured discrete results using detailed predictions of thermal-hydraulic contours or line curves, demonstrating the contribution of this work. The validated CFD model can also assess the applicability of various h-correlations for the HCT that can be adopted in system codes for safety analyses of NPPs with HCTHXs.

2. Mathematical Model and Numerical Treatment

In this study, a 3D CFD methodology was developed to simulate the non-uniform circumferential distribution of single-phase heat transfer characteristics in an HCT. Before the governing equations are presented, we list the following assumptions:

• We set uniform distributions of velocity and temperature at the inlet.
• The pressure was set at the outlet boundary condition (BC).
• According to the test powers [21], constant heat flux was set at the wall boundary and derived from the energy balance.
• RANS equations with the SST k-ω turbulence model (SSTKW) [22] were selected since the SSTKW offers better predictions for the flow conditions of adverse pressure gradients, a swirling pattern, and secondary flow due to the centrifugal and gravitational forces in an HCT.

2.1. Governing Equations

Continuity Equation

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}(\rho u_i)=0$$

(1)

Momentum Equation

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}}(\rho u_i{u}_j)=-{\displaystyle \frac{\mathsf{\partial }p}{\mathsf{\partial }{x}_i}}+{\displaystyle \frac{\mathsf{\partial }{\tau }_{ij}}{\mathsf{\partial }{x}_j}}+\rho g_i$$

(2)

where,

$${\tau }_{ij}={\mu }^{*}{\displaystyle \frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}}; {\mu }^{*}=\mu +{\mu }_t$$

(3)

Energy Equation

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}(\rho Cp{u}_{i}T)={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}({\lambda }^{*}{\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }{x}_i}})$$

(4)

where,

$${\lambda }^{*}=\text{total conductivity}=\lambda +{\lambda }_t$$

(5)

$${\lambda }_t=C_p\frac{{\mu }_t}{{\sigma }_t}$$

(6)

2.2. SST $k-\omega$ Turbulence Model

The turbulence kinetic energy (k) and specific dissipation rate (ω) in the SSTKW [22] can be obtained from the following transport equations:

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}(\rho u_{i}k)={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}\left[\left.(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}){\displaystyle \frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_i}}\right]\right.+G_k-Y_k$$

(7)

$${\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}(\rho u_i\omega )={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_i}}\left[\left.(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\omega }}}){\displaystyle \frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_i}}\right]\right.+G_{\omega }-Y_{\omega }+D_{\omega }$$

(8)

where,

$${\mu }_t={\displaystyle \frac{\rho k}{\omega }}{\displaystyle \frac{1}{\max \left(\frac{1}{{\alpha }^{*}},\frac{\mathsf{\Omega }{F}_2}{a_1\omega }\right)}}$$

(9)

$$\mathsf{\Omega }=\sqrt{2{\mathsf{\Omega }}_{ij}{\mathsf{\Omega }}_{ij}}$$

(10)

${\mathsf{\Omega }}_{ij}$ is the mean rate-of-rotation tensor and is defined by

$${\mathsf{\Omega }}_{ij}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}}-{\displaystyle \frac{\mathsf{\partial }{u}_j}{\mathsf{\partial }{x}_i}}\right)$$

(11)

$${\sigma }_k={\displaystyle \frac{1}{F_1/{\sigma }_{k,1}+(1-F_1)/{\sigma }_{k,2}}}$$

(12)

$${\sigma }_{\omega }={\displaystyle \frac{1}{F_1/{\sigma }_{\omega ,1}+(1-F_1)/{\sigma }_{\omega ,2}}}$$

(13)

The blending functions, F₁ and F₂, are given by

$$F_1=\tanh \left({\mathsf{\Phi }}_1^4\right)$$

(14)

$$F_2=\tanh \left({\mathsf{\Phi }}_2^2\right)$$

(15)

$${\mathsf{\Phi }}_1=\min \left[\max \left({\displaystyle \frac{\sqrt{k}}{0.09\omega y}},{\displaystyle \frac{500\mu }{\rho y^2\omega }}\right),{\displaystyle \frac{4\rho k}{{\sigma }_{\omega ,2}{D}_{\omega }^{+}{y}^2}}\right]$$

(16)

$${\mathsf{\Phi }}_2=\max \left[{\displaystyle \frac{2\sqrt{k}}{0.09\omega y}},{\displaystyle \frac{500\mu }{\rho y^2\omega }}\right]$$

(17)

$D_{\omega }^{+}$ is the positive portion of the cross-diffusion term and is determined by

$$D_{\omega }^{+}=\max \left[2\rho {\displaystyle \frac{1}{{\sigma }_{\omega ,2}}}{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_i}}{\displaystyle \frac{\mathsf{\partial }\omega }{\mathsf{\partial }{x}_i}},{10}^{-20}\right]$$

(18)

$${\alpha }^{*}={\alpha }_{\infty }^{*}\left({\displaystyle \frac{{\alpha }_0^{*}+{\mathrm{Re}}_t/R_k}{1+{\mathrm{Re}}_t/R_k}}\right)$$

(19)

$${\mathrm{Re}}_t={\displaystyle \frac{\rho k}{\mu \omega }}$$

(20)

$${\alpha }_0^{*}={\displaystyle \raisebox{1ex}{${\beta }_i$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$$

(21)

$${\beta }_i=F_1{\beta }_{i,1}+(1-F_1){\beta }_{i,2}$$

(22)

$$G_k={\tau }_{t,ij}{\displaystyle \frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}};\hspace{1em}{\tau }_{t,ij}={\mu }_t\left({\displaystyle \frac{\mathsf{\partial }{u}_i}{\mathsf{\partial }{x}_j}}+{\displaystyle \frac{\mathsf{\partial }{u}_j}{\mathsf{\partial }{x}_i}}\right)-2/3\rho k{\delta }_{ij}$$

(23)

$$Y_k=\rho {\beta }^{*}k\omega$$

(24)

$$G_{\omega }={\displaystyle \frac{\rho \alpha }{{\mu }_t}}{G}_k$$

(25)

$$Y_{\omega }=\rho {\beta }_i{\omega }^2$$

(26)

$$\alpha ={\displaystyle \frac{{\alpha }_{\infty }}{{\alpha }^{*}}}\left({\displaystyle \frac{{\alpha }_0^{*}+{\mathrm{Re}}_t/R_k}{1+{\mathrm{Re}}_t/R_k}}\right)$$

(27)

$${\alpha }_{\infty }=F_1{\alpha }_{\infty ,1}+(1-F_1){\alpha }_{\infty ,2}$$

(28)

$${\alpha }_{\infty ,1}={\displaystyle \frac{{\beta }_{i,1}}{{\beta }_{\infty }^{*}}}-{\displaystyle \frac{{\kappa }^2}{{\sigma }_{\omega ,1}\sqrt{{\beta }_{\infty }^{*}}}}$$

(29)

$${\alpha }_{\infty ,2}={\displaystyle \frac{{\beta }_{i,2}}{{\beta }_{\infty }^{*}}}-{\displaystyle \frac{{\kappa }^2}{{\sigma }_{\omega ,2}\sqrt{{\beta }_{\infty }^{*}}}}$$

(30)

The values of the empirical constants shown above are provided in

Table 1. Values of constants in SSTKW turbulence model [22].

${\mathsf{\sigma }}_{\mathit{t}}$	${\mathsf{\alpha }}_{\mathit{k},1}$	${\mathsf{\alpha }}_{\mathit{k},2}$	${\mathsf{\alpha }}_{\mathsf{\omega },1}$	${\mathsf{\alpha }}_{\mathsf{\omega },2}$	${\mathit{a}}_1$	${\mathsf{\beta }}_{\mathit{i},1}$	${\mathsf{\beta }}_{\mathit{i},2}$	${\mathsf{\beta }}_{\mathit{\infty }}^{\mathbf{*}}$	$\mathsf{\kappa }$	${\mathit{R}}_{\mathit{k}}$
0.85	1.176	1.0	2.0	1.168	0.31	0.075	0.0828	0.09	0.41	6

[22].

2.3. Numerical Treatment

The mathematical model described in the previous section comprises partial differential equations (PDEs). Using the finite difference or finite volume method, these PDEs can be discretized into algebraic equations for the numerical calculation. The second-order upwind scheme was adopted to treat the convection terms in these PDEs. The SIMPLE scheme [23] was used to solve the equations for velocities coupled with pressure. The Algebraic MultiGrid (AMG) linear solver was adopted for all equations. All simulations presented in this paper were performed using FLUENT code [24] on a PC with an Intel® Core i9-7900X CPU, and computing time required for a typical case was approximately 2 h. The convergence criteria for all of the governing equations were set such that the summation of the relative residual in every control volume is less than. The decay trend in the residual plot for each equation is also considered a criterion. Both of these criteria must be met to ensure the convergence of the numerical simulations.

3. Results and Discussion

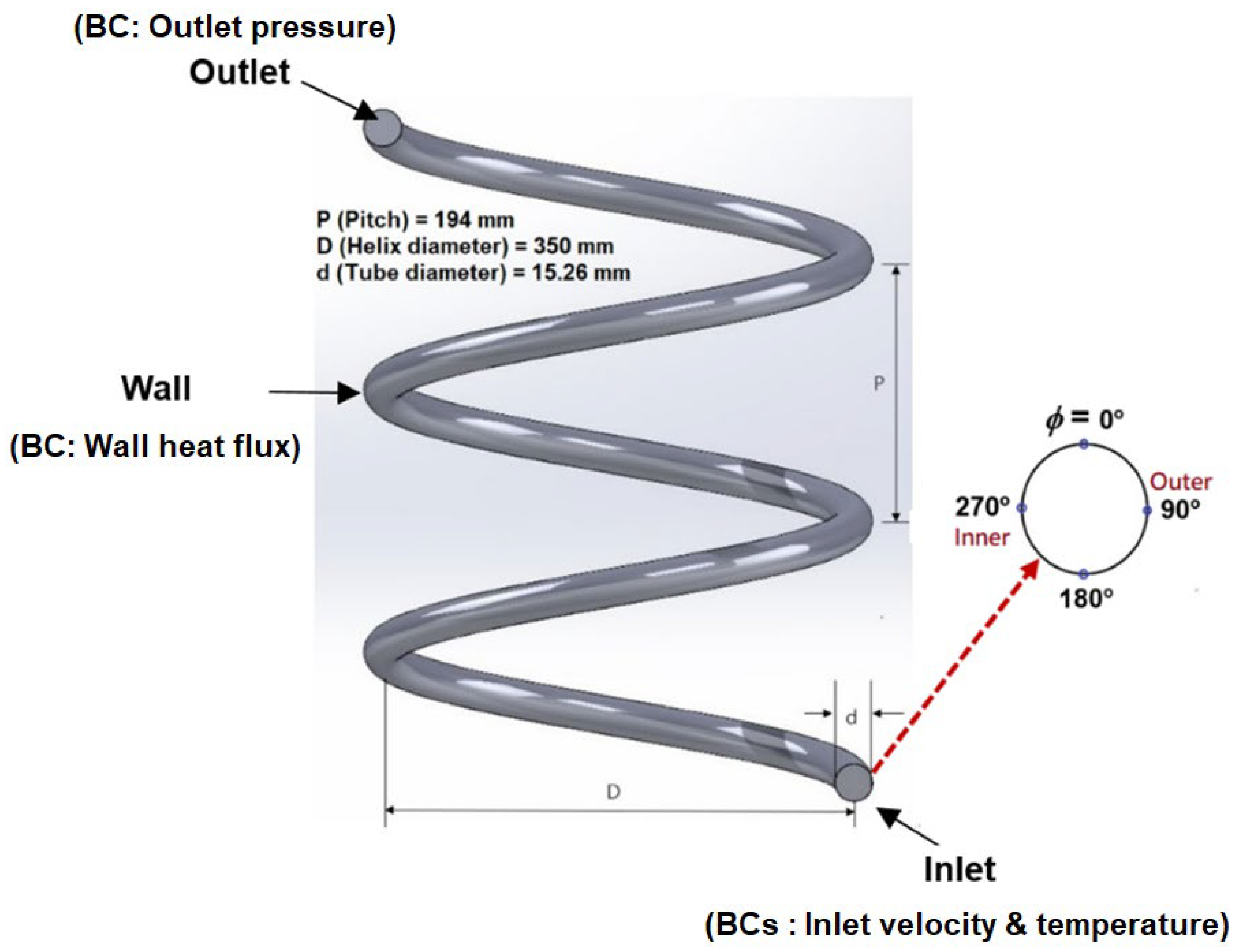
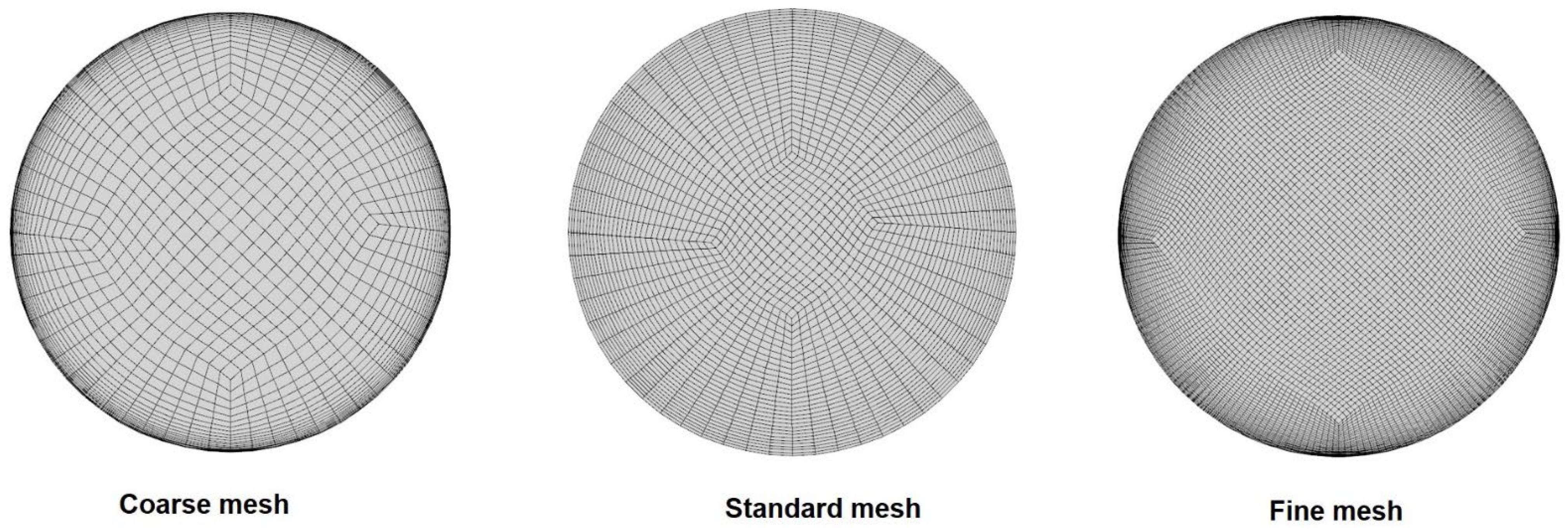
An experimental approach [21] to measuring the non-uniform circumferential distribution of wall temperature and the heat transfer coefficient in an HCT was adopted to assess the CFD methodology developed in this study. Figure 1 shows the schematics of the HCT for these simulations. The right portion of this figure shows the circumferential angle (ϕ) on the HCT wall. The corresponding mesh distributions on the cross-section of the HCT are indicated in Figure 2. Based on the requirements of the CFD Best Practice Guidelines [20], structured grids were used near the wall, and mesh-independent calculations were performed. Sensitivity simulations for the various meshes were applied on the cross-section of the HCT, including 860 (Coarse), 1425 (Standard), and 3525 (Fine) cells, respectively. The corresponding values of y+ for these three mesh models are 28.9~36.2 (Coarse), 0.8~1.2 (Standard), and 0.6~1.1 (Fine). Uniform grids along the HCT with 10° helical coil intervals were used. Constant heat flux was set at the tube wall, the inlet mass flux and temperature were set at the tube inlet, and the pressure was set at the tube outlet. The simulation conditions for all cases are listed in

Table 2. Test conditions for all simulated cases [15].

	Mass Flux (kg/m2/s)	Heat Flux (kW/m2)	Inlet Temp. (K)	Pressure (MPa)
Case 1	350	150	367.15	2
Case 2	100	50	367.15	2
Case 3	1000	245	367.15	2

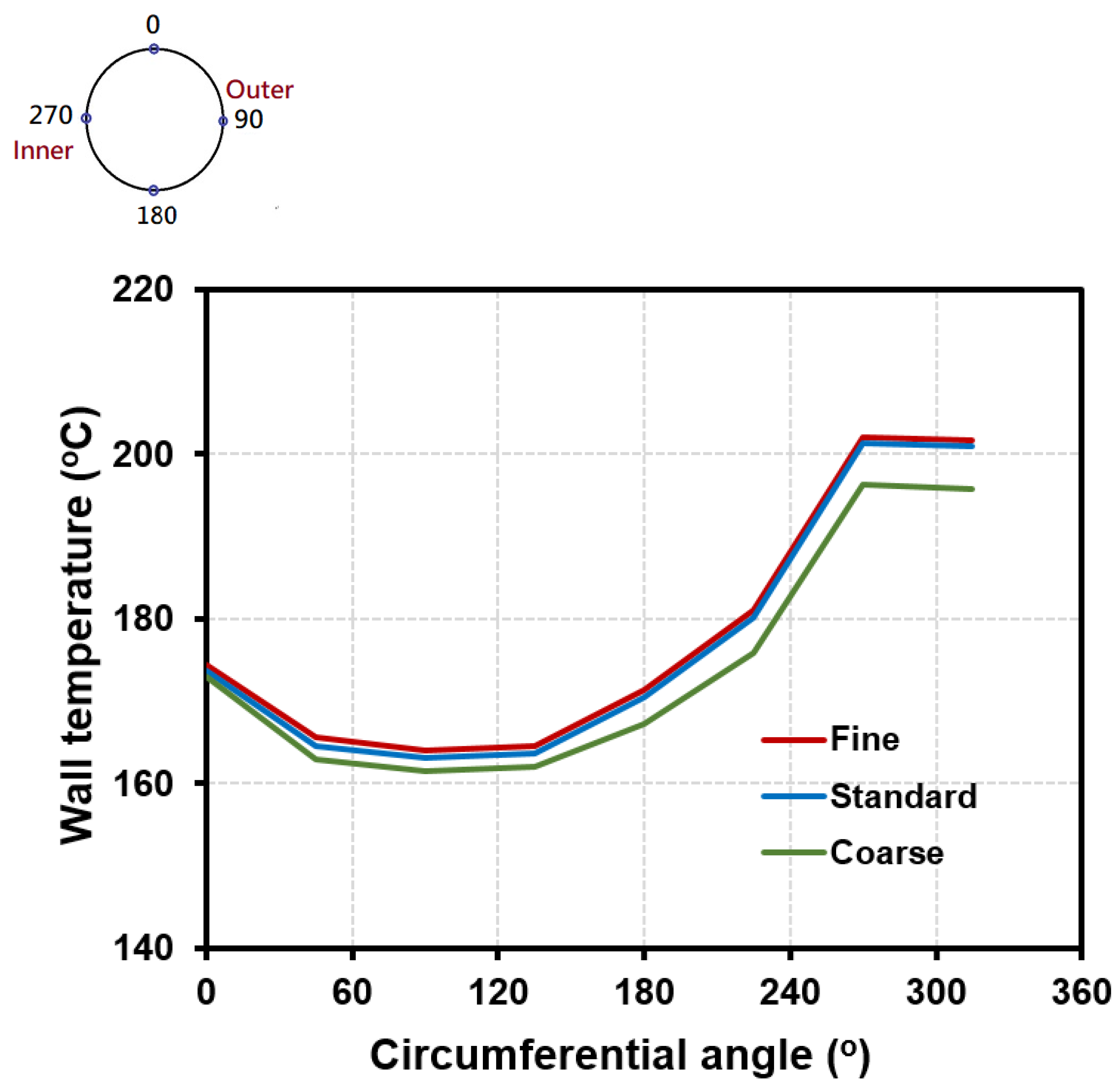
. Figure 3 compares the predicted results for the circumferential distribution of wall temperature at x = −0.147 under the coarse, standard, and fine meshes. The conditions of Case 1 in Table 2 and the SSTKW turbulence model were adopted. In this figure, the abscissa represents the circumferential angle (ϕ) of the HCT. Similar to the location index using quality (x) in the measured data presented by Wang et al., [21], x was also used as the location index of the HCT in this study. As illustrated in the upper portion of Figure 3, ϕ = 90° and 270° are the tube wall values on the outer and inner sides, respectively, of the HCT. This figure implies that the predicted result of the circumferential temperature distribution using the standard mesh is close to the result obtained using the fine mesh.

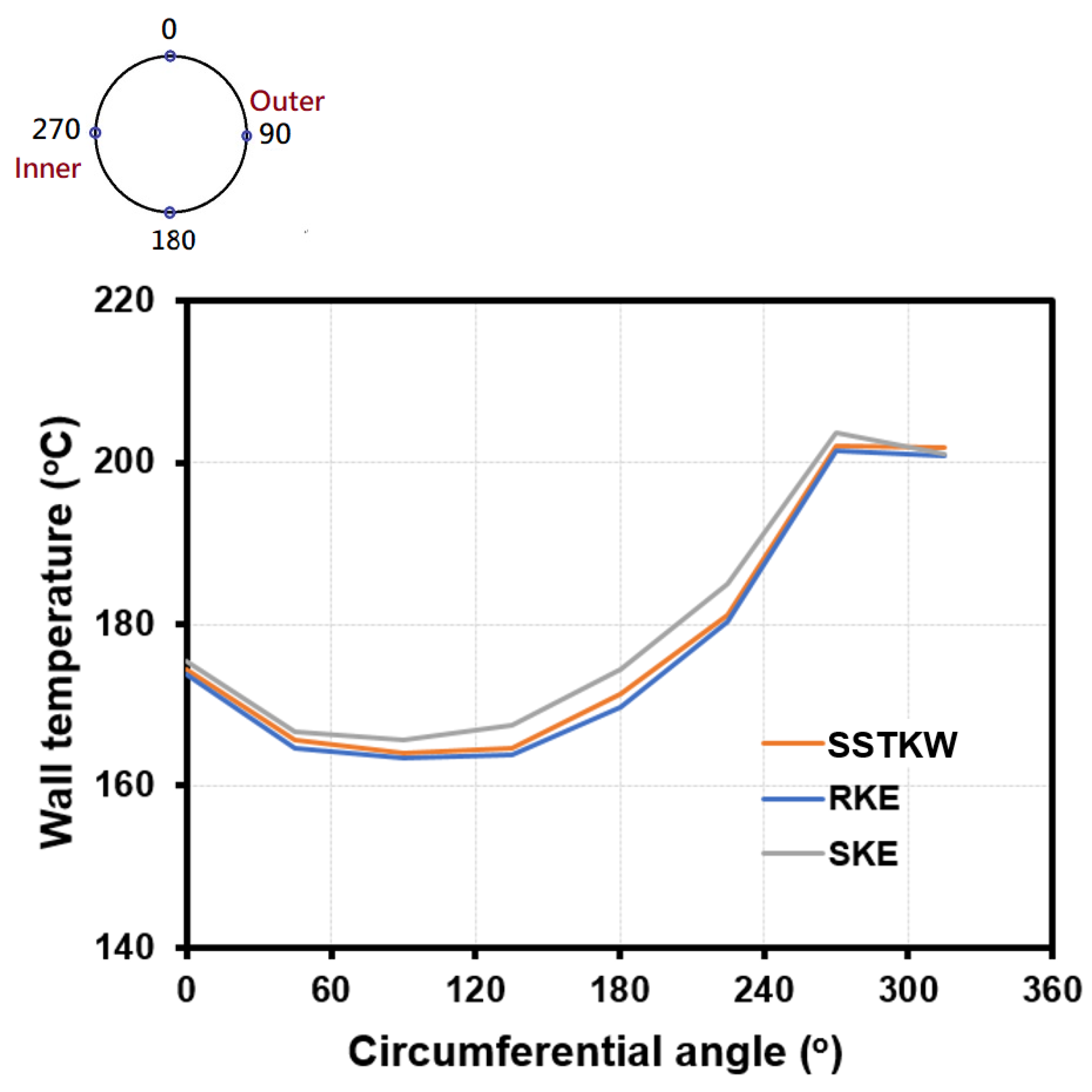
Since the BPGs provide useful guidance for single-phase applications of CFD models to nuclear reactor safety (NRS) problems, these guidelines were followed to ensure the accuracy and credibility of the CFD predictions. The essential requirements of the BPGs were applied in the mesh model; the physical models, especially the turbulence model; and in model validation. Therefore, in addition to the mesh model, sensitivity calculations for the turbulence models were also conducted, including the SKE, RKE, and SSTKW. The results of blind calculations for different turbulence models are shown in Figure 4, and the simulation conditions are the same as those in Figure 3. As shown in this figure, the predicted results of the circumferential wall temperature distribution at x = −0.147 when using the SSTKW and the RKE models are similar. The SSTKW and RKE turbulence models provide superior performance for flow characteristics with an adverse pressure gradient, recirculation, and separation, which are similar to the flow characteristics of an HCT. The SSTKW is less sensitive to the inlet turbulence properties and less restrictive than the near-wall mesh model. Therefore, the SSTKW turbulence model and standard mesh were selected for further study (Figure 5, Figure 6 and Figure 7) with the experimental data and then applied to the thermal-hydraulic characteristics of an HCT with confidence.

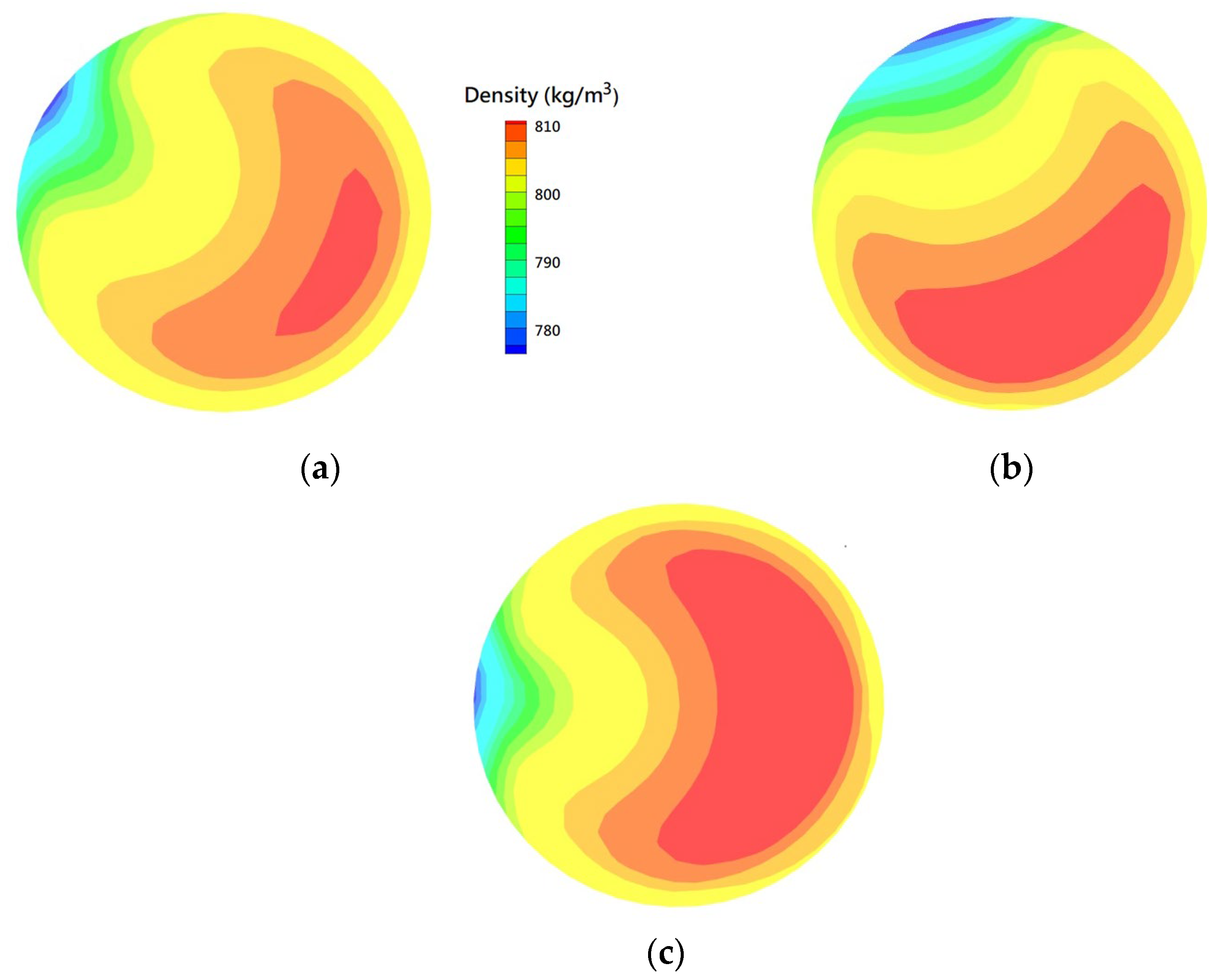
Figure 5 compares the circumferential distribution of wall temperature at x = −0.147 (L = 2.07 m) and −0.236 (L = 0.57 m) predicted by the CFD model (red dots) with the measurements (blue dots) for Case 1. It can be clearly seen in this figure that the predicted distribution agrees well with the measured distribution at these two locations. Additionally, the measured and predicted results both show a strong, non-uniform circumferential distribution of wall temperature in the HCT. As noted above, the thermal-hydraulic characteristics of an HCT are governed by centrifugal and gravitational forces. Lower-temperature water with a higher density is pushed to the outer portion of the HCT due to the centrifugal force and tends to accumulate on the lower portion of the tube due to the gravitational force. As shown in Figure 6a, the higher-density water is located near the outer and bottom-right portion of the HCT (ϕ~135°). In addition, the lower-density water with the higher-temperature water can be found near ϕ = 315°. These predicted density distributions provide clear images explaining the inhomogeneity in the circumferential distribution of the wall temperature, which is not clear from the measured results.

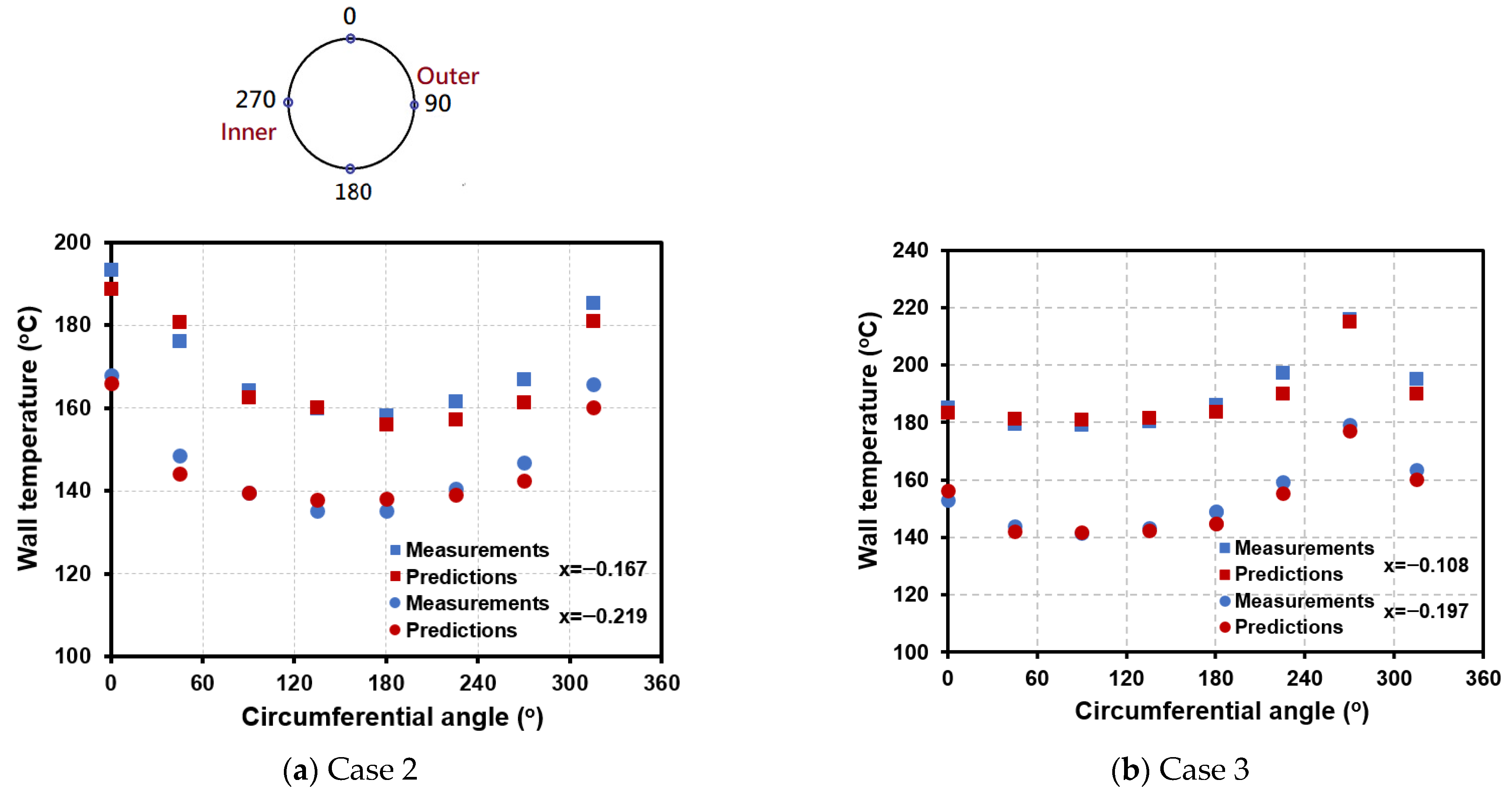
As the mass flux in the HCT decreases (i.e., Case 2), the thermal-hydraulic characteristics are governed more by the gravitational force than the centrifugal force. The lower-temperature water with the higher density accumulates in a lower portion of the HCT than in Case 1. This difference is visible in the density contours for both cases, as shown by comparing Figure 6a,b. Figure 7a shows the circumferential distributions of the wall temperature at x = −0.167 (L = 1.49 m) and −0.219 (L = 0.74 m) obtained from the CFD simulations (red dots) and the test data (blue dots) for Case 2. As shown in this figure, the lower wall temperature is located near ϕ = 180° and the higher wall temperature appears near ϕ = 360°. Both the measured and predicted results show this trend. In contrast to Case 2 with the lower mass flux, the inlet mass flux increases enough (i.e., Case 3) that the gravitational effect can be neglected, as shown in Figure 7b, which is the circumferential distribution of the wall temperature at x = −0.108 (L = 4.76 m) and −0.197 (L = 2.15 m) for Case 3. Therefore, The peak wall temperature is predicted to occur at ϕ = 270°. In Case 3, the thermal-hydraulic characteristics are symmetric along the horizontal line on the cross-section for the vertical HCT, which is clearly shown in the density contour of Figure 6c. In addition, the predicted values for the circumferential distribution of wall temperature correspond well with the measured values, which can be seen clearly in both plots in Figure 7.

The Lu number represents the ratio of the centrifugal force to buoyancy and can be written as [21]

$$Lu={\displaystyle \frac{V^2}{D\beta (T_w-T_b)g}}$$

(31)

This non-dimensional number can characterize the flow and heat transfer patterns for the HCT. In an HCT, the Lu number increases with the increasing mass flux, which also enhances the influence of the centrifugal force, and vice versa. Therefore, three simulations with Lu numbers of 1.226, 0.12, and 13.7 were conducted in this study to examine middle (centrifugal force balanced by buoyancy), low (buoyancy force dominates), and high (centrifugal force dominates) Lu numbers, respectively. 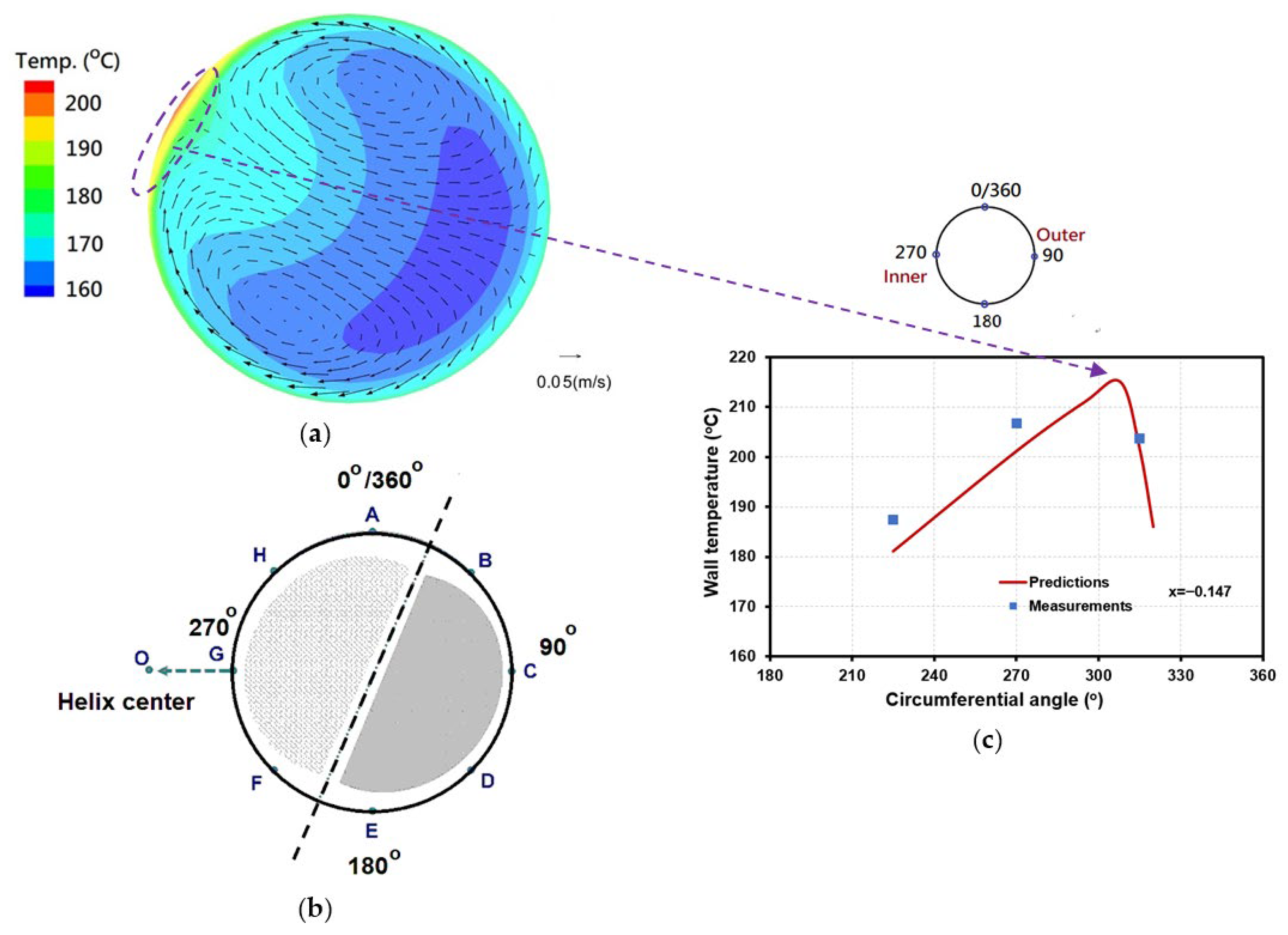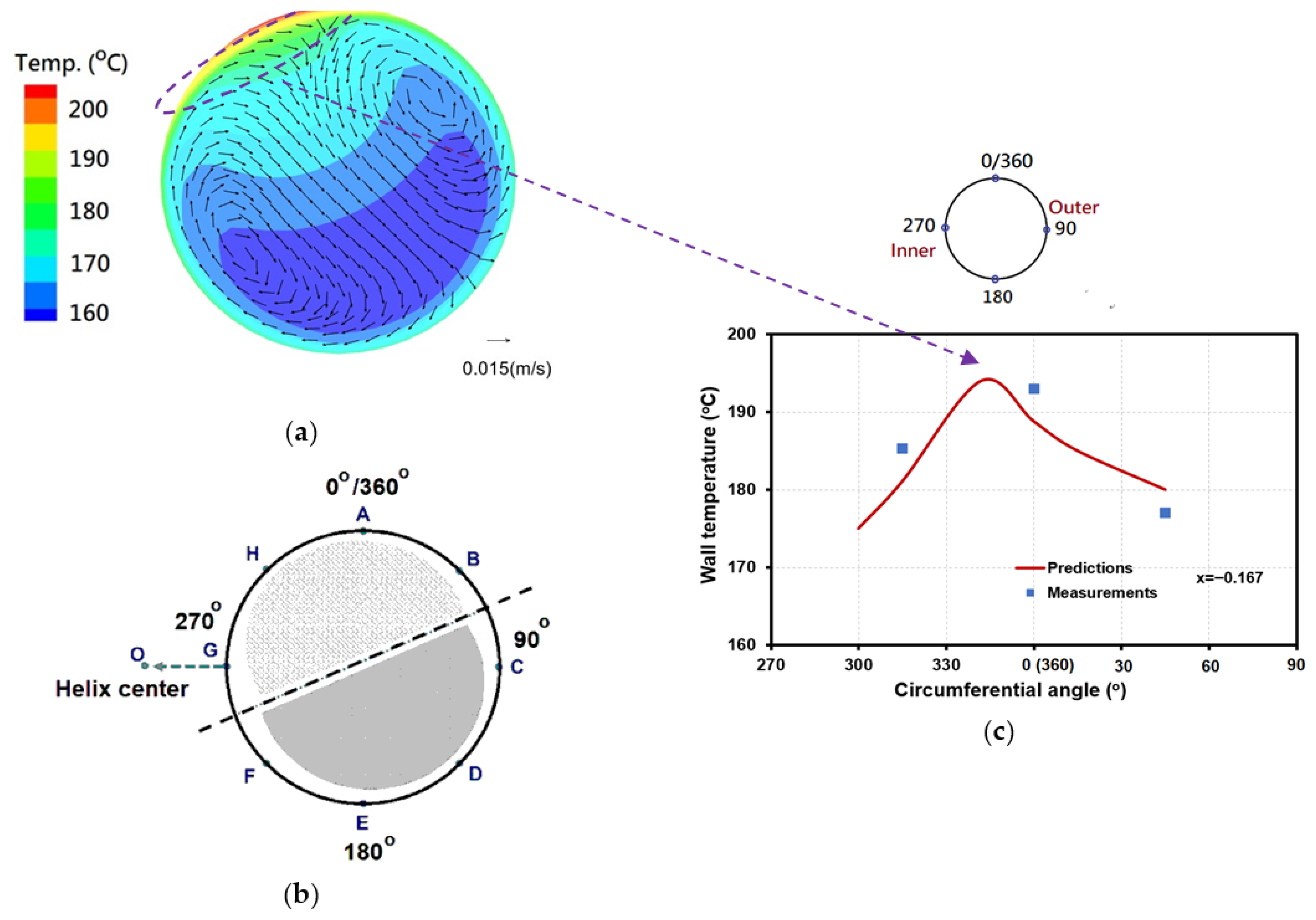Figure 8a and Figure 9a show the distribution patterns of temperature on the cross-section of the HCT for Cases 1 and 2. The density and temperature contours in Figure 6a and Figure 8a reveal that the higher heat transfer region with the lower-density and higher-temperature water is located near the upper left corner, and the lower heat transfer region with the higher-density and lower-temperature water is near the lower-right corner. These predicted results provide a clear image of two-region flow and heat transfer characteristics. This two-region heat transfer pattern was also confirmed in the experimental work of Wang et al. [15], who suggested a schematic of two-region heat transfer patterns with the higher heat transfer region in the upper-left corner and the lower heat transfer region in the lower-right corner, as shown in Figure 8b. The heat transfer flow pattern predicted from the CFD results and the schematic from [21] for Case 2 are shown in Figure 9a and Figure 9b, respectively.

The vector distributions of secondary flow in the cross-section of the HCT are also plotted on Figure 8a and Figure 9a. These plots clearly show a vortex pair of secondary flow in these HCT cross-sections. Additionally, the higher wall temperature occurs where the secondary flow abates. The temperature contour and flow vector distribution in Figure 8a imply that a higher wall temperature may occur between ϕ =270° and 315°. Based on the data from Case 1, the peak wall temperature at x = −0.147 was measured to occur at ϕ = 270°. This result was obtained from eight discrete points measured on the peripheral tube wall, which provided the circumferential distribution of the wall temperature. However, as shown in Figure 8c, the peak wall temperature was predicted to be located at ϕ~308°. This result was obtained from a line curve of the circumferential wall temperature consisting of 64 predicted points (standard mesh in Figure 2). The exact location of peak wall temperature can be captured only in the CFD results and cannot be revealed in the experimental data, which is one of the main contributions of the CFD simulation. A similar result for Case 2 is shown in Figure 9c. The peak wall temperature at x = −0.167 was measured at ϕ = 0° (i.e., 360°), but the peak wall temperature may be actually at ϕ~342°, based on the prediction. Therefore, in addition to aligning with the measured data, the results of the CFD model can help interpret the test results and expand their application.

Figure 10 compares the circumferentially averaged heat transfer coefficients in different regions, which were obtained from the measurements and predictions for Cases 2 and 3, respectively. As shown in Figure 10a, for Case 2 with Lu < 0.25, two regions with different average heat transfer values along the HCT’s circumferential wall are suggested in [15], including ϕ = 270°–45° (i.e., regions A, B, G, and H) and 90°–225° (i.e., regions C, D, E, and F). The definition of A–H regions is provided in the right portion of this plot. The former region (i.e., regions A, B, G, and H) is the lower heat transfer region where the higher-temperature water with lower density accumulates, and the latter region has the higher heat transfer. Figure 10a clearly shows that the circumferentially averaged heat transfer coefficients over the regions A, B, G, and H, the regions C, D, E, and F, and the overall circumferential wall (i.e., the defined Avg. in Figure 10a predicted by the present CFD model correspond well with the experimental data. The non-uniform distribution of the wall heat transfer coefficients is shown in both the measurements and predictions.

The correlations between the measured and predicted heat transfer coefficients in the different regions and the average value are also shown in Figure 10b for Case 3. Three regions with different heat transfer characteristics are suggested based on the measured data alone, but these characteristics are clearly visible in the predicted results in the density contour of Figure 6c. In addition, the predicted heat transfer coefficients shown in plots (a) and (b) of Figure 10 are fully developed. The heat transfer coefficient decreases from the inlet of the HCT and approaches its full value, as shown in Figure 10c for Case 3. In this plot, the longitudinal axis is the normalized heat transfer coefficient (h_norm), that is, the local h divided by the full value. The abscissa is the distance from the inlet of the HCT. A detailed observation of this plot implies that the entrance length (developing length) is about 42~50 pipe diameters (d). The correlation for the entrance length of an HCT was proposed by Saffari et al. [25]) and is expressed as a function of the Reynolds number (Re), Dean number (De), and curvature ratio (δ).

$$L/d={\delta }^{-0.1}\times {\mathit{Re}}^{1.285}\times D{e}^{-1.07}$$

(32)

Using the conditions of Case 3, the entrance length calculated using this correlation is 51.24, which is close to the range predicted in this study.

The thermal-hydraulic characteristics are fully developed when the flow passes over the coil angle (ψ) of 210°~275° based on the coil/tube diameter values, implying that the entrance effect may be neglected when evaluating the overall heat transfer characteristics of an entire HCT or HCTHX. Then, the fully developed heat transfer coefficient correlations can be applied to estimate the heat transfer capability of the HCT or HCTHX. 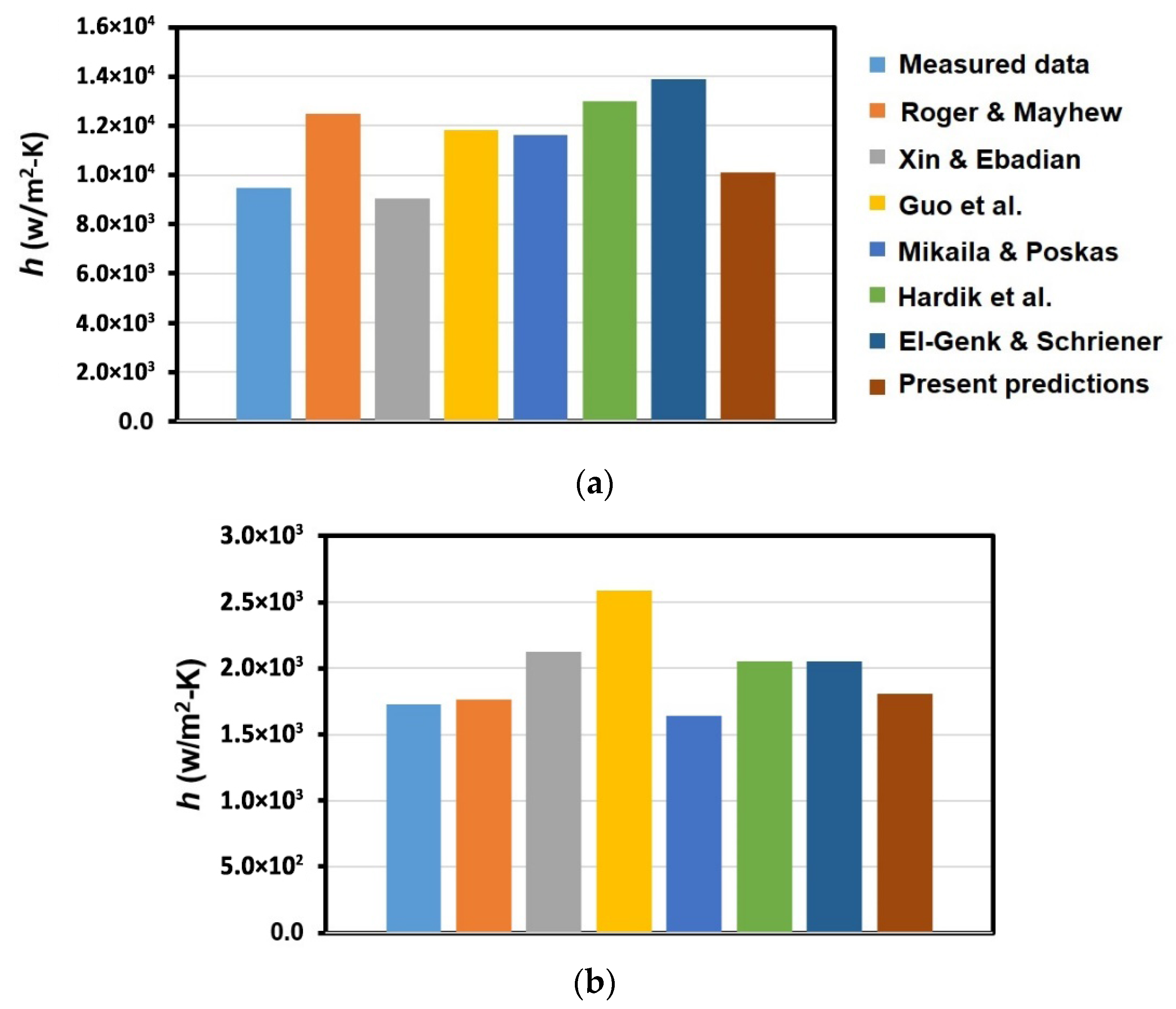Figure 11 compares the fully developed heat transfer coefficient for the HCT in the CFD model of this study, the appropriate correlations, and the experimental values for Case 2 (a) and Case 3 (b). These correlations include those proposed by Rogers and Mayhew [26], Mikaila and Poskas [27], Xin and Ebadian [28], Guo et al. [29], Hardik et al. [30], and El-Genk and Schriener [31], which Gou et al. [29] suggested are suitable for predicting the heat transfer coefficient of an HCT. Similar to the comparison in Figure 10, agreement is demonstrated between the predicted and measured h values under different flow conditions. In addition, the h value calculated with Xin and Ebadian’s correlation [28] aligns better with the data than those using the other correlations for Case 2, and the h calculated using the correlation of Rogers and Mayhew [26] or Mikaila and Poskas [27] shows better agreement with the data for Case 3. Therefore, these comparison results strong imply that the applicability of various kinds of h correlations depends on the flow conditions of the HCT, demonstrating the valuable contribution of CFD simulations in this area.

The inhomogeneity of the circumferential distribution of single-phase heat transfer characteristics in a vertical HCT is essentially due to the constant heat flux BC. In CFD simulations, this boundary condition is not suitable for investigating flow and heat transfer behaviors within the whole HCTHX, as noted in the work of Bahrehmand and Abbassi [32]. The higher wall temperature occurs near the region with inferior heat transfer under the condition of constant heat flux. The heat transfer mechanism for an HCTHX is mainly conjugated heat transfer from the hot fluid in the shell side to the cold fluid in the tube side. The wall heat flux decreases around the location with poor heat transfer capability in the tube side, suppressing this phenomenon of higher wall temperature. Therefore, this conjugated transfer effect on decreasing the non-uniform characteristics of tube wall temperature in the HCTHX can be simulated by combining the shell-/tube-side solution domains. 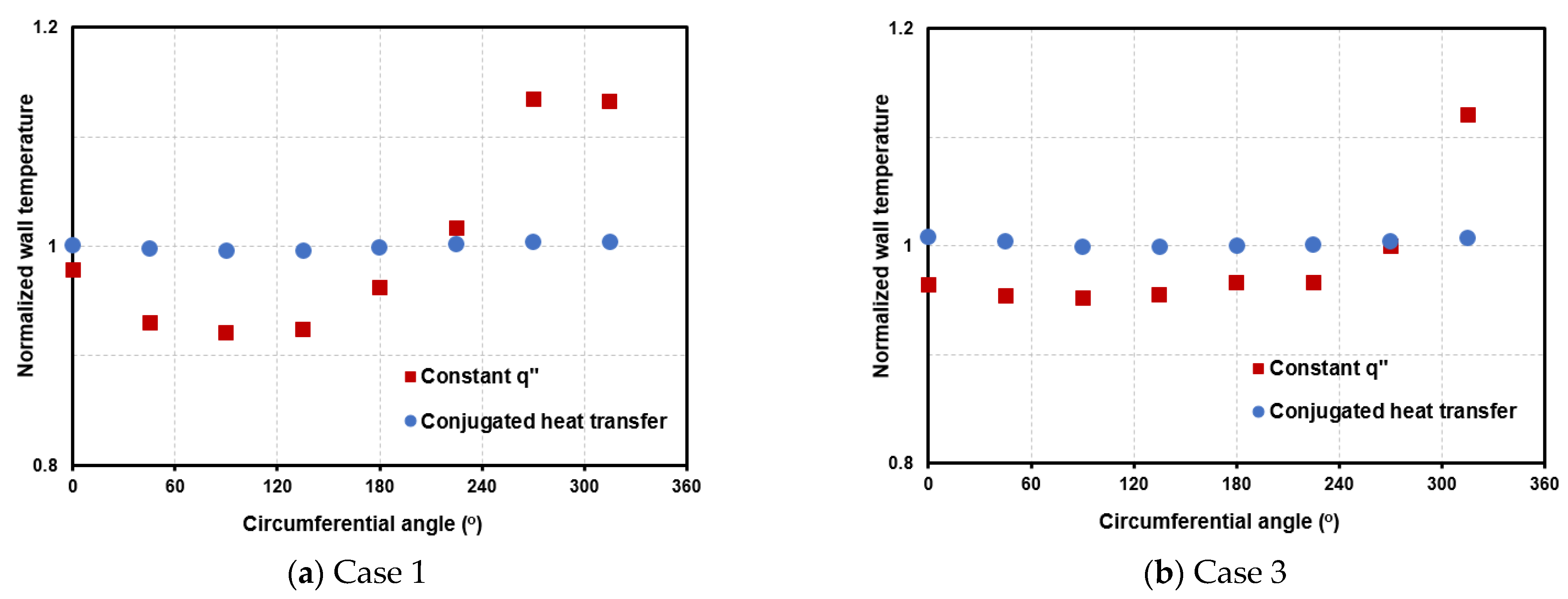The HCT shown in Figure 1 is located inside a cylindrical shell with a diameter of 750 mm. For the whole HCHX with conjugated heat transfer, the mass flow rate in the shell side is set at 0.2 kg/s. The corresponding temperature drops for the shell side are set at 35.6 °C and 58.1 °C, so that the rates of heat transfer from the shell to the tube in both cases are similar to those set in Cases 1 and 3. The inlet mass flux/temperature and pressure of the tube side for the conjugated heat transfer cases are the same as those for the constant heat flux cases. Both cases include counter-current flow, where hot (shell) and cold (tube) fluids enter opposite sides of the heat exchanger.

Figure 12 compares the circumferential dependence of the normalized temperature predicted using the constant-heat flux BC (HCT only) and the conjugated heat transfer (whole HCHX) simulations. The normalized temperature shown on the longitudinal axis is the local wall temperature divided by the average wall temperature. The simulation conditions under the constant-heat-flux cases in Figure 12a,b are similar to those for Cases 1 and 3. Figure 12 shows that the non-uniform circumferential distribution of heat transfer is essentially caused by the constant-heat-flux boundary condition on the HCT wall. This effect can be significantly reduced by actually considering conjugated heat transfer in the HCTHX. The wall heat flux would decrease (i.e., variable heat flux distribution) around the wall sites with poor heat transfer due to the lower tube flow velocity, resulting in a lower wall temperature. A more uniform circumferential distribution of the tube wall would be achieved. However, for the constant heat flux case, the wall temperature would significantly increase for the wall location with the poorest heat transfer, resulting in a non-uniform circumferential distribution of temperature. Figure 12 clearly confirms these results.

4. Conclusions

In this study, a CFD model was developed to predict the non-uniform circumferential distribution of heat transfer characteristics for single-phase convection in an HCT. The effects of inlet mass fluxes on this inhomogeneity were also considered. The CFD model was validated with the experiments of Wang et al. [15] using the circumferential distribution of wall temperature and the heat transfer coefficient under various inlet mass fluxes. The values and locations of the peak wall temperature predicted by this model correspond well with the measured values. The inhomogeneity of flow and heat transfer in an HCT are essentially caused by the centrifugal and gravitational forces, which depend on the inlet mass flux. These non-uniform characteristics can be clearly explained using the predicted density and temperature contours and secondary flow vectors on a cross-section of the HCT. These calculated results can provide a detailed visualization of the thermal-hydraulic characteristics of an HCT, which are seldom captured by measurements. This is one of the main contributions of CFD simulations. Further simulations were also performed using the conjugated heat transfer from the hot fluid in the shell side to the cold fluid in the tube side. Compared with the simplified constant heat flux BC, this conjugated heat transfer is the actual heat transfer phenomenon in an HCTHX. The results of the comparison clearly show that the inhomogeneity of the circumferential distribution of the single-phase heat transfer characteristics of an HCT is essentially caused by the assumption of a constant-heat-flux BC. These characteristics can be suppressed by considering conjugated heat transfer, which is the actual type of heat transfer in HCTHXs.