Initiating Event Frequencies for Internal Flooding and High-Energy Line Break PRAs
Abstract
1. Introduction
2. Technical Approach
2.1. Overview
2.2. Technical Enhancements from Previous Revision
2.2.1. Expanded Coverage of Piping Cases
2.2.2. Incorporation of Aging Effects
2.2.3. Enhanced Conditional Probability of Rupture Model
2.2.4. Adjusting Flood Frequencies for Enhanced Integrity Management
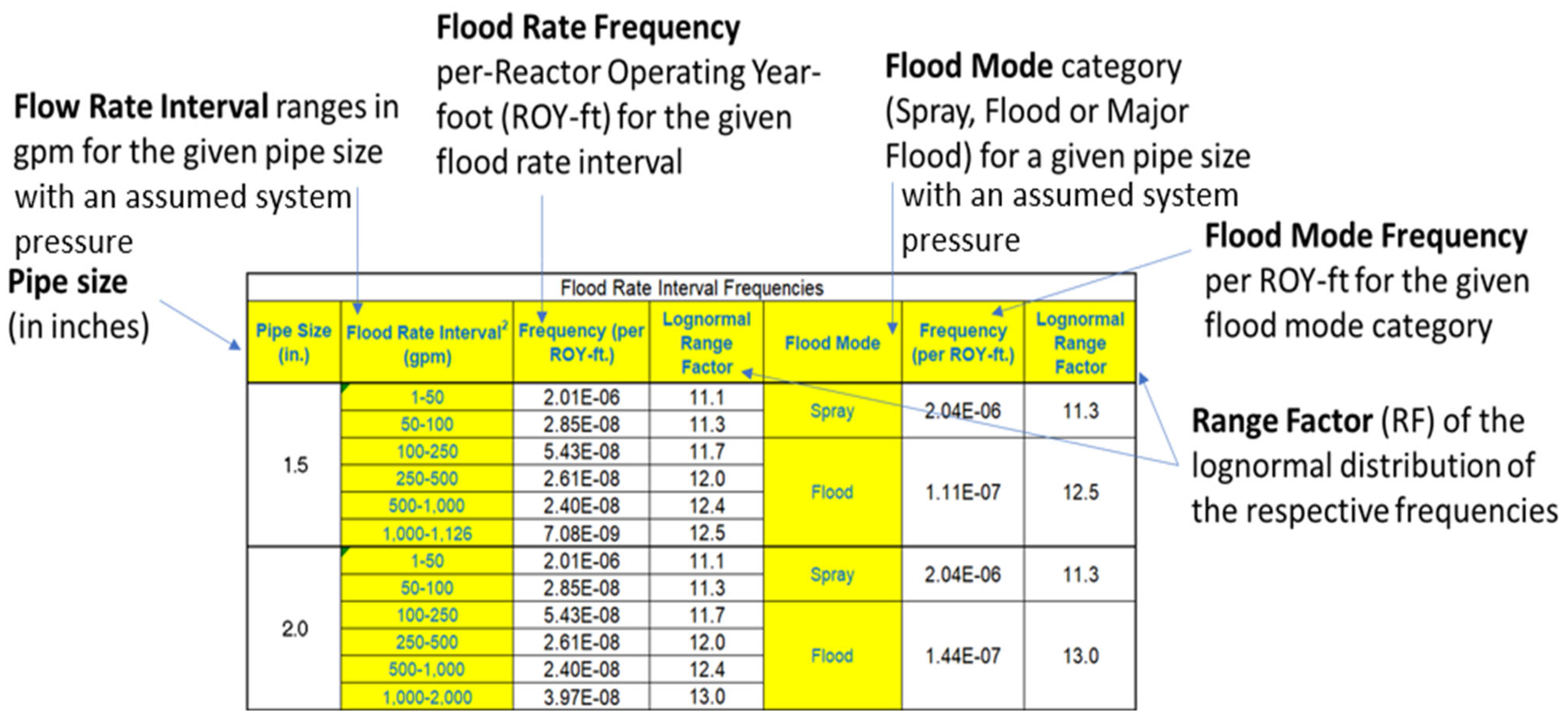
2.2.5. Expanded Set of Flood Frequency Metrics
- Cumulative break frequency of different break sizes and flood rates
- Flood frequencies for basic flood modes (spray, flood, and major flood)
- Flood frequencies for more refined flood rate intervals
2.2.6. Roadmap
2.2.7. Service Experience Data
- “Non-through wall defect” or “Wall Thinning”—a Code-rejectable defect that requires repair or replacement according to the prevailing codes and standards.
- “Pinhole leak”— characterized by both defect size and leak rate; the leak rate is equal to a “perceptible” leakage that is less than, or much less than 1 gpm.
- “Leak”—through-wall defects that are normally expected to have leak rates ≥ 1 gpm.
- “Major structural failure” (MSF)—a complete loss of structural integrity and consequential significant through-wall flow rate.
2.3. Pipe Rupture Model
- = total rupture frequency for pipe category i defined by analysis case and pipe size for rupture mode x at pipe age t.
- = failure rate of pipe category i.
- = conditional rupture probability (CRP) of rupture mode (i.e., severity of rupture) x given failure of pipe component i. See Section 4 for development of the CRP model.
- = age factor for component i at pipe age t to account for in-service degradation due to aging of the component. See Section 3 for the derivation of aging factors.
- = integrity management factor for component i and rupture mode x; this factor adjusts the rupture frequency to account for variable integrity management strategies such as leak detection, volumetric NDE, and in-service testing that might be different from the components in the service data. See Section 5 for the application of the Markov Model for derivation of these integrity management factors.
2.4. Treatment of Leak-Before-Break
- The failure rate provides an estimate of the frequency of precursors to leaks and ruptures.
- Conditional rupture probability (CRP)—provides an estimate of the probability that a failure produces a leak or rupture. An effective application of LBB is reflected in a low CRP for major pipe ruptures. The service data includes the benefits of LBB in that it inherently includes all expected opportunities to spot the leak that would occur at a typical plant (including things like normal operator rounds, security rounds, quarterly leak inspections, NDE inspections).
- Integrity Management Factors (Markov Model)—to account for improvements beyond typical industry practice for leak testing and non-destructive examinations, integrity management factors are applied on an as-needed basis (see Section 5).
2.5. Treatment of Uncertainty
- A RF of 2 was assigned to a value of 1 × 10−2;
- A RF of 30 was assigned to a value of 3 × 10−5;
- For specific values other than the above, a RF was calculated based on log-log linear interpolation/extrapolation between these points.
3. Conditional Rupture Probability Model
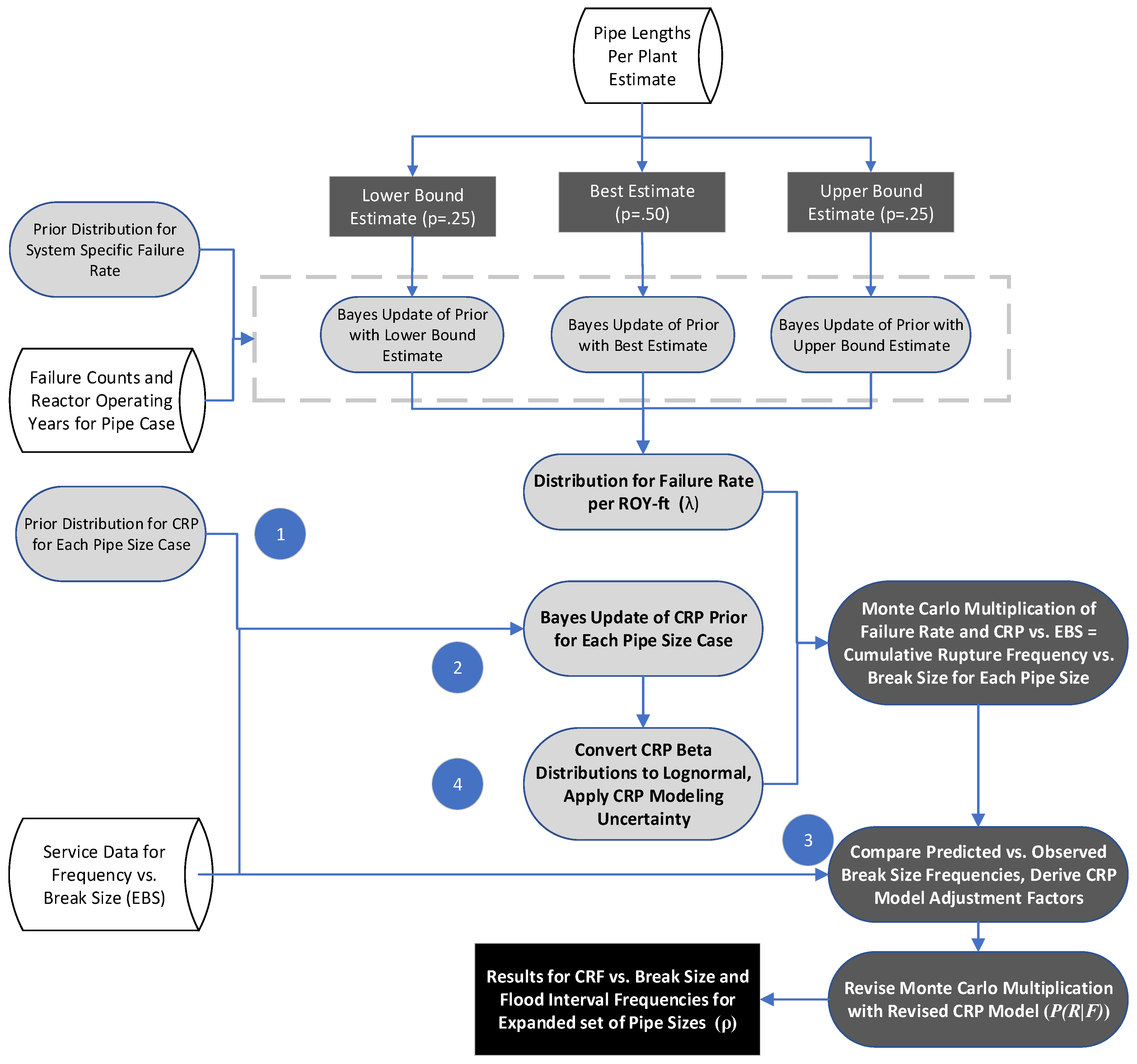
- Develop a prior distribution: A Bayes’ prior distribution is developed that incorporates insights from generic piping service experience and results of previous expert elicitations in the estimation of piping system reliability; sources for specific systems are documented in the report. This yields a table of CRP values vs. break sizes for each analyzed pipe size category. This is fitted to a CNID using the Beta Distribution by using the estimates as mean values and estimating the Beta Distribution parameters using the CNID method [17].
- Bayesian update (Stage 1): A Bayesian update of the prior distribution is performed using evidence from service experience on frequency of leaks of different sizes for systems similar to those being analyzed. This yields a new Beta Distribution and reflects the combined evidence expressed in the prior and the industry service data.
- 3.
- Bayesian update (Stage 2): A second stage Bayes’ update is applied to calibrate the CRP model to synchronize the predictions made by the pipe failure model with observed industry data on the frequency of leaks of different magnitudes. This step was added by observing that predictions made by the EPRI pipe failure model used in previous revisions to the failure report were somewhat over-estimating the frequency of leaks of different sizes observed in the industry service data.
- 4.
- Apply Modeling Uncertainty: Adjustments are made to the uncertainty distribution of the CRP model to account for modeling uncertainty, as described in Section 2.5. This includes the basic assumption in the pipe failure model that pipe failures can be regarded as precursors to pipe ruptures of various sizes. This is done by converting the means of the Beta distribution from the Bayesian update of the CRP priors to means of a lognormal distribution in which the lognormal range factor (RF) expresses a larger degree of uncertainty than is reflected in the Bayes’ updated Beta Distribution. Lognormal range factors were assigned using systematic rules, as described in Section 2.5.
4. Evaluation of Aging Factors
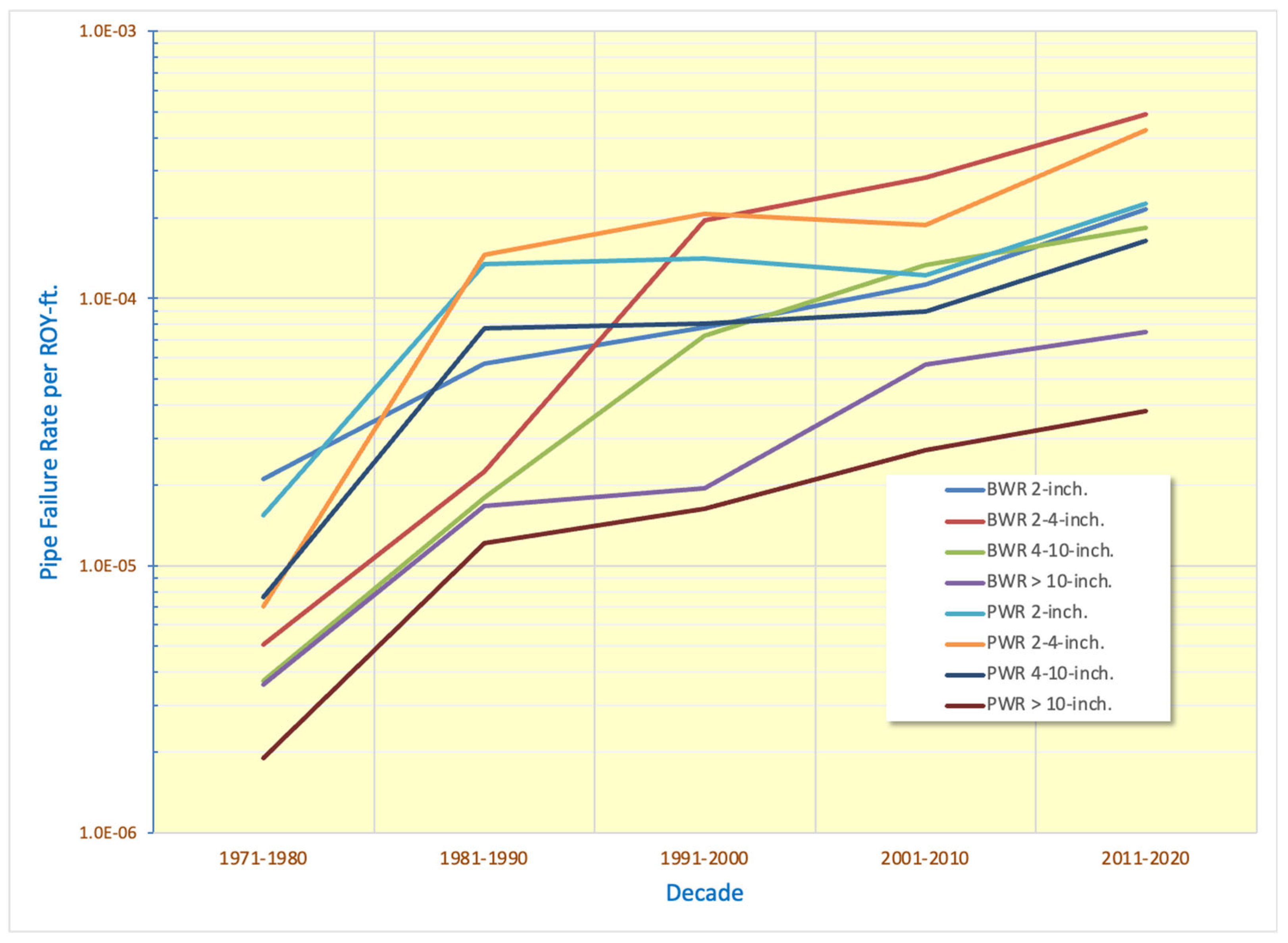
4.1. Trends in Piping System Failure Rates
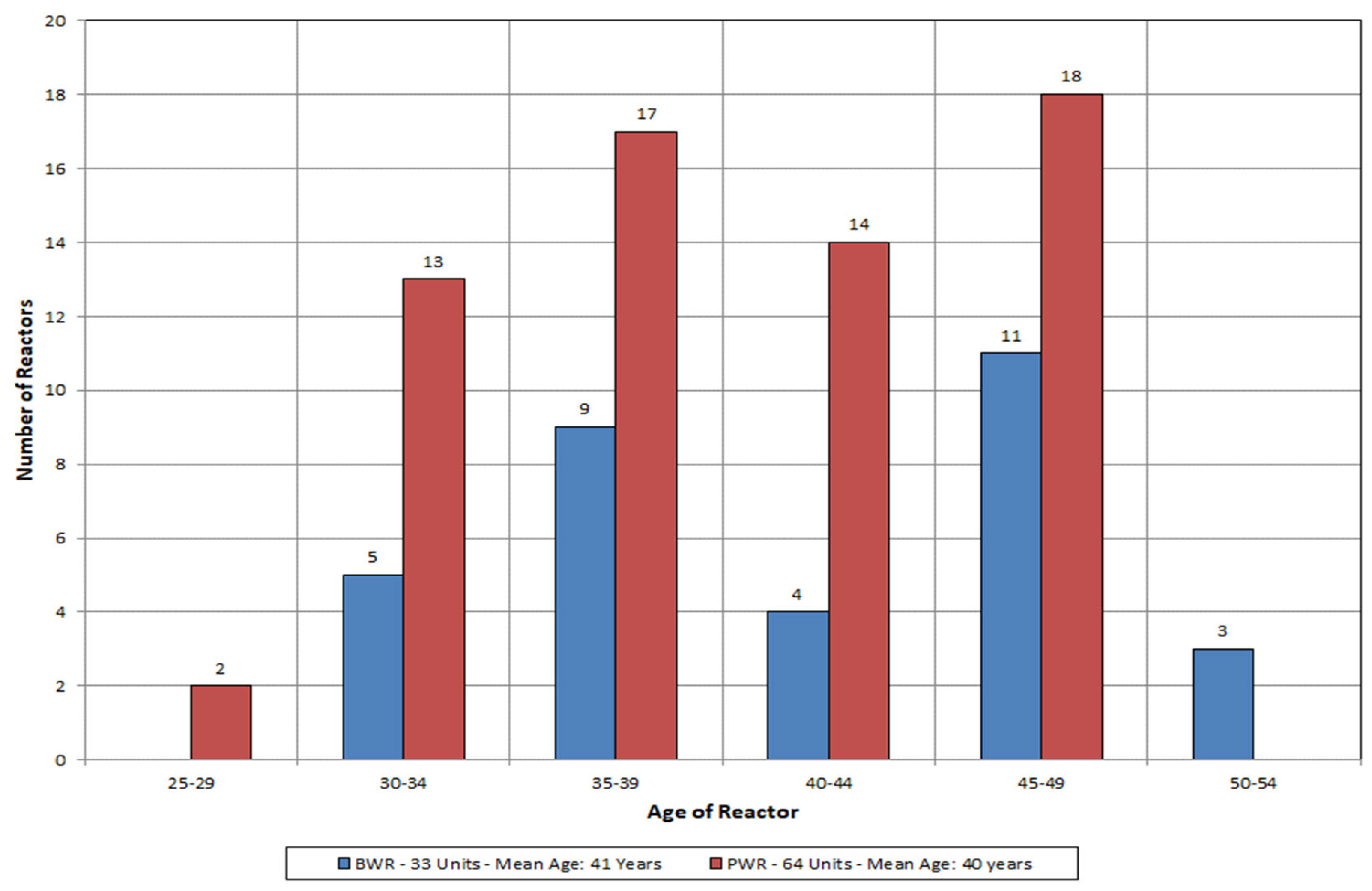
- Aging plant fleet and accumulation of pipe damage from degradation mechanisms. As shown in Figure 3 below, of the current U.S. plant fleet, 50 reactor units have entered an extended period of operation (i.e., ≥40 years).
- New operating experience data. The database that is the source of the pipe failure rate estimates is continuously updated and maintained. The overall body of service experience data has been substantially expanded since the first EPRI ‘pipe rupture frequency’ report was issued in 2006.
- Enhancements in reliability and integrity management. The plant license renewal initiatives together with applications of non-destructive examination (NDE) techniques and inspection qualification processes have evolved since the first EPRI ‘pipe rupture frequency report’ was issued. Embedded in the operating experience data are effects of NDE, replacement of pipe segments, improvements to leak tests and inspections, and changes in the reporting of pipe failures.
4.2. Aging Factor Model
- For each calculation case (system, pipe diameter, and type of raw water for the service water system), organize the pipe failure population by time period in which a failure was observed:
- ⚬
- Pool data by pipe size for each of the three cases:
- ▪
- BWR ASME Class 3 Service Water;
- ▪
- PWR ASME Class 3 Service Water;
- ▪
- Fire Protection (all failure modes).
- Segment data into time intervals; because of the size of the pipe failure populations for the two system groups, different approaches were used in the processing the data:
- ⚬
- The service water pipe failure population was fairly evenly spread across the five decades, 1971 to 2020, so the failure population was placed in ten 5-year bins.
- ⚬
- The bulk of the fire protection failure population was primarily from the 1990–2020 time period, so the failure population was placed in five 10-year bins.
- For each case and time interval, determine the average age of the piping systems that produced the pipe failures.
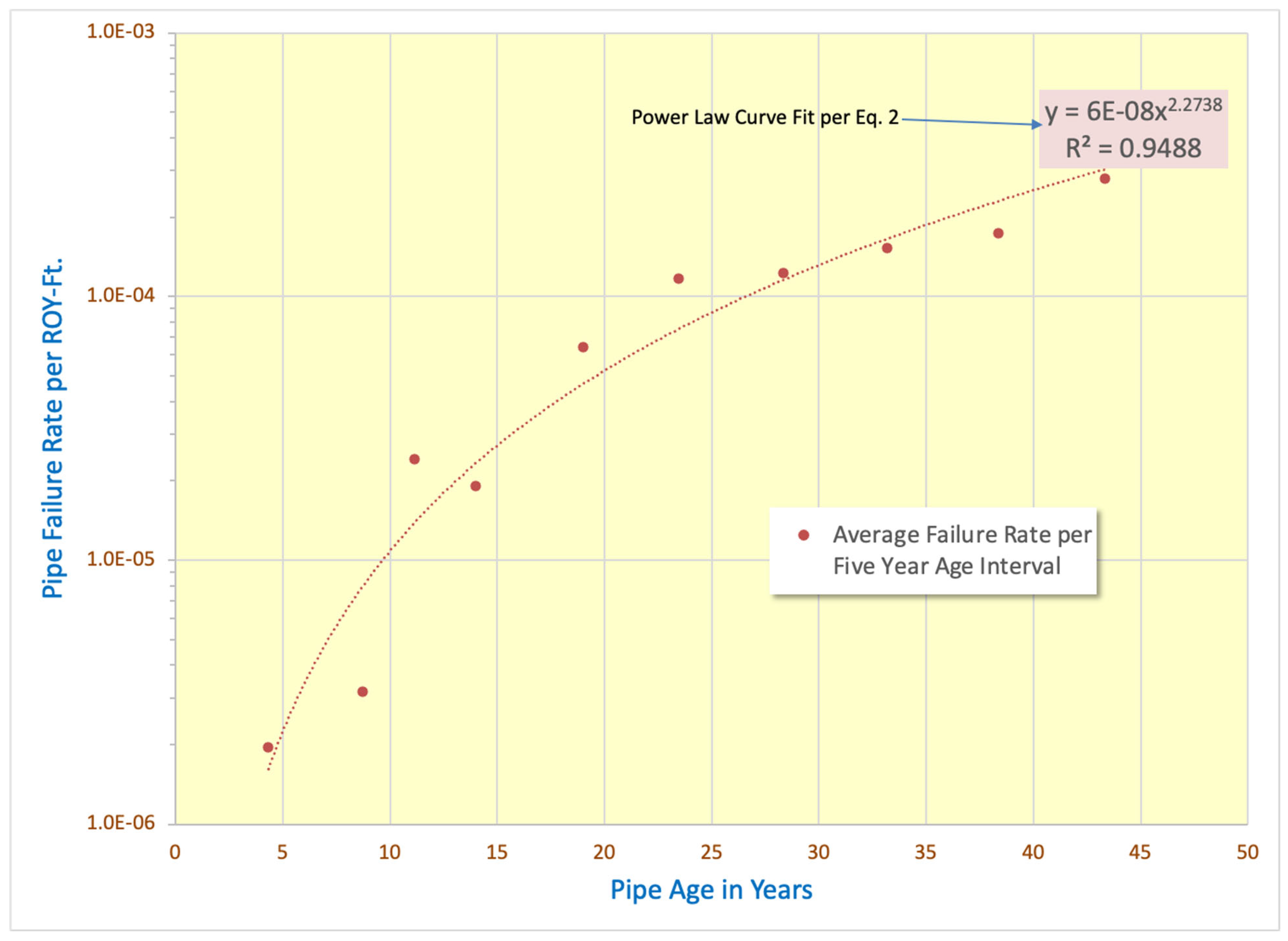
- Using the Constrained Noninformative Distribution (CNID) method [17] with a prior failure rate of 2.0 × 10−5 per ROY-ft based on the generic data in Reference [11], calculate the temporal failure as the average failure rate for that interval. This is accomplished by performing a Bayes’ update of the failure rate using the number of observed pipe failures and reactor operating years and feet of piping for that time interval as the evidence to update the prior. The prior failure rate is reduced to 2 × 10−6 per ROY-ft in the first interval to prevent too much influence by the prior to the zero failure cases.
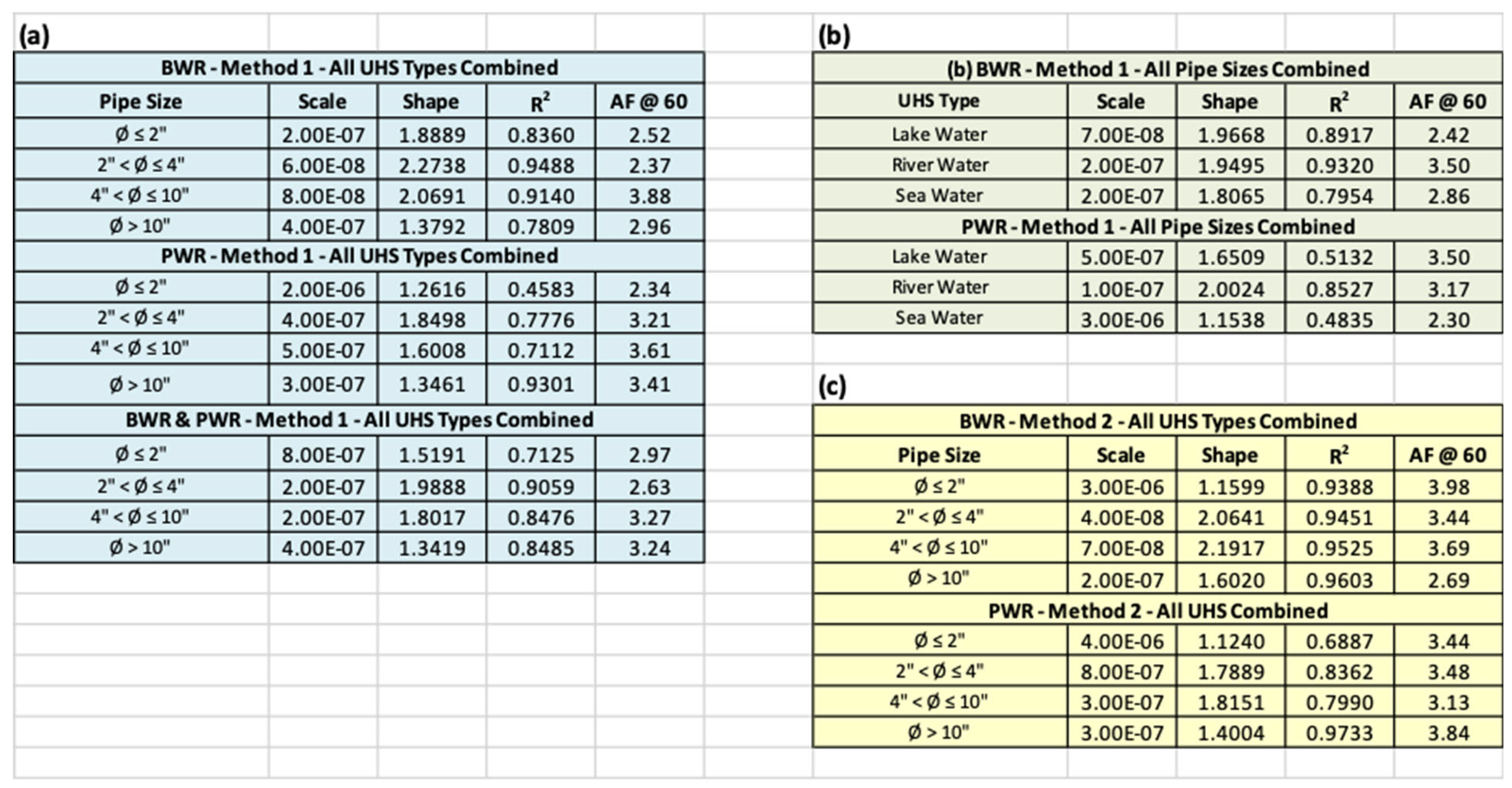
- Using Microsoft® Excel, plot a line of best-fit through the scatter plots of failure rate vs. plant age (Figure 4), resulting in a log-linear power model with scale and shape factors. For each respective calculation case, the age factor Ait is determined from the following:
| = Aging factor at pipe age t for component i defined by system, design, or code class and pipe size; | |
| = Scale parameter for component i; | |
| = Shape parameter for component i; | |
| = Average pipe failure rate for component i . |
4.3. Review of Aging Factor Approach
- Completeness of input data over time (i.e., failure reporting)
- Understanding the “outliers” in the failure population and how to handle in trend analysis.
- Data pooling strategies to overcome sparsity of data while accounting for the following:
- ⚬
- Influence of water source (sea, lake, river);
- ⚬
- Pipe size;
- ⚬
- Influence of plant type;
- ⚬
- Influence of time interval (5 yr v. 10 yr bins);
- ⚬
- Trend model selection;
- ⚬
- Assumptions on data window.
- It has clearly defined scope and limitations;
- It is based on the most relevant data and uses appropriate analysis methods;
- It has sufficiently considered the range of modeling assumptions, and appropriately applied a balance of statistical significance and engineering judgement;
- The final results are consistent with expectations based on review of the experience data;
- The approach, results, and expected application of the results are clearly documented in the final report [1].
5. Evaluation of Integrity Management Factor
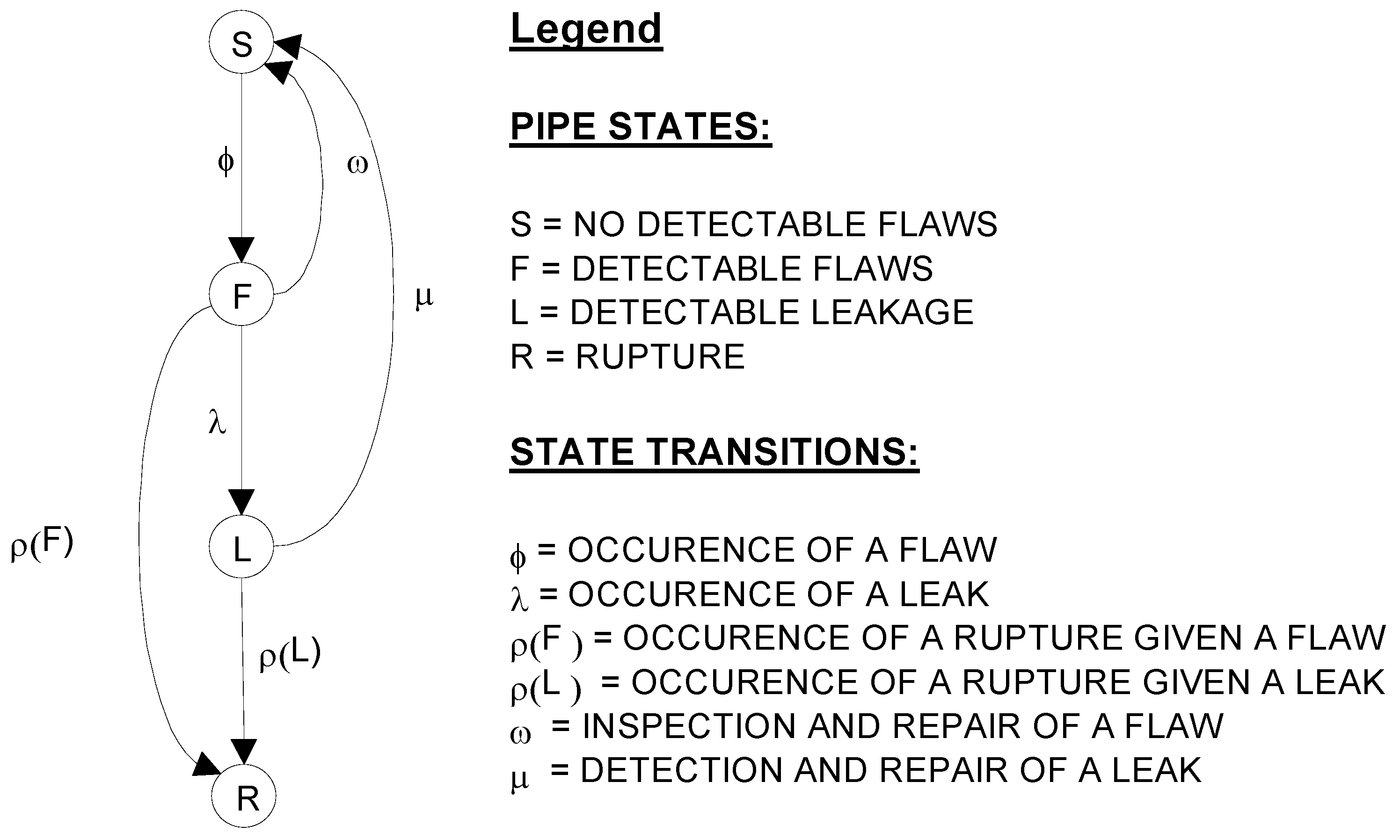
5.1. Markov Model Overview
- PI = probability that a piping element with a flaw will be inspected per inspection interval. When locations for the inspection are fixed, this term is either 0 or 1, depending on whether the pipe segment is inspected.
- PFD = probability that a flaw will be detected given that this segment is inspected. This parameter is related to the reliability of NDE inspection and is a conditional probability given that the location being inspected has a flaw that meets the criteria for repair according to the ASME code.
- TFI = mean time between inspections for flaws (inspection interval).
- TR = mean time to repair when detected. There is an assumption in this model that any significant flaw that is detected will be repaired. Because TFI, which is measured in years, is normally much greater than TR which is measured in hours, the results of applying the Markov model are not sensitive to assumptions regarding TR.
- PLD = probability that the leak in the segment will be detected per inspection.
- TLI = mean time between inspections for leaks.
- TR = as defined above but for full power applications. This time should be the minimum of the actual repair time and the time associated with any technical specification limiting condition for operation (LCO) if the leak rate exceeds technical specification requirements.
Technical reviews of the Markov model have been performed by the staff, a staff contractor (Ref. [12]), and by independent peer reviewers for EPRI. These efforts provided a detailed review of the model and its ability to support the proposed licensing application. The conclusion of the reviews is that the proposed four-state Markov model as described in EPRI-TR-110161 is both sound and appropriate as a first-order model of pipe rupture. The staff adopts the analysis of the Markov model and the Bayesian updating set forth in the contractor report (Ref. [8]). The contractor report is available in the Commission’s Public Document Room, which is located in the Gelman Building at 212 L St, N.W., Washington, D.C., 20003, under accession number 9909300045. Based on that analysis, the staff finds that the model can be used as a basis for the estimation of pipe rupture frequencies to be used instead of the bounding pipe failure frequencies in support of the change in risk estimates as part of an application that uses the EPRI RI-ISI methodology.
5.2. How the Markov Model Is Used in This Study
- Iix(t) = integrity management factor for component i for RIM strategy x at piping system t. As shown in this equation, this factor can be expressed as a product of separate integrity management and piping system factors. The RIM strategy includes a specification of how often leak tests and inspections and NDE are performed on the piping system component and how effective they are.
- hix(t) = hazard rate (time-dependent rupture mode frequency) for component I at piping system t and RIM strategy x. This is determined from the solution of the ordinary differential equations that describe the Markov model as explained more fully below. The piping system is set at the average piping system in the plant population responsible for the failure rate and conditional rupture frequency estimates.
- hiBASE(t) = hazard rate (time-dependent rupture mode frequency) for component i at piping system of t and RIM strategy corresponding to an “average” component in the service data.
- Adjusting service data to derive additional piping cases: To estimate the failure rates and rupture frequencies for non-safety-grade SW piping using data from safety grade piping which has stricter integrity management requirements. In this case, failure rates and rupture frequencies for ASME Class 3 SW piping are derived from the service data; Equation (5) is then evaluated for the RIM strategy of no leak testing and no ISI.
- Accounting for plant-specific integrity management enhancements: In the second application, additional RIM strategies are evaluated that could be used to reduce the failure rates and rupture frequencies below those reflected in the service data by conducting more inspections and tests than are reflected in the service data.
5.3. Specific RIM Strategies Used in Flood Frequency Data
5.3.1. RIM-0 Standard Industry Practice
5.3.2. RIM-1 Enhanced Leak Testing
5.3.3. RIM-2 Robust Leak Testing
5.3.4. RIM-3 Robust Leak Testing and Enhanced NDE
5.3.5. RIM-4 Robust Leak Testing and Robust NDE
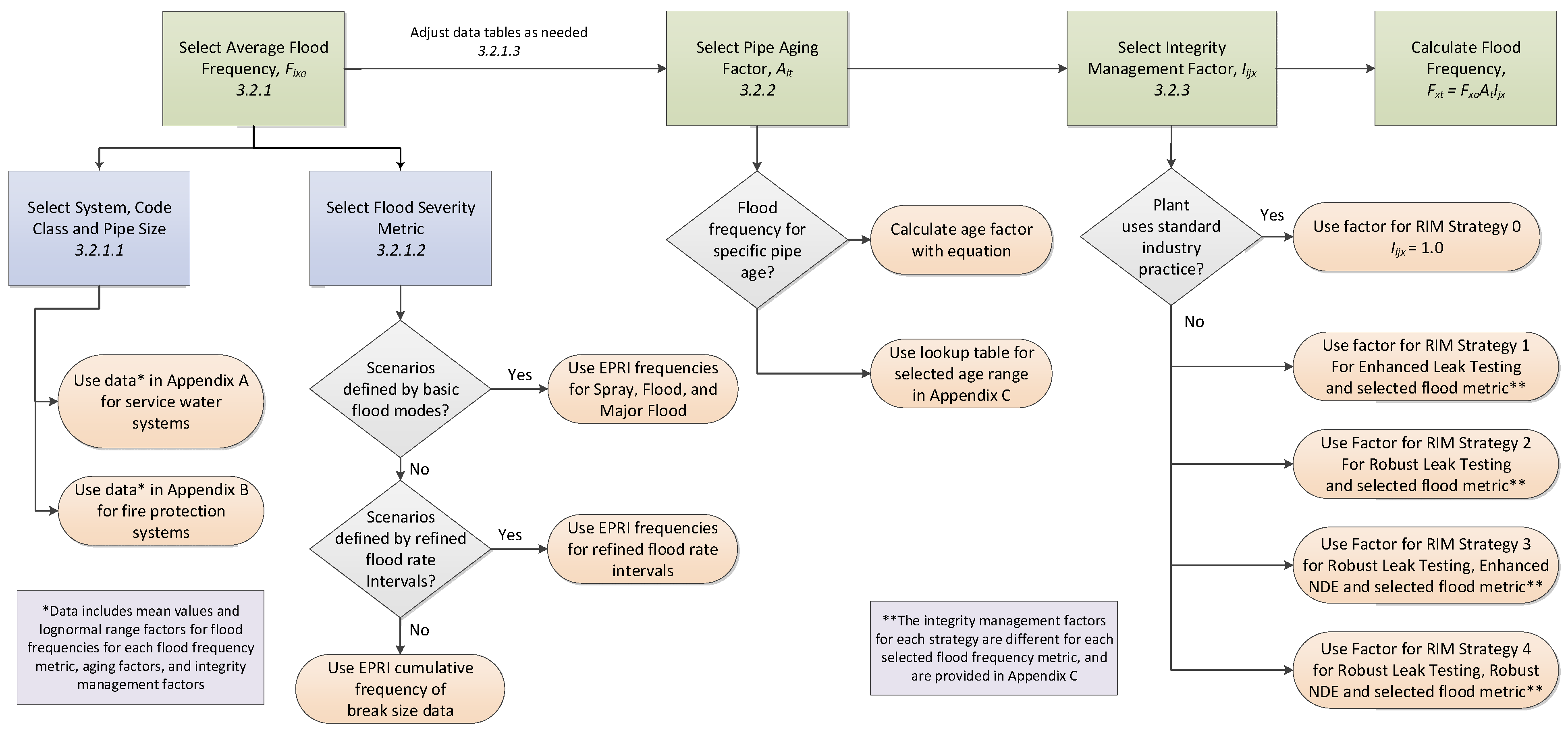
6. Roadmap for Selection and Application of Flood Frequency Parameters
- Appendix A: Service Water System Data Tables
- Appendix B: Fire Protection System Data Tables
- Appendix C: Service Water and Fire Protection Systems Adjustment Factors Data Tables
- Appendix D: Other Water Systems Data Tables
- Appendix E: FRANX Files
- Appendix F: Internal Flooding Event Database
- Appendix G: Documentation of Independent Review
- Appendix H: PIPExp Database

7. Trends in Flood Frequency Estimates
8. Summary and Conclusions
- Compared with the previous revision in Reference [2] the service experience with piping systems that have been used has been expanded from 2010 to 2020.
- A wider scope of piping systems is now supported in terms of piping system design codes, pipe materials, and pipe sizes. These cases demonstrate the advantages in replacing carbon steel pipe with corrosion-resistant materials that reduce susceptibility to corrosion-related damage mechanisms that are present in raw water systems and high-energy piping.
- A larger set of flood frequency metrics has been included to facilitate use of the pipe failure data in performing internal flooding and high-energy line break PRAs.
- The flood frequencies provided address the aging of piping systems associated with degradation mechanisms and trends in reporting. This is the first time a generic database developed to support industry PRAs has explicitly addressed the impact of aging on component failure rates.
- The ability to adjust the flood frequencies to account for enhanced integrity management strategies has been improved and is more easily applied. As demonstrated in the development of risk-informed inservice inspection programs, enhancements to the procedures for inspection of leaks and performance of non-destructive examinations can greatly reduce the frequency of pipe ruptures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pipe Rupture Frequencies for Internal Flooding Probabilistic Risk Assessments, Revision 5; EPRI: Palo Alto, CA, USA, 2023; p. 3002024904.
- Pipe Rupture Frequencies for Internal Flooding PRAs, Revision 3; EPRI: Palo Alto, CA, USA, 2013; p. 3002000079.
- Piping System Failure Rates for Corrosion Resistant Service Water Piping; EPRI: Palo Alto, CA, USA, 2014; p. 3002002787.
- Pipe Rupture Frequencies for Internal Flooding PRAs, Technical Update for High Energy Line Piping; EPRI: Palo Alto, CA, USA, 2017; p. 3002009993.
- Guidelines for Performance of Internal Flooding Probabilistic Risk Assessment; EPRI: Palo Alto, CA, USA, 2009; p. 1019194.
- ASME/ANS RA-S-1.1-2022; Standard for Level 1/Large Early Release Frequency Probabilistic Risk Assessment for Nuclear Power Plant Applications. American Society of Mechanical Engineers and American Nuclear Society: New York, NY, USA, 2022.
- Fleming, K.N.; Lydell, B.O.Y. Database Development and Uncertainty Treatment for Estimating Pipe Failure Rates and Rupture Frequencies. Reliab. Eng. Syst. Saf. 2004, 86, 227–246. [Google Scholar] [CrossRef]
- Revised Risk-Informed In-Service Inspection Procedure; Rev. B-A; EPRI: Palo Alto, CA, USA, 1999; p. TR-112657.
- Fleming, K.N. Markov Models for Evaluating Risk Informed In-Service Inspection Strategies for Nuclear Power Plant Piping Systems. Reliab. Eng. Syst. Saf. 2004, 83, 27–45. [Google Scholar] [CrossRef]
- Piping System Reliability and Failure Rate Estimation Models for Use in Risk-Informed In-Service Inspection Applications; EPRI: Palo Alto, CA, USA, 1998; p. TR-110161.
- Piping System Failure Rates and Rupture Frequencies for Use in Risk-Informed In-Service Inspection Applications; EPRI: Palo Alto, CA, USA, 1999; p. TR-111880.
- Martz, H. Final (Revised) Review of the EPRI-Proposed Markov Modeling/Bayesian Methodology for Use in Risk-Informed Inservice Inspection of Piping in Commercial Nuclear Power Plants; Los Alamos National Laboratory: Los Alamos, NM, USA, 1999; p. TSA-1/999-164. [Google Scholar]
- U.S. Nuclear Regulatory Commission. Safety Evaluation Report Related to Revised Risk-Informed In-Service Inspection Evaluation Procedure; Rev. B; EPRI: Washington, DC, USA, 1999; p. TR-112657, This is included in Reference [8]. [Google Scholar]
- Poloski, J.P.; Marksberry, D.; Atwood, U.C. Rates of Initiating Events at U.S. Nuclear Power Plants: 1987–1995; NUREG/CR-5750; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 1999.
- U.S. Nuclear Regulatory Commission. Estimating Loss-of-Coolant Accident (LOCA) Frequencies Through the Elicitation Process; NUREG-1829; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2008.
- FRANX Version 11 Packaged in Phoenix Architect Version 2.0a; EPRI: Palo Alto, CA, USA, 2023; p. 3002026269.
- U.S. Nuclear Regulatory Commission. Handbook for Parameter Estimation for Probabilistic Risk Assessment; NUREG/CR-6823; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2003.

| System 1 | Reactor Type Cases | Type Cases | Pipe Class Cases | Nominal Pipe Size (in.) Cases |
|---|---|---|---|---|
| Service water | BWR, PWR | Lake, River, Sea | ASME Class 3 Carbon Steel, ASME Class 3 Corrosion-Resistant Steel 2, ASME B31.1 Carbon Steel (non-safety) | 2, 3, 4, 6, 10, 12, 16, 18, 20, 24 |
| Fire protection | All | With and Without WH protection | Non-safety | 4, 6, 8, 10, 12, |
| SIR outside containment | All | N/A | ASME Class 3 | 4, 6, 10, 14, 24 |
| CCW and CST 3 | All | N/A | Non-safety | 4, 6, 10, 14, 24 |
| FWC outside containment | Stainless steel 4, Carbon steel (FAC susceptible) | Non-safety | 3, 4, 6, 10, 18, 24, 42 | |
| HP steam outside containment | Stainless steel 4, Carbon steel | Non-safety | 3, 4, 6, 10, 18, 24, 42 | |
| LP and EXT steam 5 | Stainless steel 4, Carbon steel | Non-safety | 3, 4, 6, 10, 18, 24, 42 | |
| Circulating water | All | Piping, Expansion joint, MOV body | Non-safety | 72″ 6 |
| Plant level floods | All | All | All | All |
| Analysis Step | Uncertainty Treatment |
|---|---|
| 1. Establish Prior Distribution for failure rate. | The Constrained Non-Informative Distribution method of Reference [17] is used to characterize uncertainty in the prior. The mean value is anchored to system specific pipe failure rates developed for EPRI RISI program in Reference [8]. |
| 2. Collect failure data for each analysis case and pipe size. | Develop point estimate of pipe failure rate for each component i. li = Number of failures/(pipe length per plant x reactor operating years). |
| 3. Estimates of pipe lengths per plant for representative sample of plants. | |
| 4. Calculate reactor operating years of experience relevant to pipe analysis case. | |
| 5. Characterize uncertainty in the estimated pipe lengths per plant [10,13]. | Perform 3 Bayes’ updates of the CNID prior distribution for the failure rate li for each component i; one for the best estimate of pipe length, one assuming pipe length is 50% higher, and one assuming pipe length is 50% lower. This yields 3 Gamma distributions for li, one for each estimate of pipe length per plant. |
| Using engineering judgment, assign a 50% probability that the best estimate of pipe length is the correct value, 25% probability that the lower estimate is correct, and 25% that the upper estimate is correct. | |
| Using Monte Carlo simulation, calculate a mixture distribution combining the above Gamma distribution using the stated probability weights. This yields one uncertainty distribution of li for each component i. | |
| 6. Develop prior distribution for the conditional probability of rupture, . | Use engineering judgement based on insights from analysis of service data, results of probabilistic fracture mechanics analyses, and expert elicitation to estimate the probabilities for discrete levels of break size. Use CNID method using the BETA distribution to characterize the prior distributions for each break size using these probabilities as mean values. |
| 7. Collect industry data on the frequency of leaks and floods with different flood rates applicable to component i. Convert to equivalent break sizes. | Perform Bayes update of the prior distributions to obtain Bayes’ posterior distributions for each conditional probability of rupture size. This yields new conjugate BETA distributions for each |
| 8. Apply adjustment factors to value of to ensure that that industry wide flood frequencies predicted by the pipe failure model agree with the observed industry data. [New to this revision]. | Adjustment factors are developed by comparing the predicted frequencies of different break size against the observed frequencies from the service data. The former are obtained multiplying the mean values of and times the pipe component exposure to obtain the predicted industry wide frequency of leaks of different sizes. Adjustment factors are calculated to make the predictions consistent with the industry data. These are used to modify the values to ensure agreement. |
| 9. Apply modeling uncertainty to account for the modeling assumption that each pipe failure is a precursor to a more severe pipe rupture. | Convert Bayes’ posterior BETA distributions from Step 7 to lognormal distribution by matching the mean values and assignment of range factors that increase with decreasing rupture probability. |
| 10. Develop overall uncertainty in the pipe rupture frequency for each value of ρix. | Perform Monte Carlo uncertainty analysis to combine the uncertainties in and . Fit the resulting distributions to lognormal distributions by matching the means and estimating the range factor (RF) from the Monte Carlo distribution percentiles: RF = SQRT(95%tile/5%tile). |
| 11. Develop flood frequency metrics for use in IFPRA. | Convert results from Step 9 into different forms including the following:
|
| 12. Develop aging factors, Ait in Equation (1) to convert time-averaged flood frequencies developed in Step 11 to flood frequencies dependent on the pipe age. See Section 4 for details regarding the development and application of aging factors. | Estimate the pipe failure rates, λi in Equation (1), by pipe system age; develop correlation between failure rate and pipe age; develop aging factors for each pipe case. |
| 13. Develop integrity management factors, Iix in Equation (1), to account for integrity management strategies for inspections for leaks and flaws in piping system. | Use the Markov Model [9] to derive integrity management factors for each pipe case. A factor 1.0 is used when standard industry practices are followed, and values less than 1 are estimated to account for selected strategies where more advanced procedures for detecting for leaks and inspecting for flaws via non-destructive examination are employed. Specific values are associated with the level of rigor of the selected strategy and are defined in [1]. |
| Analysis Group | Failure Rate Variables | Number of Analysis Cases | ||
|---|---|---|---|---|
| Plant Type | Pipe Size | UHS Type | ||
| 0 | Variable and Pooled | Pooled | Pooled | 3 |
| 1 | Variable | Variable | Variable | 24 |
| 2 | Variable and Pooled | Variable | Pooled | 12 |
| 3 | Variable and Pooled | Pooled | Variable | 6 |
| 4 | Variable and Pooled | Variable | Pooled | 9 |
| Pipe Age (Years) | Pipe Size (Inches) | |||
|---|---|---|---|---|
| ≤2″ | 2″ to 4″ | 4″ to 10″ | >10″ | |
| 5 (or less) | 0.03 | 0.01 | 0.02 | 0.10 |
| 10 | 0.10 | 0.04 | 0.10 | 0.25 |
| 15 | 0.21 | 0.10 | 0.22 | 0.44 |
| 20 | 0.35 | 0.19 | 0.40 | 0.65 |
| 25 | 0.53 | 0.32 | 0.63 | 0.88 |
| 30 | 0.73 | 0.49 | 0.92 | 1.14 |
| 35 | 0.96 | 0.69 | 1.27 | 1.41 |
| 40 | 1.22 | 0.94 | 1.68 | 1.69 |
| 45 | 1.51 | 1.23 | 2.14 | 1.99 |
| 50 | 1.82 | 1.56 | 2.66 | 2.30 |
| 55 | 2.16 | 1.94 | 3.24 | 2.62 |
| 60 | 2.52 | 2.37 | 3.88 | 2.96 |
| Symbol | Definition | How it is Quantified in This Study |
|---|---|---|
| PI | Probability per inspection interval that the pipe element will be inspected | This parameter is set to 1 for components assumed to be part of an NDE ISI program and 0 if no inspections are performed. |
PFD | Probability per inspection that an existing flaw will be detected | This parameter is set to 0 for no NDE, 0.5 for enhanced NDE, and 0.9 for robust NDE. This metric is used to provide a degree of confidence that each inspection will identify a detectable flaw according to ASME NDE criteria. |
| PLD | Probability per detection interval that an existing leak will be detected | This is a function of the reliability of the test being performed for leak detection. This parameter is set to 0.5 for enhanced leak testing and 0.9 for robust leak testing. |
| TFI | Flaw inspection interval; mean time between in-service inspections | This parameter is set to 10 years for enhanced NDE and robust NDE. |
| TLD | Leak detection interval; mean time between leak inspections | Leak inspections are assumed to be performed once per quarter year for enhanced and robust leak testing |
| TR | Mean time to repair the piping element given detection of a critical flaw or leak | This parameter is set to 200 h in this study, and the results are not sensitive to this assumption. |
| l | Failure rate for leaks | Taken as the failure rate for the smallest equivalent break size (EBS) evaluated in this study—0.32 in; note that this l is somewhat different from that used in Equation (1). This version includes all failures involving leaks, whereas the Equation (1) version includes all failure modes involving repair and replacement, which includes leaks as well as non-leak events. |
| f | Occurrence rate for detectable flaws | This rated is assumed to be a multiple (4) of the total failure rate for the component; consistent with assumptions used for LWR RI-ISI [8] |
| ρ(F) | Rupture frequency given a flaw | This is the rupture frequency for each EBS evaluated in this study. The model is evaluated for each EBS in the pipe failure model. |
| r(L) | Rupture frequency given a leak | This rate is assumed to be the rupture frequency given a severe loading condition (for example, water hammer) derived from service data (2 × 10−2 per year), consistent with assumptions used for LWR RI-ISI evaluations [8]. |
| hBASE(t) | Hazard rate for Base RIM strategy at time t | Hazard rate determined by solving the differential equations for the Markov model with the input parameters as defined in this table set to match the average industry RIM strategies. For ASME Class 3 SW systems, the average component is characterized by 5% of the components being subjected to NDE exams every 10 years for augmented inspection programs 1, the remaining 95% not being subjected to NDE, and 100% of the components being subjected to a system leak test once every refueling outage—which occurs (on average) once every 18 months. Time t is set at the average age of component that was used to develop the failure rate estimates. |
| hx(t) | Hazard rate for variable RIM strategy at time t | The hazard rate is the time dependent rupture frequency of the component with component age. In this version of the hazard rate, the input parameters defined in this table are set to match the parameters of a specific RIM strategy designated as x. |
| Name | Description | Elements of Strategy |
|---|---|---|
| RIM-0 | Standard Industry Practice | Maintain current procedures and practice for leak inspections and non-destructive examinations (NDE). |
| RIM-1 | Enhanced Leak Testing | Develop written procedure for performance of quarterly leak inspection that identifies all pipe sections for which this strategy is to be implemented. Implementation of the procedures should be capable of performing visual examination of applicable pipe sections that are effective in identifying the presence of leaks. At least 50% of the applicable pipe sections should be accessible for the visual exams to verify leak-tight integrity over the sections of piping system that the integrity management factor is being applied to. If there is water on the floor, source of leakage should be determined. If the applicable pipe section is determined to be leaking, the leak should be repaired or replaced. This strategy is simulated in the Markov model, assuming quarterly leak testing at a 50% probability of finding and repairing a detectable leak and no NDE. Maintain current procedures and practice for leak inspections and non-destructive examinations (NDE) for other pipe sections. |
| RIM-2 | Robust Leak Testing | Develop written procedures for performance of quarterly leak inspection that identifies all pipe sections that are applicable to the RIM-2 strategy. Implementation of the procedures should be capable of performing white glove examination, or equivalent, of applicable pipe sections that are effective in identifying the presence of leaks. At least 90% of the applicable pipe sections should be accessible for the visual exams to verify leak-tight integrity over the sections of piping system that the integrity management factor is being applied to 1. If there is water on the floor, source of leakage should be determined. If the applicable pipe section is determined to be leaking, the leak shall be addressed by appropriate repair and replacement. This strategy is simulated in the Markov model, assuming quarterly leak testing at a 90% probability of finding and repairing a detectable leak and no NDE. Maintain current procedures and practice for leak inspections and non-destructive examinations (NDE) for other pipe sections. |
| RIM-3 | Robust Leak Testing and Enhanced NDE | Same leak testing as in RIM-2 with additional 10-year NDE that has the capability to detect a flaw in the applicable pipe sections that exceeds the NDE criteria for repair with a 50% probability of finding a detectable flaw. If the applicable pipe section is determined to be leaking in the quarterly leak inspection or if a flaw exceeding the repair criteria is found in the 10-year NDE, the leak or flaw shall be addressed by appropriate repair and replacement. This strategy is simulated in the Markov model, assuming quarterly leak testing at a 90% probability of finding and repairing a detectable leak combined with a 10-year NDE with a 50% probability of finding and repairing a detectable flaw. Maintain current procedures and practice for leak inspections and non-destructive examinations (NDE) for other pipe sections. |
| RIM-4 | Robust Leak Testing and Robust NDE | Same leak testing as in RIM-3 but with a 10-year NDE that has the capability to detect a flaw in the applicable pipe sections that exceeds the NDE criteria for repair with a 90% probability of finding a detectable flaw. If the applicable pipe section is determined to be leaking in the quarterly leak inspection or if a flaw exceeding the repair criteria is found in the 10-year NDE, the leak or flaw shall be addressed by appropriate repair and replacement. The locations covered by this strategy should be incorporated into the plant’s existing augmented ISI programs. This strategy is simulated in the Markov model, assuming quarterly leak testing at a 90% probability of finding and repairing a detectable leak combined with a 10-year NDE with a 90% probability of finding and repairing a detectable flaw. Maintain current procedures and practice for leak inspections and non-destructive examinations (NDE) for other pipe sections. |
| Flood Rate 1 Interval (gpm) | RFI IM Factor | ||||
|---|---|---|---|---|---|
| RIM-0 | RIM-1 | RIM-2 | RIM-3 | RIM-4 | |
| 1–50 | 1.00 | 0.98 | 0.97 | 0.24 | 0.23 |
| 50–100 | 1.00 | 0.81 | 0.75 | 0.20 | 0.18 |
| 100–250 | 1.00 | 0.65 | 0.56 | 0.16 | 0.14 |
| 250–500 | 1.00 | 0.56 | 0.45 | 0.14 | 0.11 |
| 500–1000 | 1.00 | 0.51 | 0.39 | 0.13 | 0.10 |
| 1000–2000 | 1.00 | 0.46 | 0.32 | 0.11 | 0.079 |
| 2000–10,000 | 1.00 | 0.42 | 0.28 | 0.10 | 0.068 |
| 10,000–100,000 | 1.00 | 0.38 | 0.24 | 0.094 | 0.058 |
| 100,000–288,186 | 1.00 | 0.36 | 0.20 | 0.087 | 0.050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by Electric Power Research Institute, Inc. (“EPRI”). Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fleming, K.N.; Lydell, B.O.Y.; Presley, M.; Mosleh, A.; Chalgham, W. Initiating Event Frequencies for Internal Flooding and High-Energy Line Break PRAs. J. Nucl. Eng. 2025, 6, 37. https://doi.org/10.3390/jne6030037
Fleming KN, Lydell BOY, Presley M, Mosleh A, Chalgham W. Initiating Event Frequencies for Internal Flooding and High-Energy Line Break PRAs. Journal of Nuclear Engineering. 2025; 6(3):37. https://doi.org/10.3390/jne6030037
Chicago/Turabian StyleFleming, Karl N., Bengt O. Y. Lydell, Mary Presley, Ali Mosleh, and Wadie Chalgham. 2025. "Initiating Event Frequencies for Internal Flooding and High-Energy Line Break PRAs" Journal of Nuclear Engineering 6, no. 3: 37. https://doi.org/10.3390/jne6030037
APA StyleFleming, K. N., Lydell, B. O. Y., Presley, M., Mosleh, A., & Chalgham, W. (2025). Initiating Event Frequencies for Internal Flooding and High-Energy Line Break PRAs. Journal of Nuclear Engineering, 6(3), 37. https://doi.org/10.3390/jne6030037







