Deterministic Data Assimilation in Thermal-Hydraulic Analysis: Application to Natural Circulation Loops
Abstract
1. Introduction
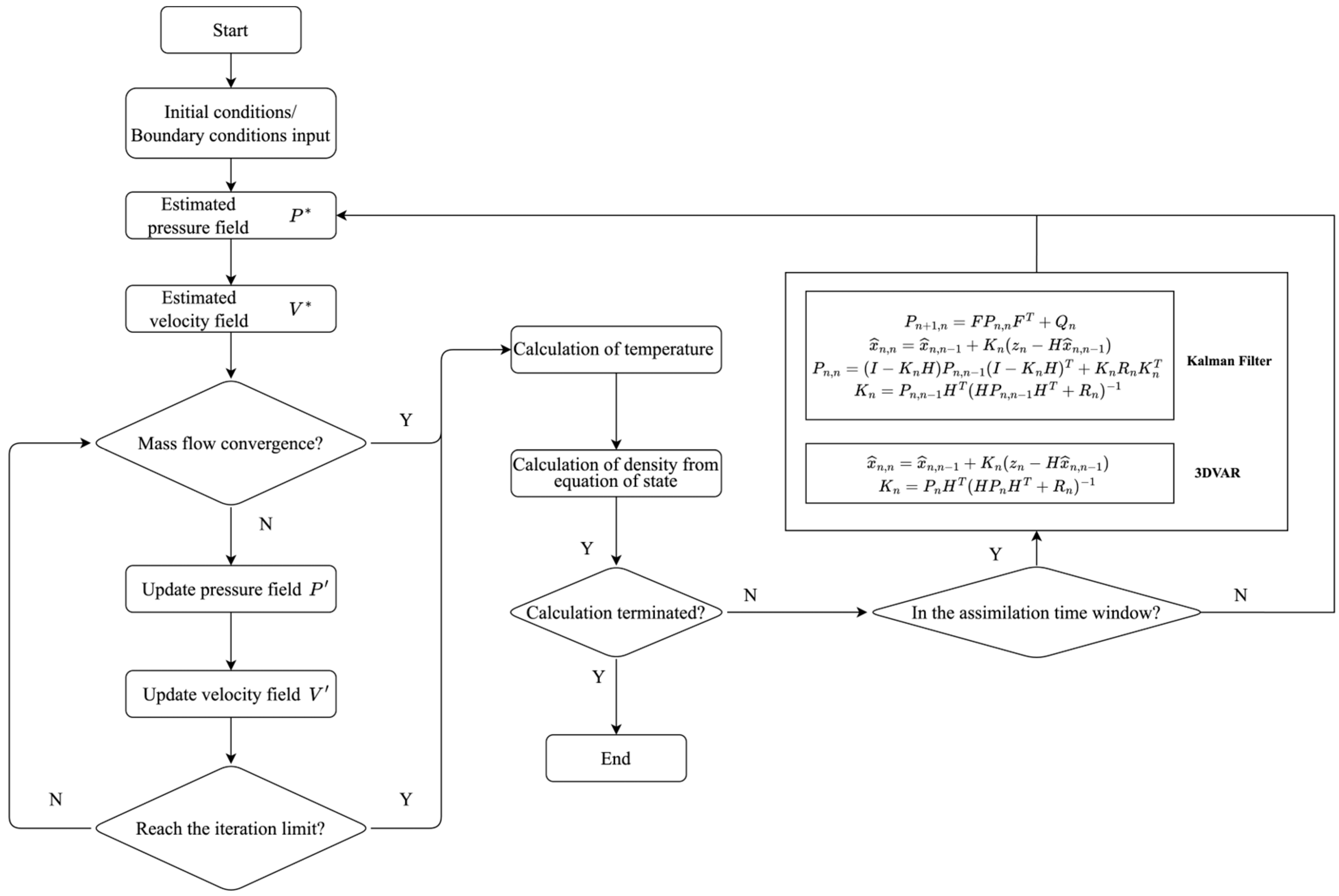
2. Deterministic Data Assimilation Methods
2.1. Kalman Filter
2.2. Three-Dimensional Variational Data Assimilation
3. Case Study of Natural Circulation Loops
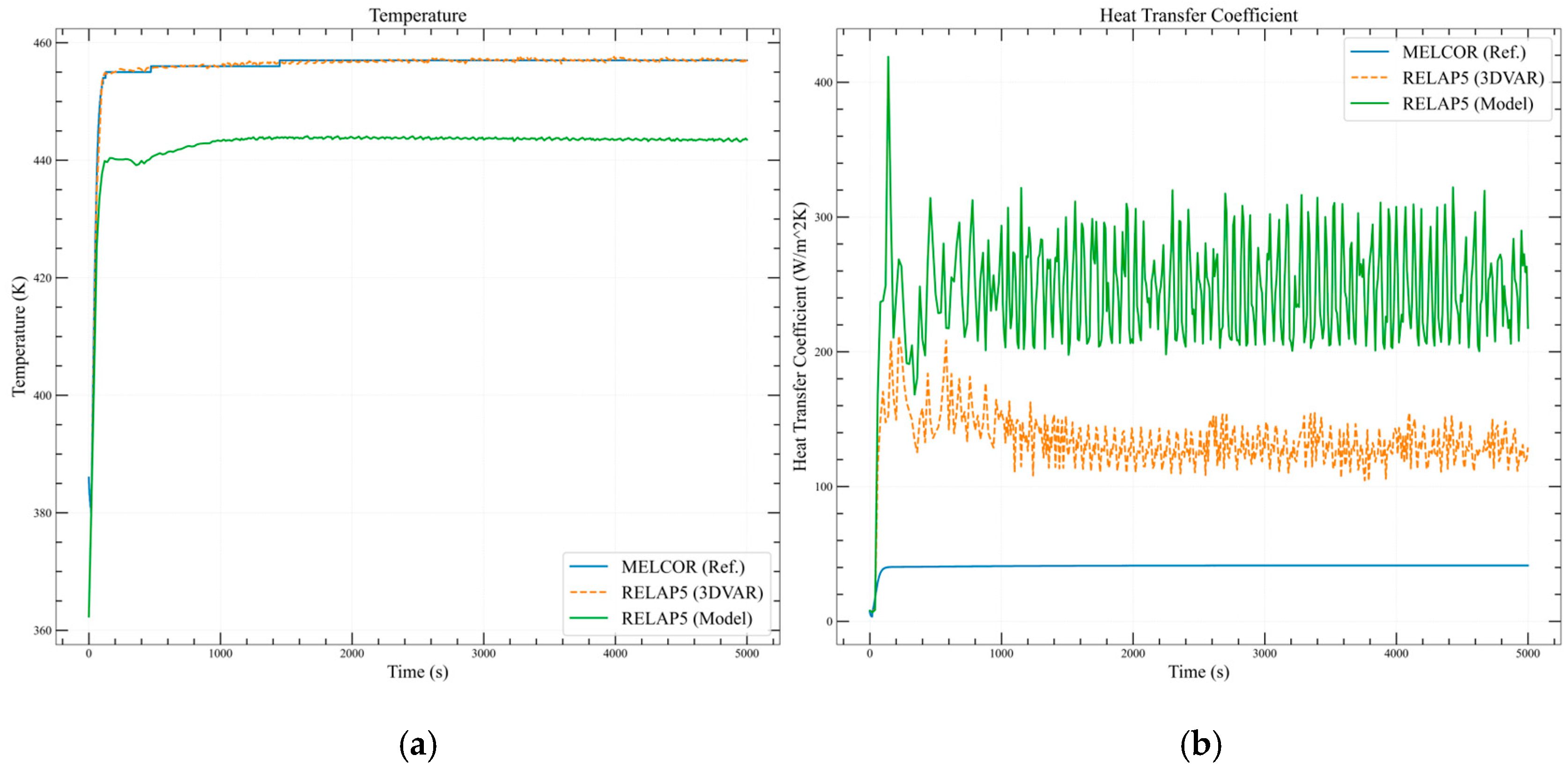
3.1. One-Dimensional Single-Phase Natural Circulation Loop
3.1.1. Model Description
3.1.2. Fixed Wall Temperature Case
3.1.3. Time-Varying Wall Temperature Case
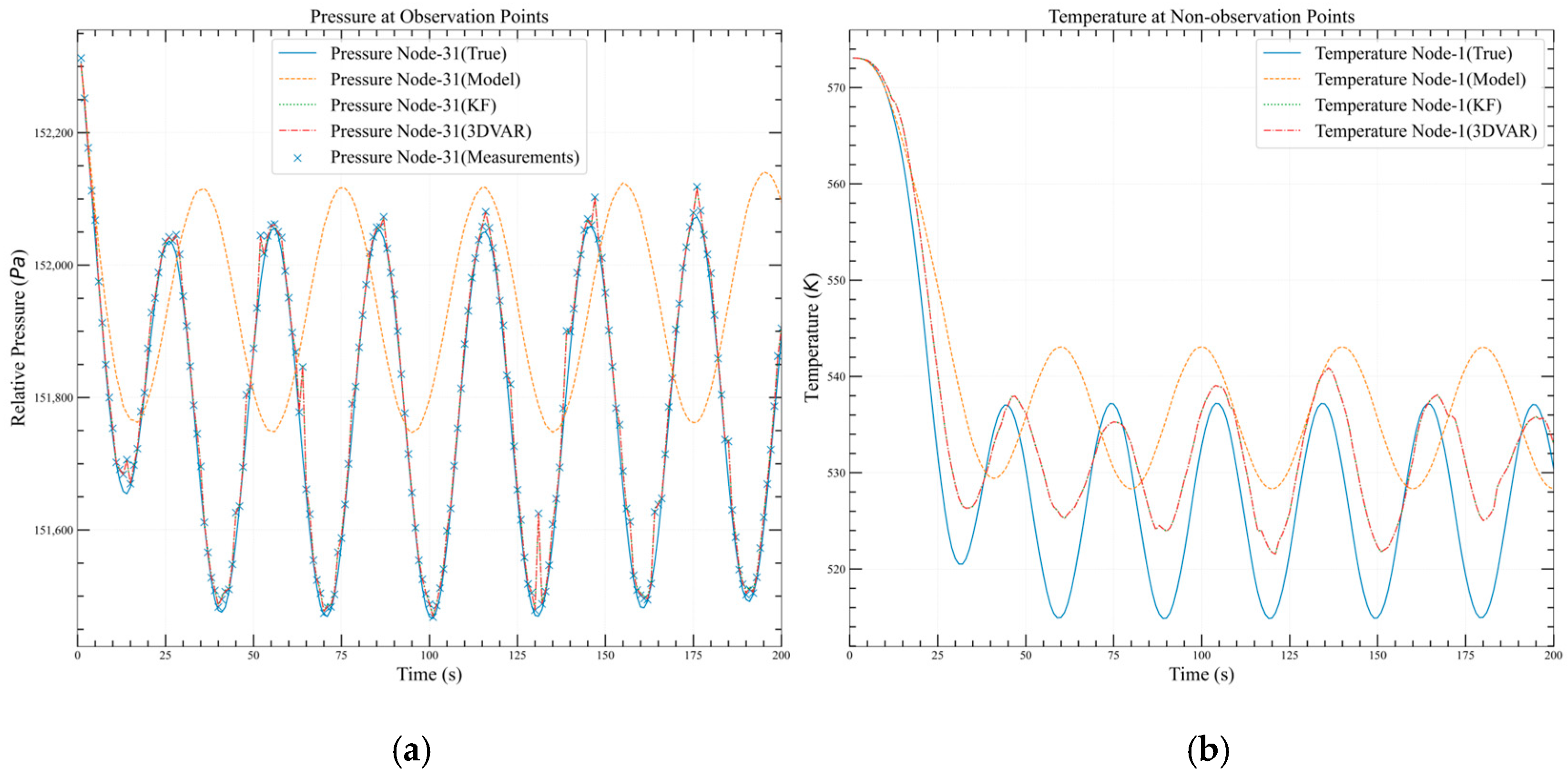
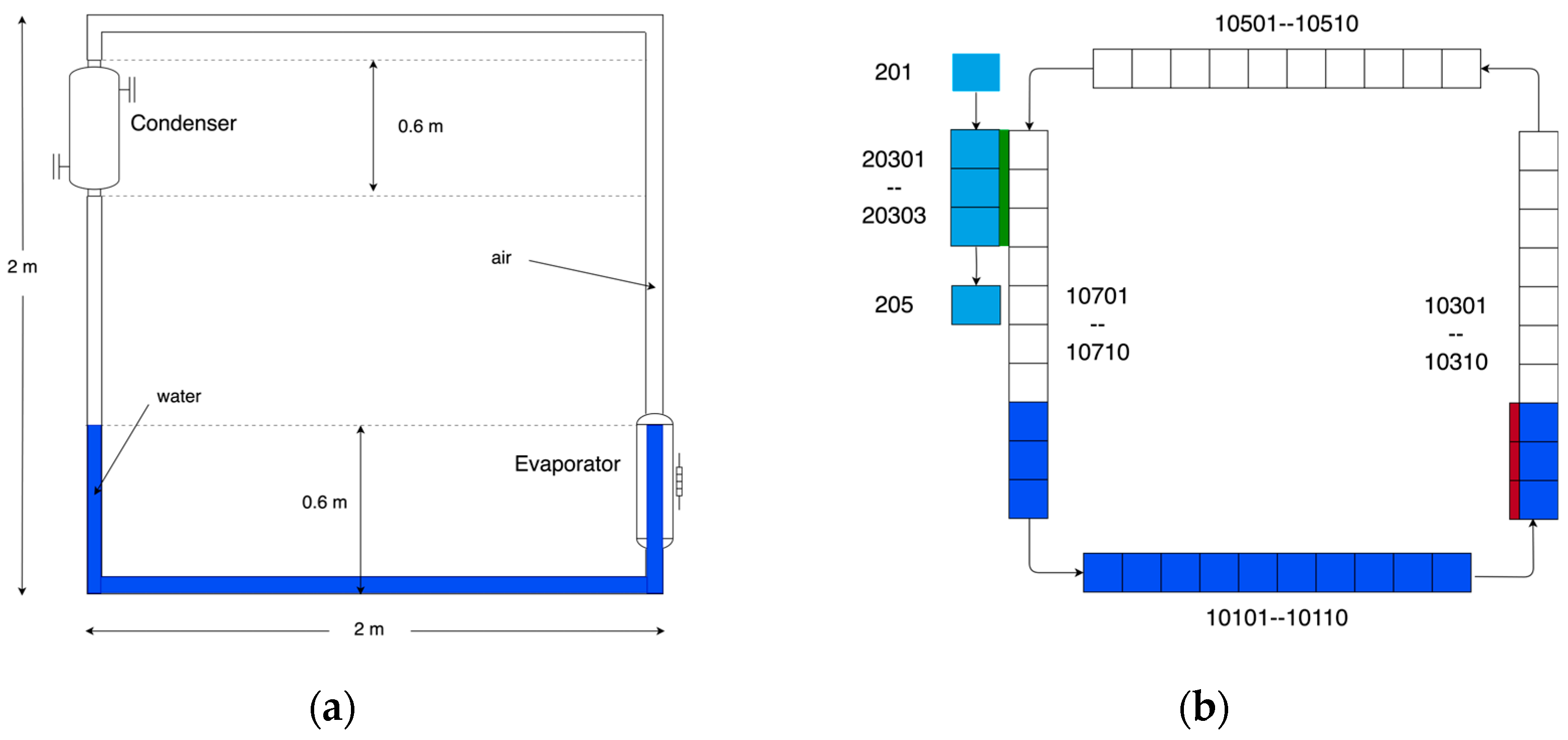
3.2. One-Dimensional Two-Phase Natural Circulation Loop
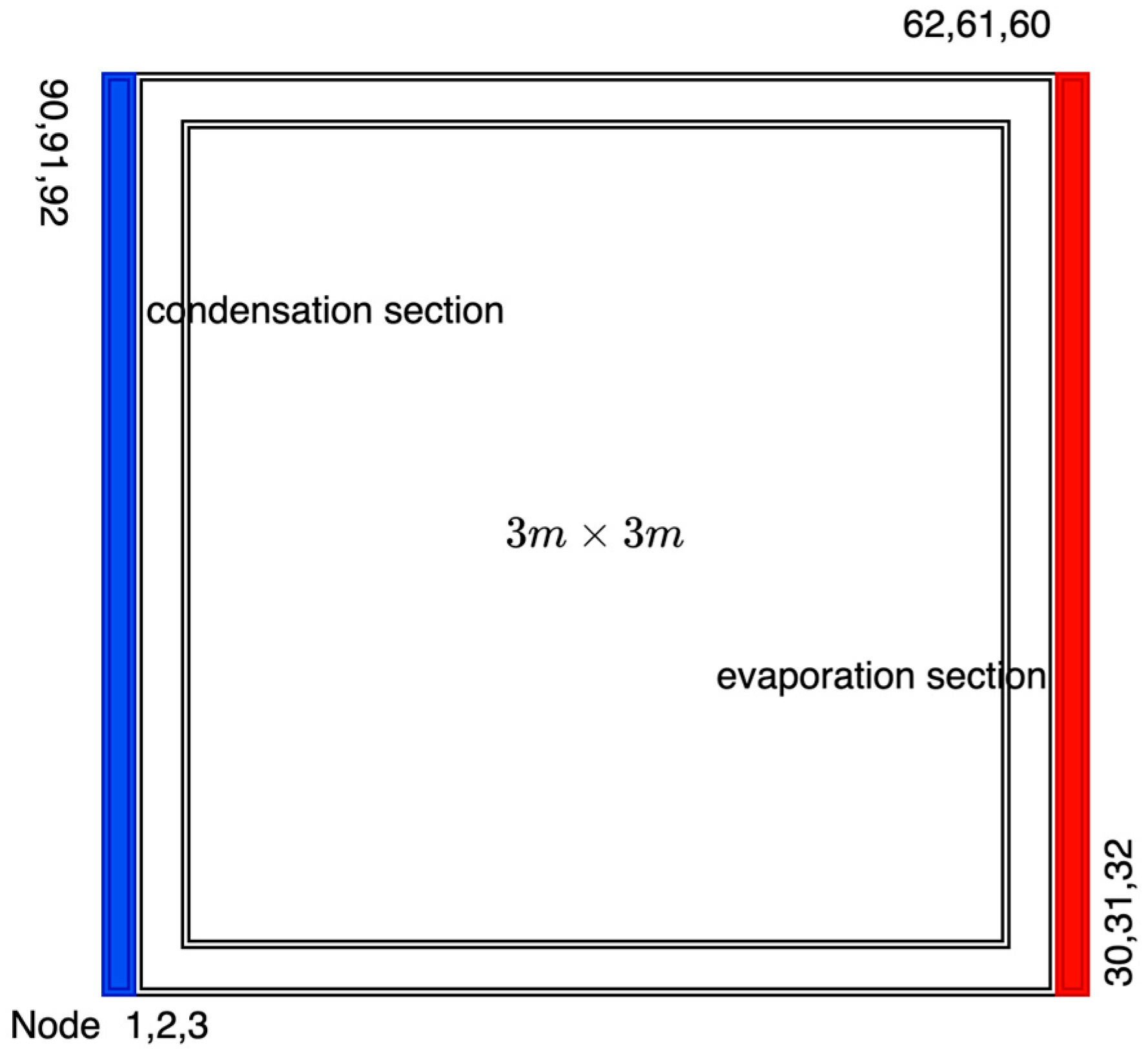
3.3. One-Dimensional Two-Phase Natural Circulation Loop Under Ocean Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lorenc, A.; Bell, R.; Macpherson, B. The Meteorological Office analysis correction data assimilation scheme. Q. J. R. Meteorol. Soc. 1991, 117, 59–89. [Google Scholar] [CrossRef]
- Carrassi, A.; Bocquet, M.; Bertino, L.; Evensen, G. Data assimilation in the geosciences: An overview of methods, issues, and perspectives. Wiley Interdiscip. Rev. Clim. Change 2018, 9, e535. [Google Scholar] [CrossRef]
- Chenyu, J.; Jun, Y.; Ke, X.; Zhanyu, H.; Ming, Y. Coupling of adjoint-based Markov/CCMT predictive analytics with data assimilation for real-time risk scenario forecasting of industrial digital process control systems. Process Saf. Environ. Prot. 2023, 171, 951–974. [Google Scholar] [CrossRef]
- Jahja, M.; Farrow, D.; Rosenfeld, R.; Tibshirani, R.J. Kalman filter, sensor fusion, and constrained regression: Equivalences and insights. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Nadler, P.; Arcucci, R.; Guo, Y.-K. Data assimilation for parameter estimation in economic modelling. In Proceedings of the 2019 15th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Sorrento, Italy, 26–29 November 2019. [Google Scholar] [CrossRef]
- Beyou, S.; Cuzol, A.; Gorthi, S.S.; Mémin, E. Weighted ensemble transform Kalman filter for image assimilation. Tellus A Dyn. Meteorol. Oceanogr. 2013, 65, 18803. [Google Scholar] [CrossRef]
- Mons, V.; Chassaing, J.-C.; Gomez, T.; Sagaut, P. Reconstruction of unsteady viscous flows using data assimilation schemes. J. Comput. Phys. 2016, 316, 255–280. [Google Scholar] [CrossRef]
- Gong, H. Data Assimilation with Reduced Basis and Noisy Measurement: Applications to Nuclear Reactor Cores. Doctoral Dissertation, Sorbonne Université, Paris, France, 2018. [Google Scholar]
- Heo, J. Optimization of Design for SMR via Data Assimilation and Uncertainty Quantification; NC State University: Raleigh, NC, USA, 2011. [Google Scholar]
- Li, K.; Chen, W.; Liang, M.; Zhou, J.; Wang, Y.; He, S.; Yang, J.; Yang, D.; Shen, H.; Wang, X. A simple data assimilation method to improve atmospheric dispersion based on Lagrangian puff model. Nucl. Eng. Technol. 2021, 53, 2377–2386. [Google Scholar] [CrossRef]
- Cacuci, D.G.; Ionescu-Bujor, M. Best-Estimate Model Calibration and Prediction through Experimental Data Assimilation—I: Mathematical Framework. Nucl. Sci. Eng. 2010, 165, 18–44. [Google Scholar] [CrossRef]
- Petruzzi, A.; Cacuci, D.G.; D’Auria, F. Best-Estimate Model Calibration and Prediction through Experimental Data Assimilation—II: Application to a Blowdown Benchmark Experiment. Nucl. Sci. Eng. 2010, 165, 45–100. [Google Scholar] [CrossRef]
- Cacuci, D.G.; Arslan, E. Reducing Uncertainties via Predictive Modeling: FLICA4 Calibration Using BFBT Benchmarks. Nucl. Sci. Eng. 2014, 176, 339–349. [Google Scholar] [CrossRef]
- Heo, J.; Kim, K.D. PAPIRUS, a parallel computing framework for sensitivity analysis, uncertainty propagation, and estimation of parameter distribution. Nucl. Eng. Des. 2015, 292, 237–247. [Google Scholar] [CrossRef]
- Shin, D.-H.; Jeong, H.-Y.; Park, M.-G.; Sohn, J.-U. Application of a combined safety approach for the evaluation of safety margin during a Loss of Condenser Vacuum event. Nucl. Eng. Technol. 2022, 54, 1698–1711. [Google Scholar] [CrossRef]
- Tiep, N.H.; Kim, K.D.; Heo, J. Improvement in the accuracy of SPACE prediction for the unblocked FLECHT SEASET reflood tests by data assimilation. Ann. Nucl. Energy 2021, 161, 108462. [Google Scholar] [CrossRef]
- Tiep, N.H.; Kim, K.-D.; Heo, J.; Choi, C.-W.; Jeong, H.-Y. A newly proposed data assimilation framework to enhance predictions for reflood tests. Nucl. Eng. Des. 2022, 390, 111724. [Google Scholar] [CrossRef]
- Yang, X.; Yang, H. Data Assimilation in Sub-Channel Analysis Model Based on Ensemble Kalman Filter. In Proceedings of the International Conference on Nuclear Engineering, Online, 8–12 August 2022. [Google Scholar] [CrossRef]
- Introini, C.; Lorenzi, S.; Cammi, A.; Baroli, D.; Peters, B.; Bordas, S. A Mass Conservative Kalman Filter Algorithm for Computational Thermo-Fluid Dynamics. Materials 2018, 11, 2222. [Google Scholar] [CrossRef]
- Introini, C.; Chiesa, D.; Lorenzi, S.; Nastasi, M.; Previtali, E.; Salvini, A.; Sisti, M.; Snoj, L.; Antonio, C. Assessment of the integrated mass conservative Kalman filter algorithm for Computational Thermo-Fluid Dynamics on the TRIGA Mark II reactor. Nucl. Eng. Des. 2021, 384, 111431. [Google Scholar] [CrossRef]
- Fang, P.; He, C.; Wang, P.; Xu, S.; Liu, Y. Data Assimilation of Steam Flow Through a Control Valve Using Ensemble Kalman Filter. J. Fluids Eng. 2021, 143, 091201. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Wu, Y.; Lang, M.; Dong, Y.; Li, F. Improving the Accuracy of RCCS Simulator Based on Ensemble Kalman Filter Algorithm. In Proceedings of the 2024 31st International Conference on Nuclear Engineering, Prague, Czech Republic, 4–8 August 2024. [Google Scholar] [CrossRef]
- Introini, C.; Lorenzi, S.; Cammi, A.; Baroli, D. A Reduced Order Kalman Filter for Computational Fluid-Dynamics Applications. Sci. Posters 2018. [Google Scholar] [CrossRef]
- Liu, C.; Fu, R.; Xiao, D.; Stefanescu, R.; Sharma, P.; Zhu, C.; Sun, S.; Wang, C. EnKF data-driven reduced order assimilation system. Eng. Anal. Bound. Elem. 2022, 139, 46–55. [Google Scholar] [CrossRef]
- Argaud, J.-P.; Bouriquet, B.; De Caso, F.; Gong, H.; Maday, Y.; Mula, O. Sensor placement in nuclear reactors based on the generalized empirical interpolation method. J. Comput. Phys. 2018, 363, 354–370. [Google Scholar] [CrossRef]
- Riva, S. Reduced Basis Methods for Data Assimilation in Real Thermal Hydraulics Systems; Polytechnic University of Milan: Milan, Italy, 2020. [Google Scholar]
- Introini, C.; Riva, S.; Lorenzi, S.; Cavalleri, S.; Cammi, A. Non-intrusive system state reconstruction from indirect measurements: A novel approach based on Hybrid Data Assimilation methods. Ann. Nucl. Energy 2023, 182, 109538. [Google Scholar] [CrossRef]
- Riva, S.; Introini, C.; Lorenzi, S.; Cammi, A. Hybrid data assimilation methods, Part I: Numerical comparison between GEIM and PBDW. Ann. Nucl. Energy 2023, 190, 109864. [Google Scholar] [CrossRef]
- Riva, S.; Introini, C.; Lorenzi, S.; Cammi, A. Hybrid Data Assimilation methods, Part II: Application to the DYNASTY experimental facility. Ann. Nucl. Energy 2023, 190, 109863. [Google Scholar] [CrossRef]
- Riva, S.; Introini, C.; Cammi, A. Multi-physics model bias correction with data-driven reduced order techniques: Application to nuclear case studies. Appl. Math. Model. 2024, 135, 243–268. [Google Scholar] [CrossRef]
- Cammi, A.; Riva, S.; Introini, C.; Loi, L.; Padovani, E. Data-driven model order reduction for sensor positioning and indirect reconstruction with noisy data: Application to a Circulating Fuel Reactor. Nucl. Eng. Des. 2024, 421, 113105. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M.; Liu, Y.; Nee, A.Y.C. Digital twin driven prognostics and health management for complex equipment. CIRP Ann. 2018, 67, 169–172. [Google Scholar] [CrossRef]
- Becker, A. Kalman Filter from the Ground Up. KilmanFilter.NET. 2023. Available online: https://www.kalmanfilter.net (accessed on 6 May 2025).
- Ahmed, S.E.; Pawar, S.; San, O. PyDA: A Hands-On Introduction to Dynamical Data Assimilation with Python. Fluids 2020, 5, 225. [Google Scholar] [CrossRef]
- Sleicher, C.A.; Awad, A.S.; Notter, R.H. Temperature and eddy diffusivity profiles in NaK. Int. J. Heat Mass Transf. 1973, 16, 1565–1575. [Google Scholar] [CrossRef]
- Cheng, X.; Tak, N.-I. Investigation on turbulent heat transfer to lead–bismuth eutectic flows in circular tubes for nuclear applications. Nucl. Eng. Des. 2006, 236, 385–393. [Google Scholar] [CrossRef]
- Giorgino, T. Computing and Visualizing Dynamic Time Warping Alignments in R: The dtw Package. J. Stat. Softw. 2009, 31, 1–24. [Google Scholar] [CrossRef]
- Gong, L.; Peng, C. Analysis of the heat-carrying performance of natural circulation loop using modified RELAP5/MOD3.4. Case Stud. Therm. Eng. 2022, 39, 102387. [Google Scholar] [CrossRef]
- Bai, T.-Z.; Peng, C.-H. Thermal hydraulic characteristics of helical coil once-through steam generator under ocean conditions. Nucl. Sci. Tech. 2022, 33, 134. [Google Scholar] [CrossRef]





| Noise | Models | Pressure | Temperature | Velocity |
|---|---|---|---|---|
| K | Model (Frobenius) | 1.0000 | 1.0000 | |
| 3DVAR (Frobenius) | 0.6298 | 0.6660 | ||
| KF (Frobenius) | 0.6298 | 0.6660 | ||
| Model (DTW) | 1.0000 | |||
| 3DVAR (DTW) | 0.5894 | |||
| KF (DTW) | 0.5895 | |||
| K | Model (Frobenius) | 1.0000 | 1.0000 | |
| 3DVAR (Frobenius) | 0.8153 | 0.7329 | ||
| KF (Frobenius) | 0.8153 | 0.7334 | ||
| Model (DTW) | 1.0000 | |||
| 3DVAR (DTW) | 0.6543 | |||
| KF (DTW) | 0.6545 |
| Noise | Models | Pressure | Temperature | Velocity |
|---|---|---|---|---|
| K. (Gauss) | Model (Frobenius) | 1.0000 | ||
| 3DVAR (Frobenius) | 0.9141 | |||
| KF (Frobenius) | 0.9141 | |||
| Model (DTW) | ||||
| 3DVAR (DTW) | ||||
| KF (DTW) | ||||
| K. (Lognormal) | Model (Frobenius) | |||
| 3DVAR (Frobenius) | 0.9222 | |||
| KF (Frobenius) | 0.9222 | |||
| Model (DTW) | ||||
| 3DVAR (DTW) | ||||
| KF (DTW) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Peng, C.; Huang, Q. Deterministic Data Assimilation in Thermal-Hydraulic Analysis: Application to Natural Circulation Loops. J. Nucl. Eng. 2025, 6, 23. https://doi.org/10.3390/jne6030023
Gong L, Peng C, Huang Q. Deterministic Data Assimilation in Thermal-Hydraulic Analysis: Application to Natural Circulation Loops. Journal of Nuclear Engineering. 2025; 6(3):23. https://doi.org/10.3390/jne6030023
Chicago/Turabian StyleGong, Lanxin, Changhong Peng, and Qingyu Huang. 2025. "Deterministic Data Assimilation in Thermal-Hydraulic Analysis: Application to Natural Circulation Loops" Journal of Nuclear Engineering 6, no. 3: 23. https://doi.org/10.3390/jne6030023
APA StyleGong, L., Peng, C., & Huang, Q. (2025). Deterministic Data Assimilation in Thermal-Hydraulic Analysis: Application to Natural Circulation Loops. Journal of Nuclear Engineering, 6(3), 23. https://doi.org/10.3390/jne6030023






