Ultra-Cold Neutrons in qBounce Experiments as Laboratory for Test of Chameleon Field Theories and Cosmic Acceleration
Abstract
1. Introduction
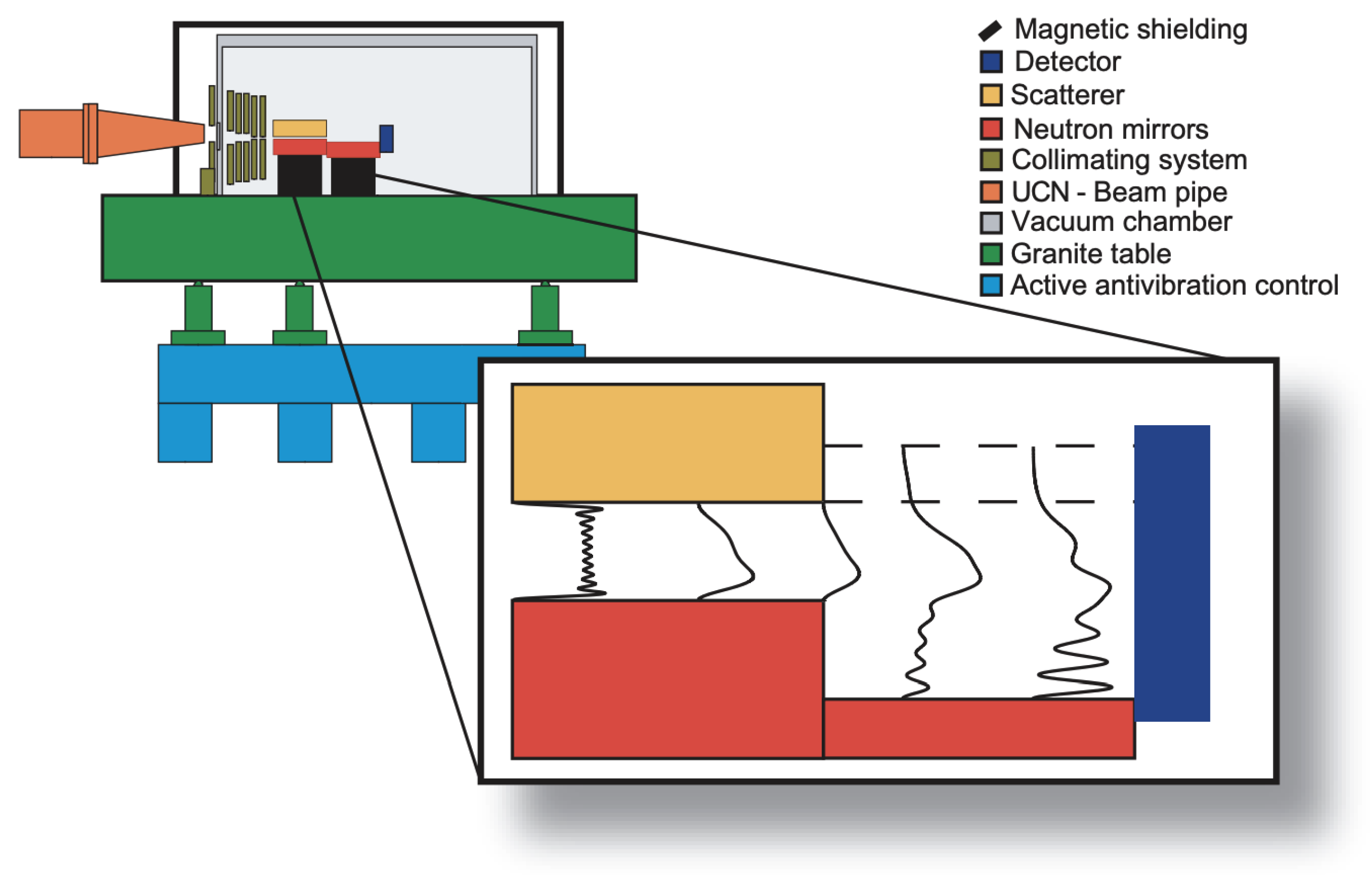
2. Wave Function of Ultra-Cold Neutrons Above a Mirror
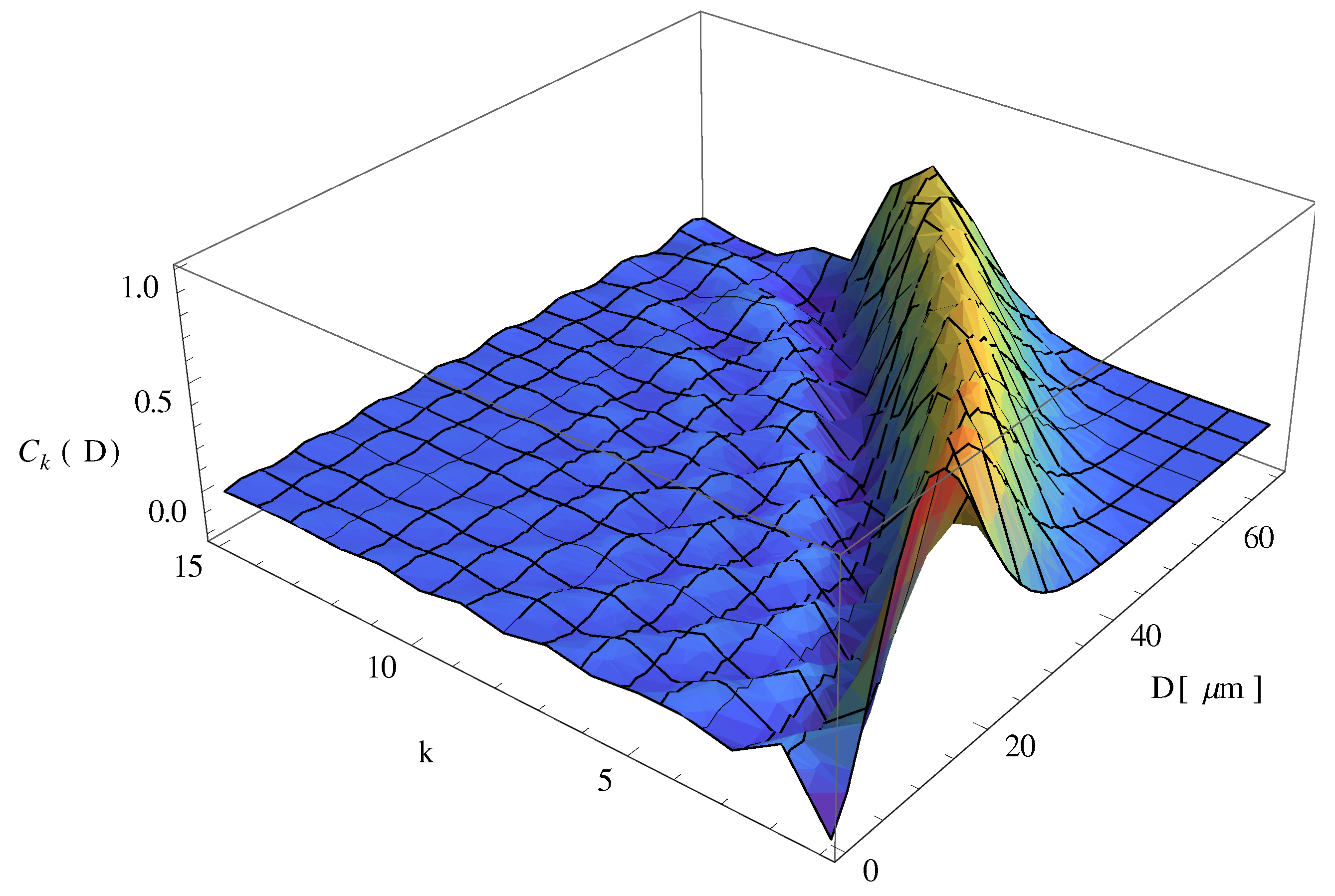
3. Chameleon Field Correction in the -Theory
4. Discussion
5. Binding Energy of Ultra-Cold Neutrons to Second-Order Perturbation Theory
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Wave Functions of Ultra-Cold Neutrons in the Gravitational Field of the Earth Between Two Mirrors and Above a Mirror
| k | (h = 31 μm) | (h = 39 μm) | (h = 47 μm) | (h = 55 μm) | (h = 63 μm) | ||
|---|---|---|---|---|---|---|---|
| 1 | −2.33811 | 1.407 | |||||
| 2 | −4.08795 | 2.461 | |||||
| 3 | −5.52056 | 3.324 | |||||
| 4 | −6.78671 | 4.086 | |||||
| 5 | −7.94413 | 4.782 | |||||
| 6 | −9.02265 | 5.432 | |||||
| 7 | −10.04020 | 6.044 | |||||
| 8 | −11.00850 | 6.627 | |||||
| 9 | −11.93600 | 7.186 | |||||
| 10 | −12.82880 | 7.723 | |||||
| 11 | −13.69150 | 8.242 | |||||
| 12 | −16.13270 | 9.712 | |||||
| 13 | −16.90560 | 10.177 | |||||
| 14 | −19.12640 | 11.514 | |||||
| 15 | −19.83810 | 11.943 | |||||
| 98.67% | 98.68% | 98.01% | 96.80% | 94.52% | |||
| 97.8% | 96.72% | 97.46% | 95.29% | 93.62% | |||
References
- Riess, A.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Larson, D.; Dunkley, J.; Hinshaw, G.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Halpern, M.; Hill, R.S.; Jarosik, N.; et al. Seven-year wilkinson microwave anisotropy probe (WMAP) observations: Power spectra and wmap-derived parameters. Astrophys. J. Suppl. 2011, 192, 16. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The hubble space telescope cluster supernova survey: V. improving the dark-energy constraints above z > 1 and building an early-type-hosted supernova sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Sanchez, A.G.; Scoccola, C.G.; Ross, A.J.; Percival, W.; Manera, M.; Montesano, F.; Mazzalay, X.; Cuesta, A.J.; Eisenstein, D.J.; Kazin, E.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the large-scale two-point correlation function. arXiv 2012, arXiv:1203.6616. [Google Scholar] [CrossRef]
- Upadhye, A.; Steffen, J.H.; Chou, A.S. Designing dark energy afterglow experiments. Phys. Rev. D 2012, 86, 035006. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef]
- Waterhouse, T.P. An Introduction to Chameleon Gravity. arXiv 2006, arXiv:astro-ph/0611816. [Google Scholar]
- Ahmadabadi, H.Y.; Sadjadi, H.M. Imprints of vector field non-standard couplings on solar neutrino flux. Phys. Lett. B 2024, 859, 139110. [Google Scholar] [CrossRef]
- Ahmadabadi, H.Y.; Sadjadi, H.M. Chameleon-neutrino conformal coupling and MSW-mediated solar neutrino deficit. Phys. Lett. B 2024, 850, 138493. [Google Scholar] [CrossRef]
- Fischer, H.; Käding, C.; Pitschmann, M. Screened Scalar Fields in the Laboratory and the Solar System. Universe 2024, 10, 297. [Google Scholar] [CrossRef]
- Silvestri, A.; Trodden, M. Approaches to understanding cosmic acceleration. Rep. Prog. Phys. 2009, 72, 096901. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The Physics of Cosmic Acceleration. Annu. Rev. Nucl. Part. Sci. 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Copel, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar]
- Wetterich, C. Cosmology and the fate of dilatation symmetry. Nucl. Phys. B 1988, 302, 668–696. [Google Scholar] [CrossRef]
- Brax, P.; Pignol, G. Strongly coupled chameleons and the neutronic quantum bouncer. Phys. Rev. Lett. 2011, 107, 111301. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Höllwieser, R.; Jenke, T.; Wellenzohn, M.; Abele, H. The influence of the chameleon field potential on transition frequencies of gravitationally bound quantum states of ultra-cold neutrons. Phys. Rev. 2013, 87, 105013. [Google Scholar]
- Jenke, T.; Cronenberg, G.; Geltenbort, P.; Ivanov, A.N.; Lauer, T.; Lins, T.; Saul1, H.; Schmidt, U.; Abele, H. A novel quantized frequency reference for dark matter and dark energy searches. arXiv 2012, arXiv:1208.3875. [Google Scholar]
- Gibbs, R.L. The quantum bouncer. Am. J. Phys. 1975, 43, 25. [Google Scholar] [CrossRef]
- Gea-Banacloche, J. A quantum bouncing ball. Am. J. Phys. 1999, 67, 776. [Google Scholar] [CrossRef]
- Wallis, H.; Dalibard, J.; Cohen-Tannoudji, C. Trapping atoms in a gravitational cavity. Appl. Phys. B 1992, 54, 407. [Google Scholar] [CrossRef]
- Nesvizhevsky, V.V.; Börner, H.G.; Petukhov, A.K.; Abele, H.; Baeßler, S.; Rueß, F.J.; Stöferle, T.; Westphal, A.; Gagarski, A.M.; Petrov, G.A.; et al. Quantum states of neutrons in the Earth’s gravitational field. Nature 2002, 415, 297. [Google Scholar] [CrossRef] [PubMed]
- Nesvizhevsky, V.V.; Börner, H.G.; Gagarski, A.M.; Petoukhov, A.K.; Petrov, G.A.; Abele, H.; Baeßler, S.; Divkovic, G.; Rueß, F.J.; Stöferle, T.; et al. Measurement of quantum states of neutrons in the Earth’s gravitational field. Phys. Rev. D 2003, 67, 102202. [Google Scholar] [CrossRef]
- Nesvizhevsky, V.V.; Petukhov, A.K.; Börner, H.G.; Baranova, T.A.; Gagarski, A.M.; Petrov, G.A.; Protasov, K.V.; Voronin, A.Y.; Baeßler, S.; Abele, H.; et al. Study of the neutron quantum states in the gravity field. Eur. Phys. J. C 2005, 40, 479–491. [Google Scholar] [CrossRef]
- Westphal, A.; Abele, H.; Baeßler, S.; Nesvizhevsky, V.V.; Protasov, K.V.; Voronin, A.Y. A quantum mechanical description of the experiment on the observation of gravitationally bound states. Eur. Phys. J. C 2007, 51, 367–375. [Google Scholar] [CrossRef]
- Abele, H.; Jenke, T.; Leeb, H.; Schmiedmayer, J. Ramsey’s method of separated oscillating fields and its application to gravitationally induced quantum phase shifts. Phys. Rev. D 2010, 81, 065019. [Google Scholar] [CrossRef]
- Suda, M.; Faber, M.; Bosina, J.; Jenke, T.; Käding, C.; Micko, J.; Pitschmann, M.; Abele, H. Spectra of neutron wave functions in Earth gravitational field. Z. Naturforsch. A 2022, 77, 875–898. [Google Scholar] [CrossRef]
- Jenke, T.; Geltenbort, P.; Lemmel, H.; Abele, H. Realization of a gravity-resonance-spectroscopy technique. Nat. Phys. 2011, 7, 468–472. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Hoedl, S.; Hoyle, C.D.; Kapner, D.J.; Upadhye, A. Particle-Physics Implications of a Recent Test of the Gravitational Inverse-Square Law. Phys. Rev. Lett. 2007, 98, 131104. [Google Scholar] [CrossRef]
- Adelberger, E.; Gundlach, J.; Heckel, B.; Hoedl, S.; Schlamminger, S. Torsion balance experiments: A low-energy frontier of particle physics. Prog. Part. Nucl. Phys. 2009, 62, 102. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.-C.; Khoury, J.; Weltman, A. Detecting dark energy in orbit: The cosmological chameleon. Phys. Rev. D 2004, 70, 123518. [Google Scholar] [CrossRef]
- Mota, D.F.; Shaw, D.J. Evading equivalence principle violations, cosmological, and other experimental constraints in scalar field theories with a strong coupling to matter. Phys. Rev. D 2007, 75, 063501. [Google Scholar] [CrossRef]
- Mota, D.F.; Shaw, D.J. Strongly coupled chameleon fields: New horizons in scalar field theory. Phys. Rev. Lett. 2007, 97, 151102. [Google Scholar] [CrossRef] [PubMed]
- Brax, P.; van de Bruck, C.; Davis, A.-C.; Mota, D.F.; Shaw, D. Detecting chameleons through Casimir force measurements. Phys. Rev. D 2007, 76, 124034. [Google Scholar] [CrossRef]
- Upadhye, A.; Gubser, S.S.; Khoury, J. Unveiling chameleon fields in tests of the gravitational inverse-square law. Phys. Rev. D 2006, 74, 104024. [Google Scholar] [CrossRef]
- Cronenberg, G.; Filter, H.; Thalhammer, M.; Jenke, T.; Abele, H.; Geltenbort, P. A Gravity of Earth Measurement with a qBOUNCE Experiment. arXiv 2015, arXiv:1512.09134. [Google Scholar]
- Hamilton, P.; Jaffe, M.; Haslinger, P.; Simmons, Q.; Müller, H.; Khoury, J. Atom-interferometry constraints on dark energy. Phys. Rev. D 2016, 94, 044051. [Google Scholar] [CrossRef]
- Abele, H.; Jenke, T.; Stadler, D.; Geltenbort, P. QuBounce: The dynamics of ultra-cold neutrons falling in the gravity potential of the Earth. Nucl. Phys. A 2009, 827, 593c–595c. [Google Scholar] [CrossRef]
- Jenke, T.; Stadler, D.; Abele, H.; Geltenbort, P. Q-BOUNCE—Experiments with quantum bouncing ultracold neutrons. Nucl. Instr. Meth. Phys. Res. A 2009, 611, 318. [Google Scholar] [CrossRef]
- Abele, H.; Leeb, H. Gravitation and quantum interference experiments with neutrons. New J. Phys. 2012, 14, 055010. [Google Scholar] [CrossRef]
- Davydov, A.S. Quantum Mechanics; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Neutron Dark Matter Decays. arXiv 2018, arXiv:1806.10107. [Google Scholar]
- Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Neutron dark matter decays and correlation coefficients of neutron β--decays. Nucl. Phys. B 2019, 938, 114–130. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Tests of the standard model in neutron β decay with a polarized neutron and electron and an unpolarized proton. Phys. Rev. C 2018, 98, 035503. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Precision analysis of electron energy spectrum and angular distribution of neutron β− decay with polarized neutron and electron. Phys. Rev. C 2017, 95, 055502, Erratum in Phys. Rev. C 2021, 104, 069901. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Höllwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Zherebtsov, O.M.; Serebrov, A.P. Deficit of reactor antineutrinos at distances smaller than 100 m and inverse β decay. Phys. Rev. C 2013, 88, 055501. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Cronenberg, G.; Höllwieser, R.; Pitschmann, M.; Jenke, T.; Wellenzohn, M.; Abele, H. Exact solution for chameleon field, self-coupled through the Ratra-Peebles potential with n=1 and confined between two parallel plates. Phys. Rev. D 2016, 94, 085005. [Google Scholar] [CrossRef]
- Beringer, J.; Arguin, J.-F.; Barnett, R.M.; Copic, K.; Dahl, O.; Groom, D.E.; Lin, C.-J.; Lys, J.; Murayama, H.; Wohl, C.G.; et al. Review of Particle Physics. Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
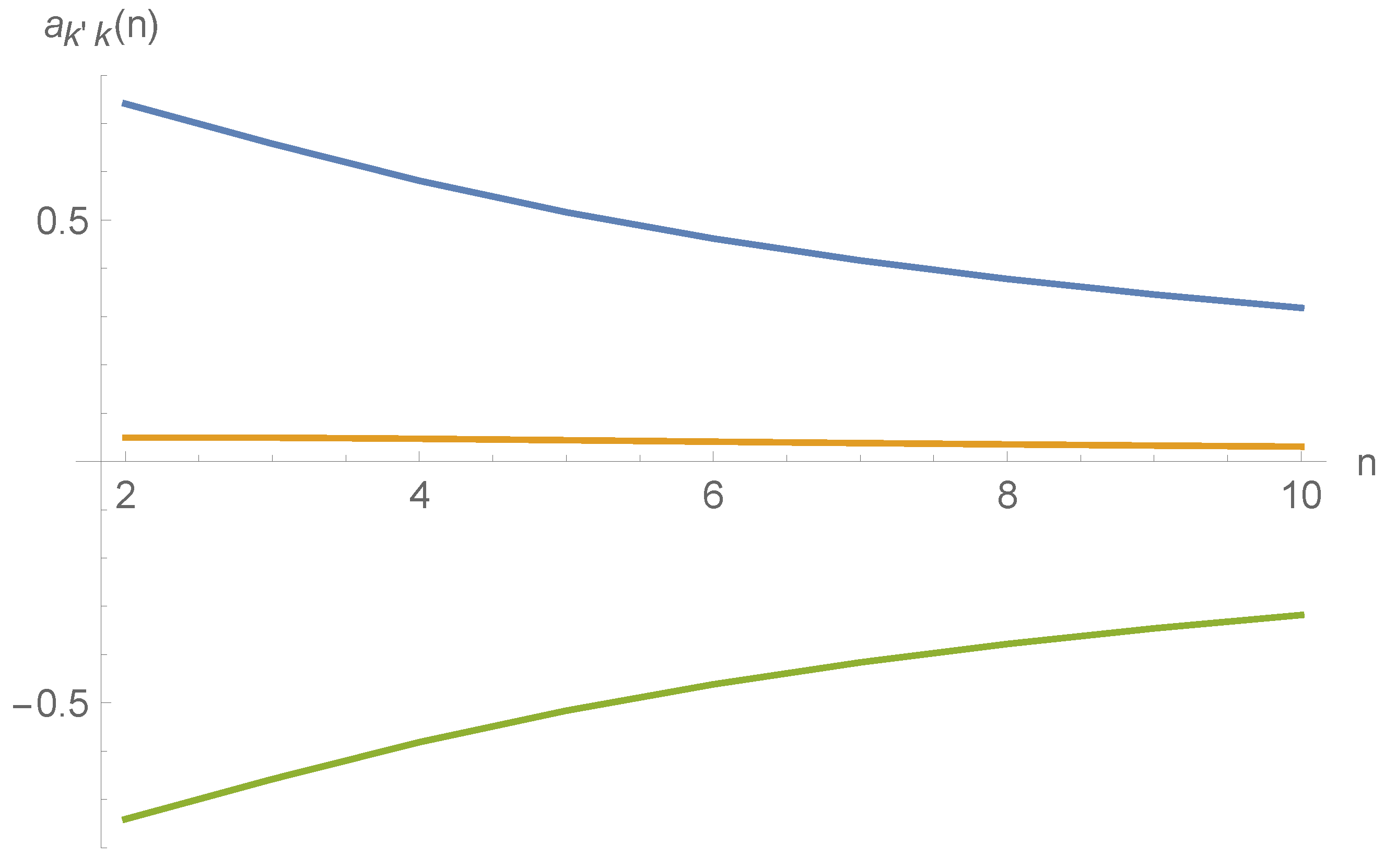

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altarawneh, D.; Höllwieser, R. Ultra-Cold Neutrons in qBounce Experiments as Laboratory for Test of Chameleon Field Theories and Cosmic Acceleration. J. Nucl. Eng. 2025, 6, 20. https://doi.org/10.3390/jne6030020
Altarawneh D, Höllwieser R. Ultra-Cold Neutrons in qBounce Experiments as Laboratory for Test of Chameleon Field Theories and Cosmic Acceleration. Journal of Nuclear Engineering. 2025; 6(3):20. https://doi.org/10.3390/jne6030020
Chicago/Turabian StyleAltarawneh, Derar, and Roman Höllwieser. 2025. "Ultra-Cold Neutrons in qBounce Experiments as Laboratory for Test of Chameleon Field Theories and Cosmic Acceleration" Journal of Nuclear Engineering 6, no. 3: 20. https://doi.org/10.3390/jne6030020
APA StyleAltarawneh, D., & Höllwieser, R. (2025). Ultra-Cold Neutrons in qBounce Experiments as Laboratory for Test of Chameleon Field Theories and Cosmic Acceleration. Journal of Nuclear Engineering, 6(3), 20. https://doi.org/10.3390/jne6030020






