Multiscale Approach of Investigating the Density of Simulated Fuel for a Zero Power Reactor
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
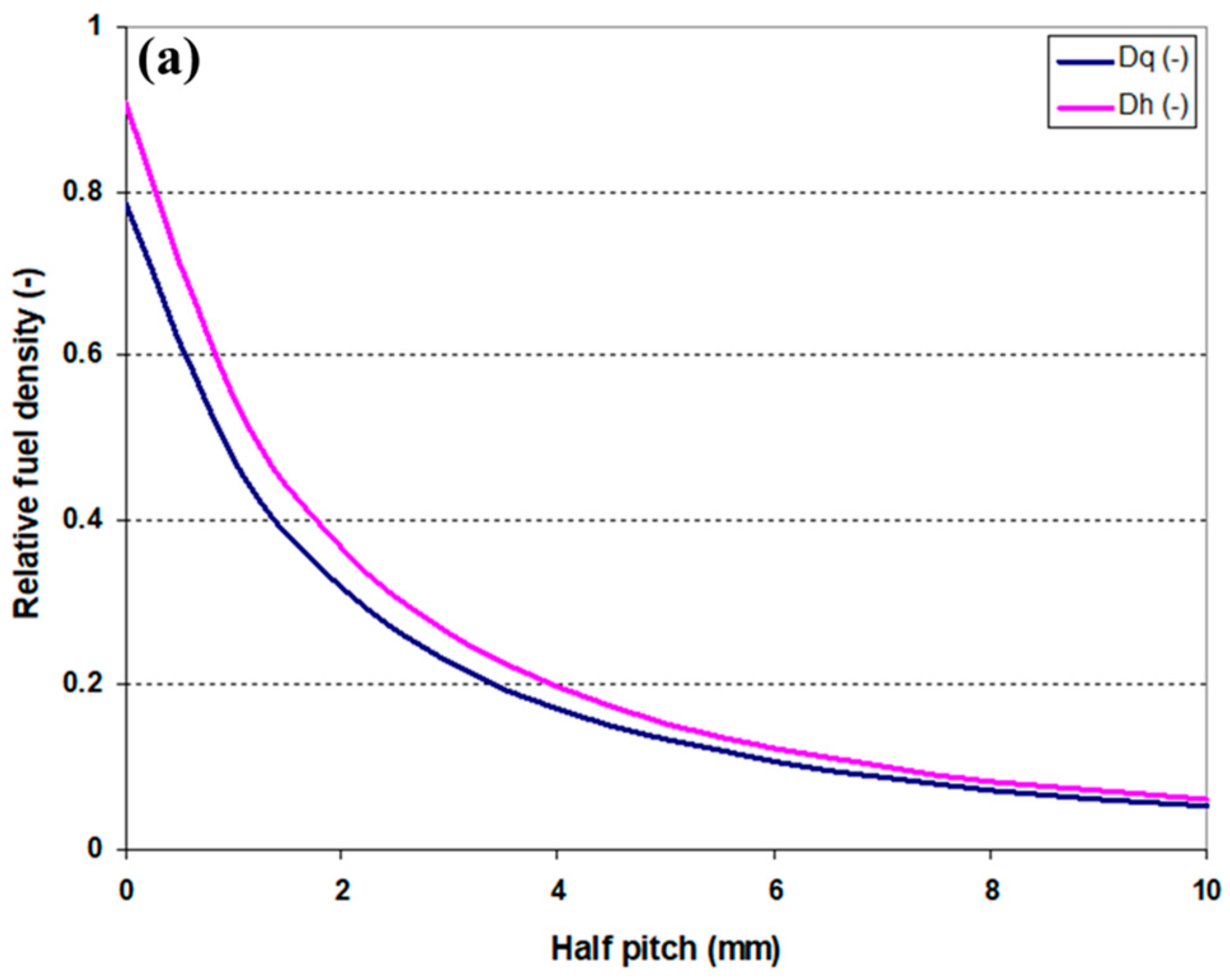
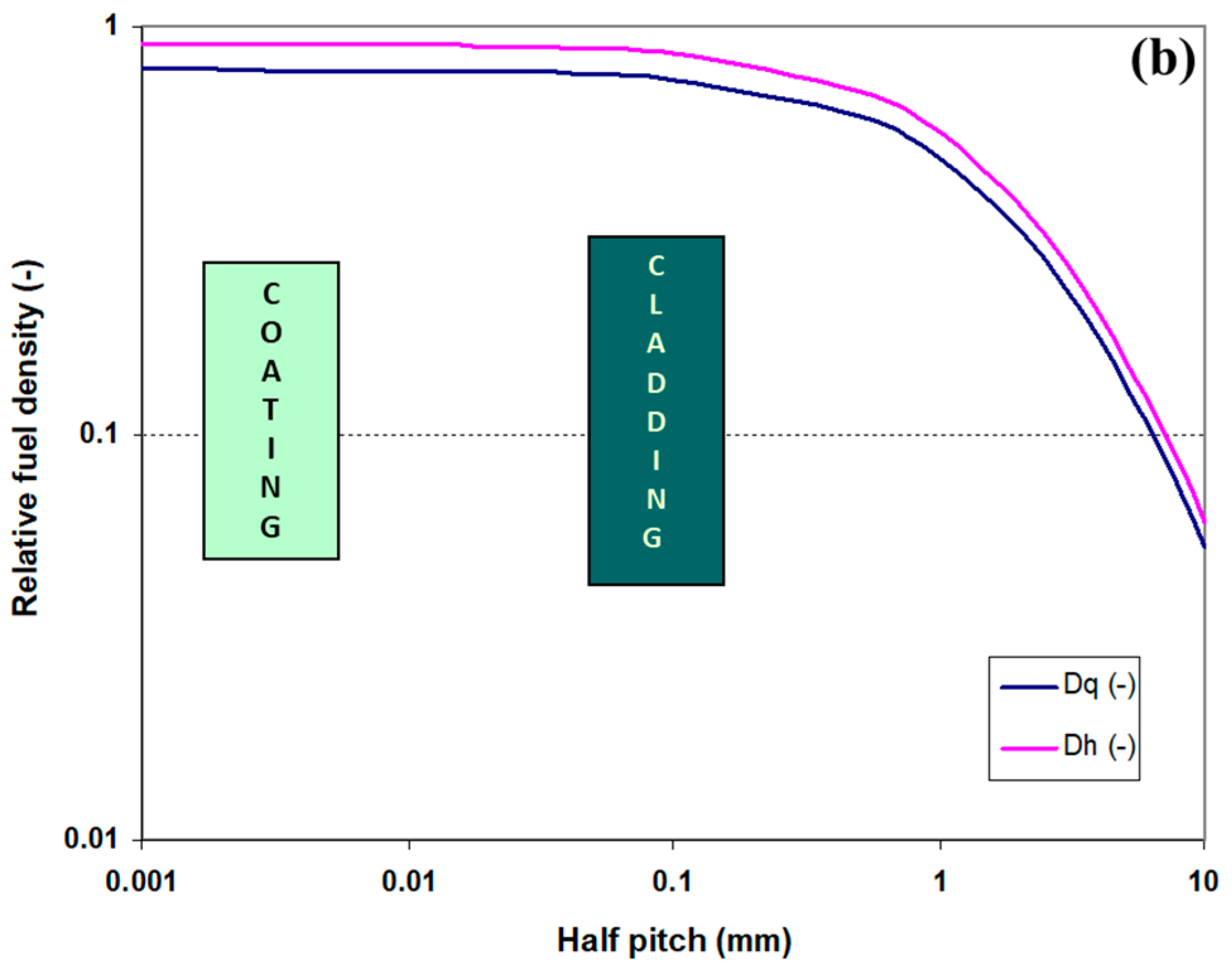
2.1.1. Fuel Element Geometry and Fuel Density in the Core
2.1.2. Geometry and Density of Fuel Pellet
2.1.3. Fuel Grain Density
2.2. Experimental Detail
2.2.1. Salt Mixture Pellet Preparation
2.2.2. Analytical Details
3. Results and Discussion
3.1. Fuel Element Geometry and Fuel Density at the Core Level
3.2. Fuel Pellet Geometry and Fuel Density
3.3. Investigation at the Microscopic Level
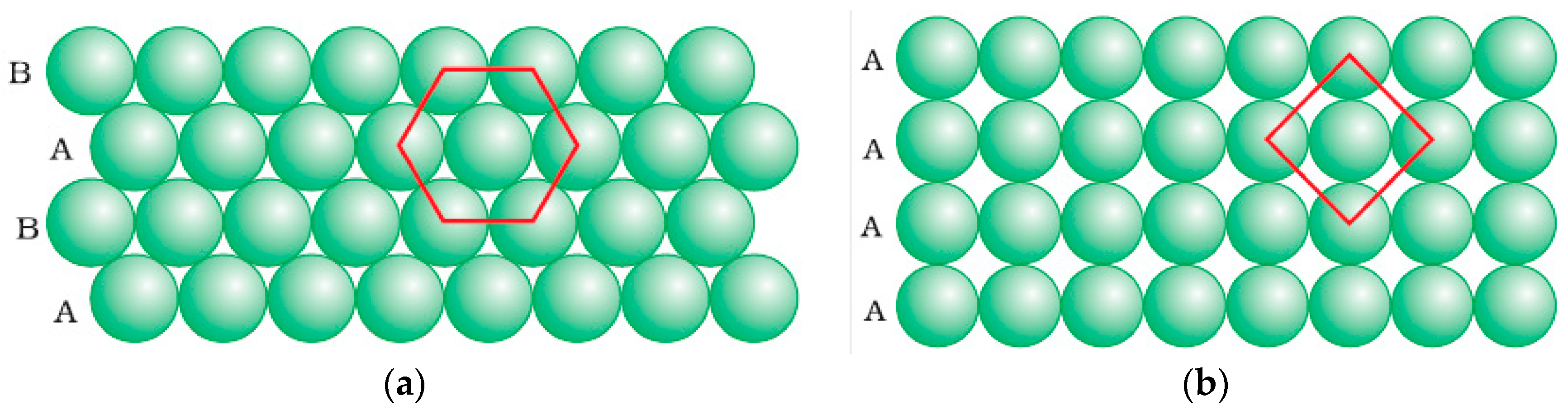
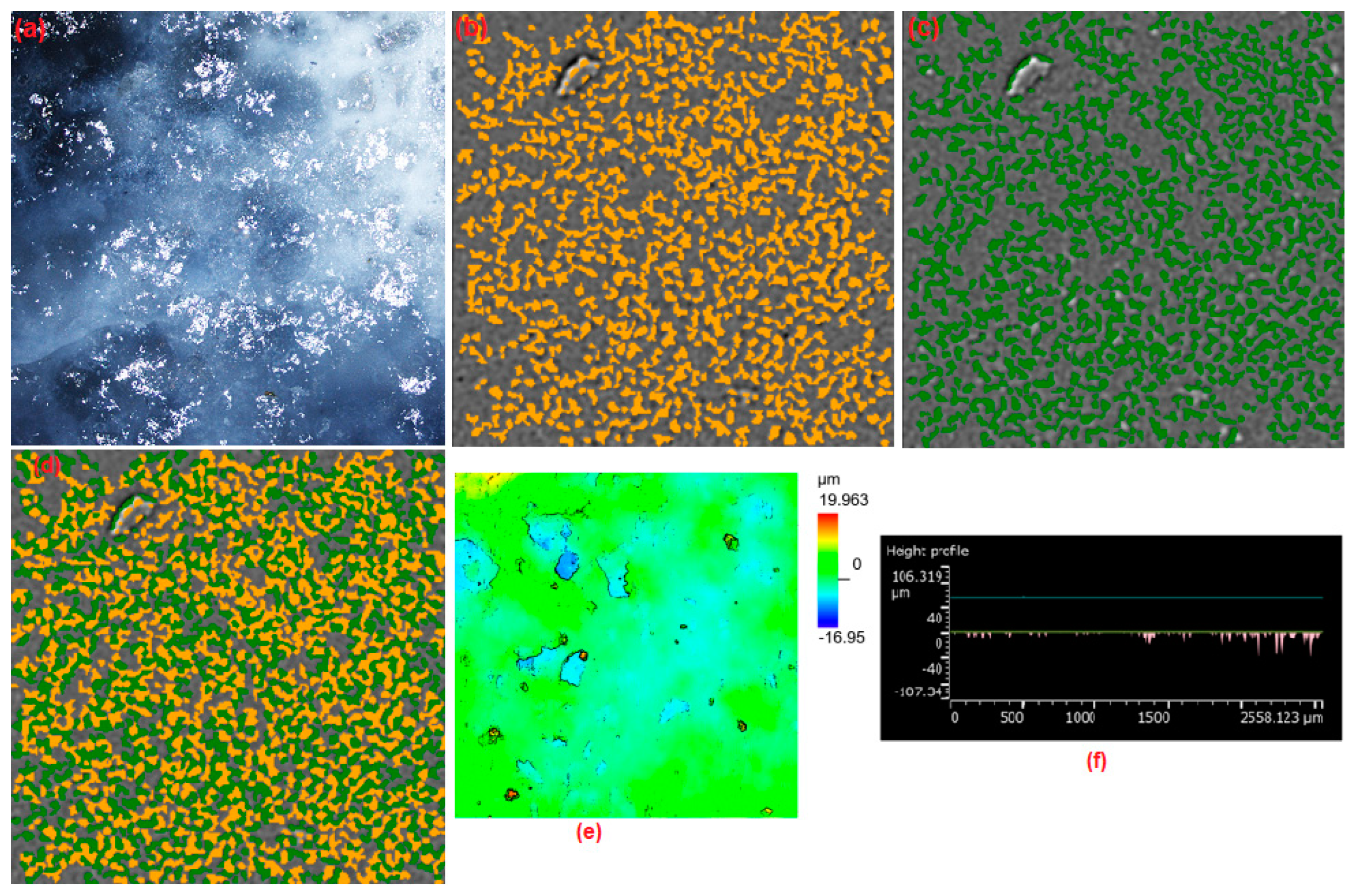
3.3.1. Two-Dimensional (2D) Surface Investigation
3.3.2. 3D Interface Investigation
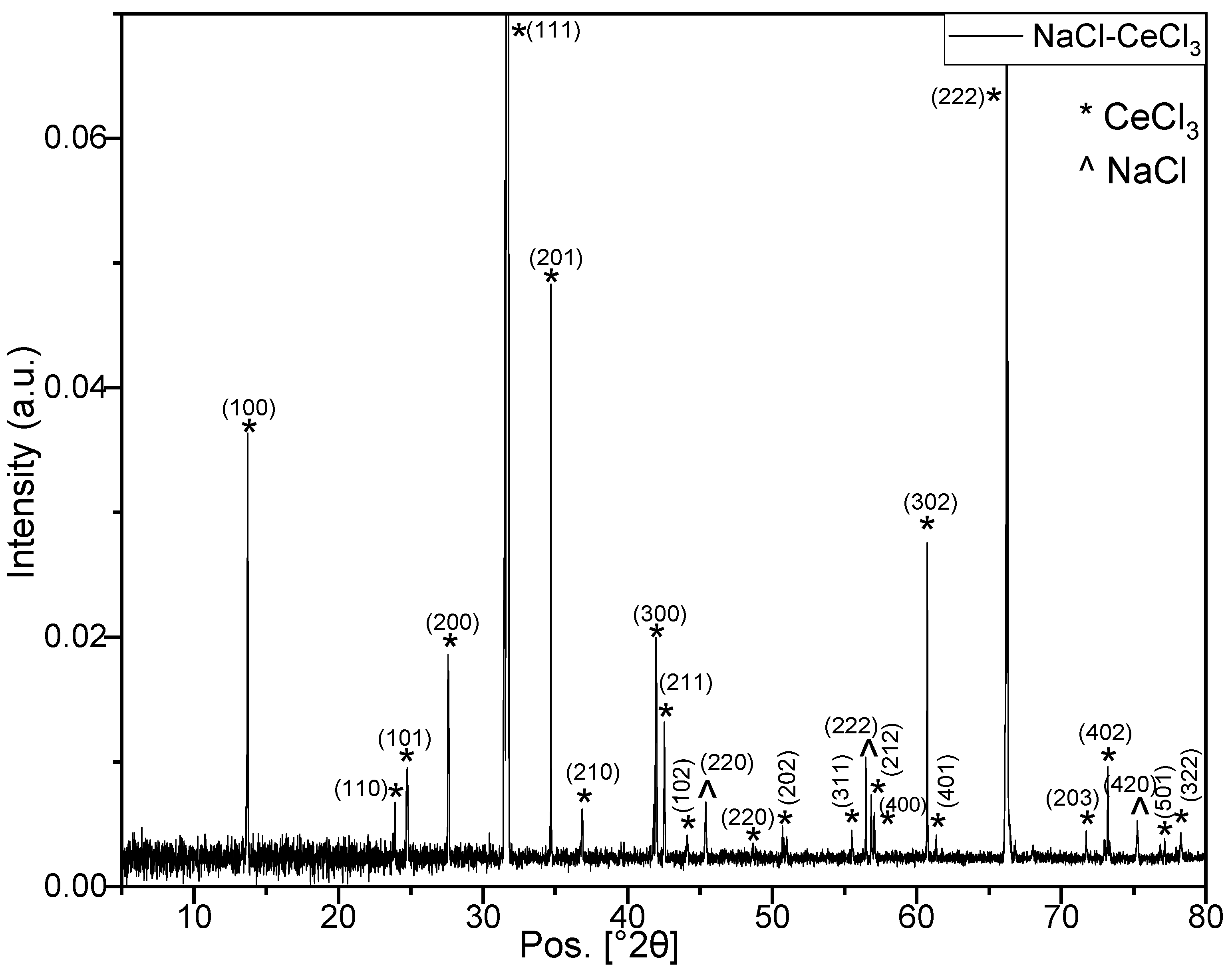
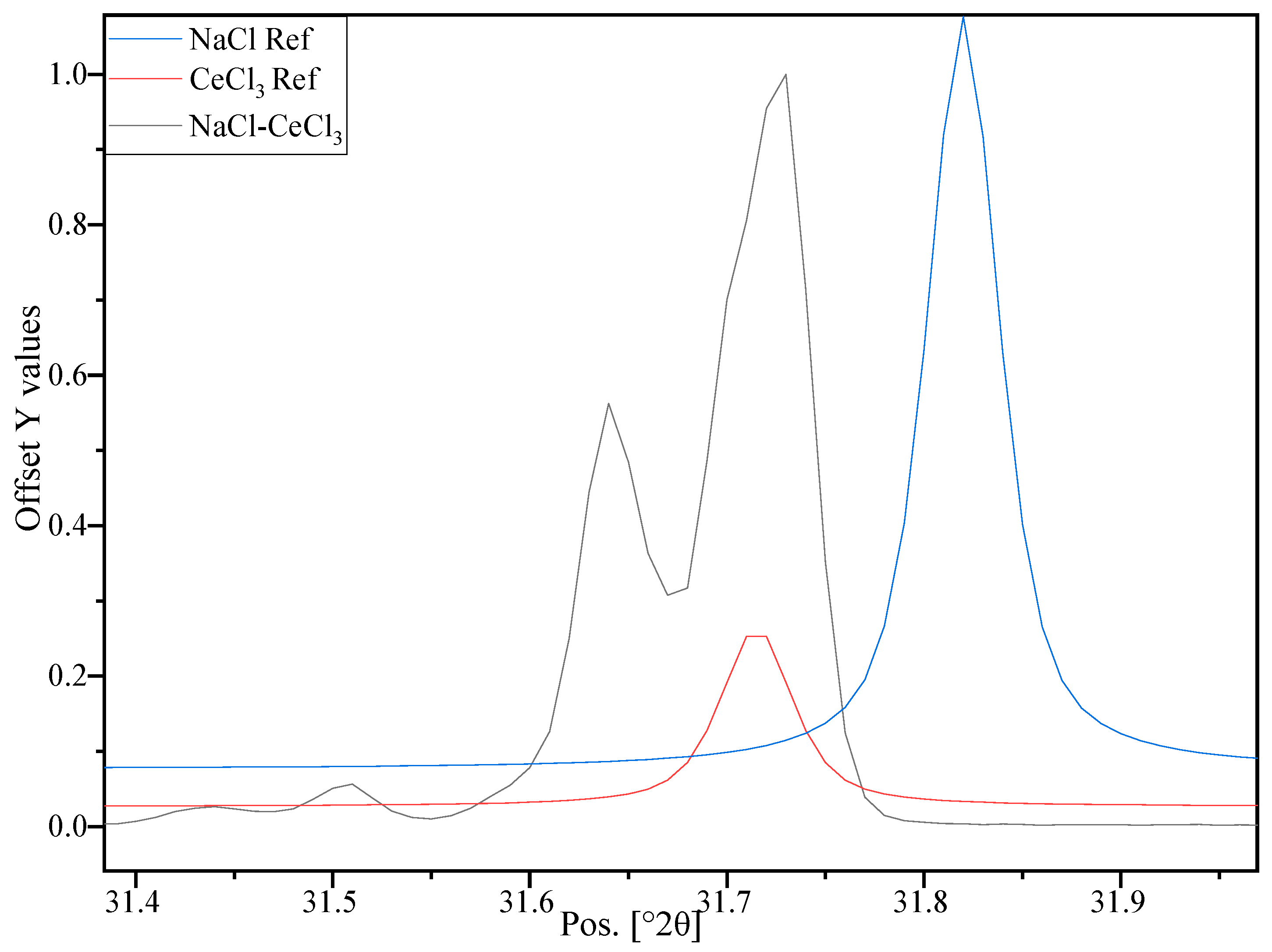
3.4. Investigation at the Nm Level—XRD Investigation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Serp, J.; Allibert, M.; Beneš, O.; Delpech, S.; Feynberg, O.; Ghetta, V.; Heuer, D.; Holcomb, D.; Ignatiev, J.; Kloosterman, L.; et al. The molten salt reactor (MSR) in generation IV: Overview and perspective. Prog. Nucl. Energy 2014, 77, 308–319. [Google Scholar] [CrossRef]
- Merk, B.; Litskevich, D.; Whittle, K.R.; Bankhead, M.; Taylor, R.J.; Mathers, D. On a long term strategy for the success of nuclear power. Energies 2017, 10, 867. [Google Scholar] [CrossRef]
- Merk, B.; Litskevich, D.; Peakman, A.; Bankhead, M. IMAGINE—A disruptive change to nuclear or how can we make more out of the existing spent nuclear fuel and what has to be done to make it possible in the UK? ATW-Int. J. Nucl. Power 2019, 64, 353–359. [Google Scholar]
- Degueldre, C.; Dawson, R.; Najdanovic, V. Nuclear fuel cycle, with a liquid ore and fuel: Toward renewable energy. Sustain. Energy Fuels 2019, 3, 1693–1700. [Google Scholar] [CrossRef]
- Choi, E.-Y.; Jeong, S.M. Electrochemical processing of spent nuclear fuels: An overview of oxide reduction in pyroprocessing technology. Prog. Nat. Sci. 2015, 25, 572–582. [Google Scholar] [CrossRef]
- Uhlir, J.; Straka, M.; Szatmary, L. Development of pyro-processing technology for thorium-fuelled molten salt reactor. In Proceedings of the 2012 International Congress on Advances in Nuclear Power Plants—ICAPP ’12, Chicago, IL, USA, 24–28 June 2012; p. 2799. Available online: www.osti.gov/biblio/22107867 (accessed on 12 September 2024).
- Ren, N.; Wu, Y.; Ma, C.; Song, L. Preparation and thermal properties of quaternary mixed nitrate with low melting point. Sol. Energy Mater. Sol. Cells 2014, 127, 6–13. [Google Scholar] [CrossRef]
- Zhu, H. Rare Earth Metal Production by Molten Salt Electrolysis; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Vahidi, E.; Zhao, F. Assessing the environmental footprint of the production of rare earth metals and alloys via molten salt electrolysis. Resour. Conserv. Recycl. 2018, 139, 178–187. [Google Scholar] [CrossRef]
- Jin, H.; Gu, Q.; Chen, B.; Tang, C.; Zheng, Y.; Zhang, H.; Jaroniec, M.; Qiao, S.-Z. Molten salt-directed catalytic synthesis of 2D layered transition-metal nitrides for efficient hydrogen evolution. Chem 2020, 6, 2382–2394. [Google Scholar] [CrossRef]
- Hu, X.; Hu, Y.; Xu, Q.; Wang, X.; Li, G.; Cheng, H.; Zou, X.; Lu, X. Molten salt-promoted Ni-Fe/Al2O3 catalyst for methane decomposition. Int. J. Hydrogen Energy 2020, 45, 4244–4253. [Google Scholar] [CrossRef]
- Sang, L.; Cai, M.; Ren, N.; Wu, Y.; Burda, C.; Ma, C. Improving the thermal properties of ternary carbonates for concentrating solar power through simple chemical modifications by adding sodium hydroxide and nitrate. Sol. Energy Mater. Sol. Cells 2014, 124, 61–66. [Google Scholar] [CrossRef]
- MacPherson, H.G. The molten salt reactor adventure. Nucl. Sci. Eng. 1985, 90, 374–380. [Google Scholar] [CrossRef]
- Forsberg, C.; Wang, D.; Shwageraus, E.; Mays, B.; Parks, G.; Coyle, C.; Liu, M. Fluoride-salt-cooled high-temperature reactor (FHR) using British advanced gas-cooled reactor (AGR) refuelling technology and decay heat removal systems that prevent salt freezing. Nucl. Technol. 2019, 205, 1127–1142. [Google Scholar] [CrossRef]
- Cisneros, A.T.; Czerwinski, K.; El-dasher, B.S.; Kerlin, W.M.; Kramer, K.; Latkowski, J.F.; Petroski, R.C.; Walter, J.C. Molten Nuclear Fuel Salts and Related Systems and Methods. U.S. Patent US20160189813A1, 30 June 2016. [Google Scholar]
- Advanced Reactors Information System (ARIS), Advances in Small Modular Reactor Technology Developments; Technical Report; IAEA: Vienna, Austria, 2018.
- Merk, B.; Detkina, A.; Litskevich, D.; Patel, M.; Noori-kalkhoran, O.; Cartland-Glover, G.; Efremova, O.; Bankhead, M.; Del Nevo, C.A. A First Step towards Zero Nuclear Waste—Advanced Strategic Thinking in Light of iMAGINE. Energies 2022, 15, 7209. [Google Scholar] [CrossRef]
- Capelli, E.; Bene, O.; Beilmann, M.; Konings, R. Thermodynamic investigation of the LiF-ThF4 system. J. Chem. Thermodyn. 2013, 58, 110–116. [Google Scholar] [CrossRef]
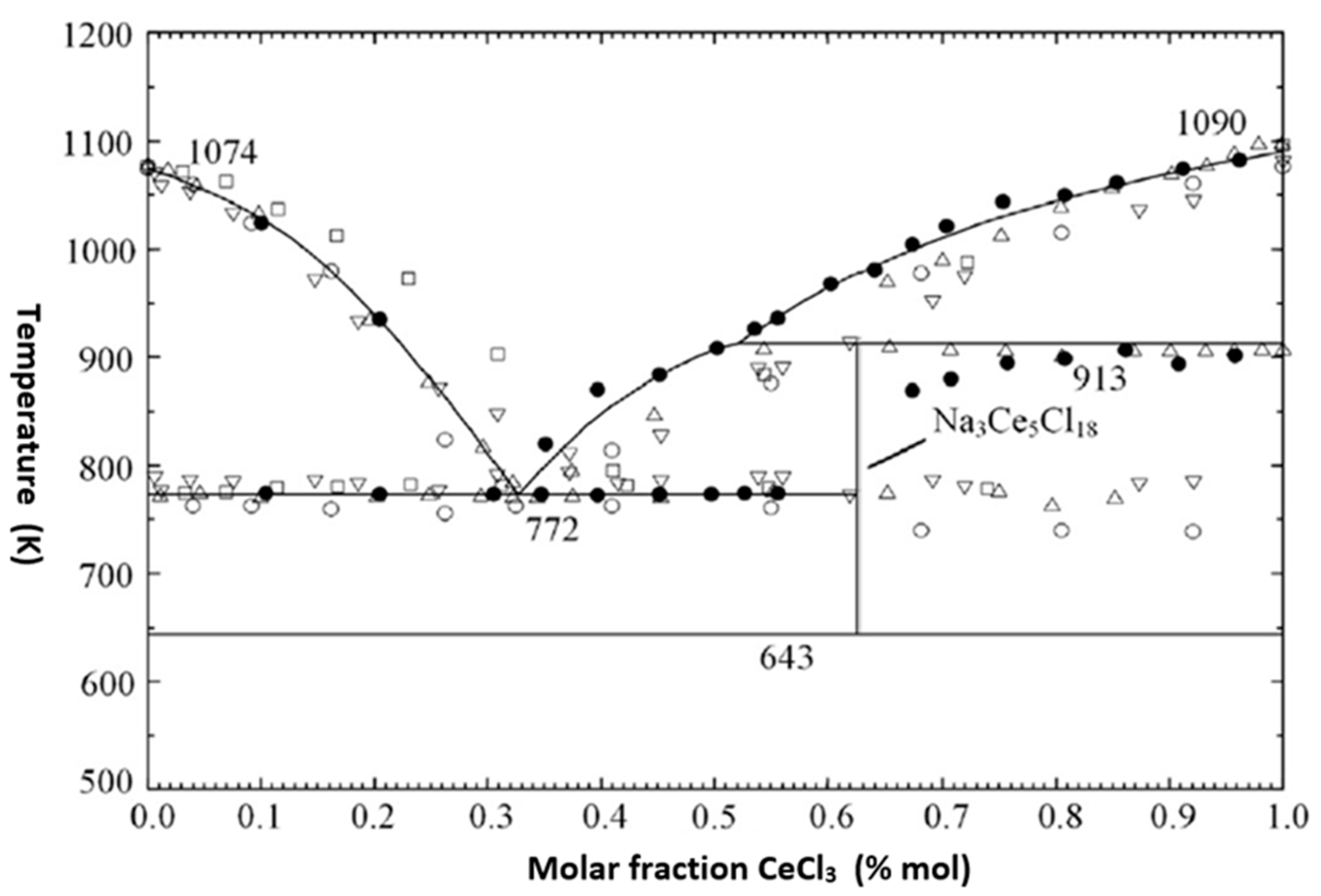
- Lu, G.; Robelin, C.; Chartrand, P.; He, M.; Wang, K. Thermodynamic evaluation and optimization of the (LiCl + NaCl + KCl + MgCl2 + CaCl2 + CeCl3) system. Fluid Phase Equilibria 2019, 487, 83–97. [Google Scholar] [CrossRef]
- Barner, H.E.; Scheuerman, R.V. Handbook of Thermochemical Data for Compounds and Aqueous Species; Wiley-Interscience: New York, NY, USA, 1978. [Google Scholar]
- Chartrand, P.; Sharma, R.; Talley, P.; Pelton, A. Coupled thermodynamic phase diagram optimizations. Calphad 1996, 20, 231–246. [Google Scholar]
- Janz, G.J. Thermodynamic and transport properties for molten salts: Correlation equations for critically evaluated density, surface tension, electrical conductance, and viscosity data. J. Phys. Chem. Ref. Data 1988, 17, 311. [Google Scholar]
- Fredrickson, G.L.; Cao, G.; Gakhar, R.; Yoo, T.-S. Molten Salt Reactor Salt Processing–Technology Status; Technical Report; Idaho National Lab. (INL): Idaho Falls, ID, USA, 2018. [Google Scholar]
- Beneš, O.; Konings, R. 3.13—Molten salt reactor fuel and coolant. In Comprehensive Nuclear Materials; Konings, R.J., Ed.; Elsevier: Oxford, UK, 2012; pp. 359–389. [Google Scholar]
- Mariani, R.D.; Vaden, D. Modeled salt density for nuclear material estimation in the treatment of spent nuclear fuel. J. Nucl. Mater. 2010, 404, 25–32. [Google Scholar] [CrossRef]
- Fermi, E. Experimental Production of a Divergent Chain Reaction. Am. J. Phys. 1952, 20, 536–558. [Google Scholar] [CrossRef]
- Yum, S.; Hursin, M.; Vasiliev, A.; Vinai, P.; Mylonakis, A.G.; Demazière, C.; Macián-Juan, R. Uncertainty analyses of neutron noise simulations in a Zero-Power reactor. Ann. Nucl. Energy 2022, 174, 109157. [Google Scholar] [CrossRef]
- Al-Jaroudi, S.S.; Ul-Hamid, A.; Abdul-Rashid, I.M.; Saner, S. Use of X-ray powder diffraction for quantitative analysis of carbonate rock reservoir samples. Powder Technol. 2007, 175, 115–121. [Google Scholar] [CrossRef]
- Degueldre, C. The Analysis of Nuclear Materials and Their Environment; Springer: Berlin/Heidelberg, Germany, 2017; p. 300. [Google Scholar]




| Pellet Components | Height (mm) | Radius (mm) | Volume (mm3) | Density (g·cm−3) | Mass (g) | Material TD * (g·cm−3) | Porosity (Φ) | Mexp (g) | Pellet Density (g·cm−3) |
|---|---|---|---|---|---|---|---|---|---|
| 70% NaCl | 0.71 (±0.01) | 3.5 (±0.01) | 27.32 (±0.53) | 2.160 | 0.02102 (±0.003) | 3.325 (±0.003) | 0.05 | 0.01997 (±0.003) | 3.16 (±0.29) |
| 30% CeCl3 | 3.970 | 0.06983 (±0.003) | 0.05 | 0.06634 (±0.003) |
| Pellet Components | Height (mm) | Radius (mm) | Volume (mm3) | Mass (g) | Pellet Density (g·cm−3) |
|---|---|---|---|---|---|
| 70% NaCl | 0.71 (±0.01) | 3.5 (±0.01) | 27.32 (±0.53) | 0.028 (±0.003) | 2.855 (±0.280) |
| 30% CeCl3 | 0.050 (±0.003) |
| Pellet Components | Height (mm) | Radius (mm) | Volume (mm3) | Mass (g) | Density (g·cm−3) | Pore Volume (mm3) | Density (g·cm−3) |
|---|---|---|---|---|---|---|---|
| 70% NaCl | 0.71 (±0.01) | 3.50 (±0.01) | 27.32 (±0.53) | 0.028 (±0.003) | 2.855 (±0.280) | 1.329 (±0.05) 2D/SEM | 3.00 (±0.23) |
| 30% CeCl3 | 0.050 (±0.003) | 1.015 (±0.005) 3D/LM | 2.97 (±0.23) |
| Diffraction Angle 2θ (°) ± 0.01 | Component | Miller Indices (hkl) | FWHM (°) ± 0.020 | Crystal Size (nm) ± 20% |
|---|---|---|---|---|
| 13.67 | CeCl3 | (100) | 0.157 | 51 |
| 23.88 | CeCl3 | (110) | 0.181 | 45 |
| 24.72 | CeCl3 | (101) | 0.151 | 54 |
| 27.55 | CeCl3 | (200) | 0.144 | 57 |
| 31.71 | CeCl3 | (111) | 0.096 | 86 |
| 34.74 | CeCl3 | (201) | 0.146 | 57 |
| 45.41 | NaCl | (220) | 0.113 | 76 |
| Level | Theoretical/Material | Fuel in Core/Assembly | Geometrical Density/Pellet | 2D SEM/Pellet | 3D LM/Pellet | XRD/Grains | |
|---|---|---|---|---|---|---|---|
| Parameter | |||||||
| Density (g·cm−3) | 3.325 | # 3.016 | 2.855 ± 0.28 | 2.51 ± 0.05 | 2.54 ± 0.05 | 3.13 ± 0.08 | |
| * 3.001 ± 0.23 | * 2.965 ± 0.23 | ||||||
| Relative density (%) | 100.00 | # 90.7 | 85 ± 8.5 | 75.5 ± 2.0 | 76.4 ± 2.0 | 94.1 ± 3.0 ° | |
| * 90.3 ± 7.0 | * 89.2 ± 7.0 | ||||||
| Porosity/void fraction (%) | 0.00 | # 9.3 | 15.0 ± 8.5 | 24.5 ± 2.0 | 23.6 ± 2.0 | 5.9 ± 3.0 | |
| * 9.7 ± 7.0 | * 10.8 ± 7.0 | ||||||
| Size Object | dm | cm | mm | µm | µm | nm | |
| Bulk | Core | Pellet | Surface | Interface | Grain | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sardar, S.; Degueldre, C.; Green, S. Multiscale Approach of Investigating the Density of Simulated Fuel for a Zero Power Reactor. J. Nucl. Eng. 2024, 5, 420-435. https://doi.org/10.3390/jne5030026
Sardar S, Degueldre C, Green S. Multiscale Approach of Investigating the Density of Simulated Fuel for a Zero Power Reactor. Journal of Nuclear Engineering. 2024; 5(3):420-435. https://doi.org/10.3390/jne5030026
Chicago/Turabian StyleSardar, Suneela, Claude Degueldre, and Sarah Green. 2024. "Multiscale Approach of Investigating the Density of Simulated Fuel for a Zero Power Reactor" Journal of Nuclear Engineering 5, no. 3: 420-435. https://doi.org/10.3390/jne5030026
APA StyleSardar, S., Degueldre, C., & Green, S. (2024). Multiscale Approach of Investigating the Density of Simulated Fuel for a Zero Power Reactor. Journal of Nuclear Engineering, 5(3), 420-435. https://doi.org/10.3390/jne5030026






