Figure 1.
(Left) General schematic of simulated configurations. (Right) Measurement configuration with three sources and 10 cm of concrete between the sources and the detector.
Figure 1.
(Left) General schematic of simulated configurations. (Right) Measurement configuration with three sources and 10 cm of concrete between the sources and the detector.
Figure 2.
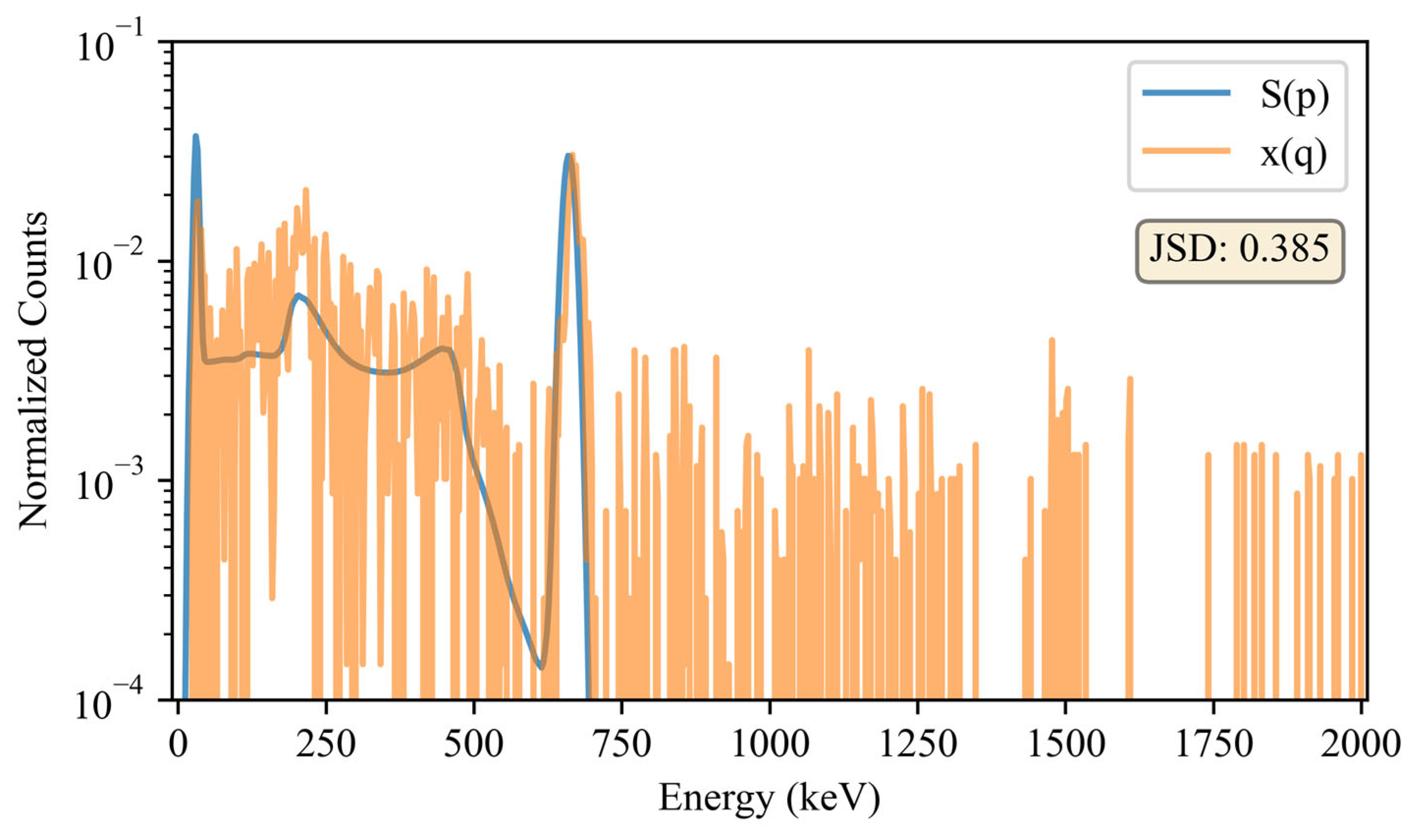
Visual comparison of the seed, , and sample, for a 137Cs source. This is one of the 10,000 baseline comparisons for 137Cs. It should be noted that counts from in the 662 keV photopeak are comparable to that of the seed, thus making it difficult to visualize the sample in this region. Also, counts with energies above the 137Cs photopeak may be attributed to pile-up and statistical uncertainties inherent in background subtraction, which was only employed for the dissimilarity calculations.
Figure 2.
Visual comparison of the seed, , and sample, for a 137Cs source. This is one of the 10,000 baseline comparisons for 137Cs. It should be noted that counts from in the 662 keV photopeak are comparable to that of the seed, thus making it difficult to visualize the sample in this region. Also, counts with energies above the 137Cs photopeak may be attributed to pile-up and statistical uncertainties inherent in background subtraction, which was only employed for the dissimilarity calculations.
Figure 3.
Baseline comparisons between the seeds, and samples, of the reference configuration. The mean line represents , while the error bars represent . These values are considered “baselines” as they will contextualize the eventual JSD comparisons between and .
Figure 3.
Baseline comparisons between the seeds, and samples, of the reference configuration. The mean line represents , while the error bars represent . These values are considered “baselines” as they will contextualize the eventual JSD comparisons between and .
Figure 4.
The average and standard deviation values for the seed-to-sample comparisons for both the and comparisons for each source (top). These comparisons were leveraged to calculate the dissimilarity measures for each isotope (bottom). The asterisk denotes the reference configuration where no domain shifts exist between the training and testing data.
Figure 4.
The average and standard deviation values for the seed-to-sample comparisons for both the and comparisons for each source (top). These comparisons were leveraged to calculate the dissimilarity measures for each isotope (bottom). The asterisk denotes the reference configuration where no domain shifts exist between the training and testing data.
Figure 5.
F1-scores for each isotope are color-coded for the four algorithms under evaluation. Predictions were made on the reference configuration where there are no domain shifts. A narrow view of the F1-scores is leveraged in this figure to enhance the interpretability of the overlapping markers. However, most other figures will provide a y-axis range of 0–1.
Figure 5.
F1-scores for each isotope are color-coded for the four algorithms under evaluation. Predictions were made on the reference configuration where there are no domain shifts. A narrow view of the F1-scores is leveraged in this figure to enhance the interpretability of the overlapping markers. However, most other figures will provide a y-axis range of 0–1.
Figure 6.
Visual comparison of the 137Cs seed, , where is the reference configuration and a 137Cs sample , where is the configuration with a standoff distance of 50 cm. Counts with energies above the 137Cs photopeak are unlikely to be attributed to pile-up but rather statistical uncertainties inherent in background subtraction, which was only employed for the dissimilarity calculations.
Figure 6.
Visual comparison of the 137Cs seed, , where is the reference configuration and a 137Cs sample , where is the configuration with a standoff distance of 50 cm. Counts with energies above the 137Cs photopeak are unlikely to be attributed to pile-up but rather statistical uncertainties inherent in background subtraction, which was only employed for the dissimilarity calculations.
Figure 7.
Dissimilarity values for the configurations with varying standoff distances. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison.
Figure 7.
Dissimilarity values for the configurations with varying standoff distances. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison.
Figure 8.
F1-scores and dissimilarity values for the 26 isotopes under varying standoff configurations. The different marker shapes represent the various configurations for the testing datasets, and the color of the markers denotes the algorithm. The asterisk indicates the reference configuration. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 8.
F1-scores and dissimilarity values for the 26 isotopes under varying standoff configurations. The different marker shapes represent the various configurations for the testing datasets, and the color of the markers denotes the algorithm. The asterisk indicates the reference configuration. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 9.
F1-scores and dissimilarity values averaged over all isotopes for each algorithm and standoff distance configuration. The different marker shapes represent the configurations for the testing datasets, and the marker colors denote the algorithms. The asterisk indicates the reference configuration. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 9.
F1-scores and dissimilarity values averaged over all isotopes for each algorithm and standoff distance configuration. The different marker shapes represent the configurations for the testing datasets, and the marker colors denote the algorithms. The asterisk indicates the reference configuration. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
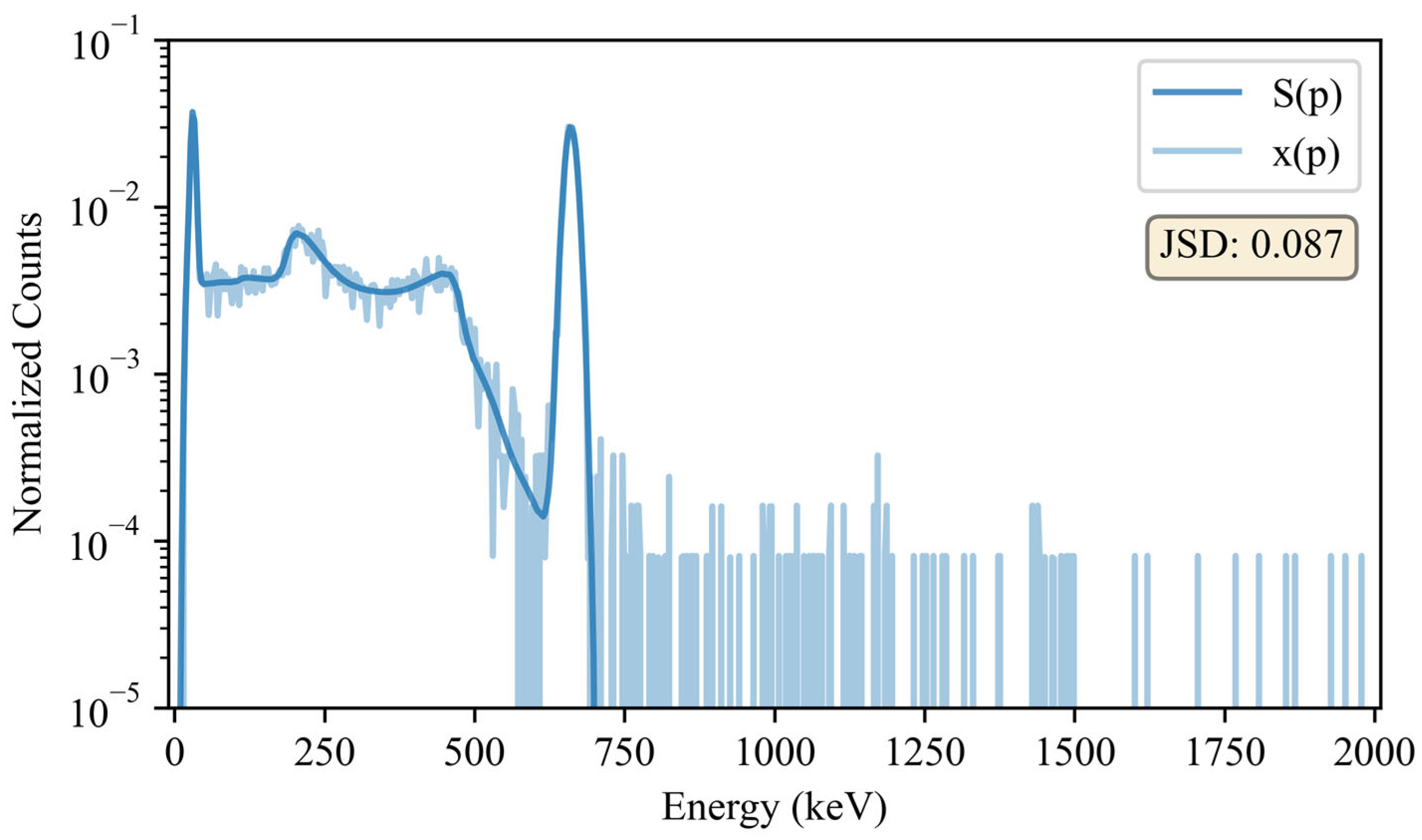
Figure 10.
Visual comparison of the 137Cs seed, , where is the reference configuration, and a 137Cs sample, , where is the configuration with shielding (AD: 10 g/cm2, AN: 20). Counts with energies above the 137Cs photopeak are unlikely to be attributed to pile-up but rather statistical uncertainties inherent in background subtraction, which was only employed for the dissimilarity calculations.
Figure 10.
Visual comparison of the 137Cs seed, , where is the reference configuration, and a 137Cs sample, , where is the configuration with shielding (AD: 10 g/cm2, AN: 20). Counts with energies above the 137Cs photopeak are unlikely to be attributed to pile-up but rather statistical uncertainties inherent in background subtraction, which was only employed for the dissimilarity calculations.
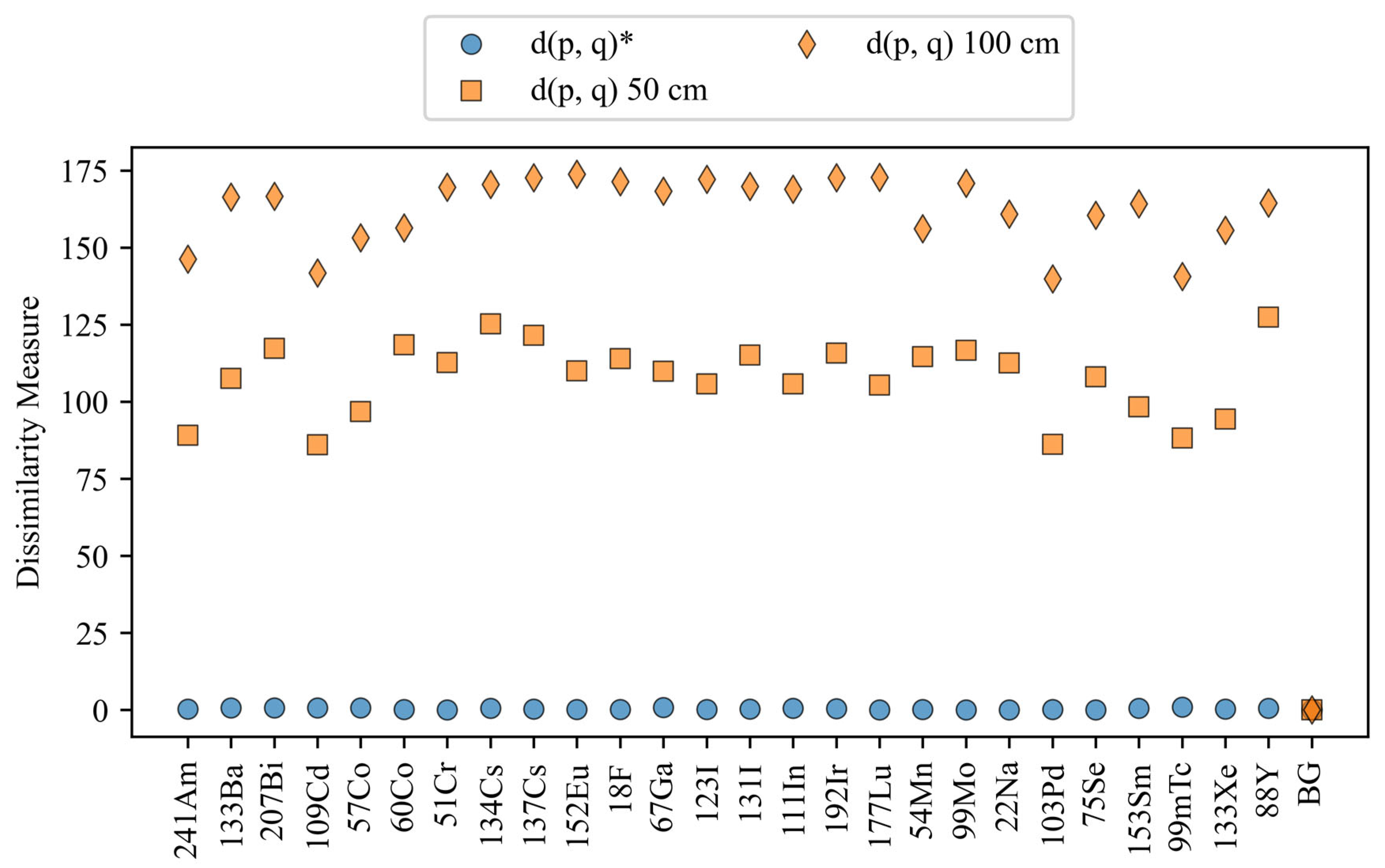
Figure 11.
Dissimilarity values for the configurations with varying shielding. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison. The different markers denote the various configurations.
Figure 11.
Dissimilarity values for the configurations with varying shielding. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison. The different markers denote the various configurations.
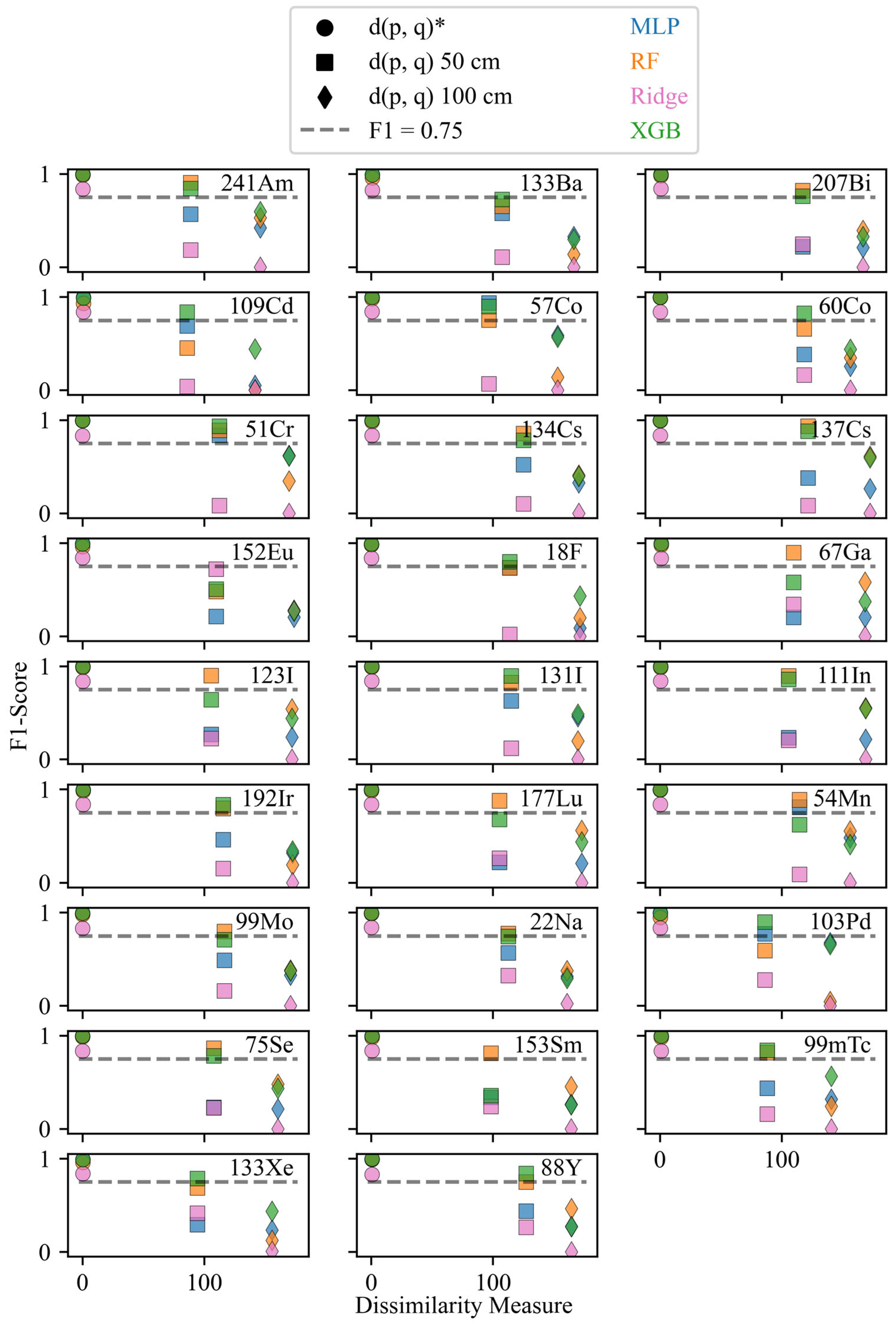
Figure 12.
F1-scores for the 26 isotopes under varying shielding configurations. The different marker shapes represent the various configurations for the testing datasets, and the marker colors denote the algorithms. The asterisk indicates the reference configuration. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 12.
F1-scores for the 26 isotopes under varying shielding configurations. The different marker shapes represent the various configurations for the testing datasets, and the marker colors denote the algorithms. The asterisk indicates the reference configuration. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 13.
Averaged F1-scores and dissimilarity values of the 26 isotopes under varying shielding configurations. The different marker shapes represent the various configurations for the testing datasets, and the marker colors denote the algorithms. The reference configuration is denoted by the asterisks. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 13.
Averaged F1-scores and dissimilarity values of the 26 isotopes under varying shielding configurations. The different marker shapes represent the various configurations for the testing datasets, and the marker colors denote the algorithms. The reference configuration is denoted by the asterisks. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 14.
Visual comparison of the background (BG) seed where is the reference configuration and a BG sample where is the configuration with a background resembling Washington, DC, USA.
Figure 14.
Visual comparison of the background (BG) seed where is the reference configuration and a BG sample where is the configuration with a background resembling Washington, DC, USA.
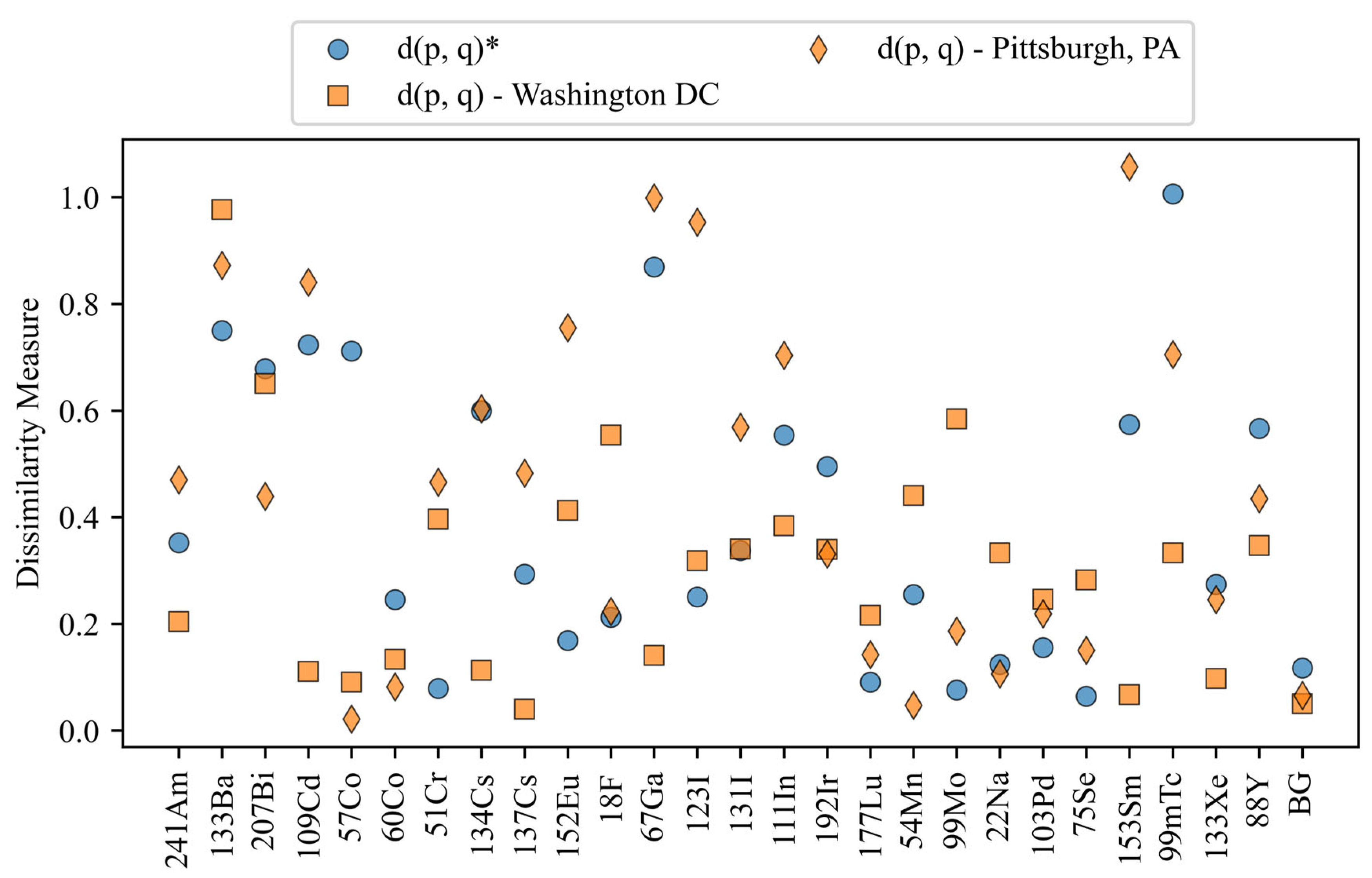
Figure 15.
Dissimilarity values for the configurations with varying backgrounds. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison. The different markers denote the different configurations. The asterisk indicates the reference configuration.
Figure 15.
Dissimilarity values for the configurations with varying backgrounds. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison. The different markers denote the different configurations. The asterisk indicates the reference configuration.
Figure 16.
F1-scores and dissimilarity values of the 26 isotopes under varying background configurations. The different marker shapes represent the various configurations for the testing datasets, and the marker colors denote the algorithms. The reference configuration is denoted by the asterisk. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 16.
F1-scores and dissimilarity values of the 26 isotopes under varying background configurations. The different marker shapes represent the various configurations for the testing datasets, and the marker colors denote the algorithms. The reference configuration is denoted by the asterisk. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 17.
Averaged F1-scores and dissimilarity values averaged over all isotopes for each algorithm and shielding configuration. The different marker shapes represent the different configurations for the testing datasets, and the marker colors denote the algorithms. The reference configuration is denoted by the asterisk. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 17.
Averaged F1-scores and dissimilarity values averaged over all isotopes for each algorithm and shielding configuration. The different marker shapes represent the different configurations for the testing datasets, and the marker colors denote the algorithms. The reference configuration is denoted by the asterisk. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 18.
Visual comparison of the 137Cs seed, , where is the reference configuration and a 137Cs sample, , where is the measured configuration with a standoff distance of 10 cm. Counts with energies above the 137Cs photopeak are unlikely to be attributed to pile-up; rather, statistical uncertainties inherent in background subtraction were only employed for the dissimilarity calculations.
Figure 18.
Visual comparison of the 137Cs seed, , where is the reference configuration and a 137Cs sample, , where is the measured configuration with a standoff distance of 10 cm. Counts with energies above the 137Cs photopeak are unlikely to be attributed to pile-up; rather, statistical uncertainties inherent in background subtraction were only employed for the dissimilarity calculations.
Figure 19.
Dissimilarity values for the configurations with measured data. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison. The different markers denote the various configurations.
Figure 19.
Dissimilarity values for the configurations with measured data. The blue circles represent the dissimilarity values for the reference configuration, and the orange markers are all of the configurations under comparison. The different markers denote the various configurations.
Figure 20.
F1-scores and dissimilarity values for the four measured sources and their corresponding configurations. The different marker shapes represent the configurations for the testing datasets, and the marker colors denotes the algorithm. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 20.
F1-scores and dissimilarity values for the four measured sources and their corresponding configurations. The different marker shapes represent the configurations for the testing datasets, and the marker colors denotes the algorithm. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 21.
Averaged F1-scores and dissimilarity values for the four measured sources and their corresponding configurations. The different marker shapes represent the configurations for the testing datasets, and the marker colors denote the algorithm. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 21.
Averaged F1-scores and dissimilarity values for the four measured sources and their corresponding configurations. The different marker shapes represent the configurations for the testing datasets, and the marker colors denote the algorithm. A dotted line at F1 = 0.75 was included as a visual reference for the performance.
Figure 22.
The markers represent F1-scores averaged over all 26 sources at the eight simulated configurations for their respective algorithms. The box plots depict the mean values (center line), interquartile range (box), and min/max values (whiskers).
Figure 22.
The markers represent F1-scores averaged over all 26 sources at the eight simulated configurations for their respective algorithms. The box plots depict the mean values (center line), interquartile range (box), and min/max values (whiskers).
Figure 23.
The markers represent F1-scores averaged over the four measured sources (133Ba, 60Co, 137Cs, 152Eu) for all twelve configurations for their respective algorithms. The box plots depict the mean values (center line), interquartile range (box), and min/max values (whiskers).
Figure 23.
The markers represent F1-scores averaged over the four measured sources (133Ba, 60Co, 137Cs, 152Eu) for all twelve configurations for their respective algorithms. The box plots depict the mean values (center line), interquartile range (box), and min/max values (whiskers).
Figure 24.
The markers represent F1-scores averaged over the four measured sources (133Ba, 60Co, 137Cs, 152Eu) at the four measured configurations for their respective algorithms. The box plots depict the mean values (center line), interquartile range (box), and min/max values (whiskers).
Figure 24.
The markers represent F1-scores averaged over the four measured sources (133Ba, 60Co, 137Cs, 152Eu) at the four measured configurations for their respective algorithms. The box plots depict the mean values (center line), interquartile range (box), and min/max values (whiskers).
Table 1.
Sources and activities (in µCi) used for the simulated data.
Table 1.
Sources and activities (in µCi) used for the simulated data.
| Source | Activity (µCi) | Source | Activity (µCi) |
|---|
| 241Am | 4.86 | 133Ba | 0.90 |
| 207Bi | 1.04 | 109Cd | 3.37 |
| 57Co | 2.04 | 60Co | 2.04 |
| 51Cr | 25.0 | 134Cs | 1.47 |
| 137Cs | 3.46 | 152Eu | 1.26 |
| 18F | 1.47 | 67Ga | 2.38 |
| 123I | 1.86 | 131I | 2.40 |
| 111In | 0.95 | 192Ir | 1.13 |
| 177Lu | 8.96 | 54Mn | 3.62 |
| 99Mo | 8.54 | 22Na | 1.13 |
| 103Pd | 8.69 | 75Se | 1.23 |
| 153Sm | 2.10 | 99mTc | 2.22 |
| 133Xe | 2.43 | 88Y | 2.05 |
Table 2.
Sources and activities (in µCi) used for the measured data.
Table 2.
Sources and activities (in µCi) used for the measured data.
| Source | Activity (µCi) | Source | Activity (µCi) |
|---|
| 133Ba | 0.34 | 60Co | 0.12 |
| 137Cs | 0.17 | 152Eu | 0.43 |
Table 3.
Training and testing measurement configurations. Simulations are denoted by “Sim”, measurements are denoted by “Meas”, AD represents the areal density for the shielding, and AN stands for the atomic number. Note that all configurations utilize the same LaBr3 IdentiFINDER detector and a live time of 30 s.
Table 3.
Training and testing measurement configurations. Simulations are denoted by “Sim”, measurements are denoted by “Meas”, AD represents the areal density for the shielding, and AN stands for the atomic number. Note that all configurations utilize the same LaBr3 IdentiFINDER detector and a live time of 30 s.
| Train/Test | Sim./Meas. | Dist. (cm) | Shielding | Background | # of Spectra | # of Counts ± IQR |
|---|
| Train | Sim. | 10 | None | Albuquerque, NM, USA | 200,000 | 13,668.2 ± 158.0 |
| Test | Sim. | 10 | None | Albuquerque, NM, USA | 50,000 | 13,667.2 ± 158.0 |
| Test | Sim. | 50 | None | Albuquerque, NM, USA | 50,000 | 2138.0 ± 62.0 |
| Test | Sim. | 100 | None | Albuquerque, NM, USA | 50,000 | 1683.3 ± 56.0 |
| Test | Sim. | 10 | AD: 5 g/cm2 AN: 6 | Albuquerque, NM, USA | 50,000 | 12,189.2 ± 149.0 |
| Test | Sim. | 10 | AD: 5 g/cm2 AN: 20 | Albuquerque, NM, USA | 50,000 | 9253.7 ± 130.0 |
| Test | Sim. | 10 | AD: 10 g/cm2 AN: 20 | Albuquerque, NM, USA | 50,000 | 7839.2 ± 119.0 |
| Test | Sim. | 10 | None | Washington, DC, USA | 50,000 | 13,668.8 ± 158.0 |
| Test | Sim. | 10 | None | Pittsburgh, PA, USA | 50,000 | 13,667.8 ± 158.0 |
| Test | Meas. | 10 | None | Fort Belvoir, VA, USA | 140 | 6997.6 ± 1773.8 |
| Test | Meas. | 50 | None | Fort Belvoir, VA, USA | 140 | 1709.00 ± 149.5 |
| Test | Meas. | 10 | 10 cm Concrete | Fort Belvoir, VA, USA | 140 | 3756.8 ± 1674.5 |
| Test | Meas. | 10 | 1 cm Lead-Pig | Fort Belvoir, VA, USA | 140 | 2521.3 ± 1085.8 |
Table 4.
Algorithms and some of their parameters for multi-isotope identification. These algorithms were all implemented in a one-vs-rest configuration with the referenced Python libraries and their corresponding default parameters.
Table 4.
Algorithms and some of their parameters for multi-isotope identification. These algorithms were all implemented in a one-vs-rest configuration with the referenced Python libraries and their corresponding default parameters.
| Classifiers | Parameters |
|---|
| Ridge Linear Model (Ridge) [32] | Alpha: 0.001 |
| Random Forest (RF) [32] | Criterion: Gini, n_estimators: 100 |
| Extreme Gradient Boosting (XGB) [33] | Objective: Binary logistic |
| Multilayer Perceptron (MLP) [32] | Solver: ADAM, Activation Function: ReLu, Hidden Layers: (512) |
Table 5.
Averaged F1-scores (over 26 sources) for the eight simulated configurations.
Table 5.
Averaged F1-scores (over 26 sources) for the eight simulated configurations.
| Configuration | MLP | RF | Ridge | XGB |
|---|
| Reference configuration | 0.995 | 0.979 | 0.837 | 0.995 |
| Standoff: 50 cm | 0.477 | 0.780 | 0.202 | 0.763 |
| Standoff: 100 cm | 0.312 | 0.351 | 0.012 | 0.434 |
| Shielding—AD: 5 gm/cm2, AN: 6 | 0.598 | 0.925 | 0.670 | 0.905 |
| Shielding—AD: 5 gm/cm2, AN: 20 | 0.480 | 0.752 | 0.658 | 0.737 |
| Shielding—AD: 10 gm/cm2, AN: 20 | 0.423 | 0.716 | 0.546 | 0.693 |
| Background—Washington, DC, USA | 0.995 | 0.979 | 0.837 | 0.995 |
| Background—Pittsburgh, PA, USA | 0.995 | 0.979 | 0.837 | 0.995 |
Table 6.
Wilcoxon signed-rank test results from
Table 5.
Table 6.
Wilcoxon signed-rank test results from
Table 5.
| Algorithm1 | MLP vs. | MLP vs. | MLP vs. | RF vs. | RF vs. | Ridge vs. |
|---|
| Algorithm2 | RF | Ridge | XGB | Ridge | XGB | XGB |
|---|
| Statistic | 6.0 | 9.0 | 6.0 | 0.0 | 17.0 | 0.0 |
| p-Value | 0.109375 | 0.25 | 0.109375 | 0.007813 | 0.945313 | 0.007813 |
| Reject null at 95.5% confidence? | No | No | No | Yes | No | Yes |
| Reject null at 99.0% confidence? | No | No | No | Yes | No | Yes |
| Reject null at 99.7% confidence? | No | No | No | No | No | No |
Table 7.
Averaged F1-scores for the four measured sources (133Ba, 60Co, 137Cs, 152Eu) for the twelve measured and simulated configurations.
Table 7.
Averaged F1-scores for the four measured sources (133Ba, 60Co, 137Cs, 152Eu) for the twelve measured and simulated configurations.
| Configuration | MLP | RF | Ridge | XGB |
|---|
| Reference configuration | 0.995 | 0.978 | 0.836 | 0.994 |
| Standoff: 50 cm | 0.387 | 0.681 | 0.267 | 0.733 |
| Standoff: 100 cm | 0.264 | 0.342 | 0.070 | 0.401 |
| Shielding—AD: 5 gm/cm2, AN: 6 | 0.783 | 0.952 | 0.639 | 0.976 |
| Shielding—AD: 5 gm/cm2, AN: 20 | 0.503 | 0.533 | 0.619 | 0.634 |
| Shielding—AD: 10 gm/cm2, AN: 20 | 0.427 | 0.533 | 0.499 | 0.627 |
| Background—Washington DC, USA | 0.994 | 0.978 | 0.838 | 0.994 |
| Background—Pittsburgh, PA, USA | 0.995 | 0.979 | 0.839 | 0.994 |
| Standoff—10 cm (measured) | 0.791 | 0.962 | 0.680 | 0.946 |
| Standoff—50 cm (measured) | 0.696 | 0.554 | 0.167 | 0.699 |
| Shielding—Concrete (measured) | 0.700 | 0.590 | 0.151 | 0.716 |
| Shielding—Lead pig (measured) | 0.669 | 0.626 | 0.403 | 0.666 |
Table 8.
Wilcoxon signed-rank test results from
Table 7.
Table 8.
Wilcoxon signed-rank test results from
Table 7.
| Algorithm1 | MLP vs. | MLP vs. | MLP vs. | RF vs. | RF vs. | Ridge vs. |
|---|
| Algorithm2 | RF | Ridge | XGB | Ridge | XGB | XGB |
|---|
| Statistic | 28.0 | 4.0 | 10.0 | 2.0 | 2.0 | 0.0 |
| p-Value | 0.423828 | 0.003418 | 0.020996 | 0.001465 | 0.001465 | 0.000488 |
| Reject null at 95.5% confidence? | No | Yes | Yes | Yes | Yes | Yes |
| Reject null at 99.0% confidence? | No | Yes | No | Yes | Yes | Yes |
| Reject null at 99.7% confidence? | No | No | No | Yes | Yes | Yes |
Table 9.
Averaged F1-scores (over the four measured sources (133Ba, 60Co, 137Cs, 152Eu) for the four measured configurations.
Table 9.
Averaged F1-scores (over the four measured sources (133Ba, 60Co, 137Cs, 152Eu) for the four measured configurations.
| Configuration | MLP | RF | Ridge | XGB |
|---|
| Standoff—10 cm (measured) | 0.791 | 0.962 | 0.680 | 0.946 |
| Standoff—50 cm (measured) | 0.696 | 0.554 | 0.167 | 0.699 |
| Shielding—Concrete (measured) | 0.700 | 0.590 | 0.151 | 0.716 |
| Shielding—Lead pig (measured) | 0.669 | 0.626 | 0.403 | 0.666 |
Table 10.
Wilcoxon signed-rank test results from
Table 9.
Table 10.
Wilcoxon signed-rank test results from
Table 9.
| Algorithm1 | MLP vs. | MLP vs. | MLP vs. | RF vs. | RF vs. | Ridge vs. |
|---|
| Algorithm2 | RF | Ridge | XGB | Ridge | XGB | XGB |
|---|
| Statistic | 4.0 | 0.0 | 1.0 | 0.0 | 1.0 | 0.0 |
| p-Value | 0.875 | 0.125 | 0.25 | 0.125 | 0.25 | 0.125 |
| Reject null at 95.5% confidence? | No | No | No | No | No | No |
| Reject null at 99.0% confidence? | No | No | No | No | No | No |
| Reject null at 99.7% confidence? | No | No | No | No | No | No |