Evaluation of δ-Phase ZrH1.4 to ZrH1.7 Thermal Neutron Scattering Laws Using Ab Initio Molecular Dynamics Simulations
Abstract
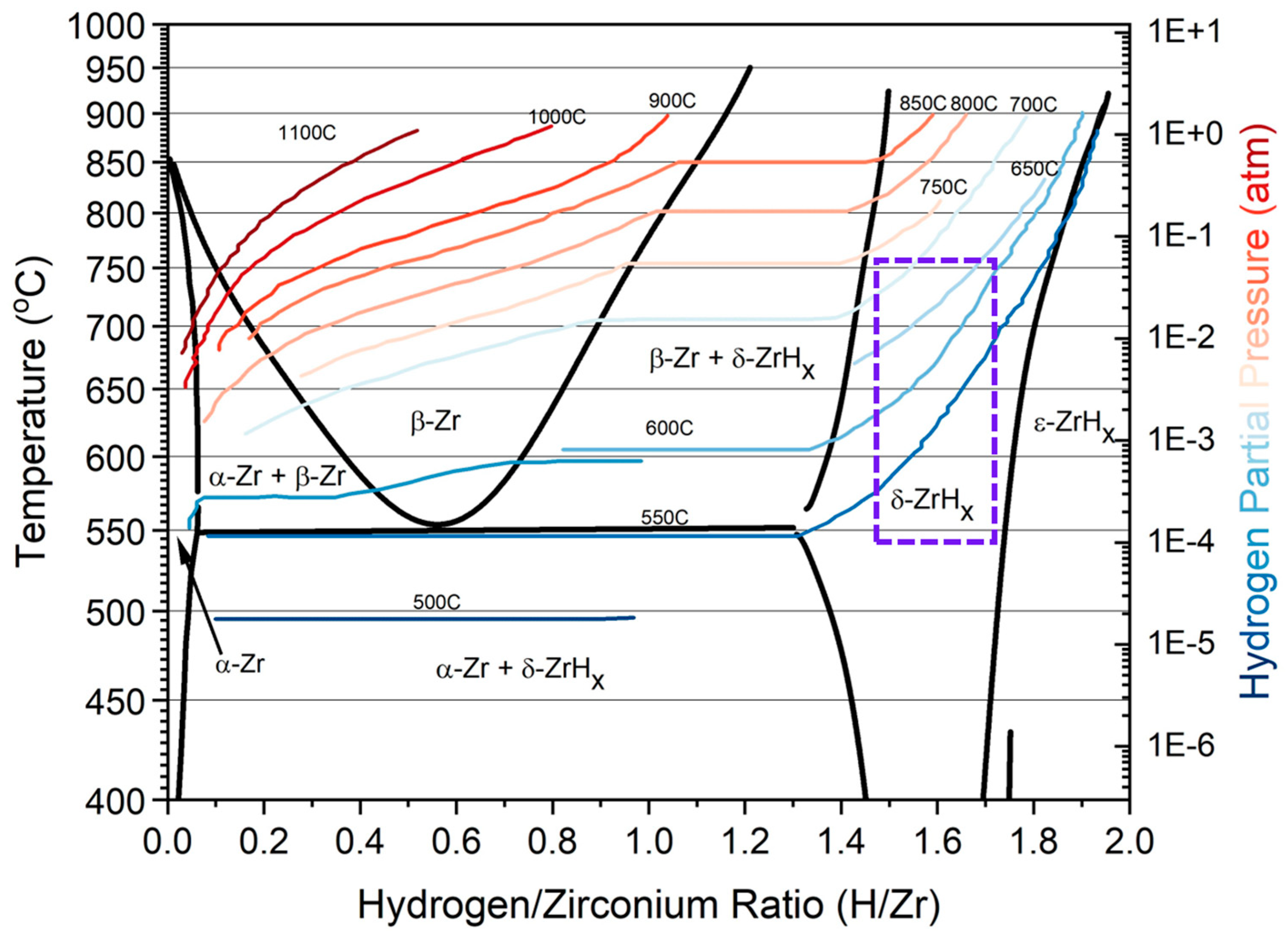
1. Introduction
2. Computational Methods
2.1. Atomic Scale Simulations
2.2. Thermal Scattering Law or S(α,β)
3. Results and Discussion
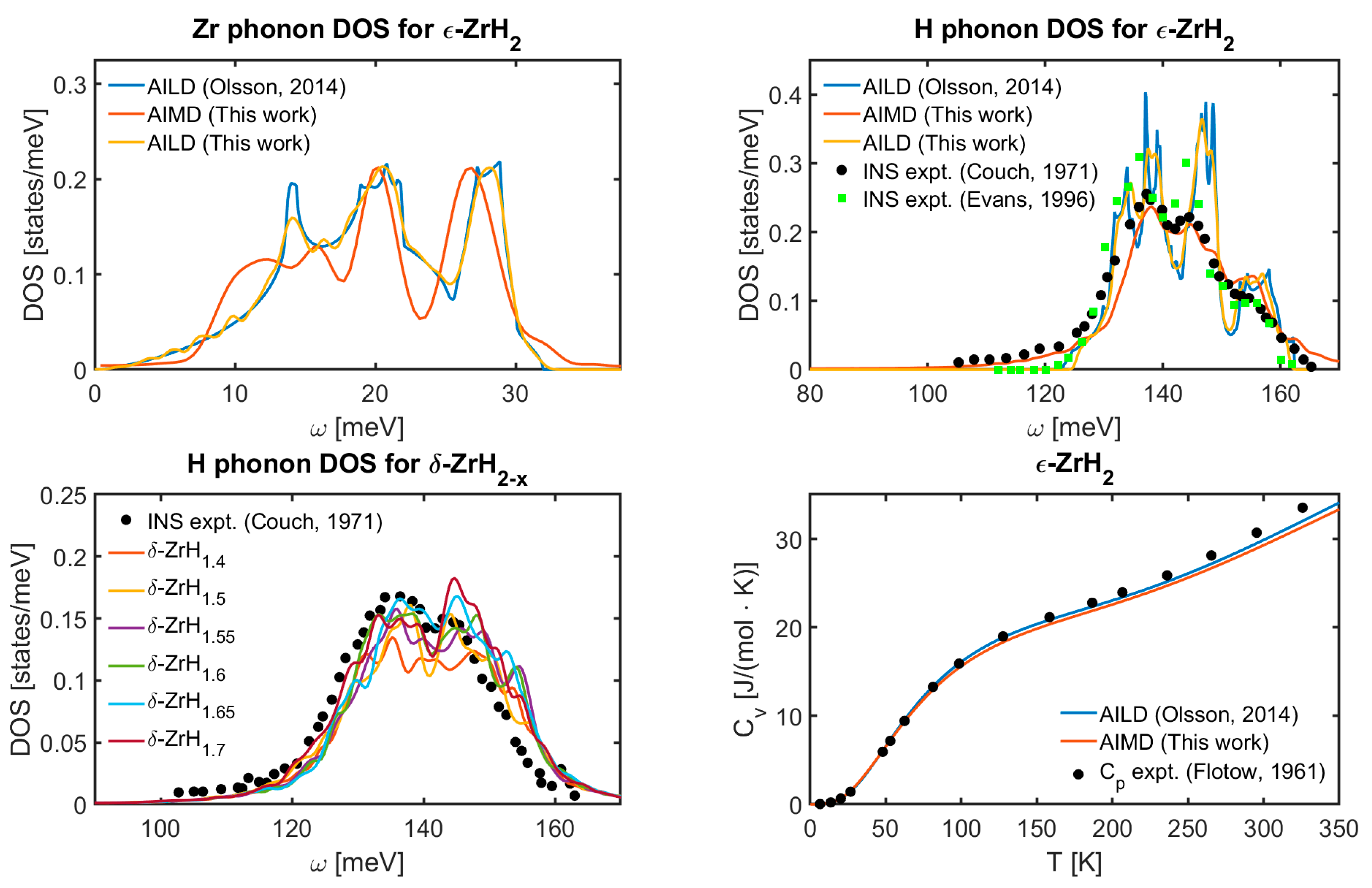
3.1. Phonon DOS
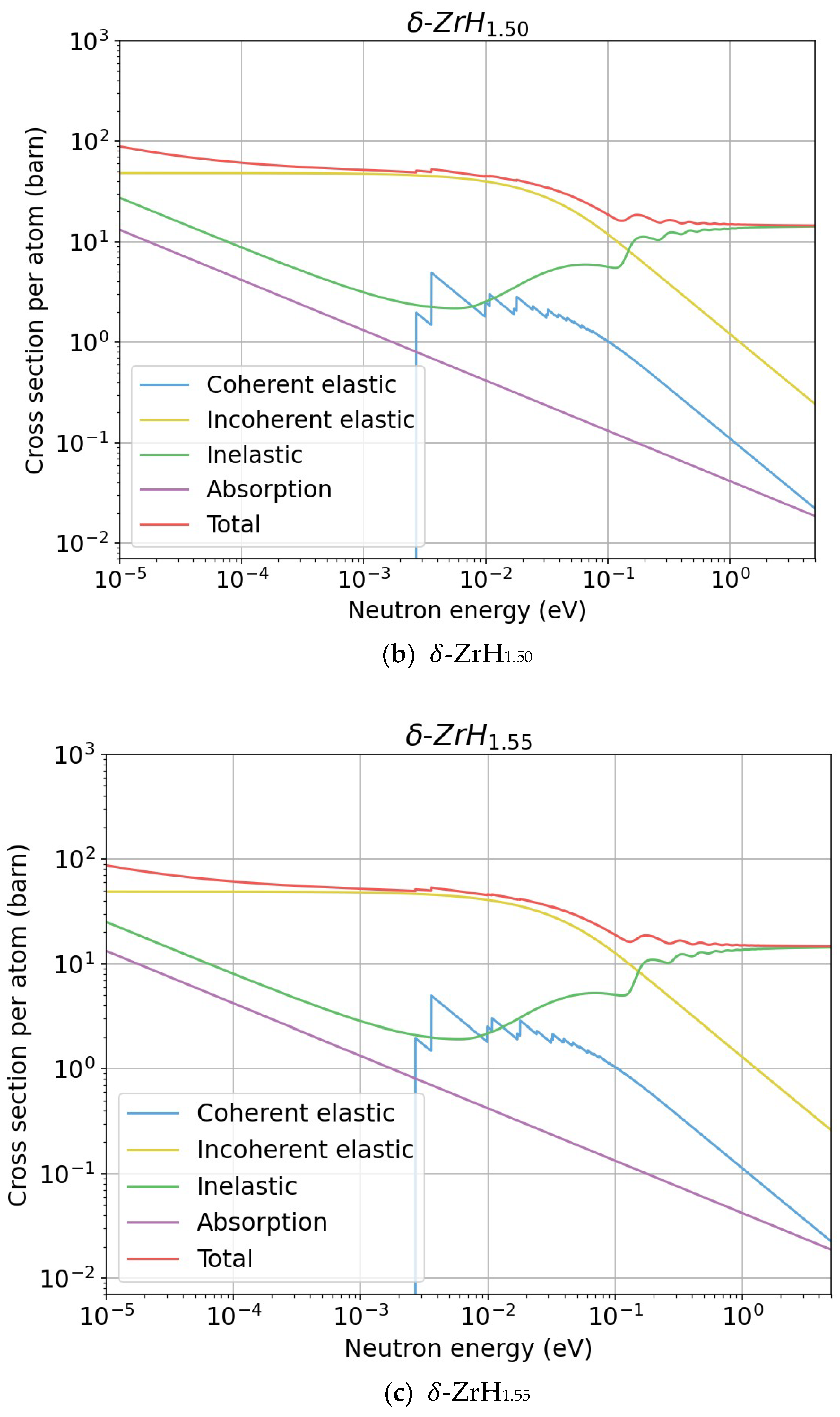
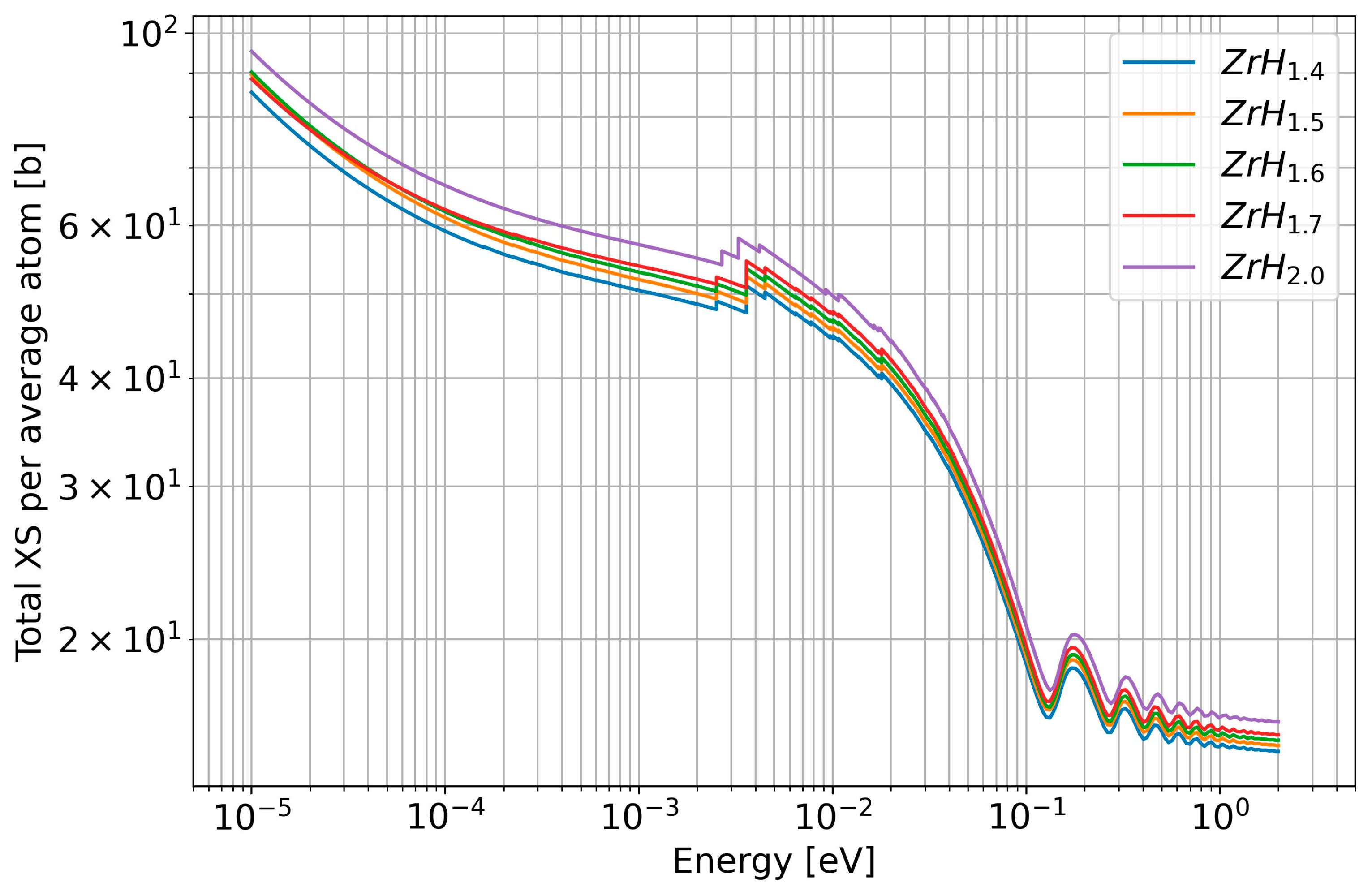
3.2. Thermal Scattering Laws (TSLs)
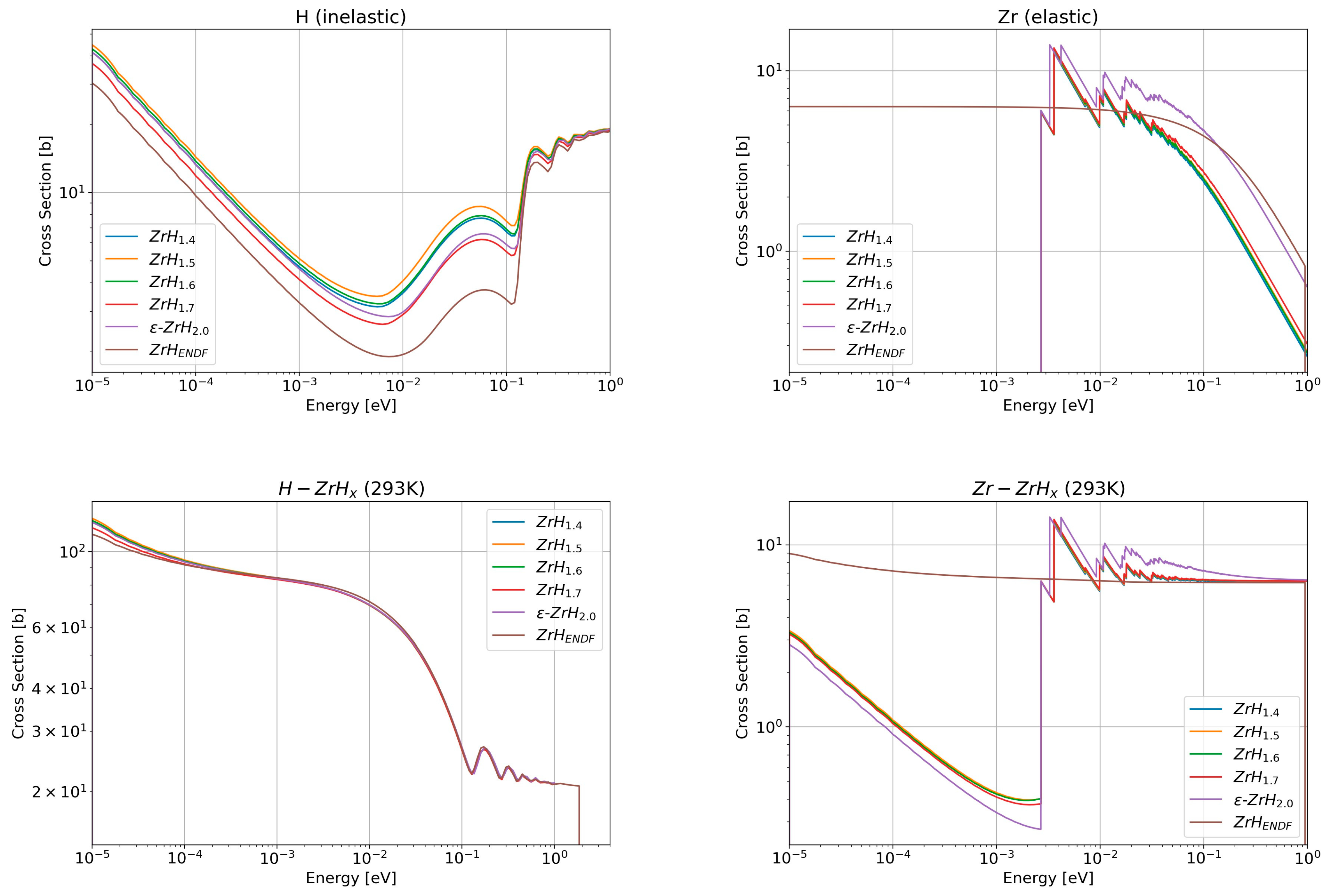
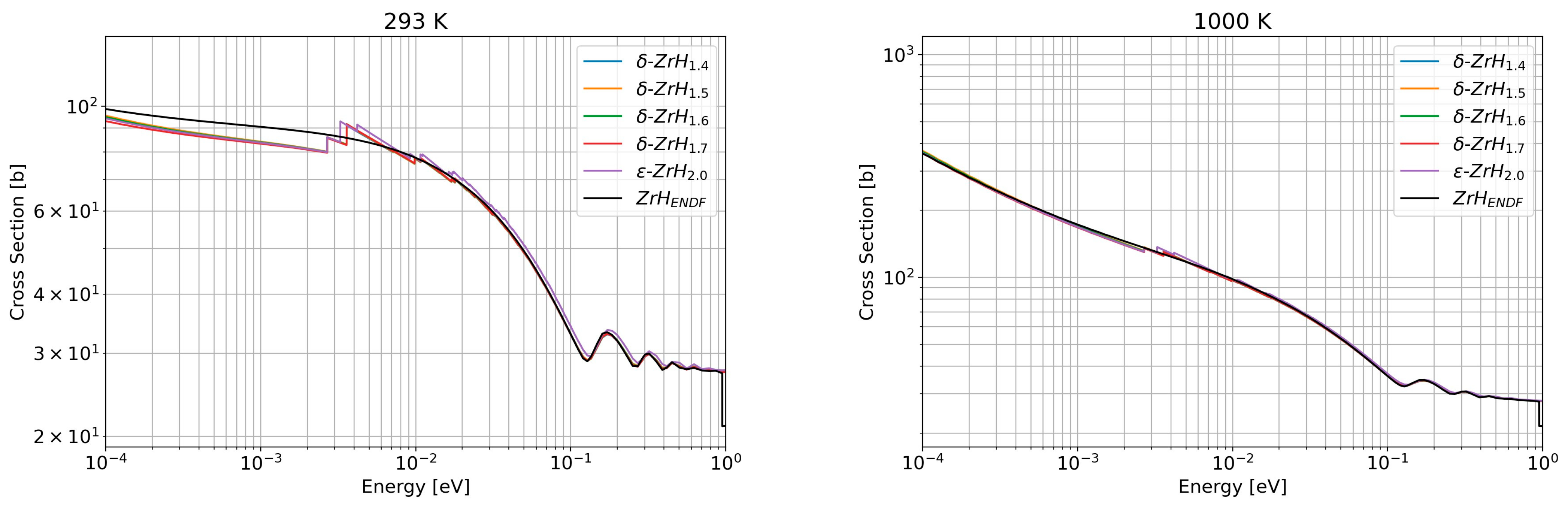
3.2.1. Benchmark with the ENDF Evaluation
3.2.2. New Evaluations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- McClure, P.R.; Poston, D.I.; Gibson, M.A.; Mason, L.S.; Robinson, R.C. Kilopower Project: The KRUSTY Fission Power Experiment and Potential Missions. Nucl. Technol. 2020, 206, S1–S12. [Google Scholar] [CrossRef]
- Poston, D.I.; Gibson, M.A.; Godfroy, T.; McClure, P.R. KRUSTY Reactor Design. Nucl. Technol. 2020, 206, 13–30. [Google Scholar] [CrossRef]
- Gibson, M.A.; Poston, D.I.; McClure, P.R.; Sanzi, J.L.; Godfroy, T.J.; Briggs, M.H.; Wilson, S.D.; Schifer, N.A.; Chaiken, M.F.; Lugasy, N. Heat Transport and Power Conversion of the Kilopower Reactor Test. Nucl. Technol. 2020, 206, 31–42. [Google Scholar] [CrossRef]
- McClure, P.R.; Poston, D.I.; Clement, S.D.; Restrepo, L.; Miller, R.; Negrete, M. KRUSTY Experiment: Reactivity Insertion Accident Analysis. Nucl. Technol. 2020, 206, S43–S55. [Google Scholar] [CrossRef]
- Sanchez, R.; Grove, T.; Hayes, D.; Goda, J.; McKenzie, G.; Hutchinson, J.; Cutler, T.; Bounds, J.; Walker, J.; Myers, W.; et al. Kilowatt Reactor Using Stirling TechnologY (KRUSTY) Component-Critical Experiments. Nucl. Technol. 2020, 206, 56–67. [Google Scholar] [CrossRef]
- Grove, T.; Hayes, D.; Goda, J.; McKenzie, G.; Hutchinson, J.; Cutler, T.; Bounds, J.; Walker, J.; Myers, W.; Sanchez, R. Kilowatt Reactor Using Stirling TechnologY (KRUSTY) Cold Critical Measurements. Nucl. Technol. 2020, 206, S68–S77. [Google Scholar] [CrossRef]
- Poston, D.I.; Gibson, M.A.; McClure, P.R.; Sanchez, R.G. Results of the KRUSTY Warm Critical Experiments. Nucl. Technol. 2020, 206, S78–S88. [Google Scholar] [CrossRef]
- Poston, D.I.; Gibson, M.A.; Sanchez, R.G.; McClure, P.R. Results of the KRUSTY Nuclear System Test. Nucl. Technol. 2020, 206, S89–S117. [Google Scholar] [CrossRef]
- Mehta, V.K.; McClure, P.; Kotlyar, D. Selection of a Space Reactor Moderator Using Lessons Learned from SNAP and ANP Programs. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Voss, S.S. Topaz II System Description; No. LA-UR--94-4; Los Alamos National Lab.: Los Alamos, NM, USA, 1994. [Google Scholar]
- Olander, D. Nuclear fuels–present and future. J. Nucl. Mater. 2009, 389, 1–22. [Google Scholar] [CrossRef]
- Lillie, A.F.; McClelland, D.T.; Roberts, W.J.; Walter, J.H. Zirconium Hydride Fuel Element Performance Characteristics; No. AI-AEC--13084; Atomics International Division: Los Angeles, CA, USA, 1973. [Google Scholar]
- Gates, J.; Denig, A.; Ahmed, R.; Mehta, V.; Kotlyar, D. Low-enriched cermet-based fuel options for a nuclear thermal propulsion engine. Nucl. Eng. Des. 2018, 331, 313–330. [Google Scholar] [CrossRef]
- Johnson, J.; Patterson, M.W.; Wagner, A.R. MARVEL Fuel Fabrication Strategy; No. INL/RPT-22-66550-Rev000; Idaho National Lab. (INL): Idaho Falls, ID, USA, 2022. [Google Scholar]
- Mehta, V.K.; Armstrong, J.; Rao, D.V.; Kotlyar, D. Capturing multiphysics effects in hydride moderated microreactors using MARM. Ann. Nucl. Energy 2022, 172, 109067. [Google Scholar] [CrossRef]
- Trellue, H.R.; Long, A.M.; Luther, E.P.; Carver, D.T.; Mehta, V.K. Effects of Hydrogen Redistribution at High Temperatures in Yttrium Hydride Moderator Material. JOM 2021, 73, 3513–3518. [Google Scholar] [CrossRef]
- Hawley, J.P.; Johnson, R.A. SNAP 10A FS-3 Reactor Performance; No. NAA-SR-11397; Atomics International Division: Canoga Park, CA, USA, 1966. [Google Scholar]
- Taylor, C.; Smith, T.; Hahn, M.; Torres, J.; Tegtmeier, E.; Nizolek, T.; Bohn, K.; Emberley, C.; Shivprasad, A.; Widgeon-Paisner, S.; et al. Properties of Uranium-Zirconium Hydride Moderated Nuclear Fuel Synthesized by Powder Metallurgy; Technical Report LA-UR-22-29969; Los Alamos National Laboratory: Los Alamos, NM, USA, 2022. [Google Scholar]
- Zuzek, E.; Abriata, J.; San-Martin, A.; Manchester, F. Phase Diagrams of Binary Hydrogen Alloys; ASM International: Materials Park, OH, USA, 2000; pp. 309–310. [Google Scholar]
- Wormald, J.; Zerkle, M.; Holmes, J. Generation of the TSL for Zirconium Hydrides from Ab Initio Methods. J. Nucl. Eng. 2021, 2, 105–113. [Google Scholar] [CrossRef]
- Zu, T.; Tang, Y.; Wang, L.; Cao, L.; Wu, H. Thermal scattering law data generation for hydrogen bound in zirconium hydride based on the phonon density of states from first-principles calculations. Ann. Nucl. Energy 2021, 161, 108489. [Google Scholar] [CrossRef]
- El Barbari, M.; El Bardouni, T.; El Yaakoubi, H.; Boulaich, Y.; Lahdour, M.; Ziani, H.; Berriban, I. First principles calculation for generating new thermal neutron scattering data for Zirconium hydride. Appl. Radiat. Isot. 2022, 187, 110313. [Google Scholar] [CrossRef]
- Švajger, I.; Fleming, N.C.; Laramee, B.; Noguere, G.; Hawari, A.I.; Snoj, L.; Trkov, A. Thermal Scattering Law Data for Zirconium Hydride from First-Principles. In Proceedings of the International Conference Nuclear Energy for New Europe, Bled, Slovenia, 6–9 September 2021; p. 307. [Google Scholar]
- Fleming, N.C.; Manring, C.A.; Laramee, B.K.; Crozier, J.P.; Lee, E.; Hawari, A.I. FLASSH 1.0: Thermal Scattering Law Evaluation and Cross Section Generation. EPJ Web Conf. 2023, 284, 17007. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Corso, A.D.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Togo, A. First-principles Phonon Calculations with Phonopy and Phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I. Implementation strategies in phonopy and phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef] [PubMed]
- Zu, T.; Xu, J.; Tang, Y.; Bi, H.; Zhao, F.; Cao, L.; Wu, H. NECP-Atlas: A new nuclear data processing code. Ann. Nucl. Energy 2019, 123, 153–161. [Google Scholar] [CrossRef]
- Gonze, X.; Jollet, F.; Araujo, F.A.; Adams, D.; Amadon, B.; Applencourt, T.; Audouze, C.; Beuken, J.M.; Bieder, J.; Bokhanchuk, A.; et al. Recent developments in the ABINIT software package. Comput. Phys. Commun. 2016, 205, 106–131. [Google Scholar] [CrossRef]
- Haeck, W.; Conlin, J.L.; McCartney, A.P.; Kahler, A.C., III. NJOY2016 Updates for ENDF/B-VIII. 0; No. LA-UR-18-22676; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2018. [Google Scholar]
- Ramić, K.; Damian, J.I.M.; Kittelmann, T.; Di Julio, D.D.; Campi, D.; Bernasconi, M.; Gorini, G.; Santoro, V. NJOY+NCrystal: An open-source tool for creating thermal neutron scattering libraries with mixed elastic support. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1027, 166227. [Google Scholar] [CrossRef]
- Kulesza, J.A.; Adams, T.R.; Armstrong, J.C.; Bolding, S.R.; Brown, F.B.; Bull, J.S.; Burke, T.P.; Clark, A.R.; Forster, R.A.A., III; Giron, J.F.; et al. MCNP® Code Version 6.3. 0 Theory & User Manual; No. LA-UR-22-30006; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2022. [Google Scholar]
- Yamanaka, S.; Yamada, K.; Kurosaki, K.; Uno, M.; Takeda, K.; Anada, H.; Matsuda, T.; Kobayashi, S. Characteristics of zirconium hydride and deuteride. J. Alloys Compd. 2002, 330, 99–104. [Google Scholar] [CrossRef]
- Bowman, R.C., Jr.; Craft, B.D.; Cantrell, J.S.; Venturini, E.L. Effects of thermal treatments on the lattice properties and electronic structure of ZrHx. Phys. Rev. B 1985, 31, 5604. [Google Scholar] [CrossRef]
- Beck, R.L. Thermophysical properties of zirconium hydride. ASM Trans. Q. 1962, 55, 556–564. [Google Scholar]
- Moore, K.; Young, W. Phase studies of the Zr-H system at high hydrogen concentrations. J. Nucl. Mater. 1968, 27, 316–324. [Google Scholar] [CrossRef]
- Hawari, A.I.; Al-Qasir, I.I.; Gillette, V.H.; Wehring, B.W.; Zhou, T. Ab initio generation of thermal neutron scattering cross sections. In Proceedings of the PHYSOR 2003, Chicago, IL, USA, 25–29 April 2004. [Google Scholar]
- Hawari, A. Modern Techniques for Inelastic Thermal Neutron Scattering Analysis. Nucl. Data Sheets 2014, 118, 172–175. [Google Scholar] [CrossRef]
- Rahman, A.; Mandell, M.J.; McTague, J.P. Molecular dynamics study of an amorphous Lennard-Jones system at low temperature. J. Chem. Phys. 1976, 64, 1564–1568. [Google Scholar] [CrossRef]
- Wormald, J.; Hawari, A. Generation of phonon density of states and thermal scattering law using ab initio molecular dynamics. Prog. Nucl. Energy 2017, 101, 461–467. [Google Scholar] [CrossRef]
- Wormald, J.; Hawari, A.I. Thermal neutron scattering law calculations using ab initio molecular dynamics. EPJ Web Conf. 2017, 146, 13002. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Nosé, S.A. unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nosé, S.A. Molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nosé–Hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Hellman, O.; Abrikosov, I.A.; Simak, S.I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 2011, 84, 180301. [Google Scholar] [CrossRef]
- Hellman, O.; Abrikosov, I.A. Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 2013, 88, 144301. [Google Scholar] [CrossRef]
- Hellman, O.; Steneteg, P.; Abrikosov, I.A.; Simak, S.I. Temperature dependent effective potential method for accurate free energy calculations of solids. Phys. Rev. B 2013, 87, 104111. [Google Scholar] [CrossRef]
- Olsson, P.A.T.; Massih, A.; Blomqvist, J.; Holston, A.-M.A.; Bjerkén, C. Ab initio thermodynamics of zirconium hydrides and deuterides. Comput. Mater. Sci. 2014, 86, 211–222. [Google Scholar] [CrossRef]
- Squires, G.L.; Leslie, G. Introduction to the Theory of Thermal Neutron Scattering; Courier Corporation: North Chelmsford, MA, USA, 1996. [Google Scholar]
- Bell, G.I.; Glasstone, S. Nuclear Reactor Theory; No. TID-25606; US Atomic Energy Commission: Washington, DC, USA, 1970.
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII. 0: The 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Zerkle, M.; Holmes, J. A thermal neutron scattering law for yttrium hydride. EPJ Web Conf. 2017, 146, 13005. [Google Scholar] [CrossRef]
- Mehta, V.K.; Cooper, M.W.; Wilkerson, R.B.; Kotlyar, D.; Rao, D.V.; Vogel, S.C. Evaluation of Yttrium Hydride (δ-YH2-x): Thermal Neutron Scattering Laws and Thermophysical Properties. Nucl. Sci. Eng. 2021, 195, 563–577. [Google Scholar] [CrossRef]
- Cai, X.-X.; Kittelmann, T. NCrystal: A library for thermal neutron transport. Comput. Phys. Commun. 2020, 246, 106851. [Google Scholar] [CrossRef]
- Trkov, A.; Brown, D.A. ENDF-6 Formats Manual: Data Formats and Procedures for the Evaluated Nuclear Data Files; CSWEG Document ENDF-102, BNL-203218-2018-INRE; Brookhaven National Laboratory: Upton, NY, USA, 2018. [Google Scholar]
- Couch, J.G.; Harling, O.K.; Clune, L.C. Structure in the Neutron Scattering Spectra of Zirconium Hydride. Phys. Rev. B 1971, 4, 2675–2681. [Google Scholar] [CrossRef]
- Evans, A.C.; Timms, D.N.; Mayers, J.; Bennington, S.M. Neutron-scattering study of the impulse approximation in ZrH2. Phys. Rev. B 1996, 53, 3023. [Google Scholar] [CrossRef]
- Flotow, H.E.; Osborne, D.W. Heat Capacities and Thermodynamic Functions of ZrH2 and ZrD2 from 5 to 350 °K and the Hydrogen Vibration Frequency in ZrH2. J. Chem. Phys. 1961, 34, 1418–1425. [Google Scholar] [CrossRef]
- Whittemore, W.L. Neutron Interactions in Zirconium Hydride; GA-4490; General Atomics: San Diego, CA, USA, 1964. [Google Scholar]
- Schmidt, U. Untersuchung derWasserstoff- und Deuteriumschwingungen in Metallhydriden, -Hydrodeuteriden und -Deuteriden Mittles Totaler Neutronen-Wirkunsquerschnitte. ATKE 1967, 12, 385. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehta, V.K.; Rehn, D.A.; Olsson, P.A.T. Evaluation of δ-Phase ZrH1.4 to ZrH1.7 Thermal Neutron Scattering Laws Using Ab Initio Molecular Dynamics Simulations. J. Nucl. Eng. 2024, 5, 330-346. https://doi.org/10.3390/jne5030022
Mehta VK, Rehn DA, Olsson PAT. Evaluation of δ-Phase ZrH1.4 to ZrH1.7 Thermal Neutron Scattering Laws Using Ab Initio Molecular Dynamics Simulations. Journal of Nuclear Engineering. 2024; 5(3):330-346. https://doi.org/10.3390/jne5030022
Chicago/Turabian StyleMehta, Vedant K., Daniel A. Rehn, and Pär A. T. Olsson. 2024. "Evaluation of δ-Phase ZrH1.4 to ZrH1.7 Thermal Neutron Scattering Laws Using Ab Initio Molecular Dynamics Simulations" Journal of Nuclear Engineering 5, no. 3: 330-346. https://doi.org/10.3390/jne5030022
APA StyleMehta, V. K., Rehn, D. A., & Olsson, P. A. T. (2024). Evaluation of δ-Phase ZrH1.4 to ZrH1.7 Thermal Neutron Scattering Laws Using Ab Initio Molecular Dynamics Simulations. Journal of Nuclear Engineering, 5(3), 330-346. https://doi.org/10.3390/jne5030022






