Abstract
Simulation modeling is crucial in support of probabilistic risk assessment (PRA) for nuclear power plants (NPPs). There is a challenge, however, associated with simulation modeling that relates to the time and resources required for collecting data to determine the values of the input parameters. To alleviate this challenge, this article develops a formalized methodology to generate surrogate values of input parameters grounded on the decomposition of phenomenological nondimensional parameters (PNPs) while avoiding detailed data collection. While the fundamental principles of the proposed methodology can be applicable to various hazards, the developments in this article focus on fire PRA as an example application area for which resource intensiveness is recognized as a practical challenge. This article also develops a computational platform to automate the PNP decomposition and seamlessly integrates it with state-of-practice fire scenario analysis. The applicability of the computational platform is demonstrated through a multi-compartment fire case study at an NPP. The computational platform, with its embedded PNP decomposition methodology, can substantially reduce the effort required for input data collection and extraction, thereby facilitating the efficient use of simulation modeling in PRA and enhancing the fire scenario screening analysis.
1. Introduction
Risk-informed applications are of great significance for the nuclear industry. Not only do they provide a means for quantitatively assessing the safety margin of as-built, as-operated plants and identifying the significant risk-contributing factors to prioritize for safety measures, but they also help improve the efficiency of operations and maintenance, for instance, by focusing inspection and surveillance resources on the risk-significant components. Probabilistic risk assessment (PRA) provides the risk information required to achieve these objectives.
Simulation modeling is crucial in support of PRA for nuclear power plants (NPPs) in certain situations, including (i) when operating experience is too limited to perform a data-driven estimation of the PRA inputs due to novel designs or the difficulty in data collection; (ii) when the relevancy of historical data to the current plant conditions is questioned, e.g., due to design or programmatic changes; (iii) when decision-makers are interested in in-depth risk information at the level of underlying phenomena; and (iv) when simulation modeling can help bring more realism to PRA by avoiding the use of overly conservative or bounding assumptions. When incorporating simulation models into PRA, careful attention should be paid to balancing the desired level of realism of the estimated risk with the time and resources required for conducting the analysis [1,2]. One of the major contributors to the time and resources required for simulation modeling is the process of collecting or extracting data, such as plant walkdowns and the review of engineering diagrams, to determine the values of the input parameters. This process is typically laborious manual work performed by an analyst.
To alleviate the challenge of input data collection for simulation models in support of PRA, this research develops a formalized methodology to generate surrogate values of input parameters while avoiding detailed data collection. The proposed methodology is grounded on the decomposition of phenomenological nondimensional parameters (PNPs). This new methodology groups multiple input quantities using a PNP that represents the underlying physical phenomena. A scientifically justifiable range for the PNP can be identified and can then be used to generate surrogate values for the physical input quantities of the simulation models; hence, the need for acquiring the precise values for the input parameters can be reduced or even avoided. Although the proposed methodology can be applicable for various hazards in PRA, this article focuses on fire PRA of NPPs as a primary application area. Fire PRA is selected since its resource intensiveness has been a long-standing challenge for the nuclear industry [3], and the experience of the authors implies that data collection to obtain input values for fire models is one of the most time-consuming activities in fire PRA [4].
Section 1.1 provides a review of recent studies addressing resource intensiveness of fire PRA for NPPs. Section 1.2 shows the contributions and organization of this article.
1.1. Recent Studies Addressing Resource Intensiveness of Fire PRA for NPPs
In recent publications, there are two main streams of research aiming to tackle the resource requirements of fire PRA for NPPs.
The first stream of research attempts to streamline the generation and quantification of fire PRA scenarios based on physical simulation outputs and contributes to the reduction of manual work and computational time to interface fire models with a plant PRA model. For instance, Prescott et al. [5,6] developed the Fire Risk Investigation in 3D (FRI3D) software which integrates multiple tools such as the existing FRANX Fire PRA model and Plant Data Model System (PDMS). FRI3D utilizes the Consolidated Model of Fire Growth and Smoke Transport (CFAST) [7] to conduct fire simulation and modeling and the Computer-Aided Fault Tree Analysis System (CAFTA) for risk analysis. This platform enables the analyst, through analyzing the full data of all components and cables, to automatically generate failure scenarios including secondary fire in the form of cable trays using the CFAST model data to determine the failed components in a scenario. Another recent study by the Korean Atomic Energy Research Institute (KAERI) [8] aims to streamline the identification and PRA modeling of fire-induced component failure modes and to automatically construct a “one-top fire event” PRA model [9]. Kang et al. [10] implemented the “mapping technique” developed by KAERI to construct and quantify a one-top fire event PRA model at Ulchin NPP Units 3 and 4. Hostikka and Keski-Rahkonen [11] automated the interface between a plant PRA model and the fire simulation, contributing to reducing the manual work needed to transfer simulation outputs to the PRA inputs. Their study developed a risk analysis tool, called Probabilistic Fire Simulator (PFS), that combines Monte Carlo simulation and CFAST to perform sensitivity analysis and estimate the distributions of the output variables of the fire model.
The second research stream focuses on creating a fast-running surrogate model for physical simulations used in fire PRA, contributing to the reduction of the computational cost for analyzing fire-induced conditions. Anderson et al. [12] reviewed the usage of machine learning in fire sciences. They highlighted that the needed data collection for training and validation of models requires excessive resources but, on the positive side, it leads to a very fast prediction of cases in the future. Hodges et al. [13] presented the utilization of a transposed convolutional neural network to predict temperatures and velocities of flow using data from FDS runs for a two-compartment configuration. As another example, Worrell et al. [14] developed metamodels of the CFAST code using machine learning methods. Sampling of input parameters and CFAST runs were executed using the Risk Analysis and Virtual Environment (RAVEN) framework, while the metamodels were trained using the R software. Their study showed that, in compartment fires at NPPs, a k-nearest neighbor model provided the best accuracy to predict the upper layer temperature and its timing.
1.2. Contributions and Paper Organization
As shown in Section 1.1, the recent studies that attempted to alleviate the resource challenges of Fire PRA focused on either (i) streamlining the interface between a physical fire model and a plant PRA model or (ii) reducing the computational cost of a physical fire simulation by building a fast-running surrogate model. Compared to the studies cited in Section 1.1, this article is unique in that it attempts to reduce the amount of effort for data collection by utilizing PNP decomposition, instead of attempting to accelerate the full data handling process or by assuming that the full input data are known to support all input parameter values.
The contributions of this article are threefold. First, the PNP decomposition methodology is developed. The concept, guiding principles, and procedures of the proposed methodology are provided and illustrated using two typical PNPs in fire PRA. Second, a new computational platform, equipped with the PNP decomposition, is developed to support the fire PRA of NPPs. This computational platform automates the PNP decomposition process and seamlessly integrates it with other fire PRA tasks, including the pre-processing of input data, verification and validation (V&V) of a fire model, generation of fire scenarios, and post-processing of outputs. This study is the first to offer a unified fire PRA computational tool equipped with PNP decomposition. Third, to demonstrate the feasibility of the proposed methodology, the computational platform is applied to a multi-compartment fire case study at an NPP. The multi-compartment fire analysis is the area where the PNP decomposition can be significantly beneficial due to its potential risk significance and the nature of its resource intensiveness [15,16,17,18,19]. In this case study, the PNP decomposition methodology is demonstrated for one of the PNPs, namely the equivalence ratio. The PNP decomposition for the equivalence ratio eliminates the need to collect detailed ventilation data.
The PNP decomposition methodology and the computational platform developed in this article can contribute to improving the fire scenario screening in fire PRA of NPPs. In the traditional screening analysis, the common approach is to use bounding or conservative values for the individual input parameters when data collection or extraction is resource-demanding [20,21]. If the fire scenario being analyzed cannot be screened out using such bounding or conservative input values, the PNP decomposition, while still avoiding the collection of detailed input data, could offer another layer of screening analysis where the input values are refined based on physical constraints generated from the PNPs.
This article is organized as follows. Section 2 shows the PNP decomposition methodology and two illustrative examples in the fire PRA context. Section 3 describes the computational platform equipped with the PNP decomposition to support the fire PRA of NPPs. Section 4 shows the application of the proposed methodology and computational platform to a multi-compartment fire scenario at an NPP. Section 5 provides concluding remarks.
2. Generation of Surrogate Values for Simulation Input Parameters Using Phenomenological Nondimensional Parameter (PNP) Decomposition
Section 2.1 describes the proposed PNP decomposition process and contrasts it to the current practice of utilizing PNPs in the fire PRA of NPPs. Section 2.2 shows the proposed procedure to operationalize the PNP decomposition methodology. Section 2.3 demonstrates the PNP decomposition procedure using two examples of PNPs in the fire PRA context.
2.1. The Concept of PNP Decomposition and Its Contrast to the Current Practice
Deduction of information about a phenomenon by dimensionless groups and variables consisting of the dependent variables and the time and space coordinates has been a common practice in most fields of engineering, particularly in the thermofluid science field. These dimensionless groups can help extend the experimental results through approximate formulae equipped with sensitivity analysis. To derive nondimensional functionality, three methods are suggested: the Buckingham theorem, nondimensionalization of the related fundamental conservation laws, and identification of the dimensional relationships by the governing physics. In the V&V study (NUREG-1824) [22] by the U.S. Nuclear Regulatory Commission (NRC) and Electric Power Research Institute (EPRI), in collaboration with the National Institute of Science and Technology (NIST), a set of six nondimensional parameters were established to easily characterize the scope of the experiments and to judge the applicability of five fire simulation tools and their ability in estimating thirteen physical quantities of interest for fire scenarios in the nuclear industry. These six nondimensional parameters are (1) fire Froude number, (2) flame length ratio, (3) ceiling jet radial distance ratio, (4) equivalence ratio, (5) compartment aspect ratio, and (6) target distance ratio [22,23,24,25,26]. These nondimensional parameters are traditionally used in fire modeling applications to determine the applicability of the V&V results from this study (NUREG-1824) to various other scales or other specific NPP fire scenarios [22]. NUREG-1824, Vol. 5 [27] provides a more detailed discussion of the V&V of CFAST [7]. In 2016, the first formal expansion of this V&V study, NUREG-1824, Supplement 1 [28], was published and the updated validation ranges for some of the nondimensional parameters were included.
The typical method of using PNPs in the V&V of fire models is illustrated in Figure 1A. Multiple dimensional parameters ( physical quantities, , in Figure 1A), with the adequate units of measurement, are grouped through a functional formula to generate a PNP. Given that the input data for these physical quantities () are collected, the PNP for the fire scenario being analyzed can be computed. The calculated PNP is used to characterize the similarities between the V&V data and an application-specific case. NUREG-1934 [29] suggests that the applicability of the V&V study to each specific application case be assessed by comparing the calculated PNPs with the validation range provided for each fire model and physical output quantity of interest. Using PNPs this way, the flow of information is from the physical quantities to the PNP.
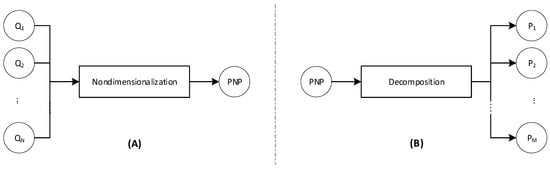
Figure 1.
(A) Nondimensionalization of N quantities into one PNP, and (B) decomposing a PNP into M physical input parameters.
In contrast, the proposed PNP decomposition approach (shown in Figure 1B) aims to generate surrogate values for the input parameters from the PNP. This process reverses the typical process of calculating a PNP from physical quantities. In the proposed PNP decomposition, the PNP is decomposed into its constituent physical parameters ( in Figure 1B), representing the surrogate values of the required input parameters for a simulation model.
The PNP decomposition should be conducted by addressing the following guiding principles.
- A.
- Balance between the precision of simulation inputs and practical constraints. An analyst should choose the level of precision of the input parameters that is sufficient to fulfill the objective of the risk-informed decision-making, given the resource constraints (e.g., labor costs for data extraction and collection) as well as other practical constraints such as scheduling and radiation dose limits. The purpose of the PNP decomposition is to enable a formalized procedure to address this balance by gradually improving the precision of the simulation input parameters used in PRA instead of resorting to an extreme bounding assumption or attempting to achieve the full precision from the beginning.
- B.
- Objective of the risk-informed decision-making of interest. The partial data and logical reasoning used in the PNP decomposition should be consistent with the objective of the intended risk-informed decision-making. For example, when the risk-informed decision-making aims to screen out non-significant scenarios and events from further detailed analysis or to determine whether a decision alternative is acceptable compared to a predefined acceptance criterion, the analyst should use conservative assumptions and approaches such that the assessed outcome is less favorable, or the risk metric is greater than expected or perceived [30]. The premise is that if the PNP is decomposed into its constituent physical parameters, representing the surrogate values of the input parameters, that would ensure that a certain hazard or event would propagate and develop in a manner harsher than reality; hence, the resultant risk information would be steered toward the safer direction.
- C.
- Knowledge about underlying physical phenomena. Physical simulation models are, by nature, the collection of the state of knowledge regarding the underlying physical phenomena in a format of numerical governing equations. In the PNP decomposition, the same knowledge about the physical phenomena should be applied to generate surrogate values of input parameters. As shown in Section 2.2, there are multiple steps in the PNP decomposition process that need to be informed by physical understanding, such as the selection of the PNP(s) to use and the identification of the justifiable value or range of the PNP.
- D.
- Validation range of the simulation model being utilized. Many correlations and computational models establish their applicability using ranges for specific parameters. It is common for these parameters to be PNPs. Typically, such ranges cover most of the potential application areas. For example, the six PNPs in fire PRA are used to check the validity of three fire simulation models to a wide range of fire scenarios in NPPs [22,28]. These PNP ranges are not measured or collected from plant-specific operations or design specifications but can be derived from the collective physical knowledge available through relevant literature and expert knowledge; hence, the workload for plant walkdowns and data collections can be reduced. Utilizing the results of validation analysis and experiments as well as PNP ranges would be valuable to guide the PNP decomposition to ensure the generated surrogate values would be applicable to the simulation model being used.
- E.
- Model behavior within the validation range. A critical approach for identifying the impact of the assumptions and utilized values of the input parameters in simulation and modeling is to conduct sensitivity analysis. This will not only substantiate that the simulation output is reasonable relative to the intended decision-making but also allow for providing more quantitative analysis on the specific values of the input parameters.
2.2. Methodological Steps for Operationalizing the Proposed PNP Decomposition Process in Support of PRA
Figure 2 shows methodological steps for operationalizing the PNP decomposition process in support of PRA.
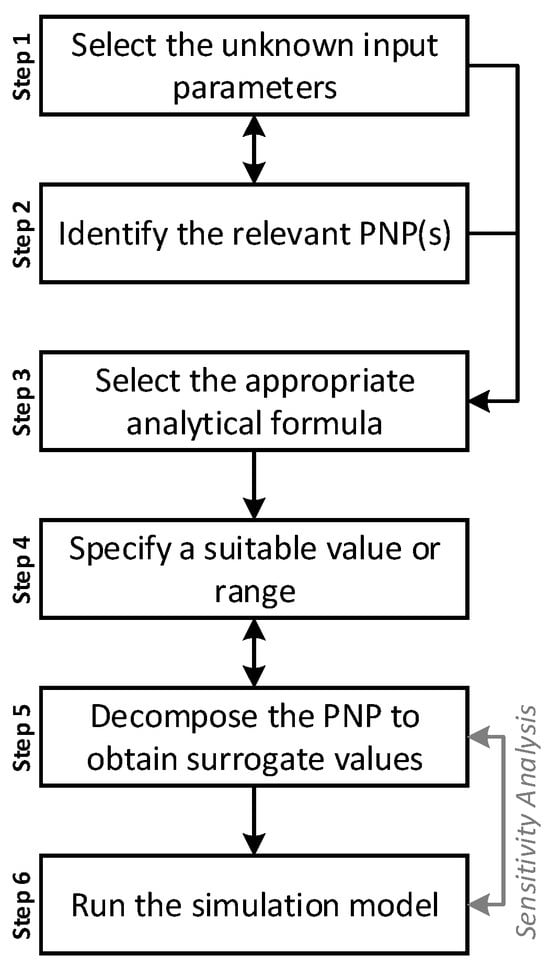
Figure 2.
Methodological steps for operationalizing the proposed PNP decomposition process.
Step 1 selects the input parameters that might impose practical and financial challenges in the data collection, design, or analysis processes for the intended simulation analysis. Principle “A” is the primary consideration in this step. The input parameters selected in this step are referred to as the “input parameters of concern”. The subsequent steps aim to determine surrogate values of these input parameters of concern based on the PNP decomposition. Meanwhile, the values of the input parameters that have not been selected in this step should be directly obtained from available data, such as design information, operational data, or physical constants.
Step 2 identifies the relevant PNP(s), including the input parameters of concern identified in Step 1. The identified PNP(s) should have proper scientific credibility and be well accepted within the scientific community in alignment with Principle “C”, i.e., the state of knowledge in the community provides a proper justification for the identified PNP(s).
It should be noted that Steps 1 and 2 may need to be implemented iteratively. For instance, the outcome of Step 2 may provide additional information that could impact the selection of the input parameters for the PNP decomposition in Step 1, e.g., the availability and characteristics of an applicable PNP identified in this step may alter the selection of input parameters of concern in Step 1.
In Step 3, an analytical formula for the PNP as a function of the input parameters of concern is selected based on credible literature and common practices in the domain of interest, considering Principle “C”.
Step 4 specifies a suitable value or range for the PNP. The proper PNP value or range should be selected considering the PNP range where the simulation model to be used has been validated (in alignment with Principle “D”). The selection of specific PNP values within the validation range can be informed by sensitivity analyses (considering Principle “E”), where the sub-range of the PNP values that result in conservative simulation output can be investigated if the conservative analysis can serve the intended risk-informed decision-making (in alignment with Principle “B”). The PNP values outside of the validation range may also be selected under certain conditions that satisfy two conditions: (i) a compelling justification exists to verify that the underlying physics still hold (considering Principle “C”), and (ii) in the direction of the deviation of the PNP values compared to the validation range, the system being analyzed is exposed to a harsher environment that intensifies or accelerates hazard progression (considering Principle “B”).
In Step 5, the PNP is decomposed to generate the surrogate values of the input parameters of concern. The surrogate values are generated by solving the PNP formula (from Step 3) to obtain the values of the input parameters of concern that result in the suitable value of the PNP specified in Step 4. If a PNP is decomposed into multiple continuous input parameters of concern, infinite combinations of their surrogate values can be identified. In this case, based on Principle “E”, sensitivity analyses can generate further insights as to the impact of the possible combinations of the surrogate input values on the intended decision (considering Principle “B”). If the sensitivity analyses show that the impact of different combinations of the surrogate values on the simulation output is negligible, a representative combination of the surrogate values (for instance, the one chosen based on industry practice) could be utilized. If the sensitivity of the simulation output to different combinations of the surrogate input values is significant, the sensitivity analyses can be used to study which combination of the surrogate input values can generate the most conservative output (i.e., based on Principle “B”, the resultant risk information would be steered toward the safer direction). This insight can help justify the final selection of the surrogate input values.
In Step 6, the simulation model is run utilizing the generated surrogate values of the input parameters to predict the key performance measures of interest. This step also conducts sensitivity analysis to provide insights on the impact of assumptions made in Step 5. The simulation output is then used as input to PRA and risk-informed decision-making.
2.3. Examples of PNPs and Their Decomposition in Fire PRA
In this section, the PNP decomposition process is demonstrated using two representative examples of PNPs commonly used in fire PRA of NPPs: the compartment aspect ratio (CAR) and the equivalence ratio. The decomposition of these two PNPs is operationalized by the computational platform developed in Section 3.
- Fire PNP Example 1: Compartment Aspect Ratio (CAR)
The CAR represents the dimensions of a specific fire room or compartment. The ratios of the length () and the width () to the ceiling height (), i.e., and , are calculated. This PNP is used as an indication of the general shape of the compartment to judge whether a room is considered a tunnel or corridor, vertical shaft, or a standard/typical room. Typical fire compartments in NPPs do not have an exact rectangular cuboid shape and, in reality, the majority of such compartments are expected to consist of connected smaller sub-rooms, mezzanine areas, buffering zones, or even have large volumes occupied by structures. In such cases, it is a common practice to represent the fire compartment in terms of volume and height (or area).
In the typical V&V practice (Figure 1A), the dimensions, , , and of a compartment would be obtained from data collection. CARs are then calculated and compared to the validation ranges. If within the validation range, the fire simulation model would be suitable in simulating such a compartment. The NUREG-1824, Supplement 1 shows that the validation range for this PNP is 0.6–8.3 [28].
In contrast, the PNP decomposition methodology (Figure 1B) reverses the process. Assume that the data available about a specific compartment is its height, . Then, the PNP decomposition procedure (Section 2.2) can be implemented as follows.
For Step 1 (select the input parameters), the input parameters of interest are the room width, , and length, . For Step 2 (identify the relevant PNP), CAR is used as the PNP. For Step 3 (determine an analytical formula for the PNP), to formulate the problem in terms of the total room area, , the two aspect ratios are multiplied to generate a single equivalent one, .
For Step 4 (specify the suitable value or range for the PNP), the lower and upper validation bounds of can be obtained from the original validation range of the aspect ratio PNP (0.6–8.3 [28]): from 0.36 (=0.62) to 68.89 (=8.32). Within this validation range, the CAR of unity, CAR 1, is chosen to avoid extreme corridor or shaft characteristics. The specific choice of the CAR value should also consider the actual characteristics of the compartment of interest and the suitability of the fire model. The actual compartment characteristics should be justified based on the existing information and knowledge (without conducting additional data collection efforts), for instance, observations from the previous plant walkdown and expert opinion from the plant field operators. Regarding the model suitability perspective, for larger CAR values (CAR 1), the characteristics of a corridor would be significant (which will require special treatment of the transport time of the combustion products and the expected non-uniform layer). In the case of lower CAR values (CAR ≪ 1), the compartment would take on the characteristics of a long shaft (which will require the consideration of parameters such as the stratification of the combustion products, the interaction of the fire plume and the enclosure boundaries, and choked flow) [22,31].
For Step 5 (decompose the PNP to generate the surrogate values of the input parameters), the two compartment dimensions are calculated by assuming a square area, i.e., . This leads to the following formulation: . It is also assumed that the height of the compartment is already established as . Assuming that the compartment represents a typical compartment, i.e., closer to a cube than a corridor or a shaft, a value of 1 is chosen (CAR 1). Therefore, the area can then be calculated as . The input parameters required are the length, , and width, , which can be calculated as follows: .
For Step 6 (run the simulation model utilizing the generated surrogate values of the input parameters), based on the above decomposition, this illustrative case can be simulated as a by by compartment (i.e., as a cube).
- Fire PNP Example 2: Equivalence Ratio ()
The equivalence ratio, , relates the energy release rate to the amount of energy release that can be supported by the mass flow rate of oxygen into the compartment. When these two quantities are equal, i.e., , the fire combustion process is provided with the exact amount of oxygen required for complete combustion. Under this condition, the flame temperature is maximized adiabatically. If the ratio is greater than one (), the fire is under-ventilated, and the fire conditions are said to be rich with fuel. If the ratio is less than one (), the fire is over-ventilated and lean with fuel. The equivalence ratio () is calculated using Equations (1) and (2).
where is the Heat Release Rate (HRR), is the heat of combustion for oxygen (), and is the mass flow rate of oxygen into the compartment estimated using Equation (2).
where is the effective area of the natural openings [], is the effective height of the natural openings [, is the density of ambient air ( at room temperature), and is the volumetric flowrate of air into the enclosure (). For a compartment with multiple natural vents, the effective area, , is calculated by summing all the vent areas, i.e., , where is the total number of vents and is the area of each individual vent. The effective height, , is calculated by weighting the height to the total vent areas, i.e., , where is the height of each vent [29,32].
In the common V&V practice (Figure 1A), the ventilation-related input variables, and , would be obtained from data collection. Then, the equivalence ratio is calculated using Equations (1) and (2) and compared to the validation range. If within the validation range, the fire simulation model would be suitable for simulating such a compartment. The NUREG-1824, Supplement 1 shows that the validation range for is 0.0–0.6 [28].
In contrast, the PNP decomposition procedure (Figure 1B) for the equivalence ratio is implemented as follows.
For Step 1 (select the input parameters), assuming the compartment only has natural openings, the input parameters of concern are the effective vent area, , and the effective vent height, . For Step 2 (identify the relevant PNP), the equivalence ratio, , is selected. For Step 3 (determine an analytical formula for the PNP), Equations (1) and (2) are utilized.
For Step 4 (specify the suitable value or range for the PNP), assuming the maximized adiabatic conditions, is used. The choice to assign unity to the equivalence ratio is to avoid under- or over-ventilation conditions for the fire while attempting to ensure that the HGL temperature is maximized conservatively.
For Step 5 (decompose the PNP to generate the surrogate values of the input parameters of concern), by reorganizing Equations (1) and (2), the two input parameters of concern identified in Step 1 can be formulated as follows: . Since there are two unknowns in this equation ( and ), there are infinite combinations that can satisfy this relationship. In this example, based on expert opinion from the plant crew, the height of the natural vent is assumed to be 1 . The equation is simplified as . By setting , the effective vent area is then obtained as . If there is significant uncertainty about the proper value of , sensitivity analysis should be conducted to assess the impact of such uncertainty and justify the choice of the specific value by either showing the uncertainty is not influential or by choosing the conservative value by taking the input value leading to the harshest condition.
For Step 6 (run the simulation model utilizing the generated surrogate values of the input parameters), based on the above decomposition, the natural vent can be modeled as a 0.266 by 1 opening.
3. Development of an Automated Platform, Equipped with the PNP Decomposition Process, for Scenario Screening in Fire PRA
This section offers a computational platform, equipped with the PNP decomposition (explained in Section 2), for scenario screening analysis in the fire PRA of NPPs. The proposed computational platform (called “SoTeRiA-Fire”) automates the PNP decomposition process and seamlessly integrates it with other fire PRA tasks.
The screening analysis in fire PRA corresponds to the Fire Scenario Selection and Analysis (FSS) element in the ASME/ANS PRA standard [20], which dominantly corresponds to Task 8 (Scoping Fire Modeling) and Task 11 (Detailed Fire Modeling) of the NUREG/CR-6850 methodology [21]. The SoTeRiA-Fire platform focuses on automating the technical fire analysis tasks in the FSS, encompassing two main features: (i) calculation of the probability of fire-induced target damage, including the evaluation of (a) the fire-generated conditions with the consideration of fire spread to secondary combustibles, (b) the safety target damage likelihood, and (c) fire detection and suppression activities; and (ii) consideration of multi-compartment fire scenarios.
Section 3.1 shows the generic fire hazard progression scenarios used as a logical basis of the SoTeRiA-Fire platform. Section 3.2 describes the SoTeRiA-Fire platform from the viewpoint of logical connections among various modules.
3.1. Fire Hazard Progression Scenarios in SoTeRiA-Fire Computational Platform
The fire hazard progression scenario in the SoTeRiA-Fire platform depicts both single- and multi-compartment fire scenarios involving potential ignition of secondary/intervening combustibles. Figure 3 shows the general event tree for the analysis in the SoTeRiA-Fire platform. The pivotal events included in Figure 3 are described in Table 1.
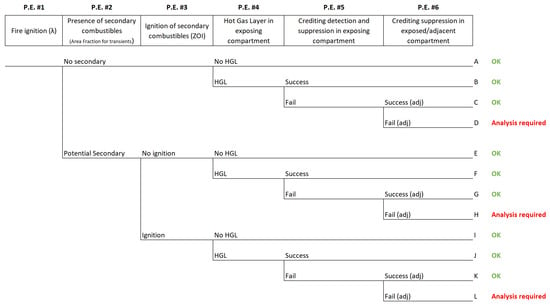
Figure 3.
General event tree of the fire hazard scenario analysis for the SoTeRiA-Fire platform.

Table 1.
Pivotal events in the fire hazard scenario logic (Figure 3).
Utilizing the results of other submodules of the SoTeRiA-Fire platform (explained in Section 3.2), the platform quantifies the frequencies of individual end states of the event tree; for instance, evaluating end states , , and which, together, constitute the total frequency for a multi-compartment scenario, computed by Equation (3).
where
- : The fire ignition frequency for scenario (1/year).
- : The failure probability of fire barriers in scenario . In this study, the generic values for different fire barrier types provided in Table 11-3 of NUREG/CR-6850, Vol. 2 [21], are utilized.
- : The probability of the presence of secondary combustibles (cable trays) in scenario .
- : The severity factor at the location of the nearest target in scenario . This can be either a safety target or secondary combustibles.
- : The probability that damaging HGL conditions exist in scenario given the status of secondary combustible ignition (), i.e., . In cases where secondary combustibles do not ignite, SoTeRiA-Fire conducts HGL analysis to estimate the damage conditions from the main fire only.
- : The non-suppression probability (NSP) for the exposing compartment (where the main initial fire is located) in scenario .
- : The NSP for the exposed adjacent compartment in scenario .
The output from Equation (3) is the updated frequency () of fire scenarios resulting in the formation of a damaging HGL in the adjacent exposed compartment.
3.2. SoTeRiA-Fire Submodules to Quantify the Fire Hazard Progression Event Tree
The SoTeRiA-Fire submodules assemble the input parameters, conduct the required input data processing, and construct the input files for the CFAST code [33]. SoTeRiA-Fire then analyzes various combinations or ranges of certain input parameters based on the fire propagation event tree (Figure 3) and prepares the outputs to be post-processed for the scenario screening. Another important function is the incorporation of the V&V process for CFAST based on NUREG-1824, Supplement 1 [28], and NUREG-1934 [29].
For pivotal event #1 in Figure 3, two types of initial ignition sources are considered: electrical enclosures modeled using NUREG-2178, Vol. 1 [34], and transient fires modeled using NUREG-2233 [35].
For pivotal events #2 and #3, if secondary or intervening combustibles exist in the scenario, CFAST predicts the temperatures and incident heat flux at the locations of the secondary combustibles, which are used to estimate the probability of a secondary combustible ignition. The platform is capable of modeling fire spread in multiple configurations of cable trays utilizing the Flame Spread over Horizontal Cable Trays (FLASH-CAT) model [36].
For pivotal event #4, the HGL temperature is computed by CFAST and compared with the cable damage thresholds [37] to estimate the time to a damaging HGL. To evaluate fire-induced cable damage, two approaches are available in SoTeRiA-Fire: the point-value damage thresholds and the heat soak method [38].
For pivotal events #5 and #6, the platform is equipped with a detection-suppression event tree and a non-suppression curve adopted from NUREG-2169 [39] to estimate NSP based on the time to damaging conditions computed by CFAST. Currently, SoTeRiA-Fire allows the user to utilize two detection and suppression event trees to calculate the total NSP: the generic event tree provided in Appendix P, NUREG/CR-6850, Vol. 2 [21], and the event tree provided in NUREG-2230 [40] which is specifically for electrical cabinet fires.
In CFAST analysis, SoTeRiA-Fire allows the user to utilize the PNP decomposition (Section 2) for generating surrogate input values. The platform is currently equipped with options for decomposing two fire PNPs, the CAR and the equivalence ratio, using the procedure illustrated in Section 2.3. These PNPs are chosen since, according to the authors’ experience in conducting fire modeling for NPPs, the use of these two PNPs can lead to a significant reduction in the resources required for input data collection.
3.2.1. Flowchart of SoTeRiA-Fire Modules
The flowchart of the SoTeRiA-Fire platform is shown in Figure 4. SoTeRiA-Fire reads the input file (spreadsheet) using the Platform (Module 1 in Figure 4). The Platform controls the information and data communication among the modules and submodules. It passes the data to the InpP (Module 2), which parses the CFAST input files and, using test processing, plugs the input values extracted from the spreadsheet into the corresponding lines in the CFAST input files.
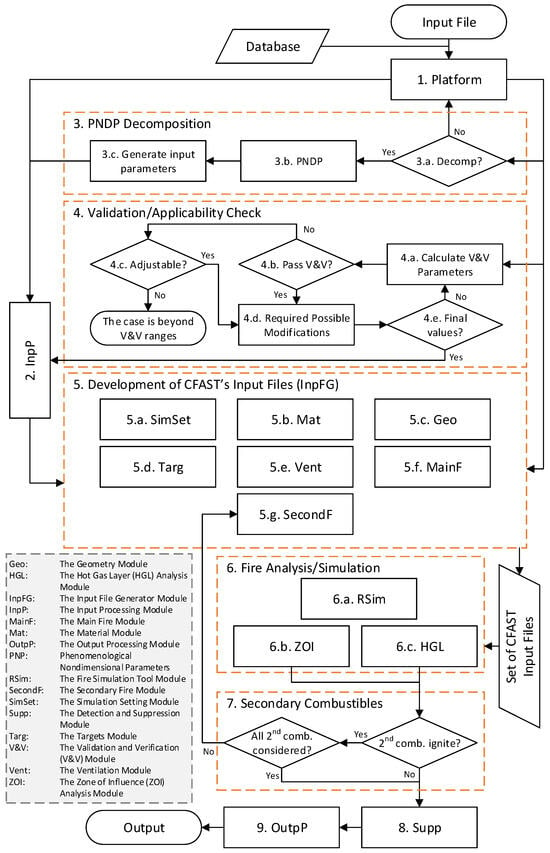
Figure 4.
Flowchart of the SoTeRiA-Fire modules and submodules.
The PNP decomposition (Module 3) can be used to generate surrogate values for some of the input parameters. Submodules 3.a, 3.b, and 3.c show a simplified representation of the PNP decomposition process described in Section 2. Currently, this module is equipped with the computational algorithm to decompose the CAR and the equivalence ratio using the procedure illustrated in Section 2.3. The surrogate values of some of the input parameters are provided to allow the InpP module to be incorporated into the CFAST input files.
Next is the V&V (Module 4), where the PNPs are evaluated (Submodule 4.a) to check the applicability of CFAST. This submodule utilizes the NUREG-1934 approach for V&V [29] with the updated experimental V&V ranges provided in NUREG-1824, Supplement 1 [28]. Once the value of the PNP is computed, it is checked against the V&V ranges (Table 3-3 in Ref. [28]). If the PNP value is within the range, the simulation tool is determined to be applicable to the problem being analyzed. If some of the PNP values fall outside of the V&V ranges, this submodule checks whether there is a possibility of adjusting them in a conservative manner that complies with regulatory and industry practices. If it is possible to adjust certain input parameters so that the corresponding PNP remains within the V&V range, these changes are made in Submodule 4.d. If the adjusted input values are confirmed by the user, they are passed to the InpP (Module 2) to be used in the CFAST input files; otherwise, the V&V is reinitiated to identify any potential modifications or to terminate the analysis.
The development of the input files of the specified fire simulation tool begins through the InpFG, Module 5. This module establishes the required communication among various submodules used to define parts of the CFAST input files. The MainF (Submodule 5.f) defines the initial or primary fire specifications and characteristics. For the definition of the secondary fire in the intervening secondary cable trays, the SecondF, Submodule 5.g, utilizes the FLASH-CAT model [36] for modeling fire spread in the cable trays. In complex cable tray configurations that have combinations of horizontal and vertical cable trays, CFAST is used iteratively to define fire propagation. If secondary combustibles exist, they are not analyzed or incorporated in the analysis until the initial primary ignition source is analyzed in Module 6, the Fire Analysis/Simulation. This is to determine, through a zone-of-influence (ZOI) analysis (Submodule 6.b) and HGL analysis (Submodule 6.c), whether the secondary combustibles ignite.
After generating the required set of the CFAST input files, the RSim, Submodule 6.a, executes the required command to run the simulation tool to generate the fire analysis results and the temperature and heat flux predictions as key performance measures. Currently, the ZOI submodule, Submodule 6.b, conducts the ZOI analysis in the vertical direction only. This approach is based on one of the assumptions of the FLASH-CAT model where the fire is assumed to be beneath the lowest tray. The ignition criteria for bulk cable/tray ignition criteria provided in FAQ 16-0011 [37] is used in the ZOI analysis. The HGL analysis is conducted in the HGL submodule, Submodule 6.c, by analyzing the temperature of the HGL developed in the compartment. One critical output from the fire analysis/simulation, Module 6, is the estimated time for a damaging HGL to occur. This time-to-damage is calculated using the cable damage/ignition criteria [37]. Either the damage threshold approach or the heat soak method [38] can be used to calculate the time-to-damaging conditions. Module 7 ensures that all the analyses and iterations over all the potential secondary combustibles are executed. These analyses are conducted by extracting data from the “compartment” data output file generated by CFAST as a .csv file.
Once the time-to-damage is obtained, the Supp, Module 8, uses it to estimate NSPs by solving detection and suppression event trees for both exposing and exposed compartments (pivotal events, #5 and #6 in Figure 3). In multi-compartment scenarios, SoTeRiA-Fire utilizes the same HGL temperature of the exposing compartment (with the initial fire) when analyzing NSP for the adjacent exposed compartment as a conservative assumption. The OutpP module, Module 9, generates the required output files, including tabulated data for the various physical outputs (e.g., the time profile for the HGL temperature), graphical plots for the time profiles of the physical outputs, and the total frequency for the fire hazard scenario by evaluating end states D, H, and L in Figure 3.
4. Application of SoTeRiA-Fire Computational Platform to Multi-Compartment Fire Analysis
In this section, the SoTeRiA-Fire platform is applied to a multi-compartment fire scenario at an NPP. The details of the case study are provided in Section 4.1. The results of the case study application are shown in Section 4.2.
4.1. Case Study Description
In this multi-compartment fire scenario, the initial ignition source in the exposing fire compartment is a transient fire, while there are two stacks of three horizontal cable trays as potential intervening combustibles. The ignition frequency of the initial transient fire is 2.84 10−5 per year [41]. The height of the transient fire base is 1.5 from the floor, while the height of the lowest cable tray is 3 m. Two different time profiles for the HRR of the transient fire are used. The first profile (referred to as Profile #1) is established based on NUREG-2233 [35], where the growth time is 218 s, the peak duration is 56 s, and the decay duration is 1295 s. The second profile (referred to as Profile #2) is established using the case study in Appendix E, NUREG-1934 [29], as a reference. In this second profile, the growth time is 480 , the peak duration is 320 s, and the decay duration is 800 s. Appendix A provides further input data used in this case study, including the material properties and the FLASH-CAT model parameters for cable trays.
The rate of fire suppression for the NSP calculation is (for transient fires, from Table 5-1 in Ref. [39]). It is assumed that HGL damaging conditions in the exposing compartment would be enough to damage safety targets in the adjacent exposed compartment. Using the conditional probabilities expressed in Equation (3), this means that the NSP of the adjacent exposed compartment (where the safety targets are located) is assumed to be equal to the NSP of the exposing compartment (with the ignition source), i.e., .
The ventilation conditions were generated based on the PNP decomposition of the equivalence ratio. Choosing to decompose the equivalence ratio was driven by the difficulty of collecting the data on the Heating, Ventilation, and Air Conditioning (HVAC) system and existing penetrations and openings in the compartment. As discussed in Section 2.3, the equivalence ratio () of unity is used. This assumption maximizes the adiabatic conditions of the flames; thus, the phenomenological understanding justifies that would lead to conservative analysis. The adequacy of this assumption is further discussed in Section 5.
4.2. Case Study Results
Table 2 shows the results for the case study obtained by the SoTeRiA-Fire platform. Four damage modes are computed by CFAST [33]: (i) surrounding gas temperature []; (ii) the target surface temperature []; (iii) target internal temperature [], i.e., the interior temperature of the target at its centerline; and (iv) the incident heat flux [], defined as the total heat flux striking the surface of the target. For each damage mode, four fire-induced damage metrics are estimated, namely the severity factor (i.e., the probability that the postulated fire would cause the target damage), the lowest cable tray ignition time [s], the time-to-damaging HGL [s], and NSP. The severity factor is computed using the NUREG/CR-6850 method (Section 8.5.5 of NUREG/CR-6850, Vol. 2 [21]). The cable ignition time and time-to-damaging HGL are computed by identifying the time for each damage parameter (i.e., temperature or heat flux) to reach the cable damage thresholds. The NSP is calculated based on Appendix P of NUREG/CR-6850, Vol. 2 [21], using the rate of fire suppression, [39].

Table 2.
Sample results for the two fire growth profiles.
Comparing the damage metrics in Table 2, the first HRR profile, compared to Profile #2, results in a shorter ignition time for the lowest cable tray, a shorter time-to-damaging HGL, and, thus, a higher non-suppression probability. This tendency is expected since the first HRR profile progresses more rapidly than the second HRR profile; therefore, damaging conditions occur sooner, which is conservative.
To demonstrate the quantification of the overall fire scenario frequency, Equation (3) is used to compute the updated ignition frequency, . In this case study, the following values and assumptions are utilized:
- , which is the ignition frequency for the transient fires in this fire compartment [41].
- , the sum of all three types of fire barriers [21].
- , because this scenario contains secondary combustibles (cable trays) and the fraction area for the transient fires is assumed to be 1 (i.e., transient fires can occur anywhere on the floor).
- computed based on the surrounding gas temperature in Table 2.
- , since CFAST outputs show that damaging HGL conditions are not reached when the secondary cable ignition does not occur.
- , since damaging HGL conditions are reached. This is expressed by identifying a time-to-damaging HGL value for the case of combined fire.
- , assuming the detection events in the fire hazard progression event tree (Figure 3) have failed.
Therefore, the updated fire ignition frequency is calculated as the following:
Thus, the total frequency of the multi-compartment scenario is reduced by five orders of magnitude compared to the initial fire ignition frequency. If the user chooses to compute the CDF for each fire scenario, the SoTeRiA-Fire platform multiplies the total fire scenario frequency with the Conditional Core Damage Probability (CCDP). For instance, in this case study, , the fire scenario CDF is computed as follows:
The computed CDF is negligibly small compared to the quantitative screening criteria in fire PRA (e.g., for the fire compartment CDF [21]), indicating that the multi-compartment fire scenario is not a major risk contributor in this case study.
The typical run time of the SoTeRiA-Fire platform for each ignition source is in the order of one to ten minutes. On average, using a typical PC, SoTeRiA-Fire takes 7.5 to process input data, prepare required variables, and construct all the required CFAST input files. It takes 37.2 to run a single case for severity factor analysis using CFAST on average, and about 50 to run a single case for HGL analysis and generate the NSP. The maximum run time (around 15–20 min) is required in cases with complex HRR profiles (e.g., multiple fire sources) and complex cable tray configurations.
4.3. Discussion: Evaluation of the Adequacy of SoTeRiA-Fire
The SoTeRiA-Fire platform intends to support the fire scenario screening; hence, the adequacy of its analysis and outputs should be discussed in the context of fire scenario screening in support of fire PRA of NPPs.
The crucial aspect of the adequacy of SoTeRiA-Fire is the validation of physical models used in the platform. SoTeRiA-Fire addresses this aspect by integrating the physical models that have been verified, validated, and documented by the NRC for the use in fire PRA of NPPs. The CFAST code, used as the core simulation model in SoTeRiA-Fire to predict the fire-induced damaging conditions for cable targets, has been verified and validated in NUREG-1824, Vol. 5 [27], and Supplement 1 [28]. As described in Section 3.2.1, the V&V module (#4 in Figure 4) implements the regulatory-accepted V&V procedure adopted from NUREG-1934 [29]. The other physical models, such as the FLASH-CAT model [36] and the HRR curve for a transient fire source [29,35], are also adopted from regulatory documents. Integrating the physical models that have been accepted and documented by the regulatory agency benefits the high quality of the SoTeRiA-Fire platform.
The adequacy of the platform in this aspect is constrained by the limitations in the state-of-practice of the available physical models and V&V procedure. One notable limitation is the implementation of the fire models beyond the experimental validation range provided in NUREG-1824, Supplement 1 [28]. In such cases, the analyst would need to assess the suitability of the fire model for the specific application being analyzed. As suggested in NUREG-1934 [29], sensitivity and comparative analyses should be performed; however, the analytical process involves subtlety, necessitating case-specific engineering judgment based on physical understanding and knowledge of the fire simulation tool. In the current SoTeRiA-Fire platform, if the case falls outside of the V&V range (as a result of Module 4 in Figure 4), the user is asked to evaluate the suitability of the fire model for the specific case being analyzed. Provided that the SoTeRiA-Fire platform is used to support the fire scenario screening, the adequacy of the analysis should be assessed based on whether a reasonably conservative output is generated, which helps avoid a false negative result in scenario screening, where the risk significant scenarios are screened out. This perspective is aligned with Principle “B” of the PNP decomposition (Section 2.1), stating that the resultant analysis should ensure that a certain hazard or event would propagate and develop in a manner harsher than reality; hence, the resultant risk information would be steered toward the safer direction.
In the case study, sensitivity analysis is conducted to test a lower equivalence ratio, varying it closer to the upper bound of the validation range of CFAST, 0.2–0.6 [28], using the second HRR profile (Profile #2). As shown in Table 3, lowering the value of the equivalence ratio led to a relatively longer time-to-damaging HGL and, thus, the NSP was lowered. This observation indicates that the surrogate values for the natural vent created using would provide reasonably conservative results, i.e., a shorter time-to-damaging HGL and an increased NSP.

Table 3.
Maximum values among all four damage modes for two values of the equivalence ratio () using HRR profile #2.
5. Concluding Remarks
Using simulation models is a crucial area of research and development for PRA of NPPs; however, the time and resources required for collecting and extracting data to determine the values of the input parameters can be significant. To address this concern, this article develops a structured methodology to generate surrogate values of simulation input parameters by decomposing phenomenological nondimensional parameters (PNPs). These surrogate values of physical input quantities are then utilized to run the simulation model in PRA, considerably reducing the data collection efforts. This study offers a methodological procedure for the proposed PNP decomposition (Section 2). This study also develops a computational platform equipped with the PNP decomposition (Section 3) for scenario screening in fire PRA. This platform (called “SoTeRiA-Fire”) integrates the PNP decomposition seamlessly with other tasks and analyses in fire scenario screening.
The SoTeRiA-Fire platform can help reduce the workload and resources for fire scenario screening as it has two crucial capabilities: (i) it enables the utilization of PNPs to augment the actual as-designed, as-operated plant data and, thus, allows an analyst to avoid making extensive data collection efforts; and (ii) offers a fire PRA platform applicable to various fire scenarios without the need to develop subroutines and codes on a case-by-case basis. The applicability of SoTeRiA-Fire is demonstrated through a multi-compartment fire case study (Section 4). In this application, the PNP decomposition methodology is demonstrated for the ventilation condition of the fire compartment with the intent of reducing the need for collecting detailed ventilation data at the scenario screening stage.
Further research should focus on conducting thorough verification of the SoTeRiA-Fire platform, integrating other fire models (in addition to CFAST) with different levels of resolution (e.g., Fire Dynamics Simulator [FDS]), and advancing the treatment of complex cable tray configurations. Currently, the SoTeRiA-Fire platform is equipped with the PNP decomposition for two fire PNPs: compartment aspect ratio and equivalence ratio. Future research can further extend the platform to incorporate other fire PNPs. Additionally, the effectiveness of SoTeRiA-Fire in reducing the resource requirement for data collection should be evaluated further. A fire PRA analyst, who conducted data collection for the case study (Section 4), estimated that, compared to the traditional approach that collects detailed ventilation data, the PNP decomposition in SoTeRiA-Fire reduces the time for data collection by 35%. Future research should perform a more formal resource analysis to establish a quantitative case for resource saving achieved by SoTeRiA-Fire grounded on the PNP decomposition.
Author Contributions
Conceptualization, S.A., T.S., S.R., E.K., S.H. and Z.M.; methodology, S.A., T.S., S.R., S.H. and Z.M.; software, S.A.; validation, S.A., T.S. and S.R.; formal analysis, S.A.; investigation, S.A., T.S., S.R., B.R. and K.K.; resources, T.S., S.R., B.R., K.K. and Z.M.; data curation, S.A.; writing—original draft preparation, S.A., T.S. and Z.M.; writing—review and editing, S.A., T.S., S.R., B.R., K.K., S.H. and Z.M.; visualization, S.A.; supervision, T.S., S.R., E.K. and Z.M.; project administration, T.S., B.R., K.K. and Z.M.; funding acquisition, T.S., S.R., E.K. and Z.M. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the U.S. Department of Energy (DOE), Office of Science, Office of Nuclear Energy, under Award Number DE-NE0008856.
Data Availability Statement
Dataset available on request from the authors.
Acknowledgments
The authors would like to thank Andrea Roy for his help with the code compilation of SoTeRiA-Fire computational platform.
Conflicts of Interest
The authors declare no conflict of interest. Authors Brian Ratte and Kristin Kaspar were employed by South Texas Project Nuclear Operating Company. Author Sean Hunt was employed by Jensen Hughes. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. Additional Fire Modeling Data for the Case Study

Table A1.
Compartment geometry and dimensions.
Table A1.
Compartment geometry and dimensions.
| Properties | Unit | Value |
|---|---|---|
| Height | 3.66 | |
| Area | 54.26 | |
| Wall, ceiling, and floor thickness | 0.3048 |

Table A2.
Thermal properties for materials used in defining compartment geometry and targets/devices.
Table A2.
Thermal properties for materials used in defining compartment geometry and targets/devices.
| Properties | Unit | Concrete | Cable Jacket |
|---|---|---|---|
| Thermal conductivity | 0.0016 | 0.000192 | |
| Density | 2400 | 1380 | |
| Specific heat | 0.75 | 1.289 | |
| Thickness of the material | 0.3048 | 0.0015 | |
| Emissivity | 0.94 | 0.95 |

Table A3.
Main fire properties.
Table A3.
Main fire properties.
| Properties | Unit | Value |
|---|---|---|
| Peak HRR (for TCCL Transient Fire) | ||
| Fire position | Compartment’s Center | |
| Height of the base of the fire | 1.5 | |
| Fire base area | 1 | |
| Heat of combustion | 20,900 | |
| Radiative fraction | 0.35 | |
| CO yield and soot yield | 0.043 and 0.052 | |
| Carbon, chlorine, hydrogen nitrogen, oxygen | 4, 0, 7, 0, 2.5 |

Table A4.
Secondary fire: cable tray fire and FLASH-CAT model properties (assuming thermoplastic [TP] cables).
Table A4.
Secondary fire: cable tray fire and FLASH-CAT model properties (assuming thermoplastic [TP] cables).
| Properties | Unit | Value |
|---|---|---|
| Lowest cable tray height | 3 | |
| Number of cable trays | 3 | |
| Spacing between cable trays | 0.47 | |
| Length of the cable trays | 2.2 | |
| Width of the cable trays | 0.45 | |
| Spread angle | Degrees (°) | 35 |
| No. of cables in a cable tray | 50 | |
| Horizontal spread rate | 3.2 | |
| Heat of combustion | 16,000 | |
| HRRPUA (TP cable) | 250 | |
| Plastic mass fraction | 0.42 | |
| Mass/length, m’ | 0.37 | |
| Char yield, ν | 0 | |
| CO yield and soot yield | 0.147 and 0.136 | |
| Carbon, chlorine, hydrogen nitrogen, oxygen | 2, 0.5, 3.5, 0, 0 |
References
- Bui, H.; Sakurahara, T.; Pence, J.; Reihani, S.; Kee, E.; Mohaghegh, Z. An algorithm for enhancing spatiotemporal resolution of probabilistic risk assessment to address emergent safety concerns in nuclear power plants. Reliab. Eng. Syst. Saf. 2019, 185, 405–428. [Google Scholar] [CrossRef]
- Alkhatib, S.; Sakurahara, T.; Reihani, S.; Kee, E.; Ratte, B.; Mohaghegh, Z. Academia-Industry Collaboration to Advance Screening Processes in Fire PRA of Nuclear Power Plants. In Proceedings of the 30th European Safety and Reliability (ESREL) Conference and the 15th Probabilistic Safety Assessment and Management (PSAM) Conference, Venice, Italy, 1–5 November 2020. [Google Scholar]
- Nuclear Energy Institute Letter to the U.S. Nuclear Regulatory Commission (NRC), “Industry Support and Use of PRA and Risk-Informed Regulation” (ADAMS Accession Number: ML13354B997). December 2013. Available online: https://adamswebsearch2.nrc.gov/webSearch2/main.jsp?AccessionNumber=ML13354B997 (accessed on 20 June 2024).
- Kaspar, K.; Ratte, B.; Billings, M.A.; Mohaghegh, Z.; Sakurahara, T.; Reihani, S.; Kee, E.; Alkhatib, S.; Albati, M.; Von Thaden, T.; et al. Integrated Fire Probabilistic Risk Assessment (PRA) Modeling in Support of Operational Efficiency; Office of Scientific and Technical Information (OSTI): Oak Ridge, TN, USA, 2022.
- Prescott, S.R.; Christian, R.; Vedros, K.G.; Lawrence, S. Industry Level Integrated Fire Modeling Using Fire Risk Investigation in 3D (FRI3D); Idaho National Laboratory (INL): Idaho Falls, ID, USA, 2021.
- Prescott, S.; Christian, R.; Sampath, R.; Biersdorf, J. Fire Risk Investigation in 3D (FRI3D) Software and Process for Integrated Fire Modeling; INL/EXT-20-59506; Idaho National Laboratory: Idaho Falls, ID, USA, 2020.
- Peacock, R.D.; McGrattan, K.B.; Forney, G.P.; Reneke, P.A. CFAST, the Consolidated Model of Fire Growth and Smoke Transport, Volume 1: Technical Reference Guide; NIST Technical Note 1889v1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023.
- Kang, D.I.; Han, S.H.; Yoo, S.Y. Development of the IPRO-ZONE for internal fire probabilistic safety assessment. Nucl. Eng. Des. 2013, 257, 72–78. [Google Scholar] [CrossRef]
- Kang, D.I.; Han, S.H.; Kim, K. An approach to the construction of a one top fire event PSA model. Nucl. Eng. Des. 2009, 239, 2514–2520. [Google Scholar] [CrossRef]
- Kang, D.; Lee, Y.; Han, S.-H. Construction and Quantification of the One Top model of the Fire Events PSA. In Proceedings of the Transactions of the Korean Nuclear Society Spring Meeting, Gyeongju, Republic of Korea, 29–30 May 2008. [Google Scholar]
- Hostikka, S.; Keski-Rahkonen, O. Probabilistic simulation of fire scenarios. Nucl. Eng. Des. 2003, 224, 301–311. [Google Scholar] [CrossRef][Green Version]
- Anderson, J.; Mossberg, A.; Gard, E.; McNamee, R. Investigating Machine Learning for Fire Sciences: Literature Review and Examples; RISE Report 2021: 59; RISE Research Institutes of Sweden: Gothenburg, Sweden, 2021; ISBN 978-91-89385-49-8. [Google Scholar]
- Hodges, J.L.; Lattimer, B.Y.; Luxbacher, K.D. Compartment fire predictions using transpose convolutional neural networks. Fire Saf. J. 2019, 108, 102854. [Google Scholar] [CrossRef]
- Worrell, C.; Luangkesorn, L.; Haight, J.; Congedo, T. Machine Learning of Fire Hazard Model Simulations for Use in Probabilistic Safety Assessments at Nuclear Power Plants. Reliab. Eng. Syst. Saf. 2019, 183, 128–142. [Google Scholar] [CrossRef]
- Vinod, G.; Saraf, R.; Ghosh, A.; Kushwaha, H.; Sharma, P. Insights from fire PSA for enhancing NPP safety. Nucl. Eng. Des. 2008, 238, 2359–2368. [Google Scholar] [CrossRef]
- Berg, H.P.; Breiling, G.; Hoffmann, H.H. Procedures and applications to enlarge the level 1+ PSA to internal fires in German nuclear power plants. Reliab. Eng. Syst. Saf. 1997, 58, 109–117. [Google Scholar] [CrossRef]
- Siu, N.O.; Melly, N.; Nowlen, S.P.; Kazarians, M. Fire Risk Analysis for Nuclear Power Plants. In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; pp. 3326–3369. [Google Scholar]
- Kahia, S.; Brinkman, H.; Bareith, A.; Siklossy, T.; Vinot, T.; Mateescu, T.; Espargillière, J.; Burgazzi, L. Report 6: Guidance Document-MAN-MADE Hazards and ACCIDENTAL AIR; 2017. Reference IRSN PSN/RES/SAG/2017-00013. Available online: http://asampsa.eu/wp-content/uploads/2017/03/ASAMPSA_E-D50.20-REPORT_6-MAN-MADE-HAZARDS-AND-ACCIDENTAL-AIRCRAFT-CRASH.pdf (accessed on 20 June 2024).
- Lybarskiy, A.; Rozin, V.; Kouzmina, I.; Kazarians, M. Development of Fire PSA Methodology and its Application in a Study for Novovoronezh-5 NPP. In Proceedings of the Probabilistic Safety Assessment and Management: PSAM 7—ESREL’04, Berlin, Germany, 14–18 June 2004; Springer: London, UK; Volume 6, pp. 1982–1987. [Google Scholar]
- ASME/ANS RA-S-1.1-2022; Standard for Level 1/Large Early Release Frequency Probabilistic Risk Assessment for Nuclear Power Plant Applications. ASME/ANS: New York, NY, USA, 2022.
- EPRI/NRC-RES Fire PRA Methodology for Nuclear Power Facilities: Volume 2: Detailed Methodology; NUREG/CR-6850, EPRI TR-1011989; Electric Power Research Institute (EPRI): Palo Alto, CA, USA; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Rockville, MD, USA, 2005.
- Verification and Validation of Selected Fire Models for Nuclear Power Plant Applications, Volume 1: Main Report; NUREG-1824, EPRI 1011999; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Rockville, MD, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2007.
- Karlsson, B.; Quintiere, J. Enclosure Fire Dynamics; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Watts, J.M., Jr.; Wieczorek, C.J. SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2015. [Google Scholar]
- Quintiere, J.G. Fundamentals of Fire Phenomena; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Quintiere, J.G. Principles of Fire Behavior, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Verification and Validation of Selected Fire Models for Nuclear Power Plant Applications, Volume 5: Consolidated Fire and Smoke Transport Model (CFAST); NUREG-1824, EPRI 1011999; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Rockville, MD, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2007.
- Verification and Validation of Selected Fire Models for Nuclear Power Plant Applications: Supplement 1; NUREG-1824 Supplement 1, EPRI 3002002182; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Washington, DC, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2016.
- Nuclear Power Plant Fire Modeling Analysis Guidelines (NPP FIRE MAG); NUREG-1934, EPRI 1023259; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Washington, DC, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2012.
- U.S. Nuclear Regulatory Commission (NRC). Glossary of Risk-Related Terms in Support of Risk-Informed Decisionmaking (NUREG-2122); U.S. Nuclear Regulatory Commission (NRC): Washington, DC, USA, 2013.
- U.S. Nuclear Regulatory Commission (NRC). Nuclear Power Plant Fire Modeling Analysis Guidelines (NPP FIRE MAG); NUREG-1934; U.S. Nuclear Regulatory Commission (NRC): Washington, DC, USA, 2012.
- Buchanan, A.H.; Abu, A.K. Structural Design for Fire Safety; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Peacock, R.D.; Reneke, P.A.; Forney, G.P. CFAST, the Consolidated Model of Fire Growth and Smoke Transport, Volume 2: User’s Guide; NIST Technical Note 1889v2; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023.
- Refining and Characterizing Heat Release Rates from Electrical Enclosures during Fire (RACHELLE-FIRE), Volume 1: Peak Heat Release Rates and Effect of Obstructed Plume; NUREG-2178, V1, EPRI 3002005578; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Rockville, MD, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2015.
- Methodology for Modeling Transient Fires in Nuclear Power Plant Fire Probabilistic Risk Assessment; Draft for Comment; NUREG-2233, EPRI 3002016054; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Washington, DC, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2019.
- McGrattan, K.; Lock, A.; Marsh, N.; Nyden, M.; Bareham, S.; Price, M.; Morgan, A.B.; Galaska, M.; Schenck, K.; Stroup, D. Cable Heat Release, Ignition, and Spread in Tray Installations During Fire (CHRISTIFIRE) Phase 1: Horizontal Trays (NUREG/CR-7010, Vol. 1); Office of Nuclear Regulatory Research: Washington, DC, USA, 2012.
- FAQ 16-0011; Cable Tray Ignition; Rev. 1; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2016.
- Refining and Characterizing Heat Release Rates from Electrical Enclosures During Fire (RACHELLE-FIRE), Volume 2: Fire Modeling Guidance for Electrical Cabinets, Electric Motors, Indoor Dry Transformers, and the Main Control Board; NUREG-2178, V2, EPRI 3002016052; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Rockville, MD, USA; Electric Power Research Institute (EPRI): Palo Alto, CA, USA, 2019.
- Nuclear Power Plant Fire Ignition Frequency and Non-Suppression Probability Estimation Using the Updated Fire Events Database: United States Fire Event Experience through 2009; 3002002936/NUREG-2169; EPRI: Palo Alto, CA, USA; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Washington, DC, USA, 2014.
- Methodology for Modeling Fire Growth and Suppression Response for Electrical Cabinet Fires in Nuclear Power Plants; 3002016051/NUREG-2230; EPRI: Palo Alto, CA, USA; U.S. Nuclear Regulatory Commission, Office of Nuclear Regulatory Research (RES): Washington, DC, USA, 2020.
- Liming, J.K. South Texas Project Electric Generating Station Fire Probabilistic Risk Assessment Upgrade Project—2018 Work Scope; Final Report, Revision 1, R-4056282-2079; ABC Consulting: Frisco, TX, USA, 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).