Abstract
The numerical analysis for the controllability assessment of a new design nuclear reactor is typically carried out by means of complex multiphysics codes, solving high fidelity partial differential equations governing the system neutronics as well as the fluid dynamics. Multiphysics codes deliver very accurate solutions at the expense of high computational times, which could be of several hours depending on the specific case study. In this work, to efficiently reduce runtimes, a sensitivity analysis (SA) is carried out to identify the most important input parameters affecting the solution of a multiphysics model developed for the controllability assessment of molten salt reactors (MSRs). The numerical modeling of these innovative systems is fundamental to allow for a safer and more sustainable power production (e.g., due to the lower radiotoxicity of the actinide inventory in MSRs and to the possibility of operation at atmospheric pressure). In this paper, four global sensitivity measures are calculated first, including the Pearson correlation coefficient, δ, Kolmogorov–Smirnov and Kuiper indices, whose results are aggregated by an ensemble strategy and confirmed by the CUmulative SUm of NOrmalized Reordered Output (CUSUNORO) plot. The results of the SA point out that the fuel density is the most important parameter yielding the largest variations in the system reactivity, fundamental for guaranteeing the MSR controllability. In light of this result, a simplified, surrogate model is then developed, which uses density as the only input parameter to determine reactivity, guaranteeing runtime reductions from several hours to a few seconds and, at the same time, a comparable level of accuracy of the multiphysics model. This result demonstrates the capability of global sensitivity analysis approaches to effectively identify the most relevant parameters in MSR systems, supporting the development of simplified, control-oriented models for these innovative reactors.
1. Introduction
Molten salt reactors (MSRs) are circulating fuel nuclear reactors in which a mixture of molten thorium and uranium fluorides acts as fuel and coolant simultaneously [1]. In recent years, MSRs are gathering a strong interest from the nuclear research community, due to their intrinsic characteristics of safety and sustainability. Thanks to the high boiling point of the molten salts, MSRs can be operated at atmospheric pressure. In addition, the adoption of a closed thorium fuel cycle may lead to an actinide inventory with lower radiotoxicity. Finally, the adoption of a liquid fuel can potentially allow for a significant plant simplification (due to the core homogeneity), as well as a greater compactness as the fission energy is directly released into the coolant [2]. For these reasons, MSRs are strong candidates for a cleaner, safer, and more sustainable power production. At the same time, MSRs raise new technical challenges that call for new simulation tools, tailored to the specificities of these innovative systems. In more detail, compared to traditional solid-fueled reactors, the circulating fuel is a distinguishing feature of MSRs [3,4], leading to completely new design and related technological challenges. Notably, the delayed neutron precursors are not spatially static, as in conventional nuclear systems, but they are dragged by the fuel mixture through the reactor and the external circuits. For this reason, delayed neutrons can be emitted in peripheral regions of the reactor, where the neutron importance with respect to reactivity is lower, or even in the external circuit, where they do not contribute at all to fissions. As a consequence, the coupling between the neutronics and thermo-fluid dynamics of the system is even stronger than in traditional reactors, since the fuel velocity field directly influences the precursor distribution.
Multiphysics approaches provide a good way to inherently couple all the physical phenomena occurring in the reactor in the same simulation environment, offering an efficient way to handle the coupling non-linearities [5]. Multiphysics models of the MSRs have been developed (Cammi et al. [6,7], Aufiero et al. [8,9], Fiorina et al. [10,11]), coupling the neutron diffusion equation with a single-phase, incompressible thermal-hydraulics model, where transport equations for the moving precursors have also been implemented [9]. Furthermore, a Finite Element multiphysics model for MSRs was developed in [12,13,14], while de Oliveira et al. proposed a Finite Volume model using the GeN-Foam code [15]. In addition, capabilities to simulate fuel salt solidification and draining transients in MSRs were developed by Tano et al. [16,17].
In some MSR designs [1], the injection of helium bubbles is foreseen for the removal of gaseous fission products. These helium bubbles not only influence reactivity, due to their negative void coefficient, but also increase the liquid fuel compressibility, which is expected to have a strong impact on fast, reactivity-driven transients, where the finite propagation velocity of pressure waves can lead to delays in the expansion reactivity feedback [18]. Therefore, careful investigation is needed in order to assess the safety of MSRs, also considering the presence of gas bubbles inside the reactor. Both the bubble motion and compressibility effects cannot be described by means of standard single-phase, incompressible thermal-hydraulics models. To address these issues, a multiphysics OpenFOAM solver has been developed in [19,20], coupling the multi-group neutron diffusion equation with a two-fluid, or Euler–Euler [21] model for two-phase, compressible thermal-hydraulics, where the motion of precursors in the liquid fuel is also considered.
These complex multiphysics tools can produce very accurate solutions, being able to catch phenomena that could not be described with simpler approaches. However, this accuracy comes at the expense of large computational times, on the order of several hours.
In order to reduce the computational time for a real-time control analysis and decision support, a surrogate model of the multiphysics model can be beneficial. In this work, sensitivity analysis (SA) methods are first used to identify the most important input parameters of the multiphysics model, to be used to build a simplified surrogate model of the MSR behavior. In general, SA methods fall into two categories: local or global. Local sensitivity approaches like the Tornado diagrams [22] focus on the simulation behavior around certain reference values of the inputs; global sensitivity methods such as the variance-based methods [23] allow the inputs to vary in their entire input [24]. It has been shown that the ensemble of different SA methods can obtain robust and reliable results [25]. In this work, we ensemble four commonly used global sensitivity methods: Pearson correlation coefficient, the Borgonovo δ index, the Kolmogorov–Smirnov index, and the Kuiper index [26]. The uncertainty in the estimates is quantified via bootstrapping and the bias-reducing bootstrap estimates [27]. The results are confirmed by a graphical method called CUSUNORO plots [28,29]. A local approach for the sensitivity analysis of the MSR was proposed in [30], based on the adjoint technique. To overcome some of the common drawbacks of local approaches, a global approach has been applied, for the first time, to study an MSR system. More specifically, local approaches evaluate the importance of one input parameter at a time (neglecting interactions), with other inputs being kept constant at their nominal value, whereas global approaches consider the interactions among all the input parameters and their variability on their whole support of distribution. Consequently, global approaches are more appropriate when applied to analyze strongly non-linear systems, such as MSRs, whose model input parameters typically interact with each other. In this frame, the paper aims at filling the gap, by proposing a global sensitivity analysis of a fast-spectrum MSR.
Following the SA, a surrogate model, based on point kinetics equations, is developed, in which only the most relevant parameters are retained. The purpose of the surrogate model is to achieve lower computational times than the high-fidelity models, providing a simulation tool that is suitable for real-time analysis. Regarding the accuracy of the new approach, the two models are compared, simulating two different accidental transients in an MSR, namely, the super-prompt-critical reactivity insertion and the loss of heat sink accidents.
Point kinetic models of the MSR were proposed in [31,32,33,34,35]. Furthermore, simplified models of MSRs were also developed by using other approaches, e.g., 1D system codes [36]. Independently from the specific approach selected to develop the simplified model, this research aims at demonstrating the suitability of global SA to provide a synthetic overview of the most relevant parameters to be used for model surrogation. In other words, the purpose of this work is (i) to identify the most relevant physical parameters affecting MSR behavior using a global SA approach, (ii) to develop a surrogate MSR model based on the reduced set of most relevant parameters identified by the sensitivity analysis, and (iii) demonstrate that this surrogate model is comparable to more complex ones in terms of accuracy but computationally cheaper. Therefore, the novelty of this work as compared to state-of-the-art literature is that it proves global SA as an effective tool in support of the development of simplified, control-oriented models of MSRs, which are suitable for real-time decision making. It is underlined that, even though point kinetics is selected to develop the surrogate model in this work, the proposed technique can be flexibly applied to any other simplified modeling approach, such as 1D system codes.
The remainder of the paper is organized as follows. Section 2 describes the main features of MSR systems. Section 3 discusses the high-fidelity model. Section 4 presents the SA methods in use. Section 5 reports the SA results. Then, in Section 6, the surrogate model is developed, and in Section 7 its results are compared to the high-fidelity model. Finally, conclusions are provided in Section 8.
2. MSRs
A schematic representation of a fast-spectrum MSR layout is shown in Figure 1 and the main design parameters are listed in Table 1. The high-fidelity simulations presented in Section 7 are carried out using the MSR system described in Figure 1 and Table 1. The salt mixture, which serves simultaneously as fuel and coolant, is circulated through 16 external circuits, where the power produced by fissions is removed by heat exchangers. The helium bubbles are injected in the cold legs, at the bottom of the system, and they are removed at the top, in the hot leg region.
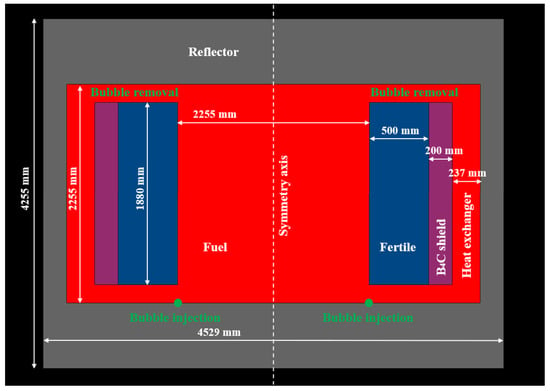
Figure 1.
Layout of the fast-spectrum MSR studied in this work.

Table 1.
Main design parameter values assumed in this work [1,16].
3. The Multiphysics High-Fidelity Model
The multiphysics high-fidelity model solves, at each time step, the system thermal-hydraulics and neutronics in two different cycles, as sketched in Figure 2. The thermal-hydraulics sub-solver is based on the standard OpenFOAM [37] solver “twoPhaseEulerFoam” for the compressible fluid and the bubble modeling, whereas neutronics is described by multi-group neutron diffusion, SP3 and discrete ordinate transport sub-solvers [19,20].
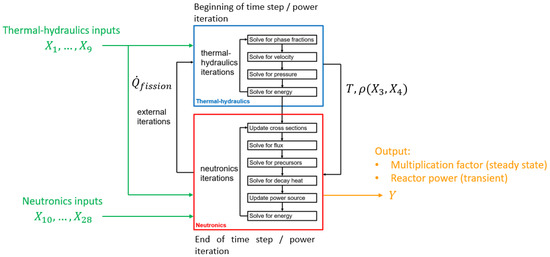
Figure 2.
Logic structure of the multiphysics solver.
The list of the inputs of the multiphysics model, is provided in Table 2, together with their uncertainty distributions. These uncertainty distributions were determined by various authors in previous works, as cited in the last column of Table 2.

Table 2.
List of the multiphysics model inputs.
The thermal-hydraulics solver, fed with the thermal-hydraulics inputs to , finds the phase fractions, the velocity of both phases, pressure, and temperature. Picard iterations are performed until convergence is reached for the solution of the thermal-hydraulic part of the problem. Then, the neutronics solver, fed with the neutronics inputs to , finds the flux, the delayed neutron precursors, and the decay heat. Once the flux (and the fission power in turn) and the decay heat are known, the volumetric power source field is updated and the energy equation is solved again (for this reason, the thermal-hydraulics inputs to are also provided to the neutronics solver). Once the new temperature and density fields of the fuel are calculated, the cross sections are updated and the cycle is repeated with Picard iterations until convergence is reached. In addition, a certain number of external iterations between the thermal-hydraulics and the neutronics sub-solvers is performed. In more detail, the temperature and the fuel density , calculated by the thermal-hydraulics solver, are passed to the neutronics cycle, whereas the fission power , calculated by the neutronics solver, is passed to the thermal-hydraulics cycle. The external iterations are particularly important in fast transients, in which the large thermal expansions due to steep power excursions have a strong impact on the fuel velocity field.
This model can be used in two different modes:
- A time-independent, criticality mode, in which the system multiplication factor is evaluated at steady-state conditions. To this aim, a power iteration routine, based on the k-eigenvalue method [48] is implemented into the neutronics module. In this case, the main output is represented by the multiplication factor.
- A time-dependent mode, for the analysis of operational as well as accidental transients. The main output provided by the transient mode is the reactor thermal power.
In both cases, the temperature and velocity fields of the fuel and of the gas bubbles, the void fraction distribution, the pressure fields, and the precursor density distributions are provided as output.
More details on the thermal-hydraulics and neutron diffusion modules are provided in the following sections.
3.1. The Thermal-Hydraulics Model
The need for a two-phase thermal-hydraulics solver is due to the presence of gaseous fission products inside the reactor. To this aim, the “twoPhaseEulerFoam” solver available in the OpenFOAM library is used, which implements a Euler–Euler approach [21]. Each phase is treated as a continuum interpenetrating each other and is described with averaged conservation equations. Due to the averaging process, phase fractions are introduced into the governing equations.
The “twoPhaseEulerFoam” solver is selected since it is well established in the OpenFOAM community and widely validated for a broad range of applications, spacing from turbulent, multiphase flows to boiling flows, chemical engineering and pharmaceutical applications, and powder technology applications. For a detailed overview, the reader is referred to [42].
Compared to other approaches for bubbly flows (e.g., Lagrangian–Lagrangian and Eulerian–Lagrangian), the Euler–Euler approach is characterized by lower computational requirements, and therefore is suitable for the simulation of high-Reynolds and large-scale systems, which is the case for the MSFR. In fact, considering an average fuel density of 4125 kg/m3, an average fuel velocity of about 1.2 m/s, a diameter of 2.26 m, and a dynamic viscosity of 10−2 Pa s [1], the Reynolds number is in the order of 106, implying a fully turbulent flow regime. For these reasons, the Euler–Euler approach is the preferred method for many practical applications and is adopted also in this work. Furthermore, the adoption of a Euler–Euler approach is compatible with the gas fractions expected in fast-spectrum MSRs implementing helium bubbling for fission gas removal, typically in the order of 1% [18,19,20].
The mass and momentum conservation equations for the two phases read:
A mass source term is considered in the continuity equation to model gas injection and extraction in the reactor. The term appears in the averaged momentum equations of each phase due to non-linearity, which requires closure equations. This term considers the momentum transfer between the two phases, due to the forces acting at the liquid–gas interface, namely the lift, the drag, virtual mass forces, and turbulent dispersions. Several models are implemented into the solver to describe the inter-phase terms and to close the momentum equation [49,50]. These closure models usually depend on the bubble diameter, which is sampled as described in Table 2.
The energy equations for the two-phases for the “twoPhaseEulerFoam” read:
where is an inter-phase heat transfer coefficient resulting from the averaging process and is the temperature difference between the two phases. Also in this case, different models are implemented in the solver and can be chosen to describe , closing the energy equation [51]. In addition, the Lahey k-ε turbulence model [52] was adopted to account for the contribution of the dispersed gaseous phase on eddy viscosity.
3.2. The Neutronics Model
The one-speed formulation of the diffusion equation is adopted in this work:
Note that the neutron velocity is not sampled, since its relative uncertainty is nearly zero, and therefore negligible compared to those of the cross sections and of the diffusion coefficient. The macroscopic cross sections are evaluated by assuming a logarithmic dependence on temperature and a linear dependence on density and on the void fraction due to the helium bubbles, according to the following relation:
with . The reference term is a group-constant cross section evaluated by Monte Carlo simulation at reference temperature and density , while is calculated by logarithmic interpolation of two cross sections values, obtained at and at a different temperature (always by Monte Carlo simulation). The suitability of Equation (4) to account for temperature and density feedback on macroscopic cross sections has been verified in [19,20] and validated in [53].
The diffusion coefficient is evaluated with a similar expression:
The source terms represent the fission neutrons, the scattering neutrons, and the delayed neutrons, respectively, and are evaluated as follows:
Due to these explicit terms, an iterative procedure among the several groups is required to achieve convergence for the neutronics description. Albedo boundary conditions are adopted at the top and bottom walls of the reactor (axial reflectors) and at the radial wall (blanket salt), in order to limit the domain of the equation set of neutronics to the fuel salt circuit only [8,54].
The precursor balance equations include the diffusion and the transport term to allow for the fuel motion (neglecting the precursor mass transfer from the liquid to the gas phase):
The turbulent Schmidt number is set to 0.85, even if no data are specifically available for the diffusion of species in the MSR salt [8].
In order to properly consider the decay heat during accidental transients, the solver is provided with equations that consider the behavior of the isotopes responsible for the decay heat, subdivided in “decay heat groups” in a manner similar to the precursor groups. Actually, the equations implement the balance for the precursor concentration multiplied by the average energy released by that decay group:
where, again, the decay constants are fixed and do not need to be sampled. The decay heat is of interest for a more accurate evaluation of power density and of temperature evolution during transients. It is assumed that the decay heat is deposited in situ (i.e., where the corresponding precursors decay) without considering photon transport.
In addition, a power iteration routine, based on the k-eigenvalue method [48], is implemented in the neutronics module of the solver for the calculation of the multiplication factor.
4. Global SA Methods
In global SA, the model inputs are considered as random variables following certain probabilistic distribution. The uncertainty in the inputs propagates through the model to the output so that the output (i.e., the multiplication factor) is also a random variable. To identify the most important input parameters affecting the output , the degree of statistical dependence between and is of concern. The stronger the statistical dependence, the more important we consider the corresponding parameter. Global sensitivity measures are developed to measure the statistical dependence. For example, the Pearson correlation coefficient (or Pearson product-moment correlation coefficient) is defined as [55]:
where denotes the covariance between and , and are the corresponding standard deviations, whereas the moment-independent Borgonovo index, Kolmogorov–Smirnov (KS) index , and Kuiper (KU) index are provided in Equations (11)–(13), respectively [26]:
where the marginal cumulative distribution function (cdf) and density function (pdf) of are denoted by and and the cdf and pdf of the model output by and , respectively.
To keep the computational burden under control, we use a given-data approach to estimate the above sensitivity indices () [26]. For quantifying the uncertainty in the estimates, the ensemble-based approach proposed in [25] is adopted. Specifically, we ensemble the rankings of by considering their sum aggregation , i.e., the ranking of the sum aggregation is calculated by first taking the sum of the ranking positions of each sensitivity index, then sorting the input parameters according to corresponding .
The results are confirmed by a graphical visualization tool called the CUSUNORO plot [28,29]. The CUSUNORO curve for a parameter at its quantile is given by:
The curve shows the average change in the standardized output to the mean when the associated input parameter changes to a given quantile . If the corresponding parameter has a significant effect on the model output, the curve has large dispersion from the zero-horizontal line at any . One can also obtain the monotonicity information of the corresponding from the CUSUNORO plot.
5. SA Results
The SA methods introduced in Section 4 were applied to analyze the MSR model, using a Monte Carlo sample of size . We used the given-data principle to estimate the Pearson correlation coefficient, Borgonovo , KS and KU indices. The bias-reducing bootstrap estimation scheme was used to obtain the error bands.
Figure 3 shows boxplots of bootstrap estimates of the four global sensitivity measures, with the bootstrap size of 100. All four indices rank the fuel density parameters and as the most important input parameters; the fuel density parameters are significantly more important than the others, as indicated by their higher sensitivity estimates that are non-overlapping with the others. The boxplots also suggest that the remaining inputs, except for the fuel density parameters, have limited effects on the output reactor power, and their ranking is not clear.
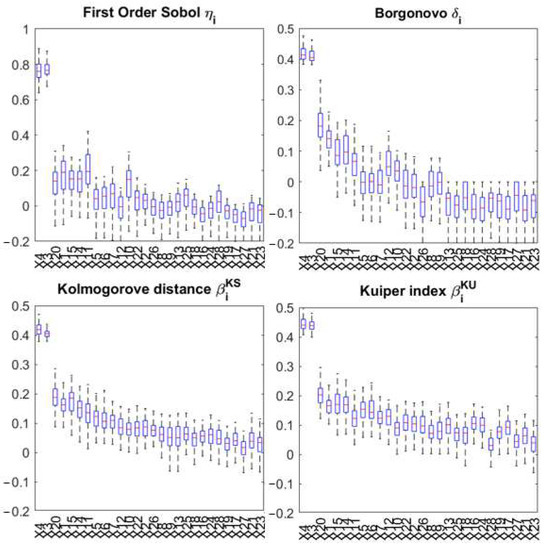
Figure 3.
Boxplots of bootstrap estimates for global sensitivity measures with n = 50 MSR runs.
Table 3 shows the ranking obtained by the bootstrap mean of , together with the sum ensemble ranking . Again, the fuel density parameters and are ranked as the first and the second, followed by the neutronics parameter , the mean bubble diameter , and the neutronics parameter .

Table 3.
Input variable ranking obtained with MSR runs.
The CUSUNORO plot in Figure 4 is obtained using the same dataset, where each curve refers to an input parameter. The magnitudes of the deviations from the zero horizontal line can be used to infer information about the strength of the impact. The CUSUNORO plot shows a clear agreement with the previous results: the fuel density parameters (blue -o-) and (red -∆-) are significantly more important than the others.
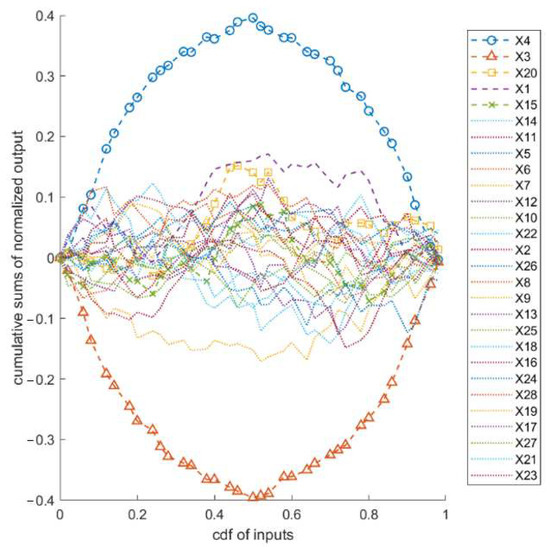
Figure 4.
The CUSUNORO plot with n = 50 MSR runs.
Furthermore, curves above the horizontal zero line signal a decreasing effect; curves below the horizontal zero line suggest the opposite. From Figure 4, one observes that has a decreasing effect on the output reactor power, whereas shows an increasing effect.
6. The Surrogate Model
The high-fidelity multiphysics model presented in Section 3 can produce very accurate solutions, being able to catch phenomena that could not be described with simpler approaches. However, this accuracy comes at the expense of large computational times, which can be as high as about 24 h in three-dimensional full core simulations. Due to this drawback, the high-fidelity model is not adequate for real-time control and decision support. To overcome this issue, a simplified surrogate model is developed in Matlab®, suitable for the real time analysis of the MSR.
As pointed out by the SA results in Section 5, the effect of the density parameters on reactivity are far more important than all the other model parameters. In the light of this, a surrogate model is developed, only considering the density feedback on reactivity.
Point kinetics equations [56] are selected for the estimation of the fission power. In order to simplify the model as much as possible, only one group is considered for the delayed neutron precursors:
where and are the fission power and the precursor density, normalized to their initial values [57]:
The effective delayed neutron fraction is evaluated by [9] and it accounts for the fact that, due to the fuel motion, some of the precursors decay outside of the reactor, where they do not contribute to the fission chain reactor. The other kinetics parameters are obtained by means of Monte Carlo simulation. The density feedback on reactivity is described by means of the following relation:
where the density feedback coefficient is evaluated by Monte Carlo simulation. The Doppler reactivity feedback and leakage effects are not included on purpose, to demonstrate that the density feedback alone is able to correctly reproduce transients, as suggested by the results of the global sensitivity analysis (which points out that density is the most relevant parameter affecting reactivity).
On the other hand, thermal-hydraulics is described by means of the following equation:
where , and are the average, the inlet, and the outlet fuel temperatures, respectively. Assuming for simplicity that:
Equation (20) can be rewritten as follows:
All the parameters appearing in Equations (15) to (22) are listed in Table 4. The effective delayed neutron fraction is calculated in [8] and accounts for precursor transport within the liquid fuel, while the other neutronics parameters are calculated by Monte Carlo simulation. The thermophysical properties and flow parameters can be found in [1,16]. Note that none of these parameters are among the 28 listed in Table 2. Their nominal values are used to define the initial conditions of the system, whereas transients are evaluated considering only the density variations, which are described by the following equation:

Table 4.
Input parameter values adopted in the surrogate model [1,8,16].
Therefore, the density coefficients and are the only two parameters retained from the high-fidelity model. Thanks to these parameters, density variations throughout the transient can be evaluated, which in turn are used to evaluate reactivity by means of Equation (17).
7. Comparison between the Surrogate and High-Fidelity Models
In this section, the surrogate model developed in Section 6 is tested against the high-fidelity multiphysics model. To this aim, two case studies are analyzed: a super-prompt-critical 500 pcm reactivity insertion, starting from zero power, and a loss-of-heat-sink accident. Due to strong nonlinearity, these transients constitute a tough test set to verify the surrogate model. Additionally, the selected case studies are of great interest from an engineering point of view, representing accidental scenarios that could take place in MSRs. Please note that the high-fidelity simulations are carried out using the geometry presented in Figure 1.
7.1. Super-Prompt-Critical Reactivity Insertion
In this section, the accidental super-prompt-critical reactivity insertion is studied. The initial fuel temperature is equal to 900 K. Zero power is approximated with an initial power of 3 MW; in addition, zero void fraction is assumed during the transient. It is also assumed that the heat exchanger secondary temperature is equal to and that perfect heat transfer takes places between the primary and secondary loops. In this way, does not change with time. This simplifying assumption is made in both the high-fidelity and surrogate calculations, so that results are coherent each with the other. This assumption allows for simpler modeling of the heat exchanger, avoiding accounting for the secondary loop. At the same time, this simplification is not expected to significantly affect the accuracy of results, since the transient characteristic time (few milliseconds) is much lower than the fuel recirculation time (around 4 s [45]).
In Figure 5, the power excursions resulting from the reactivity insertion evaluated by the multiphysics solver is plotted with a blue line, whereas the surrogate model results are in green. Compared to the multiphysics model, the surrogate model correctly describes the system dynamics, well predicting both the height as well as the shape of the power excursion. In more detail, the peak power predicted by the two curves only differs by 8%. The surrogate model curve shows a slight delay (~0.7 ms) with respect to the high-fidelity model. It is underlined that the macroscopic effect of the transient on the reactor is more determined by the peak power, rather than by the time delay between the two curves. In this regard, the surrogate model can accurately predict the peak power, thus, constituting a useful tool for the analysis of these reactivity-driven accidental transients.
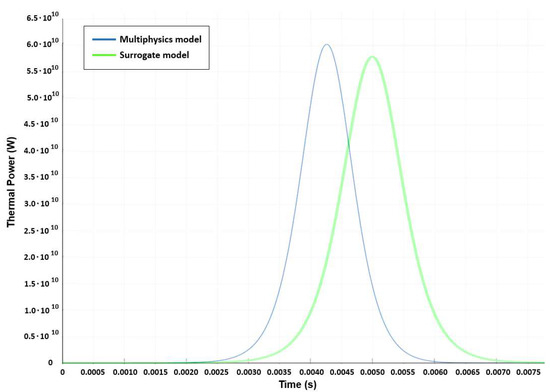
Figure 5.
Power transient predicted by the multiphysics (blue curve) and by the surrogate model (green curve).
Concerning runtimes, the high-fidelity simulation is carried out in about 10 h on a cluster, using a 2 × 24-core Intel Xeon 8160 CPU, whereas the surrogate model requires less than one second on a laptop with an Intel i7-6700HQ CPU. Therefore, the computational burden reduction is clear, at the expense of slightly less accurate results.
7.2. Loss of Heat Sink
In this section the loss-of-heat-sink accident is studied. The accident is modeled as a sudden drop to zero of the heat transfer coefficient in the heat exchanger. As the initial condition, the reactor is considered at nominal power (3000 MW) and operating temperature (973 K). The time evolution of the core power following the accident is plotted in Figure 6. Due to the absence of cooling, the inlet temperature is time dependent and always equal to the outlet (and average) temperature.
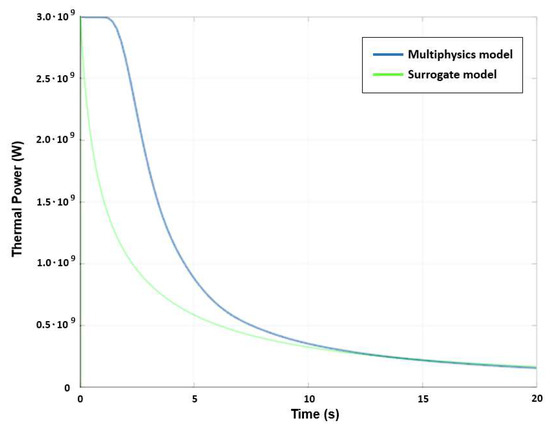
Figure 6.
Power transient predicted for the loss-of-heat-sink accident by the multiphysics (blue curve) and the surrogate models (green curve).
The multiphysics and surrogate model predictions are in good agreement, only differing by a delay (~1 s) in the first part of the transient. This is because in the high-fidelity model the fuel takes a finite time to circulate through the primary loop, thus, delaying the density feedback on reactivity. Indeed, the recirculation time is 4 s [45], and the fuel takes about 1 s to move from the heat exchanger to the reactor cold leg. This effect cannot be observed when simulating the accident using the surrogate model (since the model is zero-dimensional), thus, explaining the 1 s delay between the two simulations. This small discrepancy, however, is not expected to have a macroscopic effect on the reactor during the accidental transient.
The high-fidelity simulation takes about 2 h on a cluster, using a 2 × 18-core Intel Xeon 8160 CPU, whereas the surrogate model requires less than one second on a laptop with an Intel i7-6700HQ CPU. Again, the adoption of the surrogate model allows for a strong reduction of runtime while preserving accuracy.
8. Conclusions
The analysis of MSRs is typically carried out by means of complex multiphysics tools, coupling neutronics, thermal-hydraulics, and precursor transport in the same simulation environments. These high-fidelity models can provide a very accurate solution, since they are able to describe physical phenomena that could not be caught by simpler approaches. However, their high computational requirements hinder their application for real-time control and decision support.
To overcome this issue, an SA was carried out on a multiphysics model coupling multi-group neutron diffusion equations with a two-phase, compressible thermal-hydraulics solver for MSR reactivity control. The SA results showed that, among all the model parameters, density is by far the one affecting the reactivity the most. In light of this, a surrogate model was developed, based on point kinetics equations, in which the reactivity feedback depends solely on the fuel density.
The surrogate model was, then, tested against the high-fidelity one, using the simulations of two different accidental transients in an MSR, namely, the super-prompt-critical reactivity insertion and the loss of heat sink accidents. The results point out that the two approaches yield very similar results, in terms of accuracy. However, the surrogate model runtimes are four orders of magnitude lower, compared to the high-fidelity ones, making it suitable for real time analysis. In particular, the surrogate model can be useful for control purposes, allowing for fast estimations of fission power variations resulting from reactivity insertions or changes in important design parameters such as the fuel temperature or the fuel flow rate. Even though point kinetics were selected to develop the surrogate model, it is worth noting that the proposed technique can be applied to any other simplified modeling approach (e.g., to a 1D system code).
The results of this research point out that global sensitivity analysis approaches are an effective tool to support the development of simplified models of MSR systems, thanks to their ability to identify the most relevant physical parameters. Due to their simplicity, these models can be employed for control purposes, unlike more complex high-fidelity models whose computational requirements are too high to be used for real-time decision-making.
Author Contributions
Conceptualization, E.C., X.L., A.C., F.D.M. and E.Z.; methodology, E.C., X.L., A.C., F.D.M. and E.Z.; software, E.C., X.L. and F.D.M.; investigation, E.C., X.L. and F.D.M.; resources, A.C., F.D.M. and E.Z.; data curation, E.C., X.L. and F.D.M.; writing—original draft preparation, E.C., X.L. and F.D.M.; writing—review and editing, E.C., X.L., A.C., F.D.M. and E.Z.; supervision, A.C., F.D.M. and E.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Research data will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Latin symbols | |
| Delayed neutron precursor density, m−3 | |
| Neutron diffusion coefficient, m | |
| Decay heat precursor density, W m−3 | |
| Specific enthalpy, J kg−1 | |
| Modified thermal diffusivity, J m−1 s−1 K−1 | |
| Specific kinetic energy, J kg−1 | |
| Effective multiplication factor, − | |
| Inter-phase heat transfer coefficient, W m−3 K | |
| Inter-phase momentum transfer, kg m−2 s−2 | |
| Pressure, Pa | |
| per cent mille (=105) | |
| Power source density, W m−3 | |
| Mass source, kg m−3 s−1 | |
| Time, s | |
| Velocity, m s−1 | |
| Neutron velocity, m s−1 | |
| Greek symbols | |
| Gas fraction, − | |
| Delayed neutron precursor fraction, − | |
| Decay heat energy fraction, − | |
| Inter-phase temperature difference, K | |
| Delayed neutron precursor decay constant, s−1 | |
| Decay heat precursor decay constant, s−1 | |
| Dynamic viscosity, Pa s | |
| Kinematic viscosity, m2 s-1 | |
| Mean neutrons per fission, − | |
| Density, kg m−3 | |
| Macroscopic cross section, m−2 | |
| Neutron flux (diffusion equation), m−2 s−1 | |
| Subscripts–superscripts | |
| Absorption | |
| Bubble | |
| Delayed | |
| Fission | |
| Decay heat | |
| Neutron energy group | |
| Phase | |
| Delayed neutron precursor group | |
| Liquid | |
| Decay heat precursor group | |
References
- Gerardin, D.; Allibert, M.; Heuer, D.; Laureau, A.; Merle-Lucotte, E.; Seuvre, C. Design evolutions of Molten Salt Fast Reactor. In Proceedings of the International conference on Fast Reactors and Related Fuel Cycles: Next Generation Nuclear Systems for Sustainable Development (FR17), Yekaterinburg, Russia, 26–29 June 2017. [Google Scholar]
- Fiorina, C. The Molten Salt Fast Reactor as a Fast-Spectrum Candidate for Thorium Implementation. PhD Thesis, Politecnico di Milano, Milan, Italy, 2013. [Google Scholar]
- Serp, J.; Allibert, M.; Beneš, O.; Delpech, S.; Feynberg, O.; Ghetta, V.; Heuer, D.; Holcomb, D.; Ignatiev, V.; Kloosterman, J.L.; et al. The molten salt reactor (MSR) in generation IV: Overview and perspectives. Prog. Nucl. Energy 2014, 77, 308–319. [Google Scholar] [CrossRef]
- Dolan, T.J. Molten Salt Reactors and Thorium Energy; Woodhead Publishing Series in Energy; Elsevier Ltd.: Cambridge, MA, USA, 2017. [Google Scholar]
- Ragusa, J.C.; Mahadevan, V.S. Consistent and accurate schemes for coupled neutronics thermal-hydraulics reactor analysis. Nucl. Eng. Des. 2009, 239, 566–579. [Google Scholar] [CrossRef]
- Cammi, A.; Di Marcello, V.; Luzzi, L.; Memoli, V.; Ricotti, M.E. A Multi-Physics Modelling Approach to the Dynamics of Molten Salt Reactors. Ann. Nucl. Energy 2011, 38, 1356–1372. [Google Scholar] [CrossRef]
- Cammi, A.; Fiorina, C.; Guerrieri, C.; Luzzi, L. Dimensional Effects in the Modelling of MSR Dynamics: Moving on from Simplified Schemes of Analysis to a Multi-Physics Modelling Approach. Nucl. Eng. Des. 2012, 246, 12–26. [Google Scholar] [CrossRef]
- Aufiero, M.; Brovchenko, M.; Cammi, A.; Clifford, I.; Geoffroy, O.; Heuer, D.; Laureau, A.; Losa, M.; Luzzi, L.; Merle, E.; et al. Calculating the effective delayed neutron fraction in the Molten Salt Fast Reactor: Analytical, deterministic and Monte Carlo approaches. Ann. Nucl. Energy 2014, 65, 390–401. [Google Scholar] [CrossRef]
- Aufiero, M.; Cammi, A.; Geoffroy, O.; Losa, M.; Luzzi, L.; Ricotti, M.E.; Rouch, H. Development of an OpenFOAM model for the Molten Salt Fast Reactor transient analysis. Chem. Eng. Sci. 2014, 111, 78–90. [Google Scholar] [CrossRef]
- Fiorina, C.; Aufiero, M.; Cammi, A.; Franceschini, F.; Krepel, J.; Luzzi, L.; Mikityuk, K.; Ricotti, M.E. Investigation of the MSFR core physics and fuel cycle characteristics. Prog. Nucl. Energy 2013, 68, 153–158. [Google Scholar] [CrossRef]
- Fiorina, C.; Lathouwers, D.; Aufiero, M.; Cammi, A.; Guerrieri, C.; Kloosterman, J.L.; Luzzi, L.; Ricotti, M.E. Modelling and analysis of the MSFR transient behaviour. Ann. Nucl. Energy 2014, 64, 485–498. [Google Scholar] [CrossRef]
- Tiberga, M.; Lathouwers, D.; Kloosterman, J.L. A discontinuous Galerkin FEM multi-physics solver for the molten salt fast reactor. In Proceedings of the International Conference on Mathematics and Computation Methods Applied to Nuclear Science and Engineering, M&C 2019, Portland, OR, USA, 25–29 August 2019. [Google Scholar]
- Alsayyari, F.; Tiberga, M.; Perkó, Z.; Lathouwers, D.; Kloosterman, J.L. A nonintrusive adaptive reduced order modeling approach for a molten salt reactor system. Ann. Nucl. Energy 2020, 141, 107321. [Google Scholar] [CrossRef]
- Tiberga, M.; Hennik, A.; Kloosterman, J.L.; Lathouwers, D. A high-order discontinuous Galerkin solver for the incompressible RANS equations coupled to the k-ε turbulence model. Comput. Fluids 2020, 212, 104710. [Google Scholar] [CrossRef]
- De Oliveira, R.G.G.; Mikityuk, K. Analytical solutions to a coupled fluid dynamics and neutron transport problem with application to GeN-Foam verification. Ann. Nucl. Energy 2018, 121, 446–451. [Google Scholar] [CrossRef]
- Tano, M.; Rubiolo, P.; Doche, O. Progress in modeling solidification in molten salt coolants. Model. Simul. Mater. Sci. Eng. 2017, 25, 074001. [Google Scholar] [CrossRef]
- Tano, M.; Rubiolom, P.; Giraus, J.; Ghetta, V. Multiphysics study of the draining transient in the molten salt fast reactor. In Proceedings of the 2018 International Congress on Advances in Nuclear Power Plants (ICAPP 18), Charlotte, NC, USA, 8–11 April 2018. [Google Scholar]
- Cervi, E.; Lorenzi, S.; Cammi, A.; Luzzi, L. Development of a multiphysics model for the study of fuel compressibility effects in the Molten Salt Fast Reactor. Chem. Eng. Sci. 2019, 193, 379–393. [Google Scholar] [CrossRef]
- Cervi, E.; Lorenzi, S.; Cammi, A.; Luzzi, L. Development of an SP3 neutron transport solver for the analysis of the Molten Salt Fast Reactor. Nucl. Eng. Des. 2019, 346, 209–219. [Google Scholar]
- Cervi, E.; Lorenzi, S.; Luzzi, L.; Cammi, A. Multiphysics analysis of the MSFR helium bubbling system: A comparison between neutron diffusion, SP3 neutron transport and Monte Carlo approaches. Ann. Nucl. Energy 2019, 132, 227–235. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. PhD Thesis, Imperial College London, London, UK, December 2002. Available online: https://spiral.imperial.ac.uk/handle/10044/1/8110 (accessed on 9 October 2022).
- Howard, R.A. Uncertainty about Probability: A Decision Analysis Perspective. Risk Anal. 1988, 8, 91–98. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Borgonovo, E.; Plischke, E. Sensitivity Analysis: A Review of Recent Advances. Eur. J. Oper. Res. 2016, 3, 869–887. [Google Scholar] [CrossRef]
- Di Maio, F.; Nicola, G.; Borgonovo, E.; Zio, E. Invariant methods for an ensemble-based sensitivity analysis of a passive containment cooling system of an AP1000 nuclear power plant. Reliab. Eng. Syst. Saf. 2016, 161, 12–19. [Google Scholar] [CrossRef][Green Version]
- Borgonovo, E.; Hazen, G.; Plischke, E. A Common Rationale for Global Sensitivity Measures and their Estimation. Risk Anal. 2016, 36, 1871–1895. [Google Scholar] [CrossRef]
- Efron, B.; Gong, G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am. Stat. 1983, 37, 36–48. [Google Scholar]
- Plischke, E. An effective algorithm for computing global sensitivity indices (EASI). Reliab. Eng. Syst. Saf. 2010, 94, 354–360. [Google Scholar] [CrossRef]
- Borgonovo, E.; Lu, X.; Plischke, E.; Rakovec, O.; Hill, M.C. Making the most out of a hydrological model data set: Sensitivity analyses to open the model black-box. Water Resour. Res. 2017, 53, 7933–7950. [Google Scholar] [CrossRef]
- Jeong, Y.S.; Cervi, E.; Cammi, A.; Ninokata, H.; Bang, I.C. Adjoint-based sensitivity analysis of circulating liquid fuel system for the multiphysics model of molten salt reactor. Int. J. Energy Res. 2020, 44, 1–16. [Google Scholar] [CrossRef]
- Zhang, D.; Qiu, S.; Su, G. Development of a safety analysis code for molten salt reactors. Nucl. Eng. Des. 2009, 239, 2778–2785. [Google Scholar] [CrossRef]
- Zhang, D.; Qiu, S.; Su, G.; Liu, C.; Qian, L. Analysis of the neutron kinetics for a molten salt reactor. Prog. Nucl. Energy 2009, 51, 624–636. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, D.; Xiao, Y.; Tian, W.; Su, G.; Qiu, S. Simulation of unprotected loss of heat sink and combination of events accidents for a molten salt reactor. Ann. Nucl. Energy 2013, 53, 309–319. [Google Scholar] [CrossRef]
- Suzuki, N.; Shimazu, Y. Reactivity-Initiated-Accident Analysis without Scram of a Molten Salt Reactor. J. Nucl. Sci. Technol. 2007, 45, 575–581. [Google Scholar] [CrossRef]
- Cammi, A.; Di Marcello, V.; Guerrieri, C.; Luzzi, L. Transfer Function Modelling of Zero-Power Dynamics of Circulating Fuel Reactors. J. Eng. Gas Turbines Power 2011, 133, 1–8. [Google Scholar] [CrossRef]
- Stempiewicz, M.M.; Roelofs, F. Molten salt modelling in SPECTRA applied to MSRE. Nucl. Eng. Design 2021, 384, 111483. [Google Scholar] [CrossRef]
- OpenFOAM, 2013. OpenFOAM Documentation. Available online: http://www.openfoam.org/docs/ (accessed on 9 October 2022).
- Descamps, M.N.; Oliemans, R.V.A.; Omms, G.; Mudde, R.F. Air-water flow in a vertical pipe: Experimental study of air bubbles in the vicinity of the wall. Exp. Fluids 2008, 45, 357–370. [Google Scholar] [CrossRef][Green Version]
- Lage, P.L.C.; Esposito, R.O. Experimental determination of bubble size distributions in bubble columns: Prediction of mean bubble diameter and gas hold up. Powder Technol. 1999, 101, 142–150. [Google Scholar] [CrossRef]
- Lathouwers, D. Modelling and Simulation of Turbulent Bubbly Flow. PhD Thesis, Delft University of Technology, Delft, The Netherlands, December 1999. [Google Scholar]
- Engel, J.R.; Steffy, R.C. Xenon Behavior in the Molten Salt Reactor Experiment; ORNL-TM-3464; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1971. [Google Scholar]
- Cervi, E. An Innovative Multiphysics Modelling Approach for the Analysis and the Development of the Generation IV Molten Salt Fast Reactor. PhD Thesis, Politecnico Di Milano, Milano, Italy, July 2020. [Google Scholar]
- Sohal, M.; Ebner, M.; Sabharwall, P.; Sharpe, P. Engineering Database of Liquid Salt Thermophysical and Thermochemical Properties; INL-EXT-10-18297; Idaho National Laboratory: Idaho Falls, ID, USA, 2013. [Google Scholar]
- Ignatiev, V.V.; Feynberg, O.; Merzlyakov, A.; Toropov, A. Progress in development of MOSART concept with Th support. In Proceedings of the ICAPP ’12, Chicago, IL, USA, 24–28 June 2012. [Google Scholar]
- Lorenzi, S.; Cammi, A.; Luzzi, L.; Pini, A.; Allibert, M.; Gérardin, D.; Heuer, D.; Laureau, A.; Merle, E.; Lathouwers, D.; et al. TEC1.1 Plant Database for the System and Safety Analysis of the MSFR, SAMOFAR Safety Assessment of the Molten Salt Fast Reactor—MSFR; Internal Report, Euratom Grant Agreement 661891—Samofar; Euratom: Rome, Italy, 2016. [Google Scholar]
- Leppänen, J.; Pusa, M.; Viitanen, T.; Valtavirta, V.; Kaltiaisenaho, T. The Serpent Monte Carlo code: Status, development and application in 2013. Ann. Nucl. Energy 2015, 82, 142–150. [Google Scholar] [CrossRef]
- Santamarina, A.; Bernard, D.; Blaise, P.; Coste, M.; Courcelle, A.; Huynh, T.D.; Jouanne, C.; Leconte, P.; Litaize, O.; Ruggiéri, J.-M.; et al. The JEFF-3.1.1 Nuclear Data Library, JEFF Report 22, OECD/NEA. 2009. Available online: https://www.oecd-nea.org/jcms/pl_14470/the-jeff-3-1-1-nuclear-data-library?details=true (accessed on 9 October 2022).
- Bell, G.I.; Glasstone, S. Nuclear Reactor Theory; Van Nostrand Reinhold Company: New York, NY, USA, 1970. [Google Scholar]
- Gidaspow, D. Multiphase Flow and Fluidization; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Enwald, H.; Peirano, E.; Almstedt, A.E. Eulerian Two-Phase Flow Theory Applied to Fluidization. Int. J. Multiph. Flow 1996, 22, 21–66. [Google Scholar] [CrossRef]
- Ranz, W.E.; Marshall, W.R. Evaporation from droplets. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Lahey, R.T. The simulation of multidimensional multiphase flows. Nucl. Eng. Des. 2005, 235, 1043–1060. [Google Scholar] [CrossRef]
- Cervi, E.; Cammi, A. An Arbitrary Lagrangian-Eulerian, coupled neutronics-shock physics model for the analysis of shockwave compression of solid fissile materials. Ann. Nucl. Energy 2020, 141, 107322. [Google Scholar] [CrossRef]
- Fiorina, C.; Hursin, M.; Pautz, A. Extension of the GeN-Foam neutronic solver to SP3 analysis and application to the CROCUS experimental reactor. Ann. Nucl. Energy 2017, 101, 419–428. [Google Scholar] [CrossRef]
- Pearson, K. On the General Theory of Skew Correlation and Non-linear Regression; Dulau & Co.: London, UK, 1905. [Google Scholar]
- Lamarsh, J.R. Introduction to Nuclear Reactor Theory; American Nuclear Society: LaGrange Park, IL, USA, 2002. [Google Scholar]
- Cervi, E.; Cammi, A.; Di Ronco, A. Stability analysis of the Generation-IV nuclear reactors by means of the root locus criterion. Prog. Nucl. Energy 2018, 106, 316–334. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).