Neural Network Based Deep Learning Method for Multi-Dimensional Neutron Diffusion Problems with Novel Treatment to Boundary
Abstract
:1. Introduction
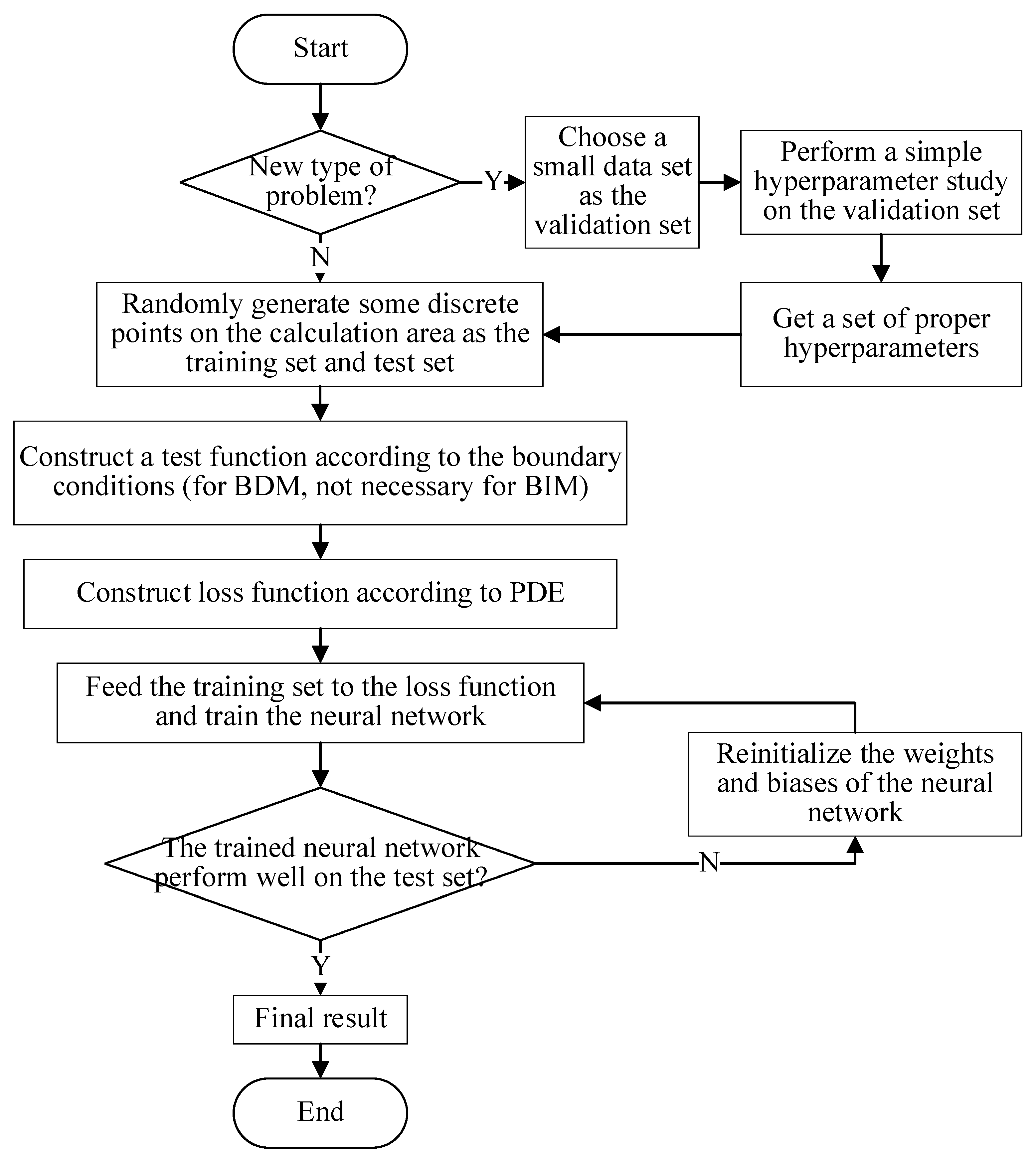
2. Methodology
2.1. Dimensionless Neutron Diffusion Equation
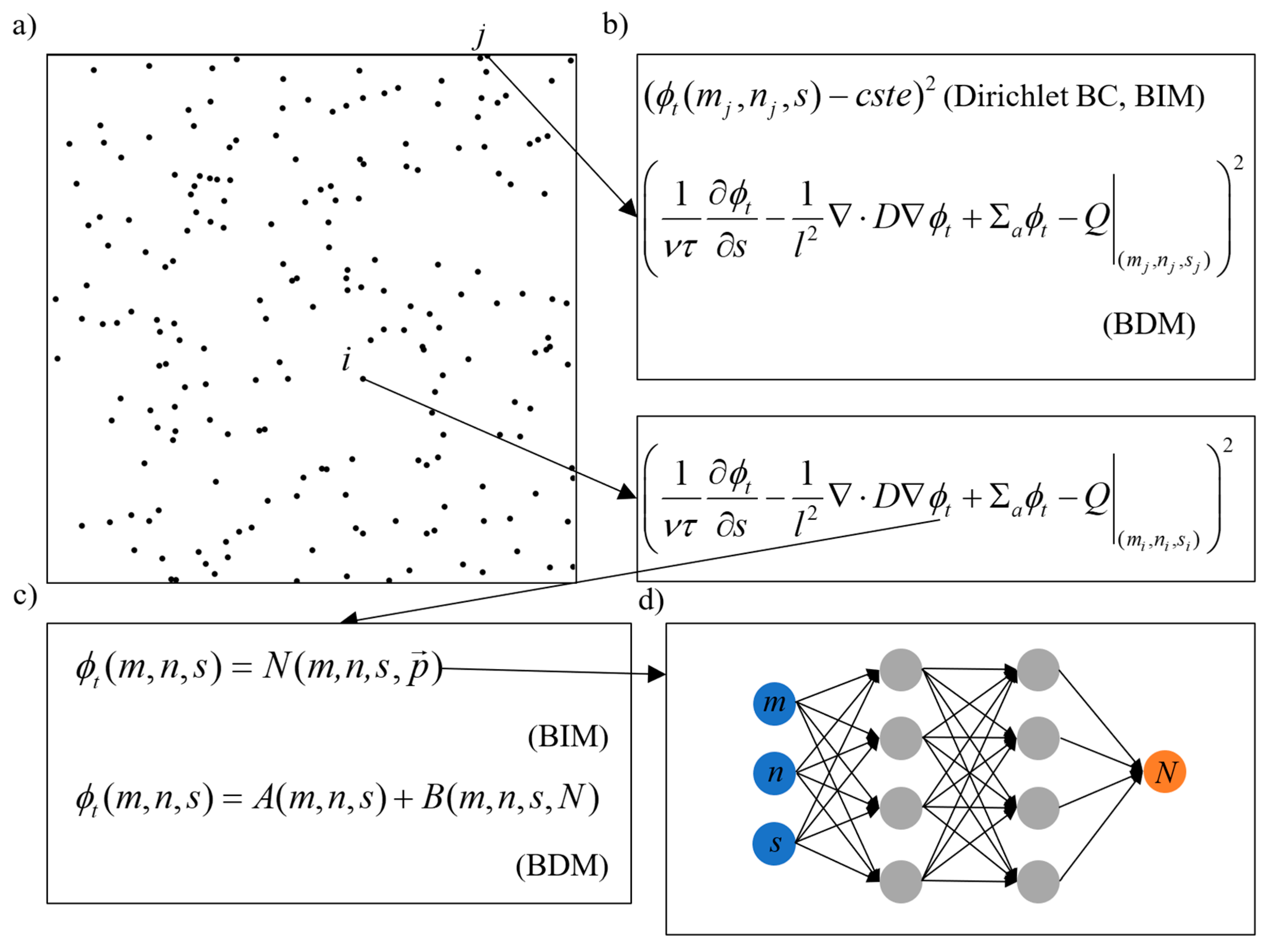
2.2. BDM and BIM
2.3. Trial Functions for Special BCs in BDM
3. Results and Discussion
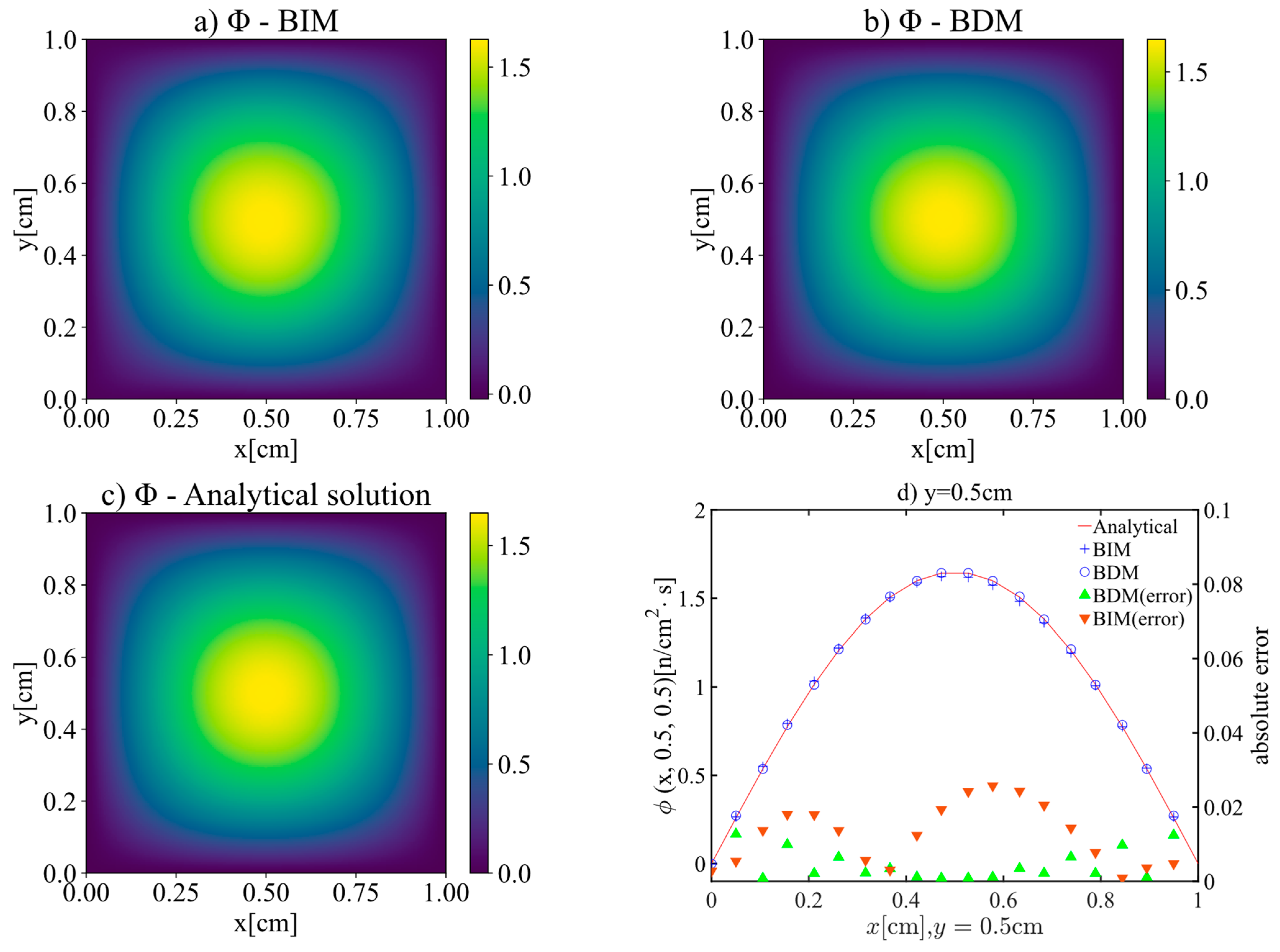
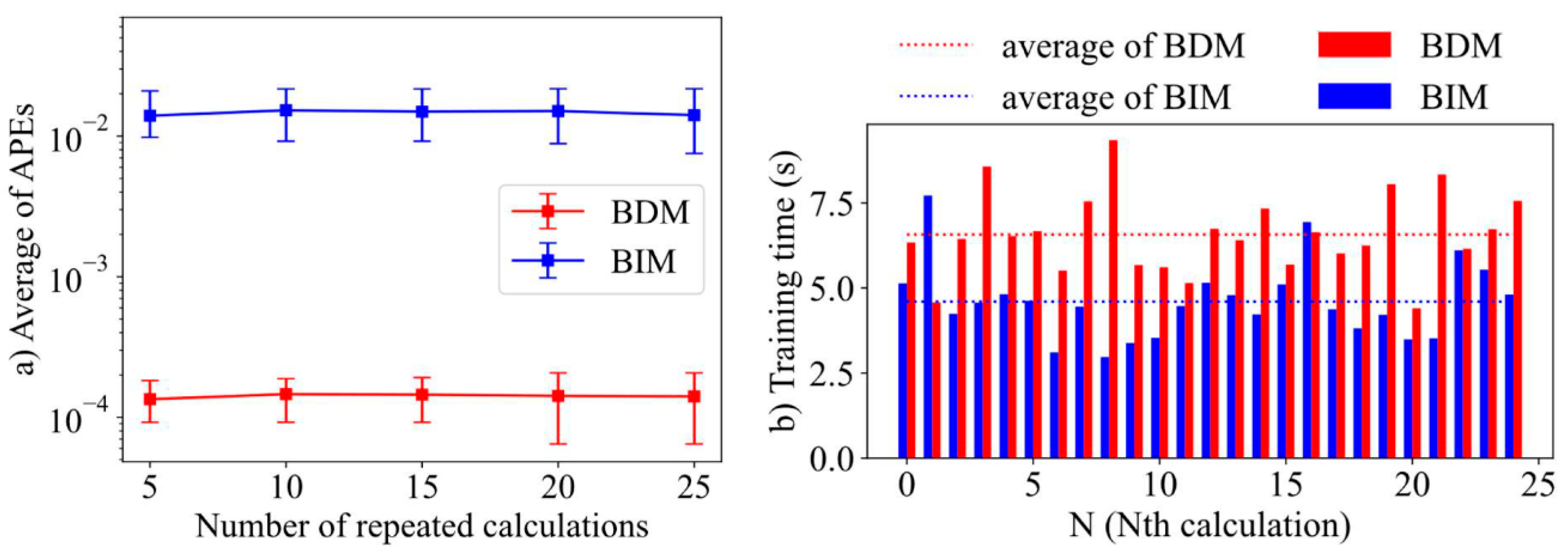
3.1. Case 1—Comparison of BDM and BIM
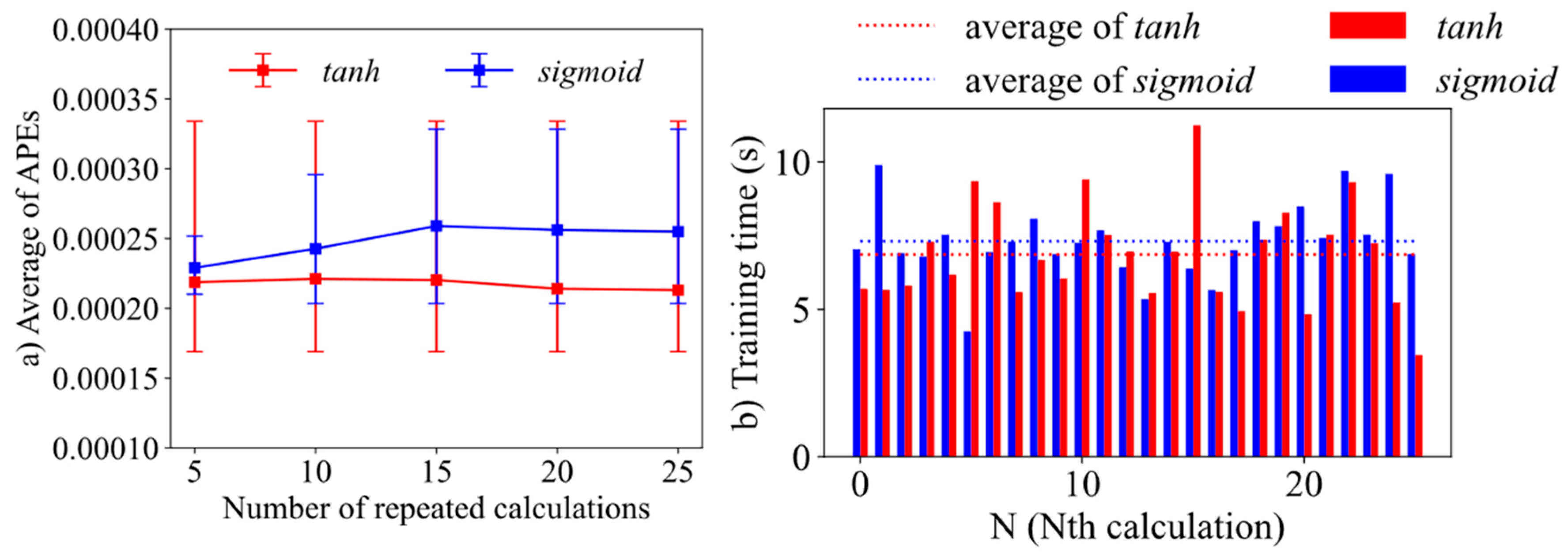
3.2. Case 2—Choice of Activation Function
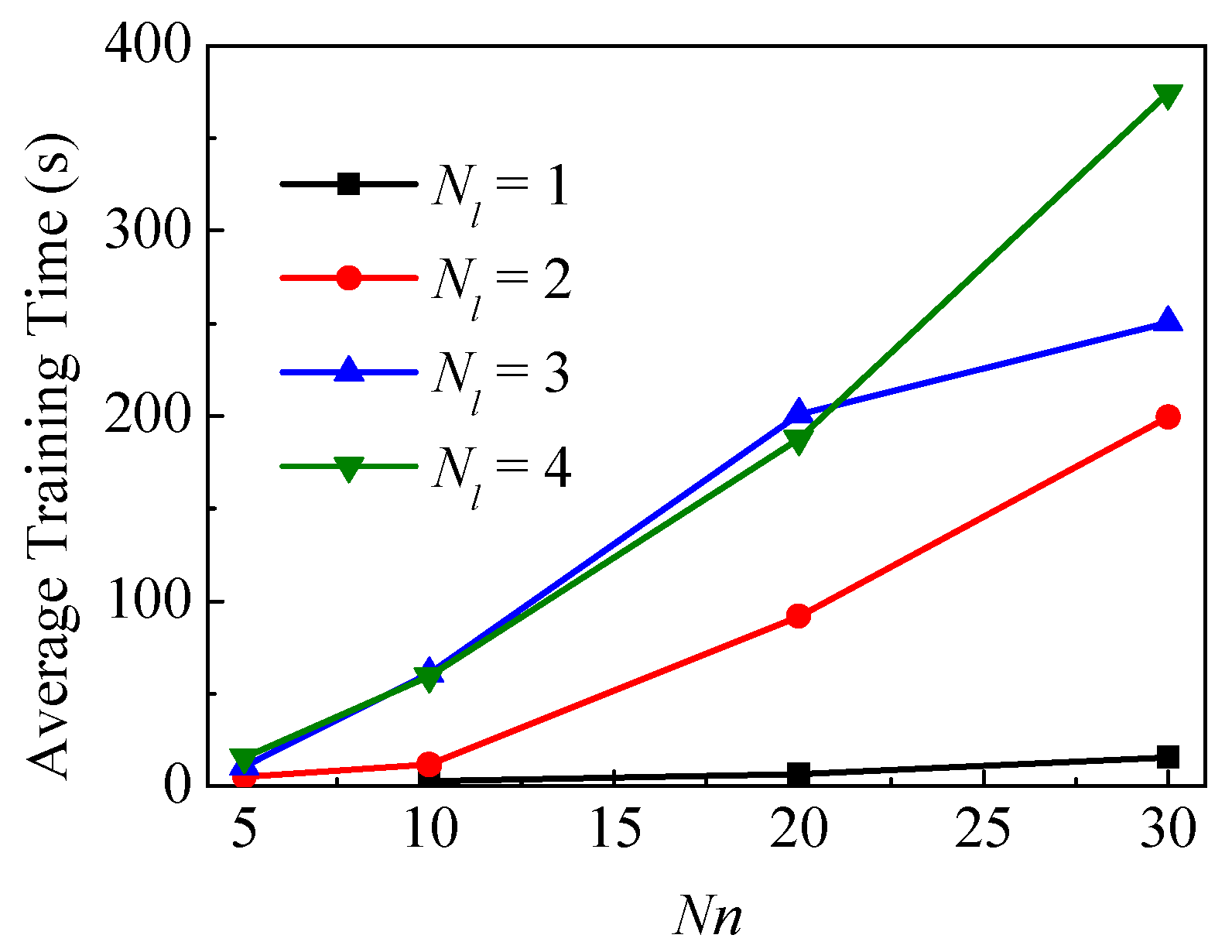
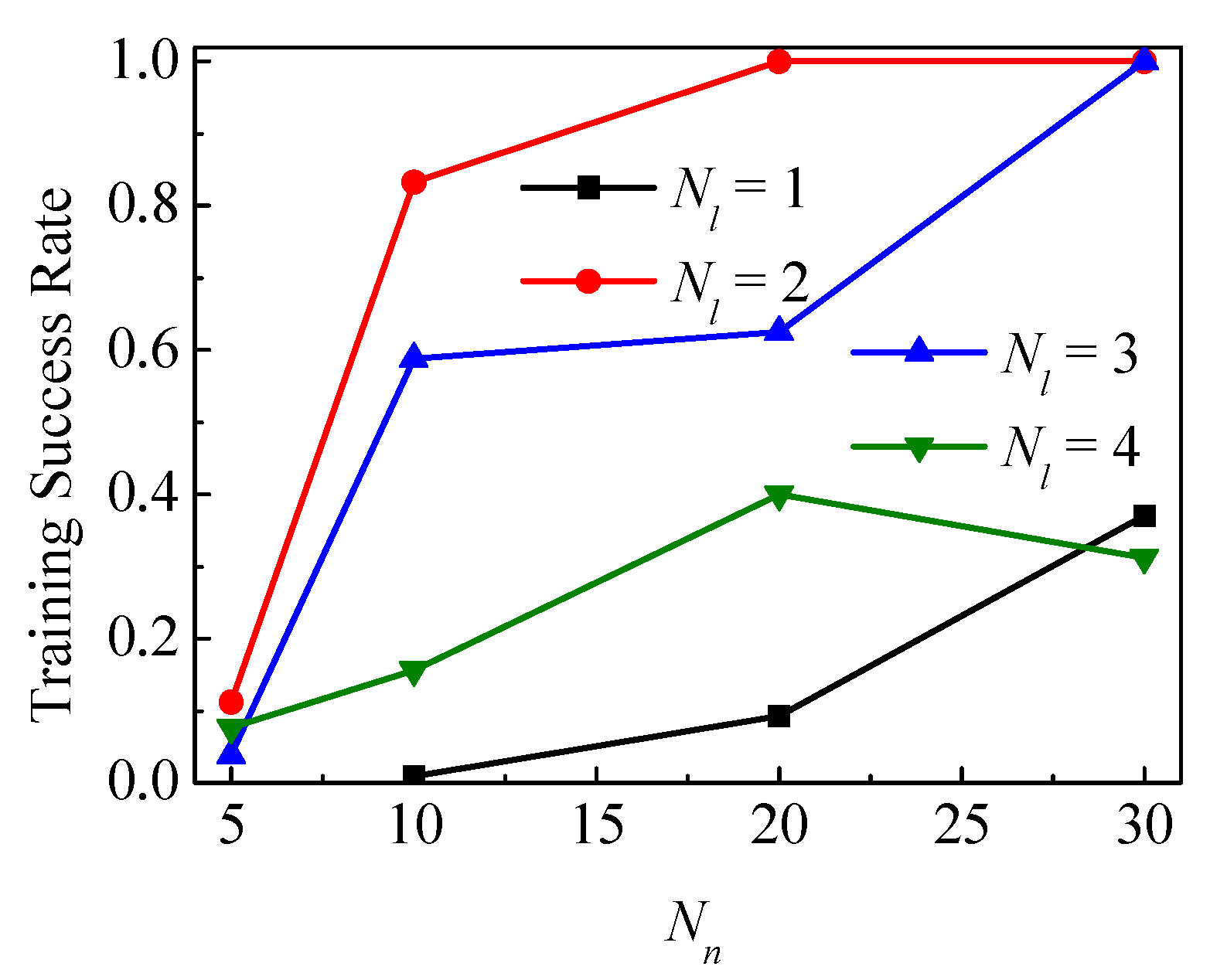
3.3. Case 3—Impact of Hyperparameters
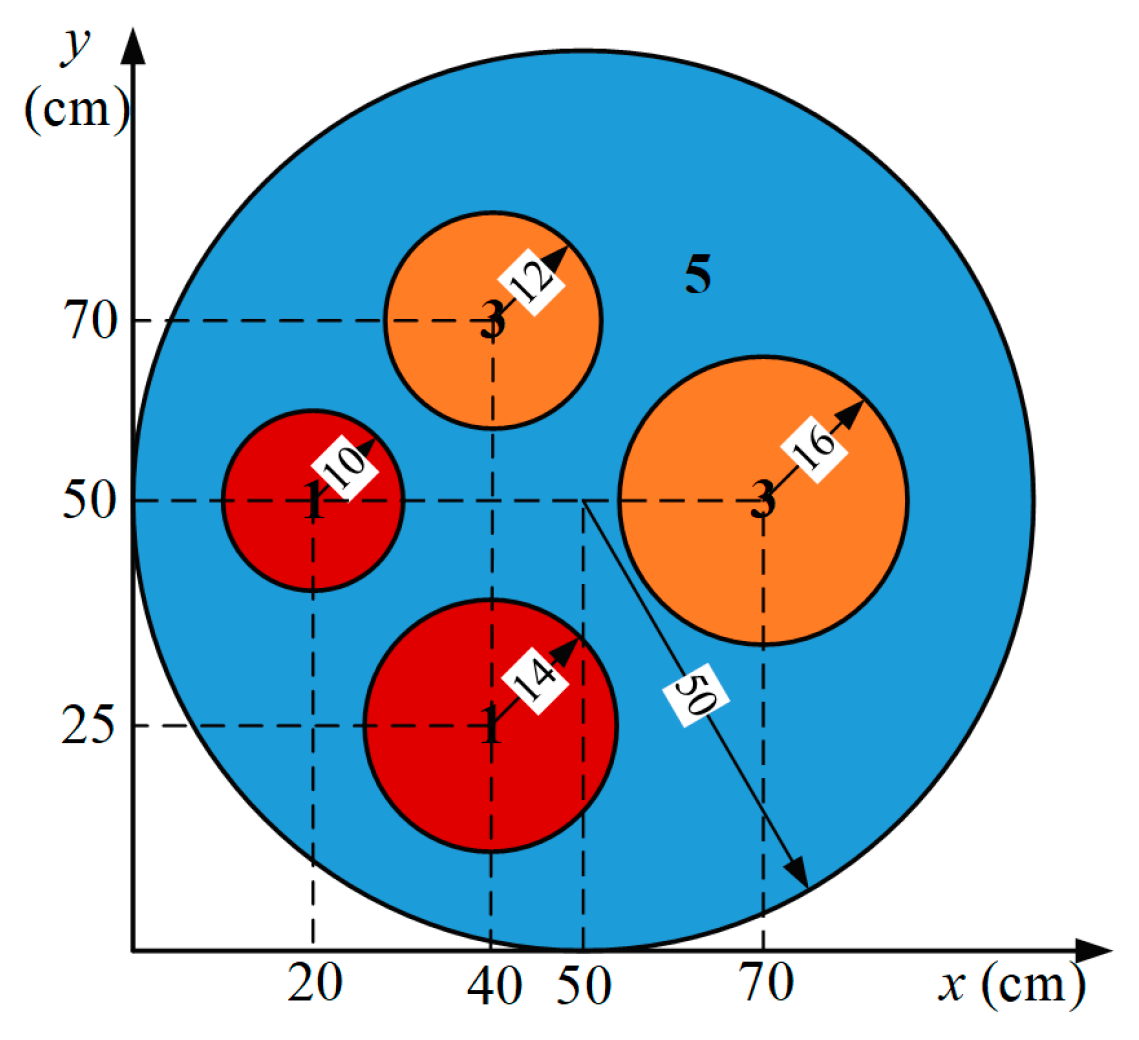
3.4. Case 4—Application in Complex Geometry
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Bell, G.I.; Glasstone, S. Nuclear Reactor Theory; US Atomic Energy Commission: Washington, DC, USA, 1970.
- Duderstadt, J.J. Nuclear Reactor Analysis; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- Kang, C.M.; Hansen, K. Finite element methods for reactor analysis. Nucl. Sci. Eng. 1973, 51, 456–495. [Google Scholar] [CrossRef]
- Varga, R.S. Numerical solution of the two-group diffusion equations in xy geometry. IRE Trans. Nucl. Sci. 1957, 4, 52–62. [Google Scholar] [CrossRef]
- Vondy, D.; Fowler, T.; Cunningham, G. VENTURE: A Code Block for Solving Multigroup Neutronics Problems Applying the Finite-Difference Diffusion-Theory Approximation to Neutron Transport; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1975. [Google Scholar]
- Dodson, Z.; Kochunas, B.; Larsen, E. The Stability of Linear Diffusion Acceleration Relative to CMFD. J. Nucl. Eng. 2021, 2, 336–344. [Google Scholar] [CrossRef]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Bao, H.; Dinh, N.; Lin, L.; Youngblood, R.; Lane, J.; Zhang, H. Using deep learning to explore local physical similarity for global-scale bridging in thermal-hydraulic simulation. Ann. Nucl. Energy 2020, 147, 107684. [Google Scholar] [CrossRef]
- Elhareef, M.H.; Wu, Z.; Ma, Y. Physics-informed deep learning neural network solution to the neutron diffusion model. In Proceedings of the the International Conference on Mathematics and Computation Methods Applied to Nuclear Science and Engineering (M&C 2021), Raleigh, NC, USA, 3–7 October 2021. [Google Scholar]
- Kim, T.K.; Park, J.K.; Lee, B.H.; Seong, S.H. Deep-learning-based alarm system for accident diagnosis and reactor state classification with probability value. Ann. Nucl. Energy 2019, 133, 723–731. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Zhang, Q.; Zhang, J.; Liang, L.; Zhao, Q.; Wu, H.; Cao, L. Application of deep neural network for generating resonance self-shielded cross-section. Ann. Nucl. Energy 2020, 149, 107785. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural language processing (almost) from scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Hermann, K.M.; Kocisky, T.; Grefenstette, E.; Espeholt, L.; Kay, W.; Suleyman, M.; Blunsom, P. Teaching machines to read and comprehend. Adv. Neural Inf. Process. Syst. 2015, 28, 1693–1701. [Google Scholar]
- Jean, S.; Cho, K.; Memisevic, R.; Bengio, Y. On using very large target vocabulary for neural machine translation. arXiv 2014, arXiv:1412.2007. [Google Scholar]
- Wang, W.; Song, W.; Chen, C.; Zhang, Z.; Xin, Y. I-vector features and deep neural network modeling for language recognition. Procedia Comput. Sci. 2019, 147, 36–43. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, D.; Lee, D.-J. IIRNet: A lightweight deep neural network using intensely inverted residuals for image recognition. Image Vis. Comput. 2019, 92, 103819. [Google Scholar] [CrossRef]
- Tompson, J.J.; Jain, A.; LeCun, Y.; Bregler, C. Joint training of a convolutional network and a graphical model for human pose estimation. Adv. Neural Inf. Process. Syst. 2014, 27, 1799–1807. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.-r.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Sainath, T.N.; Kingsbury, B.; Mohamed, A.-r.; Dahl, G.E.; Saon, G.; Soltau, H.; Beran, T.; Aravkin, A.Y.; Ramabhadran, B. Improvements to deep convolutional neural networks for LVCSR. In Proceedings of the 2013 IEEE Workshop on Automatic Speech Recognition and Understanding, Olomouc, Czech Republic, 8–12 December 2013; pp. 315–320. [Google Scholar]
- Fujii, M.; Takahashi, A.; Takahashi, M. Asymptotic expansion as prior knowledge in deep learning method for high dimensional BSDEs. Asia-Pac. Financ. Mark. 2019, 26, 391–408. [Google Scholar] [CrossRef] [Green Version]
- Galib, S.M. Applications of Machine Learning in Nuclear Imaging and Radiation Detection; Missouri University of Science and Technology: Rolla, MO, USA, 2019. [Google Scholar]
- Galib, S.; Bhowmik, P.; Avachat, A.; Lee, H. A comparative study of machine learning methods for automated identification of radioisotopes using NaI gamma-ray spectra. Nucl. Eng. Technol. 2021, 53, 4072–4079. [Google Scholar] [CrossRef]
- Sasaki, M.; Sanada, Y.; Katengeza, E.W.; Yamamoto, A. New method for visualizing the dose rate distribution around the Fukushima Daiichi Nuclear Power Plant using artificial neural networks. Sci. Rep. 2021, 11, 1857. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Jentzen, A.; Weinan, E. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef] [Green Version]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef] [Green Version]
- Abadi, M. TensorFlow: Learning functions at scale. In Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming, Nara, Japan, 18–24 September 2016; p. 1. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Pozulp, M.M.; Brantley, P.S.; Palmer, T.S.; Vujic, J.L. Heterogeneity, hyperparameters, and GPUs: Towards useful transport calculations using neural networks. In Proceedings of the the International Conference on Mathematics and Computation Methods Applied to Nuclear Science and Engineering (M&C 2021), Raleigh, NC, USA, 3–7 October 2021. [Google Scholar]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef] [Green Version]
- Multiphysics, C. Introduction to Comsol Multiphysics®; COMSOL Multiphysics: Burlington, MA, USA, 1998; Volume 9, p. 2018. [Google Scholar]
- Li, Y.Z.; Wu, H.C.; Cao, L.Z. Unstructured triangular nodal-SP3 method based on an exponential function expansion. Nucl. Sci. Eng. 2013, 174, 163–171. [Google Scholar] [CrossRef]




| v (cm/s) | D (cm) | ϕ1 (n·cm−2·s−1) | τ (s) | l (cm) | Σa (cm−1) | |
|---|---|---|---|---|---|---|
| Value | 1.0 | 0.001 | 1.0 | 1.0 | 1.0 | 0 |
| D (cm) | l (cm) | Σa (cm−1) | Q1 (n·cm−3·s−1) | |
|---|---|---|---|---|
| Value | 2/3 | 100 | 0.5 | 1.0 |
| Area No. | D (cm) | Σa (cm−1) | Q (n·cm−3·s−1) |
|---|---|---|---|
| 1 | 0.5556 | 0.07 | 0.79 |
| 3 | 0.4762 | 0.04 | 0.43 |
| 5 | 0.3704 | 0.01 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Wang, Y.; Ma, Y.; Wu, Z. Neural Network Based Deep Learning Method for Multi-Dimensional Neutron Diffusion Problems with Novel Treatment to Boundary. J. Nucl. Eng. 2021, 2, 533-552. https://doi.org/10.3390/jne2040036
Xie Y, Wang Y, Ma Y, Wu Z. Neural Network Based Deep Learning Method for Multi-Dimensional Neutron Diffusion Problems with Novel Treatment to Boundary. Journal of Nuclear Engineering. 2021; 2(4):533-552. https://doi.org/10.3390/jne2040036
Chicago/Turabian StyleXie, Yuchen, Yahui Wang, Yu Ma, and Zeyun Wu. 2021. "Neural Network Based Deep Learning Method for Multi-Dimensional Neutron Diffusion Problems with Novel Treatment to Boundary" Journal of Nuclear Engineering 2, no. 4: 533-552. https://doi.org/10.3390/jne2040036
APA StyleXie, Y., Wang, Y., Ma, Y., & Wu, Z. (2021). Neural Network Based Deep Learning Method for Multi-Dimensional Neutron Diffusion Problems with Novel Treatment to Boundary. Journal of Nuclear Engineering, 2(4), 533-552. https://doi.org/10.3390/jne2040036







