Neural Network Approaches for Mobile Spectroscopic Gamma-Ray Source Detection

Abstract

Artificial neural networks (ANNs) for performing spectroscopic gamma-ray source identification have been previously introduced, primarily for applications in controlled laboratory settings. To understand the utility of these methods in scenarios and environments more relevant to nuclear safety and security, this work examines the use of ANNs for mobile detection, which involves highly variable gamma-ray background, low signal-to-noise ratio measurements, and low false alarm rates. Simulated data from a 2” × 4” × 16” NaI(Tl) detector are used in this work for demonstrating these concepts, and the minimum detectable activity (MDA) is used as a performance metric in assessing model performance.In addition to examining simultaneous detection and identification, binary spectral anomaly detection using autoencoders is introduced in this work, and benchmarked using detection methods based on Non-negative Matrix Factorization (NMF) and Principal Component Analysis (PCA). On average, the autoencoder provides a 12% and 23% improvement over NMF- and PCA-based detection methods, respectively. Additionally, source identification using ANNs is extended to leverage temporal dynamics by means of recurrent neural networks, and these time-dependent models outperform their time-independent counterparts by 17% for the analysis examined here. The paper concludes with a discussion on tradeoffs between the ANN-based approaches and the benchmark methods examined here.

1. Introduction

Two key elements of nuclear safety and security are the ability to detect the presence of radioactive sources and to correctly identify radionuclides. Data-driven methods for discerning between background radiation and anomalous radiological sources using spectroscopic gamma-ray measurements have long been used to meet these needs [1]. Artificial neural networks (ANNs) [2,3] are one class of methods previously introduced for gamma-ray source identification. To perform identification, ANNs, also referred to simply as neural networks, are used to determine a function which maps a given gamma-ray spectrum to the types of radionuclides, or lack thereof, that are observed in the spectrum.

ANNs are of particular interest for detection and identification due to their ability to leverage information across the entire gamma-ray spectrum. Previous studies (e.g., refs. [4,5,6]) have demonstrated benefits to using full-spectrum techniques, namely, increased detection sensitivity over methods that only consider regions of the gamma-ray spectrum. Specifically, methods that incorporate information from the entire gamma-ray spectrum are capable of building more accurate models of gamma-ray sources and background. Additionally, ANNs have the advantage of being modular computational tools, allowing for flexibility in network design. The variety of network architectures resulting from this flexibility is one element to the success of ANNs in fields such as computer vision. This is in contrast to other methods for spectral analysis, such as non-negative matrix factorization (NMF), which generally take a limited, but well-defined, functional form.

Despite several previous research efforts, most ANN-based source identification in the literature has not been studied for one common use case: mobile radiological source search. In this application, vehicles equipped with radiation detection sensors are used to detect and identify radiological sources, often times in urban areas with highly variable background radiation. While the objective in mobile detection is inherently the same as laboratory-based applications of ANNs, there are operational challenges that must be taken into account for an algorithm to be used effectively on a mobile system. In particular, these systems are intended to detect weak gamma-ray sources using medium-energy-resolution gamma-ray detectors (e.g., NaI(Tl)) moving through environments that vary greatly in gamma-ray count rate and energy distributions, while operating at a relatively low false alarm rate (FAR) (e.g., 1/8 h${}^{-1}$). Previous applications using ANNs for identification, however, have generally been developed for applications with different requirements than mobile detection. For example, ref. [3] used a stationary detector configuration (i.e., constant background) in a laboratory, high signal-to-noise ratio (SNR) measurements, and a relatively high FAR of 5%. Knowing this, the intentions of this paper are:

• Introduce the use of ANN-based spectral anomaly detection and show improvements over simpler linear models.
• Evaluate current state-of-the-art identification networks under operationally relevant conditions, and benchmark against a non-ANN method.
• Improve upon state-of-the-art identification networks by introducing the use of recurrent neural networks.
• Provide a comprehensive description of neural networks for detection and identification that, when accompanied with quantitative results, better inform practitioners of current tradeoffs.

The remainder of this paper is outlined as follows. Section 2 provides a review of related research, a detailed overview of the networks studied in this work, and a description of the data and metrics used in analyzing their performance. Section 3 quantifies the performance of various models, including benchmark methods. Lastly, Section 4 concludes with a discussion o considerations when choosing between methods to use in practice, along with additional directions of research to consider.

2. Methods

2.1. Artificial Neural Networks

The objective of spectral radionuclide identification is to produce a function $f\left(\mathbf{x}\right)\in {\{0,1\}}^N$ which maps a gamma-ray spectrum $\mathbf{x}\in {\mathbb{R}}_{+}^d$ to an output vector corresponding to the presence or absence of N different sources of interest. In spectral anomaly detection, the procedure simply outputs a binary value $f\left(\mathbf{x}\right)\in \{0,1\}$ indicating the presence or absence of an anomalous source, without attempting to identify sources. Neural networks are a general data-driven method for performing function approximation, and are capable of producing functions for performing detection and identification.

The first applications of neural networks for source identification were examined between the early 1990s and 2000s [2,7,8,9,10], with networks that mapped input spectra to the relative amount of known background and sources contained within the spectrum. More recently, modern approaches to perform identification using neural networks have been developed [3,11,12,13,14,15], using methods similar to those seen since the deep learning boom of the early 2010s (e.g., ref. [16]). Recent research in the area (e.g., refs. [12,13,14]) has emphasized methodologies that are more applicable to nuclear safety and security, however, due to a lack of a characterization of these methods under operationally-relevant conditions, compared to a known benchmark method, the utility of these methods remains unclear. Additionally, the use of neural networks for spectral anomaly detection has not been previously studied, and this work begins by briefly introducing networks that can be used to accomplish this.

Neural networks are used to form a function f which operates on an input $\mathbf{x}$ (e.g., an image or gamma-ray spectrum), producing an output $\widehat{\mathbf{y}}=f\left(\mathbf{x}\right)$. The function f consists of a series of relatively simple operations, which are parameterized by a set of learned model parameters $\mathcal{P}$. Neural networks can generally be considered a composition of l different functions, that is,

$$f\left(\mathbf{x}\right)=f_l\left(f_{l-1}(\cdots \left(f_2\left(f_1\left(\mathbf{x}\right)\right)\right))\right),$$

(1)

where the output of composed function up to $f_i$ is referred to as the $i\mathrm{th}$ layer, denoted by ${\mathbf{h}}^{\left(i\right)}$. Equation (1) specifically defines a feedforward neural network, which can be represented as a directed acyclic graph. This is in contrast to a recurrent neural network (RNN), which contains cycles and is used for modeling sequential data. Section 2.3 introduces the use of RNNs for performing spectral identification using temporal sequences of spectra.

For a defined functional form of f, the parameters $\mathcal{P}$ are estimated from examples of pairs of inputs $\mathbf{x}$ and corresponding target values of output $\mathbf{y}$, such that $\widehat{\mathbf{y}}=f\left(\mathbf{x}\right)\approx \mathbf{y}$. The functional form of commonly-used layer types are provided in Appendix A. The following sections provide functional forms of f for accomplishing both detection and identification, as well as the procedure for estimating $\mathcal{P}$.

2.2. Spectral Anomaly Detection using Autoencoders

Generally speaking, spectral anomaly detection can be performed by generating an estimate $\widehat{\mathbf{x}}$ of the background in an input spectrum $\mathbf{x}$, and computing an error measure $D(\mathbf{x},\widehat{\mathbf{x}})$ between the two. $D(\mathbf{x},\widehat{\mathbf{x}})$ is chosen to measure differences between the two inputs, and a threshold T is set, either empirically or analytically using statistical principles, to alarm on spectra that exceed this threshold. Autoencoders [17,18] are a type of neural network suitable for performing the background estimation required for anomaly detection. Autoencoders are used to produce an output that is approximately equal to the input, meaning a function f is learned such that

$$\widehat{\mathbf{x}}=f\left(\mathbf{x}\right)\approx \mathbf{x}\in {\mathbb{R}}_{+}^d.$$

(2)

Undercomplete autoencoders, which perform dimensionality reduction to learn salient features about the input data, are examined in this work. Note that it is not expected for an undercomplete autoencoder to reproduce the input exactly, but instead that it returns a denoised copy of the input. The general architecture for an undercomplete autoencoder is to reduce the dimensionality using an encoder, then increase to the input dimensionality using a decoder. For anomaly detection, the parameters $\mathcal{P}$ of f are learned from background spectra, and ideally, spectra containing anomalous sources are reconstructed less accurately, resulting in higher detection metrics.

Counts in the input spectra are assumed to be Poisson-distributed, leading to the use of a Poisson negative log-likelihood loss function of the form

$$-lnp\left(\mathbf{X}\right|\widehat{\mathbf{X}})=\sum _{i=1}^n\sum _{j=1}^d{\widehat{x}}_{ij}-x_{ij}ln{\widehat{x}}_{ij}+ln{x}_{ij}!,$$

(3)

for a mini-batch $\mathbf{X}\in {\mathbb{R}}^{n\times d}$ of n d-dimensional spectra and corresponding autoencoder output $\widehat{\mathbf{X}}$. By minimizing the loss function in Equation (3), the network seeks a solution $\widehat{\mathbf{X}}$ that is the Poisson mean of the input $\mathbf{X}$ (i.e., $\mathbf{X}\sim \mathrm{Poisson}(\widehat{\mathbf{X}})$), meaning that $\widehat{\mathbf{X}}$ provides a denoised version of the input. Deviance [19] is used here as a goodness-of-fit measure between input spectra and their corresponding autoencoder reconstructions. In essence, deviance gives a measure of the difference between an ideal model where each parameter is known exactly (i.e., $p\left(\mathbf{x}\right|\mathbf{x})$), and the model determined from maximum likelihood estimation (i.e., $p\left(\mathbf{x}\right|\widehat{\mathbf{x}})$). For a spectrum $\mathbf{x}$ and associated reconstruction $\widehat{\mathbf{x}}$, the Poisson deviance is computed as

$$D(\mathbf{x},\widehat{\mathbf{x}})=2\sum _{i=1}^d{\widehat{x}}_i-x_i+x_{i}ln\frac{x_i}{{\widehat{x}}_i}$$

(4)

and used as a detection metric. The detection threshold is produced empirically from known background data. Specifically, $D(\mathbf{x},\widehat{\mathbf{x}})$ is computed on background spectra, giving a distribution of test statistics, and for a given FAR, a threshold is empirically set using this distribution.

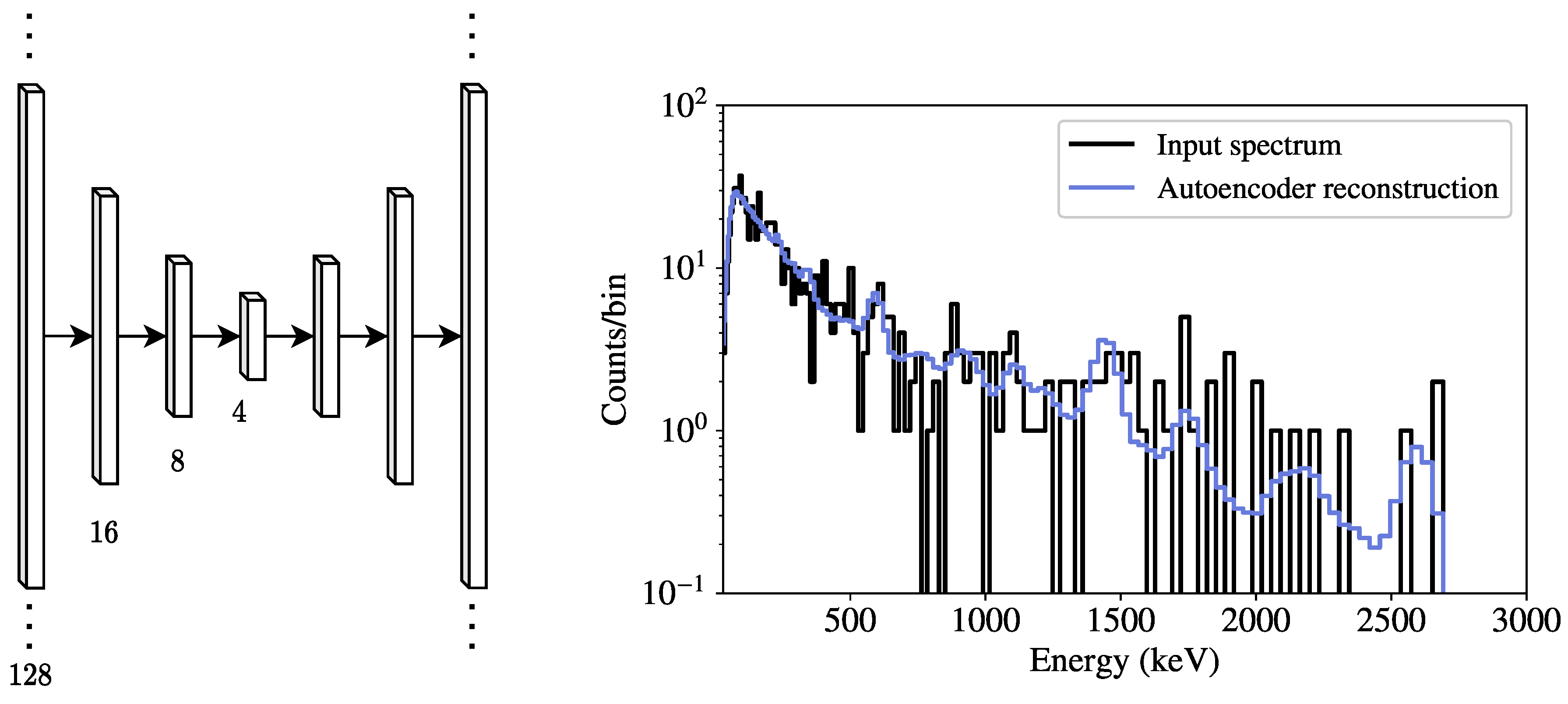
Encoders and decoders can be built from arbitrary combinations of dense and convolutional layers. Both dense autoencoders (DAE) and convolutional autoencoders were seen to perform comparably during experimentation, but only DAEs are examined here due to their relative simplicity. In this work, only symmetric DAEs (i.e., decoders that mirror the encoders) are considered here, as it reduces the hyperparameter search space. A DAE with five hidden layers (seven layers total when including the input and output), each using a rectified linear unit (ReLU) activation function, is used to demonstrate spectral anomaly detection. This particular configuration was seen to perform sufficiently well for this initial assessment and the hyperparameter space explored. The number of neurons in each dense layer is found via a random optimization, described further below.

Figure 1 shows a diagram of an example dense autoencoder, along with a sample input spectrum $\mathbf{x}$ and its corresponding reconstructed spectrum $\widehat{\mathbf{x}}$. By training the autoencoder using the Poisson loss in Equation (3), $\mathbf{x}$ can be seen as a sample from a Poisson distribution with mean rate $\widehat{\mathbf{x}}$. As a result, $\widehat{\mathbf{x}}$ contains smoothened spectral features corresponding to background peaks (e.g., ⁴⁰K at 1460 keV) and the associated downscattering continuum, seen in Figure 1.

2.3. Source Identification

In performing identification, an input spectrum $\mathbf{x}$ is mapped to an output vector $\widehat{\mathbf{y}}$ indicating the presence or absence of a source. In many common applications of neural networks for classification, the mapping from $\mathbf{x}$ to $\widehat{\mathbf{y}}$ involves encoding one or more classes of instances present in $\mathbf{x}$ as $\widehat{\mathbf{y}}$ (e.g., an image $\mathbf{x}$ containing a dog, encoded in $\widehat{\mathbf{y}}$). In gamma-ray spectroscopy, however, background contributions will always be present in a given spectrum, and sources will appear in different proportions, or sources could potentially be shielded by attenuating material. As a result, the standard method of directly predicting a vector $\widehat{\mathbf{y}}\in {\{0,1\}}^N$, with a 1 at element i indicating the presence of class i, is generally not performed. Instead, the output $\widehat{\mathbf{y}}$ is treated as the proportion of each source and background to the spectrum, such that ${\sum }_i{\widehat{\mathbf{y}}}_i=1$, meaning the network is performing regression. To achieve this behavior, the output of the network $f\left(\mathbf{x}\right)$ is passed to the softmax function, defined as

$$\mathrm{softmax}\left(z_i\right)=\frac{exp\left(z_i\right)}{{\sum }_{j}exp\left(z_j\right)},$$

(5)

for each network output $z_i\in \mathbb{R}$, which outputs values between 0 and 1.

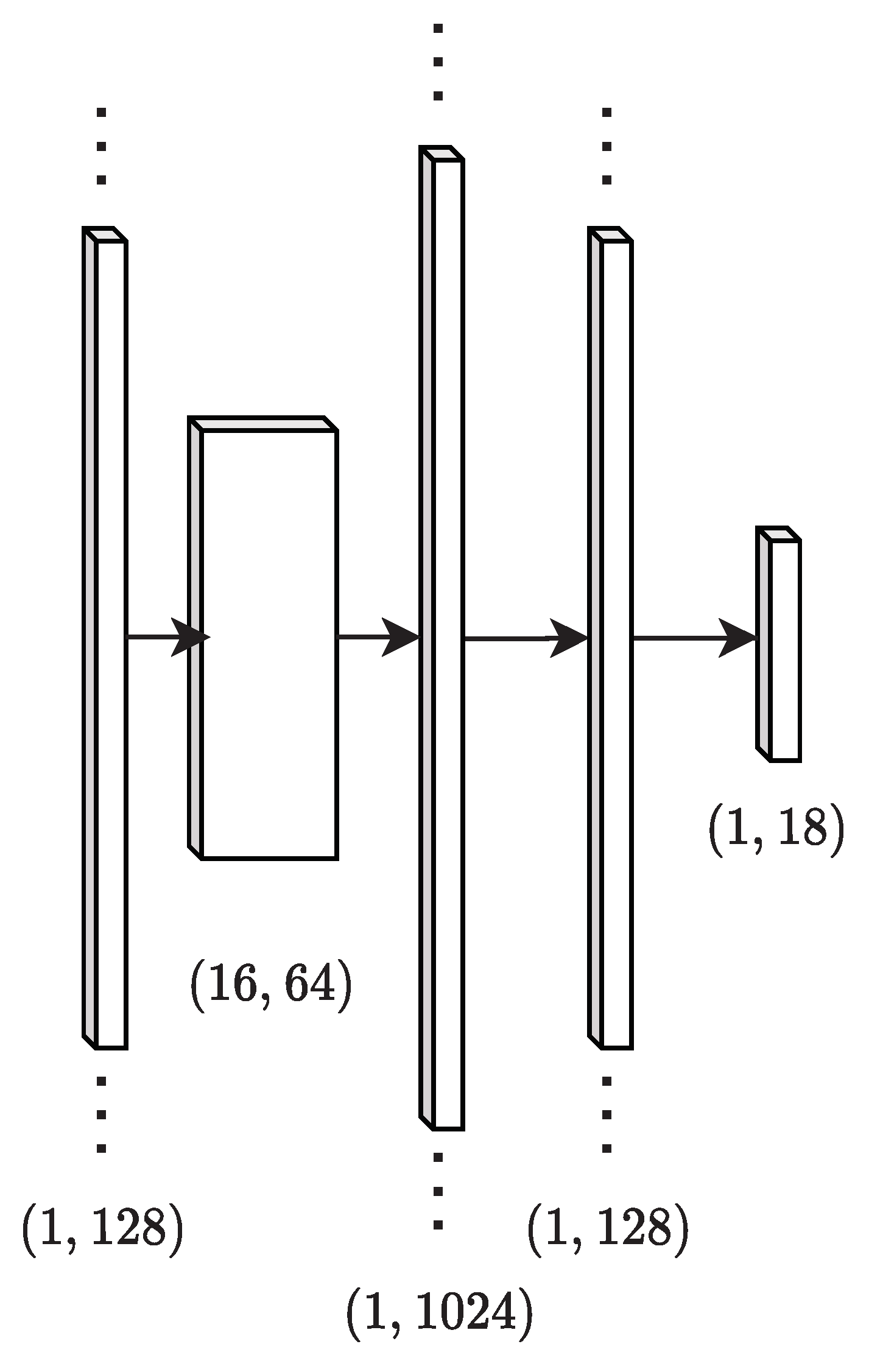
A common approach to such classification problems (e.g., in the form of AlexNet [16]) is to use a series of convolutional layers followed by dense layers. Specifically, one or more convolutional layers are used to produce convolutional feature maps, and these feature maps are flattened into a 1-dimensional vector, as done in refs. [12,13], which is then transformed using dense layers. This work makes use of a network with one convolutional layer followed by a max pooling layer and two dense layers, shown in Figure 2. Additional layers did not enhance performance for the experiments performed and hyperparameter search space used in this work. Identification networks are trained using mini-batches of spectra $\mathbf{X}$ containing known proportions of source and background $\mathbf{Y}$. The cross-entropy loss function is used in optimizing network parameters, having the form

$$\mathcal{L}(\mathbf{Y},\widehat{\mathbf{Y}})=-\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^{N+1}{y}_{ij}ln{\widehat{y}}_{ij},$$

(6)

where $y_{ij}$ and ${\widehat{y}}_{ij}$ are the elements of $\mathbf{Y}$ and $\widehat{\mathbf{Y}}$, respectively. Minimizing cross-entropy loss is equivalent to minimizing the Kullback-Leibler (KL) divergence, which is a measure between two probability distributions $\mathbf{y}$ and $\widehat{\mathbf{y}}$. The KL divergence, and thus cross-entropy, is appropriate in this case since the true value of fractional source and background contributions $\mathbf{y}$ and the corresponding estimate $\widehat{\mathbf{y}}$ can be treated as probability distributions (i.e., $y_i\in [0,1]$ and $\sum y_i=1$). Cross-entropy is used here over the KL divergence, however, simply because it is more common for network-based applications.

Feedforward networks, which include the ANN-based identification methods from previous studies, treat sequential measurements as independent—no information from one measurement is passed to the following. In mobile detection, however, there is generally a relationship between sequential measurements—both background and source contributions to spectra generally do not vary abruptly. As a result, recent measurements can potentially be used to inform the current measurement being processed. For example, if source $s_i$ was present in a spectrum at time t, it is more likely that the spectrum at $t+1$ also contains source $s_i$ than another source $s_j$. In other words, leveraging temporal information has the potential to improve classification, and thus the ability to accurately detect weaker sources.

RNNs are capable of sharing information contained in hidden states between sequential inputs, or in this case, sequences of spectra. This work makes use of Elman layers [20], which are an extension of fully-connected layers. In addition to transforming the state ${\mathbf{h}}^{\left(i\right)}$ to ${\mathbf{h}}^{(i+1)}$, as done in dense feedforward layers, Elman layers also feed the output at time t, ${\mathbf{h}}_t^{(i+1)}$, as an input at time $t+1$:

$${\mathbf{h}}_{t+1}^{(i+1)}=\sigma (\mathbf{W}{\mathbf{h}}_{t+1}^{\left(i\right)}+\mathbf{U}{\mathbf{h}}_t^{(i+1)}+\mathbf{b}),$$

(7)

where $\mathbf{W}$, $\mathbf{U}$, and $\mathbf{b}$ are learned parameters, and $\sigma$ is a nonlinear activation function, described further in Appendix A. There are additional types of recurrent layers, such as long short-term memory modules [21] and gated recurrent units [22], and these more sophisticated modules generally excel at modeling long time sequences where salient information is spread through the sequence. Due to the simple time dependence of the source models examined in this work, this paper only examines Elman layers for relating sequential spectra. In this work, the first dense layer following the flattening of convolutional features is replaced with an Elman layer, allowing for information from previous spectra ${\mathbf{h}}_{t+1}^{\left(i\right)}$ to be used in performing inference on new spectra (i.e., computing ${\mathbf{h}}_{t+1}^{(i+1)}$).

In training feedforward networks, mini-batches of spectra are used, where each spectrum contains a random radionuclide with a source activity randomly sampled uniformly from a predefined range. To provide additional variability in training data, a random source-detector angle $\theta$ (see Appendix B) is used for each spectrum, but a fixed standoff distance of 10 m is used since the activity sampling provides variability in SNR. Additionally, pure background is included for the model to appropriately learn background features in the absence of source. RNNs, however, need to learn the temporal dynamics of sources, meaning that mini-batches cannot simply contain random samples of spectra with different physical parameters—the data must include series of spectral measurements of the detector moving past the source. Instead of training the network on random mini-batches of spectra in the form of a matrix ${\mathbf{X}}_i\in {\mathbb{R}}^{n\times d}$, 3-dimensional tensors ${\mathbf{X}}_i\in {\mathbb{R}}^{r\times n\times d}$ are used, where r refers to a number of runs of data which model the kinematics of a detector moving past a source. With this approach, the network simultaneously learns the mapping between input spectra and relative source contributions and also the temporal behavior of the detector past sources.

2.4. Performance Evaluation and Data

The performance of each method discussed in this work is evaluated by injecting sources with known properties (e.g., activity, distance to detector, etc.) into sequences of background spectra. Source spectra, generated to model the effect of a detector system moving past a stationary source, are added to the background spectra, and algorithms are evaluated on these injection spectra. The outputs of the detection and identification methods are then used to compute the probability of detection, which is the fraction of runs in which the source was successfully detected or identified. The probability of detection is computed as a function of source activity, and the minimum detectable activity (MDA) [5,6] is computed, giving a single measure for how well a given method performs at a particular FAR. Suppose a source with activity A is injected into R different runs, resulting in D detections. The probability of detection is simply $p=D/R$, and as a function of activity, this ratio is modeled with a sigmoid function q of the form

$$q(A;\mu ,\sigma )=\frac{1}{1+e^{-(A-\mu )/\sigma }},$$

(8)

where $\mu$ and $\sigma$ are estimated empirically from p using least squares. Figures illustrating the sigmoid behavior of the probability of detection as a function of activity are omitted here for brevity, and we refer the reader to refs. [5,6] for examples. Using these estimated parameters, the MDA is computed as

$$\mathrm{MDA}\left(p_0\right)=\mu -\sigma ln(p_0^{-1}-1)$$

(9)

for some target detection probability $p_0$. In this work, $p_0=0.95$ is used. Note that theoretical lower bounds for MDA can be estimated for each method [6], which can be useful in assessing potential performance improvements for a given algorithm.

The runs of sequential background spectra are generated from simulations of a detector system moving through an urban environment, originating from a dataset produced as part of a public data competition [23,24]. List-mode gamma-ray events were produced from a 2” × 4” × 16” NaI(Tl) detector moving through a simulated urban environment. Only runs that do not contain anomalous sources, 4900 in total, are used in this work to produce data for training and evaluation. Runs are then divided into training and testing data using a 90–10% split; 4410 runs of training spectra are used as background for learning and validating models parameters, and the 490 testing runs are used for quantifying performance via source injection. Note that the test set only refers to a background dataset that are neither used in training nor validation, and that sources are injected into this background. 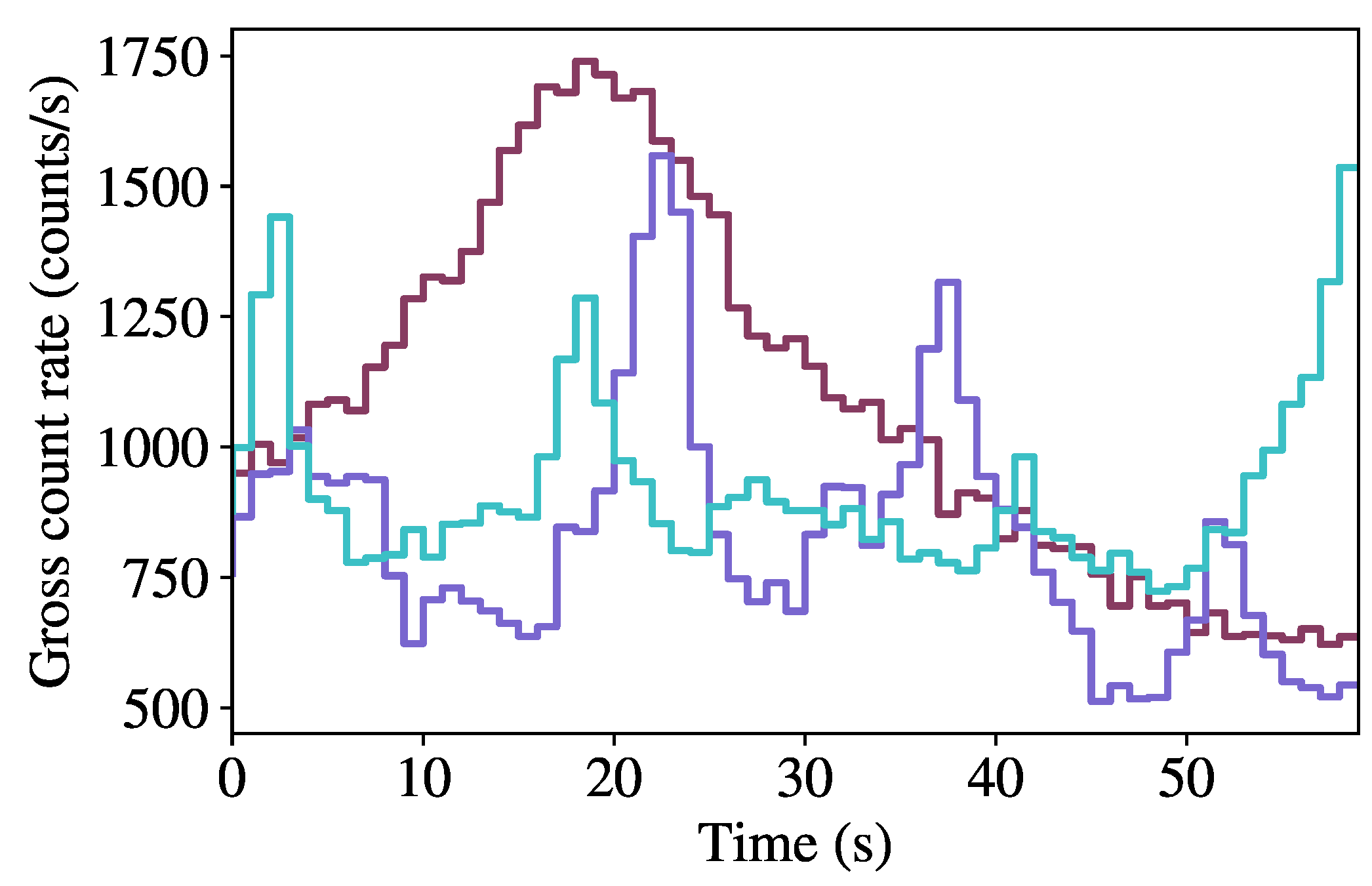Figure 3 shows the background count rate as a function of time for the first 60 s of three randomly-sampled runs, highlighting the variability in background rates within the dataset.

Spectra are formed by binning events between 30 and 3000 keV using 128 bins with widths that increase as the square root of energy and with a 1-s integration time. Note that square root binning is used both in attempt to put full-energy peaks on a similar scale (i.e., span a similar number of bins independent of gamma-ray energy), and to reduce sparsity in spectra, particularly at higher energies where there are fewer counts. Neither the temporal nor spectral binning schemes are optimized, and results can potentially improve by tuning these values. Experimenting with binning schemes commonly reported by fielded systems (e.g., 1024 linearly-spaced bins) is worth examining from a practical standpoint, however, it is beyond the scope of this work.

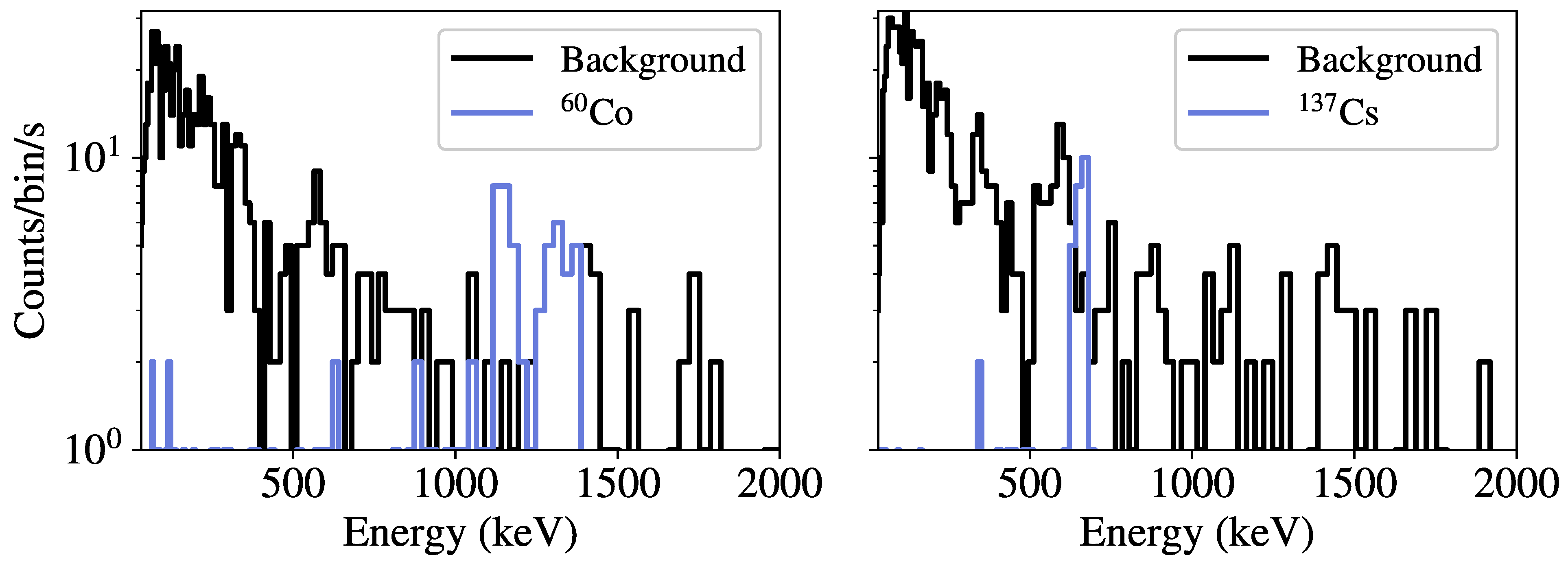
Source data are generated separately from background, using Geant4 [25] to produce list mode data. Appendix B provides a detailed description of the procedure used for generating source spectra. Seventeen source types are generated using this procedure: ¹⁹⁸Au, ¹³³Ba, ⁸²Br, ⁵⁷Co, ⁶⁰Co, ¹³⁷Cs, ¹⁵²Eu, ¹²³I, ¹³¹I, ¹¹¹In, ¹⁹²Ir, ⁵⁴Mn, ¹²⁴Sb, ⁴⁶Sc, ⁷⁵Se, ¹¹³Sn, and ²⁰¹Tl. Figure 4 gives examples of spectra from low-activity ⁶⁰Co and ¹³⁷Cs sources compared to randomly-sampled background spectra. Note that the injected sources are simulated independently in vacuum, meaning the effects of environmental scattering or occlusions are not contained in the resulting spectra. In modeling the kinematics of the detector past the source, a vehicle speed of $v=5$ m/s, along a straight line, and a standoff distance $r_0=10$ m are used. According to information provided as part of the competition, the detector speed used in generating a given background run was a constant value ranging between 1 m/s and 13.1 m/s. However, the detector speed for each run was not provided as part of the original data competition, meaning the speed v used in modeling the source kinematics is not necessarily the same. While not ideal, this discrepancy is not believed to affect the conclusions drawn from these analyses, as the speed used here (5 m/s) is in the range of values used to produce the background data.

2.5. Model Optimization

In this context, optimization refers to the process of using a dataset $\mathcal{X}$, split into training and validation subsets, to update model parameters $\mathcal{P}$, generally by some variation of stochastic gradient descent, such that the loss evaluated on $\mathcal{X}$ decreases with number of training iterations, or epochs. The elements of optimization, as they pertain to the current analyses, are briefly discussed in this section.

2.5.1. Training, Validation, and Early Stopping

First, the training set is subdivided into a set used for updating model parameters, also referred to as training data, and a validation set used for assessing model performance during optimization. During each epoch, the model parameters are updated based on each mini-batch of training data, and following these parameter updates, the error is computed on the validation data, giving a sense for how accurately the model is performing on data that was not used to update model parameters. The validation set is used to assess the generalization capabilities of the model, and in particular, it is used to indicate when the optimization procedure should cease. Initially, the loss from both the training and validation sets will decrease, however, there will often be a point at which the training loss continues to decrease, while the validation loss increases—a sign of overfitting. Early stopping is the method of stopping the training process once the validation loss begins to increase for some number of iterations, referred to as the patience. In this work, early stopping with a patience of 10 iterations is used in training each network.

2.5.2. Data Preprocessing and Batch Normalization

Models often converge faster when performing input data preprocessing and feature rescaling within the network [26]. During the experimentation for this work, a linear rescaling based on the mean and standard deviation of training data, referred to as standardization, was found to perform well for both detection and identification networks. Standardization transforms an input spectrum $\mathbf{x}$ to ${\mathbf{x}}^{\prime }$ as

$${\mathbf{x}}^{\prime }=\frac{\mathbf{x}-\mathit{\mu }}{\mathit{\sigma }+ϵ},$$

(10)

where $\mathit{\mu }$ and $\mathit{\sigma }$ are the mean spectrum and standard deviation, respectively, and $ϵ$ is a small positive constant to avoid division by 0. Furthermore, features in the network’s hidden layers can be standardized, referred to as batch normalization [27] which additionally has a regularizing effect. In this work, DAEs and feedforward identification networks use batch normalization.

2.5.3. Optimizer and Regularization

This work uses the Adam optimizer [28] with an initial learning rate of ${10}^{-3}$ for performing parameter optimization. The learning rate is reduced by a factor of 10 when the validation loss does not decrease for 5 trials, reducing the maximum step size, as the model is presumably near a local minimum. To reduce overfitting, an L2 penalty is used, controlled by a coefficient $\lambda$. Additionally, dropout [29], in which neurons are randomly set to 0 with some probability p ($p=0.5$ here), is used in the identification networks following the convolutional layer and after the first dense layer. Note that the initial learning rate and dropout probability were deemed to work sufficiently well during manual experimentation and are not optimized further.

2.5.4. Hyperparameter Optimization

The optimization procedure is performed for a given model architecture, dataset, and hyperparameter configuration. Hyperparameters refer to parameters that are not learned (i.e., they are configured prior to training), and generally determine a network’s modeling capacity. In the discussion so far, some hyperparameters include the number of neurons in a layer, number of convolutional kernels in a layer, and the L2 regularization coefficient $\lambda$. Because of the impact that hyperparameters have on model performance, care must be taken to choose optimal values. Common methods for performing hyperparameter optimization include grid search, random search, and Bayesian optimization. A joint optimization of all hyperparameters is beyond the scope of this work, and instead, this work does a partial optimization: a subset of hyperparameters for a model are fixed, determined from manual experimentation, and a random search [30] is performed with remaining hyperparameters.

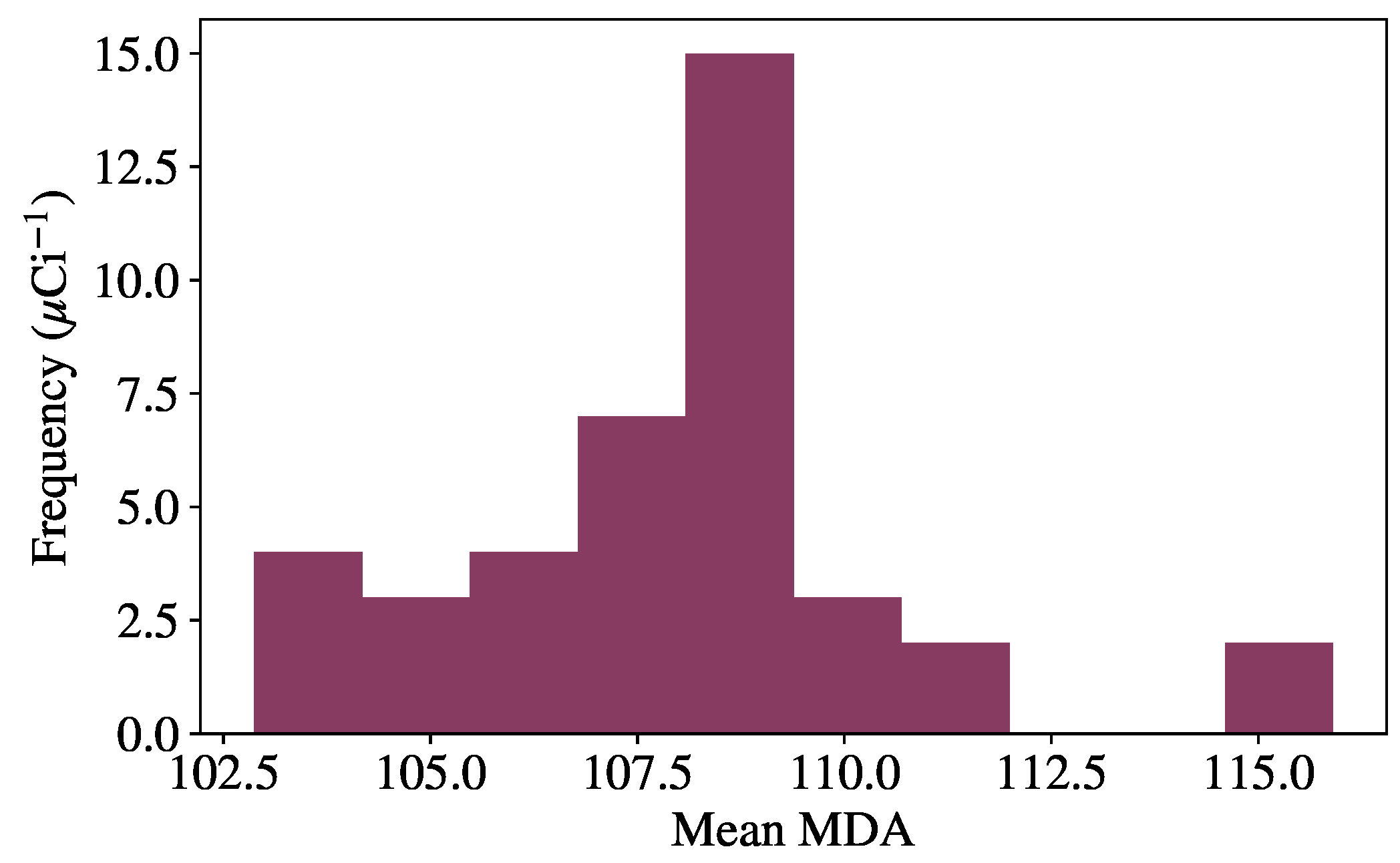
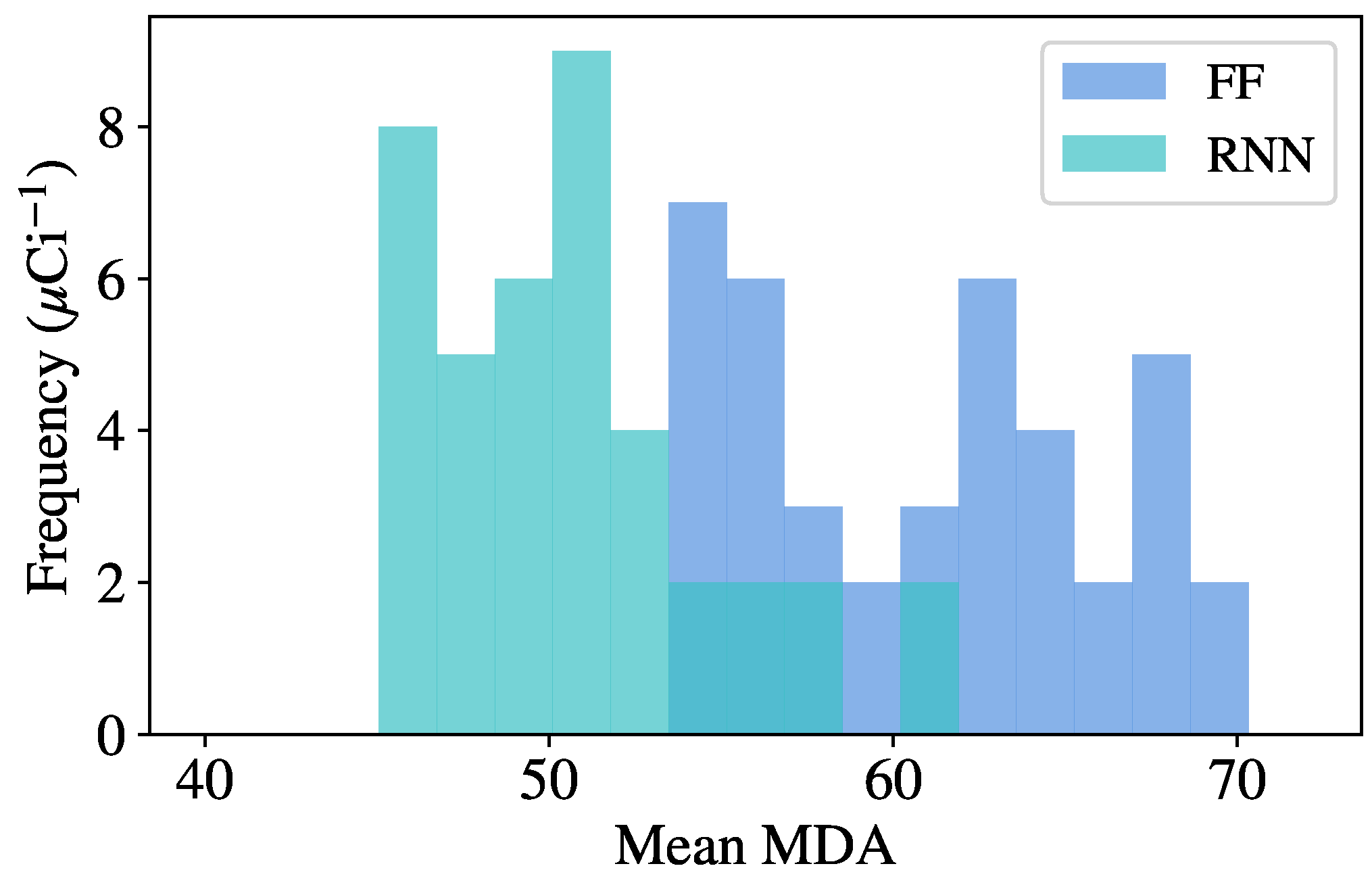
To perform the random optimization, the following procedure is used. First, the variable hyperparameters are randomly sampled from a predefined space, and the model is trained and validated using the procedure previously described. Once a model has finished training, source injection is performed on background data from the validation set, giving an initial MDA for each source. Many models are trained using this procedure, and the model resulting in the lowest mean MDA across all sources is used to evaluate the final test set, as the model has shown the greatest generalization capabilities on unseen data. This optimal model is then evaluated on the test set and compared to benchmark algorithms. The specific hyperparameters tuned for each model are described in the following section with the results.

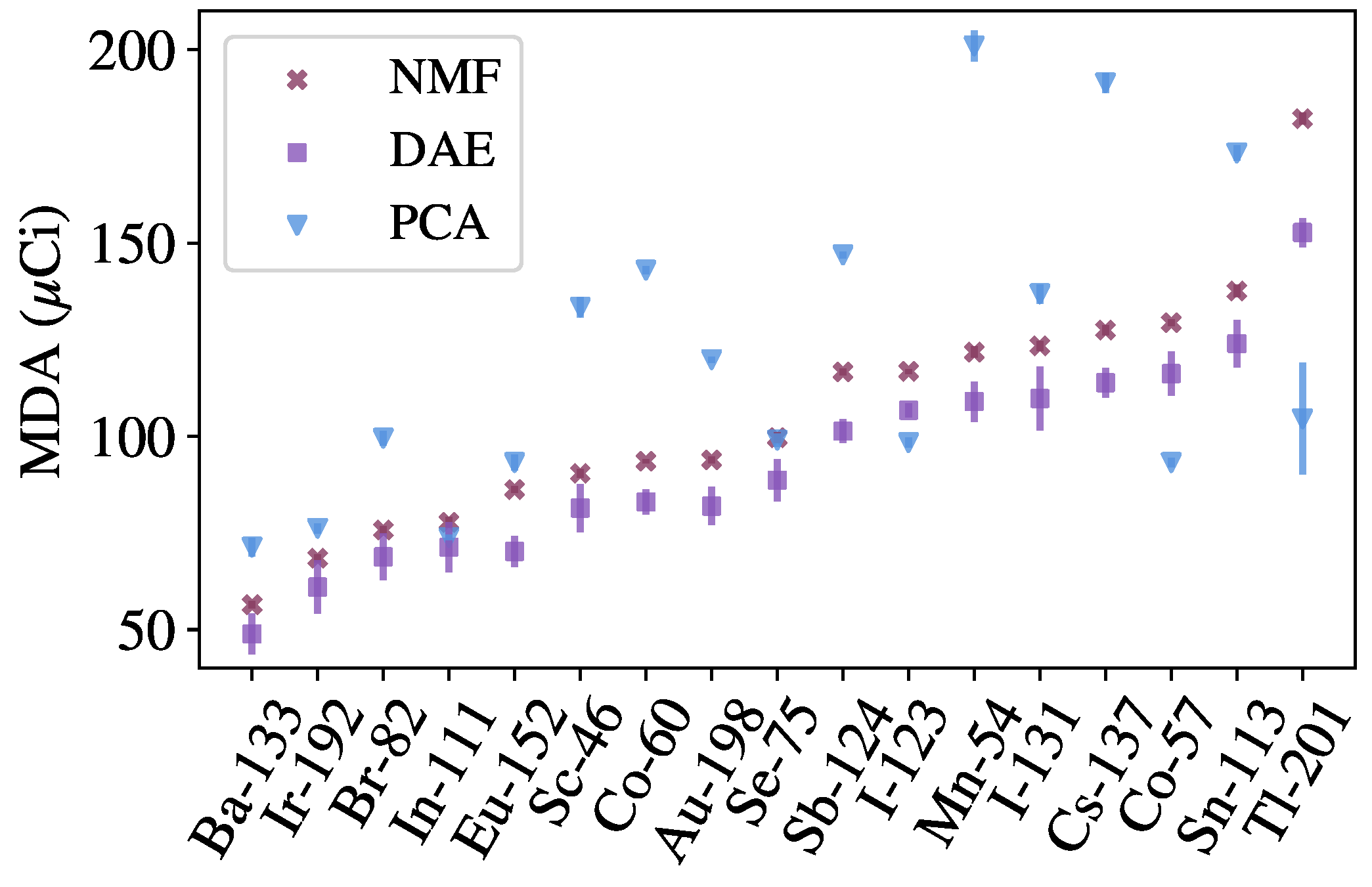
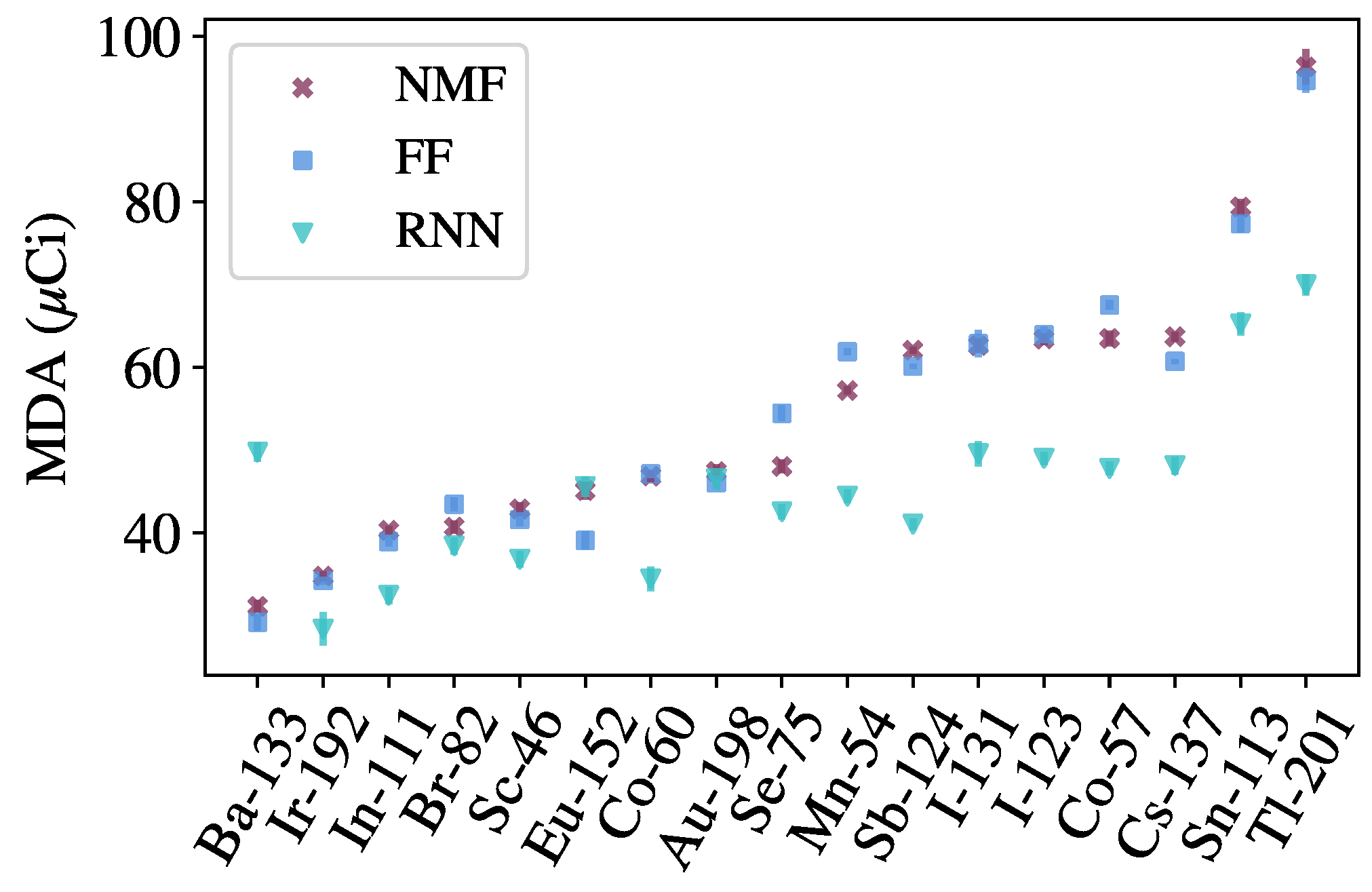
2.6. Benchmarking

The methods discussed in this work are benchmarked against approaches from recent literature. In particular, anomaly detection methods based on Principal Component Analysis (PCA) and Non-negative Matrix Factorization (NMF) are used to benchmark the autoencoder methods [6]. Both methods are linear models that operate similar to the autoencoders, in that the models are used to provide approximations of background spectra, and detection metrics are computed between the inputs and approximations. To perform the approximation, both methods can be thought of as performing a matrix decomposition $\mathbf{X}=\mathbf{AV}$, where $\mathbf{X}$ is a matrix of training data, and $\mathbf{A}$ and $\mathbf{V}$ are generally low-rank matrices with k degrees of freedom, or components. The NMF-based method also uses the Poisson deviance as a detection metric, whereas the PCA-based method, based on previous literature [31], uses the following detection metric:

$$D(\mathbf{x},\widehat{\mathbf{x}})=\frac{\parallel \mathbf{x}-\widehat{\mathbf{x}}{\parallel }_2}{\sqrt{{\parallel \mathbf{x}\parallel }_1}},$$

(11)

where the subscripts 1 and 2 denote the L1 and L2 norms, respectively.

An identification method, also based on NMF, is used to benchmark the identification networks. The components $\mathbf{V}$, learned from background data, are augmented with templates for each source of interest, allowing for reconstructions of spectra containing both background and sources. A likelihood ratio test is performed, providing a detection metric for each source of interest. Both the detection and identification methods set thresholds based on distributions of metrics produced from evaluating on background data. See ref. [6] and the references therein for additional details about the benchmarking methods.

3. Results

3.1. Anomaly Detection

Values of $\lambda$ are randomly sampled between 1 and 100 using a uniform distribution. The number of neurons in each hidden layer (three values in total for a symmetric DAE with five hidden layers), are randomly sampled under the constraint that each value decreased to center of the network. The number of neurons in the outermost values is sampled uniformly between 3 and 24. An example random configuration is (11, 7, 4), which means the number of features for all hidden layers in the network is (11, 7, 4, 7, 11). A total of 40 DAEs are trained using mini-batches of 512 randomly-sampled spectra. For each model, a threshold on the deviance test statistic is set using a FAR of 1/8 h${}^{-1}$.

Figure 5 shows a histogram of the mean MDA across all sources injected into the validation background set for the 40 different models. From this optimization, a model corresponding to $\lambda =$ 55.53 and number of neurons per layer (7, 3, 2, 3, 7) is used for evaluation on the test set. Both the PCA- and NMF-based models are evaluated on the validation dataset, each indicating that a $k=1$ component model was sufficient. Note that using a single component to represent either linear models reflects a lack of true variability in the background data for the number of spectral bins used, as many real-world datasets have been seen to yield higher numbers of components.

Figure 6 shows a comparison of the optimized DAE and linear models evaluated on each source injected into the background test set. These results show that the autoencoder-based detection method generally outperform both the NMF- and the PCA-based methods. On average, the autoencoder provides a 12% and 23% improvement over NMF- and PCA-based detection methods, respectively. The discrepancy between the PCA-based detection method and the others is likely due to the detection metric used for the PCA-based approach, which comes from previous literature [31].

To assess timing performance, the average runtime per spectrum is computed for each method. Specifically, 100 background runs are randomly sampled, and the average runtime on a per-spectrum basis is computed over each run. The averages from all 100 runs are then averaged and presented here. The reason for averaging over runs is to provide a direct comparison with the RNN-based method in the next section, which is evaluated on series of spectra. The average per-spectrum runtime for the NMF-, PCA-, and DAE-based detection methods are 0.37 ms, 0.05 ms, and 0.02 ms, respectively, when evaluated on a 3.50 GHz Intel i7-5930K CPU.

3.2. Identification

Values of $\lambda$ for both feedforward and recurrent identification networks are randomly sampled between 10${}^{-3}$ and 10 using a log-uniform distribution. For the single convolutional layer used, the number of kernels is sampled between 8 and 64, and the number of output neurons of the first dense layer, or the recurrent layer in the case of RNNs, is sampled uniformly between 32 and 256. Feedforward models are trained using mini-batches of 256 spectra, and recurrent models are trained with mini-batches of 32 runs of spectra. For a given model, thresholds for each source are set using empirical values of outputs generated from background data to achieve an overall FAR of approximately 1/8 h${}^{-1}$. Due to simultaneously testing for multiple sources, a Bonferroni correction [32] is used to achieve the target FAR, resulting in an effective FAR for each source which is simply the target FAR divided by the number of sources (i.e., 1/(8 × 17) h${}^{-1}$).

The optimization procedure is repeated 40 times for both types of models, resulting in the values ($\lambda$, $n_{\mathrm{kernels}}$, $n_{\mathrm{neurons}}$) of (0.49, 64, 66) for the feedforward networks, and (0.0013, 32, 115) for the RNNs. The distribution of MDA over the validation set for all of the 40 trials in the optimization routine is shown for both feedforward and recurrent models in Figure 7. This shows that, while there are outliers, the distribution of MDA for RNNs is generally lower than that for feedforward networks, indicating that RNNs often perform better at the same FAR. Figure 8 shows a comparison of the mean MDA for optimized feedforward and recurrent identification networks compared to the NMF-based identification benchmark. This figure indicates that the NMF-based detection method and feedforward network perform roughly the same at the same FAR, while the RNN-based identification method often provides an improvement, as expected. Specifically, the RNN is seen to provide a 17% improvement over the feedforward network. As with the detection methods, the average per-spectrum runtime is computed for the NMF-based identification, feedforward network, and recurrent network, yielding 9.54 ms, 0.07 ms, and 0.05 ms, respectively.

4. Conclusions

The goals of this work were to introduce spectral anomaly detection using autoencoders, establish a baseline of current state-of-the-art identification networks relative to simpler methods, and improve upon the current state-of-the-art using recurrent neural networks. In doing so, ANN-based detection showed a 12% and 23% improvement over the NMF- and PCA-based detection models, respectively, while the current state-of-the-art ANN-based identification was on par with the NMF-based identification method. Furthermore, the ANN-based methods showed a reduction in computational time. The improvement in detection performance and reduction in computation time make ANN-based detection a compelling candidate. Regarding identification, the reduction in runtime while achieving similar performance to NMF, an established benchmark method, makes ANN-based identification worth considering for practical applications as well. Lastly, ANN-based identification was seen to improve, on average, with the use of recurrent layers, meaning that computationally-inexpensive performance improvements can be made by including temporal modeling.

Despite the encouraging results, the use of neural networks over linear models involves tradeoffs. Networks require significantly more overhead in the form of data preparation, model design, optimization, etc. Meanwhile, methods such as NMF generally require significantly less in this regard—NMF simply needs to be performed on a matrix of input spectra using a single hyperparameter k, the number of components. However, much of the overhead with networks comes at a fixed cost; the computational burden of networks at runtime is generally significantly lower than iterative methods (e.g., NMF). For this reason, the networks examined here may be more practical than NMF-based detection or identification in scenarios with limited computational resources, for example, in low- power applications.

Though the intention here was to evaluate network-based approaches in operationally-relevant conditions, the performance in many realistic scenarios remains unclear. For one, models must be able to generalize to new environments, meaning these methods should be assessed on real-world data with higher spectral variability. While efforts were made to provide variable background in generating the original simulated data, effects such as elevated radon levels following rain and gain drift were not included. Additionally, other scenarios of practical interest include having multiple sources in a run, either at the same location or at various points in a run, and examining the effect of shielding sources. Future efforts should then assess the impact of shielding and combinations of sources, similar to that of ref. [3], under operationally-relevant conditions.

Due to the number of parameters and operations, neural networks are generally not as interpretable as other methods such as NMF [6,33], though this is an active area of research [34]. The nature of nuclear safety and security, the primary application of such algorithms, warrants tools and methods for introspection of networks to better assess behavior. For example, in the case of NMF, an alarm for a ¹³⁷Cs source corresponds to an excess of counts associated with the ¹³⁷Cs template, which an operator can interpret and act on. However, it is not clear how identification networks could be interpreted, due to the number of interconnected parameters involved in making a decision—the operator must simply trust that the network is behaving correctly. Additional research is needed in the area of interpretability of spectral models, for example, understanding convolutional kernels as with ref. [13], or generating saliency maps which relate the most significant input features in determining a given network output.