1. Introduction
OpenMC is a Monte Carlo particle transport code developed with an emphasis on reactor analysis calculations [
1]. The software and its accompanying Python application programming interface (API) has the ability to generate multigroup cross sections (MGXS) [
2] from the continuous-energy (CE) calculation. OpenMC also contains a multigroup (MG) transport solver [
3]. This MG capability was specifically implemented to enable the quantification of the errors associated with commonly made approximations to the neutron transport approximation, whether they be spatial, angular, or related to the generation of the MGXS. Accordingly, this paper describes work to use this capability to investigate the errors introduced by assuming that the energy spectra used to create group-wise cross sections is separable in angle and energy. This approximation is commonly known as the flux separability approximation (FSA).
This paper will begin describing the FSA, and then proceed to analyze the effects of this approximation on a simplistic 1D slab problem. From here, the paper will extend the evaluation to more practical and realistic applications. Finally, the findings will be summarized and conclusions made.
2. Flux Separability Approximation
The generation and use of MGXS data in practice relies on the application of the FSA. This approximation assumes that the energy dependence of the angular flux is not a function of the neutron angle. This allows the angular dependence to be removed from MGXS data. This approximation is provided in Equation (1) for the case of the total cross section. In Equation (1), E is the neutron energy, r is the position vector, Ω is the direction vector, g is the energy group index,
is the macroscopic total cross section,
is the angular neutron flux,
is the scalar neutron flux. In the FSA, the angle dependence is assumed separable from energy dependence, allowing it to be withdrawn from the integrand and ultimately cancelled. The result of this is an angle-independent MGXS.
This approximation cannot be expected to perform well in cases when the angle- and energy-dependence of the neutron flux are correlated. This may physically occur within strongly-absorbing materials or near material discontinuities. In these cases, neutrons travelling in opposite directions can have entirely different within-group energy spectra because of the differing absorption or scattering characteristics of a region. A simple example of such a scenario is a slab of a fissile material surrounded by a moderator. In this case most fast fission neutrons will be travelling away from the fissile material while most thermal neutrons will be travelling from the moderator into the fissile material. This strong relationship between energy and angle would be ignored by the FSA, though it can be mitigated by increasing the number of groups.
A common way to approximately treat this effect is with the consistent-P
N and extended transport approximations derived by Bell, Hansen, and Sandmeier [
4], or to utilize reaction rate adjustment factors, such as superhomogenization factors, to account for the discrepancy [
5,
6]. A more rigorous approach is to represent the angle dependence of the MGXS data explicitly.
Cross sections can be generated for this more rigorous approach via the openmc.mgxs module of the OpenMC Python API where polar and azimuthal tally filters are used to create MGXS data that is a histogram representation of a function of the neutron’s direction of motion. The OpenMC MG solver can then use this data to perform neutron transport without making the FSA.
3. Evaluation of Flux Separability Approximation Errors
This section will examine the effect of relaxing this FSA for three models of increasing complexity: (1) the 1D slab case discussed above; (2) a 2D pressurized water reactor (PWR) pin cell; and (3) a 2D metal-fueled, sodium-cooled, steel-reflected, fast reactor (SFR). The 1D slab case is used to explore the errors associated with the FSA. The subsequent cases evaluate if these findings hold for more realistic analyses.
For each of these models, a CE OpenMC simulation with ENDF/B-VII.1 cross sections will be used to generate the MGXS for the given model, group structure, and with or without the FSA. All MGXS libraries developed herein will use the OpenMC MGXS Python API interface and its methods discussed in [
2]. Tracklength estimators are used for all reaction rates and fluxes, except for generating the scattering matrices and fission energy spectra that use analog estimators for the relevant reaction rates and flux. The spatial homogenization was performed over problem-specific spatial domains to be discussed later.
The angle-dependent MGXS libraries are generated by setting the number of polar and azimuthal angles in the MGXS Python API. This adds the polar or azimuthal a neutron angle filter with the specified number of equal-width bins to the CE OpenMC reaction rate and flux tallies used to create the MGXS. The models in this work only applied the azimuthal filter; this captures the primary angle-dependent effects while keeping stochastic error low.
The scattering change-in-angle (µ) is represented with an 11-bin histogram instead of the typical Legendre expansion. Legendre scattering is supported by the OpenMC MG solver; however, the Legendre expansion truncation error can yield a negative probability distribution for µ, especially in cases with a large number of energy groups. These negative probability distributions can introduce non-negligible error in a Monte Carlo MG computations. Therefore using a sufficiently discretized histogram representation of the probability distribution for µ precludes this error from being present.
Once the MGXS library is generated, all cases will then use this library instead of the CE data to re-evaluate the same model using the MG Monte Carlo solver in OpenMC.
All of the models are isothermal at 294 K. The CE and MG cases were run with 200 inactive batches and 3000 active batches of 50,000 histories per batch (150 million active histories). All computations were performed with OpenMC version 0.11.
3.1. 1D Slab Model
When describing the FSA, a slab of fuel next to a slab of moderator was used as an example to highlight how the neutron flux’s energy- and angle- dependence can be correlated. This 1D slab model examines this phenomena in a simple to evaluate and visualize scenario.
3.1.1. Model Definition
This 1D model is a 2.0 cm slab of fuel followed by a 0.4 cm slab of zirconium, and a 1.6 cm slab of borated water, yielding a total model thickness of 4 cm. Reflective boundary conditions are applied on all surfaces, making this infinite in the Y and Z dimensions, and a repeating array in the X dimension.
The fuel is 3.1 w/o-enriched UO2 at a total material atom density of 6.864 × 10−2 atom/b-cm. The zirconium is simply elemental zirconium at an atom density of 4.255 × 10−3 atom/b-cm. The borated water has a total atom density of 6.627 × 10−2 atom/b-cm with 720 ppm of elemental boron. The CE OpenMC eigenvalue for this case is 1.14670 ± 0.00008.
3.1.2. Examination of Spatial Homogenization and Multigroup Approximation Errors
This section will progress through an examination of this model’s sensitivity to the choices made to represent the space, energy, and scattering angle dependence.
The first case considered was a discretization of the 4 cm slab into 10 equal-width cross section homogenization regions, producing a 1-group MGXS library spanning 0 to 20 MeV. The boundaries of these 10 homogenization regions do not cross material domains and thus there is no mixing of materials within a region. When these 1-group cross sections were generated by the OpenMC CE solver and used in the MG solver, the resultant eigenvalue is 1.15907 ± 0.00003 for an eigenvalue bias of 1237 pcm.
Figure 1 provides the neutron flux across this domain as tallied across 25 equal-width meshes. In this and later figures for this model, the red is the fuel, gray is the zirconium, and blue is the water. The vertical dotted lines denote the cross section homogenization boundaries; i.e., the region between the dotted lines will use the same MGXS throughout. Finally, the dark blue line is the flux computed with CE data, and the orange line is that computed when using the MG data generated from the CE calculation. At a high level,
Figure 1 shows that the MGXS are not allowing enough neutrons to escape the fuel.
Next, the homogenization regions were subdivided into three regions per original region to explore if these errors are due to spatial homogenization error. When doing so, the eigenvalue bias stayed roughly the same at 1230 pcm. Next, a fine-mesh was used for the MGXS regions near the material interfaces. Specifically, 60 cross section homogenization regions were applied from 1.8 cm to 2.6 cm (i.e., 0.2 cm left of the fuel-zirconium interface to 0.2 cm right of the zirconium-water interface). This also had negligible effect on the eigenvalue or the flux distribution. Therefore, it is concluded that the spatial mesh of the MGXS is not a dominant source of the eigenvalue and flux errors and that 10 regions is sufficient.
The next potential source of error is the energy group discretization. The previous 1-group analysis was then re-performed with 2-, 3-, 4-, and 47-group structures. The 2-group structure has a breakpoint at 0.625 eV; the 3-group structure adds a breakpoint at 0.82 MeV, the 4-group structure adds an additional breakpoint at 100 eV. The 47-group structure is the HELIOS 47-group structure [
7].
Table 1 provides quantitative measures for the improvement of the solution with increasing groups. The first metric is the standard eigenvalue bias. The bias significantly decreases as the number of groups increases, which is the typical and expected behavior. The second metric provided in
Table 1 is the root-mean-squared-error (RMSE) of the MG and CE fluxes by group and spatial mesh. The results show that, generally, as the number of groups increases, the RMSE of the fluxes generally decreases as well.
Figure 2 provides a qualitative indication of the performance of the flux distribution with increasing groups. Here, the one-group flux (i.e., the summation of flux over all groups) throughout the problem domain is plotted for the 2-, 3-, 4-, and 47-group cases. These results show that the low errors of the 2-group case were due to a fortuitous cancellation of errors as the flux distribution is too large in the fuel. The 4- and 47-group cases are noticeably closer to the CE reference solution than the other group structures.
3.1.3. Examination of Flux Separability Approximation Errors
The magnitude of the error introduced by the FSA is now evaluated using the angle-dependent MGXS tallying and transport capability of OpenMC. The same group structures and spatial discretization discussed in the previous section were used, but the MGXS were generated across histogram bins spanning the azimuthal angle space of [−π, π). 1, 4, 8, 12, and 16 equal-width azimuthal bins were examined.
Table 2 provides the quantitative error metrics for the eigenvalue and flux distributions when varying both the groups and the number of azimuthal angle bins. The results show that the addition of 4–8 azimuthal angles is enough in some cases to reduce the eigenvalue bias substantially; more than 12 provides diminishing returns. These results also show that 8 azimuthal angle bins and 1 group produces a smaller eigenvalue bias than the standard 47-group MGXS with the FSA (the 1 angle bin case in
Table 2). Interestingly, the angle-dependent MGXS provide limited improvement for cases with a large number of groups and angles; this could be due to the stochastic uncertainty present in the MGXS data that is introduced when energy and angle tallies are further discretized for these cases. This was not explored further.
Figure 3 provides the spatial flux distribution for the cases with 4, 8, 12, and 16 angle bins and 4 groups for the total flux (i.e., 0 to 20 MeV). These flux distributions show that the MG flux is qualitatively converging to the CE flux as the number of angle bins are increased.
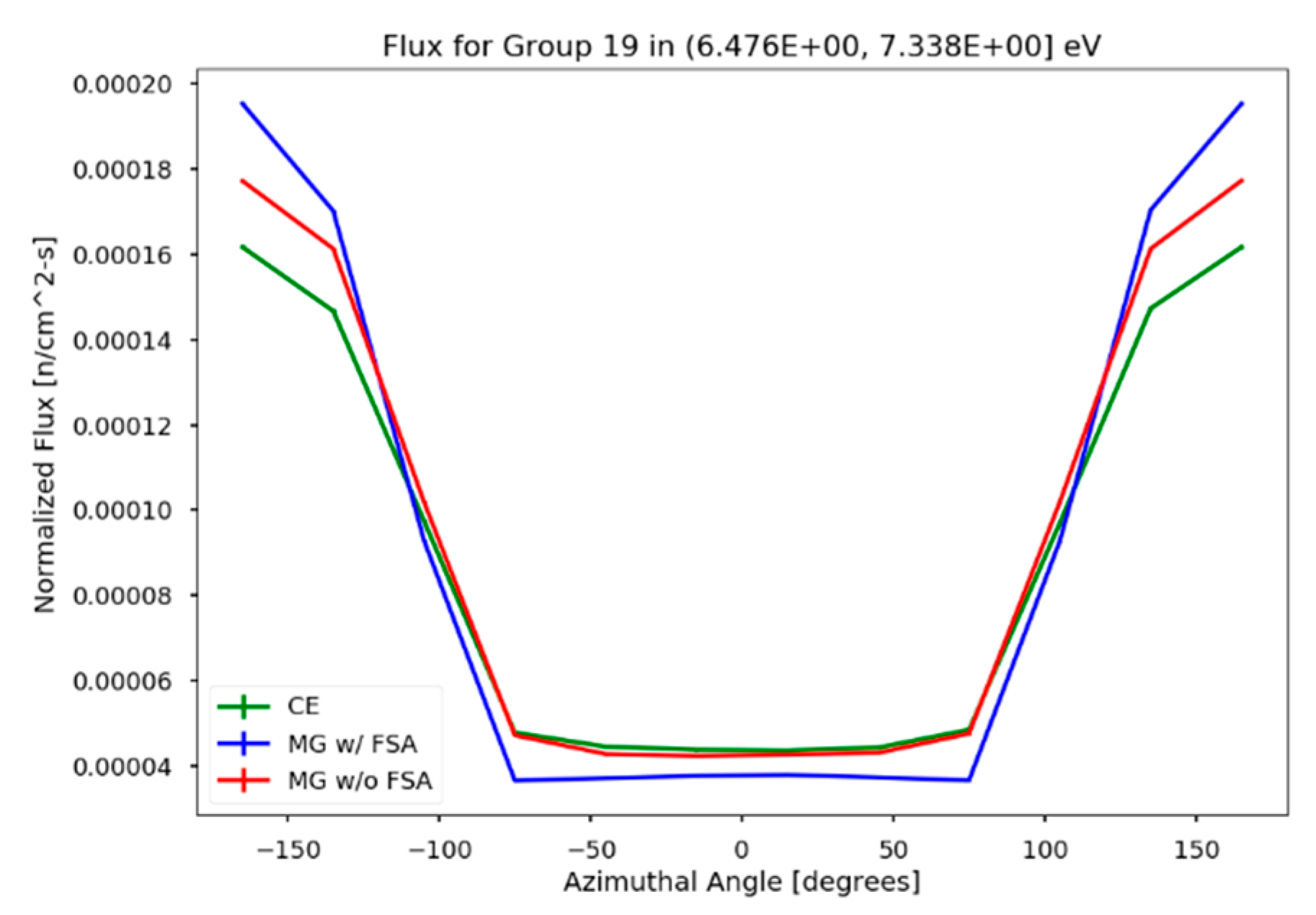
To examine the benefit that angle-dependent MGXS brings specifically in capturing resonance self-shielding, consider the behavior of neutrons near the fuel/cladding interface and at energies at and around the strong 238U absorption resonance at 6.67 eV. Such neutrons travelling to the fuel from the cladding have not been shielded by this strong resonance, while neutrons travelling outward from the fuel have. The CE solution will naturally capture this behavior. An MG solution will only capture this if the MGXS capture the behavior. MGXS generated with the FSA will be weighted by neutrons of all directions of motion, yielding an MGXS weighted over all directions. Therefore the streaming of neutrons into and out of the fuel can only capture the average behavior over all directions. Conversely, angle-dependent MGXS will have MGXS values specific to the particle direction of interest, and thus will have an angular flux closer to the CE prediction.
Figure 4 provides the angular flux in the fuel region immediately adjacent to the cladding of the slab model. This angular flux is from group 19 of the 47-group structure; this group contains the 6.67 eV
238U resonance. The azimuthal angular flux for the CE, flux-separability approximation based MGXS flux (“MG w/FSA”), and angle-dependent MGXS flux (“MG w/o FSA”) are included in the figure. Here, 0 degrees is oriented along the X-axis, and thus is the direction of neutrons leaving the fuel. As expected, the use of angle-dependent MGXS reduces the error compared to the flux computed with the FSA-based MGXS.
In summary, this 1D slab case has shown that: (1) the FSA may be important in scenarios where there is a large energy-angle correlation to the flux, including when resonance self-shielding is prominent; and (2) the MGXS approximation errors that are typically subdued by more neutron energy groups could also be mitigated with the application of angle-dependent MGXS.
3.2. 2D PWR Pin Cell
The next case to consider is a 2D PWR pin cell case to evaluate if the 1D slab findings hold in a more relevant scenario. This pin cell will use the same materials and general arrangement as the 1D slab; however, the geometry will be more representative of those encountered during typical reactor analysis calculations. This section will first discuss the specifics of the model and then discuss how the errors behave when the FSA is relaxed.
3.2.1. Model Definition
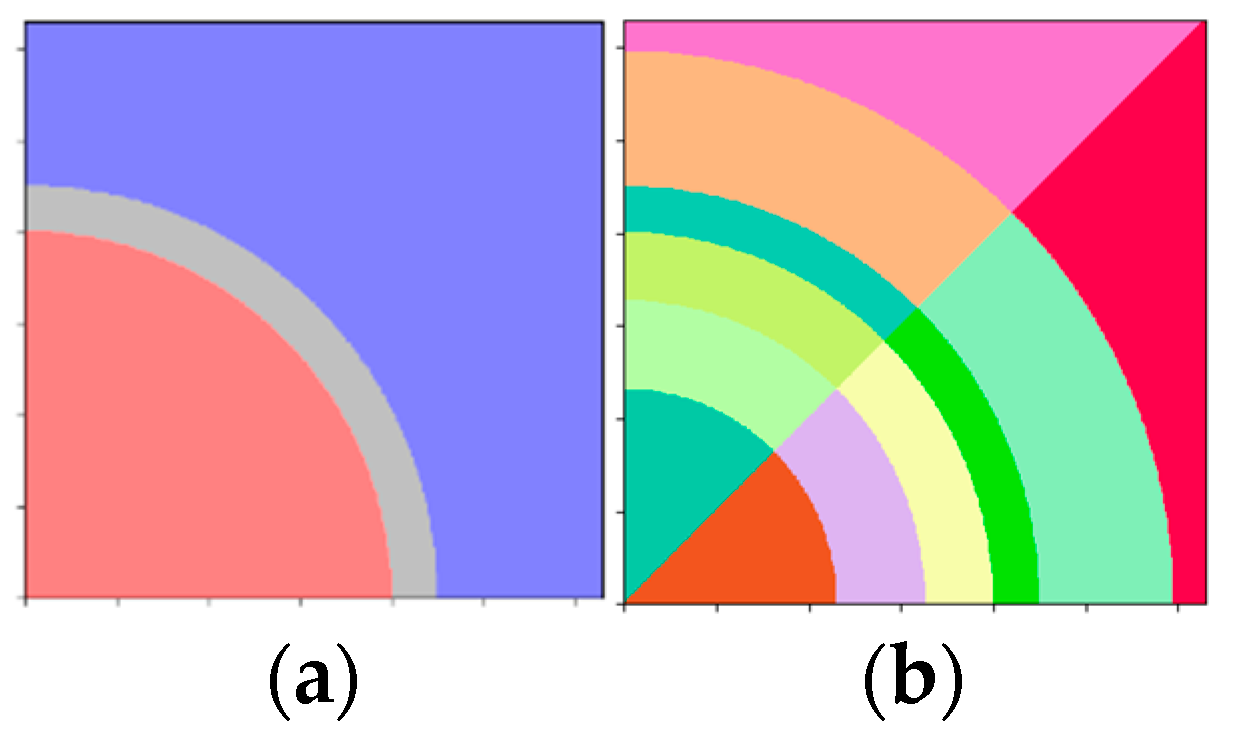
The fuel pin has a radius of 0.4 cm, the cladding thickness is 0.05 cm, and the pin pitch is 1.26 cm. No fuel-cladding gap is included. Only the upper-right quadrant of the pin cell is included in the OpenMC model. The resultant geometry is shown in the left side of
Figure 5. The material coloring of the left-hand-side of
Figure 5 is the same as was utilized for the 1D slab case: red is fuel, gray is cladding, and blue is the borated water. The MGXS homogenization regions are shown on the right hand side with each region having a color distinct from the neighboring region. These regions have three equal-area fuel rings, one cladding ring, and two equal-area water rings. Each of the above rings are further subdivided into two azimuthal regions. The CE OpenMC eigenvalue for this case is 1.22022 ± 0.00007.
3.2.2. Examination of Flux Separability Approximation Errors
To evaluate the errors associated with the FSA, the MG evaluations were performed with the same 1-, 2- 3-, 4-group, and 47-group structures used in the 1D slab case. In addition to varying the number of groups, each group structure also applied 1, 4, 8, 12, and 16 azimuthal angle bins. The 1-angle-bin case is equivalent to employing the FSA. Each of these cases employed 11-bin histogram scattering as previously discussed.
The eigenvalue biases and flux RMSEs for each of these cases are tabulated in
Table 3. Starting with the MGXS with the FSA (the 1-angle bin case) the MG eigenvalue is shown shifting from a −80 pcm to +301 pcm as the number of groups are increased to 47. This indicates that the discretization strategy has led to a fortuitous cancellation of error. This is consistent with the findings of Gibson [
5] and Park [
6], who both analyzed a similar pin cell model with different MGXS generation and MG transport solvers.
Table 3 shows that increasing the number of azimuthal angle bins to the MGXS library (relaxing the FSA) can significantly reduce the eigenvalue biases and flux RMSEs for some cases. The cases which see little change in the eigenvalue or flux RMSE are those whose errors are already reasonably low.
The qualitative effect of the introduction of the angle-dependent MGXS are shown in
Figure 6. In this figure, the MG-to-CE total flux distribution ratios are plotted for the 1, 4, 8, and 12 azimuthal angle bin cases for the 47-group case. The FSA case is provided in the top left, the 4-angle-bin case is in the top right, 8 bins in the lower-left, and 12 bins in the lower-right. All four cases share the coloring scheme shown in the lower-right figure’s color scale: red and blue denote ± 0.3% error, respectively. This figure agrees with the flux RMSE for the 47-group case in that the error is reduced significantly by the introduction of four angle bins, with a more modest reduction thereafter. Otherwise, these flux distributions show similar behavior to that observed with the 1D slab case wherein relaxing the FSA allowed neutrons to more effectively stream out of the fuel region.
3.3. 2D Sodium-Cooled Fast Reactor
The third case examined in this paper is a 2D metal-fueled, sodium-cooled, steel-reflected, fast reactor, based on the FASTER test reactor design [
8], but modified to remove the thermal test region.
3.3.1. Model Definition
The whole-core layout of this reactor is shown in
Figure 7. The metallic fuel used in this reactor is a UPuZr alloy (19 w/o U, 6 w/o Pu). The uranium is of natural enrichment and the plutonium is reactor-grade. The fuel is clad in HT-9 stainless steel that is also used for in-core structural components. The control rods are composed of B
4C. The 2D slice for this model was taken from the active core region that contains the inserted primary control rods. The material constituents of each assembly are homogenized, an approximation typically made in fast reactor analysis. All computations were performed on a one-third-core model. OpenMC computes a CE eigenvalue of 1.13528 ± 0.00006 for this model.
3.3.2. Examination of Flux Separability Approximation Errors
To evaluate the errors associated with the FSA, the MGXS were generated with 1-group, 33-group, and 70-group structures, with the latter two being the fast reactor-specific ANL33 and ANL70 group structures defined in Appendix D of [
9]. Unique MGXS were generated for each of the hexagonal assemblies in the third-core model. In addition to varying the number of groups, each group structure also applied 1, 6, 12, 16, and 18 azimuthal angle bins. Each of these cases employed 11-bin histogram scattering as previously discussed. The error metrics for each of these cases are provided in
Table 4.
Employing the FSA (the 1-bin row of
Table 4), it is evident that even 70 groups is not enough to reduce the eigenvalue bias to less than around 1000 pcm. However, as in the previous thermal reactor problems, the eigenvalue bias and the flux RMSE are reduced when the FSA is relaxed and more than 6 angular bins are introduced. These results show that the eigenvalue biases in the 1-bin cases are driven by the FSA. Once again, the error could be reduced by introducing a polar angle dependency, but that was not explored further.
As this case is a whole-core model, the changes in the fission rate distribution will be displayed instead of the flux due to the high importance of the fission rate distribution to core design. Therefore
Figure 8 provides the MG-to-CE total fission distribution ratios for the 33-group case. The left hand side provides the ratio obtained from the MGXS using the flux-separability approximation whereas the right hand is for the case of 12-angle bins. Both the left- and right-hand side figures use the same ratio scale as is shown on the right, where red and blue indicate a 6% over-prediction and 6% under-prediction by the MG solver, respectively. This comparison shows that employing the MGXS defined with 12 angles has resulted in a significant improvement in the fission rate distribution (reducing predicted power peaking by around 6%), especially near the fuel-reflector interface where the within-group energy spectra varies strongly with angle.
4. Conclusions
This work used the OpenMC capabilities for MGXS-generation and subsequent MG transport to isolate the errors introduced by the commonly made flux separability approximation. This evaluation was performed using a 1D slab, a 2D PWR pin cell, and a 2D SFR core. It was found that relaxing the FSA by introducing angle-dependent MGXS can significantly reduce the eigenvalue bias by hundreds of pcm and local flux uncertainties by several percent.
This work showed that these FSA errors can become significant at energies at or near strong cross section resonances. These errors are typically managed by increasing the number of energy groups used in a deterministic neutron transport analysis, a practice which results in a roughly linear increase in the computational costs. If these errors were more directly addressed by relaxing the FSA by using angle dependent MGXS, fewer energy groups would be required for the same levels of accuracy. Doing so adds complexity to the MG processing stage, decreases MGXS library generality, and could increase the MGXS memory storage and memory access costs if more angles are used than groups saved for a given application. However, these downsides should be investigated to see how they compare with the benefits of decreased transport solution computational costs and/or increased accuracy.
Author Contributions
Conceptualization, A.G.N.; methodology, A.G.N.; software, P.K.R., W.B. and A.G.N.; formal analysis, A.G.N.; investigation, A.G.N.; resources, P.K.R.; writing—original draft preparation, A.G.N.; writing—review and editing, P.K.R. and W.B.; visualization, A.G.N.; supervision, A.G.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne National Laboratory’s work was supported by the U.S. Department of Energy, Office of Nuclear Energy under contract DE-AC02-06CH11357.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B. OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Boyd, W.; Nelson, A.G.; Romano, P.K.; Shaner, S.; Forget, B.; Smith, K. Multigroup Cross-Section Generation with the OpenMC Monte Carlo Particle Transpoort Code. Nucl. Technol. 2019, 205, 928–944. [Google Scholar] [CrossRef]
- Nelson, A.G.; Shaner, S.; Boyd, W.; Romano, P.K. Incorporation of a Multigroup Transport Capability in the OpenMC Monte Carlo Particle Transport Code; Transactions of the American Nuclear Society: Washington, DC, USA, 2017; Volume 117, pp. 679–681. [Google Scholar]
- Bell, G.I.; Hansen, G.E.; Sandmeier, H.A. Multitable Treatments of Anisotropic Scattering in SN Multigroup Transport Calculations. Nucl. Sci. Eng. 1967, 28, 376–383. [Google Scholar] [CrossRef]
- Gibson, N.A. Novel Resonance Self-Shielding Methods for Nuclear Reactor Analysis. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Park, H.; Joo, H.G. Practical Resolution of Angle Dependency of Multigroup Resonance Cross Sections Using Parametrized Spectral Superhomogenization Factors. Nuclear Eng. Technol. 2017, 49, 1287–1300. [Google Scholar] [CrossRef]
- Stamm’ler, R.J. HELIOS Methods; Studsvik Scandpower: Wilmington, NC, USA, 2003. [Google Scholar]
- Grandy, C.; Belch, H.; Brunett, J.; Heidet, F.; Hill, R.; Hoffman, E.; Jin, E.; Mohamed, W.; Moisseytsev, A.; Passerini, S.; et al. FASTER Test Reactor Preconceptual Design Report; Argonne National Laboratory: DuPage County, IL, USA, 2016; ANL-ART-40. [Google Scholar]
- Lee, C.H.; Yang, W.S. MC2-3: Multigroup Cross Section Generation Code for Fast Reactor Analysis; Argonne National Laboratory: DuPage County, IL, USA, 2013; ANL/NE-11-41 Rev.2. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).