Abstract
Utilising molten salt as coolant instead of carbon dioxide in traditional advanced gas-cooled reactors (AGRs) can potentially increase their core power density, simplify the safety case and shorten the time needed for the development of the fluoride-salt-cooled high-temperature reactor (FHR). However, the change of coolant has a strong impact on the system behaviour. Therefore, a new type of fuel assembly is required. However, the design of a new assembly is affected by a wide range of parameters. Systematic search through all the potential configurations is prohibitively computationally expensive. In this work, a multi objective particle swarm optimisation (MOPSO) algorithm is utilised to identify the most attractive candidate configurations for the hybrid AGR-like FHR assembly. The first optimisation step targets basic design parameters such as radius and enrichment of the fuel pins, their number and arrangement. MOPSO is based on the concept of Pareto dominance, which is used to determine the flight direction of the simulated particles. The outcome of the optimisation process provides insight on families of possible solutions, which described by the Pareto front.
1. Introduction
It is expected that the next generation of nuclear power reactors (Gen-IV) must surpass the current reactors in operation (Gen-III/III+), in terms of safety, economy, generated waste and proliferation [1]. However, the development effort for Gen-IV reactors is substantial and slow, with the latest assessments predicting the deployment of these reactors no earlier than 2030 [1]. Some argue that, realistically, this might actually be closer to 2050 [2]. Currently, there are five commercial Gen-IV reactors in operation in Russia, India and China. However, judging by the latest world tendencies, the near future of Gen-IV reactors is not bright (e.g., ASTRID project termination [3]). Thus, the near future of nuclear power generation will likely be based on light water reactors (LWRs), as advanced systems are yet to reach technological maturity and address all the open technological issues they face.
To speed up the development of Gen-IV reactors and shorten the time for their commercialisation, a study is underway at the University of Cambridge—the Advanced Gas-cooled Reactor (AGR) Technologies for Enabling Molten Salt-cooled Reactors Designs (AGRESR). The project aims to take of-the-shelf technologies available from the UK AGRs to speed up the development of the fluoride-salt-cooled high-temperature reactors (FHRs) [4]. The FHRs are a type of molten salt reactors (MSR) where a salt is used as coolant while the fuel remains in a solid form. The FHR concept presents several advantages over traditional LWRs. First, the reactor operates at lower pressure as the coolant never reaches it boiling temperature, even in an accident situation, no forced removal of material (on-line processing) from the core is required, and low-pressure operation relaxes many constraints on structural integrity for high pressure operation, effectively implying that the system does not require an expensive pressure vessel and high-pressure piping. Second, in case of an accident, the reactor can rely on natural convection to provide the decay heat removal from the fuel to an external heat sink. Finally, the FHR can be viewed as an incremental step between the current generation of reactors and the Gen-IV MSRs with molten fuel.
The FHR core is graphite-moderated, operates at high temperatures (about 700 °C) and low pressure. Some variations of FHR design feature pin-type fuel compacts TRISO particles in graphite matrix [4]. Many of these characteristics resemble the design of British AGRs, making them attractive candidates for technological adaptation. Although, AGRs deployment was a long and difficult process, all issues were eventually resolved and the current fleet of 14 reactors has a remarkable operating and safety record [5,6]. Thus, years of expertise of AGR construction and operation, in high temperature operation (outlet temperature is about 630 °C), manufacturing and construction of large concrete pressure vessel for relevant temperature range, and online refuelling, can be adapted for the design of and AGR-like FHR.
Replacing the AGR CO2 coolant with a typical MSR salt—a mix of lithium fluoride (LiF) and beryllium fluoride (BeF2) known as FLiBe with 7Li enrichment of 99.996% to reduce tritium build-up in the system, as it also has a strong impact on the system’s neutronics [7]. The higher density of the salt (about 1000 times higher than CO2) and relatively light isotopes in the salt make the coolant temperature coefficient an important safety parameter for optimisation because the salt contributes significantly to the neutron moderation. First analysis of AGR-like FHR [8,9] identified several possible design configurations. Unlike previous studies, which were based on an exhaustive search through the design space, the current study presents a more systematic approach based on a multi-objective particle swarm optimisation (MOPSO) [10]. The first results presented in this paper aim at optimising two parameters: first, maximising the beginning of cycle (BOC) infinite medium multiplication factor, second, minimising the coolant temperature coefficient.
2. Methodology
2.1. AGR Reference Geometry
AGRs use slightly enriched UO2 fuel. The enrichment varies between approximately 1.16 and 2.1 w/o of 235U. The fuel is encased in a stainless steel (type ATI 20–25+ Nb) cladding and bound together in a graphite double sleeve (Figure 1) the fuel element contains 36 fuel pins with a central tie-bar, which is used to pull the fuel assembly out of the core. The element dimensions are summarised in Table 1.
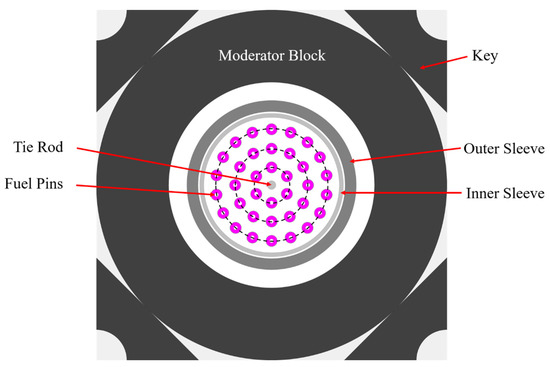
Figure 1.
Representative AGR fuel element cross-section.

Table 1.
Main geometrical dimensions of AGR fuel element [5,6].
2.2. Multi-Objective Particle Swarm Optimisation
Particle swarm optimisation (PSO) [11] is a Nature-inspired algorithm based on the schooling pattern of a swarm. The PSO algorithm basis is the evolution of swarm members (known as particles), which investigate an n-dimensional space in search of the best global solution. The particle position is determined by evaluation of the target function, while the evolution made by adjusting the particle velocity in respect to the best personal position and the best swarm known position. PSO shown to deal well optimising non-linear and discrete single objective problems. PSO presents several advantages over more traditional approaches such as genetic algorithms (GAs) [12,13]. GAs rely on some genetic operators like crossover, mutation, selection, etc. with many user-defined parameters, while in PSO, only a few parameters are adjustable. It also generally requires a lower computational effort than GA, because the PSO structure allows one to check simultaneously for local and global best values, while a GA evaluates only the current state. Finally, the PSO algorithm particles have memory of previous fitness values. The mentioned advantages make PSO an attractive candidate for multi-objective optimisation.
Thus, extending the PSO to treat multi-objective problems has a potential to benefit from the advantages mentioned above. The approach chosen in this study is to use a traditional PSO to identify Pareto front of non-dominant solutions [14] and it is rather straightforward. The historical record of best solutions found by a particle could be used to store non-dominated evaluation of the optimisation function generated in previous iterations. The use of the global attraction mechanism combined with previous solutions memory of previously found non-dominant population would motivate convergence towards Pareto front of non-dominating solutions. The MOPSO algorithm summarised in Algorithm 1, where the target function for this study is maximising the BOL infinite multiplication factor, while minimising the coolant temperature coefficient. The optimisation parameters and their boundaries summarised in Table 2.
where is the inertia weight (usually 0.4); and are random numbers in the range [0..1]; and are the personal and the global learning coefficient; is the best position that particle remembers; is a value taken from the repository; is the current value of particle . The selection of is made as following—the nD cubes containing more than a single particle are assigned a fitness equal to the result of dividing any number greater than 1 (in this work assumed 7) by the number of particles that they contain. This aims to reduce the fitness of those nD cubes that contain large number of particles (i.e., fitness sharing [15]). Then, a roulette-wheel selection applied to identify the nD cube from which the particle will be selected. Once the cube was selected, a particle from within it is obtained randomly. In the current analysis, 50 particles are sampled over 100 iteration, with a repository size of 50.
| Algorithm 1: MOPSO algorithm [10] | |
| 1: | Initialise the population POP and initial velocity: |
| 1a: | FOR I = 0 to MAX % MAX = number of particles |
| 1b: | Initialize POP(i) |
| 1c: | VEL(i) = 0 |
| 2: | Evaluate each of the particles if POP |
| 3: | Store the positions of the particles that represent non-dominated vectors in the repository REP |
| 4: | Generate n-dimensional (nD) cubes of the search space explored, and locate the particles using the nD cubes as coordinate system where each particle’s coordinates are defined according to the values of its objective functions. |
| 5: | Initialise the memory of each particle |
| 5a: | FOR I = 0 to MAX |
| 5b: | PBEST(i) = pop(i) |
| 6. | WHILE itr < itrMAX DO % itrMAX = maximum number of iterations |
| 6a: | Compute the velocity, VEL(i), of each particle using expression in Equation (1) |
| 6b: | Compute new particle position POP(i) = POP(i) + VEL(i) |
| 6c: | Apply boundary condition of new particle positions |
| 6d: | Evaluate each particle in POP |
| 6e: | Update the contents of REP together with the geographical representation of the particles within the nD cubes. This update consists of inserting all the non-dominated locations into the repository. Any dominated locations in the repository is eliminated. |
| 6f: | IF current position is better than personal best, then PBEST(i) = POP(i) |
| 6g: | itr = itr + 1 |
| 7 | END WHILE |

Table 2.
Optimisation parameters for different test cases.
2.3. WIMS Transport Code
The Winfrith improved multi-group scheme (WIMS) is a general-purpose code for reactor for 2D lattice and 3D full core calculations, using the 172-energy group JEFF-3.1.2 library [16]. The code is capable of performing calculations for any type of nuclear system using deterministic transport. Therefore, utilising WIMS as the neutronic solver in the current work reduces the computation time required to obtain the results for a single MOPSO generation, in comparison to previous AGR-like FHR analysis [8] where the objective functions evaluations were performed with a Monte Carlo code. The AGR-like FHR solutions obtained though collision probabilities modules PIJ, a module to evaluate first flight collision probabilities, and PIP, which provides the solution to the transport equation for an eigenvalue problem. It should be noted that WIMS nuclear data library currently lacks temperature dependency for FLiBe isotopes. Therefore, the system is treated at 300 K for the current study. The temperature effect is accounted for through the thermal expansion effect using the following relationship for the salt density as a function of temperature (where is in Kelvin) [17]:
3. Results and Discussions
As mentioned previously, the objective of the optimisation is to maximise the infinite multiplication factor and minimise the coolant temperature coefficient. The simulations results are summarised in Figure 2. Each figure shows the relationship between the two-optimisation parameters, where the red lines represent the converged Pareto front. The first notable trend is that the lower the infinite multiplication factor, the higher the salt reactivity feedback. In test cases 1 and 2, where the main moderator block maintains the same dimension as the reference AGR (test case 1 is subcase of test case 2), none of the examined configurations have a negative coolant temperature coefficient (CTC). However, when the graphite block size is decreased (test case 3 and 4), negative CTC values start to appear (Figure 2c,d). The size of the block increases the appearances of cases with low CTC and k-inf, observed by the shift of the inflection point in the Pareto front (Figure 2). For small graphite blocks, moderation mainly occurs in the salt and, for low enrichment cases, the reduction in moderation shifts the spectrum to higher energies, which leads to an increase in 238U absorption. On the other hand, a higher enrichment is required to overcome the parasitic absorption in the salt, for example, case 4 exhibits lower k-inf values in comparison to case 3 for the same enrichment levels (Figure 3ai,bi). In the case with the original block size (Figure 2b), the governing mechanism is the reduction of absorption in the salt, which increases the number of neutrons escaping and thermalizing in the graphite, consequently leading to positive CTC. Therefore, the size of the graphite block has a significant impact on the configuration behaviour, which shifts the Pareto front denoted by ‘2’ downwards.
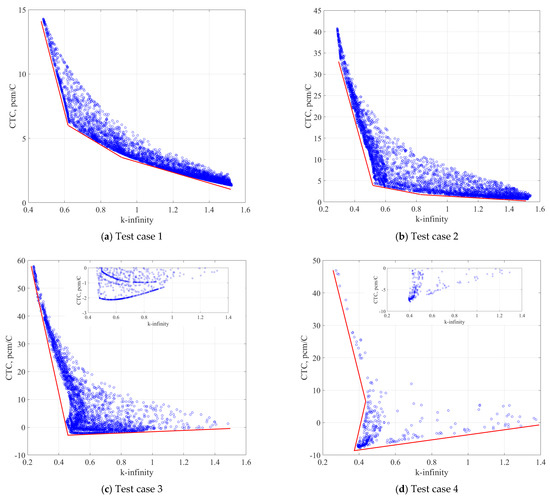
Figure 2.
MOPSO results and Parte front for the different test cases (a) Test case 1. (b) Test case 2. (c) Test case 3. (d) Test case 4.
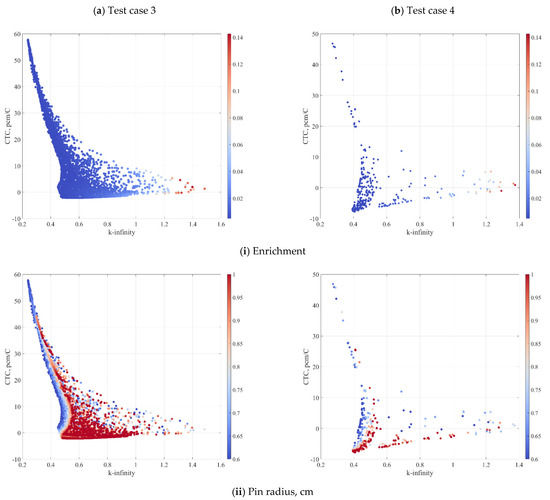
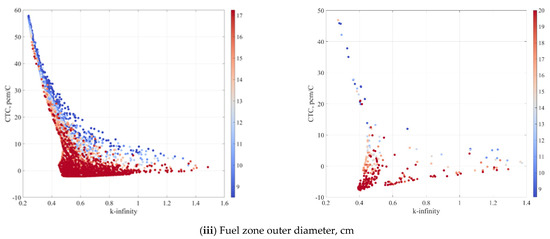
Figure 3.
Correlation between k-inf, CTC and a selected parameter (a) Test case 3—(i) Enrichment, (ii) Pin Radius, (iii) Fuel zone outer diameter; (b) Test case 4—(i) Enrichment, (ii) Pin Radius, (iii) Fuel zone outer diameter.
It should be noted that case 4 appears to have a smaller number of particles (realisations). However, this is just an artefact of overlapping points. The main reason for this phenomenon was a not particularly successful sample of the initial population, which could be addressed by sampling more particles from this region of the search space.
All the results presented in Figure 2 converge on a similar Pareto front, which is divided into two distinct zones. In test cases 1 and 2 (Figure 2a,b), it is seen that it would be worthwhile allowing a higher enrichment, which will allow configurations to reach higher k-inf values. On the other hand, when the block becomes smaller, the second trend of the front reverses. The second observed trend in test cases 3 and 4 (Figure 2c,d) is showing an increase rather than decrease observed in previous cases. Thus, unlike in the previous cases, an increase of reactivity will not be desirable. The zoomed-in plots in Figure 2c,d show the region from which an optimal case can be selected, with negative CTC values and k-inf greater than unity to ensure a feasible cycle length.
The swarm cloud presented in Figure 2 does not provide an understanding on how each one of the optimisation parameters influences the objective function. The multi-dimensionality of the problem requires to breakdown the relationships into sets of two creating a correlation matrix. The correlation between different parameters of test cases 3 and 4 are shown in Figure 3. Configuration that satisfy the optimisation target, in those cases, have higher enrichment (above 8%), thick pins (r~1 cm), and more importantly, bigger fuel cluster (smaller moderator block). It can be seen that the most influential parameter is the size of the moderator block. Furthermore, none of the viable configurations is similar to that of a typical AGR (Figure 1); the configurations require large number of pins with higher diameter and smaller graphite block.
Based on the presented results, the best-suited (k-inf higher than unity and negative CTC) configuration for the AGR-like FHR has somewhat different core lattice geometry from that of a typical AGR. The best-suited configuration has a smaller moderator block, higher enrichment (above 4 o/w), with pin radius of above 0.8 cm, large number of pins in the outer assembly ring (above 10), and with the largest numbers of pins on the innermost ring (4 or 6).
4. Conclusions
This paper summarises the first step in the optimisation of a new AGR-like FHR assembly configuration. The optimisation process proposed is based on the MOPSO algorithm. The objective was selected to be the infinite multiplication factor, as a surrogate measure for cycle length, and CTC, as a measure of safety. Thus, the objective was to simultaneously maximise k-inf and minimise CTC. The results obtained show that in order to reach a viable configuration, one should consider reducing the size of the graphite block. The original block size configuration did not meet the expected negative CTC value criterion for the fresh configuration. However, the obtained Pareto front indicates that an increase in the excess reactivity would reduce the CTC making it negative as desired. In the smaller block configuration, the Pareto front changed its shape, so that an increase in reactivity will lead to a positive CTC. The results showed the capability of MOPSO process to identify possible configuration candidates. However, a more detailed analysis including thermal-hydraulic feedback, to estimate the maximum possible power uprate, and burnup calculation, to estimate the cycle length, are needed to show the benefits of the AGR-like FHR over a typical AGR.
Author Contributions
Conceptualization, M.M.; methodology, M.M.; formal analysis, M.M.; investigation, M.M. and E.S.; resources, E.S.; writing—original draft preparation, M.M.; writing—review and editing, E.S.; visualization, M.M.; funding acquisition, E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the UK Engineering and Physical Sciences Research Council under grant EP/R029113/1—AGR Technology for Enabling Salt-cooled Reactor Designs (AGRESR).
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gen-4 International Forum (GIF). Annual Report 2017; OECD Nuclear Energy Agency: Paris, France, 2017. [Google Scholar]
- Murphy, C.; Safonov, V. What Will Be Required for a Significant Expansion of Global Nuclear Energy? Bulletin of the Atomic Scientists. Available online: https://thebulletin.org/2019/06/what-will-be-required-for-a-significant-expansion-of-global-nuclear-energy/ (accessed on 20 June 2019).
- Reuters. France Abandons Research into Fourth-Generation Nuclear-Le Monde. Available online: https://www.reuters.com/article/france-nuclearpower-astrid/france-abandons-research-into-fourth-generation-nuclear-le-monde-idUSL5N25Q1MU (accessed on 30 August 2019).
- Forsberg, C.; Peterson, P.F. Basis for fluoride salt–cooled high-temperature reactors with nuclear air-brayton combined cycles and firebrick resistance-heated energy storage. Nucl. Technol. 2016, 196, 13–33. [Google Scholar] [CrossRef]
- Nonbol, E. Description of the Advanced Gas Cooled Type of Reactor (AGR); Riso National Laboratory: Roskilde, Denmark, 1996. [Google Scholar]
- Britich Electricity International. Modern Power Sation Practice—Nuclear Power Generation, 3rd ed.; Littler, J.D.J., Davies, E.J., Johnson, H.E., Kirkby, F., Myerscough, P.B., Wright, W., Eds.; Pergamon Press: London, UK, 1992. [Google Scholar]
- Margulis, M.; Shwagerus, E. Advanced gas-cooled reactors technology for enabling molten-salt reactors design—Estimation of coolant impact on neutronic performance. Prog. Nucl. Energy 2020, 125, 103382. [Google Scholar] [CrossRef]
- Xing, Z.; Shwageraus, E. Design space exploration studies of an FHR concept leveraging AGR technologies. In Proceedings of the International Congress on Advances in Nuclear Power Plants, Fukui-Kyoto, Japan, 24–28 April 2017; ICAPP: Fukui, Japan; Kyoto, Japan, 2017. [Google Scholar]
- Xing, Z.; Shwageraus, E. Molten salt coolant reactivity fedback in alternative FHR designs. In Physics of Reactors; PHYSOR: Cancun, Mexico, 2018. [Google Scholar]
- Coello, C.C.; Lechuga, M. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kaushik, A.; Kumar, H. Performance evaluation between GA versus PSO. Int. Res. J. Eng. Technol. 2016, 3, 103–110. [Google Scholar]
- Lima, C.A.S.; Lapa, C.M.F.; Pereira, C.M.D.N.; Da Cunha, J.J.; Alvim, A.C.M. Comparison of computational performance of GA and PSO optimization techniques when designing similar systems—Typical PWR core case. Ann. Nucl. Energy 2011, 38, 1339–1346. [Google Scholar] [CrossRef]
- Seah, C.-W.; Ong, Y.-S.; Tsang, I.W.; Jiang, S. Pareto rank learning in multi-objective evolutionary algorithms. In Proceedings of the WCCI 2012 IEEE World Congress on Computational Intelligence, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Proceedings of the Second International Conference on Genetic Algorithms on Genetic Algorithms and Their Application, Cambridge, MA, USA, 12 August 1987. [Google Scholar]
- Lindley, B.; Hosking, J.; Smith, P.; Powney, D.; Tollit, B.; Newton, T.; Perry, R.; Ware, T.; Smith, P. Current status of the reactor physics code WIMS and recent developments. Ann. Nucl. Energy 2017, 102, 148–157. [Google Scholar] [CrossRef]
- Romatoski, R.; Hu, L. Fluoride salt coolant properties for nuclear reactor applications: A review. Ann. Nucl. Energy 2017, 109, 635–647. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).