Data-Driven Modelling and Simulation of Fuel Cell Hybrid Electric Powertrain
Abstract
1. Introduction
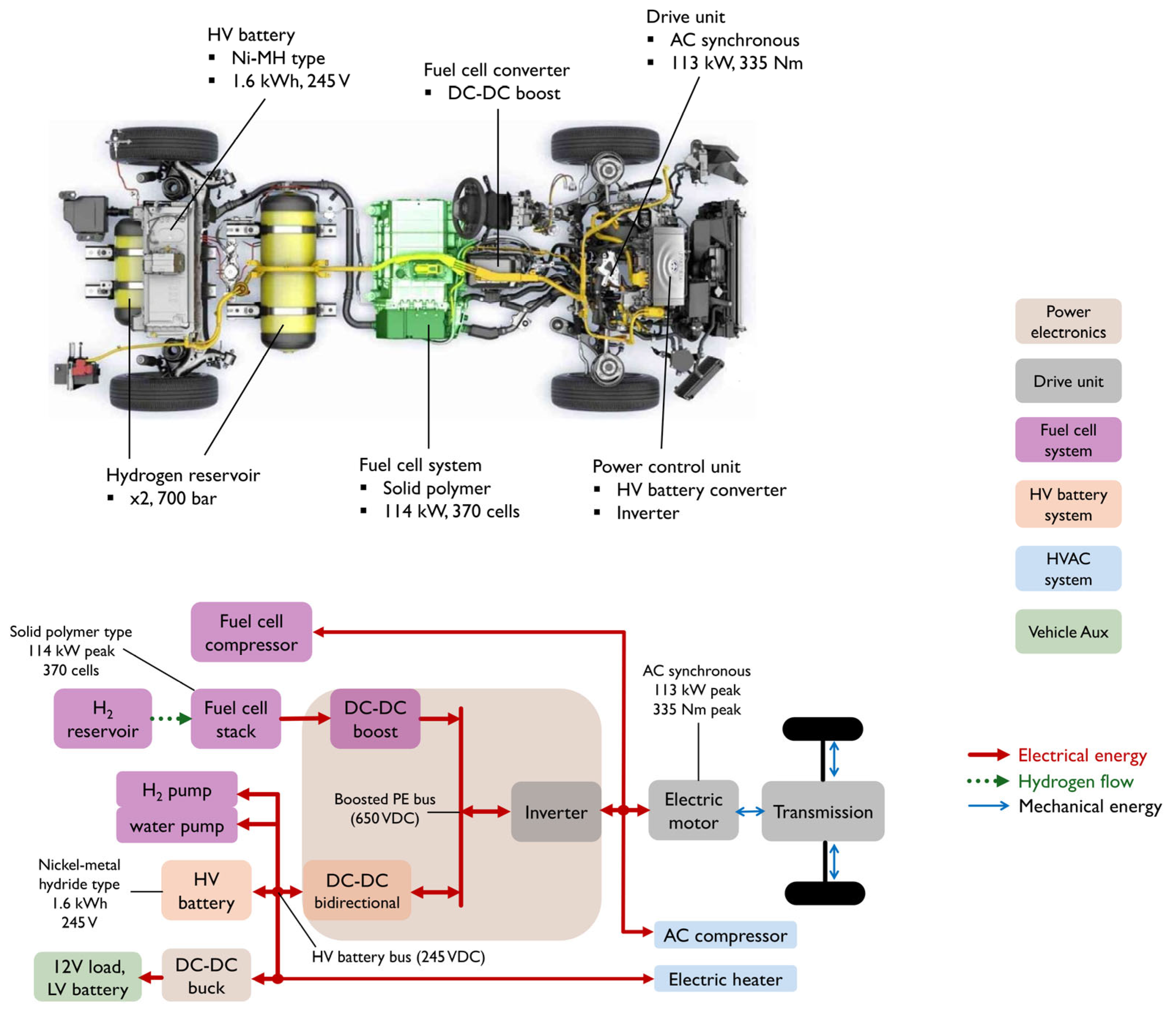
2. Hybrid Powertrain Layout and Modelling
2.1. Drivetrain Power Demand
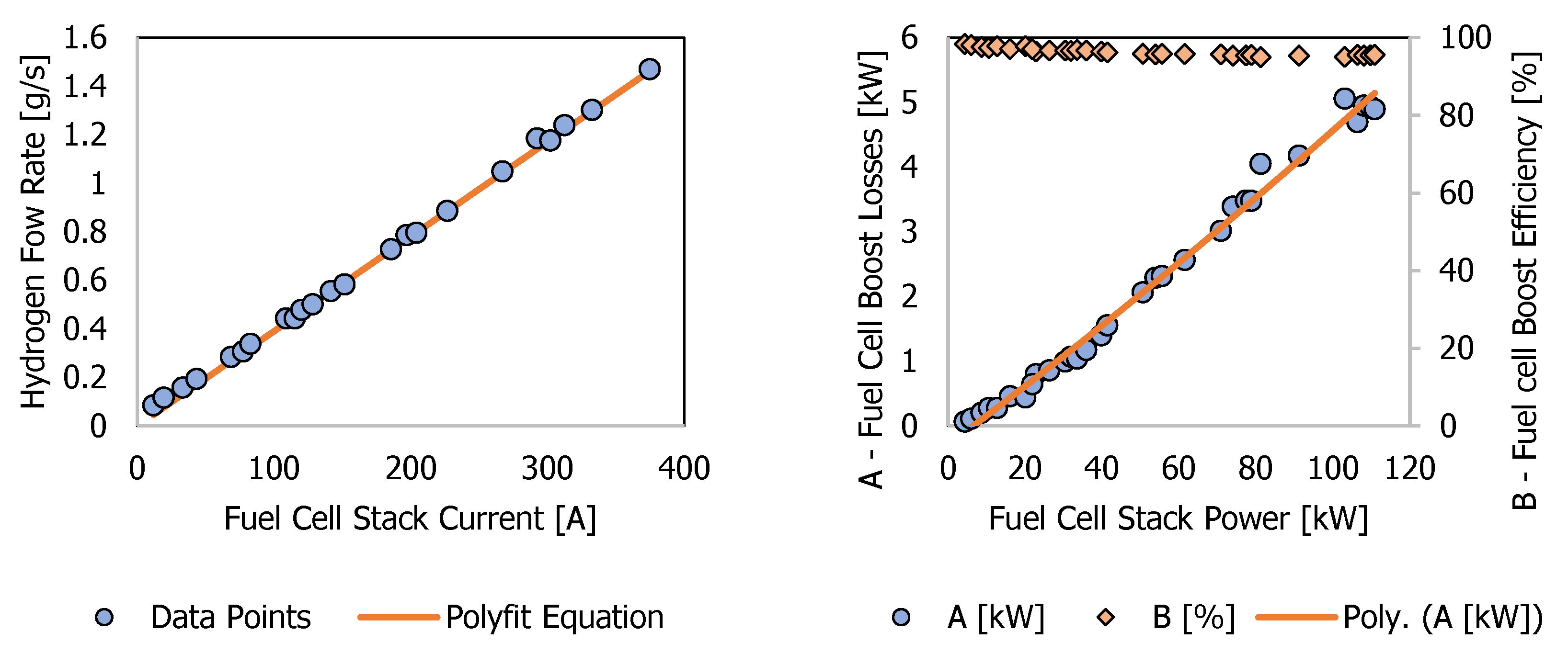
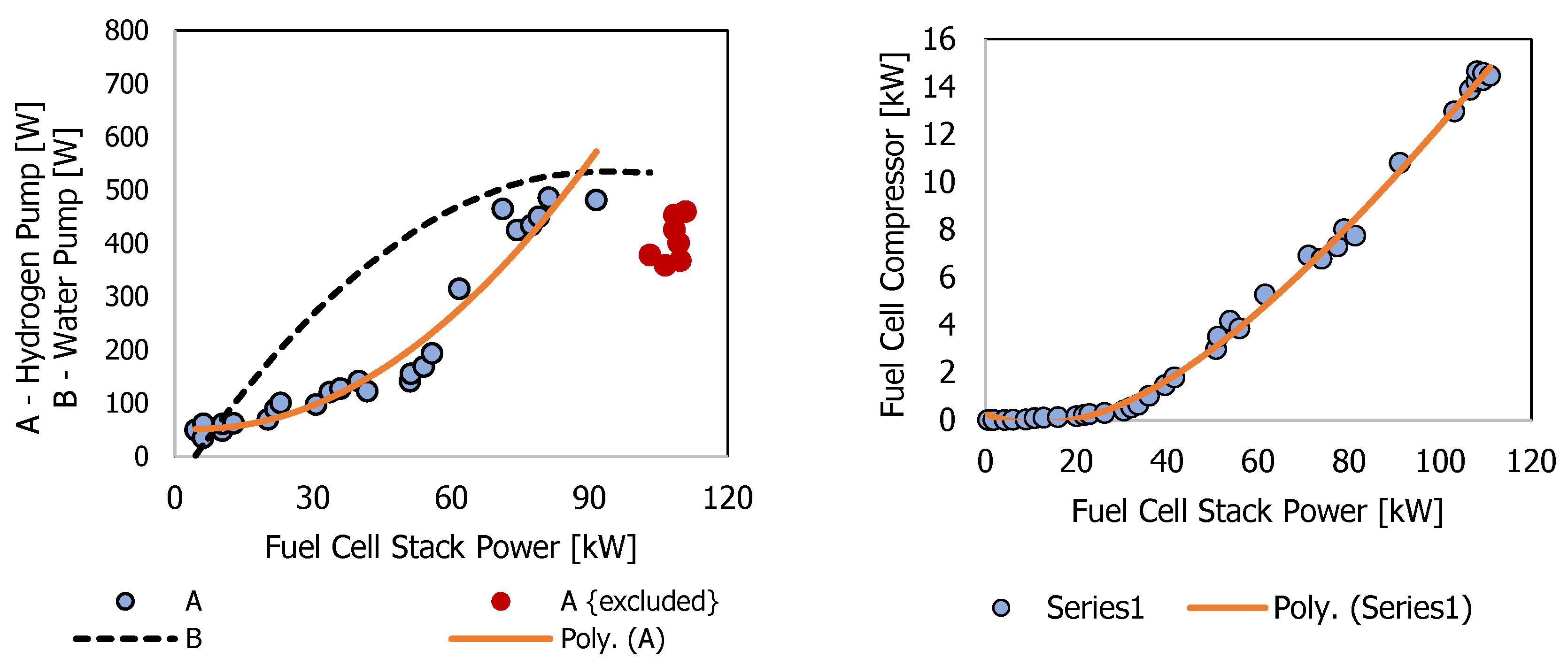
2.2. Hybrid System
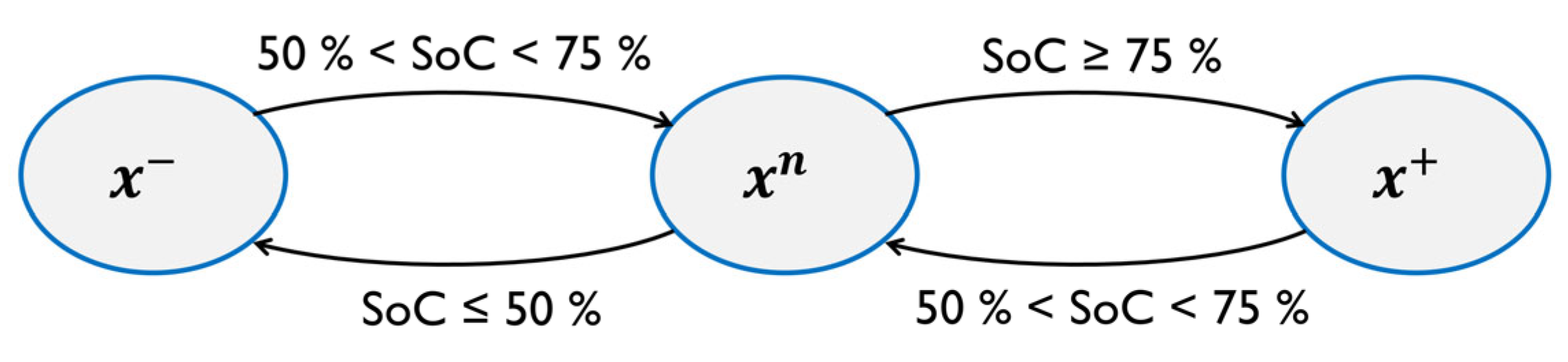
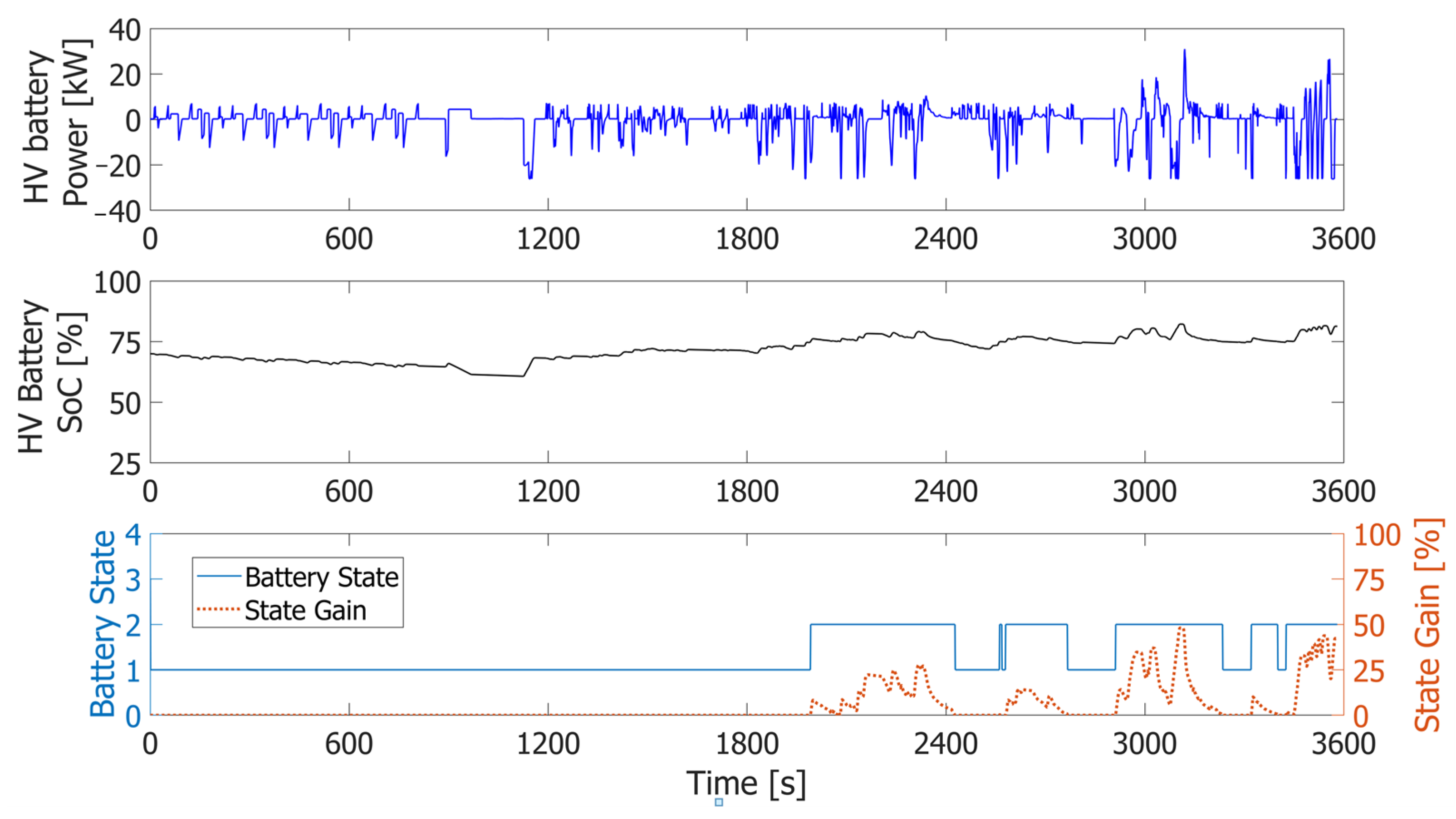
2.3. Power Management System
3. Simulation Results and Discussion
- (1)
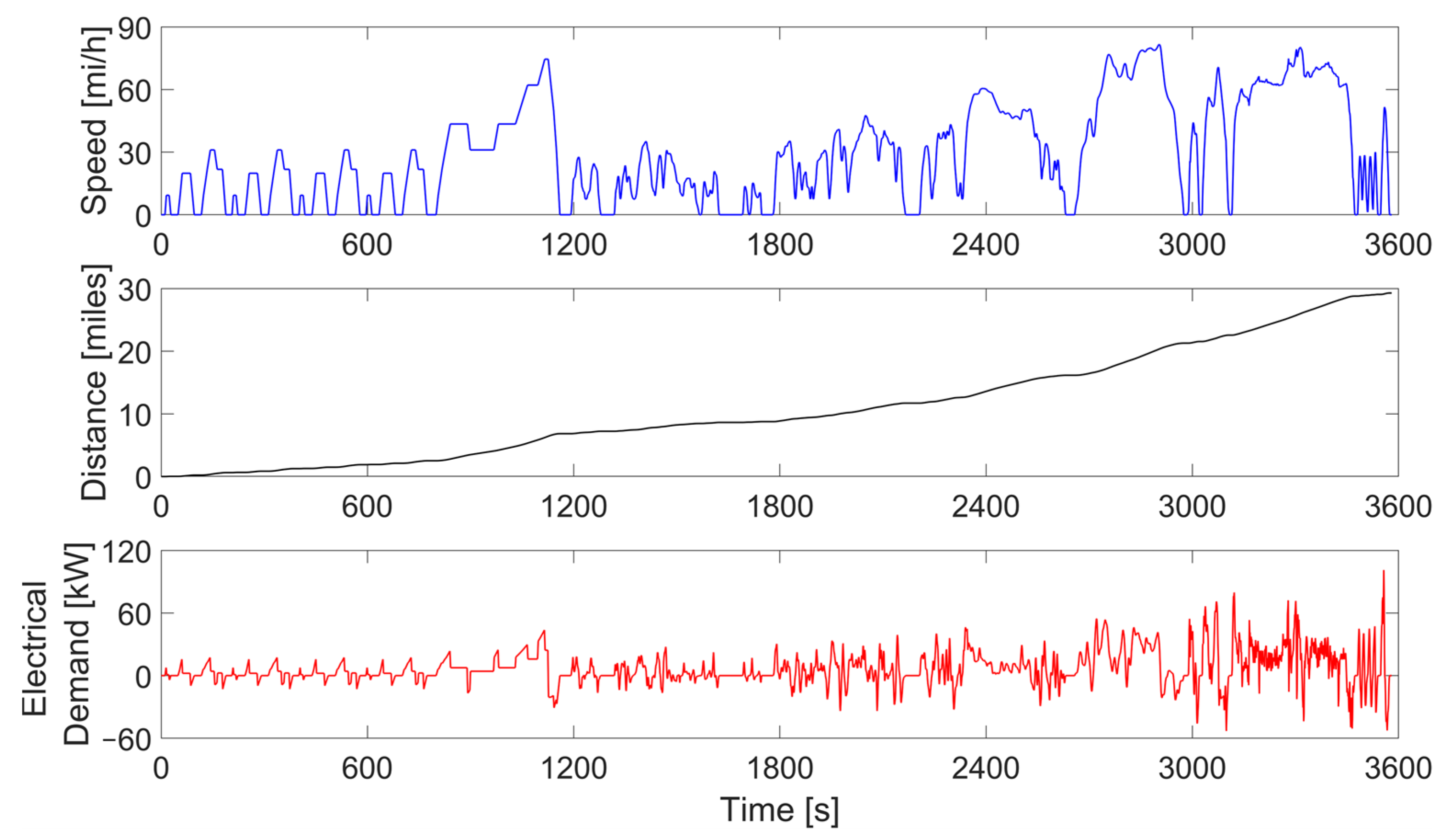
- A combination of three synthetic driving cycles (Figure 2). This composite cycle consists of a sequential combination of three widely used endurance tests: NEDC (1180 s), WLTP Class 3 (1800 s) and US06 (600 s). This cycle is used to capture baseline performance and evaluate the proposed power allocation strategy.
- (2)
- A driving scenario to benchmark against actual data from the Toyota Mirai [23] and compare with a similar tiered frequency-splitting power allocation method [26,27,28]. For benchmarking purposes, various statistical measures are evaluated to highlight the merits and limitations of the proposed approach.
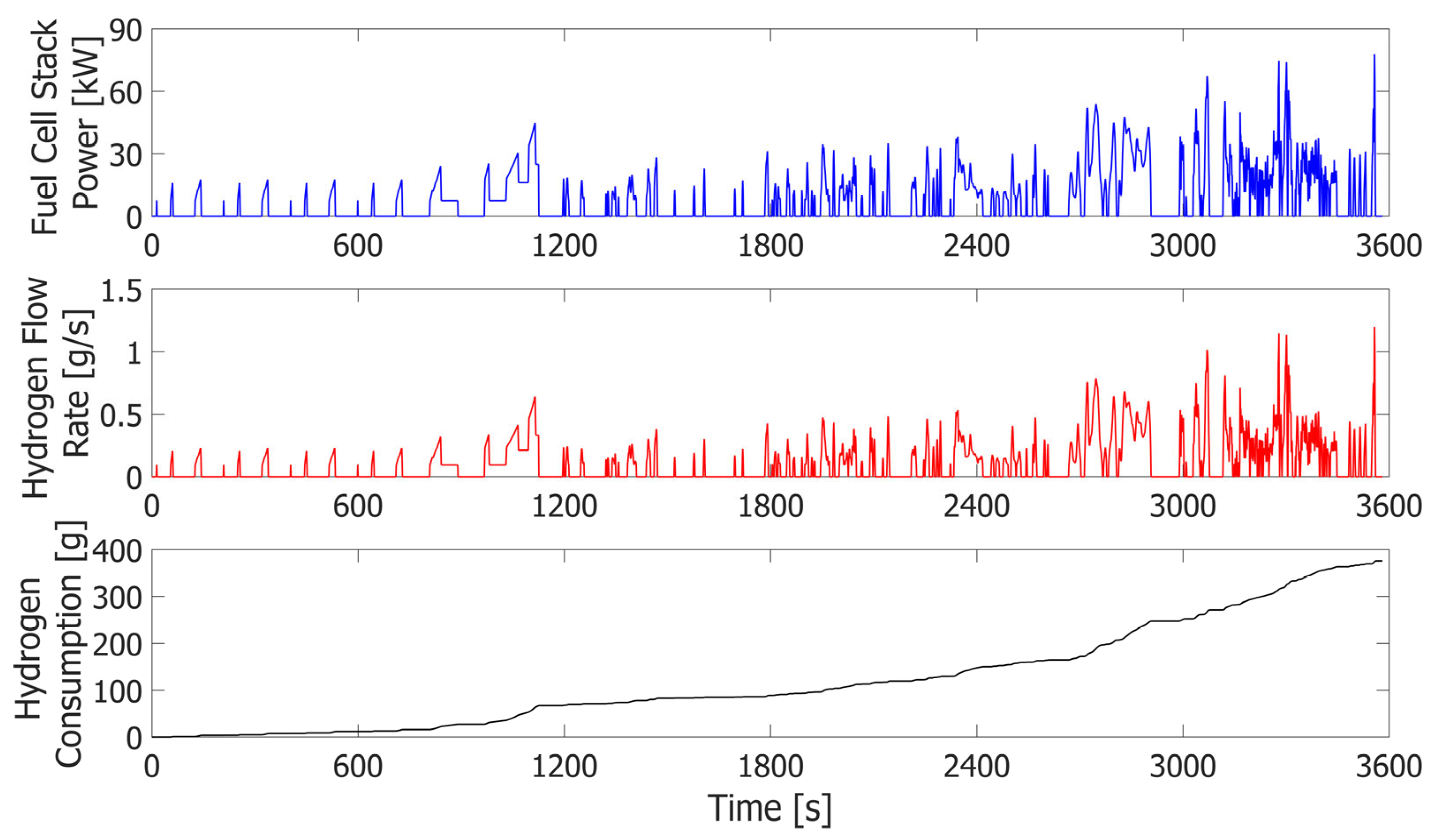
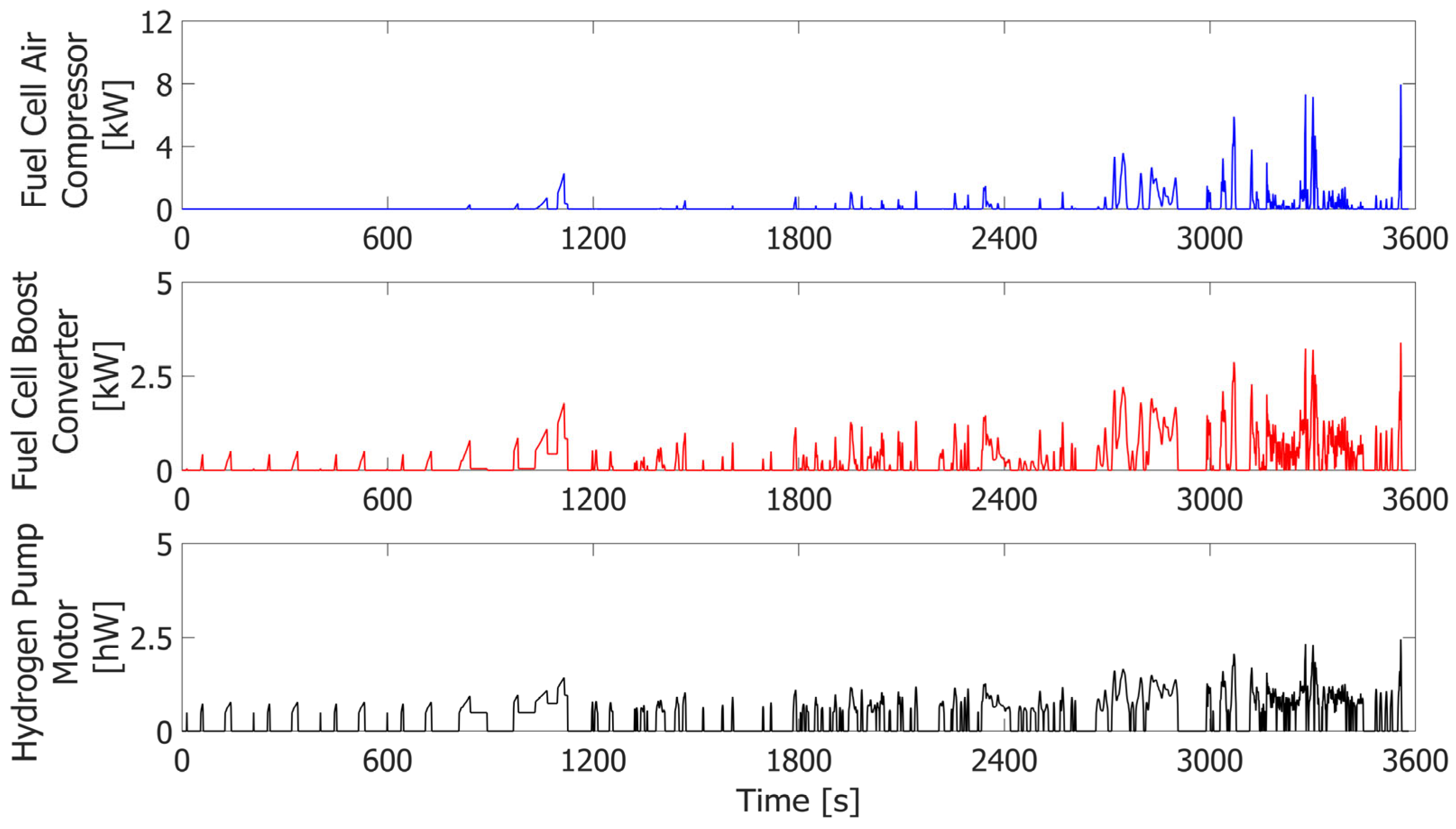
3.1. Baseline Performance
3.2. Performance Benchmarking
- The total hydrogen consumed in kg.
- The cost factor in euros (EUR) per kilogram is adopted from [30] and based on the green hydrogen production pathway.
- Overall efficiency (eta) expressed in both miles per kilogram and miles per EUR.
- Δidle is the % of total driving time during which the fuel cell stack remains idle.
- Δramp is the % of total driving time during which the fuel cell power change rate exceeds 10 kW/s.
- Δswitch is the % of total driving time spent switching between idle and active states.
- The percentage of total driving time during which the HV battery’s SoC exceeds the soft limits (50% < SoC < 75%).
- The number of instances where the battery power exceeds the 30 kW peak threshold.
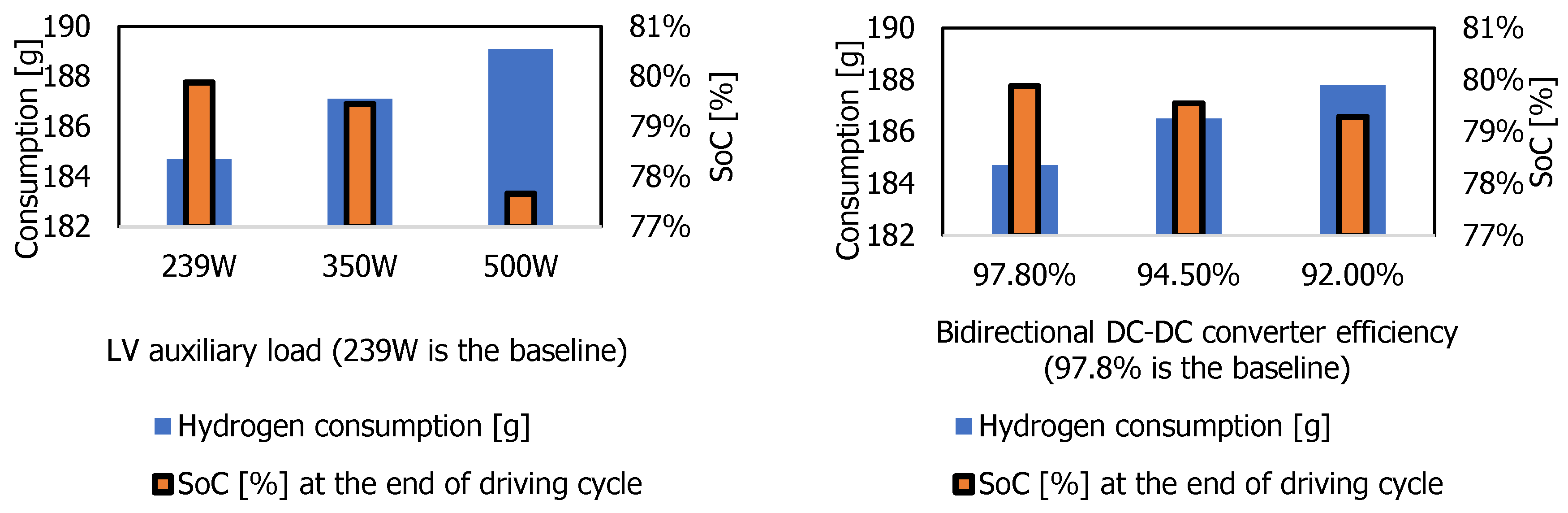
3.3. Sensitivity and Emission Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 5 × 10−7 | 0.0006 | −0.2483 | 318.27 | 0.0039 | −8 × 10−6 | 0.0026 | −0.0541 |
| 0.1886 | 0.0691 | −0.649 | 53.253 | 12.1 | 4 × 10−5 | 0.0443 | −0.291 |
References
- Jayakumar, A.; Madheswaran, D.K.; Kannan, A.; Sureshvaran, U.; Sathish, J. Can hydrogen be the sustainable fuel for mobility in India in the global context? Int. J. Hydrogen Energy 2022, 47, 33571–33596. [Google Scholar] [CrossRef]
- Togun, H.; Basem, A.; Abdulrazzaq, T.; Biswas, N.; Abed, A.M.; Dhabab, J.M.; Chattopadhyay, A.; Slimi, K.; Paul, D.; Barmavatu, P.; et al. Development and comparative analysis between battery electric vehicles (BEV) and fuel cell electric vehicles (FCEV). Appl. Energy 2025, 388, 125726. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.; Mohamed, A.; Ker, P.; Majlan, E.; Daud, W.W. Optimization of energy management system for fuel-cell hybrid electric vehicles: Issues and recommendations. Appl. Energy 2018, 228, 2061–2079. [Google Scholar] [CrossRef]
- Carignano, M.; Costa-Castelló, R. Toyota Mirai: Powertrain model and assessment of the energy management. IEEE Trans. Veh. Technol. 2023, 72, 7000–7010. [Google Scholar] [CrossRef]
- Nonobe, Y. Development of the fuel cell vehicle MIRAI. IEEJ Trans. Electr. Electron. Eng. 2016, 12, 5–9. [Google Scholar] [CrossRef]
- Tanaka, Y. Development of the mirai fuel cell vehicle. In Hydrogen Energy Engineering; Springer: Berlin, Germany, 2016; pp. 461–475. [Google Scholar]
- Legala, A.; Kubesh, M.; Chundru, V.R.; Conway, G.; Li, X. Machine learning modeling for fuel cell-battery hybrid power system dynamics in a Toyota Mirai 2 vehicle under various drive cycles. Energy AI 2024, 17, 100415. [Google Scholar] [CrossRef]
- Iqbal, M.; Laurent, J.; Benmouna, A.; Becherif, M.; Ramadan, H.S.; Claude, F. Ageing-aware load following control for composite-cost optimal energy management of fuel cell hybrid electric vehicle. Energy 2022, 254, 124233. [Google Scholar] [CrossRef]
- Manoharan, Y.; Hosseini, S.E.; Butler, B.; Alzahrani, H.; Foua, B.; Ashuri, T.; Krohn, J. Hydrogen Fuel Cell Vehicles; Current Status and Future Prospect. Appl. Sci. 2019, 9, 2296. [Google Scholar] [CrossRef]
- Tokieda, J.; Ozawa, T.; Yoshida, T.; Aida, S.; Oya, L. The MIRAI Life Cycle Assessment Report; Toyota Motor Corporation: Toyota City, Japan, 2015. [Google Scholar]
- Davis, S.; Williams, R.B.; Moore, S. 2016 Vehicle Technologies Market Report; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2016. [Google Scholar]
- Available online: https://global.toyota/pages/global_toyota/mobility/technology/toyota-technical-review/TTR_Vol66_E.pdf (accessed on 10 July 2025).
- Lohse-Busch, H.; Stutenberg, K.; Duoba, M.; Iliev, S. Technology Assessment of a Fuel Cell Vehicle: 2017 Toyota Mirai (No. ANL/ESD-18/12); Argonne National Laboratory (ANL): Argonne, IL, USA, 2018. [Google Scholar]
- Usmanov, U.; Ruzimov, S.; Tonoli, A.; Mukhitdinov, A. Modeling, simulation and control strategy optimization of fuel cell hybrid electric vehicle. Vehicles 2023, 5, 464–481. [Google Scholar] [CrossRef]
- Hua, Z.; Li, X.; Bai, H.; Zhao, D.; Wang, Y.; Dou, M.; Liu, C. Nonintrusive Condition Monitoring of FCEV Using System-Level Digital Twin Model. IEEE Trans. Transp. Electrif. 2023, 10, 1314–1323. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cennamo, E.; Cordiner, S.; Mulone, V.; Pasqualini, F.; Boot, M.A. Digital twin of a hydrogen Fuel Cell Hybrid Electric Vehicle: Effect of the control strategy on energy efficiency. Int. J. Hydrogen Energy 2023, 48, 20971–20985. [Google Scholar] [CrossRef]
- Bartolucci, L.; Cennamo, E.; Cordiner, S.; Mulone, V.; Pasqualini, F.; Boot, M.A. Digital Twin of Fuel Cell Hybrid Electric Vehicle: A detailed modelling approach of the hydrogen powertrain and the auxiliary systems. In E3S Web of Conferences; EDP Sciences: London, UK, 2022; Volume 334, p. 06003. [Google Scholar]
- Iqbal, M.; Becherif, M.; Ramadan, H.S.; Badji, A. Dual-layer approach for systematic sizing and online energy management of fuel cell hybrid vehicles. Appl. Energy 2021, 300, 117345. [Google Scholar] [CrossRef]
- Available online: https://media.toyota.co.uk/wp-content/uploads/sites/5/pdf/210223M-Mirai-Tech-Spec.pdf (accessed on 10 July 2025).
- Available online: https://khkgears.net/new/gear_knowledge (accessed on 10 July 2025).
- Available online: https://motoranalysis.com/motoranalysis-pm/ (accessed on 10 July 2025).
- Huang, Q.; Huang, Q.; Guo, H.; Cao, J. Design and research of permanent magnet synchronous motor controller for electric vehicle. Energy Sci. Eng. 2023, 11, 112–126. [Google Scholar] [CrossRef]
- Available online: https://www.anl.gov/taps/d3-2016-toyota-mirai (accessed on 10 July 2025).
- Iqbal, M.; Benmouna, A.; Becherif, M.; Mekhilef, S. Survey on battery technologies and modeling methods for electric vehicles. Batteries 2023, 9, 185. [Google Scholar] [CrossRef]
- Available online: https://uk.mathworks.com/help/autoblks/ref/drivecyclesource.html (accessed on 10 July 2025).
- Badji, A.; Abdeslam, D.O.; Becherif, M.; Eltoumi, F.; Benamrouche, N. Analyze and evaluate of energy management system for fuel cell electric vehicle based on frequency splitting. Math. Comput. Simul. 2020, 167, 65–77. [Google Scholar] [CrossRef]
- Iqbal, M.; Ramadan, H.S.; Becherif, M. Health-aware frequency separation method for online energy management of fuel cell hybrid vehicle considering efficient urban utilization. Int. J. Hydrogen Energy 2021, 46, 16030–16047. [Google Scholar] [CrossRef]
- Snoussi, J.; Elghali, S.B.; Benbouzid, M.; Mimouni, M.F. Optimal sizing of energy storage systems using frequency-separation-based energy management for fuel cell hybrid electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 9337–9346. [Google Scholar] [CrossRef]
- Huo, H.; Cai, H.; Zhang, Q.; Liu, F.; He, K. Life-cycle assessment of greenhouse gas and air emissions of electric vehicles: A comparison between China and the US. Atmos. Environ. 2015, 108, 107–116. [Google Scholar] [CrossRef]
- Durkin, K.; Khanafer, A.; Liseau, P.; Stjernström-Eriksson, A.; Svahn, A.; Tobiasson, L.; Andrade, T.S.; Ehnberg, J. Hydrogen-powered vehicles: Comparing the powertrain efficiency and sustainability of fuel cell versus internal combustion engine cars. Energies 2024, 17, 1085. [Google Scholar] [CrossRef]
- Tang, O.; Rehme, J.; Cerin, P. Levelized cost of hydrogen for refueling stations with solar PV and wind in Sweden: On-grid or off-grid? Energy 2022, 241, 122906. [Google Scholar] [CrossRef]
- Gerloff, N. Comparative Life-Cycle-Assessment analysis of three major water electrolysis technologies while applying various energy scenarios for a greener hydrogen production. J. Energy Storage 2021, 43, 102759. [Google Scholar] [CrossRef]

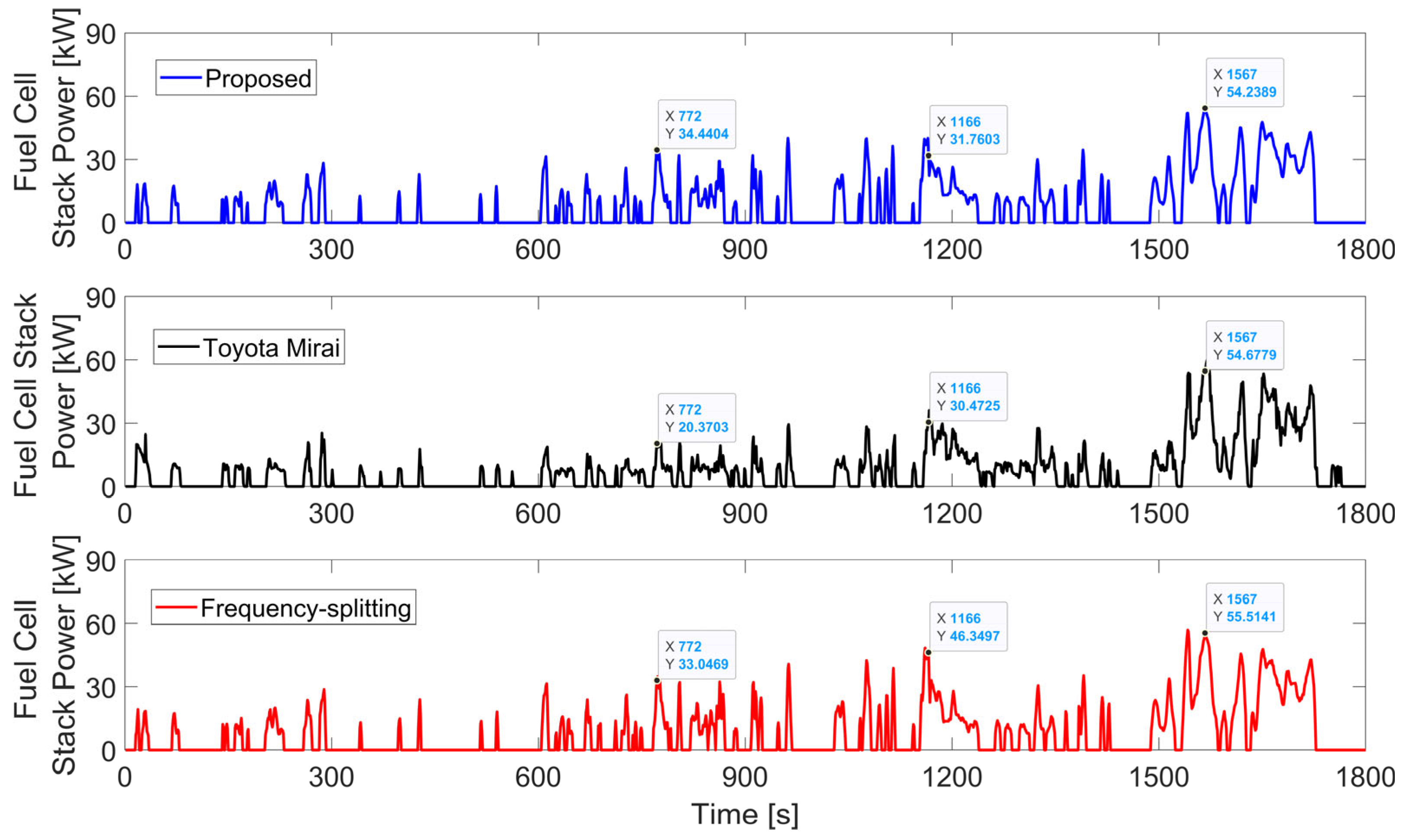
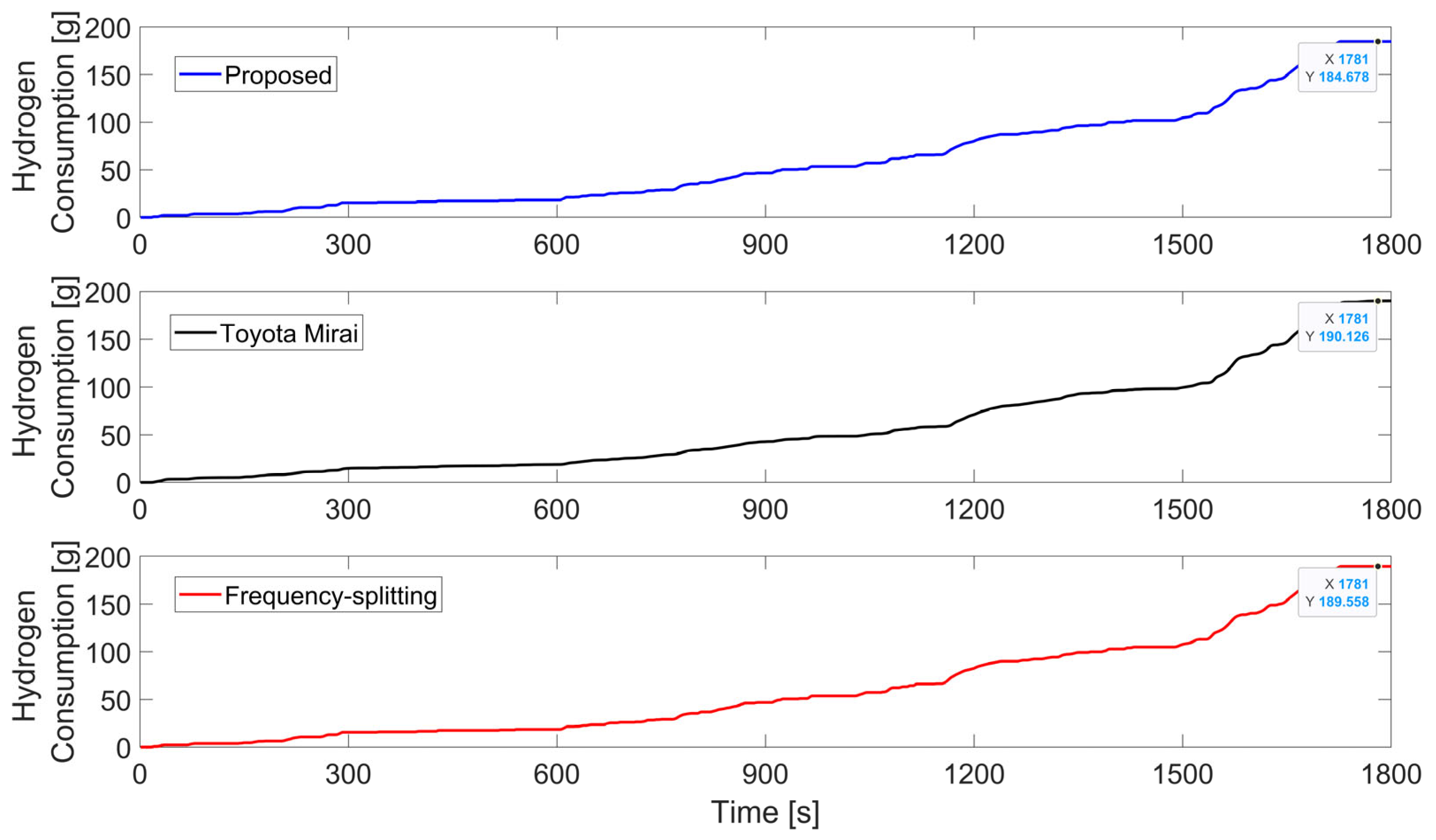
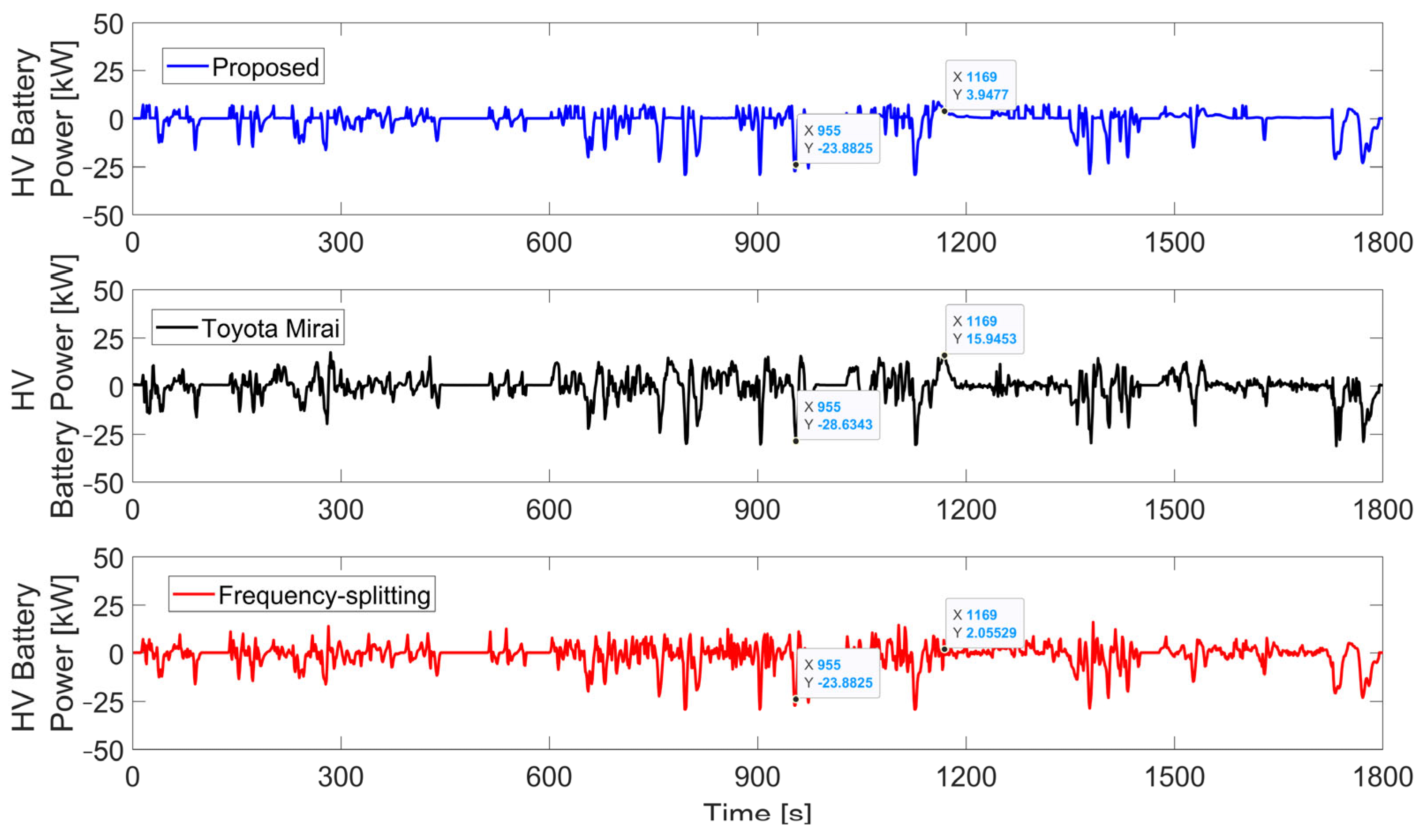
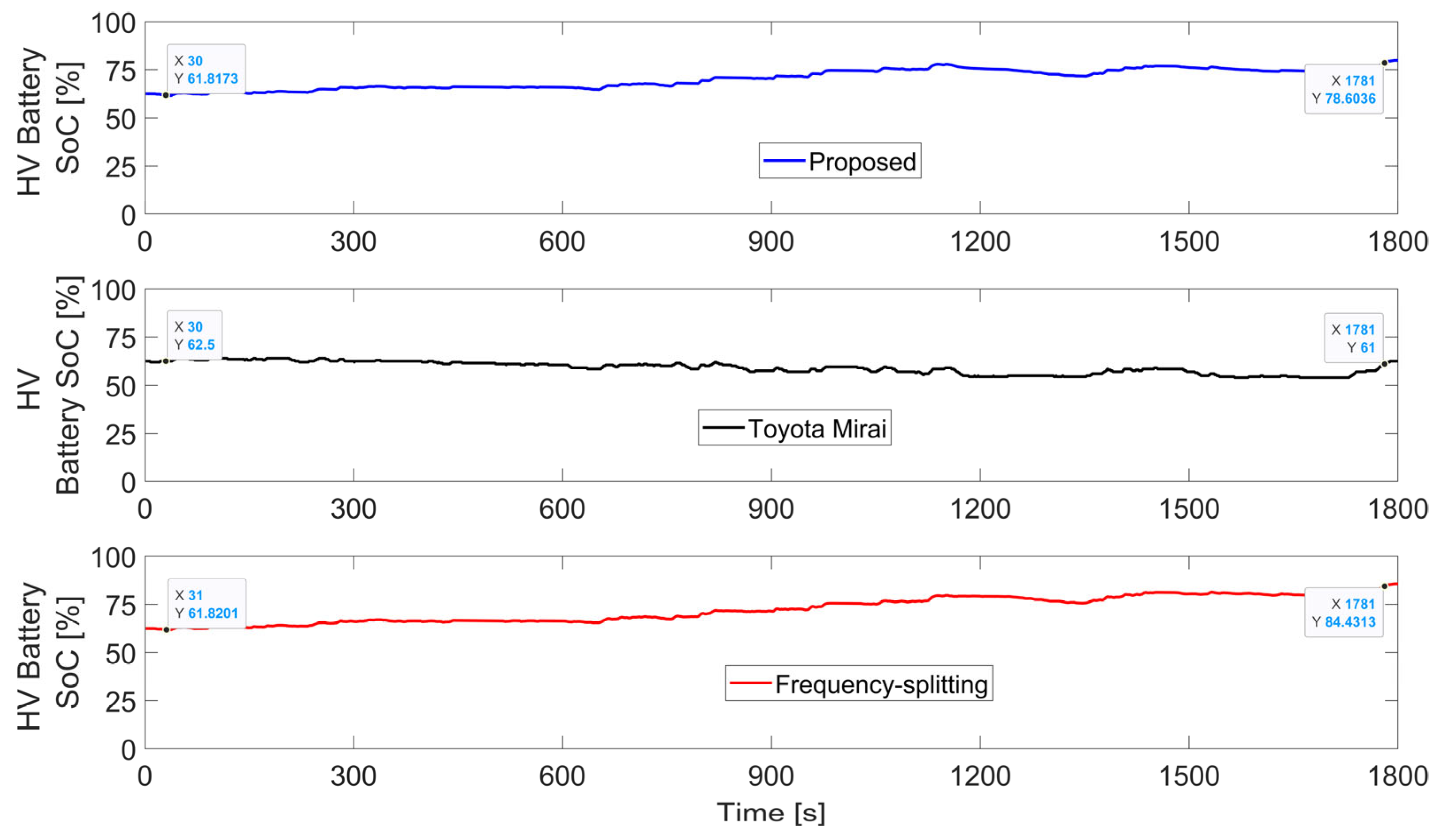
| Method (WLTP C3 Cycle) | Operational Characteristics | Battery Degradation | Fuel Cell Degradation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Fuel h2 Consumed | Price Factor | Miles | Eta | Eta | ΔSoC | Nbattery | Δidle | Δramp | Δswitch | |
| [kg] | [EUR/kg] | - | [mi/kg] | [mi/EUR] | [%] | - | [%] | [%] | [%] | |
| Proposed | 0.185 | 13 | 14.44 | 78.20 | 6.015 | 11.87 | 0 | 30.53 | 1.648 | 3.072 |
| Toyota Mirai data [23] | 0.190 | 75.89 | 5.838 | 0 | 2 | 20.72 | 1.551 | 2.796 | ||
| Frequency splitting, inspired by [26,27,28] | 0.189 | 76.19 | 5.86 | 23.01 | 0 | 30.49 | 3.11 | 4.01 | ||
| Method, Dataset and/or Study (WLTP—14.44 mi) | Fuel h2 Consumed | Range | SoCinit | SoCfinal | ΔSoC-RMSE |
|---|---|---|---|---|---|
| [kg] | [mi/kg] | [%] | [%] | [%] | |
| Proposed—state transition | 0.185 | 78.20 | 62.5 | 79.8 | 17.3 |
| Toyota Mirai data [23] | 0.190 | 75.89 | 61.9 | 0.6 | |
| Frequency splitting, idealised [26,27,28] | 0.189 | 76.19 | 85.66 | 23.01 | |
| Mirai simulation [4] | 0.188 | 76.81 | 61.7 | 0.8 | |
| Equivalent consumption minimisation [14] | 0.166 | 86.93 | 47.39 | 15.11 | |
| Rule-based [14] | 0.197 | 73.3 | 63.29 | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iqbal, M.; Benmouna, A.; Becherif, M. Data-Driven Modelling and Simulation of Fuel Cell Hybrid Electric Powertrain. Hydrogen 2025, 6, 53. https://doi.org/10.3390/hydrogen6030053
Iqbal M, Benmouna A, Becherif M. Data-Driven Modelling and Simulation of Fuel Cell Hybrid Electric Powertrain. Hydrogen. 2025; 6(3):53. https://doi.org/10.3390/hydrogen6030053
Chicago/Turabian StyleIqbal, Mehroze, Amel Benmouna, and Mohamed Becherif. 2025. "Data-Driven Modelling and Simulation of Fuel Cell Hybrid Electric Powertrain" Hydrogen 6, no. 3: 53. https://doi.org/10.3390/hydrogen6030053
APA StyleIqbal, M., Benmouna, A., & Becherif, M. (2025). Data-Driven Modelling and Simulation of Fuel Cell Hybrid Electric Powertrain. Hydrogen, 6(3), 53. https://doi.org/10.3390/hydrogen6030053






