Impact of Hydrogen Release on Accidental Consequences in Deep-Sea Floating Photovoltaic Hydrogen Production Platforms

Abstract

Hydrogen is a potential key component of a carbon-neutral energy carrier and an input to marine industrial processes. This study examines the consequences of coupled hydrogen release and marine environmental factors during floating photovoltaic hydrogen production (FPHP) system failures. A validated three-dimensional numerical model of FPHP comprehensively characterizes hydrogen leakage dynamics under varied rupture diameters (25, 50, 100 mm), transient release duration, dispersion patterns, and wind intensity effects (0–20 m/s sea-level velocities) on hydrogen–air vapor clouds. FLACS-generated data establish the concentration–dispersion distance relationship, with numerical validation confirming predictive accuracy for hydrogen storage tank failures. The results indicate that the wind velocity and rupture size significantly influence the explosion risk; 100 mm ruptures elevate the explosion risk, producing vapor clouds that are 40–65% larger than 25 mm and 50 mm cases. Meanwhile, increased wind velocities (>10 m/s) accelerate hydrogen dilution, reducing the high-concentration cloud volume by 70–84%. Hydrogen jet orientation governs the spatial overpressure distribution in unconfined spaces, leading to considerable shockwave consequence variability. Photovoltaic modules and inverters of FPHP demonstrate maximum vulnerability to overpressure effects; these key findings can be used in the design of offshore platform safety. This study reveals fundamental accident characteristics for FPHP reliability assessment and provides critical insights for safety reinforcement strategies in maritime hydrogen applications.

1. Introduction

Deep-sea floating photovoltaic hydrogen production (FPHP) technology represents an innovative paradigm for renewable hydrogen generation, emerging as a critical energy frontier due to its strategic advantages in spatial resource utilization, enhanced power generation efficiency, and green hydrogen potential. The International Energy Agency (IEA) projects global hydrogen demand exceeding 150 million tons by 2030 [1], with green hydrogen constituting over 60% of the supply. This is a stark contrast to its current penetration rate (<1%), underscoring the dual urgency for technological breakthroughs and robust safety controls. China’s national hydrogen strategy prioritizes offshore renewable hydrogen [2], driving development of over 50 offshore wind-to-hydrogen projects by 2025 with a 300,000-ton annual capacity, while coastal provinces advance “Marine Energy Island” initiatives, integrating floating photovoltaics (PV) with offshore electrolysis for scalable production [3].

The FPHP platform investigated in this study comprises three core modules: photovoltaic power generation, seawater electrolysis for hydrogen production, and hydrogen storage tanks. These components collectively fulfill hydrogen synthesis and storage objectives. The historical precedent for PV-related risks is exemplified by the severe Chikura floating solar power plant fire in Japan [4]. The storage of large quantities of high-pressure hydrogen presents a significant hazard potential. Leakage can readily form extensive combustible clouds; subsequent ignition may trigger cascading disasters, including fires and explosions. The current review underscores that while substantial research focuses on hydrogen production systems, the assessment of hydrogen leakage and explosion hazards within the FPHP platform remains limited. Scholarly studies systematically addressed the hydrogen facility safety, establishing assessment frameworks for refueling stations [5,6]. Ingrid et al. conducted risk analysis to derive emergency responses for hydrogen incidents [7]. FPHP feasibility studies have elucidated safety mechanisms governing electrolyzer operations while optimizing engineering designs and protective measures [8,9,10,11]. A risk assessment of the entire system was conducted by Kumar et al. [12], which focused on the safety, environmental protection, and financial viability of infrastructure in the offshore green hydrogen system. Hydrogen leakage presented multi-phase risks spanning production, delivery, and end-use operations, fundamentally amplifying deflagration risks during inadvertent releases [13]. The presence of compressor equipment and a cylindrical hydrogen storage tank led to accelerated flame propagation and higher overpressure peaks [14]. An explosion model was modified [15] to extend the flame critical radius and flame speed, providing an accurate prediction across a wide range of hydrogen–air mixtures. Wang et al. established a numerical model for characterizing hydrogen vapor cloud explosions (HVCEs); this work systematized the wind intensity effects on HVCEs’ structural response [16]. Employing computational fluid dynamics (CFD), potential work for explosion modeling during hydrogen leakage in confined or open space was demonstrated [17,18,19], and relevant prediction models for explosion characteristics and hazards were proposed. Hajji and Qian analyzed hydrogen leakage dynamics dependencies on orifice geometry, location, and discharge velocity [20,21], which revealed enhanced near-surface combustible cloud accumulation. Total hydrogen inventory critically determines the spatial morphology of cloud boundaries along release vectors [22], while concentration gradients govern dispersion via natural convection. Thermal radiation models incorporated flame temperature dependencies for jet fire prediction [23,24,25], while mixture non-ideality studies demonstrated anomalous dispersion [26]. Operational protocols addressed parametric correlations for liquid hydrogen leakage [27,28], with fundamental research characterizing spontaneous ignition [29] and obstacle-driven flame acceleration [30]. Systematic experiments characterized critical deflagration parameters—flame temperature, peak overpressure (0.14–0.36 MPa), and duration—and revealed ignition location distribution as the primary determinant of explosion severity [31,32]. Obstacles in constrained configurations accelerated flame fronts and amplified the blast intensity by 18–34% [33,34], while open-space HVCEs exhibited directional shockwave propagation that was modulated by crosswinds [35]. Integrated ANSYS CFX (R19.1)/Fault Tree Analysis provided an emergency response framework for high-pressure leakage scenarios [36], supported by Type IV tank tests deriving shockwave attenuation relationships [37], as shown in

Table 1. Parameters of Type IV hydrogen tank ignition tests [38].

Item	Distance from Source/m	Peak Overpressure/kPa
Value	1.9	300
	4.2	83
	6.5	41
	Observed fireball diameter exceeded 7.7 m.

. Molkov and Kashkarov established an analytical model for shockwave prediction during high-pressure tank ruptures, incorporating real gas effects and chemical energy release with experimental validation [38]. Pu et al. developed a simplified algebraic model based on acoustic theory for a rapid hazard assessment of HVCEs [39], while a proprietary numerical code solving multi-component reaction equations was implemented to simulate HVCEs in high-pressure storage systems [40].

The novel approach proposed in this study is a combination of a theoretical model and a numerical method, which collectively enables the generation of effective data. On the one hand, the influence mechanism of offshore factors on the characteristics of hydrogen vapor cloud explosions is still unclear. As a highly developing technology for hydrogen production in the future, relevant technical specifications of safety protection for the FPHP platform are still being explored at present. On the other hand, damage evaluations of FPHP hydrogen vapor cloud explosions are employed to generate predictions, representing an additional effort to enhance the effectiveness of the FLACE-based models and facilitate the application in marine conditions associated with the prevention strategy in practice. This study recreates the accident scene of the FPHP and obtains the key parameter characteristics, such as the flow field distribution and concentration dispersion, during the hydrogen leakage process. By analyzing the flame behavior and shock wave propagation laws in the marine environment, the accident consequences after the failure of the FPHP are addressed. Based on the influence of factors, such as sea surface wind velocity, different leakage ruptures, and ignition positions, this study further quantifies the characteristic parameters, such as shock wave overpressure and flame temperature, as well as their spatio-temporal evolution characteristics. This study reveals the core risk chain of the FPHP platform and proposes that there are potential risks during the operation of the FPHP. This study aims to provide data support and scientific references for the design, safety protection, and emergency response of FPHPs.

2. Numerical Method

2.1. Scenario Modeling

The FPHP involved in this study is built on an open water area along the coast of China, as shown in Figure 1. The entire platform consists of two main parts: one is the photovoltaic module, and the other is the hydrogen production platform. The photovoltaic system comprises floating photovoltaic panels supported by pontoons. The size of the photovoltaic panel is 1.65 × 1.0 × 0.05 m (height × width × thickness). The pontoon is used to support the photovoltaic panels to float stably on the water’s surface, with dimensions of 0.75 m × 0.3 m × 0.1 m. Photovoltaic systems directly convert solar energy into electrical energy through photovoltaic panels, which include independent photovoltaic power generation systems. The power generation system is composed of a controller, an inverter, and circuits, together with electronic components and mechanical parts. The function of an inverter is to transform direct current energy into fixed-frequency and fixed-voltage or frequency-regulated and voltage-regulated alternating currents. Its dimensions are 0.5 × 0.3 × 0.7 m. It is composed of an inverter bridge, control logic, and filter circuits. The hydrogen production platform consists of equipment such as water purification and proton exchange membrane (PEM) electrolyzer, as well as a compressor and hydrogen storage tank. When there is sufficient sunlight on the sea surface, the photovoltaic modules convert solar energy into electricity and store it. The reverse osmosis device includes a high-pressure pump that drives seawater through the reverse osmosis membrane. Due to the different specific concentrations of solutes, the pressure inside and outside the semi-permeable membrane is formed differently, thereby achieving seawater desalination. Meanwhile, the photovoltaic modules supply power to the electrolytic cell, generating hydrogen through electrolytic reactions. The generated hydrogen is stored in the hydrogen storage device via the compressor.

This modeling sets the high-pressure hydrogen storage area in the accident zone. The height of a single hydrogen storage tank is 8 m, and the diameter is 1.5 m. There are two high-pressure hydrogen storage tanks, with a working pressure of 35 MPa. The density of liquid hydrogen in the tank is 23.3 kg/m³, and the total amount of hydrogen filled is 329.03 kg. The parameters are shown in

Table 2. The physical parameters of the materials in the hydrogen storage tank.

Material	Density/kg/m−3	Critical Temperature/K	Critical Pressure/MPa	Heat of Vaporization/kJ·kg−1	Specific Heat Ratio	Heat Value/MJ/kg	Explosion Limits
Hydrogen	0.089	33.25	1.313	305	1.4	140	4–75%

in detail. The leakage position of the hydrogen near the high-pressure hydrogen storage tank is set, and the release and dispersion process of hydrogen is explored by simulating the rupture of the high-pressure hydrogen storage tank. The leakage orifice diameters of hydrogen release are modeled with a range from 25 mm to 100 mm, and the initial state of the leakage is a two-phase medium with gas/liquid. In terms of the grid setting, a total of 39,904 grids were set up. The local densification of the grid was carried out at the hydrogen leakage location of the hydrogen storage tank, while the grids outside the accident area were gradually thinned. The simulation of this accident sets the marine environmental temperature at 293.15 K, the average humidity at 86.1%, and the atmospheric stability at D. The boundary condition for the hydrogen leakage direction is “WIND”, and for the other directions, it is “Plane-Wave”. The initial turbulence intensity was set at 0.1, and the turbulence length scale was 0.01 m. Considering the effect of sea surface wind conditions, the average sea surface wind velocity was set successively from 0 m/s to 20 m/s. Ignition sources may occur at different locations on the entire FPHP. In this study, through hazard source identification, it was determined that the areas near high-pressure hydrogen storage tanks, electrolyzers, and inverters were the regions with the highest frequency of ignition sources. The location of the ignition source will have an impact on the consequences and damage intensity caused by HVCEs.

2.2. Governing Equation

The hydrogen leakage accident that occurred during the operation of the FPHP, after going through leakage and dispersion, eventually formed a combustible hydrogen cloud, which is divided into three stages. At the initial stage, when hydrogen leaks due to pressure difference between internal pressure of storage tank and atmospheric pressure, a significant density difference occurs between hydrogen and air, therefore a jet forms at leakage point. Jet flow is a phenomenon where a fluid accelerates its flow in the environment through a small hole or nozzle, thereby being released at high velocity. It often occurs in liquids and gases. Due to the significant density difference between hydrogen and air, and the driving force for the continuous movement of the jet after it is discharged, which is affected by both momentum and buoyancy, this type of hydrogen leakage belongs to a buoyancy jet. In the second stage, the momentum required by the early jet is the initial kinetic energy and velocity difference caused by the pressure difference. The leaked high-velocity hydrogen gas continuously sucks in the air and constantly exchanges mass, energy, and momentum with the surrounding environment, continuously expanding the range where the jet phenomenon occurs. In the final stage, after being at a certain distance away from the leakage point, the buoyancy generated by the density difference becomes the main factor affecting the jet. Since the density of hydrogen is much lower than that of the surrounding ambient gas, this jet is a positive buoyancy jet. In the model construction of this study, the continuity equation and the law of conservation of physics are involved when gases flow [41,42,43]. Basic laws of conservation of physics include the laws of conservation of mass, conservation of energy, and conservation of momentum. The flow contains different components and involves component transport equations as well as turbulence models. The continuity equation is shown as Equation (1).

$${\displaystyle \frac{\partial {\rho }_{\mathrm{m}}}{\partial \mathrm{t}}}+\nabla •\left({\rho }_{\mathrm{m}}{\overrightarrow{\upsilon }}_{\mathrm{m}}\right)=0,$$

(1)

where ρ_m is the density of mixtures, kg/m³; ${\overrightarrow{\upsilon }}_{\mathrm{m}}$ is the average velocity of mass, kg/(m²·s).

The equation of conservation of mass is as follows:

$${\displaystyle \frac{\partial \rho }{\partial \mathrm{t}}}+{\displaystyle \frac{\partial \left(\rho {\mu }_{\mathrm{x}}\right)}{\partial \mathrm{x}}}+{\displaystyle \frac{\partial \left(\rho {\mu }_{\mathrm{y}}\right)}{\partial \mathrm{y}}}+{\displaystyle \frac{\partial \left(\rho {\mu }_{\mathrm{z}}\right)}{\partial \mathrm{z}}}=0,$$

(2)

where μ_x, μ_y, and μ_z are the velocities in the x, y, and z directions, respectively, m/s.

The equation of conservation of momentum is as follows:

$${\displaystyle \frac{\partial \left({\rho }_{\mathrm{m}}{\overrightarrow{\upsilon }}_{\mathrm{m}}\right)}{\partial \mathrm{t}}}+\nabla \left({\rho }_{\mathrm{m}}{\overrightarrow{\upsilon }}_{\mathrm{m}}{\overrightarrow{\upsilon }}_{\mathrm{m}}\right)=-\nabla \rho +\nabla •\left[{\mu }_{\mathrm{m}}\left(\nabla {\overrightarrow{\upsilon }}_{\mathrm{m}}+\nabla {\upsilon }_{\mathrm{m}}^{\mathrm{T}}\right)\right]+{\rho }_{\mathrm{m}}\mathrm{g}+\overrightarrow{\mathrm{F}}-\nabla \left({\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{n}}{\alpha }_{\mathrm{k}}{\rho }_{\mathrm{k}}{\overrightarrow{\upsilon }}_{\mathrm{dr},\mathrm{k}}{\overrightarrow{\upsilon }}_{dr,k}}\right),$$

(3)

where α_k is the volume fraction of phase k; n is the phase number; μ_m is the mixture viscosity, Pa·s; ${\overrightarrow{\upsilon }}_{\mathrm{d}\mathrm{r},\mathrm{k}}$ is the drift velocity of the second phase k, m/s; $\overrightarrow{F}$ is the volume force, N.

The equation for energy conservation is as follows:

$${\displaystyle \frac{\partial {\displaystyle {\sum }_{\mathrm{k}}{\alpha }_{\mathrm{k}}{\rho }_{\mathrm{k}}{E}_{\mathrm{k}}}}{\partial \mathrm{t}}}+\nabla •{\displaystyle {\sum }_{\mathrm{k}}{\alpha }_{\mathrm{k}}{\upsilon }_{\mathrm{k}}}\left({\rho }_{\mathrm{k}}{E}_{\mathrm{k}}+\mathrm{p}\right)=\nabla •\left({\mathrm{k}}_{\mathrm{eff}}\nabla \mathrm{T}-{\displaystyle {\sum }_{\mathrm{k}}{\displaystyle {\sum }_{\mathrm{j}}{\mathrm{h}}_{\mathrm{j},k}}}{J}_{j,k}+{\tau }_{eff}•\upsilon \right)+S_h,$$

(4)

where k_eff is the effective electrical conductivity; k_t is the turbulent thermal conductivity defined by the k-ε turbulence model, W/(m·K); h_j,k is the enthalpy of species j in phase k; J_j,k is the diffusion flux of species j in phase k; S_h is the heat source item.

The equation for component transport can be shown in Equation (5):

$${\displaystyle \frac{\partial \left(\rho {\mathrm{c}}_{\mathrm{s}}\right)}{\partial \mathrm{t}}}+{\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left(\rho {\mu }_{\mathrm{j}}{\mathrm{c}}_{\mathrm{s}}\right)={\displaystyle \frac{\partial }{\partial {\mathrm{x}}_{\mathrm{j}}}}\left[D_{\mathrm{s}}{\displaystyle \frac{\partial \left(\rho {\mathrm{c}}_{\mathrm{s}}\right)}{\partial {\mathrm{x}}_{\mathrm{j}}}}\right]+S_{\mathrm{s}},$$

(5)

where c_s is the volume fraction of the source term.

The gas leakage models are the ideal gas model and the AN-EOS model. When the internal pressure of the small hole is lower than 10 MPa, the error of choosing the ideal gas model is relatively small. The maximum pressure of the high-pressure hydrogen storage tank carried by the ship is 35 MPa, and the pressure at the leakage position is set at 10 MPa. The pressure ratio inside and outside the small hole is compared at the leakage position with a value containing the adiabatic gas coefficient. If the ratio is greater than the numerical value, hydrogen leakage is in a subsonic flow state. If the ratio is less than or equal to the value, hydrogen leakage is in a supersonic flow state.

According to the complexity of gas dispersion, classical models have been proposed, such as the Gaussian model, the BM model, and the Sutton model. The Gaussian model is used in this study, and the expression of gas concentration distribution in the plume model is shown as Equation (6).

$$\mathrm{c}\left(x,y,z,H\right)={\displaystyle \frac{Q}{{\left(2\pi \right)}^{\frac{2}{3}}{\sigma }_x{\sigma }_y{\sigma }_z}}\exp \left[-{\displaystyle \frac{{\left(x-ut\right)}^2}{2{\sigma }_x^2}}\right]\exp \left(-{\displaystyle \frac{y^2}{2{\sigma }_y^2}}\right)\left[\exp \left(-{\displaystyle \frac{{\left(z-H\right)}^2}{2{\sigma }_z^2}}\right)+\exp \left(-{\displaystyle \frac{{\left(z+H\right)}^2}{2{\sigma }_z^2}}\right)\right],$$

(6)

where c(x,y,z,H) is the concentration at a certain point in the space, kg/m³; u is the average wind velocity in m/s; t is the hydrogen dispersion time, s; σ_x, σ_y, and σ_z are the coefficients in the downwind direction, crosswind direction, and vertical wind direction, respectively; H is the height, m.

2.3. Model Validation

To verify the effectiveness of the numerical methods in predicting hydrogen leakage and dispersion from hydrogen storage tanks in the FPHP platform, a physical model of the actual experiment is accurately replicated in FLACS-based modeling [44]. Numerical simulation was set according to the experimental conditions, and the simulation calculation results were systematically compared and analyzed with the experimental data to evaluate the accuracy of this simulation method. The experiment for model verification aimed to analyze the dispersion, concentration distribution, and variation law of leaked gas at different locations. The experiment was completed in an unconfined space. To simulate the external ventilation conditions in an open space and create stable laminar flow conditions in a low wind velocity environment, the experimental space was enclosed by a roof with a height of 5.2 m and vertical walls that were spaced 6.4 m apart from each other. An experimental site with a length of 11 m, a width of 3 m, and a height of 3 m was constructed inside the space. A sonic anemometer was installed 2 m above the ground at the air inlet. Its main function was to precisely measure the wind direction and wind velocity. Sensors were respectively set at a position 2 m above the ground in the middle of the experimental area and at the outlet of the leaked gas. The gas release process of the failure source, with the aid of the storage cylinder device, was conducted, which was placed 10 m away from the leakage outlet. The leakage hole was located on the centerline of the inner surface of the wind tunnel, nearly 0.01 m above the ground, and its diameter was 0.02 m. When gas was released, 6 monitoring points (MP) were set along the ground centerline, and the THY-TB10 sensor device was used to measure the gas concentration at different positions. The settings of the verification model are consistent with the experimental layout, and four different leakage rates were set at 8.8 m/s, 10.6 m/s, 13.3 m/s, and 15.9 m/s, respectively. The scenario model established by FLACS was compared with the experimental tests, and the simulation results can be seen in Figure 2. A comparison with experimental data shows that the maximum deviation between the concentration data obtained by the FLACE-based model and experimental tests occurs at the peak point time, with a deviation of 9.47%. The deviation between the numerical simulations and experimental data reflects the homogenization when setting the boundary conditions of the current model, such as setting the wind velocity to a constant value, etc. In addition, it may be the influence of many factors during the experimental process. The above-mentioned problems have been improved in existing models and simulation processes. Based on this, the simulation results of hydrogen leakage and dispersion in the FPHP platform constructed by FLACS in this study display certain validity and accuracy.

3. Results and Discussion

3.1. Hydrogen Dispersion with Different Rupture Sizes Induced by Platform Failure

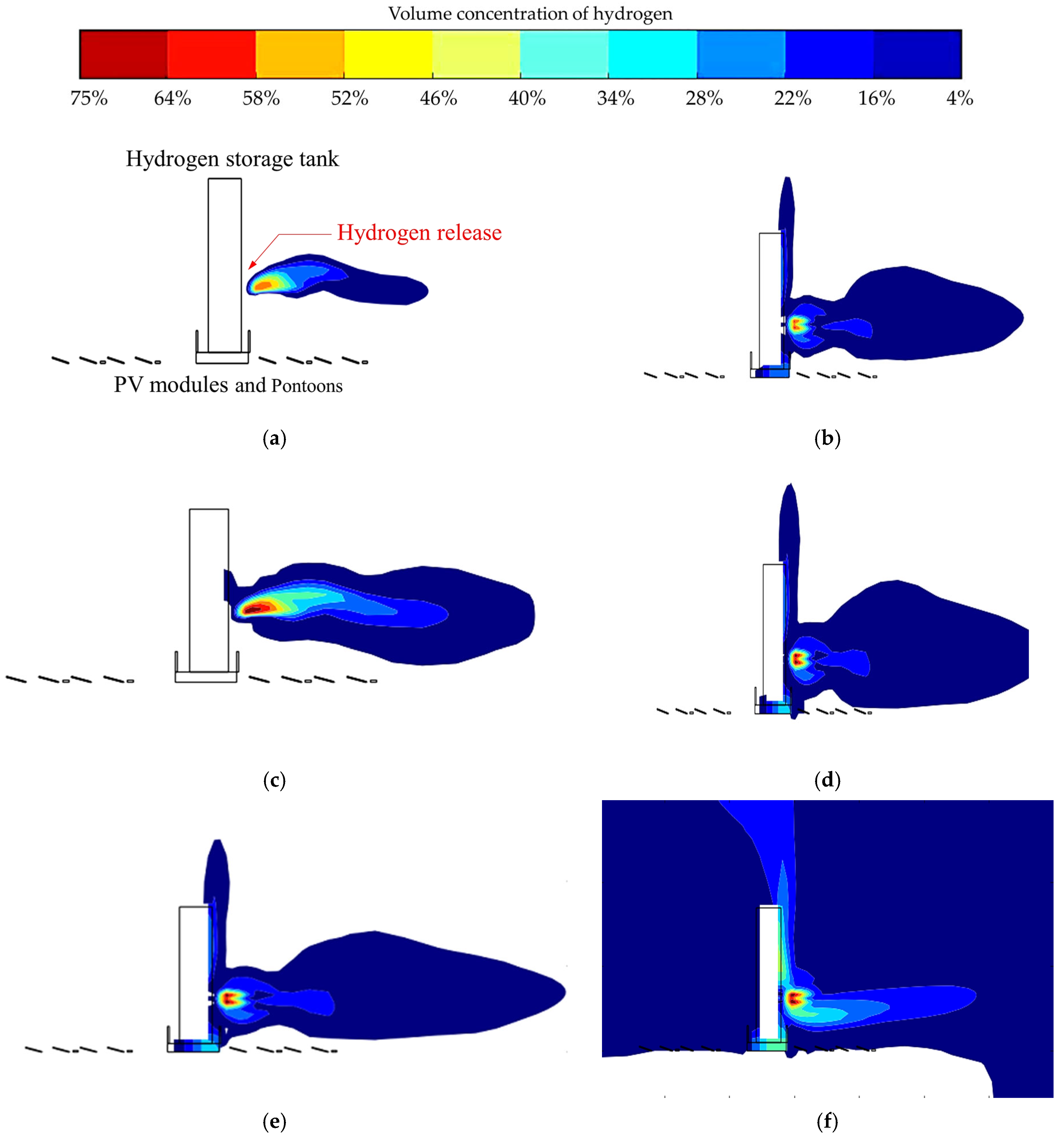
There are safety risks in the long-term operation of FPHP in an offshore environment, especially in areas with high-pressure hydrogen storage devices; more attention should be paid to safety protection measures. Figure 3 shows the gas concentration distribution when hydrogen leakage occurs horizontally in the hydrogen storage tank of FPHP with a failure rupture of 25 mm. As the leakage time continued to increase, the range of vapor cloud was formed by the hydrogen leakage expanded. The entire dispersion range was roughly divided into two parts. The first part was the dispersion in the horizontal direction along the leakage point. This direction was an unconfined area where hydrogen disperses in open space without obstacles. Within 2.0 s to 8.0 s of leakage duration, the dispersion of combustible vapor cloud was distributed in a willow leaf-like pattern on the horizontal plane. The hydrogen gas reached 10.1 m and 14.2 m, respectively, in the horizontal direction. Between 8.0 s and 14.0 s of hydrogen leakage in FPHP, the vapor cloud formed by hydrogen leakage grew and widened rapidly, further increasing the possibility of HVCE accidents. When the hydrogen leaked for 14.0 s, it reached 18 m along the horizontal direction, and the width expanded from 2.2 m to 8.3 m. The vapor cloud that was formed by hydrogen leakage reached its maximum volume and filled the entire area. Another part spreads vertically upward along the hydrogen storage tank. Due to the low volumetric energy density of hydrogen, it needs to be stored under high pressure during the preparation process. High-pressure hydrogen storage tanks are usually prone to local failure, which leads to the formation of small-sized ruptures. When a compressed medium in a high-pressure hydrogen storage tank communicates with the outside through a small-sized rupture, it disperses to the external environment in the form of a jet release. A small amount of hydrogen vapor cloud then accumulated above the rupture point of storage tank. This part of the gas was not yet within an explosion range. Between 8.0 s and 14.0 s of hydrogen leakage in FPHP, as the leakage duration continued to increase, a large amount of hydrogen accumulated near the rupture point. The blocking effect of the hydrogen storage tank prevented hydrogen from moving horizontally. Due to the momentum conservation, it dispersed in the vertical space. Hydrogen was dispersed in a vertical area with a height of approximately 13.4 m. After some of the hydrogen exceeded the hydrogen storage tank, it began to extend in horizontal space, and the vertical distance was 16.1 m.

Figure 4 demonstrates the hydrogen dispersion process along the horizontal direction with a rupture diameter of 50 mm in the hydrogen storage tank of FPHP. Due to an increase in rupture size, the leakage volume of hydrogen increased. Gas concentrations in the horizontal and vertical directions and the range of vapor cloud formation are significantly larger compared to the 25 mm case. In a scenario where the rupture diameter is 50 mm, more hydrogen disperses along the direction of the leakage outlet. A hydrogen cloud formed by hydrogen spreads horizontally to a distance of 11 m. As the rupture diameter increases, the hydrogen leakage in a high-pressure hydrogen storage tank goes up accordingly. Strong jets form initial momentum, prompting more hydrogen to disperse horizontally. At 8.0 s of hydrogen leakage, a hydrogen vapor cloud with a rupture of 50 mm disperses to 15.7 m. Meanwhile, the width of the hydrogen cloud increases from 2.1 m to 7.3 m. In a scenario where the hydrogen leakage rupture is 50 mm, within 8.0 s of hydrogen leakage occurrence, hydrogen above the leakage outlet has not reached the explosion limit range. This is similar to hydrogen dispersion in an accident scenario with a leakage rupture of 25 mm. When hydrogen leakage occurs in FPHP at 14.0 s, the vertical dispersion height of hydrogen (50 mm rupture case) is approximately 13.3 m. When hydrogen leakage occurs for 25.0 s, there is a risk of HVCE within the hydrogen dispersion range. Figure 4c shows the concentration distribution of hydrogen dispersion along the horizontal direction when the leakage rupture is 100 mm. Hydrogen is instantly ejected from the leakage point, and the kinetic energy of the fluid in space increases. Due to an increase in leakage rupture, the length and width of the hydrogen vapor cloud are larger than those in the 50 mm rupture case. The horizontal dispersion distance of the hydrogen vapor cloud reaches 15.7 m, and the width of the vapor cloud reaches 3.2 m, both of which are larger than the hydrogen vapor cloud with the rupture case of 50 mm. The hydrogen vapor cloud accumulated above the leakage point (reached explosion limits), which spread upward along the vertical direction. The dispersion concentration of hydrogen in space thus reached the explosive limit range. From 14.0 s of hydrogen leakage occurrence to 23.0 s, in the horizontal direction, the hydrogen concentration increased. In vertical space, the hydrogen dispersion width was greater than in the 50 mm rupture case. Obviously, due to an increase in hydrogen leakage rupture, the amount of hydrogen leakage continued to rise, leading to an enhanced risk of HVCEs in the deep-sea FPHP platform.

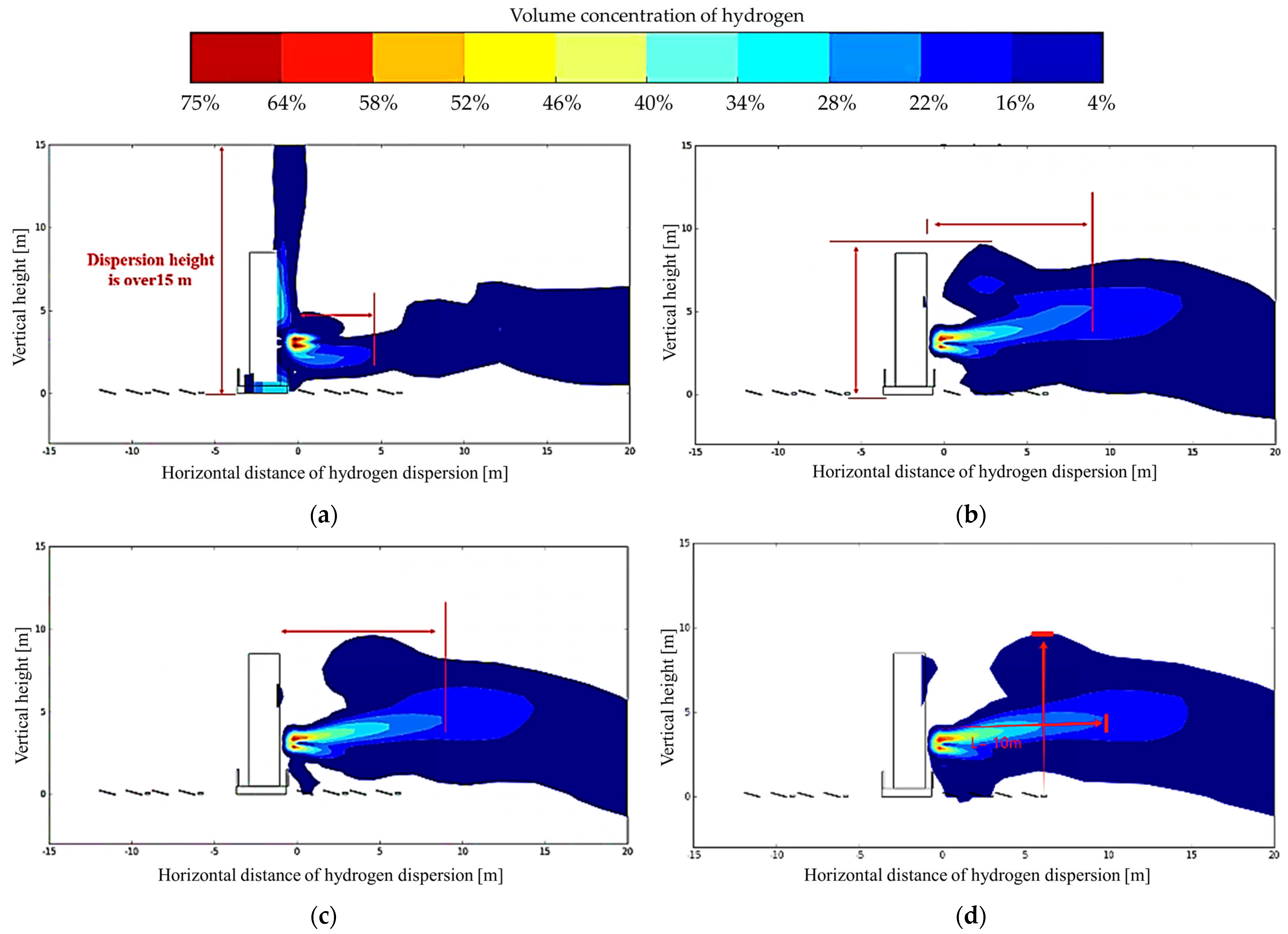
When the sea surface condition approaches a windless state, the hydrogen leakage accident in FPHP is shown in Figure 5a. Due to different pressure ratios between the leakage source and the marine environment, the hydrogen jet release is in different flow states at the failure location. If the internal pressure of the hydrogen storage tank is close to atmospheric pressure, the pressure ratio is lower than the critical pressure ratio of leaked hydrogen. In this accident scenario, hydrogen is in a fully expanded state at the leakage location, and the leakage form is a subsonic jet. When the hydrogen storage tank in FPHP fails, it is obvious that the pressure ratio at the inner and outer interfaces of the failure rupture is higher than the critical pressure of hydrogen. The velocity at the leakage location is close to the local sound velocity, and hydrogen leakage is in an under-expansion state. Due to the pressure being higher than atmospheric pressure, hydrogen further expands when leaving the rupture point, forming a supersonic flow. When a failure of a high-pressure hydrogen storage tank occurs at 23.0 s, the hydrogen concentration on FPHP is monitored to exceed 52%. When the failure time of the hydrogen storage tank exceeds 50.0 s, high-concentration leakage begins to spread to the photovoltaic modules. Due to the inherent characteristics of hydrogen, it gradually undergoes an upward floating behavior during the process of leaked hydrogen dispersing to the marine surroundings. When the sea surface wind velocity increased to 10 m/s, the wind force effect thus significantly inhibited the ability of hydrogen cloud clusters to draw air in all directions. The dominant role of the wind field prompts hydrogen cloud clusters to break through the original dispersion pattern and instead disperse in a directional manner along the wind direction. Downwind direction becomes the core direction for hydrogen to draw in air, expanding the dispersion distance along the horizontal direction. When the wind velocity from no wind to the sea surface is 10 m/s, the hydrogen dispersion distance along the horizontal direction increases by 5.5 m. The increase in sea surface wind velocity weakens the dispersion distance in vertical space, which expands the vertical dispersion distance to 8.3 m.

Comparisons between Figure 5b,c show that the hydrogen concentration at the boundary decreases continuously with elevated wind velocity at the sea surface. Figure 5b indicates that when the hydrogen concentration is 40.7%, the hydrogen disperses horizontally to a position of 10.1 m. While in Figure 5c, hydrogen disperses horizontally to a position of 8.3 m. The results reveal that in the scenario of downwind leakage, wind force on the sea surface has a dual effect on hydrogen dispersion. On the one hand, wind on the sea surface transports hydrogen to spread further away. On the other hand, high wind velocity significantly reduces the volume of high-concentration hydrogen vapor clouds by rapidly diluting hydrogen. As the sea surface wind velocity continues to increase, the horizontal force of airflow significantly strengthens. This significantly increases the difficulty for hydrogen to draw air upwards, forcing hydrogen to mainly disperse along the ground. From the perspective of hydrogen dispersion characteristics, a high wind velocity can not only drive vapor clouds to migrate to the distal end, but it also reduces the concentration during the dispersion process of hydrogen vapor clouds. By comparing Figure 5c,d, it indicates that the increase in sea surface wind velocity significantly weakens the ability of hydrogen to draw air around. Specifically, the greater wind velocity at the sea surface, a lower vertical upward dispersion height of hydrogen, and its dispersion pattern gradually flattens. It is worth noting that when the sea surface wind velocity is lower than 10 m/s, the hydrogen dispersion distance is positively correlated with wind velocity. That is, elevated wind force can effectively push a vapor cloud mass to move along the wind direction, promoting the continuous expansion of the hydrogen dispersion range. When the sea surface wind velocity increases to over 15 m/s, the hydrogen dispersion pattern gradually changes under the action of strong winds. These findings suggest the obvious characteristics of near-ground hydrogen dispersion. The strong sea surface wind force has accelerated the dispersion and dilution process of the hydrogen vapor cloud. Meanwhile, due to the directional enhancement effect of gas flow on hydrogen, it is difficult for hydrogen to extend further in the horizontal direction. As a result, the dispersion distance gradually shortens as the wind velocity further increases. Within 25.0 s of hydrogen leakage, hydrogen formed a large-scale mixed vapor cloud near FPHP. The hydrogen vapor cloud is within the explosion limit concentration range of hydrogen/air. Once it encounters a heat source or flame propagation, it causes a large-scale HVCE around FPHP.

In this study, the critical wind velocity at the sea surface is further analyzed. The critical wind velocity and distribution of combustible vapor clouds are discussed by adding different conditions, such as sea surface wind velocities of 15 m/s, 16 m/s, 17 m/s, 18 m/s, 19 m/s, and 20 m/s. The entire hydrogen leakage process is mainly affected by both wind velocity and buoyancy, and the combustible vapor cloud moves in a horizontal direction. The different horizontal dispersion distances of the hydrogen vapor cloud under different sea surface wind velocities. When the sea surface wind velocity is less than 16 m/s, as the sea surface wind velocity increases, the distance that the hydrogen vapor cloud disperses horizontally along the sea surface wind velocity remains above 18.2 m. When the sea surface wind velocity is greater than 16 m/s, with an increase in wind velocity, the distance that the hydrogen vapor cloud disperses horizontally along the wind velocity remains basically unchanged and is maintained at 15.3 m. Analysis suggests that within a certain range of sea surface wind velocity, when hydrogen leaks downwind, the wind force can carry the hydrogen vapor cloud to spread to more distant positions. Based on data-based simulations of hydrogen dispersion changes along the leakage direction under different wind velocity conditions, it is found that wind force has a significant effect on the vertical dispersion process of hydrogen vapor clouds. After hydrogen leakage occurs, when the wind velocity is lower than 16 m/s, while hydrogen leaks horizontally, it also undergoes vertical dispersion in the vertical direction. When the sea surface wind velocity increased to 19 m/s, a strong wind significantly weakened the ability of the hydrogen vapor cloud to draw in surrounding air, forcing the vapor cloud to move horizontally along the wind direction. It significantly compresses the dispersion distance of hydrogen in vertical space. Further observations reveal that when the sea surface wind velocity reaches 19 m/s and 20 m/s, respectively, the dispersion range of hydrogen vapor cloud in both the horizontal and vertical directions shows a gradually shrinking trend. This phenomenon indicates that the increase in sea surface wind velocity can accelerate the dilution process of hydrogen and effectively reduce the spatial proportion of high-concentration hydrogen vapor clouds. As the wind velocity at the sea surface continues to increase, the difficulty for hydrogen to draw air upwards increases sharply, causing its dispersion form to be increasingly close to the ground. High-intensity wind velocity has a dual effect on hydrogen dispersion. On the one hand, strong winds drive hydrogen vapor clouds to spread to more distant areas. On the other hand, elevated wind intensities accelerate the dilution of hydrogen concentration and change the spatial distribution characteristics of vapor clouds. As the wind velocity on the sea surface keeps increasing, the vertical upward dispersion height of hydrogen becomes lower and lower. Under the dominant effect of strong wind force, the dispersion pattern of hydrogen undergoes a significant transformation, showing obvious characteristics of near-ground dispersion. Meanwhile, high-velocity airflow accelerates the mixing process of hydrogen with the surrounding air, greatly enhancing dilution efficiency. Under the influence of these dual factors, the effective dispersion distance of hydrogen does not extend with the increase in wind velocity. Instead, it shows a shrinking trend with increasing wind velocity. With an increase in wind velocity on the sea surface, hydrogen vapor clouds spread close to the ground. Leaked hydrogen accumulates between devices, such as photovoltaic panels and inverters. Impacts of the sea surface wind conditions on these areas are limited, and it takes a relatively long time to dissipate.

3.2. Effect of Ignition Position on Hydrogen Explosion-Driven Thermal Damage

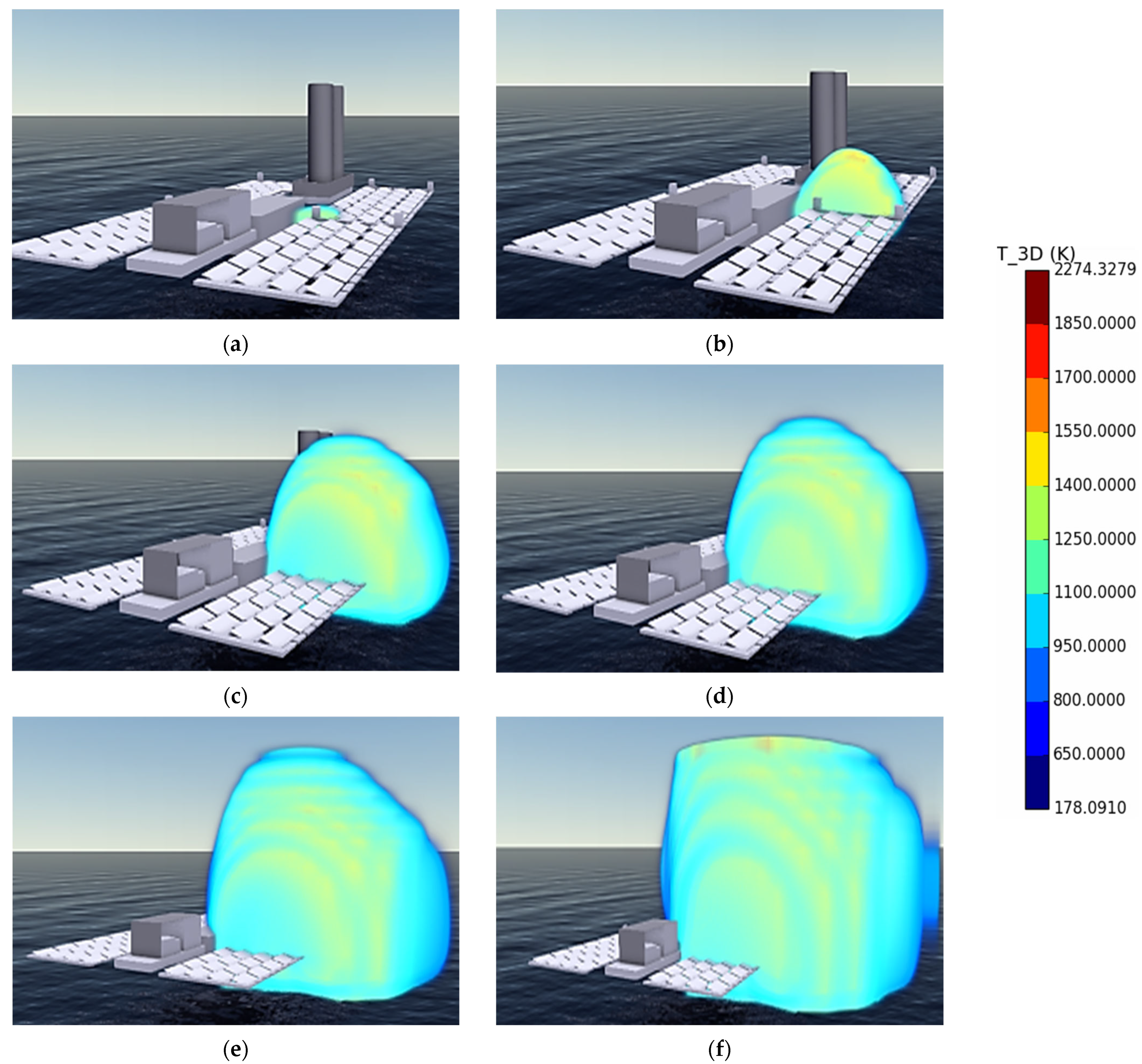
In a deep-sea FPHP platform, flames are most likely to occur near hydrogen storage tanks, electrolyzers, and inverters. This further triggers the risk of HVCEs. In this study, ignition points were set at three different positions, such as the hydrogen storage tank, electrolytic cell, and inverter, to explore the influence of different ignition positions on thermal hazards caused by HVCEs. Figure 6 indicates the variation trend of thermal radiation of the ignition source near the hydrogen storage tank over time. At the initial stage of HVCE, the temperature of the explosive fireball is the highest at this time, reaching 1850.1 K. Due to the abundance of combustible materials and high heat released by a HVCE, the affected area at this time is relatively small. When the duration time of a HVCE is 3000 ms, the flame begins to develop into an ellipsoid with a long axis. High-temperature flames completely cover the horizontal photovoltaic panels, and the temperature in the photovoltaic panel area reaches over 1550 K. The temperature remains at a relatively high level, but it is slightly lower than that at approximately 2000 ms. At nearly 4000 s after a HVCE occurs, the flame continued to spread outward. As the flame continues to spread, when the occurrence time of a HVCE is approximately 5000 ms, it has reached the boundary of the entire system platform. Since there are no obstacles blocking the ignition point of the hydrogen storage tank, the spread pattern of flame is completely dominated by the HVCE’s intensity and the form of combustible vapor cloud. The thermal radiation produced by a HVCE reveals a certain geometric regular distribution in its propagation pattern.

Figure 7 shows the variation trend of the thermal radiation of the ignition source near the electrolytic cell over time. Compared with the flame propagation ignited near a hydrogen storage tank, the temperature of the hydrogen cloud ignited near the electrolytic cell is lower, and the time to reach the peak temperature is longer. As shown in Figure 7, when the HVCE time of the hydrogen/air vapor cloud is 500 ms, the flame temperature reaches 920.2 K. At this time, the maximum temperature of the flame is much lower than that of the vapor cloud near the hydrogen storage tank because the concentration of the hydrogen vapor cloud at this location is relatively low. When a HVCE occurs at nearly 1000 ms, the peak temperature of the flame produced by a HVCE reaches approximately 1040.5 K. The HVCE-driven flames have completely covered the photovoltaic panels in the horizontal direction. When a HVCE occurs at 3000 ms, the area covered by the flame has already exceeded the positions of the hydrogen storage tanks and photovoltaic panels in the horizontal direction. High temperatures formed by a HVCE are spherical, with a diameter of approximately 15.5 m. The peak temperature of the flame generated by a HVCE reaches 1255.5 K. After 4000 ms of a HVCE, the high temperature formed by the combustion flame has reached the regional boundary. The minimum temperature at the boundary at this time is 680.3 K. Compared with the thermal effect formed by igniting near the hydrogen storage tank, the thermal effect formed by igniting in the electrolytic cell is spherical. Analysis suggests that this is because the area near the hydrogen storage tank is less affected by the hydrogen jet.

Hydrogen leakage at the deep-sea FPHP platform causes HVCEs and generates intense thermal damage. The significant hazard of accidents is that high temperatures prompt structural melting and deformation. When there is electrical equipment on the spot, high temperatures and combustion will further cause larger-scale disasters. Due to the strong suddenness of HVCEs, flames and high temperatures generated within the near-ground range near the explosion source spread extremely fast, and the affected area is wide. The degree of thermal damage to structures within a certain range can be determined based on the high temperatures formed by a HVCE. Figure 8 demonstrates the variation trend of HVCE-driven flames from the ignition source near the inverter over time. As shown in Figure 8, thermal damage caused by the flames from ignition near the inverter is similar to the effect caused by ignition near the electrolytic cell. When a HVCE occurs for nearly 500 ms, the peak temperature of the flames reaches approximately 1100 K. The high temperature of the flames formed by a HVCE will melt the inverter. At 1000 ms after a HVCE occurred, flames produced by the explosion had completely covered the photovoltaic panel area. The peak temperature of the flames produced by a HVCE goes up to about 1640.2 K, and the minimum temperature at the boundary is approximately 920.7 K. When the explosion of hydrogen gas transportation occurs in 2000 ms, the flames continue to spread outward and horizontally, with a diameter of over 20 m. After 4000 ms of a HVCE, flames spread over the local area boundary of the FPHP platform. Compared with the above conditions, the peak time of the ignition condition in the inverter area is in the middle of the two, and its peak temperature is also in the middle of the two, which corresponds to the concentration of the hydrogen at each point after leakage. The local deflagration and instantaneous high temperature caused by the failure of the hydrogen storage tank both result in local or overall permanent deformation of the structure within a certain range of the sea surface platform. For structural materials in offshore areas far from the explosion source, their performance is damaged and deteriorated due to HVCE-driven high temperatures. Furthermore, the high temperature of the flames reduces the safety of the structures, such as masonry, and shortens their service life. In addition, high-temperature flames generated by HVCEs cause on-site workers to suffer burns of varying degrees, and in severe cases, even direct death.

This study numerically simulated a HVCE that was triggered by two distinct ignition sources within the deep-sea FPHP platform: the static electricity and the hot surface that was induced by equipment overheating. Comparative analysis reveals significant differences between these ignition mechanisms in terms of the triggering processes, energy transfer modes, and consequence profiles. For such offshore FPHP platforms, the hydrogen storage tank area constitutes the primary at-risk zone for electrostatic ignition, where friction-induced static charges may accumulate despite the humid marine environment. Conversely, regions surrounding high-temperature equipment (e.g., electrolyzers and compressors) are susceptible to hot-surface ignition. Notably, seawater cooling proves inadequate to significantly dissipate heat from these surfaces.

In electrostatic ignition scenarios, a spherical flame kernel develops at the spark location, progressing readily to detonation within the turbulence fluctuation of hydrogen/air vapor clouds. The resulting HVCE-driven fireball envelops the entire hydrogen/air vapor cloud with instantaneous thermal radiation. The peak temperatures reach 2200–2800 K, and the time of duration is less than 500 ms. The detonation generates shockwaves propagating at a velocity of 2000 m/s, with the peak overpressure at the epicenter measuring between 8.5 bar and 10.0 bar. In the hot-surface ignition scenarios, the results indicate that the localized combustion effects dominate. The hydrogen adjacent to the hot surface ignites, forming discrete fireballs of HVCEs. The subsequent flame spread and thermal radiation transfer are strongly influenced by buoyancy-driven hydrogen dispersion. It is found that the localized temperatures attain 1500–2000 K, with duration scaling with the hydrogen release time (seconds to tens of seconds). Flame propagates along the hot surface as columnar-shaped jets, exhibiting HVCE-driven deflagration characteristics. In addition, the results indicate that the subsonic flame speeds (3–50 m/s) in deep-sea FPHP platforms generate HVCE peak overpressures of approximately 4.5 bar.

3.3. Shock Wave Propagation of Hydrogen Explosion by Elevated Sea Surface Wind Intensity

When a hydrogen leakage accident occurs in a deep-sea FPHP platform, there is a coupling relationship between the occurrence area and the sea surface wind velocity. The concentration distribution and influence range of leaked gas in a complex layout area show an irregular situation. To explore the influence of sea surface wind velocity on the hydrogen leakage process of the FPHP platform, accidental scenarios with different sea surface wind velocities, such as 0 m/s, 5 m/s, 10 m/s, 15 m/s, and 20 m/s, are conducted, and phased analyses are carried out on the hydrogen dispersion behavior within the platform. The first stage is the change in initial hydrogen leakage and dispersion behavior of the hydrogen storage tank when the sea surface is calm, as shown in Figure 9. The second stage is a variation in the hydrogen dispersion range under different sea surface wind velocities after a period of time since the hydrogen storage tank failure, as shown in Figure 10. In the early stage of a hydrogen leakage accident, the sea surface wind velocity mainly acts on the hydrogen concentration distribution near the rupture source. In an accident scenario without the influence of sea surface wind force, hydrogen releases at high velocity will not only move forward rapidly along the centerline of the hydrogen jet but also spread around the leakage point of the hydrogen storage tank. 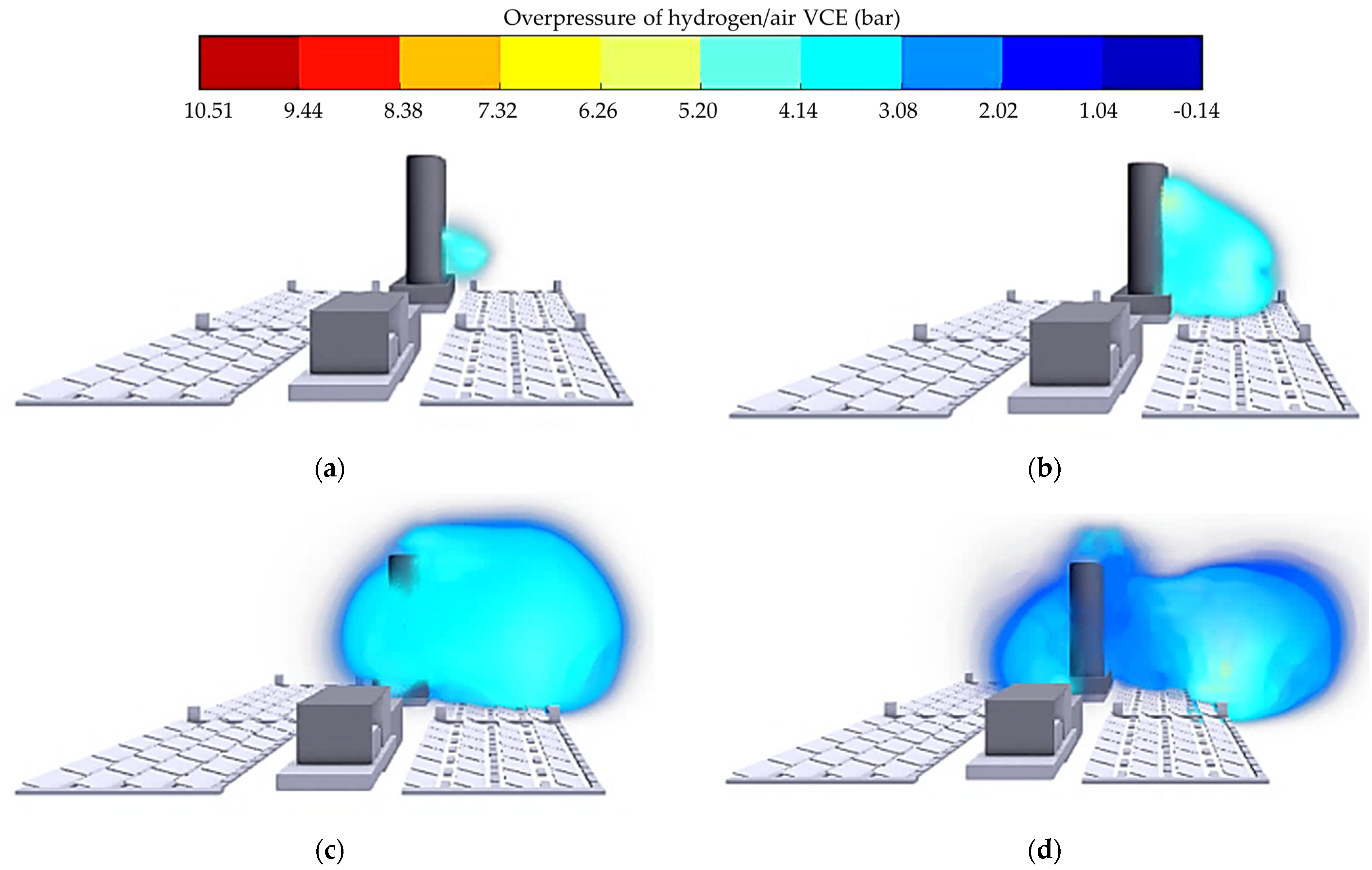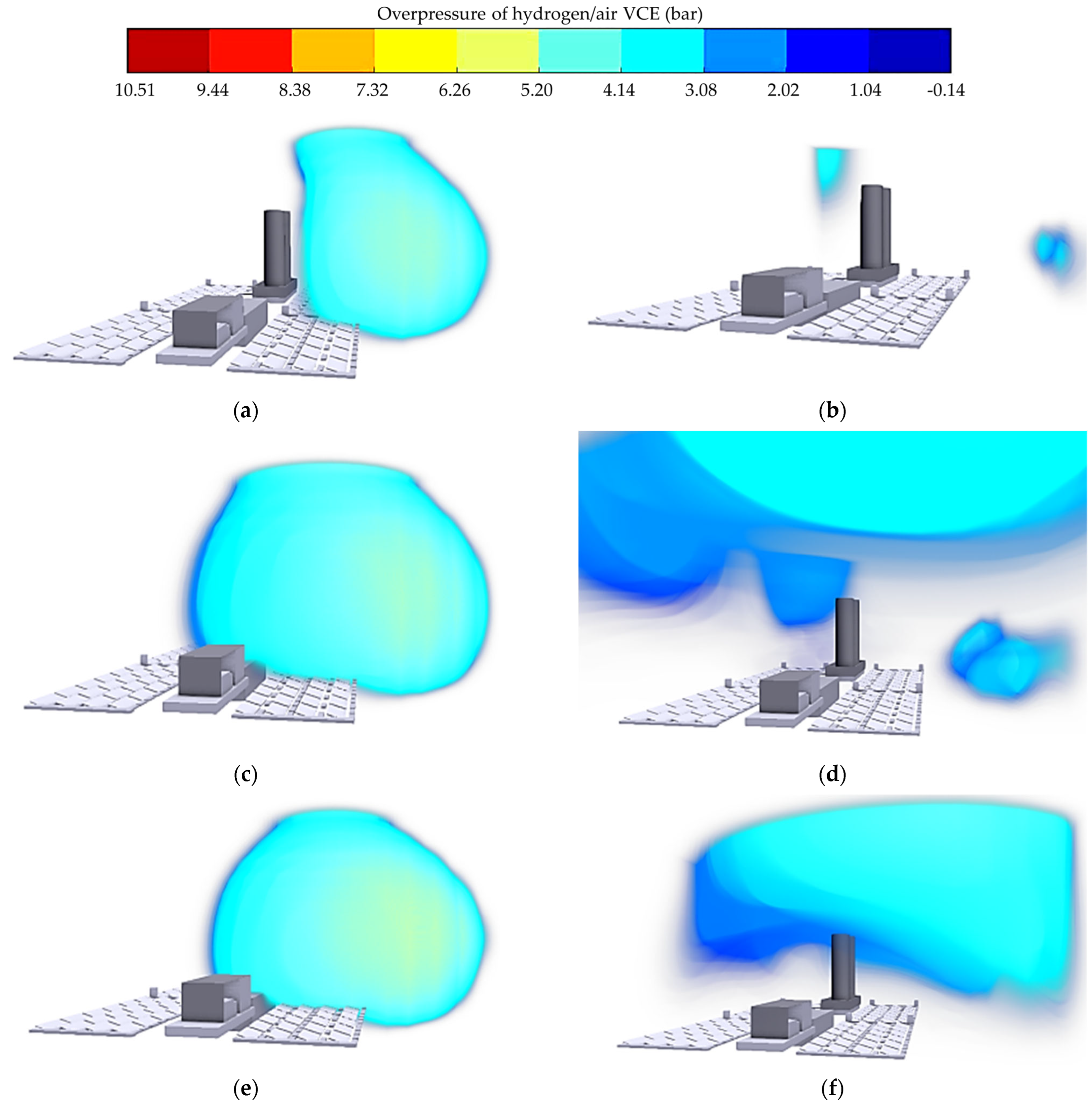Figure 9 indicates the variation trend of the overpressure of a shock wave generated by a HVCE over time after hydrogen leaked horizontally for 25 s and ignited under a windless force on the sea surface. At 500 ms after the HVCE occurs, overpressure begins to spread outward from the hydrogen storage tank, as shown in Figure 9. Overpressure near the hydrogen storage tank is high, and the diameter of the explosion range is around 5.4 m, which is relatively small. When a HVCE occurs at 1000 ms, the explosion diameter increases to 10.7 m. The shock wave reaches the vicinity of the photovoltaic panels. The overpressure near the photovoltaic panel is 3.4 bar, and peak overpressure reaches approximately 3.7 bar. When the occurrence time of a HVCE is 1500 ms, the range of the shock wave completely covers the hydrogen storage tank and photovoltaic panel area. The range of the shock wave reaches its maximum and spreads in a spherical pattern. When a HVCE occurs at 2000 ms, the shock wave spreads in all directions, and overpressure gradually decreases as the distance increases.

As the sea surface wind velocity increases to 10 m/s, the hydrogen concentration changes towards the area outside the deep-sea FPHP platform decreases. The movement of the hydrogen vapor cloud is still not significant. As the sea surface wind velocity further increases to 15 m/s and 20 m/s, the area of the hydrogen vapor cloud along the vertical direction gradually shrinks, and the dispersion height in vertical space begins to show a significant downward trend. When the sea surface wind velocity increases to 10 m/s, it reaches a Grade 5 wind standard. Due to the constraints of wind conditions, the hydrogen jet at the rupture point of the hydrogen storage tank mainly spreads along the near-surface after emerging. Figure 10a,d show the variation trends of the overpressure generated by a HVCE over time after hydrogen leaks horizontally for 25.0 s under a wind velocity of 10 m/s and is ignited. When the occurrence time of a HVCE is 500 ms, the diameter formed by the shock wave is over 10.5 m, which is larger than the range of the shock wave in a windless state, and the maximum hyperpressure reaches 3.8 bar. When the occurrence time extends to 1750 ms, the range of the shock wave further enhances. However, due to the influence of wind force, the shock wave begins to propagate along the wind direction, with peak pressure reaching 3.6 bar and a dispersion diameter being approximately 14.9 m. Compared with a windless situation, the action range of the shock wave is larger, and the shock wave forms an overpressure of 3.4 bar at the photovoltaic panel. Meanwhile, the shock wave propagated horizontally under the influence of the wind force and, instead, moved away from the hydrogen storage tank. After the occurrence time of a HVCE exceeds 1750 ms, the shock wave further spreads along the wind direction under the influence of wind velocity, moves away from the photovoltaic panel and reaches the regional boundary. The dispersion distance extends to the maximum value. With an elevated wind velocity (nearly 10 m/s), it can significantly affect the propagation range of the shock wave. It makes the shock wave propagate along the wind direction, away from the hydrogen storage tank and photovoltaic panels, and to a certain extent, reduces the occurrence of further disasters in this area. In practical design for safety protection, coupling effects between differential hydrogen dispersion characteristics and enhanced wind conditions should be systematically considered. Traditional mist curtain systems exhibit limited efficacy under the above accidental scenarios, necessitating integration with porous energy-absorbent materials. Obstacles inadvertently amplify the shock wave propagation and resultant destruction, which requires identifying critical obstacle locations for retrofitting with inert gas-purging systems to mitigate cascading hazards.

When the sea surface wind velocity increases to 15 m/s, enhanced wind conditions limit the ability of hydrogen vapor clouds to draw air in all directions, prompting hydrogen vapor clouds to move downwind, thus expanding the distance of hydrogen dispersion. Figure 10b,e show the variation trends of overpressure generated by a HVCE over time when the wind velocity is 15 m/s. With the occurrence time of a HVCE being 500 ms, compared with a wind velocity of 10 m/s, its explosion range is wider. Shock wave propagation can reach 20.1 m horizontally and 15.3 m vertically. When the occurrence time of a HVCE is 1750 ms, the shock wave accumulates above the area after the hydrogen explosion. Compared with the sea surface wind velocity of 10 m/s, the shock wave does not propagate along the wind direction. Instead, a high wind velocity suppresses the flow of hydrogen vapor clouds. Figure 10c,f demonstrate the variation trends of the overpressure generated by a HVCE over time when the sea surface wind velocity is 20 m/s. The peak overpressure of a HVCE increases to 3.7 bar, and the overpressure near the photovoltaic panel reaches 3.4 bar. The arrival time of the shock wave is earlier than that when the wind velocity is 15 m/s. When the occurrence time of a HVCE is 1750 ms, the explosion range is maximum at this time. The shock wave propagates along the horizontal direction for a distance of 20.1 m and a longitudinal height of 15.2 m. The results indicate that when the sea surface wind velocity goes up to 10 m/s, the influence range of overpressure expands significantly. Meanwhile, the propagation velocity of the shock wave has also significantly accelerated. When the sea surface wind velocity exceeds 15 m/s, the greater sea surface wind velocity limits the range of the shock wave. Due to the enhanced wind conditions, the vertical spatial dispersion of the hydrogen/air vapor cloud is restricted. It leads to confining more vapor clouds to perigee, thereby enhancing the destructive effect of the shock waves on equipment. Upon wind velocities exceeding critical thresholds at sea level, initially, the promotional effect on shock wave propagation transitions to measurable suppression. This phenomenon necessitates dynamic adaptation of monitoring equipment positioning on FPHP platforms, corresponding to the migration of peak destruction epicenters under marine environmental forcing. A synergistic protection strategy is implemented whereby annular water curtains (over 200 L/min·m² coverage intensity) automatically engage when wind velocities surpass 15 m/s to obstruct hydrogen dispersion pathways. In addition, the system monitors directional variance rates, triggering immediate nano-aerosol suppressant injection when the fluctuation exceeds 45°/min to achieve flame front-quenching and propagation arrest.

The TNT equivalent method assumes an energy equivalence between flammable material and TNT [45,46]. The equivalent mass of TNT is calculated using Equation (7), derived from the total heat of material combustion.

$$W_{TNT}={\displaystyle \frac{\eta W{Q}_c}{Q_{TNT}}},$$

(7)

where η denotes the empirical explosion efficiency, W is the mass of flammable material, Q_c is the heat of combustion of flammable material, Q_TNT is the heat of combustion of TNT, and W_TNT is the mass of TNT (kg).

For gaseous deflagrations, η typically ranges from 2% to 15%. The explosion effects are assessed using experimental data that are scaled to the equivalent mass of TNT W_TNT. Within this framework, scaled distance Z is defined by Equation (8), enabling practical computational implementation.

$$Z={\displaystyle \frac{R}{{W_{TNT}}^{1/3}}},$$

(8)

where R is the distance from the central point of the gas explosion.

The prediction is given as semi-empirical curves on the coordinate system of scaled distance Z and maximum overpressure P_m. Henrych [47] proposed one of the most common attenuation laws for shock wave induced by gas explosion in free-field which is expressed as the following equation.

$${\left.{\mathsf{\Delta }P}_m\right|}_{Henrych}=\left\{\begin{array}{c}{\displaystyle \frac{14.072}{Z}}+{\displaystyle \frac{5.54}{Z^2}}-{\displaystyle \frac{0.357}{Z^3}}+{\displaystyle \frac{0.00625}{Z^4}} if 0.05\le Z \le 0.3\\ {\displaystyle \frac{6.194}{Z}}-{\displaystyle \frac{0.326}{Z^2}}+{\displaystyle \frac{2.132}{Z^3}} if 0.3\le Z \le 1\\ {\displaystyle \frac{0.662}{Z}}+{\displaystyle \frac{4.050}{Z^2}}+{\displaystyle \frac{3.288}{Z^3}} if 1 \le Z\end{array}\right.,$$

(9)

Mills [48] investigated the applicability of Sachs’ scaling law to gas explosions in an unconfined environment at overpressures of up to 0.1 MPa. By integrating similarity theory and numerical methodology, he proposed a refinement of established free-field overpressure decay laws through the modification of evaluation distance. This approach yields a modified overpressure–distance decay relationship related to the TNT explosion-driven shock wave, as shown in Equation (10). The theoretical framework established above enables a quantitative assessment of physical explosion in a gas leakage scenario. The accuracy and applicability of the proposed model are empirically validated against full-scale experimental data.

$${\left.{\mathsf{\Delta }P}_m\right|}_{Mills}={\displaystyle \frac{0.108}{Z}}-{\displaystyle \frac{0.114}{Z^2}}+{\displaystyle \frac{1.772}{Z^3}}$$

(10)

Figure 11 shows the overpressures on the photovoltaic panels and inverters after HVCE occurs in the deep-sea FPHP platform. If the influence of enhanced wind force on the sea surface is not considered, the evolution law of the shock wave generated by the explosion conforms to the overpressure–distance decay relationship proposed by Mills. With an increase in sea surface wind velocity, turbulence induced by high wind velocity enhances the reaction rate of combustion, causing peak overpressure to rise for a period of time. Therefore, the wind velocity on the sea surface will affect the intensity of the shock wave. Figure 11a presents the overpressure effect of a HVCE-driven shock wave on a photovoltaic panel structure in the FPHP platform under the influence of different sea surface wind velocities. It can be seen from the figure that the enhancement of sea surface wind force has a significant impact on the action time of the shock wave. In an accident scenario where sea surface wind velocity is less than 5 m/s, the effect trend of a HVCE-driven shock wave on a photovoltaic panel structure is relatively consistent. With a low sea surface wind velocity, the time when the first peak overpressure occurs in the photovoltaic panel-laying area is approximately 1084 ms. In an accident scenario of low sea surface wind velocity, peak overpressure shows 2.476 bar. At this point, brick structures are 50% destroyed, and self-restraining steel structures are destroyed in the low sea surface wind velocity case. Under the effect of secondary shock wave propagation, the photovoltaic panel-laying area formed a second peak of overpressure. The overpressure data relatively decreases, with a value of 0.271 bar. When the sea surface wind velocity moved to 10 m/s, the time when the first overpressure peak occurred did not change significantly. In a scenario of high sea surface wind velocity, the peak overpressure data that were monitored in the photovoltaic panel area increased to 2.112 bar. Since an increase in sea surface wind velocity has a significant impact on the dispersion range of a hydrogen vapor cloud, the variation law of overpressure also changes. It can be known from Figure 11a that when the sea surface wind velocity increases to 15 m/s, the rising rate of pressure was monitored in the area where the photovoltaic panels were laid decreases. The occurrence time of peak overpressure is prolonged compared with the accident scene under weak wind conditions, and the maximum overpressure is approximately 1.461 bar. If the sea surface wind velocity continues to increase to 20 m/s, the findings indicate that the area where the photovoltaic panels are laid is less affected by HVCE-driven shock waves. The peak overpressure of the shock wave is only 0.249 bar.

Figure 11b shows the variation trend of the shock waves generated by a HVCE near the inverter under different sea surface wind velocities. The propagation process of the shock wave near the inverter is affected by wind conditions on the sea surface. Meanwhile, due to a greater number of obstacles around the inverter, overpressure fluctuates to varying degrees over time. Under weak wind conditions on the sea surface, the peak overpressure formed by the shock wave around the inverter is 3.701 bar. Severe displacement of the steel structure is triggered, or serious damage to earthquake-proof structures occurs. When the sea surface wind velocity reaches 10 m/s, a shock wave generates the first peak overpressure at the inverter, and the overpressure is approximately 2.079 bar. Subsequently, overpressure shows a decreasing change until secondary peak overpressure (P_m = 1.251 bar) occurs at 3871 ms after the explosion. As the sea surface wind velocity increases to 15 m/s, the peak overpressure time formed by the shock wave around the inverter is delayed. However, the duration of peak overpressure relatively increases, and the average overpressure remains at around 1.521 bar. If strong wind conditions occur on the sea surface, the overpressure data monitored around the inverter are relatively small. As shown in Figure 11a, the maximum overpressure that can be generated in this accident scenario is 0.427 bar. Without concrete, slab-brick structures with a thickness of 0.2–0.3 m are broken, and the building is almost completely destroyed. The results reveal that the enhancement of wind force promotes a shortening of time for the shock wave to reach peak overpressure, and the peak value shows a significant increase. However, this research also finds that with an increase in sea surface wind velocity, the peak overpressure effect generated after a HVCE is weakened somewhat, and the effect time is continuously delayed in the FPHP platform.

4. Conclusions

This current study extensively examines the damage effects of a hydrogen–air vapor cloud explosion with multifactor scenarios on a deep-sea floating photovoltaic hydrogen production platform through numerical simulations. The hydrogen release diameters varied from 25–100 mm for an individual effect and 0–20 m/s each for a combined wind effect, and were analyzed to illustrate the damage mechanism induced by a HVCE around the deep-sea FPHP platform. In conclusion, the main insights are as follows:

• The critical content of failure rupture is related to the unconfined hydrogen vapor cloud range. As the rupture diameter increases, the high-concentration range of hydrogen/air mixtures decreases in the horizontal direction due to the fluctuation in the rupture pressure drop rate; however, this remains almost unchanged with the limited increase in vertical space.
• The increases in wind intensity accelerate the hydrogen dilution process and effectively reduce the spatial proportion of high concentration in hydrogen vapor clouds. As a critical threshold of shock wave suppression effect with the wind velocity beyond 16 m/s is captured, hydrogen accumulates between devices (e.g., PV panels and inverters). A synergistic protection strategy is implemented whereby annular water curtains automatically engage when the wind velocities surpass 15 m/s to obstruct the hydrogen dispersion pathways.
• Comparison of flame spread behaviors with different ignition positions (e.g., close to storage tank, PV module, and inverter), proximal to storage tanks, led to rigorous protection protocols that were imperative due to the potential for catastrophic large-scale damages, whereas the PV module or inverter zones necessitate preventive measures, targeting electrical ignition sources as primary detonation initiators.
• Subsequent shock wave propagation is strongly influenced by buoyancy-driven hydrogen dispersion across the sea surface wind intensity. Under meteorologically stable marine conditions with minimal wind variability, overpressure effects on FPHP platforms are significantly amplified, establishing hazards as the safety design consideration for protection systems.
• For future research, the proposed safety recommendations have potential applications in addressing multi-stage decision-making problems, particularly where the FPHP system design and emergency operations are predefined. The findings are especially useful in scenarios characterized by numerous design parameters and significant uncertainties. Differentiated safety protocols must address distinct hazard mechanisms, as well as the physical impacts that require containment-specific countermeasures, while chemical ignition risks demand fundamentally different mitigation strategies. The optimal designs proposed in Section 3 inherently embody this compartmentalization philosophy, providing tailored protection that is aligned with zone-specific vulnerability profiles.
• This study provides a valid analysis of wind velocity magnitude variations over marine environments. A limitation of this study is the exclusion of FLACS-based model mismatches, which are critical in actual FPHP applications. Currently, the simulation framework prescribes constant wind velocities and invariant directional vectors, deviating from real-world transient wind dynamics. Furthermore, multi-physics coupling between hydrogen dispersion and fluctuating sea surface temperature/humidity gradients remains unexplored. These identified limitations constitute priority investigative vectors for subsequent research extensions in the future.