Abstract
A comprehensive 3D Multiphysics model was developed to simulate a plate fin heat exchanger designed for hydrogen liquefaction, incorporating an ortho-para hydrogen conversion catalyst in the hot fin channel. The model encompassed the 3D serrate fin structure, turbulent flow within the cold fin channel, and porous flow through the catalytic hot fin channel. Species transportation within the hot fin channel is coupled with ortho-para hydrogen conversion kinetics, while heat transfer mechanisms between the hot and cold fin channels are rigorously accounted for. Additionally, the state-of-the-art equation of state is employed to accurately describe the thermodynamic properties of ortho- and para-hydrogen within the model. Numerous operational parameters, including the gas hourly space velocity, cold gas velocity, ortho-para hydrogen conversion kinetics, and operating pressure, were systematically varied to identify the kinetic and heat transfer constraints during the heat exchanger operation. The findings revealed that the ortho-para hydrogen conversion kinetic parameter predominantly governs operations requiring high gas hourly space velocity, particularly in large-scale hydrogen liquefaction processes. Furthermore, a significant pressure drop within the catalytic filled channel was observed; however, operating at higher pressure mitigates this issue while mildly enhancing ortho-para hydrogen conversion kinetics.
1. Introduction
Liquid hydrogen (LH2) plays a pivotal role in large-scale and long-distance storage and the distribution of hydrogen, despite its inherent challenges of high energy consumption [1]. A significant aspect of this challenge relates to the ortho- to para-hydrogen conversion (OPC) during the liquefaction process. At ambient temperatures, hydrogen gas consists of 75% ortho-hydrogen and 25% para-hydrogen. However, at the normal boiling temperature of LH2 (20.3 K), the equilibrium shifts dramatically with para-hydrogen concentration reaching 99.8%. To reduce boil off so that long term storage of LH2 is achievable, the ortho-hydrogen must be converted to para form in the presence of a catalyst during the hydrogen liquefaction process. Otherwise, the heat generated due to the exothermicity of the OPC leads to an increase of LH2 evaporation, since the enthalpy difference between ortho- and para-hydrogen exceeds the latent heat of LH2 evaporation [2].
To improve the energy efficiency of hydrogen liquefaction, a continuous cooling during the OPC process has been suggested by Lipman [3] based on the thermodynamic principle that power requirements are minimized by removing heat at the highest possible temperature. Modelling results also suggest that the specific energy consumption for continuous-conversion based process is 21.8% and 28.7% lower than the adiabatic and isothermal ones [4]. This continuous cooling approach is commonly implemented in practical commercial processes using catalyst-filled plate-fin heat exchangers (CPFHEs) [5,6].
Plate-fin heat exchangers (PFHEs) are extensively utilized in cryogenic applications due to their high specific surface area and compactness [7]. Typically constructed from aluminium for its excellent thermal conductivity and strength at cryogenic temperatures, PFHEs employ a configuration of fins and parting sheets to create separate flow passages for hot and cold media. The theoretic analysis of PFHEs has been well established [8,9]. The introduction of a catalyst into PFHEs, however, complicates the design in several ways. Firstly, catalyst filling alters the heat transfer characteristics of the heat exchanger within the hot flow channel. Secondly, the OPC, an exothermic reaction, introduces varying kinetics along its path, thereby increasing the thermal load on the heat exchanger. Thirdly, the catalyst-filled hot channel acts as a packed-bed chemical reactor, constrained by the kinetics of the OPC. Given the increased complexity of CPFHEs, mathematical modelling approaches are commonly employed for theoretical analyses and design optimization.
Early efforts in modelling CPFHEs were pioneered by Meagher [10], who applied classic correlations for heat transfer and pressure drop in both the open passage (cold channel) and catalyst-filled passage (hot channel) of a CPFHE. His work utilized a simplified one-dimensional finite difference approach coupled with a logarithmic model of OPC kinetics based on Hutchinson et al. [11], providing initial insights into the prediction of the hydrogen liquefaction process. Wilhelmsen et al. [12] presented a steady-state one-dimensional mathematical model that incorporates the geometry of the heat exchanger, nonequilibrium ortho-para conversion, and correlations to account for the pressure drop and heat transfer coefficients due to the possible boiling/condensation of the refrigerant at the lowest temperatures. Based on available experimental data, a kinetic model with four parameters was developed. This approach achieved a close prediction of experimental data with an average deviation of 2.2%. Donaubauer et al. [13] developed a pseudo-homogeneous model for the CPFHE, considering energy balance, mass balance, and momentum balances. Kinetic models based on first-order and Langmuir-Hinshelwood approaches were derived and confirmed the first-order approaches as the most suitable model. Park et al. [14] studied CPFHEs numerically by developing a model including the continuity equation, momentum equation, and energy equation to describe the fluid flow and heat transfer. The numerical model provided insights into pressure drop mechanisms in the porous region filled with an ortho-para catalyst through the development of a new correlation. O’Neill et al. [15] developed a comprehensive one-dimensional mathematical model that included OPC kinetics, heat transfer dynamics, and pressure drop considerations with more precise accounting for catalyst fraction effcorreects. The results suggest that the outlet parahydrogen fraction is determined to be about 10 times more sensitive to the reaction rate relative to heat transfer.
Despite these advancements, existing models for CPFHEs predominantly remain one-dimensional, with separate descriptions of controlling physics based on classic correlations. In this case, the mechanisms of flows (turbulent flow in open channel and porous flow in catalyst-filled channel), heat transfer between the channels and parting sheets, and OPC kinetics are determined separately and how these mechanisms interact with each other is not fully understood.
Recently, a pioneering 3D model based on ANSYS® Fluent® has emerged [16], aiming to capture the complex flow and heat transfer processes within CPFHEs. The flow and heat transfer process of hydrogen in the cold sides is described by the mass conservation equation, momentum conservation equation, and energy conservation equation. However, to simplify the flow and heat transfer process in the hot channel, the porous media model and Ergun equation were applied in the model. The equation of state (EoS) of ortho-parahydrogen was also fitted with piecewise polynomial functions. The flow and heat transfer performance and the efficiency of OPC in the CPFHE were quantitatively evaluated, and the effects of the structural parameters of fins on the flow and heat transfer coupled with the OPC are analysed. Zhu et al. [17] established a three-dimensional model of the CPFHE and revealed the local thermal non-equilibrium effect in the heat exchanger, which is most significant at the inlet of the porous medium, while the fluid and the solid reach an approximately thermal equilibrium in the fully developed section inside the heat exchanger. The model also suggests that excellent heat transfer performance and catalytic efficiency can be achieved when the Reynolds number is in the range of 170 to 300.
The simulation of a practical plate fin heat exchanger filled with an ortho-para hydrogen conversion catalyst presents significant challenges due to its multifaceted nature involving multiple physics phenomena. These include turbulent flow in the cold channel, porous flow and the OPC catalytic reaction in the catalyst-filled hot channel, and heat transfer between the cold and hot channels. The complexity is further compounded when these flows are coupled within a three-dimensional structure. Nevertheless, this comprehensive approach is indispensable for elucidating the controlling mechanisms governing the operation of the CPFHE.
To address these challenges, thisstudy have employed COMSOL Multiphysics® 6.2 software, a versatile simulation platform capable of fully coupled Multiphysics modelling, to establish a 3D-based CPFHE model. This work aims to predict the overall performance of CPFHEs while exploring the impact of two primary controlling mechanisms—i.e., OPC kinetics and heat transfer dynamics. This endeavour not only provides valuable insights into CPFHE operation but also lays the groundwork for future advancements towards optimizing CPFHE designs.
2. Three-Dimensional Modelling
2.1. PFHE Geometry
The 3D geometry of a primitive serrated fin with front and back fins is shown in Figure 1a. To characterise the serrated fins, there are four dimensions to be considered, which are fin altitude (ac), fin thickness (tc), fin spacing (sc), and serration length (lc). The stagged length of front and back fin (ls) is half of the fin spacing. It is not the intention for this study to optimize these structure parameters of fins for improved heat transfer performance, so all the structure parameters are taken from the literature [10] without changes.
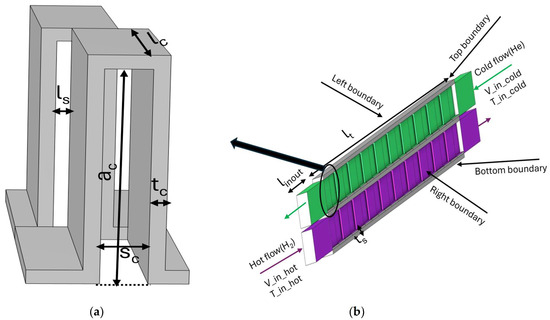
Figure 1.
(a) Primitive serrated fin structure; (b) 3D structure of PFHE formed from the primitive serrated fin.
Figure 1b illustrates the 3D configuration of the PFHE constructed using periodic arrangements of these primitive serrated fins. The PFHE incorporates double-layered flow channels for the cold and hot media, separated by parting sheets with a thickness of ts. In this configuration, both the hot and cold channels share identical structural parameters for the fins. To ensure well-developed flow within the heat exchanger, the total effective length (lt) of the heat exchanger is set as 20 times of the serration length. Additionally, to minimize inlet/outlet flow end effects, free-flow zones extending to 2.5 times the serration length (linout) are incorporated before and after the flow path separately, as suggested by Xu et al. [16]. The structure is shown in Figure 1b. Detailed dimensions of the structural parameters are provided in Table 1, resulting in a highly specific heat transfer area of 1857 m2/m3

Table 1.
Structure parameters of the PFHE.
2.2. Model Description
The mathematical model for the CPFHE is developed under the following specified conditions:
- (1)
- The cold channel operates with helium as the working fluid, while hydrogen is used on the hot channel. The hydrogen is a mixture of ortho- and para-form with the given concentration.
- (2)
- The catalyst particles are uniformly filled exclusively in the hot side of fin channel, maintaining fixed porosity and permeability in the catalyst bed.
- (3)
- Both the flow dynamics and heat transfer in the cold and hot channels, as well as the OPC kinetics in the hot channel, are assumed to be at steady state.
The modelling approach for the CPFHE involves solving a set of governing equations.
- (1)
- Mass and momentum conservation equations: These equations describe the flow behaviour in both the cold and hot channels separately, accounting for their distinct flow characteristics.
- (2)
- Species transport equation: This equation governs the transport of ortho- and para-hydrogen species in the hot channel with consideration of the OPC kinetics.
- (3)
- Heat transfer equation: This equation governs the transfer of heat between the cold and hot channels and the parting sheet, taking into account the enthalpy changes due to the OPC reaction.
The problem is a typical multiphysical simulation in computational modelling where different aspects of a physical systems were needed to be integrated, and the interactions among them was required to be handled. In order to achieve this, the simulations were conducted using the commercial software package COMSOL Multiphysics® 6.2. The software provides a robust platform for integrating and solving these multi-physics phenomena. A brief introduction of the theory for modelling and selection of physics interfaces from the software are given in the following sections, and a detailed description can be found elsewhere [18].
2.2.1. Flow Characteristics
Due to the different nature of flow patterns, fluid flow in the hot and cold channels were treated separately. The fluid dynamics inside the cold channel of the CPFHE was modelled using the Navier–Stoke equation. The continuity equation and momentum equations were given as
Since the flow in the cold channel is in the turbulent flow range, the standard k-epsilon (k-ϵ) model for turbulence flow was adopted, as given by
The value of constant is given as = 0.09, = 1.00, = 1.3, = 1.44, and = 1.92.
Due to the presence of catalyst particles in the hot channel of CPFHE, the fluid flow was modelled as porous medium flow and was given by the Brinkman equation, which extends Darcy’s law to describe the dissipation of the kinetic energy by viscous shear, similar to the Navier–Stokes equations.
The built-in physical interfaces in COMSOL as turbulent flow (spf) and free and porous flow (fp) were selected accordingly. Both flows are treated as compressible flows with Mach numbers less than 0.3. The velocity field and pressure profile are the dependent variables for both channels and will be solved separately.
2.2.2. Species Transportation
The chemical species (ortho- and para-hydrogen in this simulation) present inside the hot channel are subject to diffusion and convection, in addition to the OPC chemical reaction. The species transportation equation is given as
The mixture averaged approximation model is selected in calculating the diffusion model, given as
The conversion of orthohydrogen (H2,o) to parahydrogen (H2,p) is exothermic and is described by the following:
H2,o ⇌ H2,p ΔH = −Qconv
Kinetic models selected from the literature will be tested and applied to calculate the reaction rate (R), while the heat of reaction will be calculated from the equation of state of ortho- and para-hydrogen. These will be discussed in the next section.
The built-in physical interfaces in COMSOL as Transport of Concentrated Species (tcs) and Chemistry (chem) were selected for modelling. The mole concentrations of species are the dependent variables and will be solved.
2.2.3. Heat Transfer
Without considering the work undertaken by pressure change and viscous dissipation, the heat transfer equation following energy balance is given as
The built-in physical interfaces in COMSOL, i.e., heat transfer in solids and fluids (ht), were selected, where the porous medium property has been also added to the physics in describing the heat transfer in the porous media. To simplify the model, the viscous dissipation during the flow is not considered in the energy balance. The temperature is the dependent variable and will be solved.
2.2.4. Multiphysics Coupling
When the previous individual physical interface was set up, it was identified that these physical interfaces are Multiphysics in nature—i.e., the heat transfer physics (ht) is coupled with the velocity field of the cold and hot channels, which were calculated from two flow physics (spf and fp). In this case, the nonisothermal flow Multiphysics interfaces in COMSOL are being enabled. Two nonisothermal flow Multiphysics coupling (nitf1, nitf2), which coupled the spf and ht and fp and ht, were added into the model.
2.3. Material Property
Aluminium was selected as the material of construction for the fins and parting sheet in the model in order to mimic the actual industrial liquefaction process. The catalyst used is hydrous ferric oxide, commercially available under the trade name Ionex® [19]. The physical properties of the material are given in Table 2.

Table 2.
Physical properties of solid materials used in the model.
Accurately determining thermophysical properties such as densities, viscosities, and thermal conductivities of fluids, including both cold (helium) and hot (hydrogen) media, is crucial for the precise simulation of the hydrogen liquefaction process.
State-of-the-art EoS for para-hydrogen, ortho-hydrogen, and normal hydrogen were developed by Leachman et al. [20]. The EoS is implemented in the thermodynamic property package, namely RefProp®, which was developed by the National Institute of Standards and Technology (NIST) [21]. It provides comprehensive thermodynamic property data necessary for modelling cryogenic processes accurately.
In this work, helium is selected as the cold media to cool hydrogen down to cryogenic temperature and facilitate the ortho- to para-conversion. The thermodynamic properties of helium are also obtained from RefProp® to ensure consistency and accuracy in the simulation model.
Due to the absence of a direct interface between COMSOL Multiphysics® and RefProp®, a CAPE-OPEN interface [22] was utilized. This interface facilitates seamless interoperability between COMSOL Multiphysics® and RefProp®, enabling the simulation software to access and utilize the thermodynamic properties calculated by RefProp®.
2.4. Boundary Conditions and Solver Setting
The CPFHE operates as a counter-current model for hot and cold fluids. A practical heat exchanger can involve multi fins in the width direction. Due to computation resource limitations, it is impractical to increase the number of fins in the width direction beyond what is shown in Figure 1b. Therefore, asymmetric boundary conditions are applied to the left and right boundaries, while periodic boundary conditions are applied to the top and bottom boundaries. In this way, the 3D structure can be expanded effectively without increasing the computation resources. The details are given in the list below.
Fluid Flow Calculation (spf and fp)
- Inlet Boundary: Normal inflow velocity is specified. The inlet velocity for the cold flow is denoted as V_in_cold and for the hot flow as V_in_hot.
- Outlet Boundary: Specified as a pressure boundary with suppressed backflow.
- Wall Boundary: Non-slip wall boundary condition is applied to all walls.
- Asymmetric Boundaries: Left and right boundaries are set as asymmetric to accommodate the flow dynamics.
Ortho-para hydrogen concentration calculation (tcs)
- Inlet Boundary: Specified as normal hydrogen consisting of 75% ortho-hydrogen and 25% para-hydrogen.
- Reaction Source: Includes a reaction source term considering the production of para-hydrogen from the OPC.
- Asymmetric Boundaries: Left and right boundaries are set as asymmetric to capture concentration gradients effectively.
Temperature calculation (ht)
- Inlet Boundary: Fixed temperature is specified. The inlet temperature for the cold flow is T_in_cold and for the hot flow is T_in_hot.
- Heat Source: Includes a heat source term accounting for the heat generated by the OPC reaction.
- Boundary Conditions: Left and right boundaries are set as asymmetric, while the top and bottom boundaries are set as periodic to simulate continuous heat exchange.
Solver Settings
- Dependent variable: A segregated solver is employed to solve for eight dependent variables, which includes pressure (P1), velocity (v1), turbulent dissipation rate (ɛ) and turbulent kinetic energy (k) for the cold channel, pressure (P2) and velocity (v2) for the hot channel, temperature (T) for the entire heat exchanger, and parahydrogen mass fraction (ω) in the hot channel.
- Relative Tolerance: A relative tolerance of 1E-3 is set for each variable to ensure numerical stability and accuracy.
3. Results and Discussion
3.1. Model Verification
3.1.1. Mesh Size Setting
COMSOL Multiphysics® utilizes the finite element method (FEM) for computation. In FEM calculations, the modelling space is discretized using a mesh, and the accuracy of the solution depends directly on the mesh size. A refined mesh leads to a solution that more closely approximates the true solution.
For the simulation, a user-controlled mesh was employed. Free triangular mesh with distribution was applied to the three parting sheets, while a free tetrahedral mesh was used for the flow domain. To accurately capture thin boundary layers along the no-slip boundaries in the fluid flow domain, a boundary layer mesh with dense element distribution for normal to selected boundaries was applied. The boundary layer consists of five layers with a stretch factor of 1.2.
A simple case was configured for the simulation. The case does not include the OPC reaction but has the following conditions:
- Both hot and cold flow inlet velocity set to V_in_cold = V_in_hot = 5 m/s;
- Hot flow inlet temperature, T_in_hot = 77 K and cold flow inlet temperature, T_in_cold = 60 K.
The results were obtained by solving the model with progressively finer meshes. Four different mesh sizes were tested:
- Coarse mesh with 890,000 elements;
- Normal mesh of 2.21 million elements;
- Fine mesh of 4.46 million elements;
- Finer mesh of 8.87 million elements.
All the mesh sizes can produce similar temperature distribution profiles of the PFHE, as showing in Figure 2a that are derived from the results of the fine mesh. This profile is characteristic of a counterflow heat exchanger. Uniform temperature differences between the cold and hot fluid along the flow path is evident, which is favourable for a uniform rate of heat transfer throughout the heat exchanger.
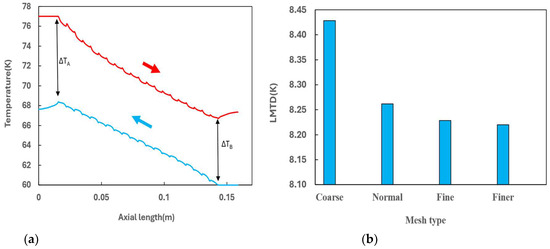
Figure 2.
(a) Temperature profile along the flow path for the hot ( ) and cold (
) and cold ( ) channels derived from fine mesh; (b) Effect of the mesh size on the logarithmic mean temperature difference.
) channels derived from fine mesh; (b) Effect of the mesh size on the logarithmic mean temperature difference.
 ) and cold (
) and cold ( ) channels derived from fine mesh; (b) Effect of the mesh size on the logarithmic mean temperature difference.
) channels derived from fine mesh; (b) Effect of the mesh size on the logarithmic mean temperature difference.
To facilitate the comparison of results from different mesh sizes, the logarithmic mean temperature difference (LMTD), which determines the temperature driving force for heat transfer in heat exchangers, was utilized.
LMTD is defined as
Figure 2b displays the LMTD changes with the mesh size. As the mesh becomes finer, LMTD starts to converge, showing negligible differences between the fine and finer meshes. Considering both the computation time and the accuracy of the results, the fine mesh with 4.46 million elements was selected for further studies. A snapshot of the fine mesh for the 3D model is shown in Figure 3.
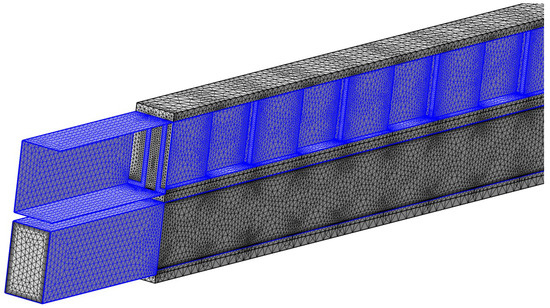
Figure 3.
Fine mesh used for model simulation; Note: two boundaries have been removed from the top channel to demonstrate the mesh inside the flow channel.
3.1.2. Verification of Heat Transfer
The performance of traditional PFHEs with serrated fin structures in the absence of catalysts have been extensive studied. The first objective of this study is to validate the developed model’s accuracy in term of the prediction of heat transfer performance and pressure loss of the PFHE.
To validate the modelling results, simulation cases were configured to calculate the overall heat transfer coefficient (U) of the heat exchanger. In the simulation, the gas velocity in the cold channel was varied, while the gas velocity of hot channel remained constant. U is calculated based on
The Colburn number (j) is commonly used to characterize the heat transfer performance. The Colburn number for serrated fins has been empirically correlated with the Reynold number of flow and the fin structure parameters, given as [23]:
The hydraulic diameter of the fin is used for calculating the Reynold number and is defined from fin structural parameters, given as
The heat transfer coefficient (h) for both the cold and hot channels can be derived from the Colburn number, which is given as
Given that the heat transfer areas in both the cold and hot channels are the same in the model, the overall heat transfer coefficient can be expressed as
Comparing the overall heat transfer coefficient between the simulated case (Us from Equation (14)) and the analytic correlation case (Ua from Equation (18)) provides an indication of the model’s accuracy. The comparison—varying the Reynolds number of the cold flow while keeping the Reynold number of hot flow fixed—is presented in Figure 4.

Figure 4.
Comparing the overall heat transfer coefficient derived from the numerical simulation and analytic correlation approach.
The model predicts that the overall heat transfer coefficient increases with the increase of gas velocity, with Us ranging between 70 to 110 W/m2·K across the specified Reynold number range of the cold flow. The reported heat transfer coefficient for forced convention in the PFHE typically ranges between 35 to 350 W/m2·K [24], and the model prediction falls within this range.
Quantitatively, however, the simulation results exhibit up to an approximately 30% discrepancy compared to the results derived from the analytical correlation (Ua). This discrepancy could be due to different reasons. On one side, the derivation of the correlated Colburn number with the Reynold number (Equation (15)) was originally developed for a steam-air system [24], where the wall temperature remains constant due to steam condensation—a condition significantly different from our cryogenic modelling system. On the other hand, the experimental data used for the derivation of the Colburn number correlation reports an error band of approximately 20% [23]. Considering these factors, the accuracy of the current model is deemed acceptable within practical engineering tolerances.
3.1.3. Verification of Pressure Drop
The model was further verified in terms of friction associated with pressure drops (Δp). To achieve this, a simulation case was established to calculate the pressure loss correlation with the gas flow Reynold number. In this simulation, the inlet gas velocity of the cold channel was varied, and the pressure loss (Δp) was computed. The Fanning friction factor (fF), a dimensionless number used to analyse fluid friction in pipes, can be determined from the pressure loss as
The fanning friction factor for serrated fins, correlated with the Reynolds number and fin structure parameters, has been derived from the literature [23], given as
The comparison of fF,s and fF,a is shown in Figure 5. The model predicts that fF,s decreases with the increase of Re, which fits with the trend derived from the analytical correlation (fF,a). At a low Reynold number, the simulated results agree well with the value derived from the correlation. However, discrepancies increase with the increase of the Reynold number, reaching up to 20% at a Reynold number of 3000.
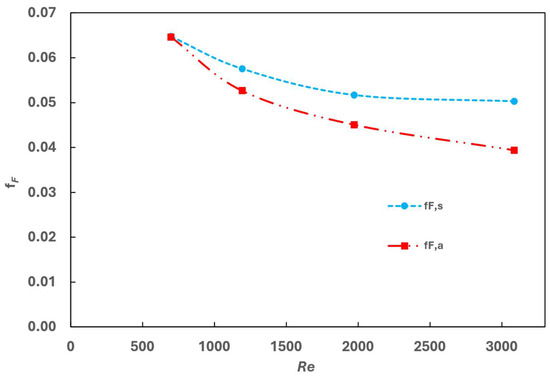
Figure 5.
Comparing the fanning friction factor derived from the simulation and analytical correlation.
Potential reasons for these discrepancies include the accuracy limitations of the k-ϵ model in simulating turbulence flow at a high Reynold number. Additionally, the derivation of the Fanning friction factor (Equation (20)) correlation is reported with an experimental error band of approximately ±20% [23].
With the verification results and the above considerations, the validity of the developed 3D model can be confirmed with an acceptable level of accuracy in predicting the heat transfer and pressure loss characteristics of the PFHE.
3.1.4. Verification of Kinetic Models
Three kinetics models for the OPC reaction that were developed in the literature are evaluated here.
Model 1, the Langmuir–Hinshelwood (LH) kinetic model [13], is given as follows:
The parameters are given in Table 3.

Table 3.
Parameters for the LH kinetic model.
Model 2: The first order kinetic model is expressed as the following equations (Equations (24) and (25)) [13]
The parameters are given in Table 4.

Table 4.
Parameters for the first order kinetic model.
Model 3: The Elovich kinetic model is expressed as the following equation (Equations (26) and (27)) [12]
and n = a
The kinetic parameters are given in Table 5.

Table 5.
Parameters for the Elovich kinetic model.
For all three models, is the equilibrium ortho concertation, which is temperature dependent and can be calculated as [10]
Hutchinson [11] conducted extensive experimental work to measure the OPC kinetics at LN2 temperature under various pressure using a 1/4” OD × 1/8” ID copper tube reactor with a length of 5 inches. To verify the kinetic models, a simulation case based on an isothermal plug flow model was set up. In the plug flow model, the inlet gas velocity was varied, resulting in a range of gas hourly specific velocities (GHSV, min−1), defined as the actual flow rate per unit bulk volume of the catalyst, and the outlet parahydrogen concentration was predicted.
The simulation case was compared with the experimental data at a pressure of 2.06 bar and temperature of 76 K [11]. The comparison is given in Figure 6. It is evident that only the Elovich model can quantitatively predict the experimental data, while the other two models yielded significantly different results. It is not clear as to the cause of such significant deviation of the other two kinetic models at this stage. Therefore, the Elovich kinetic model was chosen for further studies.
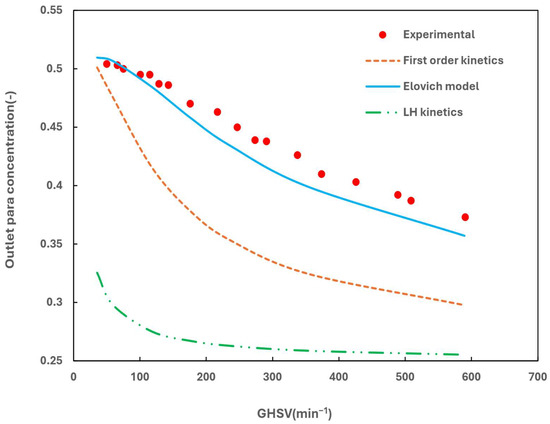
Figure 6.
Comparing the experimental results with simulated results from different kinetic models.
It is important to note that Hutchinson defines GHSV as the actual flow rate per unit bulk volume of the catalyst. This definition complicates comparisons across different temperatures and pressures. Therefore, another definition is also used in this study, known as the Gas Hourly Space Velocity at Standard Temperature and Pressure (GHSV_STP, min−1), which represents the flow rate at a standard temperature and pressure (STP) per unit bulk volume of the catalyst. Generally, GHSV_STP is larger than GHSV.
3.2. General Description of the Features of CPFHE
This section provides a general description of a default simulation case of the CPFHE focused on the hot channel. The simulated parameters are set as follows: T_in_hot = 77 K, V_in_hot = 0.2 m/s (corresponding to GHSV_STP = 465 min−1), T_in_cold = 60 K, and V_in_cold = 5 m/s, while the pressure is maintained at the atmosphere level. It is noted that the simulated case exhibits a significant mass ratio between the cold side and the hot side (m_cold/m_hot = 63.8), indicating that the heat transfer is not the controlling factor in the scenario.
The present study employs a three-dimensional approach, enabling the observation of the actual flow field in both channels. To visualize the velocity distribution more clearly, a 2D velocity profile of a section of the cross-section of the hot channel (parallel to the flow direction with 0.003 m above the bottom parting sheet) is shown in Figure 7.
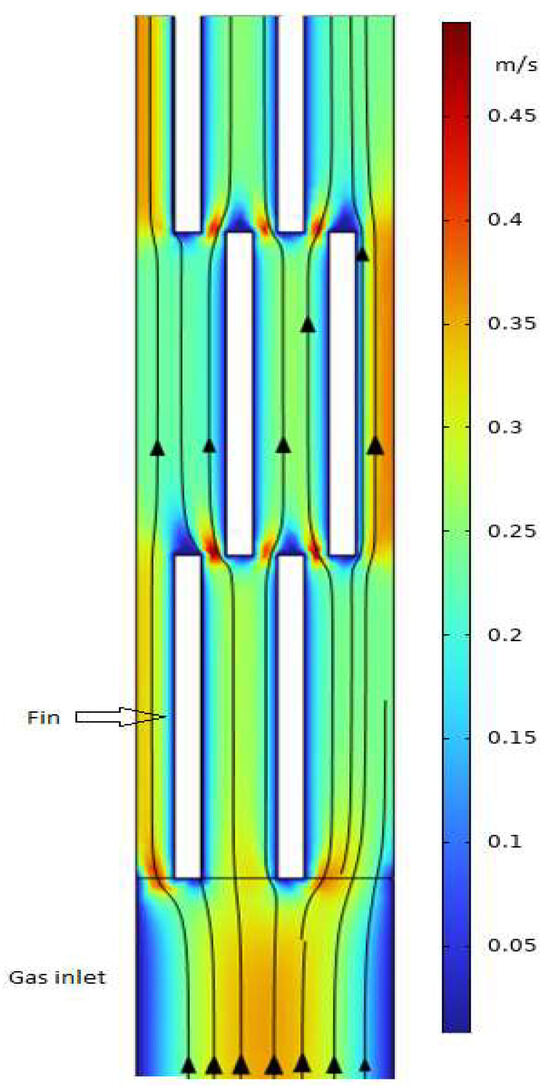
Figure 7.
Velocity profile of the hot channel.
The model accurately predicts the wall effect on the flow field, where the flow velocity is zero at the wall. A boundary layer grows over the fin surface and is abruptly disrupted at the end of the fin length. Additionally, a low-velocity zone is observed at the tip of the fin outlet, while velocities are high at the gap between the front and back fins. The periodic variations in gas velocity contribute to improved heat transfer performance [25]. It is anticipated that a shorter fin length could enhance heat transfer performance due to the increased frequence of high and low velocity changes and the shorter boundary layer; however, this may lead to an increase of pressure loss. This analysis aligns with the findings of Xu et al. [16], who systematically studied the effect of a structure parameter of a PFHE on both heat transfer performance and pressure loss.
A temperature profile of the cross-section fin channels (taken vertically to the flow direction, positioned 0.05 m away from the hot inlet) and temperature distribution along the fin width (taken at half of the fin height) are showing in Figure 8. Observations indicate that the temperature distribution on the hot side is more unform compared to the cold side, attributed to the presence of catalyst particles. The temperature of the parting sheet is closer to that of the hot side, suggesting that the primary heat transfer resistance occurs on the cold side. The temperature distribution along half of the fin height further illustrates these characteristics, emphasizing the influence of the catalyst presence on thermal uniformity and heat transfer dynamics within the plate fin heat exchanger.
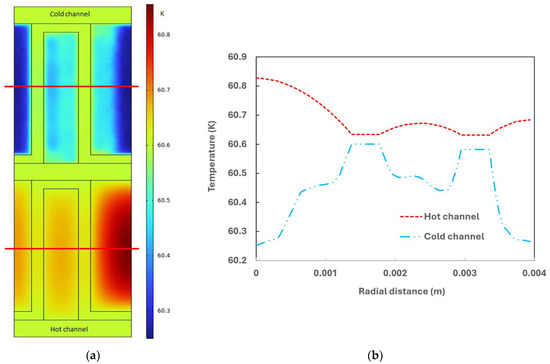
Figure 8.
(a) Temperature profile inside the fin channel; (b) Temperature distribution along the fin width at half fin height.
Parahydrogen distribution in one of the hot channels is illustrated in Figure 9. The concentration of para-hydrogen is non-uniform within the small fin channel and shows a reverse correlation with the temperature. Specifically, the para concentration is higher at the fin wall due to lower temperatures, while it decreases towards the middle of the fin. This observation suggests that despite the compact geometry, there is room for improvement in heat transfer within the fin channels.
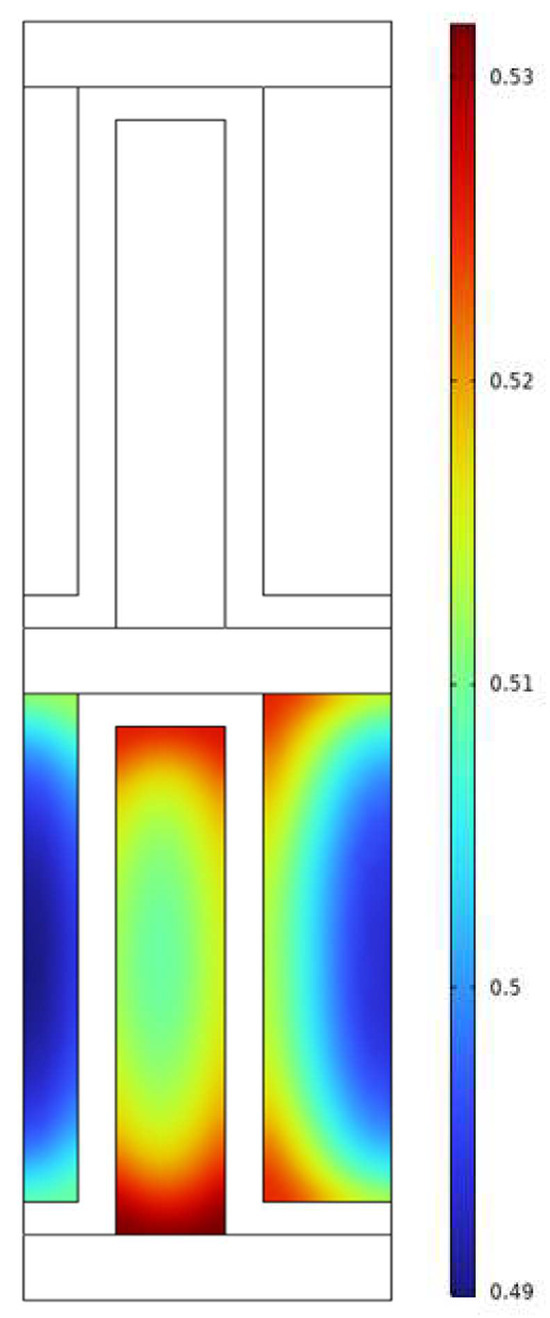
Figure 9.
Parahydrogen concentration profile inside the hot fin channel.
The previous discussion reveals a non-uniform distribution of temperature in both the hot and cold channels and a non-uniform distribution of parahydrogen concentration within the hot channel of the CPFHE. For a practical performance analysis, focusing on the average values is of interest. The average temperature distribution along the axial length of the hot side is presented in Figure 10.
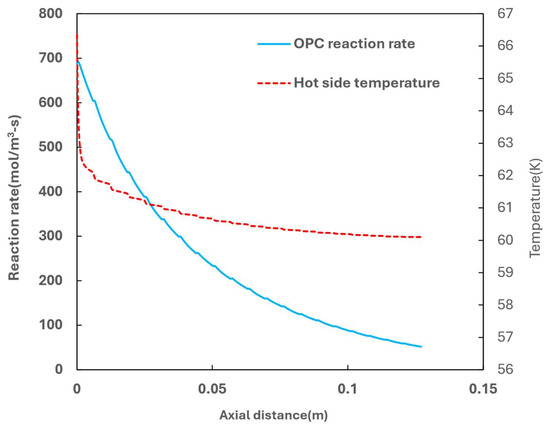
Figure 10.
Temperature profile and OPC reaction rate along the flow axial distance.
In the simulated case, due to the significant flow of cooling media, the hot side experience rapid cooling, resulting in a pronounced temperature drop at the inlet. From a heat transfer perspective, this operation model is suboptimal, leading to increased losses due to inefficient utilization of the cold energy. However, this cooling pattern is desirable from the OPC kinetics standpoint. The OPC kinetics are driven by the difference between the para concentration and equilibrium para concentration, where the latter is temperature-dependent. As illustrated in Figure 10, the maximum kinetics rate occurs at the inlet of the hot side, followed by a decrease along the flow direction.
Figure 11 depicts the para concentration along the axial length of flow direction, accompanied by the calculated equilibrium para concentration using Equation (28). The equilibrium para concentration stabilizes shortly after the inlet, while the actual para concentration increases gradually due to the kinetic constraints.
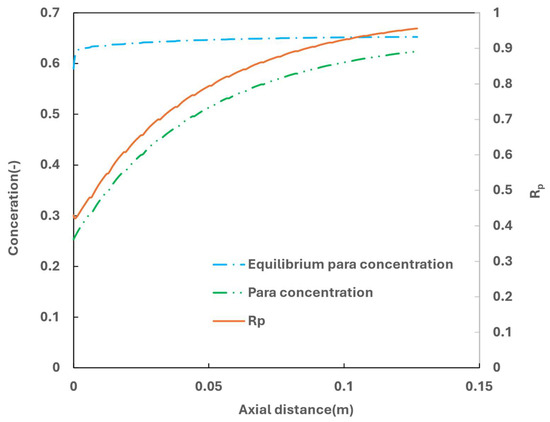
Figure 11.
Para concentration along the flow axial distance.
To assess the efficiency of the OPC reaction, a parameter Rp, defined as the ratio of actual para concertation to the equilibrium para concentration, is used to quantify the analysis. Achieving Rp = 1 indicates that the para concentration has reached equilibrium, so the entropy loss due to ortho para conversion will be minimized. In the simulated case with the specified GHSV-STP, Rp at the heat exchanger exit reaches 0.95.
3.3. Sensitivity Analysis of CPFHE Model
This section conducts a sensitivity analysis to investigate the performance of the CPFHE by varying the heat transfer parameters (through changing the gas flow velocities in the cold and hot channels), OPC kinetics (through changes in the kinetic constant), and reaction pressure. This approach aims to deepen our understanding of CPFHE performance. The Reynold number (based on hydraulic diameter) for the hot side ranges from 50 to 220, while it varies between 800 to 3300 on the cold side.
3.3.1. GHSV Effect
To investigate the effect of GHSV, the inlet velocity of the hot side was varied while keeping other parameters constant.
As the inlet velocity of the hot side increases (resulting in an increase in GHSV or a decrease in the mass flow ratio between cold and hot media, i.e., m_c/m_h), the heat transfer U also increases, as shown in Figure 12, indicating an overall improvement in heat transfer performance of the heat exchanger. This improvement is further validated by the increase in outlet temperature of the cold side with higher hot side velocity. It is important to note that in this analysis, the cold media flow is always in excess (m_c/m_h > 10), ensuring that heat transfer is not the constrained factor.
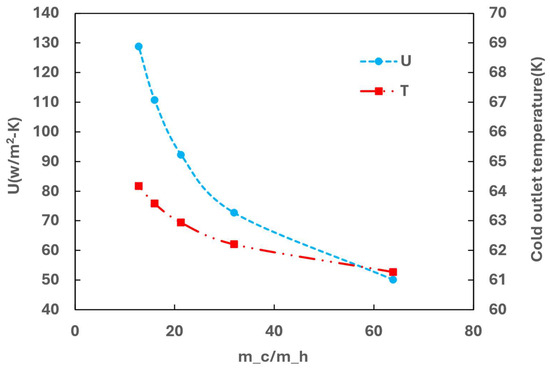
Figure 12.
Effect of GHSV on heat transfer performance.
Figure 13 illustrates the variation of Rp at the heat exchanger outlet with GHSV-STP. It is observed that Rp decreases as GHSV-STP increases. At a low GHSV (approximately 500 min−1), Rp can reach 0.95, indicating a close approach to equilibrium. However, at a higher GHSV (around 2300 min−1), Rp drops significantly to 0.64. The low para concentration at the outlet suggests that the kinetic is the constraint of the CPFHE.
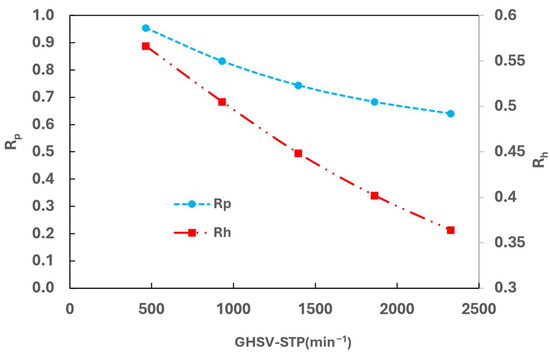
Figure 13.
Effect of GHSV-STP on OPC efficiency.
In terms of heat transfer, cold media is utilized to remove both heat generated from the OPC reaction and the latent heat of the hot media. To quantify this, another parameter, Rh, defined as the ratio of the heat required to remove the OPC reaction to the total required heat, is also plotted in Figure 13. Rh decreases as GHSV increases, indicating that more heat is used to remove the latent heat of hydrogen than the OPC reaction heat.
The study of GHSV presents conflicting outcomes where an improvement in heat transfer coincides with a decrease in the OPC efficiency with the increase of hot flow velocity.
3.3.2. Cooling Effects
For large-scale hydrogen liquefiers, it is crucial that the heat exchanger efficiently handles high volumes of gas flow at a fixed catalyst volume (i.e., large GHSV-STP) without compromising Rp. In our analysis, achieving Rp of 0.95 at GHSV-STP of 2300 min−1 was set as the goal, although this specific GHSV value may not be directly applied to any practical hydrogen liquefication applications.
Figure 14 illustrates the effects of heat transfer by varying the flow rate of cold media at a fixed GHSV-STP of 2300 min−1. The heat transfer coefficient (U) initially increases rapidly with the increasing flow rate of the cold media, and it becomes less responsive at a higher flow rate. Conversely, the outlet temperature of cold media decreases with a higher flow rate, indicating the inefficient utilization of cold energy and potential for increased entropy loss.
Figure 14.
Effect of cold flow rate on heat transfer performance.
At a high GHSV-STP of 2300 min−1, although increasing the flow rate of cold media improves heat transfer, Rp remains at approximately 0.65, as shown in Figure 15. Simultaneously, Rh stabilizes around 0.35. This suggests that at a high GHSV, kinetic limitations predominate, limiting the production of para and rendering cooling less impactful. To achieve a higher Rp under these conditions, improving the kinetics parameters of the current catalyst would be necessary.
Figure 15.
Effect of cold flow rate on OPC efficiency.
The cooling effect studies demonstrate scenarios where increasing the flow rate of cold media enhances the heat transfer but does not have any positive effects on OPC efficiency.
3.3.3. OPC Kinetic Effects
The performance was further investigated by varying the OPC reaction rate at a fixed GHSV-STP of 2300 min−1, where the reaction rate of the original value of the Elovich model was increased five and ten times. Figure 16 illustrates the effect of the OPC reaction rate and cold flow rate on the overall heat transfer coefficient.
Figure 16.
Effect of OPC reaction rate on the heat transfer performance.
It is evident that increasing the reaction rate significantly enhances the overall heat transfer coefficient. The OPC reaction is exothermic, and the higher reaction rate leads to increased heat released from the OPC reaction. The heat release elevates the local temperature within the catalyst channel, creating a stronger driving force for heat transfer between the hot and cold channels. Consequently, this results in a higher overall heat transfer coefficient, which is advantageous from a heat transfer point of view.
Figure 17 shows that as the reaction rate increases, Rp initially increases with the increasing cold flow rate, stabilizing at higher values for a larger cold flow. This indicates that at lower cold flow rates, increased kinetic parameters may make heat transfer the limiting factor. In such cases, enhancing the heat transfer by increasing the cold flow can improve the OPC efficiency.
Figure 17.
Effect of kinetic parameters on OPC efficiency.
Additionally, Rp increases significantly with a higher reaction rate. At the heat exchanger outlet, Rp reaches 0.92 with five times of the original reaction rate and exceeds 0.98 at ten times of the reaction rate for a large cold flow. The high Rp is favourable from a kinetic standpoint.
OPC kinetic studies demonstrate scenarios where increasing the OPC reaction rate improves both heat transfer and OPC efficiency simultaneously.
3.3.4. Effect of Operating Pressure
The effect of operating pressure in the hot channel on OPC performance was investigated at a constant GHSV-STP of 2300 min−1. To achieve this, the inlet velocity of hot media was adjusted accordingly as operating pressure increased. Figure 18 plots the Rp as a function of the operating pressure ranging from 1 to 30 bars.
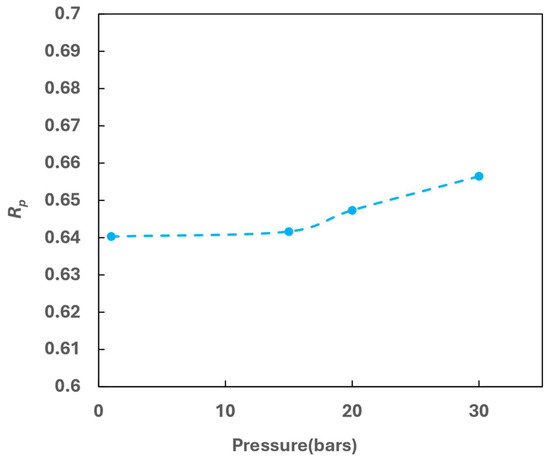
Figure 18.
Effect of operating pressure on OPC efficiency.
The results indicate that operating pressure positively impacts OPC performance, leading to improved para concentration. The increase in para concentration at higher pressure could be attributed to enhanced physical adsorption of hydrogen on the catalyst surface [26]. Experimental data by Weitzel [27] also support this observation, showing a small but definite increase in conversion over a pressure range of 1.37 to 27.6 bar (20 to 400 psig). The model predictions align with these trends. However, this improvement is relatively minor as indicated by the increase in Rp by a little over 0.015 in the pressure range employed.
3.3.5. Pressure Drop
With the development of catalysts of improved kinetics, achieving a high Rp at a large GHSV is feasible. However, incorporating catalysts into the hot channel increases the pressure drop, especially at a high GHSV, resulting in significant energy loss.
To quantify the pressure drop in the hot channel, a simulated case was set up to derive the pressure drop varying with hot gas velocity (accordingly with the GHSV_STP). The results are given in Figure 19. The simulation results clear indicate that the pressure drop increases linearly with the increase of gas velocity.
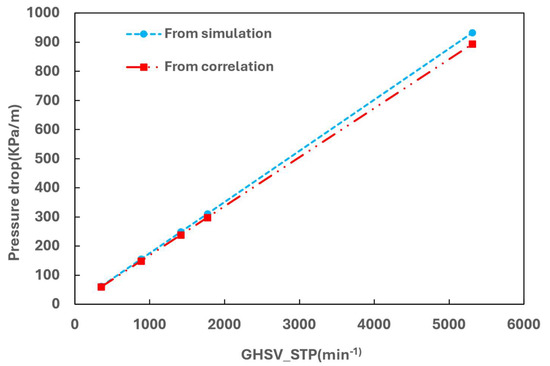
Figure 19.
Effect of gas velocity on the pressure drop of the catalytic bed.
The actual frictional pressure drop in the hot channel with the catalyst includes contributions from both the catalyst bed and the heat transfer fins. It has been noted that the contribution from the fins can be neglected, as it is one to two orders of magnitude lower than that of the packed bed [10]. Thus, the pressure drop can be estimated using Darcy’s law as expressed as
The pressure drop calculated using Darcy’s law is also plotted in Figure 19 for comparison, showing good agreement with the simulated results. It is evident that increasing GHSV results in a high pressure drop, with the pressure drop reaching approximately 400 kPa/m at a GHSV of 2300 min−1, which is substantial.
3.4. Discussion
Due to their compact nature, PFHEs are widely utilized in various energy-intensive industry processes. However, the incorporation of a catalyst into the fin channel to function as both a chemical reactor and a heat exchanger (CPFHE) has been relatively underexplored. CPFHEs face two primary constraints when applied to OPC: OPC kinetic limitations and heat transfer considerations. The optimal operation goal of a CPFHE is to achieve a high Rp under high GHSV while maintaining a thermally efficient design, necessitating an optimized cooling system inherently coupled with the OPC reaction.
PFHE can achieve a high heat transfer surface area up to 1000 m2/m3. Additionally, the small hydraulic diameter of inserted fins enhances the fluid turbulence, thereby boosting the local convective heat transfer coefficient. From a chemical reactor point of view, the hot channel side of the CPFHE functions as micro fix-bed reactor, with the reactor size determined by GHSV. The preferred GHSV value for the OPC reactors is not well-documented in the research area. However, for reference, typical steam methane reformers operate with a GHSV range of 10,000 h−1 to 30,000h−1. Our default case operates at GHSV_STP = 465 min−1, which falls in the range.
At GHSV_STP = 465 min−1, it appears that the heat transfer is rarely the limiting factor for a CPFHE due to the high heat transfer coefficient inherent to PFHE. Close-to-equilibrium para concentration can also be achieved at this GHSV. Therefore, both heat transfer and kinetic constraint can be effectively managed.
Figure 12 presents an unoptimized scenario with high-capacity cooling, where the hot side cools rapidly, causing excessive temperature declines at the entrance. The rapid cooling enhances the OPC reaction rate but results in an unfavourable heat exchange design, as the available heat transfer area is underutilized. Moreover, rapid cooling demands increased coolant supply effort without fully utilizing cold energy [13]. This can be remedied by either increasing the hot side flow rate or decreasing the cold side flow rate to achieve an optimized heat exchanger design.
In the context of a large-scale hydrogen liquefier, high gas throughput often necessitates a large GHSV. At a large GHSV, it becomes challenging for the outlet para concentration to reach the equilibrium value. Increasing heat transfer does not significantly improve the para concentration, and a slight improvement is observed with increased reaction pressure. This underscores that kinetics are the controlling factor due to the current low catalytic activity.
According to Wilhelmsen et al. [12], doubling the catalytic activity compared to Ionex® can reduce the exergy destruction by 9%. This study investigates catalysts with five to ten times greater activity, highlighting the critical need to reach a high Rp at a high GHSV. Those catalysts with improved activity have been reported in the literature [28]. With highly active catalysts, inadequate cooling may necessitate compromising Rp. The fin structure significantly impacts heat transfer performance, which is a well-studied area beyond the scope of this work. Increasing the flow rate of both cold and heat media can enhance the heat transfer. However, increasing the hot flow rate is not advisable as para concentration is limited by the GHSV. Simulation suggests that increasing the cold flow rate can satisfy the heat transfer requirements. Importantly, the heat transfer coefficient improves with higher OPC activity, offering a dual advantage for catalysts with improved performance. Firstly, achieving a high Rp under high GHSV allows for a reduction in reactor size. Secondly, an improved heat transfer coefficient can potentially decrease the heat exchange size or lower the cold media flow rate.
One additional property that may be crucial for the newly developed catalyst is its thermal conductivity. As shown in Figure 8, there is a non-uniform temperature distribution inside the small fin channel packed with the catalyst. Increasing the gas velocity enhances convective heat transfer, which can improve temperature uniformity within the fins. However, as discussed, this approach is unsuitable for enhancing the para conversion due to the resulting high GHSV.
An alternative approach to enhancing heat transfer within the fin channels involves developing a catalyst with high thermal conductivity, thereby promoting conductive heat transfer. To validate this hypothesis, a simulation was conducted by increasing the thermal conductivity of the catalyst by a factor of 10, while keeping all other parameters consistent with those given in Figure 8. Figure 20 presents the temperature distribution across the width of the fin at half the fin height for the modified case. A noticeable improvement in temperature uniformity on the hot side is observed compared to the results in Figure 8. Consequently, this enhancement led to a 2.4% increase in the overall heat transfer coefficient.

Figure 20.
Temperature distribution along the fin width at half fin height for the case with increase of catalyst thermal conductivity.
Pressure drop is a critical consideration in the design and optimizing of CPFHEs. Minimizing pressure drop is essential from an energy-saving perspective. Designing the fin type and plate pattern plays a key role in achieving this goal, which is a topic extensively explored in existing literature [29,30]. This study specifically investigates the influence of a catalyst addition on pressure drops.
Given the current kinetic constraints, gas velocity within the catalyst bed in hot channel is limited yet still results in a significant pressure drop. The calculated pressure drop is approximately 400 kPa/m at a GHSV of 2300 min−1 when the operation is at atmosphere. The high pressure drop is inherent in fix bed reactors. In order to reduce this, two solutions have been proposed. (1) to develop a catalyst with improved activity. A catalyst with high activity will reduce the amount of catalyst used in the PFHE. This suggests that a small heat exchanger can be utilized when OPC kinetics is the control factor, thus reducing the pressure drop. (2) to rethink the strategy of how a catalyst is integrated with a heat exchanger so that a more efficient and less restrictive flow path can be reached. This will further reduce the pressure drop.
At the same time, conducting reactions at elevated pressures can help mitigate this issue. A pressure drop in the catalyst channel is directly influenced by superficial gas velocity. Operating at a higher pressure, as prescribed by the specified GHSV-STP, reduces gas superficial velocity within the catalyst bed, thereby lowering the pressure drop. For instance, at an operating pressure of 20 bar, gas superficial velocity is approximately 1/20th compared to that at atmospheric pressure, resulting in an estimated pressure loss of 20 kPa/m.
A common guideline suggests that the pressure drop should not exceed 20% of the inlet pressure [31]. For a GHSV-STP of 2300 min−1 and an operation pressure of 20 bar, the estimated pressure drop is 20 KPa/m. For a large PFHE with a length of 5 m, this translates to a pressure loss of approximately 1 bar, which can meet the pressure drop requirement.
While higher operating pressures positively impact CPFHE performance, the effect is marginal. Therefore, operating at higher pressures is recommended for CPFHE OPC efficiency.
To optimize the CPFHE design under various operating conditions, the exergy destruction analysis of CPFHEs proposed by Wilhelmsen et al. [12] can be employed. This analysis identifies the exergy destruction and lost work in CPFHEs originating from the heat transfer, pressure drops, and OPC. The existing studies primarily focus on CPFHE performance through heat transfer and OPC kinetics, with limited exploration on minimizing exergy destruction during the heat transfer process.
Furthermore, these studies are confined to an LN2 temperature at 77 K. At temperatures below 40 K, significant changes in thermodynamic properties of ortho-para hydrogen may render findings less applicable. Further research should thus explore optimizing temperatures, pressures, OPC kinetic parameters, and refrigerant compositions. This optimization should be conducted in conjunction with comprehensive process simulation utilizing the advanced 3D heat exchanger models developed in this study.
4. Conclusions
A Multiphysics model incorporating the 3D fin structure and the governing equations was developed and applied to assess the performance of a catalyst-filled plate-fin heat exchanger applied to the OPC during hydrogen liquefaction. The conclusions drawn from this study are as follows:
- (1)
- Despite the compact nature of the PFHE with large heat transfer area and millimetre-scale fin spacing, simulations reveal non-uniform temperature distribution within the fin channels. The addition of a catalyst improved the temperature uniformity, with the catalyst possessing high thermal conductivity and further enhancing this uniformity.
- (2)
- Increasing the gas velocities of both the hot and cold media in the CPFHE channels can enhance the overall heat transfer coefficient. However, higher gas velocities in the hot channel results in a large GHSV, thus compromising the OPC performance. At a GHSV-STP of 2300 min−1, the ratio of actual para concertation to the equilibrium para concentration can only reach 0.65, irrespective of the heat transfer performance.
- (3)
- In large-scale hydrogen liquefaction systems requiring high GHSVs, OPC kinetics predominately dictate CPFHE performance. Improving heat transfer alone does not enhance the OPC performance; instead, developing catalysts with enhanced activity is crucial. A catalyst with kinetics 5 to 10 times more active than the current commercial catalyst can help para concertation reaching equilibrium at a GHSV-STP of 2300 min −1.
- (4)
- Incorporating a catalyst into fin channels increases the pressure drop significantly, which can reach approximately 400 kPa/m at a GHSV of 2300 min−1. However, the increased operating pressure will mitigate this, which also positively impacts the OPC performance marginally.
- (5)
- These findings underscore the complex interplay between heat transfer, OPC catalytic activity, and pressure drops in the CPFHE design for hydrogen liquefaction. Optimizing the CPFHE operating parameters necessitates minimizing exergy destruction due to heat transfer, pressure loss, and OPC reaction.
Future research should focus on the development of a catalyst with improved OPC activity and optimization of operating conditions of PFHEs. Modelling verification with experimental data is also important for the scale up of the design of CPFHEs.
Author Contributions
Conceptualization, L.T. and D.Y.; methodology, L.T. and J.O.; formal analysis, W.T.; writing—original draft preparation, L.T.; writing—review and editing, D.Y. and W.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CSIRO H2 Future Science Platform (No: R-15641).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data and materials are available from the corresponding author upon reasonable request. The data are not publicly available due to ongoing researches using a part of the data.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| A | total heat transfer area, m2 |
| A(h,c,w) | heat transfer area of hot/cold channel/parting sheet, m2 |
| Cp | specific heat capacity, J/kg-K |
| CH2 | molar concentration of hydrogen, mol/m3 |
| Dh | hydraulic diameter of the fin, m |
| Ea | activation energy of OPC reaction, J/mol |
| Fanning friction factor from simulation/analytical correlation, - | |
| F | volume force vector, N/m3 |
| FF | viscous force due to Forchheimer and Ergun option, N/m3 |
| ha,(h,c) | heat transfer coefficient for cold/hot channel, W/m2-K |
| I | identity matrix, - |
| transport of chemical species (i) due to diffusion, mol/m2-s | |
| j(a) | Colburn number, - |
| effective thermal conductivity, W/m-K | |
| kp | permeability of catalyst bed, m2 |
| K | viscous stress tensor, Pa |
| and M | molar mass of species i and mixture, g/mol |
| Pk | production of turbulent kinetic energy, m2/s3 |
| Pc | critical pressure of hydrogen, MPa |
| P | pressure, Pa |
| Δp | pressure loss, Pa |
| q | heat flux by conduction, W/m2 |
| mass source, kg/m3-s | |
| Q | total heat transferred, W |
| Qconv | heat of conversion, J/mol. |
| reaction rate expression for the species i, mol/m3-s. | |
| Re | Reynolds number, calculated as , - |
| Tc | critical temperature of hydrogen, K |
| T | temperature, K |
| ΔT(A,B) | the temperature difference between the two fluids at end A/B, K |
| u | gas velocity, m/s |
| U(s,a) | the overall heat transfer coefficient calculated from simulation or analytical correlation, W/m2-K |
| V | velocity vector, m/s |
| mole fraction of species i and can be calculated as , - | |
| Greek symbols | |
| k | turbulent kinetic energy, m2/s2 |
| ɛ | turbulent dissipation, m2/s3 |
| porosity of catalyst bed, - | |
| fin temperature effectiveness of the cold/hot channel, - | |
| µ | fluid dynamic viscosity, Pa-s |
| eddy viscosity and is given as , m2/s | |
| mass fraction of species (i), - | |
| ρ | density, kg/m3 |
| λ(h,c,w) | thermal conductivity of fluid or hot/cold channel/parting sheet, W/m-K, |
| Subscript | |
| a | from analytic correlation |
| c | cold side |
| h | hot side |
| s | from numerical simulation |
| w | parting sheet |
References
- Al Ghafri, S.Z.S.; Munro, S.; Cardella, U.; Funke, T.; Notardonato, W.; Trusler, J.P.M.; Leachman, J.; Span, R.; Kamiya, S.; Pearce, G.; et al. Hydrogen liquefaction: A review of the fundamental physics, engineering practice and future opportunities. Energy Environ. Sci. 2022, 15, 2690–2731. [Google Scholar] [CrossRef]
- Aziz, M. Liquid Hydrogen: A Review on Liquefaction, Storage, Transportation, and Safety. Energies 2021, 14, 5917. [Google Scholar] [CrossRef]
- Lipman, M.S.; Cheung, H.; Roberts, O.P. Continuous conversion hydrogen liquefaction. Chem. Eng. Prog. 1963, 59, 49–54. [Google Scholar]
- Teng, J.J.; Wang, K.; Zhu, S.L.; Bao, S.R.; Zhi, X.Q.; Zhang, X.B.; Qiu, L.M. Comparative study on thermodynamic performance of hydrogen liquefaction processes with various ortho-para hydrogen conversion methods. Energy 2023, 271, 127016. [Google Scholar] [CrossRef]
- Krasae-in, S.; Stang, J.H.; Neksa, P. Development of large-scale hydrogen liquefaction processes from 1898 to 2009. Int. J. Hydrog. Energy 2010, 35, 4524–4533. [Google Scholar] [CrossRef]
- Xu, P.; Wen, J.; Li, K.; Wang, S.M.; Li, Y.Z. Review of the continuous catalytic ortho-para hydrogen conversion technology for hydrogen liquefaction. Int. J. Hydrog. Energy 2024, 62, 473–487. [Google Scholar] [CrossRef]
- Popov, D.; Fikiin, K.; Stankov, B.; Alvarez, G.; Youbi-Idrissi, M.; Damas, A.; Evans, J.; Brown, T. Cryogenic heat exchangers for process cooling and renewable energy storage: A review. Appl. Therm. Eng. 2019, 153, 275–290. [Google Scholar] [CrossRef]
- London, A.L.; Shah, R.K. Offset Rectangular Plate-Fin Surfaces—Heat Transfer and Flow Friction Characteristics. J. Eng. Gas Turbines Power 1968, 90, 218–228. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.Z. Layer pattern thermal design and optimization for multistream plate-fin heat exchangers—A review. Renew. Sustain. Energy Rev. 2016, 53, 500–514. [Google Scholar] [CrossRef]
- Meagher, J.P. Modelling of Hydrogen Liquefiers with Kinetic Conversion of Ortho to Para Hydrogen in Plate-Fin Heat Excahngers. Master’s Thesis, Department of Chemical and Biological Engineering, University at Buffalo, State University of New York, Buffalo, NY, USA, 2009. [Google Scholar]
- Hutchinson, H.L. Analysis of Catalytic Ortho-Parahydrogen Reaction Mechanisms. Ph.D. Dissertation, Department of Chemical Engineering, University of Colorado, Boulder, CO, USA, 1966. [Google Scholar]
- Wilhelmsen, Ø.; Berstad, D.; Aasen, A.; Neksa, P.; Skaugen, G. Reducing the exergy destruction in the cryogenic heat exchangers of hydrogen liquefaction processes. Int. J. Hydrog. Energy 2018, 43, 5033–5047. [Google Scholar] [CrossRef]
- Donaubauer, P.J.; Cardella, U.; Decker, L.; Klein, H. Kinetics and Heat Exchanger Design for Catalytic Ortho-Para Hydrogen Conversion during Liquefaction. Chem. Eng. Technol. 2019, 42, 669–679. [Google Scholar] [CrossRef]
- Park, J.; Lim, H.; Rhee, G.H.; Karng, S.W. Catalyst filled heat exchanger for hydrogen liquefaction. Int. J. Heat Mass Transf. 2021, 170, 121007. [Google Scholar] [CrossRef]
- O’Neill, K.T.; Al Ghafri, S.; da Silva Falc, B.; Tang, L.G.; Kozielski, K.; Johns, M.L. Hydrogen ortho-para conversion: Process sensitivities and optimisation. Chem. Eng. Process. Process Intensif. 2023, 184, 109272. [Google Scholar] [CrossRef]
- Xu, P.; Lei, G.; Xu, Y.Y.; Wen, J.; Wang, S.M.; Li, Y.Z. Study on continuous cooling process coupled with ortho-para hydrogen conversion in plate-fin heat exchanger filled with catalyst. Int. J. Hydrog. Energy 2022, 47, 4690–4703. [Google Scholar] [CrossRef]
- Zhu, S.L.; Teng, J.J.; Zhi, X.Q.; Bao, S.R.; Qiu, L.M.; Wang, K. Numerical study on comprehensive performance of flow and heat transfer coupled with ortho-para hydrogen conversion. Int. J. Heat Mass Transf. 2023, 201, 123653. [Google Scholar] [CrossRef]
- COMSOL. Multiphysics Reference Manual, version 6.2; COMSOL, Inc.: Stockholm, Sweden, 2023. Available online: www.comsol.com (accessed on 25 July 2024).
- Molecular Products Inc. Ionex® Type OP Catalyst. 2024. Available online: https://www.molecularproducts.com/products/ionex-type-op-catalyst (accessed on 15 January 2024).
- Leachman, J.W.; Jacobsen, R.T.; Penoncello, S.G.; Lemmon, E.W. Fundamental Equations of State for Parahydrogen, Normal Hydrogen, and Orthohydrogen. J. Phys. Chem. Ref. Data 2009, 38, 721–748. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23, NIST Reference Fluid Thermodynamic and Transport Properties, Version 10.0. 2018. Available online: https://www.nist.gov/srd/refprop (accessed on 20 March 2024).
- van Baten, J. REFPROP CAPE-OPEN Property Package Manager. 2024. Available online: https://www.amsterchem.com/refpropco.html (accessed on 20 March 2024).
- Manglik, R.M.; Bergles, A.E. Heat Transfer and Pressure Drop Correlations for the Rectangular Offset Strip Fin Compact Heat Exchanger. Exp. Therm. Fluid Sci. 1995, 10, 171–180. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Compact Heat Exchangers; Vinod Kumar Jain, Scientific International (Pvt.) Ltd.: New Delhi, Inida, 2018. [Google Scholar]
- Webb, R.L.; Kim, N.H. Principles of Enhanced Heat Transfer, 2nd ed.; Taylor & Francis Group: New York, NY, USA, 2005. [Google Scholar]
- Schmauch, G.E.; Singleton, A.H. Technical aspects of ortho-parahydrogen conversion. Ind. Eng. Chem. 1964, 56, 20–31. [Google Scholar] [CrossRef]
- Weitzel, D.H.; Van Valin, C.C.; Draper, J.W. Design data for ortho-parahydrogen converters. In Proceedings of the 1957 Cryogenic Engineering Conference, National Bureau of Standards, Boulder, CO, USA, 19–21 August 1957; Springer: Boston, MA, USA, 1960. [Google Scholar]
- Wakao, N.; Smith, J.M.; Selwood, P.W. The low-temperature orthohydrogen conversion over supported oxides and metals. J. Catal. 1962, 1, 62–73. [Google Scholar] [CrossRef]
- Wieting, A.R. Empirical Correlations for Heat Transfer and Flow Friction Characteristics of Rectangular Offset-Fin Plate-Fin Heat Exchangers. Trans. ASME 1975, 97, 488–490. [Google Scholar] [CrossRef]
- Yang, H.Z.; Li, Y.Y.; Yang, Y.; Zhu, Y.G.; Wen, J. Effect of surface efficiency on the thermal design of plate-fin heat exchangers with passages stack arrangement. Int. J. Heat Mass Transf. 2019, 143, 118494. [Google Scholar] [CrossRef]
- Pérez-Ramírez, J.; Berger, R.J.; Mul, G.; Kapteijn, F.; Moulijn, J.A. The six-flow reactor technology: A review on fast catalyst screening and kinetic studies. Catal Today 2000, 60, 93–109. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).