Hydrogen Storage Mechanism in Sodium-Based Graphene Nanoflakes: A Density Functional Theory Study
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
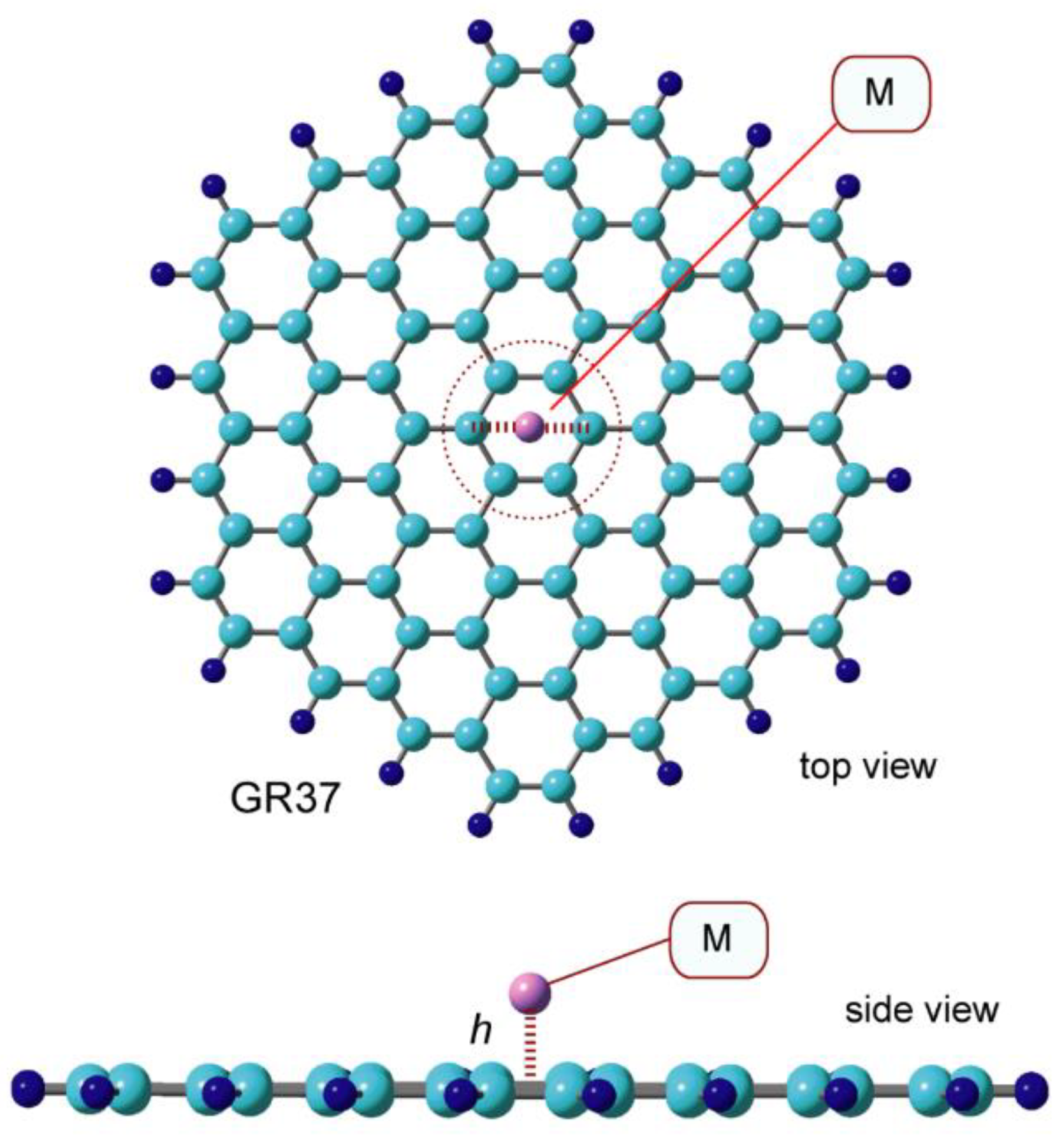
3.1. Structures of Na Doped-Graphene Nanoflakes
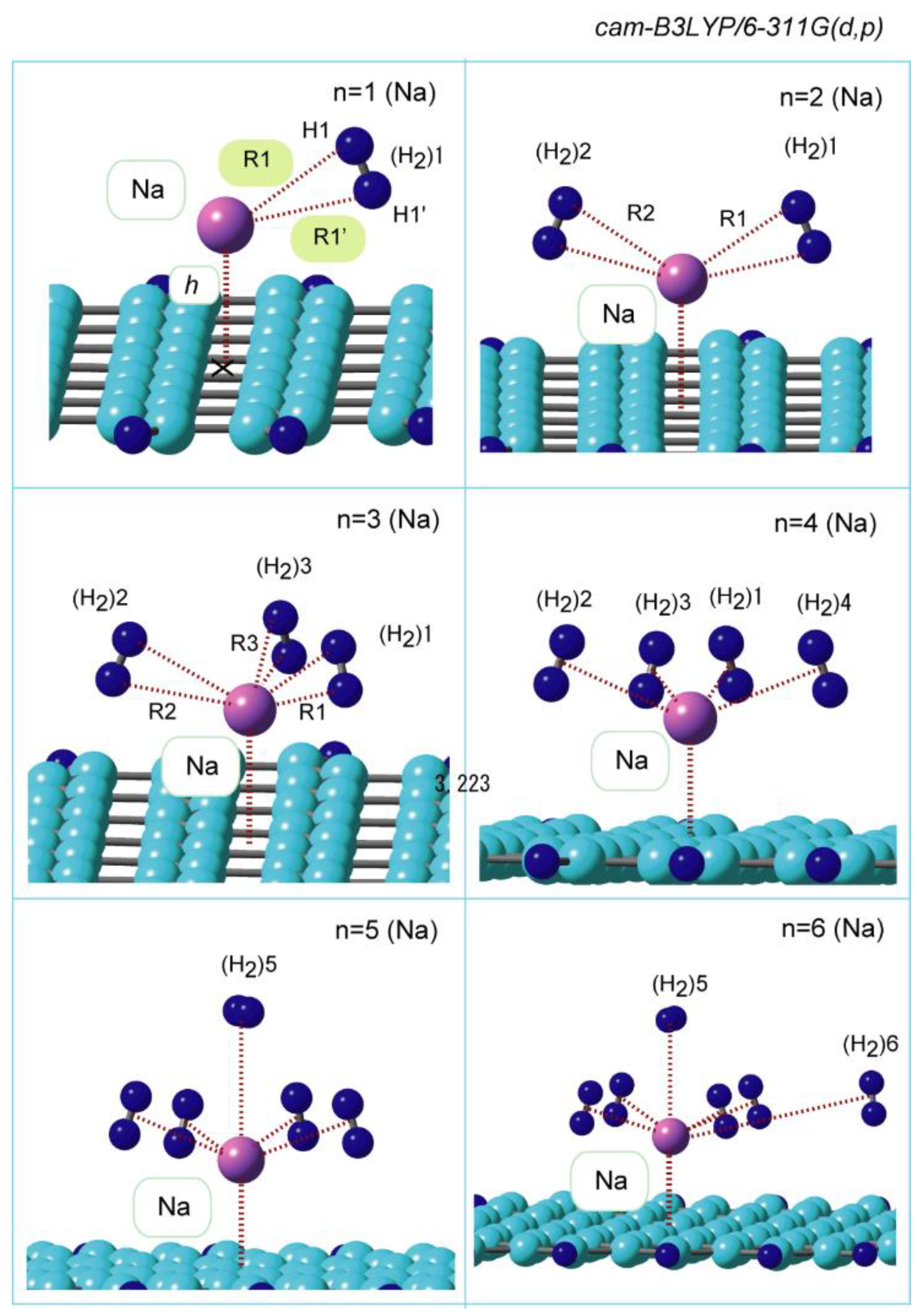
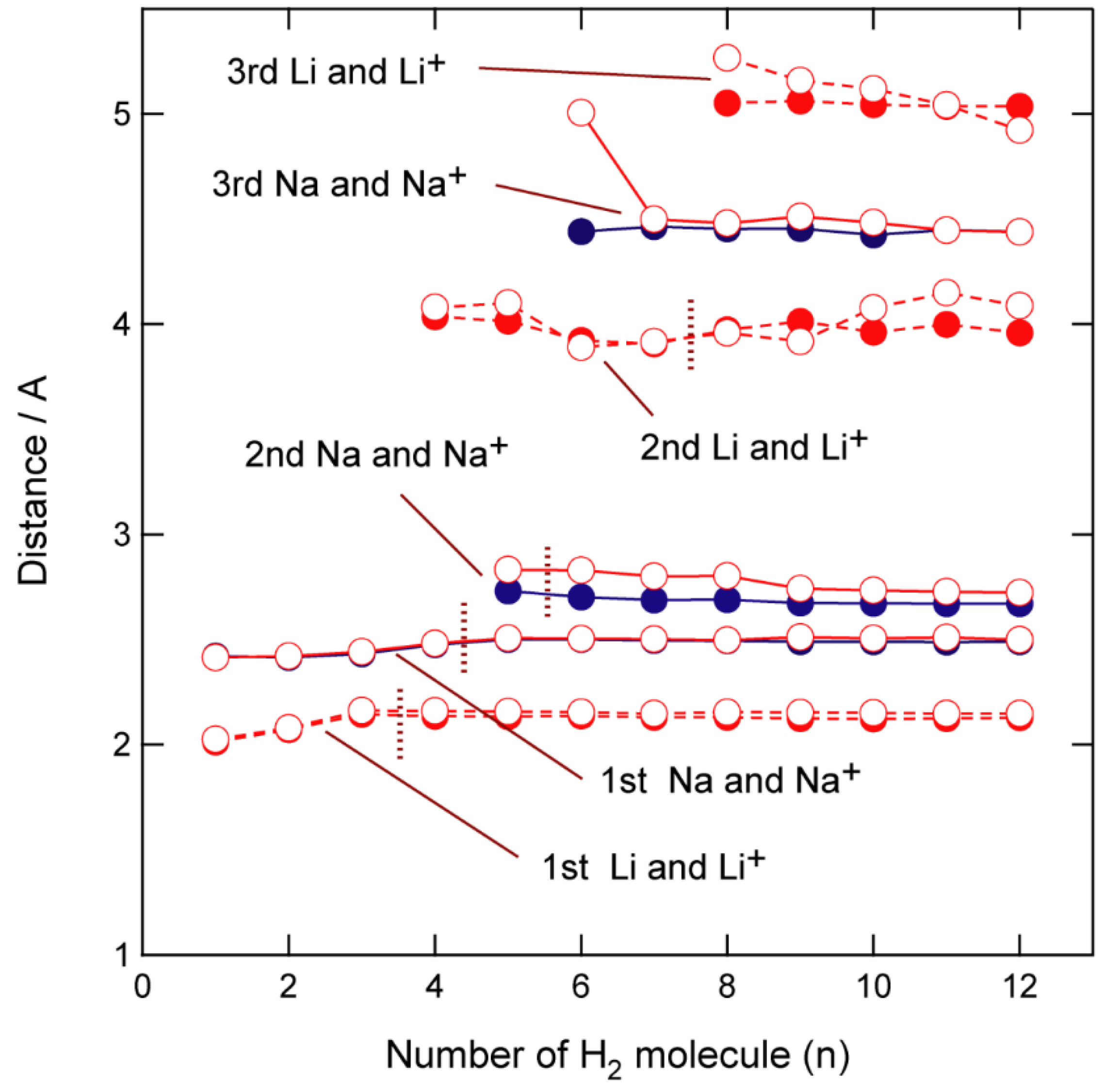
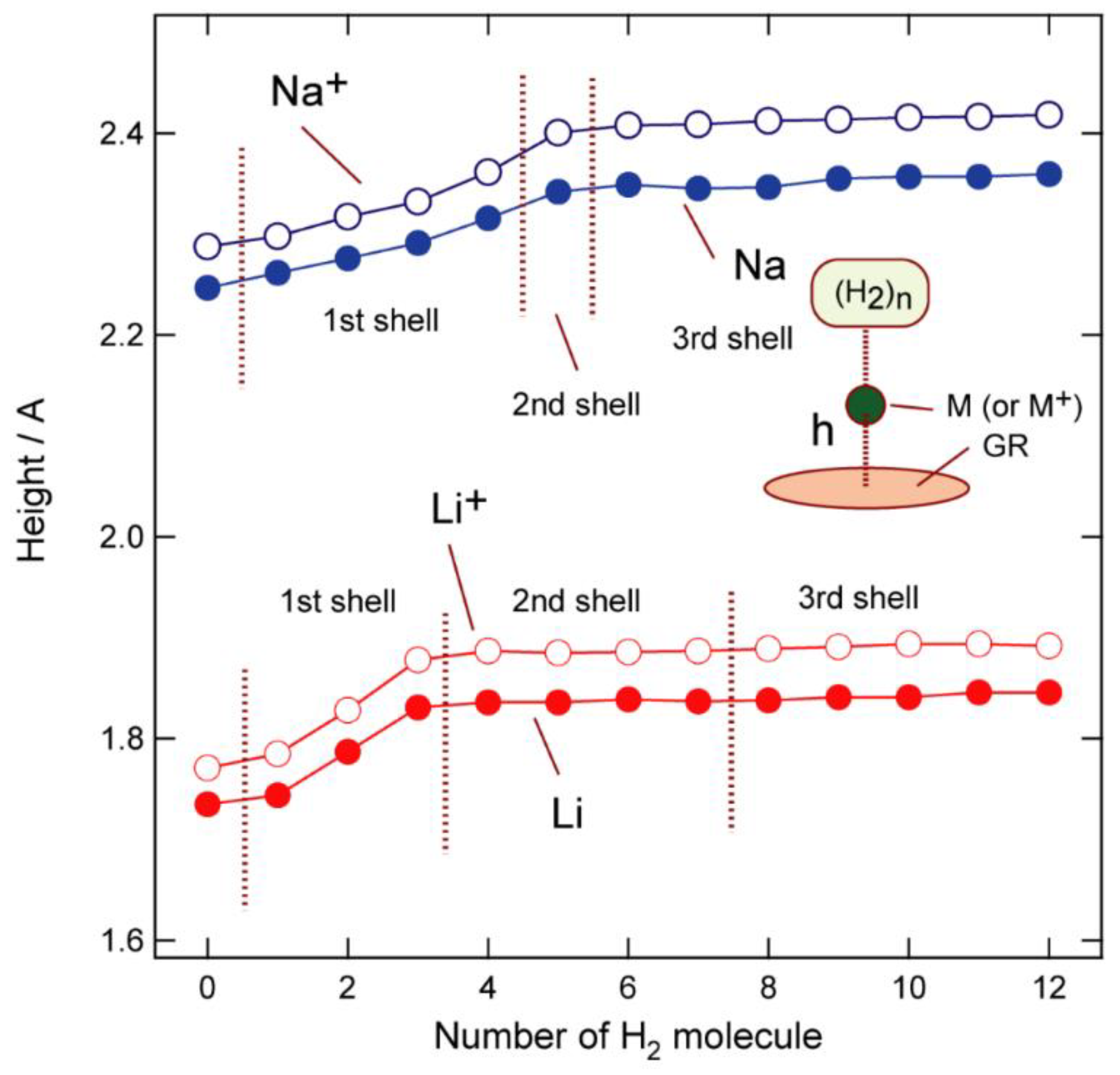
3.2. Structures of Molecular Hydrogen Bound to GR-Na
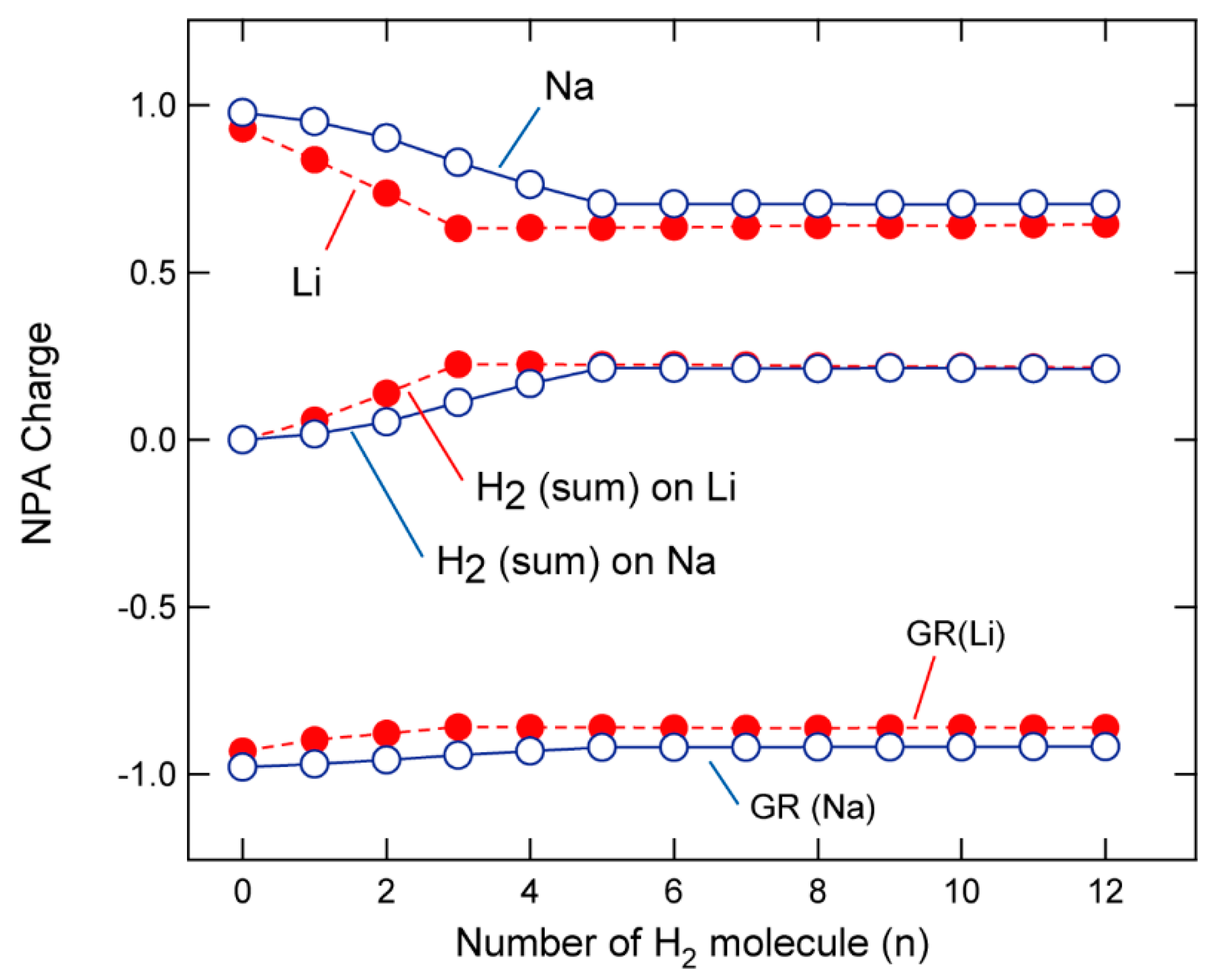
3.3. Electronic States
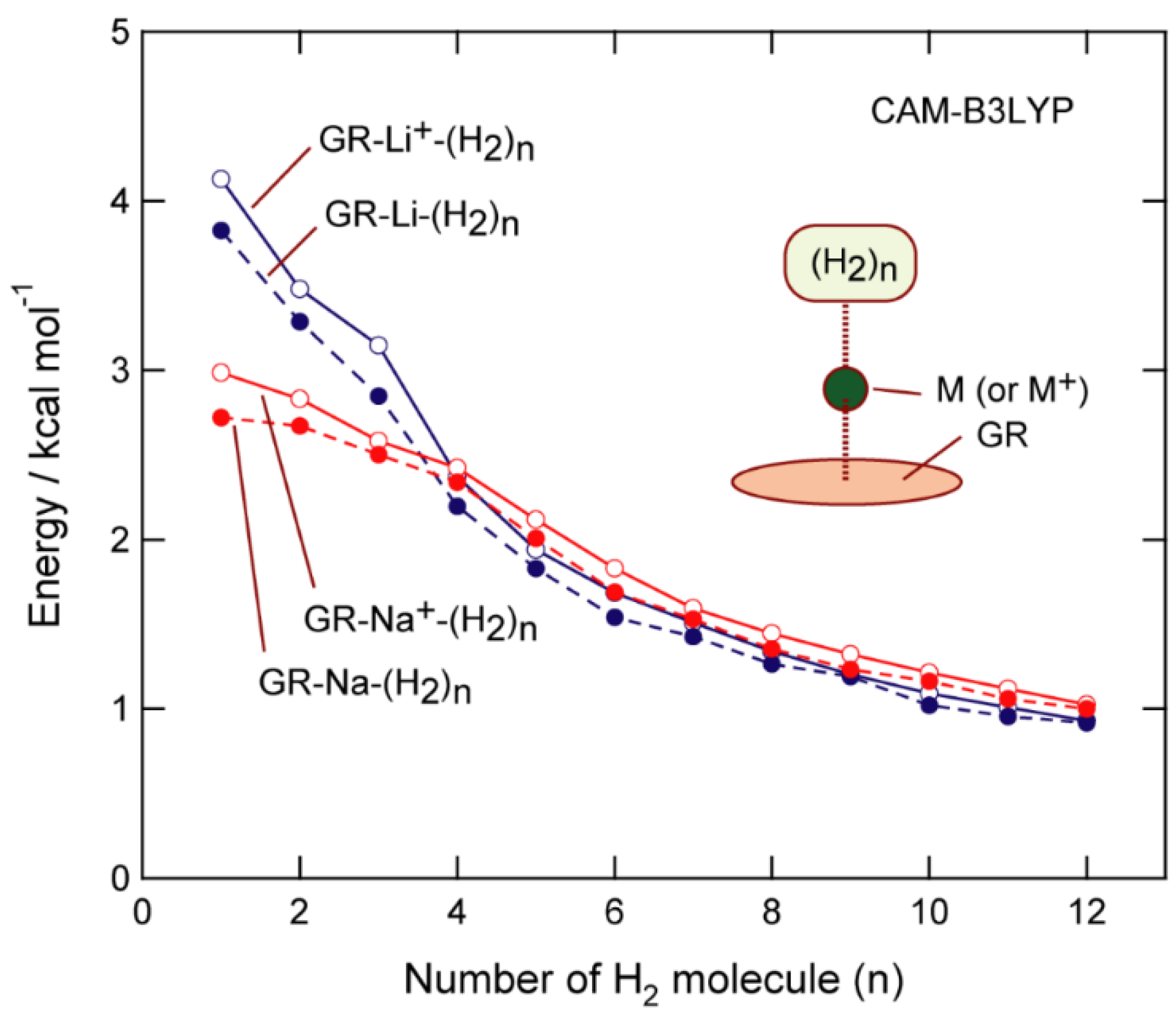
3.4. H2 Binding Energies to GR-Na
3.5. Effect of the Functional on Biding Energy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lempert, R.J. Climate Change Risk Measuring Global Climate Risk. Nat. Clim. Chang. 2021, 11, 805–806. [Google Scholar] [CrossRef]
- Rudd, J.A. From Climate Change Ignorant to Climate Change Educator. Chem. Eur. J. 2021, 27, 6107–6111. [Google Scholar] [CrossRef]
- Merino, J.G. Climate Change. Neurology 2021, 97, 657. [Google Scholar] [CrossRef]
- Unruh, C.F. Letting Climate Change. J. Am. Philos. Assoc. 2020, 7, 368–386. [Google Scholar] [CrossRef]
- Fuglie, K. Climate Change Upsets Agriculture. Nat. Clim. Chang. 2021, 11, 294–295. [Google Scholar] [CrossRef]
- Hanna, R.; Victor, D.G. Marking the Decarbonization Revolutions. Nat. Energy 2021, 6, 568–571. [Google Scholar] [CrossRef]
- Alent’ev, A.Y.; Volkov, A.V.; Vorotyntsev, I.V.; Maksimov, A.L.; Yaroslavtsev, A.B. Membrane Technologies for Decarbonization. Membr. Membr. Technol. 2021, 3, 255–273. [Google Scholar] [CrossRef]
- Bandelow, N.C.; Hornung, J.; Schröder, I.; Vogeler, C.S. Decarbonization and Climate Change. Rev. Policy Res. 2021, 38, 754–756. [Google Scholar] [CrossRef]
- Stephenson, J.R.; Sovacool, B.K.; Inderberg, T.H.J. Energy Cultures and National Decarbonisation Pathways. Renew. Sustain. Energy Rev. 2021, 137, 110592. [Google Scholar] [CrossRef]
- Shimoda, Y.; Sugiyama, M.; Nishimoto, R.; Momonoki, T. Evaluating Decarbonization Senarios and Energy Management Requirement for the Residential Sector in Japan through Bottom-Up Simulations of Energy End-Use Demand in 2050. Appl. Energy 2021, 303, 117510. [Google Scholar] [CrossRef]
- Chiaramonti, D.; Talluri, G.; Vourliotakis, G.; Testa, L.; Prussi, M.; Scarlat, N. Can Lower Carbon Aviation Fuels (LCAF) Really Complement Sustainable Aviation Fuel (SAF) towards EU Aviation Decarbonization? Energies 2021, 14, 6430. [Google Scholar] [CrossRef]
- De Silvestri, A.; Stendardo, S.; Della Pietra, M.; Borello, D. Decarbonizing Cement Plants via a Fully Integrated Calcium Looping-Molten Carbonate Fuel Cell Process: Assessment of a Model for Fuel Cell Performance Predictions under Different Operating Conditions. Int. J. Hydrogen Energy 2021, 46, 14988–15007. [Google Scholar] [CrossRef]
- Guo, Z.; Wei, W.; Chen, L.; Zhang, X.; Mei, S. Equilibrium Model of a Regional Hydrogen Market with Renewable Energy Based Suppliers and Transportation Costs. Energy 2021, 220, 119608. [Google Scholar] [CrossRef]
- Vijayakumar, V.; Jenn, A.; Fulton, L. Low Carbon Scenario Analysis of a Hydrogen-Based Energy Transition for On-Road Transportation in California. Energies 2021, 14, 7163. [Google Scholar] [CrossRef]
- Lobo, R.; Alvarez, N.; Shanov, V. Hydrogen Nanometrology in Advanced Carbon Nanomaterial Electrodes. Nanomaterials 2021, 11, 1079. [Google Scholar] [CrossRef]
- Lobo, R.; Ribeiro, J.H.F.; Inok, F. Hydrogen Uptake and Release in Carbon Nanotube Electrocatalysts. Nanomaterials 2021, 11, 975. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, X.; Liu, Y.; Zhang, L.; Hu, J.; Gao, M.; Pan, H. A Unique Double-Layered Carbon Nanobowl-Confined Lithium Borohydride for Highly Reversible Hydrogen Storage. Small 2020, 16, 202001963. [Google Scholar] [CrossRef] [PubMed]
- Yadav, S.; Tam, J.; Singh, C.V. A First Principles Study of Hydrogen Storage on Lithium Decorated Two Dimensional Carbon Allotropes. Int. J. Hydrogen Energy 2015, 40, 6128–6136. [Google Scholar] [CrossRef]
- Moon, H.S.; Lee, J.; Kwon, S.; Kim, I.T.; Lee, S.G. Mechanisms of Na Adsorption on Graphene and Graphene Oxide: Density Functional Theory Approach. Carbon Lett. 2015, 16, 116–120. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.H.; Lu, G.Q. Comparative Study of Li, Na, and K Adsorption on Graphite Using ab Initio Method. Langmuir 2004, 20, 10751–10755. [Google Scholar] [CrossRef]
- Dimakis, N.; Salas, I.; Gonzales, L.; Vadodaria, O.; Ruiz, K.; Bhatti, M.I. Li and Na Adsorption on Graphene and Graphene Oxide Examined by Density Functional Theory, Quantum Theory of Atoms in Molecules, and Electron localization Function. Molecules 2019, 24, 754. [Google Scholar] [CrossRef] [Green Version]
- El Kassaoui, M.; Houmad, M.; Lakhal, M.; Benyoussef, A.; El Kenz, A.; Loulidi, M. Hydrogen Storage in Lithium, Sodium and Magnesium-Decorated on Tetragonal Silicon Carbide. Int. J. Hydrogen Energy 2021, 46, 24190–24201. [Google Scholar] [CrossRef]
- Tachikawa, H.; Iyama, T. Mechanism of Hydrogen Storage in the Graphene Nanoflake-Lithium-H2 System. J. Phys. Chem. C 2019, 123, 8709–8716. [Google Scholar] [CrossRef]
- Tachikawa, H.; Izumi, Y.; Iyama, T.; Azumi, K. Molecular Design of a Reversible Hydrogen Storage Device Composed of the Graphene Nanoflake-Magnesium-H2 System. ACS Omega 2021, 6, 7778–7785. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.; Handy, N. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Low Atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Foster, J.P.; Weinhold, F. Natural Hybrid Orbitals. J. Am. Chem. Soc. 1980, 102, 7211–7218. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Tachikawa, H. Hydrogen atom addition to the surface of graphene nanoflakes: A density functional theory study. Apl. Surf. Sci. 2017, 396, 1335–1342. [Google Scholar] [CrossRef]
- Tachikawa, H.; Iyama, T.; Kawabata, H. Electronic structures of hydrogen functionalized carbon nanotube: Density functional theory (DFT) study. Solid State Sci. 2016, 55, 138–143. [Google Scholar] [CrossRef]
- Tachikawa, H. Ionization dynamics of water dimer on ice surface. Surf. Sci. 2016, 647, 1–7. [Google Scholar] [CrossRef]
- Tachikawa, H.; Kawabata, H. Molecular design of ionization-Induced proton switching element based on fluorinated DNA base pair. J. Phys. Chem. A 2016, 120, 1529–1535. [Google Scholar] [CrossRef] [PubMed]
- Hama, T.; Ueta, H.; Kouchi, A.; Watanabe, N.; Tachikawa, H. Quantum tunneling hydrogenation of solid benzene and its control via surface structure. J. Phys. Chem. Lett. 2014, 5, 3843–3848. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chai, J.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Ebind | Height (h) | NPA | |
|---|---|---|---|
| GR-Na | 4.4 | 2.247 | +0.978 |
| GR-Na+ | 37.5 | 2.288 | +0.979 |
| GR-Li | 17.1 | 1.736 | +0.929 |
| GR-Li+ | 52.8 | 1.771 | +0.937 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tachikawa, H.; Yi, H.; Iyama, T.; Yamasaki, S.; Azumi, K. Hydrogen Storage Mechanism in Sodium-Based Graphene Nanoflakes: A Density Functional Theory Study. Hydrogen 2022, 3, 43-52. https://doi.org/10.3390/hydrogen3010003
Tachikawa H, Yi H, Iyama T, Yamasaki S, Azumi K. Hydrogen Storage Mechanism in Sodium-Based Graphene Nanoflakes: A Density Functional Theory Study. Hydrogen. 2022; 3(1):43-52. https://doi.org/10.3390/hydrogen3010003
Chicago/Turabian StyleTachikawa, Hiroto, Heewon Yi, Tetsuji Iyama, Shuhei Yamasaki, and Kazuhisa Azumi. 2022. "Hydrogen Storage Mechanism in Sodium-Based Graphene Nanoflakes: A Density Functional Theory Study" Hydrogen 3, no. 1: 43-52. https://doi.org/10.3390/hydrogen3010003
APA StyleTachikawa, H., Yi, H., Iyama, T., Yamasaki, S., & Azumi, K. (2022). Hydrogen Storage Mechanism in Sodium-Based Graphene Nanoflakes: A Density Functional Theory Study. Hydrogen, 3(1), 43-52. https://doi.org/10.3390/hydrogen3010003





