Blocking Hydrogen Diffusion in Palladium Cathode i—Analyzed by Electrochemistry; ii—Analyzed by Chaos
Abstract
:1. Introduction
1.1. Hydrogen Interest
1.2. Electrochemistry and Chaos
- (a)
- the exchange power between adsorbed hydrogen transients,
- (b)
- the divergence topology when diffusion is blocked.
- (a)
- subsurface diffusion,
- (b)
- diffusion over the thickness of palladium.
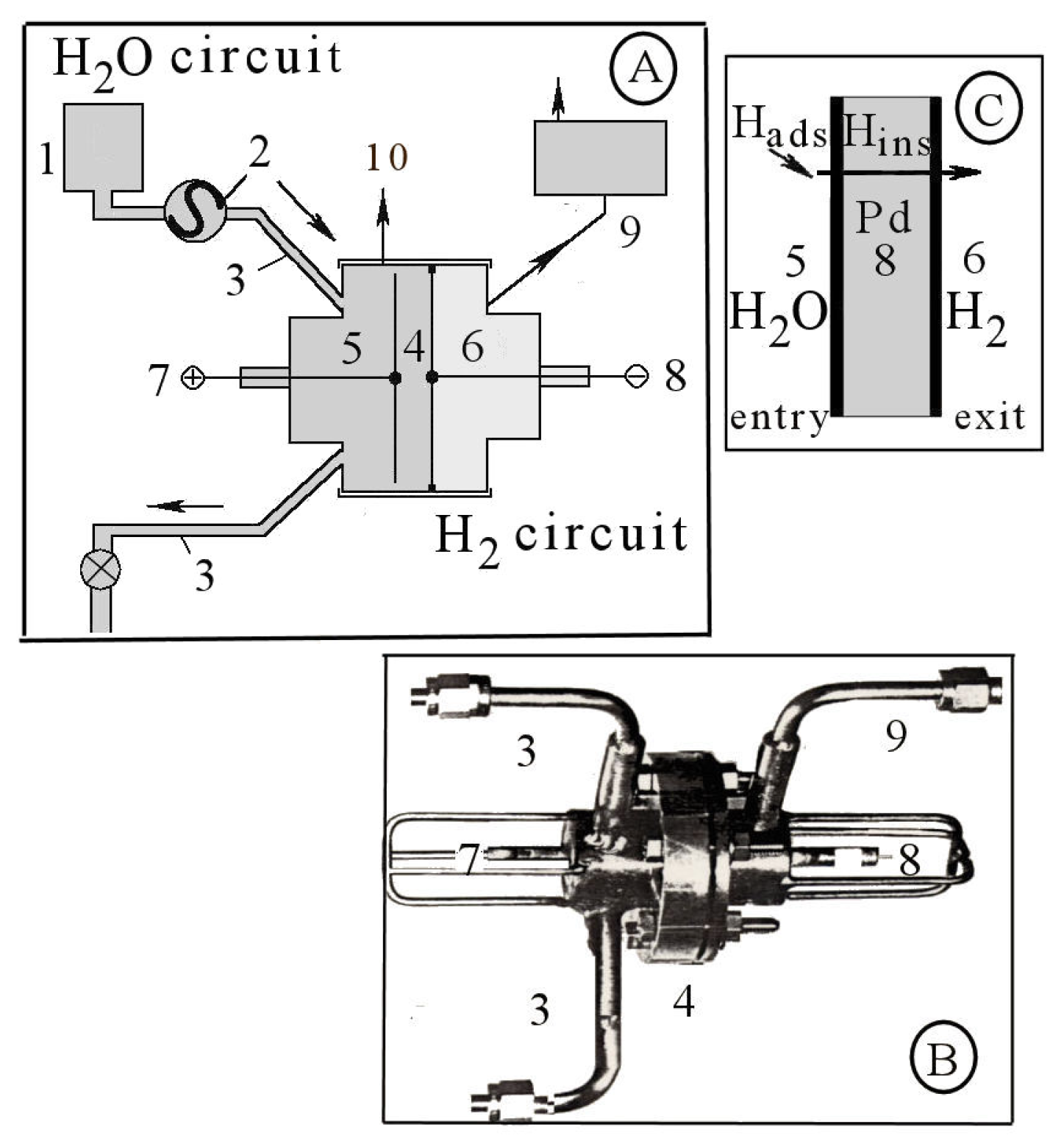
2. Methods and Materials
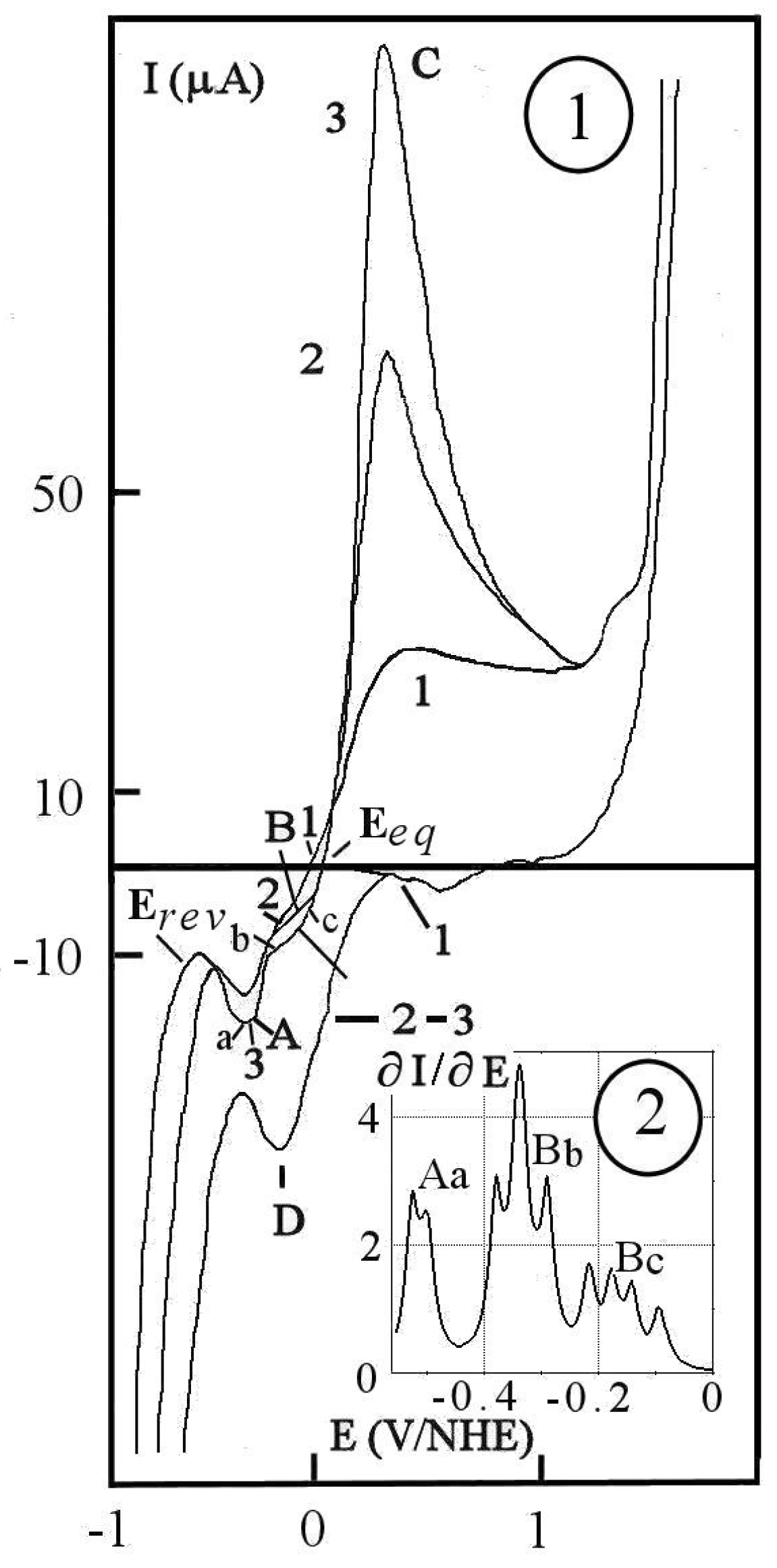
3. Scanning Voltammetry
- (A)
- peak A for hydrogen adsorption on the forward scan,
- (B)
- shoulder B for the second hydrogen adsorption,
- (C)
- peak C for oxidation of back-diffused hydrogen and palladium,
- (D)
- peak D for hydrogen adsorption on the return scan.
- (a)
- a on the peak A,
- (b)
- b between peak A and shoulder B,
- (c)
- c between shoulder and equilibrium potential.
- 1
- a model for constraint charging by mono-atomic hydrogen from the reversible potential,
- 2
- and a cathodic charging model at the equilibrium potential where the mono-atomic hydrogen intervenes.
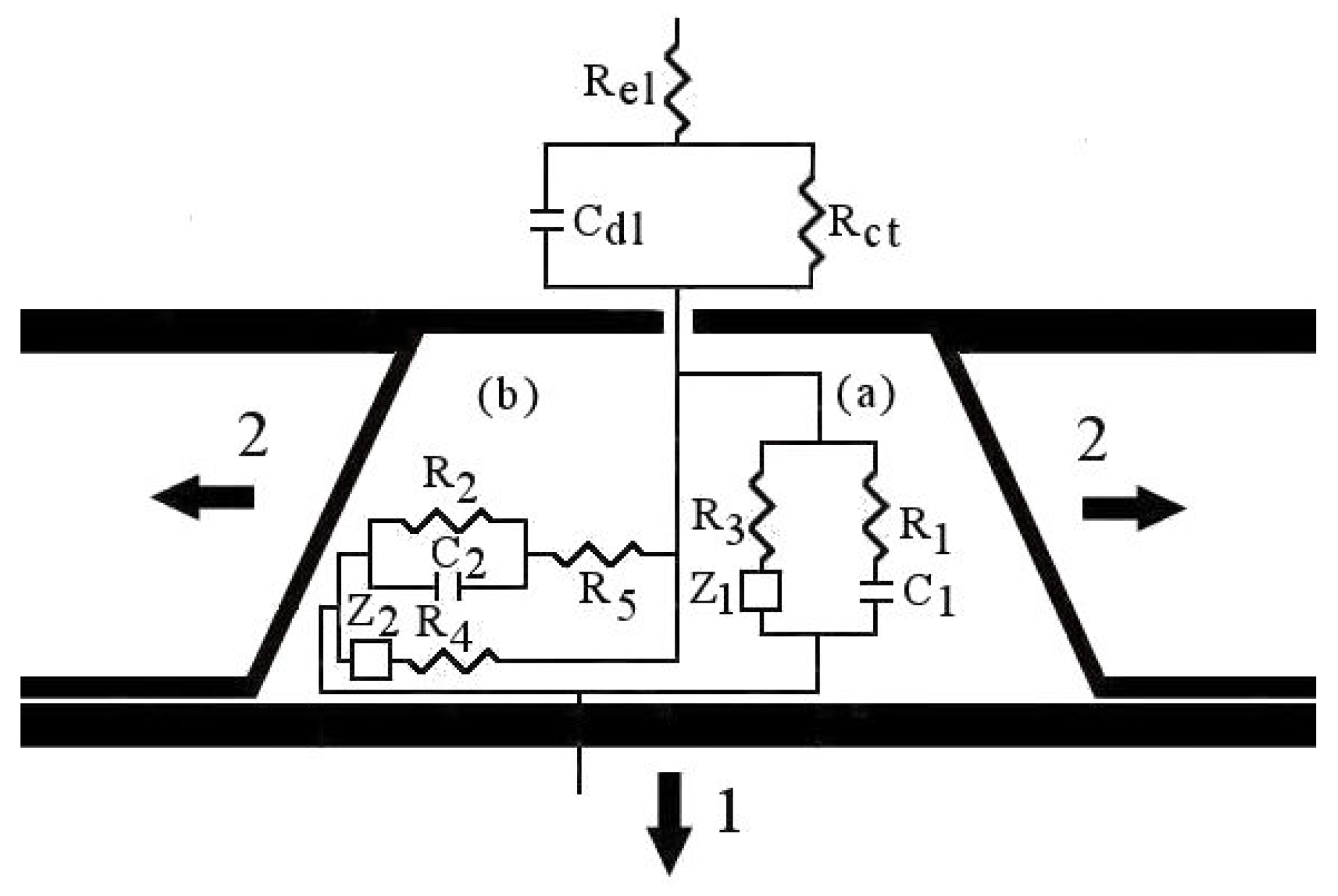
4. Electrochemical Impedance Spectroscopy
4.1. Measurements in the Reversible Potential
4.2. Transient Rearrangement and Overlapping
4.3. Measurements in the Equilibrium Potential
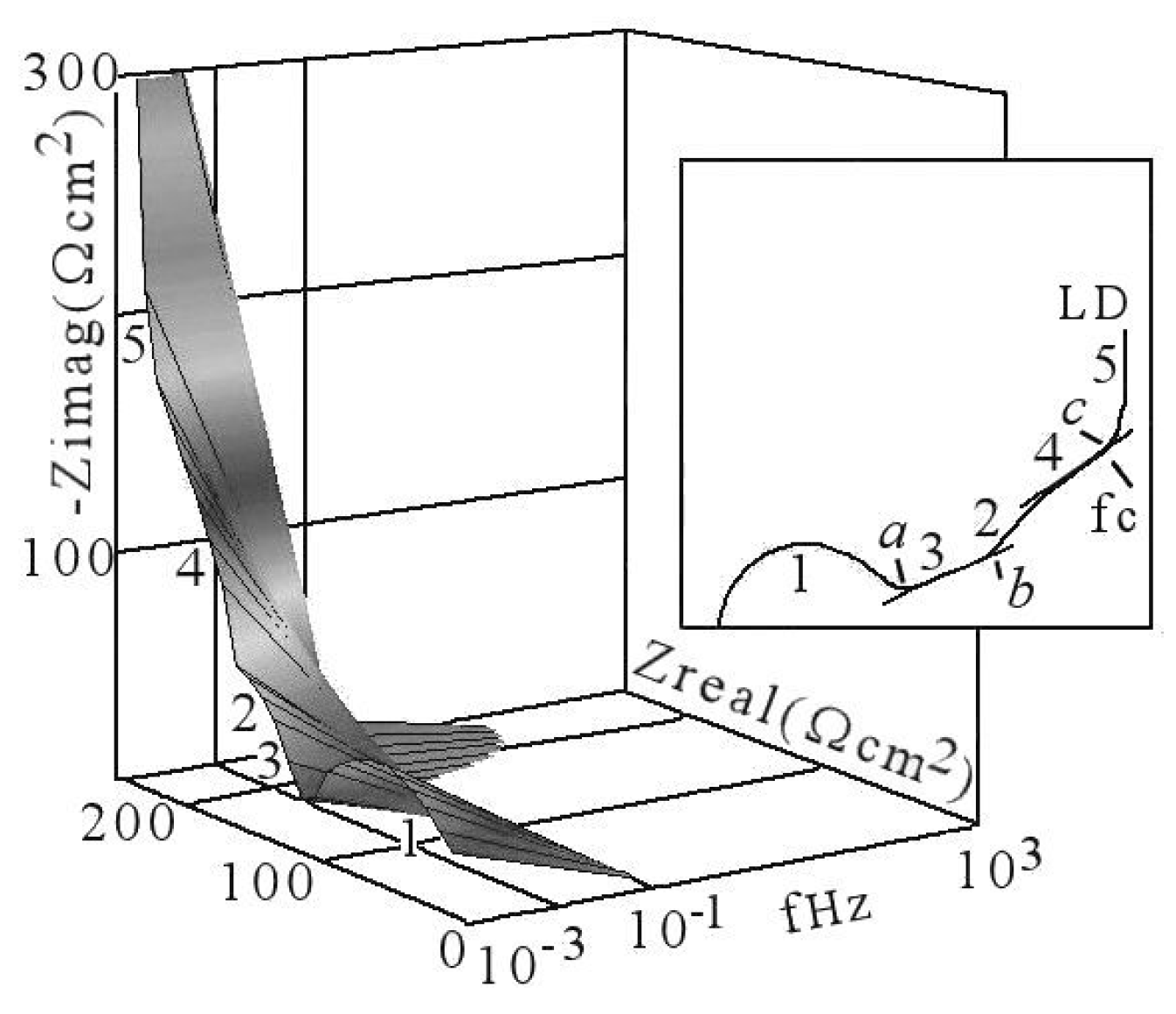
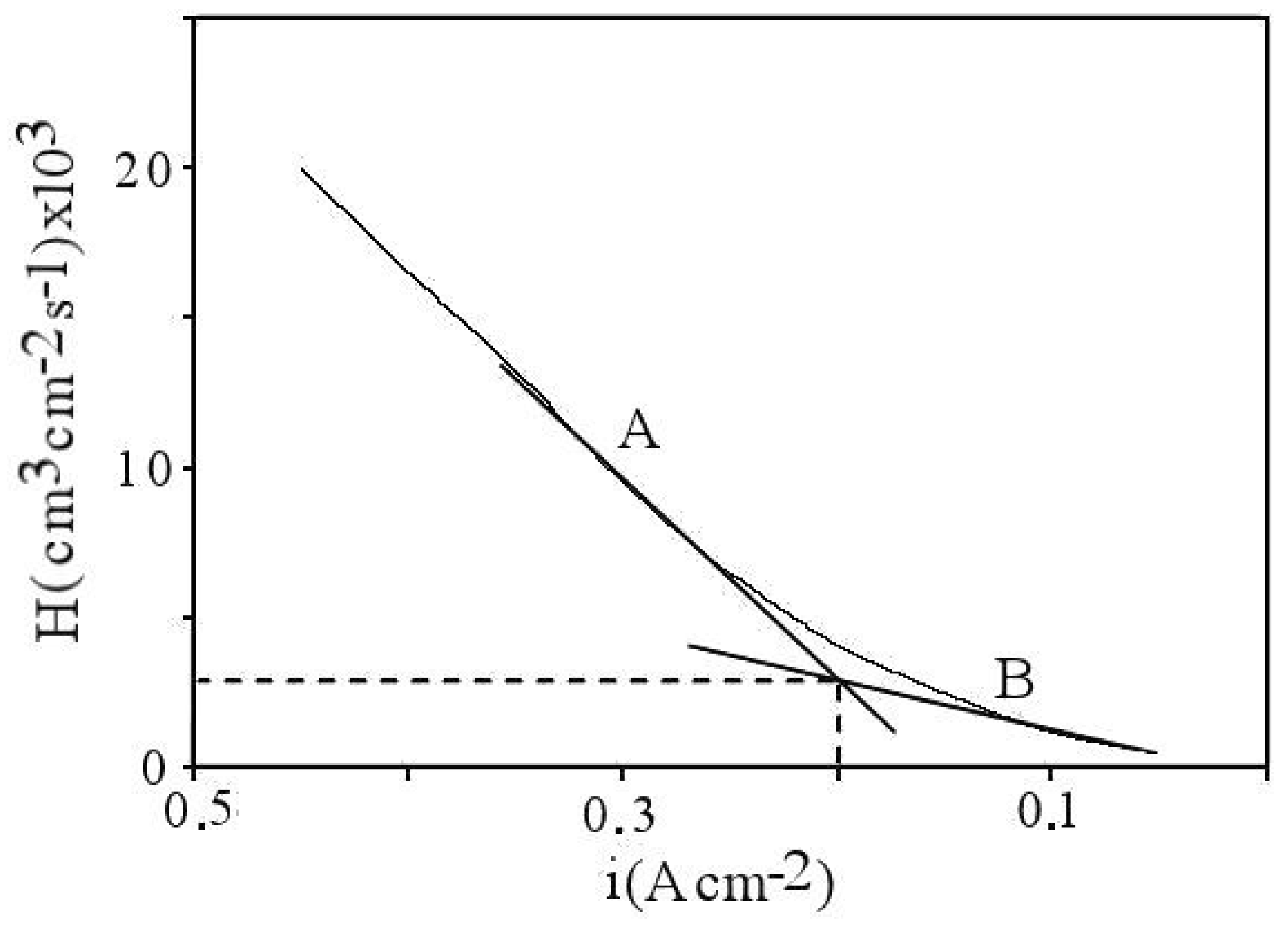
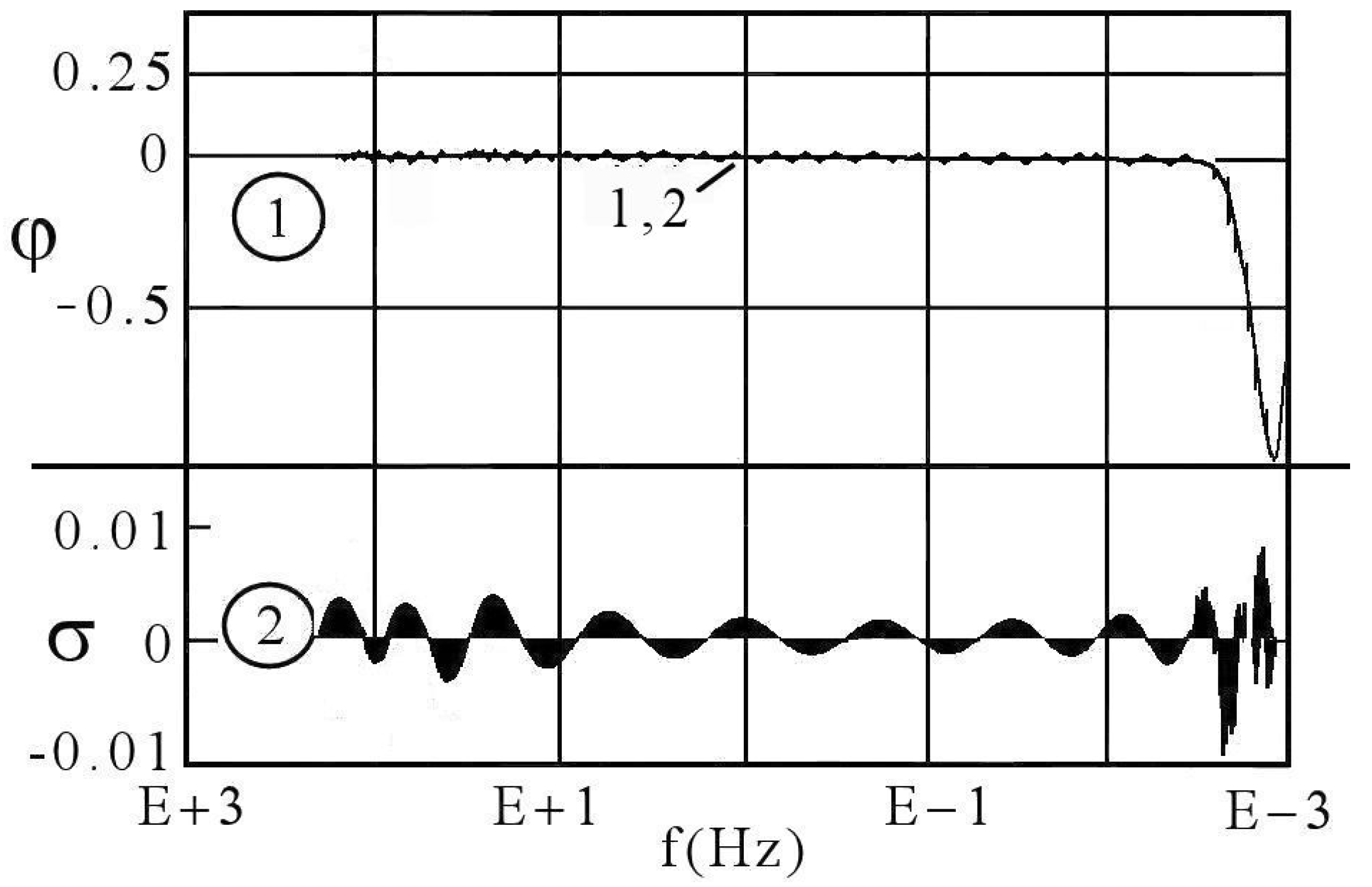
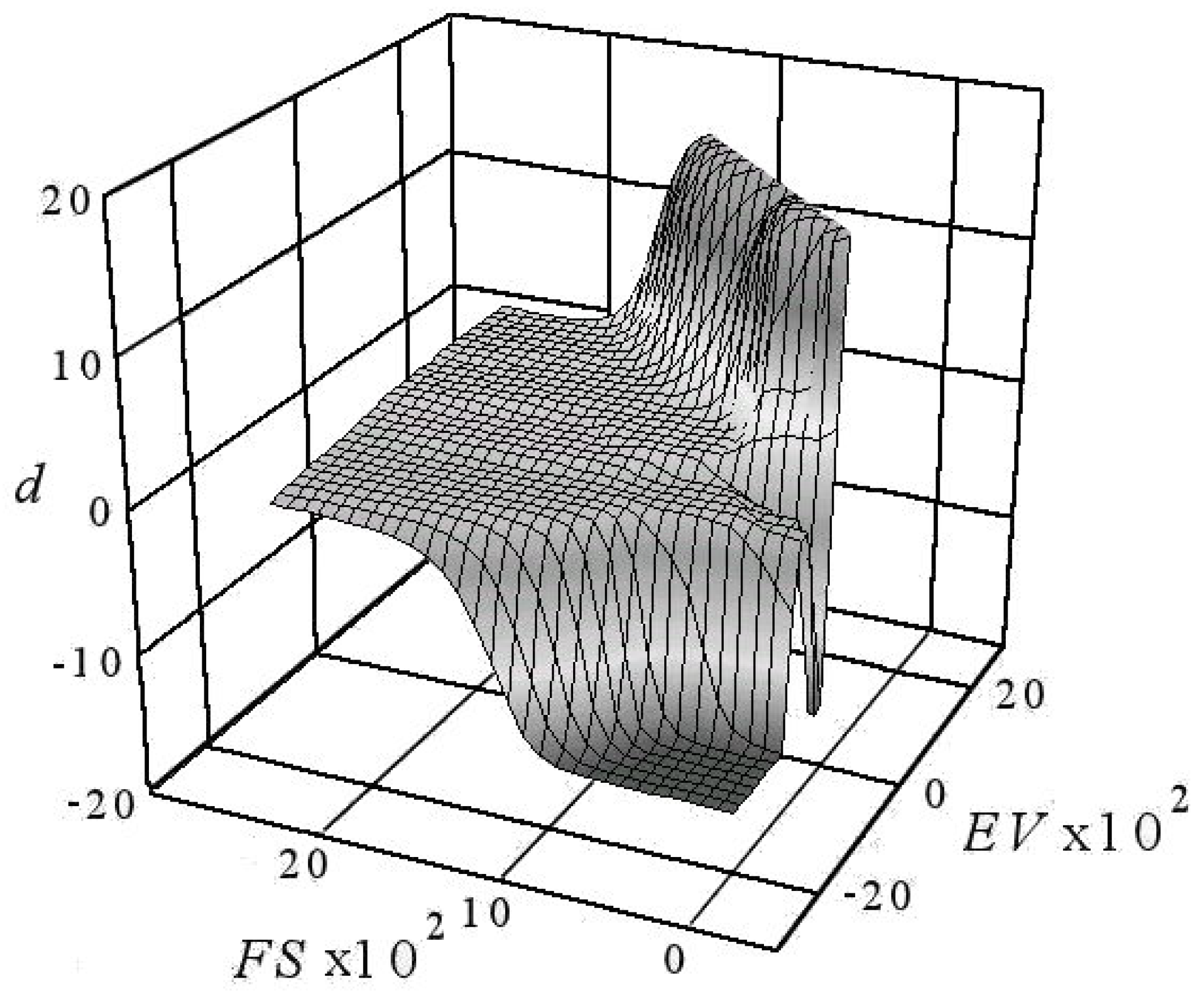
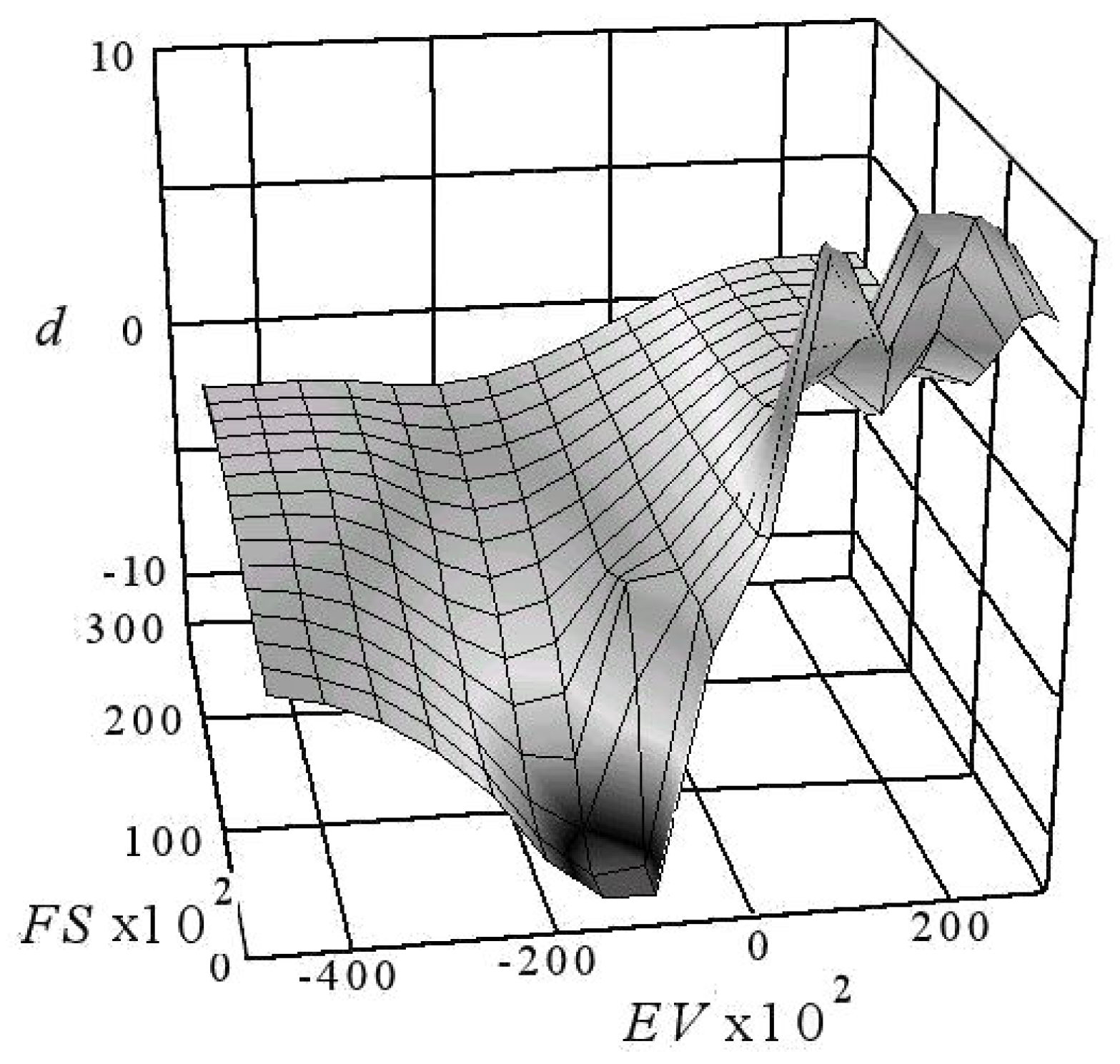
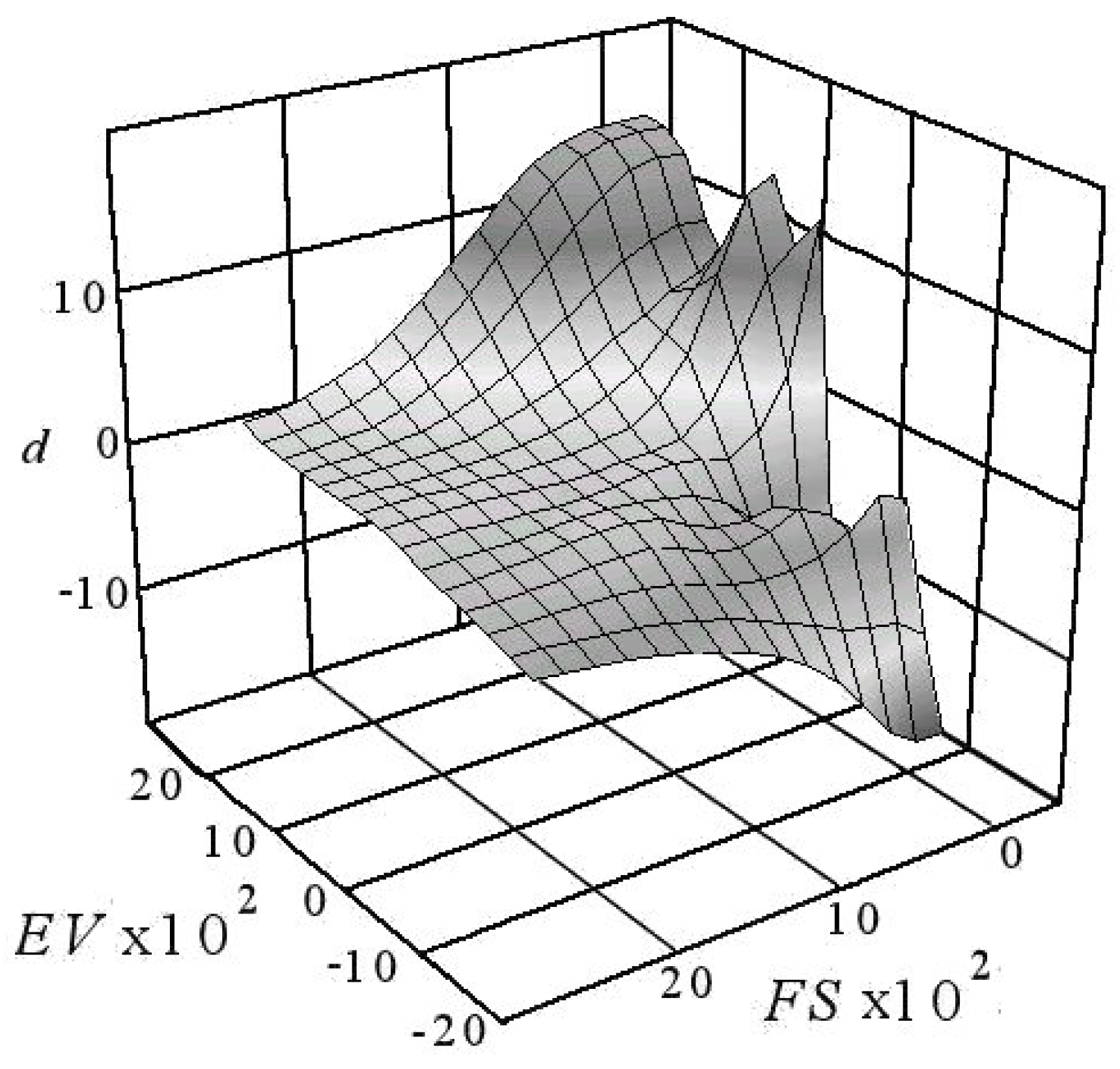
5. Interpreting the Limited Diffusion
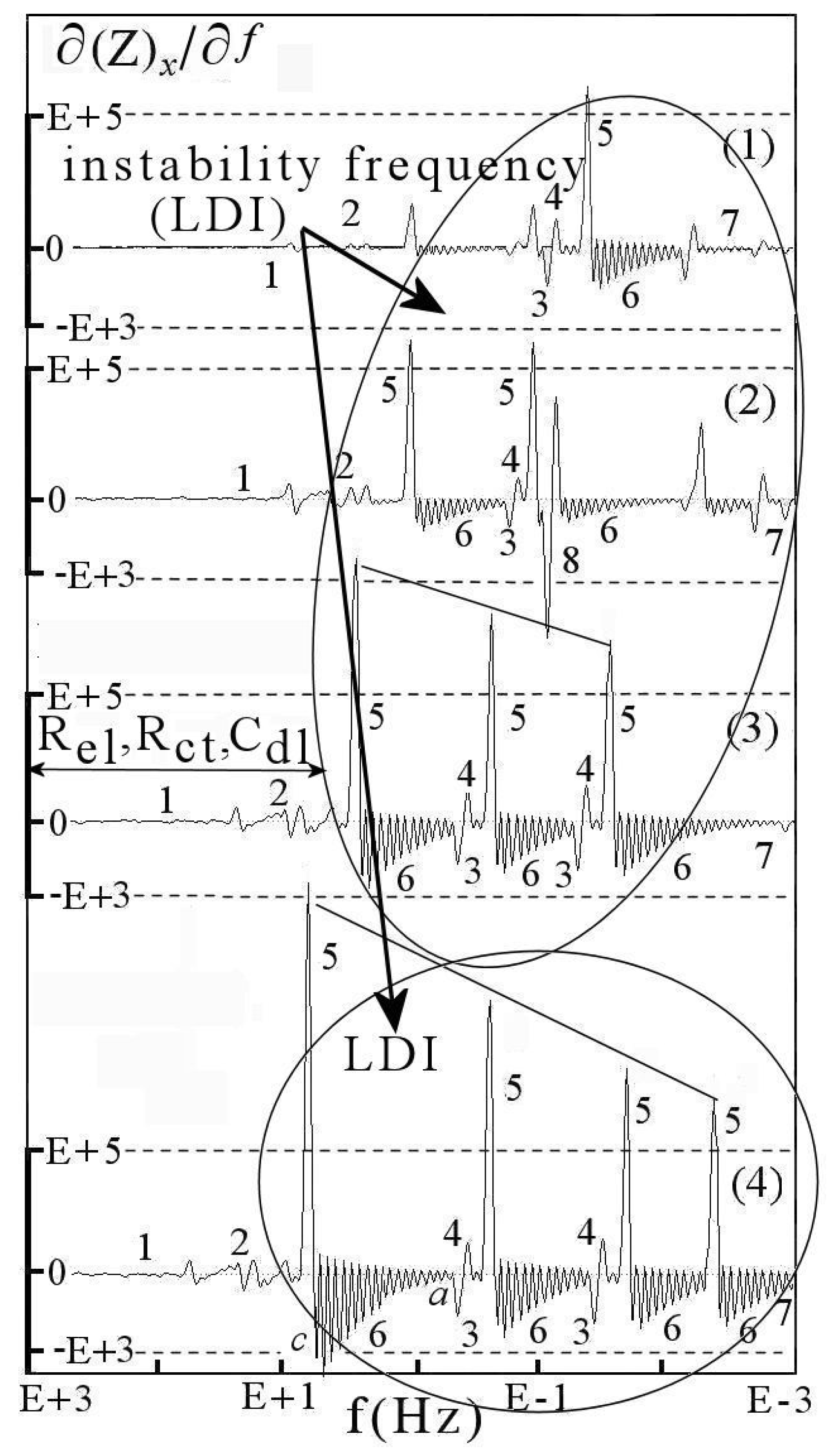
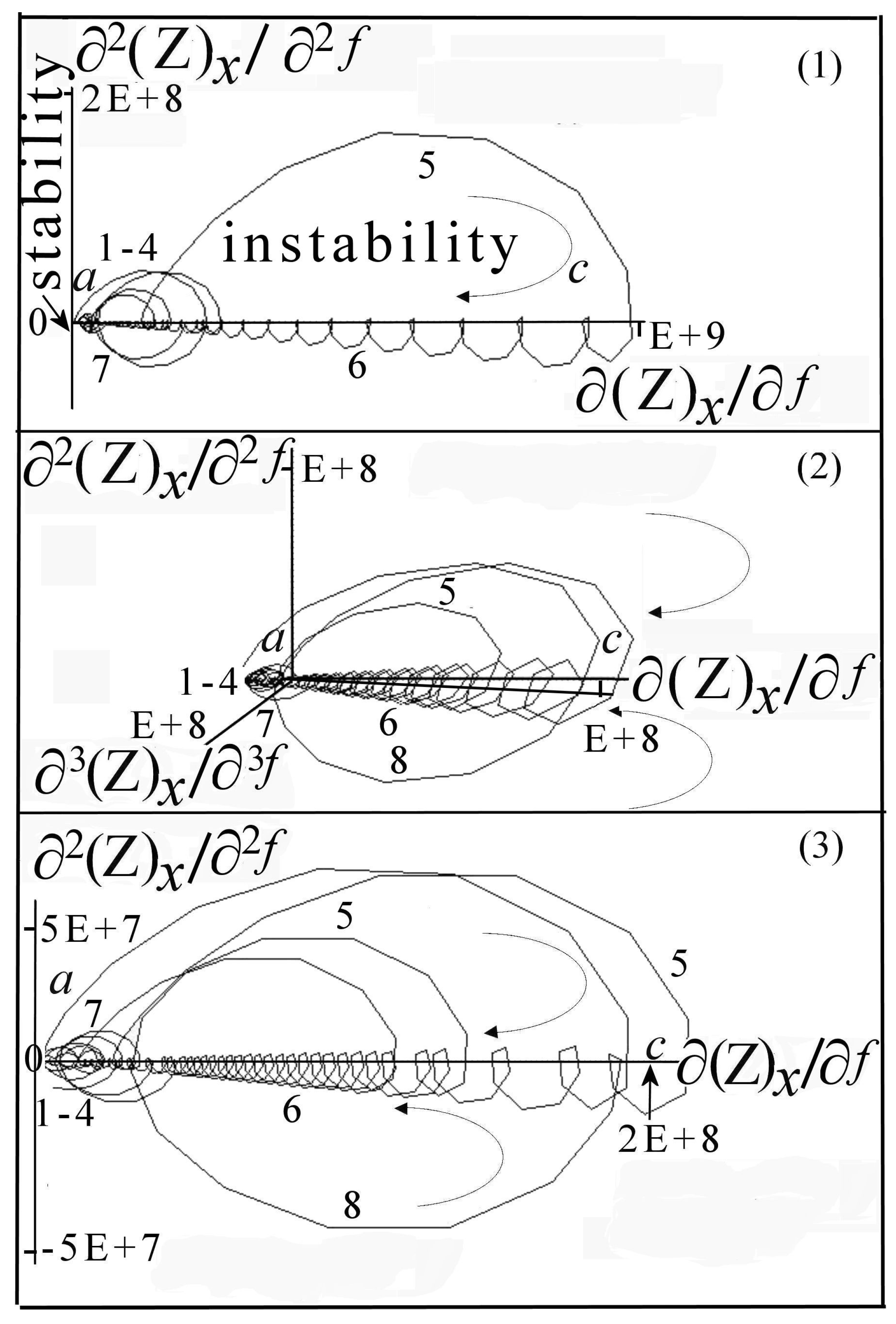
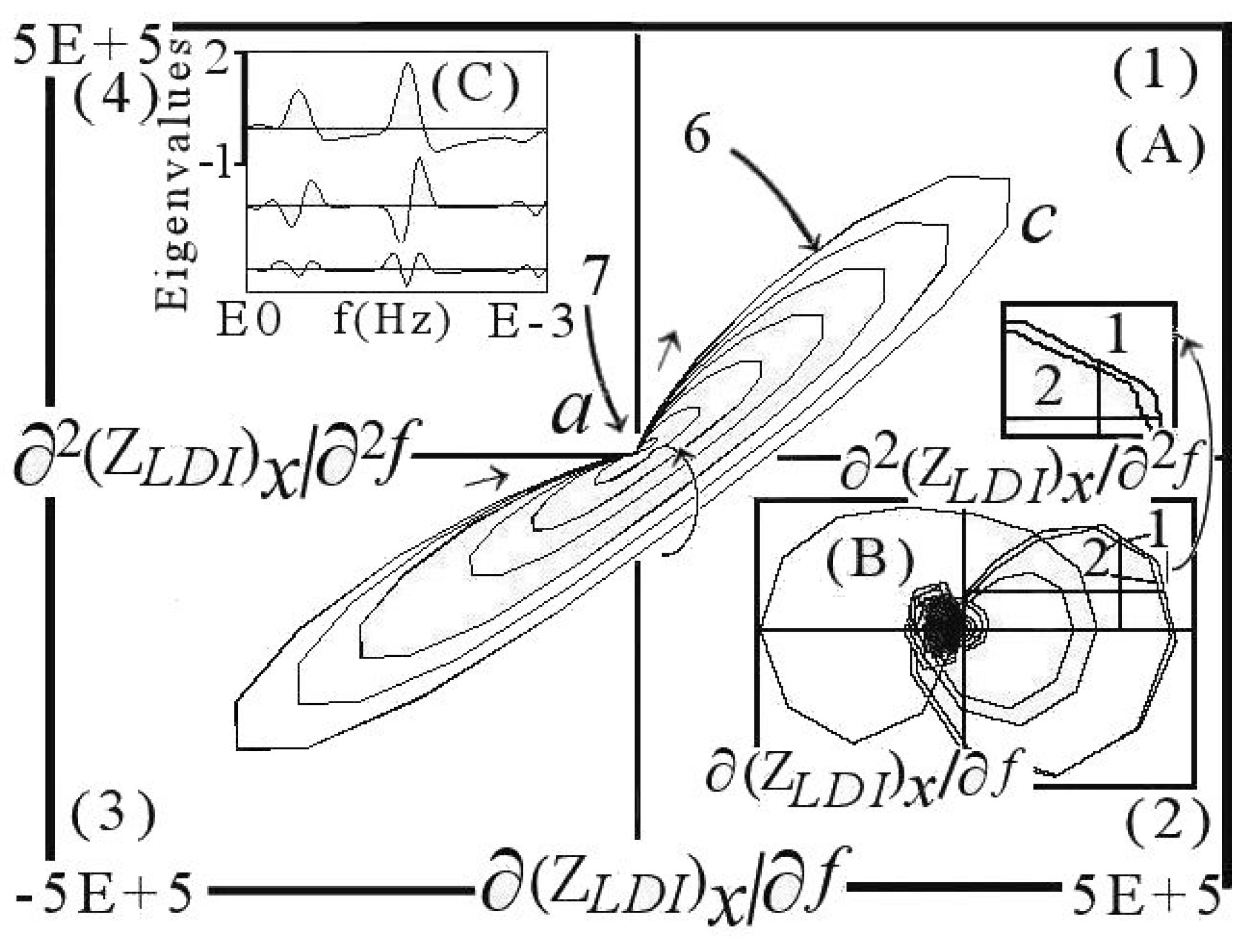
6. DescriptiveInformation of Chaos Analyzer
7. Analysis of Models and Result Projection
7.1. Measurements in the Reversible Potential
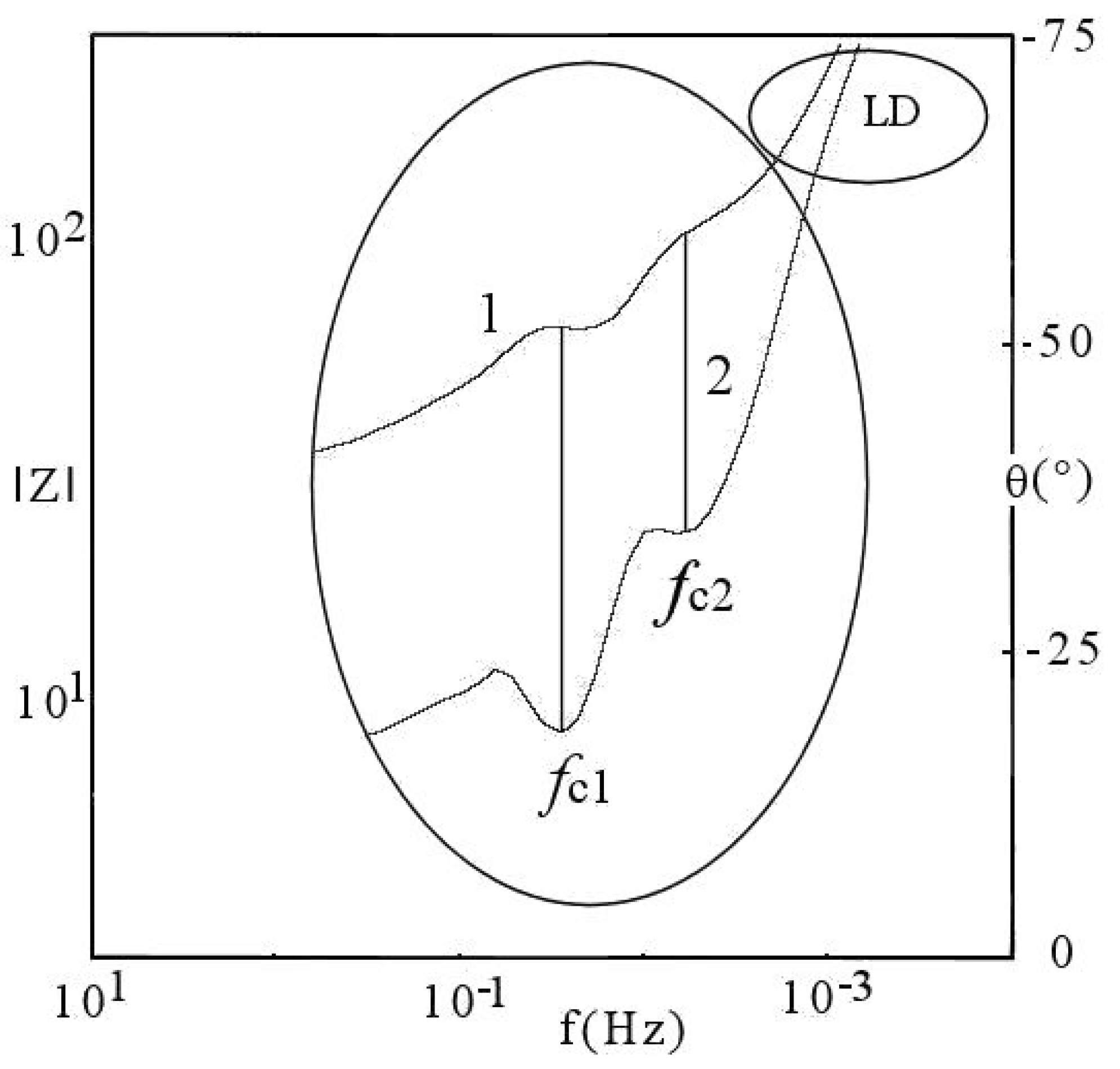
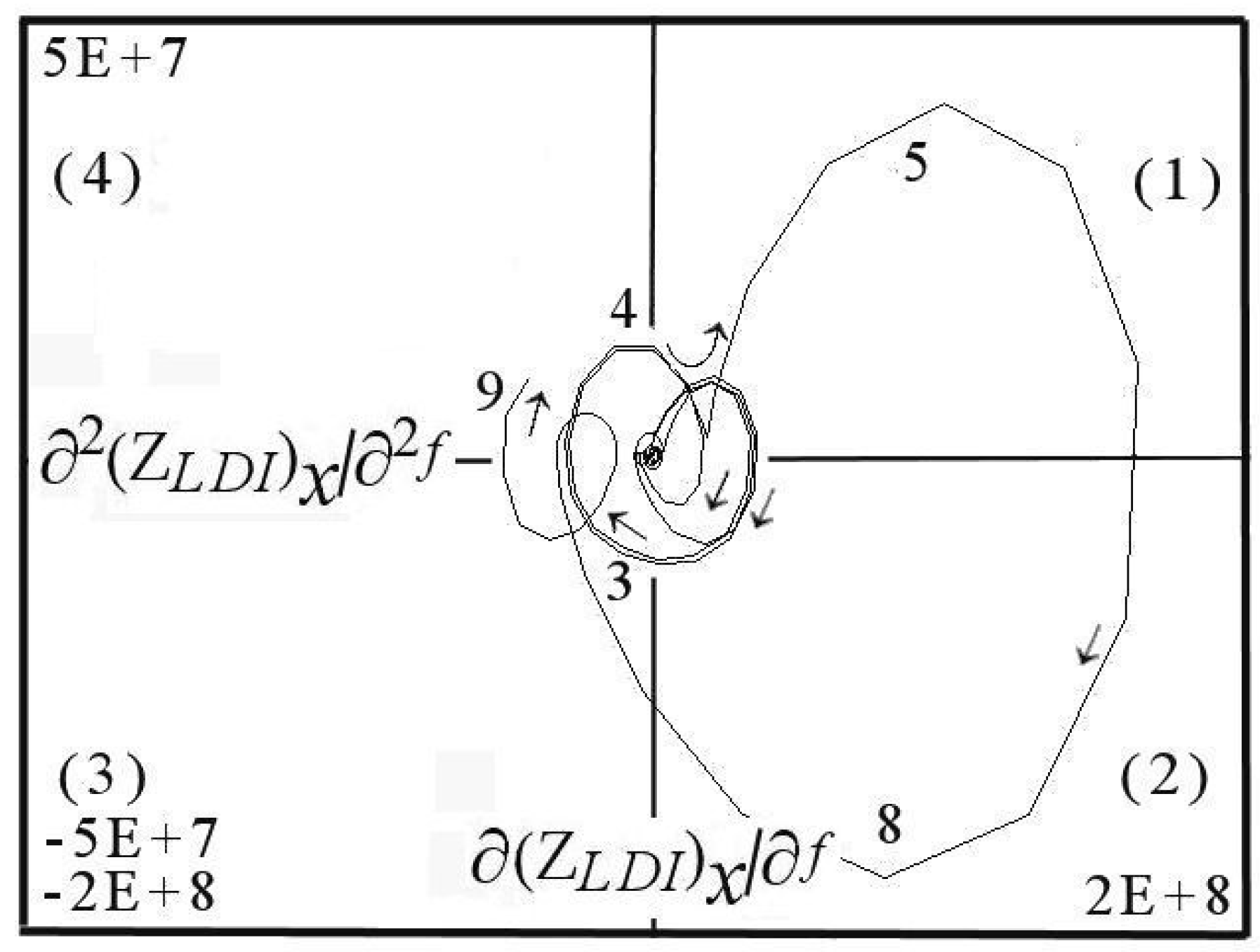
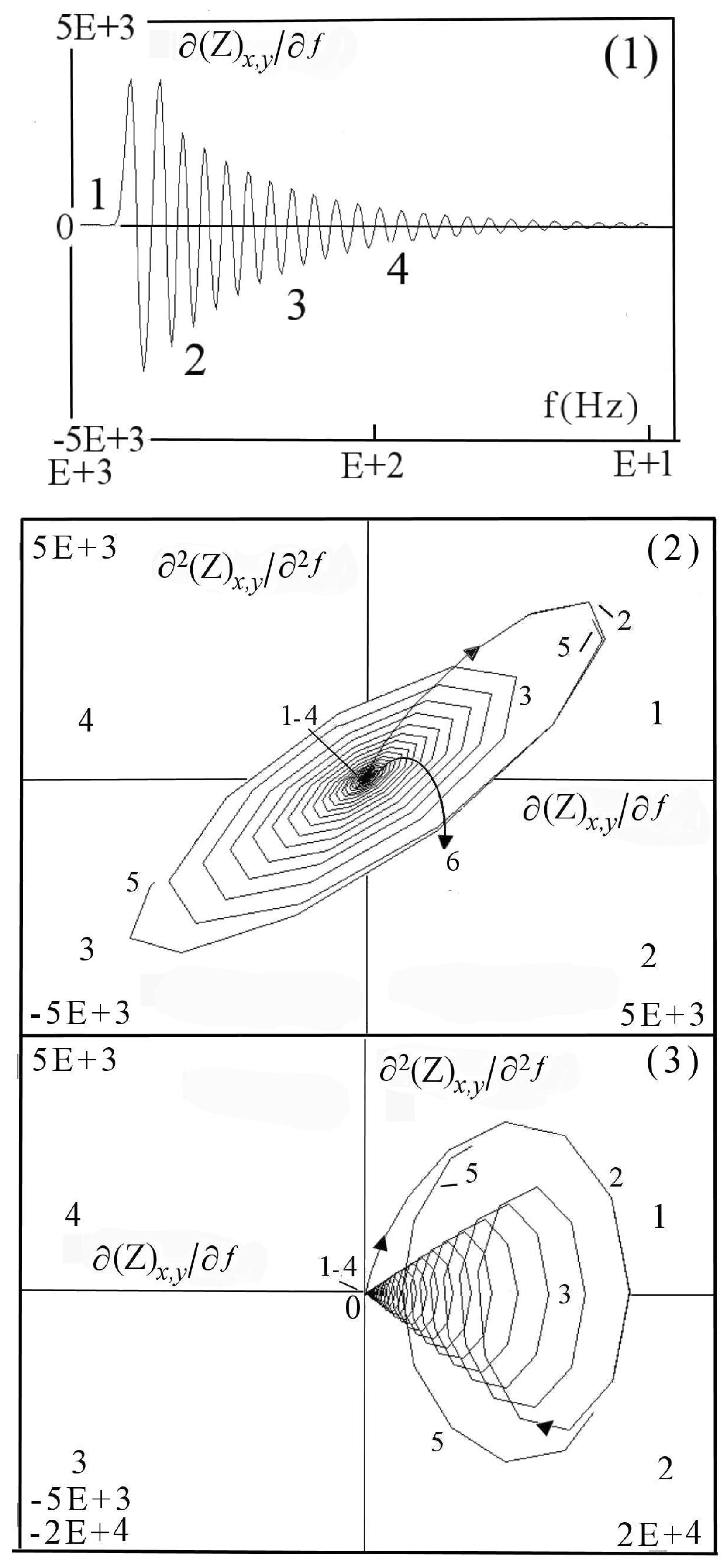
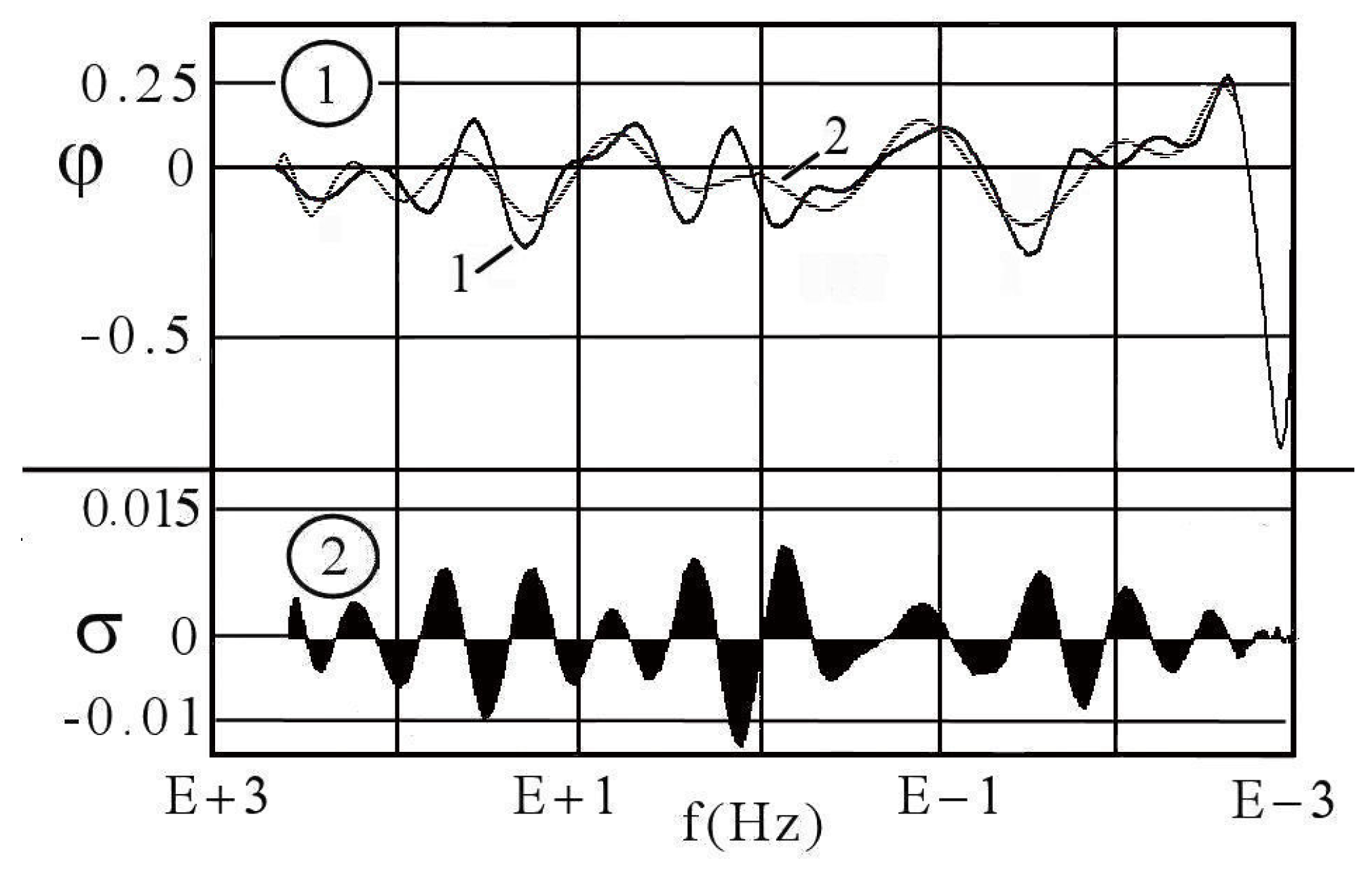
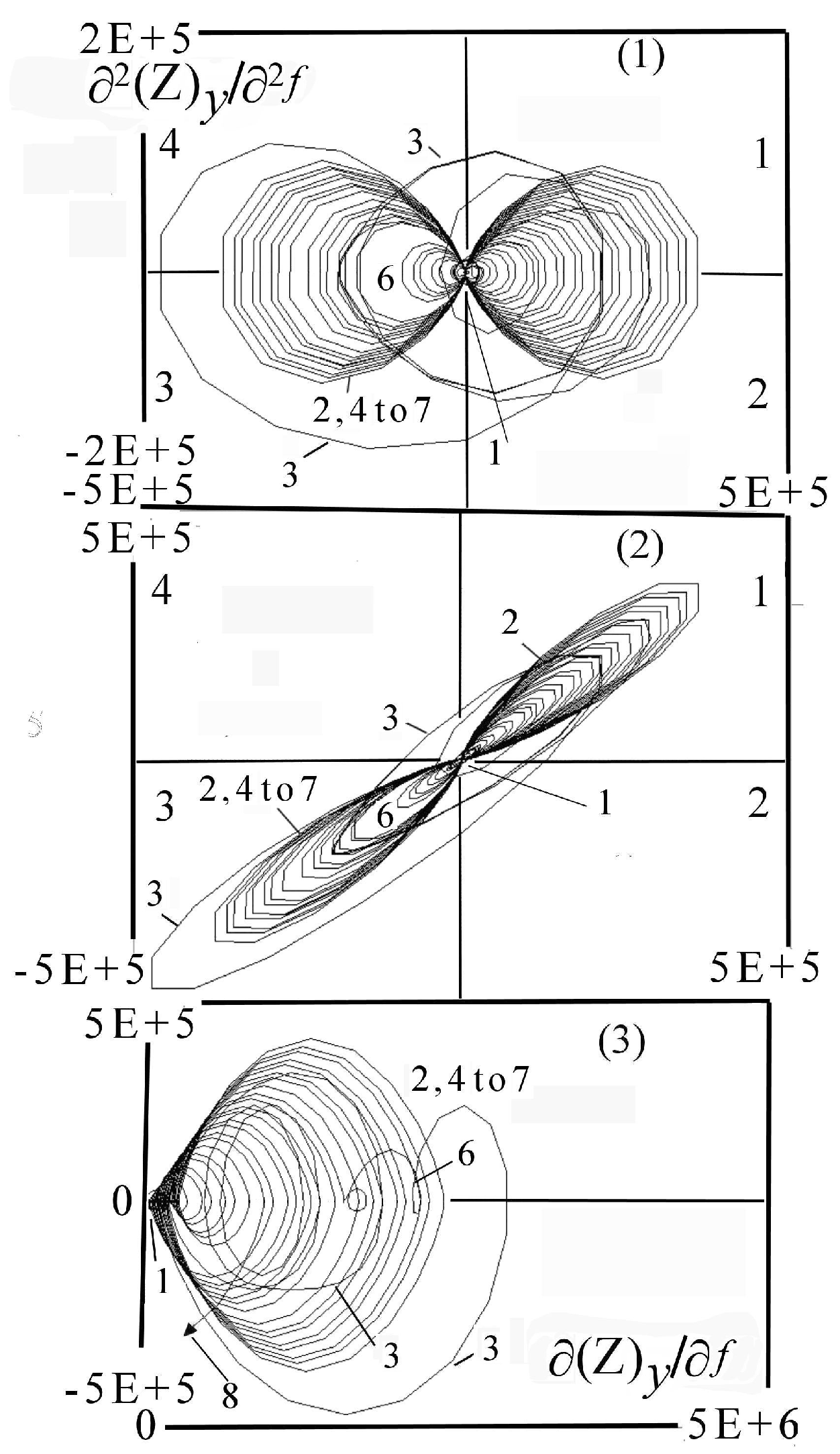
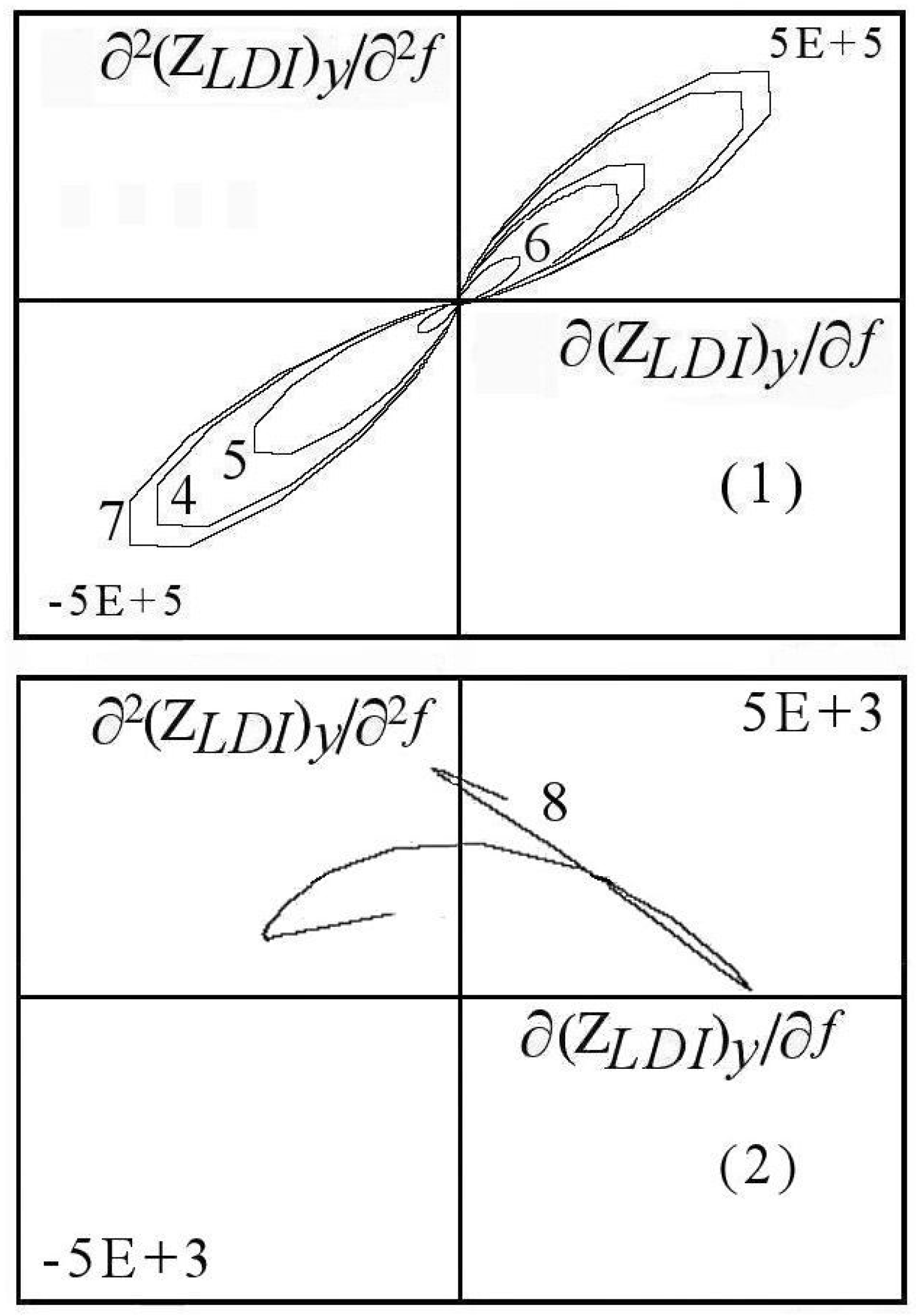
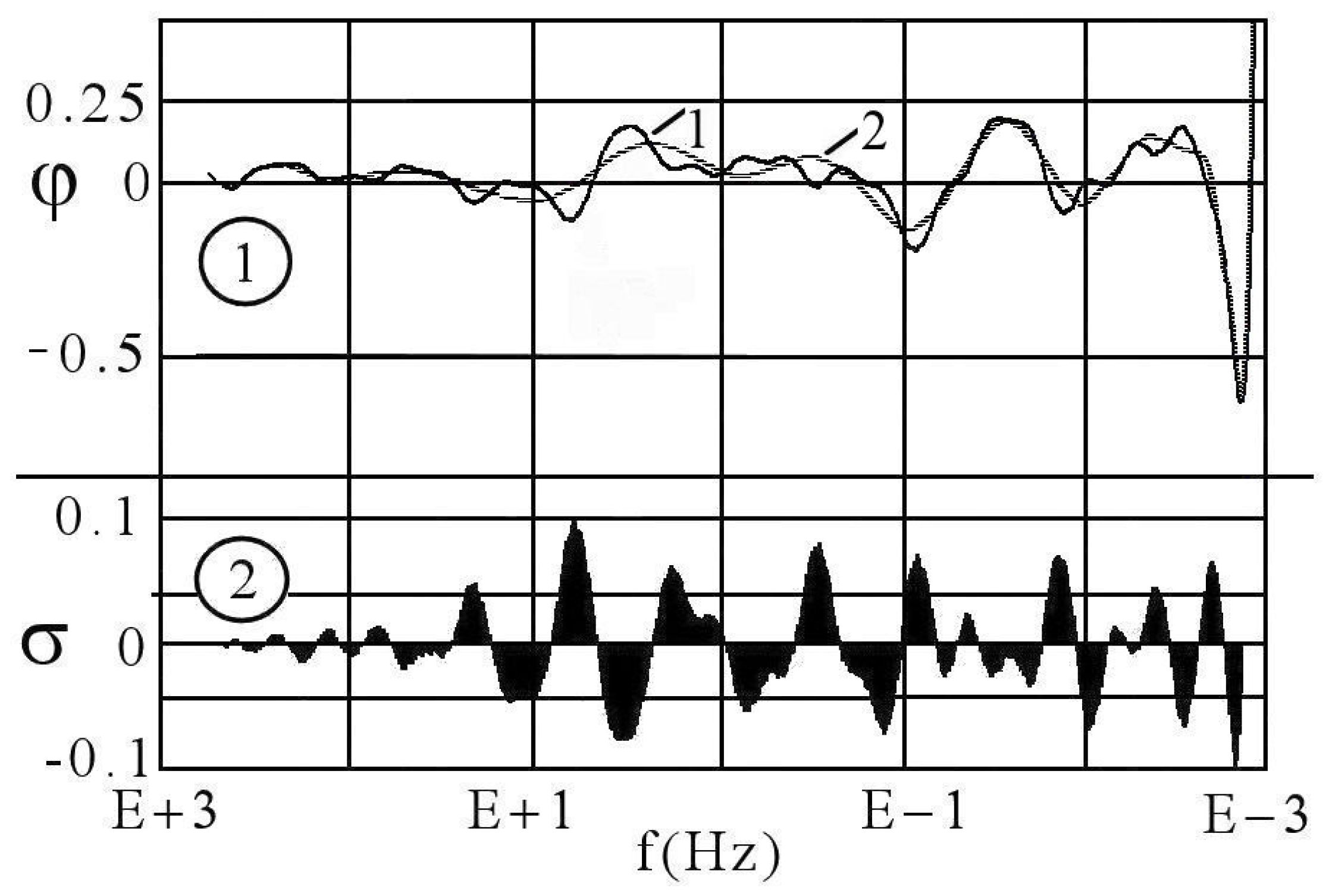
7.1.1. Aspects of Global Spectra
- (a)
- continuous line corresponding to capacitive and resistive effect (event 1),
- (b)
- minor positive instability and negative signal (events 2 to 4),
- (c)
- significant instability scaled highly positive (event 5),
- (d)
- which could be synchronized with negative signal (event 8),
- (e)
- decreasing small negative periodic oscillations (event 6),
- (f)
- and possible metastable line before stability (event 7).
7.1.2. Aspects of Local Sectors in Spectra
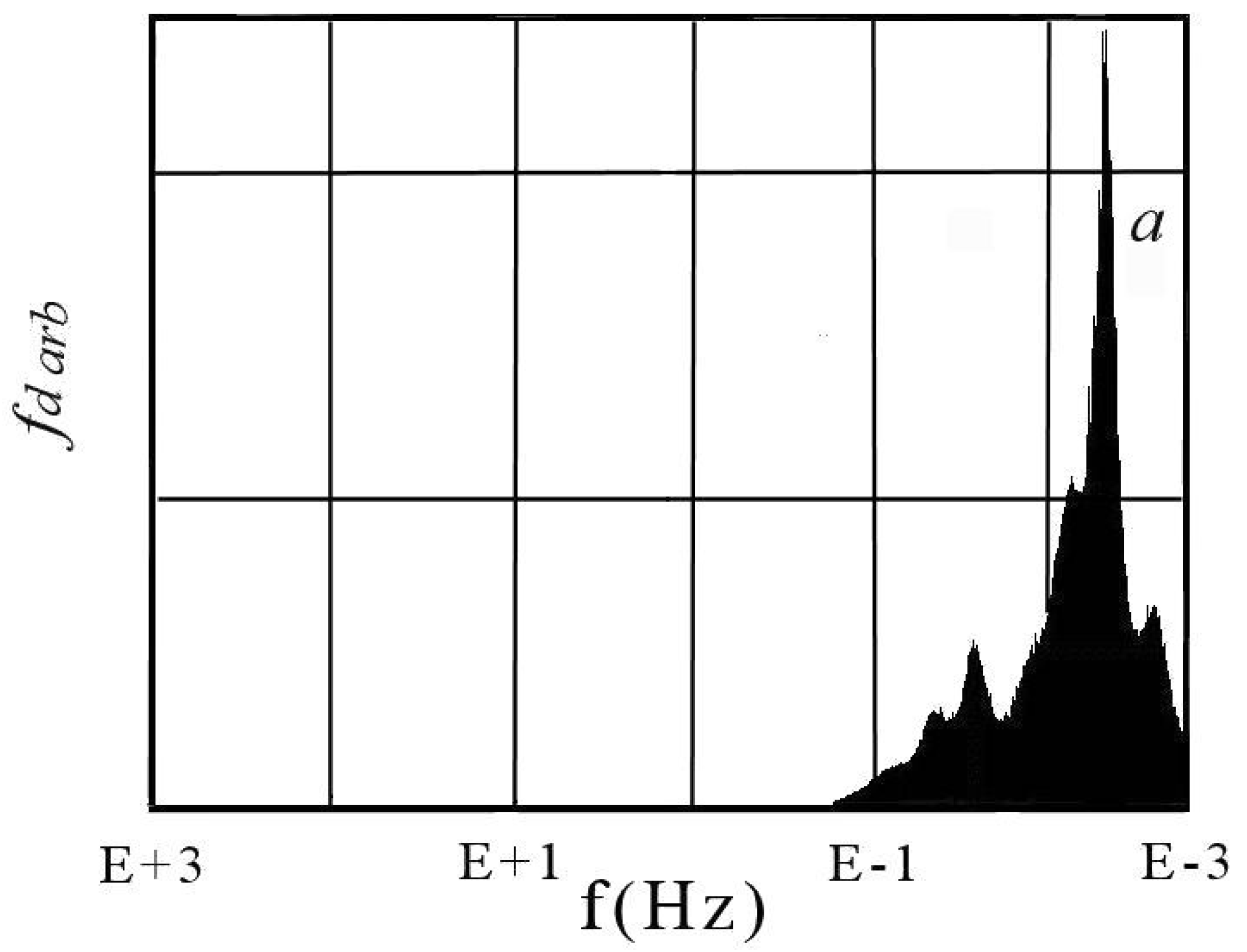
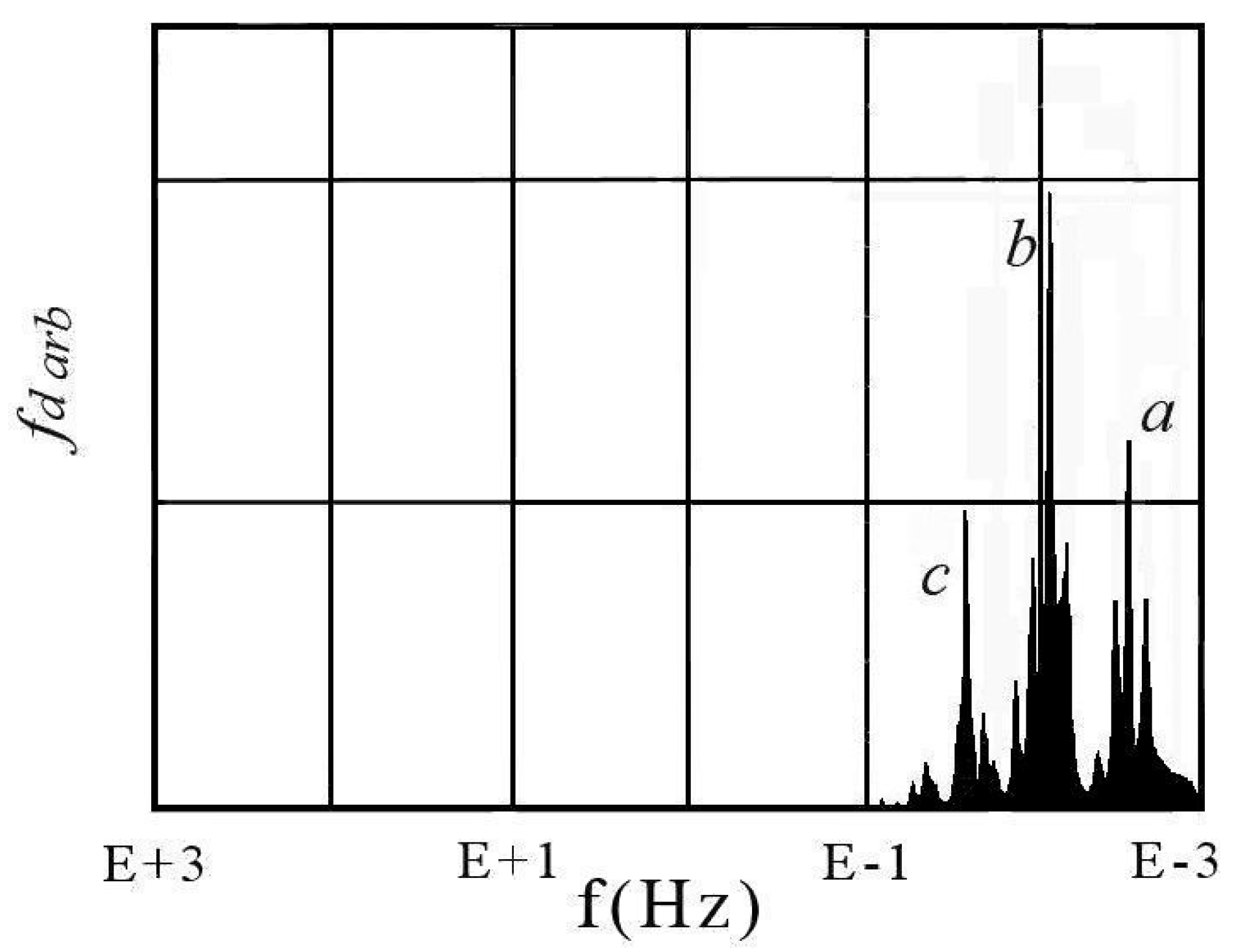
7.1.3. Aspects of Power Spectra
7.2. Transient Rearrangement and Overlapping
7.2.1. Aspects of Local Spectra at High Frequency
7.2.2. Aspects of Local Spectra at Low Frequency
7.2.3. Aspects of Power Spectra
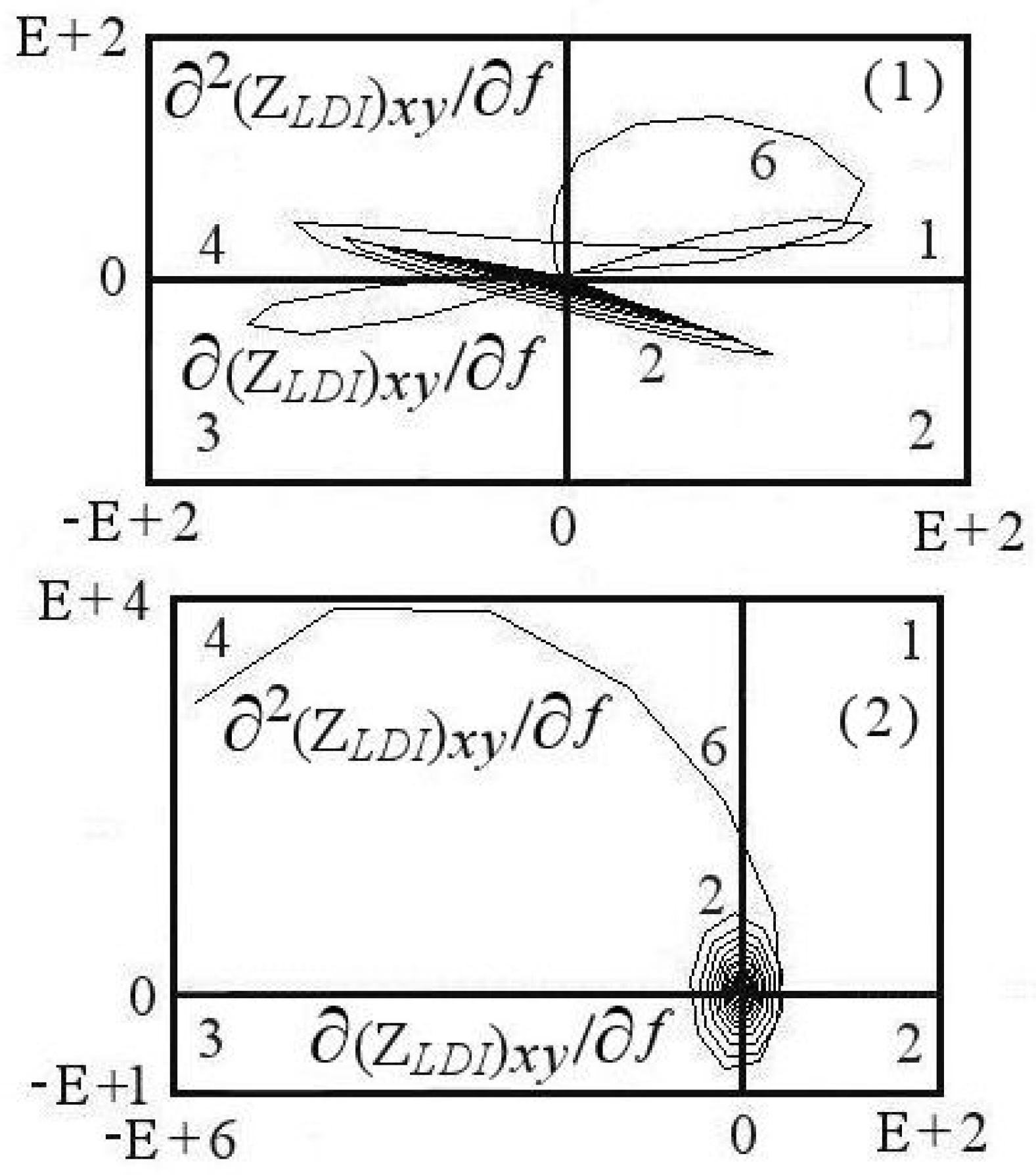
7.3. Measurements in the Equilibrium Potential
7.3.1. Aspects of Local Spectra
7.3.2. Aspects of Power Spectra
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Conde, J.J.; Marono, M.; Sanchez-Hervas, J.M. Pd-based membranes for hydrogen separation: Review of alloying elements and their influence on membrane properties. Sep. Purif. Rev. 2017, 46, 152–177. [Google Scholar] [CrossRef]
- Watanabe, N.; Yukawa, H.; Nambu, T.; Matsumoto, Y.; Zhang, G.X.; Morinaga, M. Alloying effects of Ru and W on the resistance to hydrogen embrittlement and hydrogen permeability of niobium. J. Alloys Compd. 2009, 477, 851–854. [Google Scholar] [CrossRef]
- Lasser, R. Tritium and Helium-3 in Metals, Materials Science; Springer-Verlag Series in Materials Science: New York, NY, USA, 1989; Volume 9. [Google Scholar]
- Tosti, S. Overview of Pd-based membranes for producing pure hydrogen and state of art at ENEA laboratories. Int. J. Hydrog. Energy 2010, 35, 12650–12659. [Google Scholar] [CrossRef]
- Burkhanov, G.S.; Roshan, N.R.; Kolchugina, N.B.; Korenovsky, N.L.; Slovetsky, D.I.; Chistov, E. Palladium-based alloy membranes for separation of high-purity hydrogen from hydrogen containing gas mixtures. Platin. Met. 2011, 55, 3–12. [Google Scholar] [CrossRef]
- Burkhanov, G.S.; Roshan, N.R.; Kol’chugina, N.B.; Korenovskii, N.L. Palladium rare-earth metal alloys-Advanced materials for hydrogen power engineering. Metal 2006, 15, 409–413. [Google Scholar]
- Pozio, A.; de Francesco, M.; Jovanovica, Z.; Tosti, S. Pd-Ag hydrogen diffusion cathode for alkaline water electrolysers. Int. J. Hydrog. Energy 2011, 36, 5211–5217. [Google Scholar] [CrossRef]
- Tosti, S.; Bettinali, L.; Violante, V. Rolled thin Pd and Pd-Ag membranes for hydrogen separation and production. Int. J. Hydrog. Energy 2000, 25, 319–325. [Google Scholar] [CrossRef]
- Paolone, A.; Tosti, S.; Santucci, A.; Palumbo, O.; Trequattrini, F. Hydrogen and deuterium solubility in commercial Pd-Ag alloys for hydrogen purification. ChemEngineering 2017, 1, 14. [Google Scholar] [CrossRef] [Green Version]
- Bellanger, S.; Rameau, J.J. Tritium recovery from tritiated water by electrolysis. Fusion Technol. 1999, 36, 296–308. [Google Scholar] [CrossRef]
- Muranaka, T.; Shima, N. Improved electrolyzer for enrichment of tritium concentrations in environmental water samples. Fusion Sci. Technol. 2008, 54, 297–300. [Google Scholar] [CrossRef]
- Bellanger, G. Changes of the breaking strain from content of tritium and cycling in a palladium cathode membrane. Fusion Eng. Des. 2011, 86, 357–362. [Google Scholar] [CrossRef]
- Bellanger, G. Prospecting stress formed by hydrogen or isotope diffused in palladium alloy cathode. Materials 2018, 11, 2101. [Google Scholar] [CrossRef] [Green Version]
- Thomas, J.; Hersbach, P.; Yanson, A.I.; Koper, M.T.M. Anisotropic etching of platinum electrodes at the onset of cathodic corrosion. Nat. Commun. 2016, 7, 12653. [Google Scholar] [CrossRef] [Green Version]
- Yanson, A.I.; Antonov, P.V.; Rodriguez, P.; Koper, M.T.M. Influence of the electrolyte concentration on the size and shape of platinum nanoparticles synthesized by cathodic corrosion. Electrochim. Acta 2013, 112, 913–918. [Google Scholar] [CrossRef]
- Ash, R.; Barrer, R.M. Diffusion with a concentration discontinuity: The hydrogen-palladium system. J. Phys. Chem. Solids 1960, 16, 246–252. [Google Scholar] [CrossRef]
- Xia, D.; Song, S.; Wang, J.; Shi, J.; Bi, H.; Gao, Z. Determination of corrosion types from electrochemical noise by phase space reconstruction theory. Electrochem. Commun. 2012, 15, 88–92. [Google Scholar] [CrossRef]
- Fernandez Macia, L.; Tourwe, E.; Pintelon, R.; Hubin, A. A new modeling method for determining electrochemical parameters from LSV experiments using the stochastic noise. Part I: Theory and validation. J. Electroanal. Chem. 2013, 690, 127–135. [Google Scholar] [CrossRef]
- Astafev, E. The instrument for electrochemical noise measurement of chemical power sources. Rev. Sci. Instrum. 2019, 90. [Google Scholar] [CrossRef]
- Rocha, P.R.F.; Schlett, P.; Kintzel, U.; Mailander, V.; Vandamme, L.K.J.; Zeck, G.; Gomes, H.L.; Biscarini, F.; de Leeuw, D.M. Electrochemical noise and impedance of Au electrode/electrolyte interfaces enabling extracellular detection of glioma cell populations. Nat. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Curioni, M.; Monetta, T.; Bellucci, F. Modeling data acquisition during electrochemical noise measurements for corrosion studies. Corros. Rev. 2015, 33, 187–194. [Google Scholar] [CrossRef]
- Jamali, S.S.; Zhao, Y.; Gao, Z.; Li, H.; Hee, A.C. In situ evaluation of corrosion damage using non-destructive electrochemical measurements. J. Ind. Eng. Chem. 2016, 43, 36–43. [Google Scholar] [CrossRef]
- Jamali, S.S.; Mills, D.J.; Cottis, R.A.; Lan, T.Y. Analysis of electrochemical noise measurement on an organically coated metal. Prog. Org. Coatings 2016, 96, 52–57. [Google Scholar] [CrossRef] [Green Version]
- Homborg, A.M.; Cottis, R.A.; Mol, J.M.C. An integrated approach in the time, Frequency and time-frequency domain for the identification of corrosion using electrochemical noise. Electrochim. Acta 2016, 222, 627–640. [Google Scholar] [CrossRef]
- Homborg, A.M.; van Westing, E.P.M.; Tinga, T.; Ferrari, G.M.; Zhang, X.; de Wit, J.H.W.; Mol, J.M.C. Application of transient analysis using Hilbert spectra of electrochemical noise to the identification of corrosion inhibition. Electrochim. Acta 2014, 116, 355–365. [Google Scholar] [CrossRef]
- Grafov, B.M. Theory of the first encounter with the boundary by a stochastic diffusion process in an equilibrium electrochemical RC-circuit. Russ. J. Electrochem. 2016, 52, 885–889. [Google Scholar] [CrossRef]
- Grafov, B.M. The fractal theory of electrochemical diffusion noise: Correlations of the third and fourth order. Russ. Electrochem. 2016, 52, 220–225. [Google Scholar] [CrossRef]
- Grafov, B.M. Fractal theory of electrochemical diffusion noise. Russian J. Electrochem. 2015, 51, 1–6. [Google Scholar] [CrossRef]
- Banerjee, S.; Rondoni, L. Chaos, transport and diffusion—Applications of chaos and nonlinear dynamics in science and engineering. Springer Ser. 2015, 4, 31–63. [Google Scholar]
- Garcia, E.; Hernandez, M.A.; Rodriguez, F.J.; Genesca, J.; Boerio, F.J. Oscillation and chaos in pitting corrosion of steel. Corrosion 2003, 59, 50–58. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.-J.; Xia, D.-H.; Song, S.-Z. Detection of SCC of 304 NG stainless steel in an acidic NaCl solution using electrochemical noise based on chaos and wavelet analysis. Russ. Electrochem. 2016, 52, 560–575. [Google Scholar] [CrossRef]
- Bahrami, M.J.; Hosseini, S.M.A.; Shahidi, M. Comparison of electrochemical current noise signals arising from symmetrical and asymmetrical electrodes made of Al alloys at different pH values using statistical and wavelet analysis. Part II: Alkaline solutions. Electrochim. Acta 2014, 148, 249–260. [Google Scholar] [CrossRef]
- Ortiz Alonso, C.J.; Arely, L.G.M.; Hermoso-Diaz, I.A.; Chacon-Nava, J. Detection of sulfide stress cracking in a supermartensitic stainless steel by using electrochemical noise. Int. J. Electrochem. Sci. 2014, 9, 6717–6733. [Google Scholar]
- Astafev, E.A.; Ukshe, A.E.; Dobrovolsky, Y.A. The model of electrochemical noise of a hydrogen-air fuel cell. J. Electrochem. Soc. 2018, 165, F604–F612. [Google Scholar] [CrossRef]
- Astafev, E.A.; Ukshe, A. Flicker noise spectroscopy in the analysis of electrochemical noise of hydrogen-air PEM fuel cell during its degradation. Int. J. Electrochem. Sci. 2017, 12, 1742–1754. [Google Scholar] [CrossRef]
- Lalik, E. Chaos in oscillatory sorption of hydrogen in palladium. J. Math. Chem 2014, 52, 2183–2196. [Google Scholar] [CrossRef] [Green Version]
- Denissen, P.J.; Homborg, A.M.; Garcia, S.J. Interpreting electrochemical noise and monitoring local corrosion by means of highly resolved spatiotemporal real-time optics. J. Electrochem. Soc. 2019, 166, C3275–C3283. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, X. Correlated pitting stages of 304 stainless steel with recurrence quantification analysis of electrochemical noise. Mater. Corros. 2019, 70, 197–205. [Google Scholar] [CrossRef]
- Hou, Y.; Aldrich, C.; Lepkova, K.; Machuca, L.L.; Kinsella, B. Monitoring of carbon steel corrosion by use of electrochemical noise and recurrence quantification analysis. Corros. Sci. 2016, 112, 63–72. [Google Scholar] [CrossRef] [Green Version]
- Huang, V.M.; Wu, S.-L.; Orazem, M.E.; Pebere, N.; Tribollet, B.; Vivier, V. Local electrochemical impedance spectroscopy: A review and some recent developments. Electrochim. Acta 2011, 56, 8048–8057. [Google Scholar] [CrossRef] [Green Version]
- Yule, L.C.; Daviddi, E.; West, G.; Bentley, C.L.; Unwin, P.R. Surface microstructural controls on electrochemical hydrogen absorption at polycrystalline palladium. J. Electroanal. Chem. 2020, 872, 1–9. [Google Scholar] [CrossRef]
- Bertocci, U.; Huet, F.; Nogueira, R.P.; Rousseau, P. Drift removal procedures in the analysis of electrochemical noise. Corrosion 2002, 58, 337–347. [Google Scholar] [CrossRef]
- Leban, M.; Dolecek, V.; Legat, A. Electrochemical noise during non-stationary corrosion processes. Mater. Corros. 2001, 52, 418–425. [Google Scholar] [CrossRef]
- Kearns, J.R.; Scully, J.R.; Roberge, P.R. Electrochemical Noise Measurement for Corrosion Applications; ASTM STP1277: Philadelphie, PA, USA, 1996. [Google Scholar]
- Stringer, J.; Markworth, A.J. Applications of deterministic chaos theory to corrosion. Corros. Sci. 1993, 35, 751–760. [Google Scholar] [CrossRef]
- Grafov, B.M. The Kramers-Moyal expansion for electrochemical stochastic diffusion. Russ. J. Electrochem. 2014, 50, 92–94. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L.; Johnson, G.A.; Mar, D.J. Fundamentals of synchronization in chaotic systems, Concepts and applications. Chaos-Interdiscip. Nonlinear Sci. 1997, 7, 520–543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhdanov, V.P. Dynamics of surface diffusion. Surf. Sci. 1989, 214, 289–303. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time, Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Systat Software, Inc. TableCurve 2D, Automated Curve Fitting; Systat Publisher: Chicago, IL, USA, 2002. [Google Scholar]
- Teong, S.P.; Li, X.; Zhang, Y. Hydrogen peroxide as an oxidant in biomass-to-chemical processes of industrial interest. Mater. Trans. 2019, 21, 5753–5780. [Google Scholar] [CrossRef]
- Bellanger, G. Corrosion Induced by Low-Energy Radionuclides- Modeling of Tritium and Its Radiolytic and Decay Products Formed in Nuclear Installations, in Materials Science; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Okazaki, J.; Tanaka, D.A.P.; Tanco, M.A.L.; Wakui, Y.; Mizukami, F.; Suzuki, T.M. Hydrogren permeability study of the thin Pd-Ag alloy membranes in the temperature range across the α-β phase transition. J. Membr. Sci. 2006, 282, 370–374. [Google Scholar] [CrossRef]
- Gabrielli, C.; Grand, P.; Perrot, H. Investigation of hydrogen adsorption and absorption in palladium thin films. J. Electrochem. Soc. 2004, 151, 1943–1949. [Google Scholar] [CrossRef]
- Bosch, R.W.; Moons, F.; Zheng, J.H.; Bogaerts, W.F. Application of electrochemical impedance spectroscopy for monitoring stress corrosion cracking. Corrosion 2001, 57, 532–539. [Google Scholar] [CrossRef]
- Zheng, C.; Yi, G. Investigating the influence of hydrogen on stress corrosion cracking of 2205 duplex stainless steel in sulfuric acid by electrochemical impedance spectroscopy. Corros. Rev. 2017, 35, 23–33. [Google Scholar] [CrossRef]
- Zoltowski, P. Transport of hydrogen in elastic MHn solids. In Proceedings of the International Workshop—Materials to Systems, Berhampur, Odisha, India, 19–21 December 2017; pp. 16–22. [Google Scholar]
- Tanaka, M. Electrochemical hydrogen pump using a high temperature type proton conductor under reduced pressure. J. Plasma Fusion Res. Series 2010, 9, 352–357. [Google Scholar] [CrossRef] [Green Version]
- Bockris, J.O.M. On Hydrogen Damage and the Electrical Properties of Interfaces, In Stress Corrosion Cracking and Hydrogen Embrittlement of Iron Base Alloys; Nace Publishers: Houston, TX, USA, 1974. [Google Scholar]
- Duncan, H.; Lasia, A. Mechanism of hydrogen adsorption/absorption at thin Pd layers on Au(111). Electrochim. Acta 2007, 52, 6195–6205. [Google Scholar] [CrossRef]
- Lasia, A. Applications of the Electrochemical Impedance Spectroscopy to Hydrogen Adsorption, In Evolution and Absorption into Metals, Modern Aspects of Electrochemistry; Kluwer: New York, NY, USA, 2002; Volume 35, pp. 1–49. [Google Scholar]
- Jacobsen, T.; West, K. Diffusion impedance in planar, cylindrical and spherical symmetry. Electrochim. Acta 1995, 40, 255–262. [Google Scholar] [CrossRef]
- Scully, J.R. Electrochemical Impedance—Analysis and Interpretation; STP1188—ASTM: Philadelphia, PA, USA, 1993. [Google Scholar]
- Anishchenko, V.S.; Astakhov, V.; Vadivasova, T.; Neiman, A. Nonlinear Dynamics of Chaotic and Stochastic Systems— Tutorial and modern Developments; Springer: New York, NY, USA, 2007. [Google Scholar]
- Muthuswamy, B. Implementing memristor based chaotic circuits. Int. J. Bifurc. Chaos 2010, 20, 1335–1350. [Google Scholar] [CrossRef]
- Cottis, R.; Turgoose, S.; NACE International. Electrochemical Impedance and Noise; Corrosion Testing Made Easy, Nace: Houston, TX, USA, 1999. [Google Scholar]
- Zhong, G.-Q.; Ayrom, F. Periodicity and chaos circuit. Trans. Circuits 1985, 32, 501–503. [Google Scholar] [CrossRef]
- Chua, L.O.; Lin, G.-n. Intermittency in a piecewise-linear circuit. IEEE Trans. Circuits Syst. 1991, 38, 510–520. [Google Scholar] [CrossRef]
- Bartissol, P.; Chua, L.O. The double hook. IEEE Trans. Circuits Syst. 1988, 35, 1512–1522. [Google Scholar] [CrossRef]
- Wigdorowitz, B.; Petrick, M.H. Modelling concepts arising from an investigation into a chaotic system. Mathl. Comput. Model. 1991, 15, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Madan, R.N. Chua Circuit—A Paradigm for Chaos, World Scientic; Non-Linear Science, Rabinder: Madan, Bulgaria, 1993. [Google Scholar]
- Bellanger, G.; Rameau, J.J. Determination of tritium adsorption and diffusion parameters in a palladium-silver alloy by electrochemical impedance analysis. Fusion Technol. 1997, 32, 94–106. [Google Scholar] [CrossRef]
- Chua, L.O.; Lin, G.-N. Canonical realization of Chua circuit family. IEEE Trans. Circuits Syst. 1990, 37, 885–902. [Google Scholar] [CrossRef] [Green Version]
- Limphodaen, N.; Chansangiam, P. Mathematical analysis for classical Chua circuit with two nonlinear resistors. Songklanakarin J. Sci. Technol. 2020, 42, 678–687. [Google Scholar] [CrossRef]
- Cheng, W.; Luo, S.; Chen, Y. Use of EIS, Polarization and electrochemical noise measurements to monitor the copper corrosion in chloride media at different temperatures. Int. J. Electrochem. Sci. 2019, 14, 4254–4263. [Google Scholar] [CrossRef]
- Anishchenko, V.S.; Vadivasova, T.E.; Okrokvertskhov, G.A.; Strelkova, G.I. Correlation analysis of dynamical chaos. Phys. A 2003, 325, 199–212. [Google Scholar] [CrossRef]
- Le Maitre, O.P.; Reagan, M.T.; Najm, H.N.; Ghanem, R.G.; Knio, O.M. A stochastic projection method for fluid flow. ii. Random process. J. Comp. Phys. 2002, 181, 9–44. [Google Scholar] [CrossRef] [Green Version]
- MaItre, O.P.L.; Knio, O.M.; Najm, H.N.; Ghanem, R.G. A stochastic projection method for fluid flow. i. Basic formulation. J. Comp. Phys. 2001, 173, 481–511. [Google Scholar] [CrossRef] [Green Version]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput Phys 2011, 230, 2345–2367. [Google Scholar] [CrossRef]




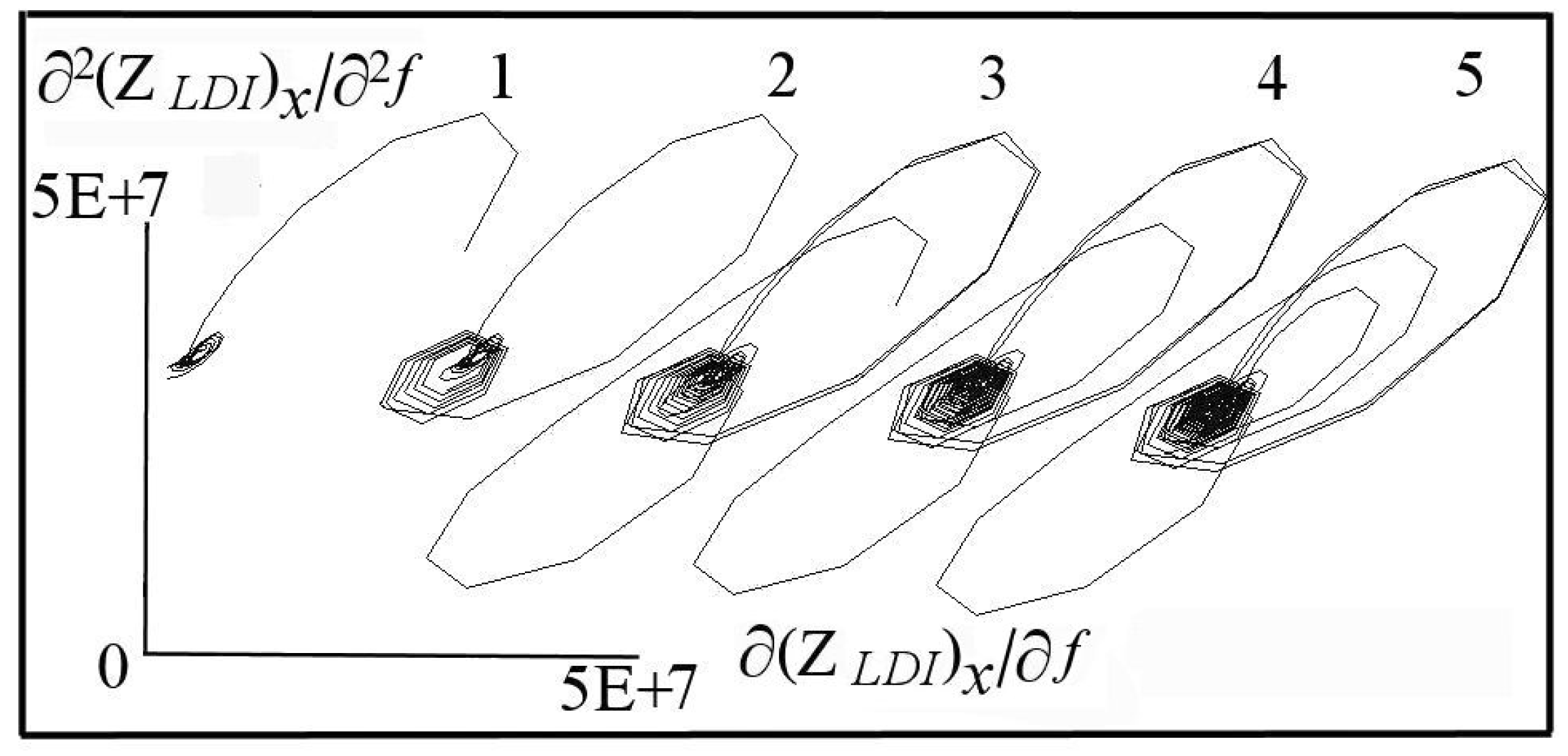



| Considered Adsorbates | Eigenvalues | ||
|---|---|---|---|
| 3 dominant adsorbates (events 4, 5, 7) | 0.983 | −1.225 | 0.731 |
| 3 dominant + 1 tiny adsorbates | 0.952 | −1.328 | 1.045 |
| 3 dominant + 2 tiny adsorbates | 0.911 | −1.373 | 1.253 |
| 3 dominant + 3 tiny adsorbates | 0.865 | −1.382 | 1.393 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellanger, G. Blocking Hydrogen Diffusion in Palladium Cathode i—Analyzed by Electrochemistry; ii—Analyzed by Chaos. Hydrogen 2022, 3, 123-160. https://doi.org/10.3390/hydrogen3010010
Bellanger G. Blocking Hydrogen Diffusion in Palladium Cathode i—Analyzed by Electrochemistry; ii—Analyzed by Chaos. Hydrogen. 2022; 3(1):123-160. https://doi.org/10.3390/hydrogen3010010
Chicago/Turabian StyleBellanger, Gilbert. 2022. "Blocking Hydrogen Diffusion in Palladium Cathode i—Analyzed by Electrochemistry; ii—Analyzed by Chaos" Hydrogen 3, no. 1: 123-160. https://doi.org/10.3390/hydrogen3010010
APA StyleBellanger, G. (2022). Blocking Hydrogen Diffusion in Palladium Cathode i—Analyzed by Electrochemistry; ii—Analyzed by Chaos. Hydrogen, 3(1), 123-160. https://doi.org/10.3390/hydrogen3010010






