Energetics of LOHC: Structure-Property Relationships from Network of Thermochemical Experiments and in Silico Methods

Abstract

The storage of hydrogen is the key technology for a sustainable future. We developed an in silico procedure, which is based on the combination of experimental and quantum-chemical methods. This method was used to evaluate energetic parameters for hydrogenation/dehydrogenation reactions of various pyrazine derivatives as a seminal liquid organic hydrogen carriers (LOHC), that are involved in the hydrogen storage technologies. With this in silico tool, the tempo of the reliable search for suitable LOHC candidates will accelerate dramatically, leading to the design and development of efficient materials for various niche applications.

1. Introduction

Power production from renewable energy technologies suffers from systematic energy fluctuations and they can be improved by the storage of excess energy. Hydrogen has been considered as a possible energy carrier for various applications. Covalent bond usage of aromatic organic molecules is one of the promising options for hydrogen storage, because hydrogen can be stored by hydrogenation and it is released by the dehydrogenation, when the hydrogen is needed. Benzene and toluene can be considered as the first generation of liquid organic hydrogen carriers (LOHC), but the harsh reaction conditions (usually around 473 K) of the dehydrogenation step have been unacceptable for designing industrial processes. In general, any olefin or aromatic compound can be considered a potential LOHC. Screening for suitable candidates for practical applications is, therefore, very demanding.

It was found that the introduction of a nitrogen atom to aromatic organic hydrides is effective for lowering of the dehydrogenation temperature [1]. This idea was realized in N-alkyl-carbazoles as the second generation of nitrogen-containing organic hydrides for hydrogen storage [2,3,4]. So far, however, no single material has been found that can meet numerous criteria expected for the inexpensive but effective hydrogen storage material that must consume and release H₂ with fast kinetics at moderate temperatures of 350–400 K. Thus, the search for new LOHC systems based on abundant and inexpensive organic compounds with a high capacity to store and release hydrogen and ideally use the same catalyst to charge and discharge hydrogen under relatively mild conditions, and compatible with existing infrastructure for transport and refuelling, is a major challenge [5]. However, an unavoidable problem that limits progress in this area is the lack of experimental thermodynamic data for promising hydrogen-reach, as well as hydrogen-lean LOHC. There is no lack of various empirical group additivity (GA) methods [6,7,8] that can give satisfactory results for simple linear and not strained molecules. However, these methods generally fail for aromatic, branched, and strained cyclic molecules [9]. In a series of our recent studies, we successfully tested quantum-chemical composite methods of G* family to provide reliable gas phase thermochemical data for N-alkyl-carbazoles [2,3,4]. The hydrogenation/dehydrogenation reactions suitable for hydrogen storage, however, usually take place in the liquid phase. Therefore, the idea of combining the quantum chemical methods with a framework based on empirical, semi-empirical and theoretical approaches leading to thermodynamic data in the liquid phase seems to be a last resort in the situation with complete information deficit. The reliable thermodynamics of chemical reactions today can only be evaluated by a reasonable combination of experimental and computational methods. By computational methods we should understand not only the quantum chemical methods, but also all possible empirical, semi-empirical, and other theoretical methods. We define the interweaving of experimental methods with computational methods as an in silico-based procedure.

The aim of this paper is to offer a network of experimental thermochemical methods (combustion calorimetry, transpiration, tensimetry, and DSC) in combination with the high-level composite quantum-chemical methods (G4 and G3MP2) and a group-additivity method developed for prediction of vaporization enthalpies of LOHC. This network of experimental and in silico methods was used for the thermodynamic analysis of the energetics and feasibility of hydrogenation/dehydrogenation reactions for a series of substituted pyrazines and quinoxalines (see Figure 1) as possible LOHC candidates.

2. Experimental Section

2.1. Materials and Purification

The commercially available samples of pyrazine derivatives (see Table S1) have been used in this work. The liquid sample of 2-methyl-quinoxaline was additionally purified by the fractional distillation and the solid sample of 2,3-dimethyl-quinoxaline was purified by the fractional sublimation in a vacuum. No impurities (greater than 0.0002 mass fraction) could be detected in both samples used for the thermochemical measurements. The degree of purity was determined using a GC equipped with a FID. A capillary column HP-5 was used with a column length of 30 m, an inside diameter of 0.32 mm, and a film thickness of 0.25 μm.

2.2. Experimental and Theoretical Thermochemical Methods

The gas-phase standard molar enthalpy of formation, ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g), of a compound under study is the comprehensive experimental thermochemical property that includes all enthalpies of phase transitions (sublimation, vaporization, and fusion) in combination with enthalpies of formation derived from the combustion enthalpy. Vapor pressures of methyl-quinoxalines at different temperatures were measured by the transpiration method. The standard molar enthalpy of vaporisation, ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$, and the standard molar enthalpy of sublimation, ${\Delta }_{\mathrm{cr}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$, were derived from vapor pressures temperature dependences. The standard molar enthalpy of fusion, ${\Delta }_{\mathrm{cr}}^{\mathrm{l}}{H}_{\mathrm{m}}^{\mathrm{o}}$, of 2,3-dimethyl-quinoxaline was measured by using the differential scanning calorimetry (DSC). The experimental procedures have been described elsewhere [10,11,12,13] and the necessary details are given in the electronic supporting information (ESI).

We used quantum-chemical methods to get theoretical gas-phase enthalpies of formation,${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_theor, of substituted pyrazines and amines. Calculations were performed with the Gaussian 09 series of programs [14]. An initial search for the stable conformers was performed with the force field method MM3 [15] and the b3lyp/6-31g(d,p) method [16]. Energies E₀ and enthalpies H₂₉₈ were calculated by using the composite G4 [17] and the G3MP2 methods [18] from Gaussian 09. Details on computational procedure were reported elsewhere [19]. The H₂₉₈-values were obtained according to the “rigid rotator”-“harmonic oscillator” approach embedded in the Gaussian 09. The enthalpies H₂₉₈-values were finally converted to the ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_theor and discussed. Calculations were performed for the most stable conformer of each compound.

3. Results and Discussion

In general, any type of unsaturated compound could be considered a hydrogen carrier. The hydrogenation of the LOHC (or the regeneration of the spent form) is thermodynamically favorable, but the dehydrogenation of the LOHC (or the release of hydrogen) exhibits the reverse process, which becomes more favorable with increasing temperature. It was theoretically evaluated that an ideal LOHC is expected to have the hydrogenation enthalpy at a level of not higher than 40 kJ·mol⁻¹/H₂ [20]. However, the reaction enthalpy should not be significantly below 40 kJ·mol⁻¹/H₂ in order to avoid thermodynamic limitations in the regeneration step. Aliphatic unsaturated compounds cannot meet this requirement. In contrast, the aromatic nitrogen-containing aromatic compounds promise to overcome the thermodynamic limitations in the regeneration step. A major advantage of heterocyclic compounds over homocyclic aromatics is the lower temperature and enthalpy of reaction for the hydrogen release through dehydrogenation [20].

3.1. Thermodynamic Background

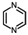
One of the typical for the hydrogen storage reactions is the hydrogenation/dehydrogenation of 2,5-dimethylpyrazine as it shown in Equation (1) below:

(1)

A chemical reaction basically takes place under thermodynamic and (or) kinetic control. The thermodynamic feasibility analysis of chemical processes enables the determination of the driving forces and could reduce the experimental efforts. Thermodynamic feasibility of a chemical process is determined by the sign of the Gibbs reaction energy,${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$, according to the Gibbs-Helmholtz equation:

$${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}} ={\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}} -T\times {\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}= -RT\times \ln K_p$$

(2)

where ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$ is the change in the free energy of a chemical reaction; ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ is the reaction enthalpy, and ${\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$ is the change in the entropy of a chemical reaction. The negative sign (${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$ < 0) provides a qualitative indication of the general feasibility. Moreover, the magnitude of the gas-phase thermodynamic equilibrium constant $K_p$ (at any temperature of interest T) provides quantitative insight into the possible yield of the desired product (e.g., for $K_p$ > 10 the yield is practically close to 99%). As a rule, the thermodynamic calculations are initially carried out at the reference temperature T = 298 K. Using the standard molar isobaric heat capacities $C_{p,\mathrm{m}}^{\mathrm{o}}$ of reaction participants, the feasibility of the reaction at any desired temperature can be derived with the aid of Kirchhoff’s law.

According to Equation (2), knowledge of standard molar enthalpies of formation and standard entropies of reaction participants is indispensable for the feasibility analysis. In the past decade, the high-level composite quantum-chemical methods become a valuable tool for obtaining theoretical ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g, 298)-values with so-called “chemical accuracy” of 4–5 kJ·mol⁻¹ [21]. These QC methods differ considerably in terms of time and computing power. The QC calculations are currently being carried out successfully to obtain ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)-values for small- and medium-sized molecules.

Predicting the entropies (required for Equation (2)) and heat capacities (required for the Kirchhoff’s Law) of organic molecules is undoubtedly a challenging task. In principle, they can be reliably calculated with help of quantum chemistry or using statistical mechanics if their structures, moments of inertia and vibration frequencies are known. The uncertainties of such calculations depend strongly on the size and flexibility of the molecules of interest. However, it is obvious from Equation (2) that the possible inaccuracy of the entropy predictions (calculated in usual units J.K⁻¹.mol⁻¹) compared to the enthalpic term (calculated in usual units kJ.mol⁻¹) can be regarded as less pronounced. At least the inaccuracy of the entropy estimates is not crucial to get a correct trend of the ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$–value.

The gas-phase thermodynamic functions ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$ and $K_p$ required for the thermodynamic analysis and optimization of the hydrogenation/dehydrogenation reactions can also be obtained with the high-level QC methods. For the practical applications the equilibrium constant, $K_p$, derived with the help of the quantum-chemistry have to be re-calculated to the liquid-phase thermodynamic equilibrium constant $K_a$. For example, for the hydrogenation reaction (1) the thermodynamic equilibrium constant $K_a$ in the liquid phase can be calculated by Equation (3):

$$K_a= K_p\times \frac{p_{2,5\text{-}\mathrm{dimethyl}\text{-}\mathrm{pyrazine}}\times p_{H2}}{p_{2,5\text{-}\mathrm{dimethyl}\text{-}\mathrm{piperazine}}}$$

(3)

where $p_i$ are the absolute vapor pressures of the pure reaction (1) participants (i), which are either available in the literature or measured by any suitable method [22]. In addition, the QC calculations can be performed at any desired temperature and the desired $K_a$-values in the liquid phase can be evaluated in the temperature range of the practical application.

The heat management of the hydrogenation/dehydrogenation reactions is based on the standard molar enthalpies of formation of reaction participants. The latter values can be obtained with the help of modern high-level QC methods for the ideal gas state. However, the hydrogenation/dehydrogenation reactions are usually carried out in the liquid phase. Therefore, the theoretical enthalpies of formation ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g) of potential hydrogen carriers, which are calculated by using the QC method have to be re-calculated into the practically relevant liquid phase values,${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq), as follows:

$${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{liq}\right) = {\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}(\mathrm{g}{)}_{\mathrm{QC}} - {\mathsf{\Delta }}_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$$

(4)

where ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$ is the standard molar vaporization enthalpy of the compound of interest. It is important that all thermochemical properties involved in Equation (4) have to be referenced to the same temperature (e.g., to the reference temperature T = 298 K). The ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq, 298 K)-values derived by Equation (4) can be further used for estimation of reaction enthalpies ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq, 298 K) (according to the Hess’s Law):

$${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{liq}\right) = {\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}(\mathrm{liq}, \mathrm{products}) - {\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}(\mathrm{liq}, \mathrm{reactants})$$

(5)

In our experiences, however, there is a more elegant and reliable access to the desired ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq, 298 K)-value over the theoretical enthalpy of a gas phase reaction, ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_QC. Indeed, the latter value can be calculated according to the Hess’s Law directly from the H₂₉₈ values available in the output of the QC method. This gas-phase ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_QC-value is related to the liquid phase reaction enthalpy, ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq), by equation:

$${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{liq}\right)= {\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}{\left(\mathrm{g}\right)}_{\mathrm{QC}}-{\displaystyle \sum }_i{\nu }_i{\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m},i}^{\mathrm{o}}$$

(6)

where ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m},i}^{\mathrm{o}}$ are the molar enthalpies of vaporization of the pure reaction participants i at the reference temperature 298 K, and ${\nu }_i$ is the stoichiometric coefficient. The required vaporization enthalpies of compounds involved in the hydrogenation reactions are measurable [22] or they can be estimated with a reasonable accuracy, e.g., by the group-additivity [6,7,8,9]. It is also important to note, that only in this case the ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_QC-values for hydrogenation/dehydrogenation reactions are calculated from enthalpies H₂₉₈ of the reaction participants, which are directly available from the Gaussian output. This option is valuable to overcome common ambiguities [23,24] associated with the quantum-chemical methods by using conventional isodesmic, homodesmic, etc. reactions [25]. Thus, the reasonable combination of experimental and theoretical methods opens up the possibility of a quick but reliable assessment of the energetics of reactions that are relevant for the hydrogen storage process.

In this work we used the data derived from traditional thermochemical methods (combustion calorimetry, vapor pressure measurements) together with the modern composite quantum-chemical methods G4 and G3MP2 methods to obtain Gibbs energies, reaction enthalpies, equilibrium constants, $K_p$, and $K_a$. These results, together with the thermodynamic functions of vaporization, derived from vapor pressure measurements, are used for the thermodynamic analysis of various nitrogen-containing LOHC hydrogenation reactions as follows.

3.2. Thermodynamics of Liquid-Gas, Crystal-Gas, and Crystal-Liquid Phase Transitions

Vapor pressures and vaporization enthalpies are an essential part of the thermodynamic analysis and they are involved in Equations (5) and (6). Results on the vapor pressure temperature dependences measured in this work by the transpiration method (see Table S2) have been used to derive the standard molar enthalpies of vaporization, ${\mathsf{\Delta }}_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$, and standard molar sublimation enthalpies,${ \mathsf{\Delta }}_{\mathrm{cr}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$, of pyrazine derivatives at different temperatures. Vapor pressures of 2-methylquinoxaline have been measured for the first time. Vapor pressures of pyrazine derivatives available in the original literature have been evaluated in the same way as our own results (see details in ESI). Results of the data evaluation are compiled in

Table 1. Compilation of enthalpies of vaporization/sublimation ${\Delta }_{\mathrm{l},\mathrm{cr}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$ for pyrazine derivatives derived in this work and from the data available in the literature.

Compound	Technique a	T-Range	$$\begin{gathered} {\Delta }_{\mathbf{l},\mathbf{c}\mathbf{r}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}} \\ ({\mathit{T}}_{\mathbf{av}}) \end{gathered}$$	$$\begin{gathered} {\Delta }_{\mathbf{l},\mathbf{c}\mathbf{r}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}} \\ (298 \mathbf{K}){ }^{\mathbf{b}} \end{gathered}$$	Ref.
		K	kJ·mol−1	kJ·mol−1
quinoxaline (cr)	DC	365	-	(66.6 ± 2.0)	[26]
				71.1 ± 0.9	Table 2
quinoxaline (liq)	CGC	298	-	58.7 ± 1.8	[27]
		298		59.9 ± 1.0	Table 3
				59.6 ± 0.9 c	average
2-methylquinoxaline (liq)	T	313.2–372.5	63.8 ± 0.3	64.4 ± 0.8	this work
2,3-dimethylquinoxaline (cr)	DC	383	103.3 ± 1.8	85.8 ± 1.8	[28]
	K	294.1–308.1	87.7 ± 0.8	87.8 ± 1.4	[29]
	T	313.2–372.5	83.3 ± 0.6	84.6 ± 0.8	this work
				85.4 ± 0.7 c	average
2,3-dimethylquinoxaline (liq)				66.7 ± 1.3	Table 2
phenazine (cr)				95.9 ± 0.4	[30]
phenazine (liq)				78.7 ± 2.3	[30]

^a Techniques: T = transpiration; DC = drop calorimetry; CGC = correlation gas chromatography; K = Knudsen effusion method. In this table, uncertainties of the vaporization/sublimation enthalpies are expressed as the expanded uncertainty (0.95 level of confidence, k = 2). They were calculated according to a procedure described elsewhere [11,12]. Uncertainties include uncertainties from the experimental conditions and the fitting equation, vapor pressures, and uncertainties from adjustment of vaporization/sublimation enthalpies to the reference temperature T = 298.15 K. ^b Vapor pressures available in the literature were treated using Equations (S3) and (S4) with help of heat capacity differences from Table S3 to evaluate the enthalpy of vaporization at 298.15 K in the same way as our own results in Table S2. ^c Weighted mean value (the uncertainty was taken as the weighing factor). Values highlighted in bold were recommended for thermochemical calculations.

.

The single experimental vaporization enthalpy for quinoxaline was reported from the Correlation-Gas-Chromatography method [27]. The enthalpies of sublimation for 2,3-dimethylquinoxaline compiled in Table 1 also agree within the combined experimental uncertainties. Vapor pressures for this compound measured in this work by the transpiration method are in agreement (see Figure S1) with those measured by the Knudsen mass-loss effusion technique [29]. Thus, the weighted average value ${\Delta }_{\mathrm{cr}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K) = (85.4 ± 0.7) kJ·mol⁻¹ was derived and applied for further thermochemical calculations.

We have carefully collected available ${\Delta }_{\mathrm{cr}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K) and ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K) data on alkyl-pyrazine derivatives (see Table S4) and together with our new complementary results on quinoxalines these data can be used for optimization of the hydrogenation/dehydrogenation reactions of LOHC.

Data on the thermodynamics of the solid-liquid phase transition for pyrazine derivatives are required for the mutual re-calculations of sublimation and vaporization enthalpies collected in Table 1 according to the general equation:

$${\Delta }_{\mathrm{cr}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}= {\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}} {+}^{ }{\Delta }_{\mathrm{cr}}^{\mathrm{l}}{H}_{\mathrm{m}}^{\mathrm{o}}$$

(7)

Thermal behavior of 2,3-dimethylquinoxaline has been studied in this work for the first time. Available experimental data on enthalpies of fusion for methyl-substituted pyrazines and quinoxalines are compiled in

Table 2. Compilation of thermodynamic data on N-containing compounds (in kJ⋅mol⁻¹) ^a.

Compounds	${\Delta }_{\mathbf{c}\mathbf{r}}^{\mathbf{l}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}$	${\Delta }_{\mathbf{c}\mathbf{r}}^{\mathbf{l}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{c}\mathbf{r}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{c}}$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{d}}$	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{cr}\right)$	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{liq}\right){ }^{\mathbf{e}}$
	at Tfus			298.15 K
1	2	3	4	5	6	7
pyrazine [19]	15.3/327.0	14.5 ± 0.4	57.5 ± 0.4	42.0 ± 0.6	145.7 ± 1.3	160.2 ± 1.4
tetra-methylpyrazine [28]	21.4/357.6	18.9 ± 0.8	76.5 ± 1.0	57.6 ± 0.9	−39.9 ± 2.0	−21.0 ± 2.2
quinoxaline	11.8/305.7 [31]	11.5 ± 0.1	71.1 ± 0.9 g	59.6 ± 0.9 c	189.8 ± 3.6 [32] g	201.3 ± 3.6
2,3-dimethylquinoxaline	22.6/378.8 f	18.7 ± 1.2	85.4 ± 0.7	66.7 ± 1.3	87.1 ± 2.4	105.8 ± 2.4
phenazine [30]	24.9/447.9	17.2 ± 2.3	95.9 ± 0.4 g	78.7 ± 2.3	235.8 ± 1.2	253.0 ± 2.6
1,3,5-triazine [33]	14.6/353.9 [34]	13.0 ± 0.5	54.2 ± 0.2 g	41.2 ± 0.5	171.7 ± 0.8	184.7 ± 0.9
di-phenylamine [35]	17.9/326.2	16.2 ± 0.5	95.2 ± 0.4 g	79.0 ± 0.8	130.5 ± 1.9	146.7 ± 2.0
tri-phenylamine	24.9/400.2 [27]	18.3 ± 2.2	108.5 ± 2.5 g	90.2 ± 1.2 [27]	235.3 ± 3.0 [36]	253.6 ± 3.7

^a Uncertainties are presented as expanded uncertainties (0.95 level of confidence with k = 2). ^b The experimental enthalpies of fusion ${\Delta }_{\mathrm{cr}}^{\mathrm{l}}{H}_{\mathrm{m}}^{\mathrm{o}}$ reported at T_fus have been adjusted to 298 K in this work according to procedure developed by Chickos and Acree [37]. ^c From Table 1 or from the original literature given in column 1. ^d Calculated in this work as the difference between column 4 and 3 in this table. ^e Calculated in this work as the sum of column 3 and 6 in this table. ^f This work ^g Calculated in this work as the sum of column 3 and 5 in this table.

. For thermochemical calculations, the experimental enthalpies of fusion measured at T_fus were adjusted to the reference temperature T = 298 K (for details see ESI).

The energetics of the solid-liquid phase transition for pyrazine derivatives are also required for the re-calculation of the standard molar enthalpies of formation in the crystal state, ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(cr), into practically more relevant standard molar enthalpies of formation in the liquid state,${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq), according to a general equation:

$${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{liq}\right) = {\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{cr}\right) + {\Delta }_{\mathrm{cr}}^{\mathrm{l}}{H}_{\mathrm{m}}^{\mathrm{o}}$$

(8)

provided that all values are adjusted to the reference temperature T = 298 K. The liquid phase enthalpies of formation of pyrazine derivatives are given in Table 2, column 7.

3.3. Consistency of Vaporization Enthalpies

Since the amount of experimental data on the vaporization/sublimation thermodynamics of quinoxalines is very limited, internal consistency needs to be proven using any kind of structure-property correlations. A valuable method to establish consistency of experimental data is the correlation gas-chromatography (CGC) [38]. In this method experimental enthalpies of vaporization ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K) are correlated with the chromatographic Kovats indices (J_x) on DB-1701 [39] (see

Table 3. Correlation of vaporization enthalpies ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (298.15 K) of alkyl pyrazines and alkyl quinoxalines, with the Kovats indices on DB-1701 ^a.

	Jxa	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}(298.15 \mathbf{K}{)}_{\mathbf{exp}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}(298.15 \mathbf{K}{)}_{\mathbf{calc}}{ }^{\mathbf{c}}$
		kJ·mol−1	kJ·mol−1	kJ·mol−1
pyrazine	822	42.0	41.2	0.8
methyl-pyrazine	908	44.0	44.4	−0.4
2,5-di-methyl-pyrazine	988	48.2	47.4	0.6
2,6-di-methyl-pyrazine	991	45.3	47.5	−2.2
ethyl-pyrazine	994	48.4	47.6	0.7
2,3-di-methyl-pyrazine	1000	47.8	47.8	0.0
tri-methyl-pyrazine	1075	52.2	50.6	1.2
2,3-di-ethyl-pyrazine	1170	53.8	54.1	−0.3
tetra-methyl-pyrazine	1274	57.6	57.9	−0.3
quinoxaline	1327		59.9	−0.3
2-methyl-quinoxaline	1421		63.3	1.1
2,3-di-methyl-quinoxaline	1506		66.5	0.2

^a Data on DB-1701 [39]. ^b Experimental data from Table S4. ^c Calculated using equation: ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (298.15 K)/(kJ·mol⁻¹) = 10.9 + 0.0369 × J_x with (R² = 0.985).

). Earlier we demonstrated that vaporization enthalpy was linearly correlated with the J_x in different homologous series of nitriles [40], aliphatic ethers [41], and alkylbenzenes [42].

For correlation with ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K)-values listed in Table 1 and Table S4, we have collected Kovats indices for low polarity gas-chromatographic column DB-1701 (see Table 3). It has turned out that the ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K)-values of pyrazine derivatives and quinoxalines exhibit very good linear correlations with the J_x-values:

$${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}(298.15 K)/(\mathrm{kJ}·{\mathrm{mol}}^{-1}) = 10.9 + 0.0369 \times J_x\hspace{1em}\mathrm{with} (R^2 = 0.985)$$

(9)

The high correlation coefficient R² = 0.985 of the ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K) = f(J_x) dependence proves the reliability and internal consistency of the enthalpies of vaporization evaluated in the Table 1. The uncertainties of the correlated results derived in Table 3 were rated with ±1 kJ·mol⁻¹.

It is also important to show the internal consistency of the datasets of the quinoline and its methyl derivatives as well as the pyrazine and its methyl derivatives, as shown in Figure S2. The difference between pairs of molecules is not expected to be the same, but the general trends appear to be consonant within a range of pyrazines, quinoxalines, and benzenes (see Figure S2).

Vapor pressures and thermodynamics of solid-vapor, liquid-vapor, and solid-liquid phase transitions of pyrazine and quinoxaline derivatives, which were evaluated in this work (see Table 1, Table 2 and Table 3) can be recommended for the thermodynamic analysis of reactions hydrogenation/dehydrogenation reactions and for the calculations of the liquid-phase thermodynamic equilibrium constants K_a of these reactions in combination with the quantum-chemical methods as follows in Section 3.7 and Section 3.8.

3.4. Standard Molar Enthalpies of Formation of Pyrazine Derivatives

Standard molar enthalpies of formation of pyrazines and quinoxalines are required for the thermodynamic analysis of the hydrogenation/dehydrogenation reactions according to the Hess’s Law (Equation (5)) or according to Equation (6). The thermochemistry of pyrazine and quinoxaline derivatives has been studied intensively in established laboratories in Porto [26,28,29,43,44]. The available experimental results together with our new measurements are compiled in

Table 4. Thermochemical data at T = 298 K (p° = 0.1 MPa) for pyrazine derivatives (in kJ·mol⁻¹) ^a.

Compounds	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}(\mathbf{liq} \mathbf{or} \mathbf{cr})$	${\Delta }_{\mathbf{l},\mathbf{c}\mathbf{r}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}(\mathbf{g}{)}_{\mathbf{exp}}$	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right){\mathbf{G}}_4{ }^{\mathbf{c}}$	d
1	2	3	4	5	6
pyrazine (cr)	145.7 ± 1.3 [19]	57.5 ± 0.4	203.2 ± 1.5	206.7	−3.5
methylpyrazine (liq)	(118.7 ± 3.5) e	44.0 ± 0.3	-	162.7	-
2,3-dimethylpyrazine (liq)	73.4 ± 2.0 [28]	47.8 ± 1.0	121.2 ± 2.2	120.7	0.5
2,5-dimethylpyrazine (liq)	67.0 ± 2.0 [43]	48.2 ± 0.5	115.2 ± 2.0	119.7	−4.5
2,6-dimethylpyrazine (cr)	(55.5 ± 3.8) e	63.5 ± 1.4	-	119.0	-
trimethylpyrazine (liq)	20.4 ± 2.2 [28]	52.2 ± 0.8	72.6 ± 2.3	77.3	−4.7
tetramethylpyrazine (cr)	−39.9 ± 2.0 [28]	76.5 ± 1.0	36.6 ± 2.2	36.9	−0.3
ethylpyrazine (liq)	98.1 ± 2.1 [44]	48.4 ± 0.9	146.5 ± 2.3	141.0	5.5
n-propylpyrazine (liq)	(66.5 ± 3.6) e	51.9 ± 1.0	-	118.4	-
2,3-diethylpyrazine (liq)	27.6 ± 2.4 [44]	53.8 ± 1.1	81.4 ± 2.6	81.3	0.1
quinoxaline (cr)	(189.8 ± 3.6) e	71.1 ± 0.9 f	262.3 ± 4.2 [29]	260.9	1.4
2-methylquinoxaline (liq)	(151.5 ± 3.6) e	64.4 ± 0.8	-	215.9	-
2,3-dimethylquinoxaline (cr)	87.1 ± 2.4 [28]	85.4 ± 0.7	172.5 ± 2.5	171.2	1.3
phenazine (cr)	235.8 ± 1.2 [30]	95.9 ± 0.4	331.7 ± 1.3	329.3	2.4

^a The uncertainties in this table are presented as expanded uncertainty with 0.95 level of confidence. ^b From Table 1. ^c Enthalpies of formation calculated by G4 were corrected with the empirical correlation: ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g, exp)/kJ.mol⁻¹ = (1.010 ± 0.003) ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(G4) + (0.7 ± 0.4) with R² = 0.9998, derived in our previous work [19]. The uncertainty is assessed to be on the level of ±3.5 kJ.mol⁻¹ [17]. ^d Calculated as the difference column 4 and 5. ^e Calculated as the difference column 5 and 3. ^f From Table 2.

.

The results for ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq or cr) from the combustion calorimetry, which are collected in Table 4, and the vaporization/sublimation enthalpies of pyrazine derivatives, which were evaluated and averaged in this work (see Table 1), were used together for the further calculation of the experimental gas phase standard molar enthalpies of formation, ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_exp at 298 K (see Table 4, column 4). Since the available for each compound data on ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(liq or cr) compiled in Table 4, column 2 are originated from single sources, they were validated with help of the QC calculations. An agreement or disagreement between the experimental (Table 4, column 4) and theoretical (Table 4, column 5) ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_G4-values could provide a criterion for the mutual validation for both results.

In order to convert the H₂₉₈ values into theoretical standard enthalpies of formation ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g) we used the atomization procedure. It is known that enthalpies of formation resulting from the atomization process have to be corrected for a systematic shift [23,24]. In order to “correct” the theoretical ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_G4 values calculated by the atomization procedure, we used the linear correlation:

$${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}(\mathrm{g}{)}_{\exp }/\mathrm{kJ}·{\mathrm{mol}}^{-1} = (1.010 \pm 0.003) {\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}(\mathrm{g}){\mathrm{G}}_4 + (0.7 \pm 0.4) \mathrm{with} R^2 = 0.9998$$

(10)

developed in our previous work [19] with a set of 18 small heterocyclic compounds similar in shape to the diazines. The “corrected” in this way theoretical ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_G4 values (Table 4, column 5) are in a good agreement with the experiment (within the boundaries of the experimental uncertainties). This agreement can be considered as an indicator for the mutual consistency of the experimental and theoretical results evaluated in this work.

3.5. Standard Molar Enthalpies of Formation of Hydrogenated Pyrazines as LOHC

Standard molar enthalpies of formation of hydrogenated pyrazines (e.g., piperazine as fully hydrogenated pyrazine) are also required for the thermodynamic analysis of the hydrogenation/dehydrogenation reactions according to the Hess’s Law (Equation (5)) or according to Equation (6). For the sake of clarity, the structures of hydrogenated pyrazine derivatives are given in

Table 5. Thermochemical data at T = 298 K (p° = 0.1 MPa) for the hydrogenated pyrazine derivatives (in kJ·mol⁻¹) ^a.

Compounds	Structure	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}} \left(\mathbf{liq}\right)$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{f}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right){\mathbf{G}}_4{ }^{\mathbf{c}}$
1	2	3	4	5
piperazine		−18.5 ± 0.8 [45]	50.1 ± 1.9 [46]	32.0 d
2-methylpiperazine		(−60.4 ± 3.6) e	50.9 ± 1.0	−9.5
2,3-dimethylpiperazine		(−94.5 ± 3.6) e	51.6 ± 1.0	−42.9
2,5-dimethylpiperazine		(−98.1 ± 3.6) e	52.4 ± 1.0	−45.7
trimethylpiperazine		(−135.3 ± 3.6) e	53.0 ± 1.0	−82.3
tetramethylpiperazine		(−171.8 ± 3.6) e	53.6 ± 1.0	−118.2
perhydroquinoxaline		(−107.5 ± 3.6) e	63.7 ± 1.0	−43.8
2-methyl-perhydroquinoxaline		(−148.8 ± 3.6) e	65.1 ± 1.0	−83.7
2,3-dimethyl-perhydroquinoxaline		(−184.6 ± 3.6) e	65.7 ± 1.0	−118.9
perhydrophenazine		(−198.0 ± 3.6) e	77.9 ± 1.0	−120.1

^a The uncertainties in this table are presented as expanded uncertainty with 0.95 level of confidence. ^b Vaporization enthalpies estimated using group-contributions listed in Table S6. ^c Enthalpies of formation calculated by G4 were corrected with the empirical correlation according to Equation (10). The uncertainty is assessed to be on the level of ±3.5 kJ.mol⁻¹ [17]. ^d For comparison for piperazine ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g)_exp = 31.6 ± 2.1 kJ·mol⁻¹ [46]. ^e Calculated as the difference column 5 and 4.

, column 2. It has turned out that the thermochemical data on piperazine derivatives are only available for the piperazine itself [45,46] (see Table 5). However, in our recent work we have shown that the group-additivity method and quantum-chemical calculations can provide reliable enthalpies of vaporization and gas-phase enthalpies of formation of various aliphatic cyclic amines (cyclohexanamine, N-methyl-cyclohexanamine, N,N-dimethyl-cyclohexanamine, and N-cyclohexyl-cyclohexanamine) [47]. The latter structures are related to the hydrogenated pyrazines investigated in this work. In the present work we propagate this combination of empirical and quantum chemical methods in order to derive the enthalpies of liquid phase formation of the LOHC candidates.

The available experimental gas-phase enthalpy of formation of piperazine have been validated with help of the G4 calculations. A very good agreement between the experimental ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_exp = 31.6 ± 2.1 kJ·mol⁻¹ and theoretical ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g)_G4 = 32.0 ± 3.5 kJ·mol⁻¹ (see Table 5) clearly demonstrated the ability of the high-level composite method G4 to provide reliable energetics of the hydrogenated pyrazine derivatives in the gas phase. However, in order to get the liquid phase ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq, 298 K)-values according to Equation (4), vaporization enthalpies of hydrogenated pyrazine derivatives are required. In a series of our recent papers [48,49,50,51,52] we have developed group-additivity parameters for prediction of ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (298 K)-values of aliphatic nitrogen-containing compounds. Compilation of the group contributions required for estimation of vaporization enthalpies of different cyclic amines is given in Table S6. These increments have been used to obtain ${\Delta }_{\mathrm{l}}^{\mathrm{g}}{H}_{\mathrm{m}}^{\mathrm{o}}$(298 K)-values for alkyl-piperazines listed in Table 5, column 4. The validation of the increments is shown in Table S7. Finally, in order to derive the liquid phase enthalpies of formation of hydrogenated pyrazines, required for thermodynamic analysis of the LOHC practical applications, we have combined the theoretical ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g, 298 K)-values from QC with vaporization enthalpies estimated by the group additivity procedure. These ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq, 298 K)-values are given in Table 5, column 3.

3.6. Energetics of the Hydrogenation Process: Structure-Energetics Relationships

When using LOHC technology for on-board energy supply in road vehicles, the energetics of the dehydrogenation/hydrogenation reaction is essential for optimizing the temperature range and the power density of the conversion units. Unfortunately, the body of thermochemical data on various LOHC compounds is very limited. For this reason, two methods (using Equations (5) and (6)) given in Section 3.1 for evaluating the reaction enthalpies ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq) have to be thoroughly validated with reliable data before using for a general thermodynamic analysis.

As an attestation, we used well-established experimental thermochemical data for piperazine ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq, 298 K) = (−18.8 ± 0.8) kJ.mol⁻¹ [46] and pyrazine ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq, 298 K) = (161.2 ± 1.7) kJ.mol⁻¹ [19] in order to calculate the experimental reaction enthalpy, ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (298 K) = (−180.0 ± 1.9) kJ.mol⁻¹ according to Equation (5) for the following reaction:

$${\mathrm{C}}_4{\mathrm{H}}_4{\mathrm{N}}_2\left(\mathrm{liq}\right) + 3 {\mathrm{H}}_2 \left(\mathrm{g}\right) = {\mathrm{C}}_4{\mathrm{H}}_{10}{\mathrm{N}}_2\left(\mathrm{liq}\right) \mathrm{with} {\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{liq}\right) = -180.0 \pm 1.9 \mathrm{kJ}·{\mathrm{mol}}^{-1}$$

(11)

For comparison, the practically indistinguishable reaction enthalpy ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq) = −178.7 kJ·mol⁻¹ (see

Table 6. Reaction enthalpies of hydrogenation/dehydrogenation of pyrazine derivatives, at T = 298 K in kJ·mol⁻¹.

Compounds a		${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{c}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right){\mathbf{G}}_4{ }^{\mathbf{d}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{liq}\right){\mathbf{G}}_4{ }^{\mathbf{e}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}({\mathbf{H}}_2){ }^{\mathbf{f}}$
pyrazine		42.0	50.1 [46]	−168.7	−178.7	−59.7
methylpyrazine		44.0	50.9	−166.3	−173.2	−57.7
2,3-dimethylpyrazine		47.8	51.6	−157.8	−161.6	−53.9
2,5-dimethylpyrazine		48.0	52.4	−159.5	−163.9	−54.6
tri-methylpyrazine		51.8	53.0	−153.8	−155.0	−51.7
tetra-methylpyrazine		57.6	53.6	−149.4	−145.4	−48.5
tert-butylpyrazine		50.5	66.5	−159.8	−175.8	−58.6
2,6-di-tert-butylpyrazine		58.4	82.2	−132.3 g	−156.1	−52.0
1,3,5-triazine		41.2 [53]	55.3	−129.0	−143.1	−47.7

^a Only the fully dehydrogenated molecules are shown. Details are given in Table S8. ^b For the fully dehydrogenated molecules. Data from Table 1. ^c For the fully-hydrogenated molecules. Vaporization enthalpies estimated using group-contributions listed in Table S6. ^d Calculated directly from H₂₉₈-values of the hydrogenation reaction participants. ^e Calculated according to Equation (6). ^f Reaction enthalpy per mole of hydrogen in kJ·mol⁻¹/H₂. The uncertainty is assessed to be on the level of ±3.5 kJ.mol⁻¹. ^g Calculated by G3MP2 according to the Hess’s Law applied to reaction: 2,6-di-tert-butyl-pyrazine + benzene = 2-tert-butyl-pyrazine + tert-butyl-benzene. Data for tert-butyl-benzene were taken from [54].

) was calculated for this reaction according to Equation (6) by using the G4 calculated gas-phase enthalpy of reaction ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_G4 combined with the experimental vaporization enthalpies of reaction participants.

Very good agreement between the “pure” experimental ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq)-value, which was derived using the Hess’s Law, and the theoretical value, which was estimated by Equation (6), was demonstrated for the typical reaction of the pyrazine hydrogenation/dehydrogenation (see Equation (11) and Table 6). This fact can serve as a successful validity test for applying the combination of QC and group additivity methods to reliably predict the enthalpies of the hydrogenation/dehydrogenation reaction.

An important remark should be made about the quantum chemical calculations. The theoretical values, ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g)_G4, of the gas phase hydrogenation reaction derived in Table 6 and discussed above were calculated according to the Hess’s Law from the H₂₉₈ values calculated by the G4 method which are directly available from the Gaussian 09 output. This way to get the ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)_G4-values is preferable in comparison (see details in ESI) to other options to calculate the reaction enthalpy based on the Hess’s Law applied for the theoretical enthalpies of formation,${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g, 298 K), calculated by any common procedures (atomization, isodesmic reactions, homodesmic reactions, etc.) [25]. This way is advantageous in order to overcome ambiguities associated with the quantum-chemical methods for calculations of ${\Delta }_{\mathrm{f}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (g, 298 K), by using conventional reactions [23,24,25].

The hydrogenation of aromatic compounds is a highly exothermic process and careful heat management is essential for the safety of the practical applications. In order to reveal the structure-energetics relationships for the hydrogenation reactions, the ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq)_G4-values for series of pyrazine derivatives (Table 6), quinoxaline derivatives (

Table 7. Reaction enthalpy of hydrogenation/dehydrogenation of quinoxaline derivatives, at T = 298 K (p° = 0.1 MPa) in kJ·mol⁻¹.

Compounds a		${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{c}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right){\mathbf{G}}_4{ }^{\mathbf{d}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{liq}\right){\mathbf{G}}_4{ }^{\mathbf{e}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}/{\mathbf{H}}_2{ }^{\mathbf{f}}$
quinoxaline		58.7	63.7	−294.7	−299.7	−59.9
2-methylquinoxaline		64.4	65.1	−289.7	−290.4	−58.1
2,3-dimethylquinoxaline		66.7	65.7	−280.3	−279.3	−55.9
2,6-dimethyl-1,5-naphthyridine		66.7	66.5	−280.6	−290.2	−58.0
phenazine		78.7 g	77.9	−435.1	−434.3	−62.0

^a Only the fully dehydrogenated molecules are shown. Details are given in Tables S5 and S9. ^b For the fully dehydrogenated molecules. Data from Table 1. ^c For the fully-hydrogenated molecules. Vaporization enthalpies estimated using group-contributions listed in Table S6. ^d Calculated directly from H₂₉₈-values of the hydrogenation reaction participants. ^e Calculated according to Equation (6). The uncertainty is assessed to be on the level of ±3.5 kJ.mol⁻¹. ^f Reaction enthalpy per mole of hydrogen in kJ·mol⁻¹/H₂. ^g from Table 4.

), pyridine derivatives (

Table 8. Reaction enthalpy of hydrogenation/dehydrogenation of pyridine derivatives, at T = 298 K (p° = 0.1 MPa) in kJ·mol⁻¹.

Compounds a		${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{c}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right){\mathbf{G}}_4{ }^{\mathbf{d}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{liq}\right){\mathbf{G}}_4{ }^{\mathbf{e}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}/{\mathbf{H}}_2{ }^{\mathbf{f}}$
pyridine		40.2	39.3 g	−178.6	−177.7	−59.2
2-methylpyridine		42.5	40.5 g	−174.7	−172.7	−57.6
4-methylpyridine		44.9	40.6 h	−175.1	−170.8	−56.9
2,6-dimethylpyridine		46.0	42.4 h	−170.9	−167.3	−55.8
2-tert-butylpyridine		42.7	57.5	−169.1	−183.9	−61.3
4-tert-butylpyridine		54.4	54.2	−170.0	−169.8	−56.6
2,6-di-tert-butylpyridine		56.6	77.1	−168.1 i	−188.6	−62.9

^a Only the fully dehydrogenated molecules are shown. Details are given in Tables S5 and S10. ^b For the fully-dehydrogenated molecules. Data from Table 1. ^c For the fully-hydrogenated molecules. Vaporization enthalpies estimated using group-contributions listed in Table S6. ^d Calculated directly from H₂₉₈-values of the hydrogenation reaction participants. ^e Calculated according to Equation (6). The uncertainty is assessed to be on the level of ±3.5 kJ.mol⁻¹. ^f Reaction enthalpy per mole of hydrogen in kJ·mol⁻¹/H₂. ^g From ref. [53]. ^h From ref. [55]. ⁱ Calculated by G3MP2 according to the Hess’s Law applied to reaction: 2,6-di-tert-butyl-pyridine + benzene = 2-tert-butyl-pyridine + tert-butyl-benzene. Data for tert-butyl-benzene were taken from [54].

), and aniline derivatives (

Table 9. Reaction enthalpy of hydrogenation/dehydrogenation of aniline derivatives, at T = 298 K (p° = 0.1 MPa) in kJ·mol⁻¹.

Compounds a		${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{b}}$	${\Delta }_{\mathbf{l}}^{\mathbf{g}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}{ }^{\mathbf{c}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right){\mathbf{G}}_4{ }^{\mathbf{d}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{liq}\right){\mathbf{G}}_4{ }^{\mathbf{e}}$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}/{\mathbf{H}}_2{ }^{\mathbf{f}}$
aniline		55.8	43.9	−185.0	−173.1	−57.7
N-methylaniline		55.0	46.4	−183.0	−174.4	−58.1
N,N-dimethylaniline		54.0	45.6	−188.6	−180.2	−60.1
N,N-diphenylamine		79.0	64.1	−386.6 i	−371.7	−62.0
tri-phenylamine		90.2 g	77.0 h	−558.0 i	−571.2	−63.5

^a Only the fully dehydrogenated molecules are shown. Details are given in Tables S5 and S11. ^b For the-fully dehydrogenated molecules. Data from Table 1. ^c For the fully-hydrogenated molecules. Data from ref. [47]. ^d Calculated directly from H₂₉₈-values of the hydrogenation reaction participants. ^e Calculated according to Equation (6). The uncertainty is assessed to be on the level of ±3.5 kJ.mol⁻¹. ^f Reaction enthalpy per mole of hydrogen in kJ·mol⁻¹/H₂. ^g From Table 4. ^h Vaporization enthalpy was estimated using group-contributions listed in Table S6. ⁱ Calculated by G3MP2.

).

It has turned out, that a consequent methylation of the pyrazine ring (methyl, dimethyl, trimethyl, and tetramethyl) significantly reduce (see Table 6) the liquid phase reaction enthalpy (from −178.7 kJ·mol⁻¹ observed for unsubstituted pyrazine to −145.4 kJ·mol⁻¹ for tetramethylpyrazine). Surprisingly, the sterically hindered tert-butylpyrazine has hydrogenation enthalpy (−175.8 kJ·mol⁻¹) comparable to the unsubstituted pyrazine, moreover the considerably more strained 2,6-di-tert-butylpyrazine also exhibit (see Table 6) substantial energetic level (−156.1 kJ·mol⁻¹). This peculiarity of the sterically strained substituted pyrazines could be interesting for practical implementation in the LOHC technology.

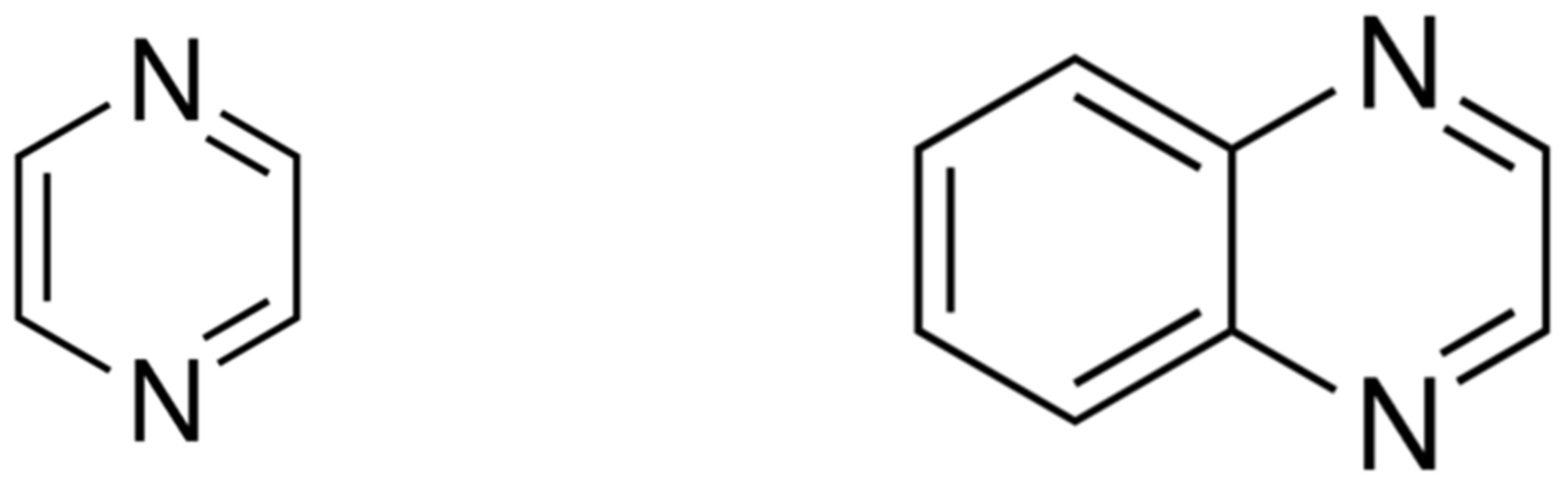
Compared to the pyrazine ring, the quinoxaline ring has a hydrogen storage capacity (5 mole H₂) about 1.7 times greater, but this benefit is energetically covered by the 1.7 times larger (see Table 7) hydrogenation enthalpy of quinoxaline (−299.7 kJ·mol⁻¹). The consequent methylation of the quinoxaline ring (methyl and dimethyl shown in Table 7) is similar to the effect on the pyrazine ring and causes a gradual decrease in the liquid phase reaction enthalpy (from −299.7 kJ·mol⁻¹ observed for unsubstituted quinoxaline to −279.3 kJ·mol⁻¹ for 2,3-dimethylquinoxaline). Displacement of methyl-substituents and nitrogen atoms on the quinoxaline aromatic rings (e.g., results for 2,3-dimethylquinoxaline and 2,6-dimethyl-1,5-naphthyridine are given in Table 7) is also not thermoneutral. Accordingly, the storage capacity (7 mole H₂) and hydrogenation enthalpy (−434.3 kJ·mol⁻¹) of phenazine are significantly larger comparable to the unsubstituted pyrazine and quinoxaline.

Hydrogenation of pyridine and its derivatives (see Table 8) seems to be energetically equal (except for crowded 2-tert-butyl- and 2,6-di-tert-butyl-pyridine,) to analogous alkyl-pyrazines (see Table 6). The sterically hindered tert-butyl-pyridines exhibit not only the highest for the pyridine series hydrogenation enthalpies, but also 2,6-di-tert-butyl-pyridines with ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq)_G4 = −188.6 kJ·mol⁻¹ is apparently a leader in the series of monoheterocyclic compounds shown in Table 6 and Table 8.

Aniline derivatives (see Table 9) can be considered as unbeatable low-cost nitrogen containing LOHC. The liquid phase hydrogenation enthalpies of aniline (−173.1 kJ·mol⁻¹), N-methyl-aniline (−174.4 kJ·mol⁻¹), and N,N-dimethyl-aniline (−180.2 kJ·mol⁻¹) listed in Table 9 are apparently on the same level as those for pyrazine and methylpyrazine (see Table 6). For diphenylamine the hydrogen storage capacity of 6 mole H₂ amounts the hydrogenation enthalpy −371.7 kJ·mol⁻¹. The increasing of hydrogen storage capacity up to 9 mole H₂ in tri-phenyl-amine has required the energetic penalty in the hydrogenation enthalpy of −571.2 kJ·mol⁻¹.

Chemical engineering of hydrogen storage frequently operates with a specific unity “reaction enthalpy per mole of hydrogen, kJ·mol⁻¹/H₂” for reaction enthalpy of the hydrogenation/dehydrogenation process. Following this line, we have calculated (see Table 6, Table 7, Table 8 and Table 9, last column) hydrogenation enthalpies of pyrazine, quinoxaline, pyridine, and aniline derivatives. Values of reaction enthalpy −59.7 kJ·mol⁻¹/H₂ calculated for unsubstituted pyrazine, −59.9 kJ·mol⁻¹/H₂ for unsubstituted quinoxaline, and 59.2 kJ·mol⁻¹/H₂ for hydrogenation of unsubstituted pyridine. Analysis of the reaction enthalpies per mole of hydrogen for miscellaneous LOHC candidates presented in Table 6, Table 7, Table 8 and Table 9 has revealed that the values scatter in very narrow range between 52 and 63 kJ·mol⁻¹/H₂. These values are not significantly higher in comparison to N-ethyl-carbazole with ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ (liq)_G4 = −50.5 kJ·mol⁻¹/H₂ [2] (considered as the most acknowledged candidate from the N-containing aromatics), as well as comparable with pure hydrocarbon LOHC such as commercially available thermofluids biphenyl (−65.4 kJ·mol⁻¹/H₂) [56], benzyltoluenes (Marlothem LH^®) and dibenzyltoluenes (Marlotherm SH^®) (−63.5 and −65.4 kJ·mol⁻¹/H₂, respectively) [57].

3.7. Thermodynamic Analysis of the Hydrogenation Process in the Gas Phase

Quantification of energetics of the hydrogenation/dehydrogenation reactions is important part of the LOHC-technology optimization. However, the general thermodynamic analysis based on standard molar Gibbs energies, ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$, provide direct access to the yield and the degree of conversion of the hydrogenation/dehydrogenation reactions. As it has been shown in previous section, the high-level composite QC methods are reliable for energetics of chemical reactions. Admittedly, the quantum chemical calculations for the ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$, and especially for $K_p$ are very demanding. In order to test the ability of the G4 method to provide reliable $K_p$—values, we have calculated standard molar Gibbs energy of the well-known ethylbenzene dehydrogenation reaction with reliable experimental data [58]. As can be seen from result given in Table S12, the excellent agreement between theoretical and experimental ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$ and $K_p$ values achieved at 298 K and 400 K provide confidence in results with G4 method calculations. Thus, in this work we used the G4 method for calculation of thermodynamic functions involved in Equation (2): the standard molar Gibbs energies, the standard molar enthalpies of formation, and the standard molar entropies of hydrogenation/dehydrogenation reactions of miscellaneous LOHC (see

Table 10. Thermodynamic analysis of pyrazine and trans-2,5-dimethylpyrazine hydrogenation reaction (according to Equation (1)), as calculated by the G4 method.

Compound	Pyrazine		2,5-Dimethylpyrazine
Thermodynamic Functions	298 K	400 K	298 K	400 K
${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$/kJ·mol−1	−58.8	−20.4	−43.1	−2.5
${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$/kJ·mol−1	−168.7	−174.3	−159.5	−165.3
${\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$/J·mol−1·K−1	−368.7	−384.8	−390.4	−407.1
$K_p$a	2.0 × 1010	4.6 × 102	3.6 × 107	2.1
$\left(\frac{p_{py\mathrm{r}azine}\times p_{H2}}{p_{pipe\mathrm{r}azine}}\right)$b	5.9	2.7	2.3	1.2
$K_a$c	1.2 × 1011	1.2 × 103	8.3 × 107	2.5

^a Calculated according to Equation (2). Details are given in Table S13. ^b Vapor pressures at 298 K and 400 K are given in Table S14. ^c Calculated according to Equation (3).

and

Table 11. Thermodynamic analysis of the hydrogenation of LOHC candidates in the gas phase (at 298 K and p° = 0.1 MPa) calculated using G4 method, thermodynamic equilibrium constant $K_p$ at 298 K.

Compounds	${\Delta }_{\mathbf{r}}{\mathbf{G}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right)$	${\Delta }_{\mathbf{r}}{\mathit{H}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right)$	${\Delta }_{\mathbf{r}}{\mathbf{S}}_{\mathbf{m}}^{\mathbf{o}}\left(\mathbf{g}\right)$	${\mathbf{K}}_{\mathbf{p}}$	${\mathbf{T}}_{\mathbf{e}\mathbf{q}}$
	kJ·mol−1	kJ·mol−1	J·mol−1·K−1		K
			Pyrazines
pyrazine	−58.8	−168.7	−368.7	2.0 × 1010	458
methylpyrazine	−52.9	−166.3	−380.5	1.8 × 109	437
2,3-dimethylpyrazine	−45.9	−157.8	−375.3	1.1 × 108	420
2,5-dimethylpyrazine	−43.1	−159.5	−390.4	8.3 × 107	408
trimethylpyrazine	−38.3	−153.8	−387.5	5.1 × 106	397
tetramethylpyrazine	−35.0	−149.4	−383.6	1.3 × 106	389
tert-butylpyrazine	−46.6	−159.8	−379.8	1.5 × 108	421
2,6-di-tert-butylpyrazine	−20.4	−132.3	−375.4	3.7 × 103	352
triazine	−18.3	−129.0	−371.3	1.6 × 103	347
			Pyridines
pyridine	−69.2	−178.6	−367.0	1.3 × 1012	487
2-methylpyridine	−61.4	−174.7	−380.2	5.7 × 1010	459
4-methylpyridine	−61.6	−175.1	−380.7	6.2 × 1010	460
2,6-dimethylpyridine	−52.0	−170.9	−398.7	1.3 × 109	429
4-tert-butyl-pyperidine	−61.4	−170.0	−364.1	5.8 × 1010	467
2,6-di-tert-butyl-pyperidine	−55.8	−168.1	−376.5	5.9 × 109	446
			Anilines
aniline	−75.5	−185.0	−367.6	1.6 × 1013	503
N-methyl-aniline	−73.5	−183.0	−367.3	7.5 × 1012	498
N,N-dimethyl-aniline	−76.5	−188.6	−376.2	2.5 × 1013	501
diphenylamine	−166.3	−386.6	−739.0	1.3 × 1029	523
triphenylamine	−224.6	−558.0	−1118.2	2.2 × 1039	499

).

For practical purpose, it has been reasonable to perform thermodynamic analysis of hydrogenation/dehydrogenation reactions at least at two significantly different temperatures. We selected the acknowledged reference temperature T = 298 K and practically relevant T = 400 K. The latter temperature represents an acceptable level for the on-board energy delivery on vehicles. Calculations at the reference temperature T = 298 K are practically irrelevant, but they help to assess the trend of the equilibrium constants $K_p$ temperature dependences.

The theoretical gas-phase thermodynamic data for hydrogenation of pyrazine and 2,5-dimethylpyrazine, including chemical equilibrium constants $K_p$ at both temperatures are collected in Table 10 and Table S13. It is obvious, that the equilibrium of the hydrogenation/dehydrogenation reactions at room temperatures is completely shifted to the left side (i.e., to the starting molecule), but the position of equilibrium is strongly temperature dependent and, already at 400 K, the dehydrogenation reactions become more thermodynamically favorable.

Thermodynamic analysis of the hydrogenation reactions of miscellaneous LOHC candidates in the gas phase calculated using G4 method is summarized in Table 11. Taking into account reversibility of the hydrogenation/dehydrogenation processes, the thermodynamic functions ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$(g), ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g), and ${\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$(g) given in Table 11 for the hydrogenation reaction will get the opposite sign for the dehydrogenation reaction. Results collected in Table 11 help to reveal that hydrogenation reactions are definitely ″driven by enthalpy″. Indeed, let us compare thermodynamic data obtained for reactions which involve methylpyrazine and tetramethylpyrazine. Both reactions exhibit quite similar reaction entropies ${\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$(g): −380.5 J·mol⁻¹·K⁻¹ for methylpyrazine and −383.6 J·mol⁻¹·K⁻¹ for tetramethylpyrazine, although the ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$(g)-values are different by only 16.9 kJ·mol⁻¹ (−166.3 kJ·mol⁻¹ for methylpyrazine and −149. 4 kJ·mol⁻¹ for tetramethylpyrazine). Nevertheless, this difference is quite decisive for the level of the gas-phase equilibrium constant $K_p$: 1.8 × 10⁹ for methylpyrazine and 1.3 × 10⁶ for tetramethylpyrazine. The similar trend was observed within all three series of the LOHC candidates—pyrazine, pyridine, and aniline derivatives. This finding has reinforced importance of precise studies of energetics of the hydrogenation/dehydrogenation process in order to select most suitable LOHC candidate and optimize conditions for application.

Equilibrium of hydrogenation/dehydrogenation processes exhibit many similarities with polymerization/depolymerization processes, because the enthalpy also drives polymerizations [59]. According to the Gibbs free energy equation (Equation (2)), the entropy term is negative. Thus, at low temperatures, the enthalpy term dominates over the entropy term, which allows hydrogenation or polymerization to occur. In polymer chemistry, ceiling temperature $T_{\mathrm{c}}$ is a practical measure of the trend of a polymer to revert to the starting monomers. At the ceiling temperature, the enthalpy term ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ and the entropy term $T\times {\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$ are equal. Above the ceiling temperature, the depolymerization begins to be thermodynamically favorable. At equilibrium ${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}$ = 0 and we can re-arrange Equation (2) to get expression ${\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$ = $T\times {\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$ leading to the definition of the ceiling temperature as the ratio ($T_{\mathrm{c}}={\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}$/${\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}$). Using this analogy with the polymerization/depolymerization processes it is practically important to define an equilibrium temperature $T_{\mathrm{eq}}$, which is able to imply the reverse of thermodynamic feasibility from hydrogenation to dehydrogenation trend:

$$T_{\mathrm{eq}}=\frac{{\Delta }_{\mathrm{r}}{H}_{\mathrm{m}}^{\mathrm{o}}}{{\Delta }_{\mathrm{r}}{S}_{\mathrm{m}}^{\mathrm{o}}}$$

(12)

This temperature could be valuable indicator for design and selection of effective LOHC. This equilibrium temperature is desired to be not too low for the hydrogenation step in order to keep acceptable reaction rates. At the same time, for the dehydrogenation step the $T_{\mathrm{eq}}$ is expected to be not too high, but sufficient for a good level of conversion and selectivity. Results for $T_{\mathrm{eq}}$ calculations according to Equation (12) for pyrazine, pyridine, and aniline derivatives are given in Table 11, last column. It is apparent from this table that alkyl-pyrazines exhibit the lowest equilibrium temperatures (except for unsubstituted pyrazine and methylpyrazine) at the level of 400 K. The pyridine derivatives show the $T_{\mathrm{eq}}$-values around 450 K and for aniline derivatives the highest $T_{\mathrm{eq}}$-values around 500 K are required. Thus, the pyrazine derivatives appear to be significantly more suitable LOHC candidates compared to the aniline derivatives. A short, but important, comment on calculations according to Equation (12) have to be done. All $T_{\mathrm{eq}}$ calculations in Table 11 have been performed by using thermodynamic functions referenced to 298 K. However, the choice of the reference temperature is generally irrelevant for this type of calculations. To set an example, for hydrogenation/dehydrogenation of 2,5-dimethylpyrazine the value $T_{\mathrm{eq}}$ = 408 K was calculated in Table 11. However, by using thermodynamic functions for this compound given in Table 10 and referenced to 400 K, the value $T_{\mathrm{eq}}$ = 406 K was estimated. The difference is marginal for theoretical and practical applications and it means that quantum-chemical calculations can be successfully applied for characterization and selection of efficient LOHC candidates.

3.8. Thermodynamic Equilibrium Constants of the Hydrogenation/Dehydrogenation Reactions from Quantum-Chemical Calculations

From a practical point of view, the most interesting thermodynamic result is the liquid phase equilibrium constant $K_a$. This constant provides preliminary information not only about the feasibility of the chemical reaction according to the Gibbs energy equation:

$${\Delta }_{\mathrm{r}}{G}_{\mathrm{m}}^{\mathrm{o}}\left(\mathrm{liq}\right) = -RT\ln K_a$$

(13)

However, it is also important to assess the expected theoretical concentrations of the reaction participants. The liquid phase equilibrium constant $K_a$ of the hydrogenation/dehydrogenation is related to the gas phase thermodynamic equilibrium constant, $K_p$, by Equation (3) (related exemplary to reactions 1 and 11, for the sake of brevity). Auxiliary data on vapor pressures at 298 K and 400 K are given in Table S14. Saturated vapor pressures for the 2,5-dimethylpyrazine and trans-2,5-dimethyl-piperazine are available in the literature (see Table S14). Using the theoretical $K_p$ calculated with help of the G4-method and presented in Table 10, the liquid phase thermodynamic equilibrium constant $K_a$ was calculated. Values of the liquid phase equilibrium constants for reaction hydrogenation of 2,5-dimethylpyrazine to trans-2,5-dimethyl-piperazine: very large $K_a$= 8.3 × 10⁷ at 298 K and very small $K_a$= 2.5 at 400 K indicate sufficient thermodynamic feasibility for the hydrogenation/dehydrogenation reversible process. This theoretical conclusion is in agreement with the practical observation for this reaction. Indeed, a new system for hydrogen storage based on the reversible interconversion between 2,5-dimethylpyrazine and 2,5-dimethylpiperazine by hydrogenation at 383 K and dehydrogenation at 411 K catalyzed by an iridium complex has been reported just recently [60]. Reversible and repetitive transformations between 2,5-dimethylpyrazine and 2,5-dimethylpiperazine, accompanied by the uptake and release of three equivalents of hydrogen was repeated almost quantitatively at least four times without any loss of efficiency [60].

As can be seen in Table 10, the contribution from multiplication of pressures ($p_{\mathrm{pyrazine}}\times p_{H2}/p_{\mathrm{piperazine}}$) in Equation (3) is altering from 1.2 to 5.9 depending on the structure of reaction participants and reaction temperature. Nevertheless, this p-factor is hardly decisive for the general level of the $K_a$ even at 400 K as compared to the level of $K_p$ (see Table 10) derived by the G4 method. This observation is of utmost importance for the successful application of quantum chemical methods to the advanced screening of suitable LOHC candidates. Indeed, even taking into account the use of time-consuming and resource-intensive high-level G* methods, the in silico assessment of reliable $K_p$-values for any hydrogenation/dehydrogenation reaction at any desired temperature opens the window of the possibility of reducing the experimental thermochemical effort and performing the general computational search for promising LOHC structures suitable for various transportation, household, etc. niche applications.

4. Conclusions

In summary, the in silico procedure, which is based on the combination of experimental and quantum-chemical results, can be practically applied to evaluate reaction parameters and yields for a wide range of hydrogenation/dehydrogenation reactions, that are involved in the LOHC-technologies. With this quantum chemical tool, the tempo of the reliable search for suitable candidates will accelerate dramatically, leading to the design and development of efficient materials for various niche applications.