A Novel Linear Evaluation of Chromatographic Peak Features in Pharmacopoeias Using an Inverse Fourier Transform Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemical Reagents and Solution Preparation for Gas Chromatography
2.2. Fourier Transform Methods in Chromatography
3. Results of Peak Width Evaluations
3.1. Symmetric Peaks
3.2. Asymmetric Peaks
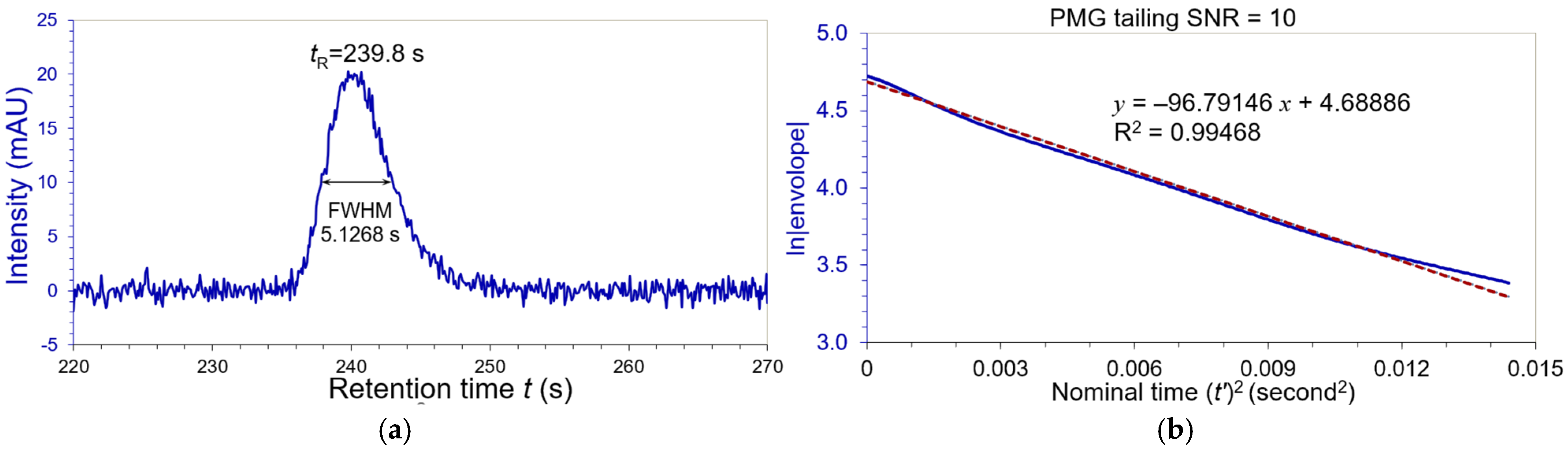
3.3. Noise Testing of Peak Width Evaluation
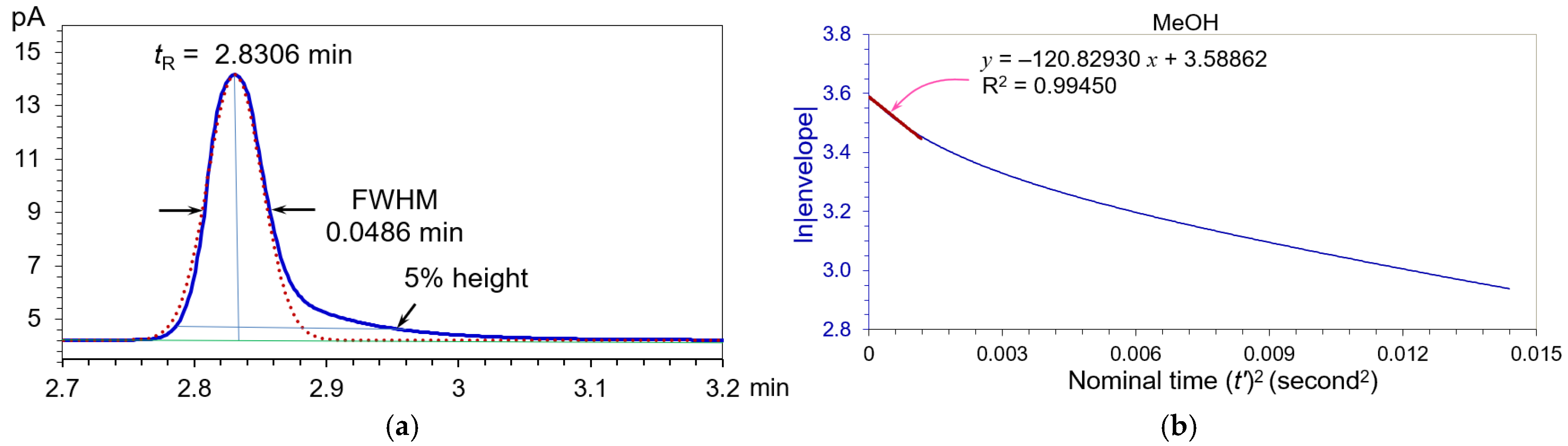
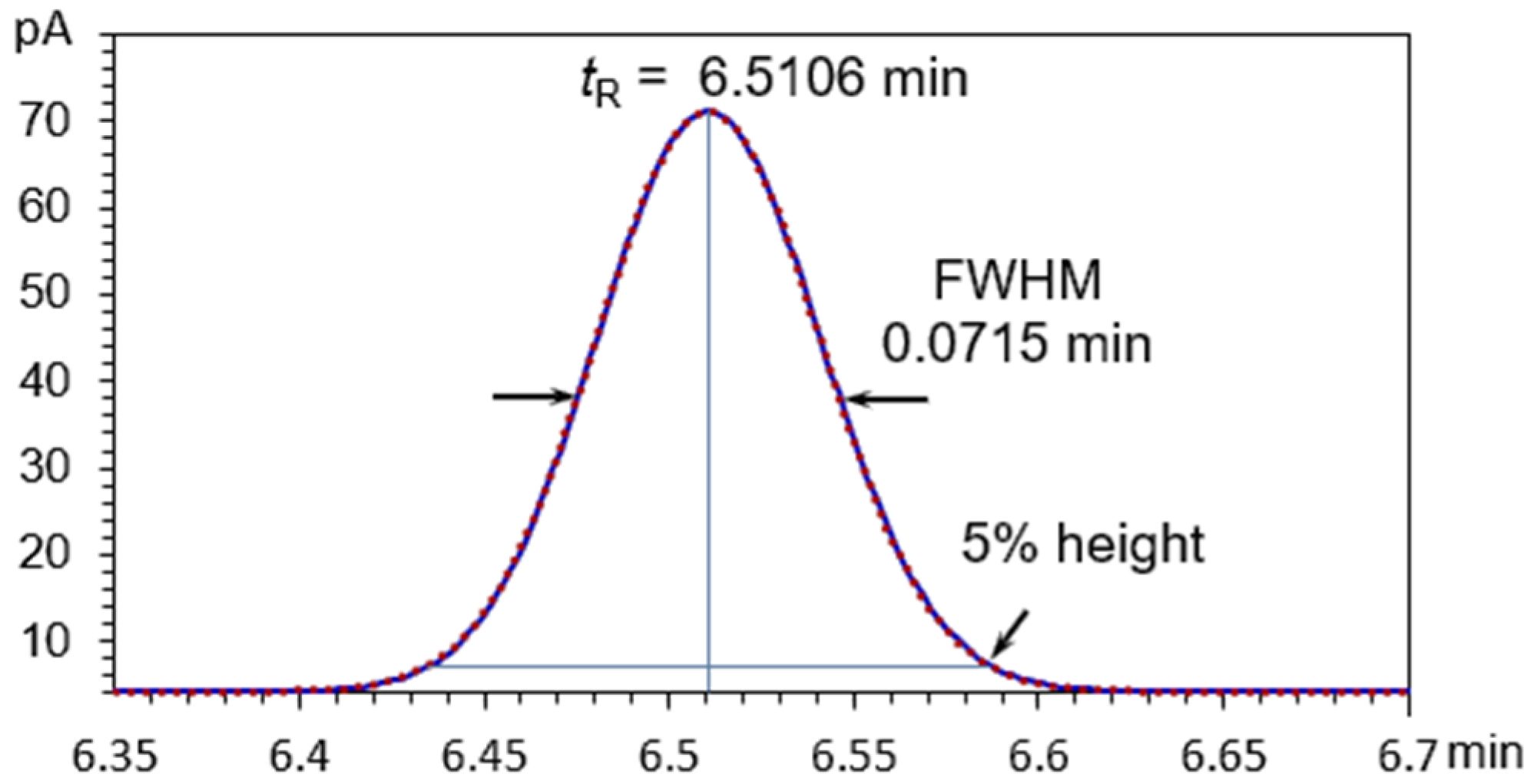
3.4. Application to Gas Chromatographic Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FT | Fourier transform |
| FWHM | Full width at half maximum |
| PMG | Polynomial modified Gaussian |
| SNR | Signal-to-noise ratio |
| USP | US pharmacopoeia |
Appendix A
References
- Martin, A.J.P.; Synge, R.L.M. A new form of chromatogram employing two liquid phases: 1. A theory of chromatography. 2. Application to the micro-determination of the higher monoamino-acids in proteins. Biochem. J. 1941, 35, 1358–1368. [Google Scholar] [CrossRef] [PubMed]
- Komsta, Ł.; Heyden, Y.V.; Sherma, J. (Eds.) Chemometrics in Chromatography; CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Dong, M.W. HPLC and UHPLC for Practicing Scientists, 2nd ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Miller, L.M.; Pinkston, J.D.; Taylor, L.T. Modern Supercritical Fluid Chromatography, Carbon Dioxide Containing Mobile Phases; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Webster, G.K.; Kott, L. (Eds.) Chromatographic Methods Development; Jenny Stanford Publishing: Singapore, 2020. [Google Scholar]
- Wan, Q.-H. Mixed Mode Chromatography: Principles, Methods, and Applications; Springer: Singapore, 2021. [Google Scholar]
- Kromidas, S. (Ed.) Optimization in HPLC, Concepts and Strategies; Wiley-VCH: Weinheim, Germany, 2021. [Google Scholar]
- Robards, K.; Ryan, D. Principles and Practice of Modern Chromatographic Methods, 2nd ed.; Academic Press: London, UK, 2021. [Google Scholar]
- Poole, C.F. (Ed.) Gas Chromatography, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Moldoveanu, S.; David, V. Essentials in Modern HPLC Separations, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Stoll, D.R.; Carr, P.W. (Eds.) Multi-Dimensional Liquid Chromatography, Principles, Practice, and Applications; CRC: Boca Raton, FL, USA, 2022. [Google Scholar]
- Hicks, M.B.; Ferguson, P.D. Practical Application of Supercritical Fluid Chromatography for Pharmaceutical Research and Development; Academic Press: London, UK, 2022. [Google Scholar]
- Fanali, S.; Chankvetadze, B.; Haddad, P.R.; Poole, C.F.; Riekkola, M.-L. (Eds.) Liquid Chromatography: Fundamentals and Instrumentation, Handbooks in Separation Science, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 1. [Google Scholar]
- Fanali, S.; Chankvetadze, B.; Haddad, P.R.; Poole, C.F.; Riekkola, M.-L. (Eds.) Liquid Chromatography: Applications, Handbooks in Separation Science, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2023; Volume 2. [Google Scholar]
- Nesterenko, P.N.; Poole, C.F.; Sun, Y. (Eds.) Ion-Exchange Chromatography and Related Techniques, Handbooks in Separation Science; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- General Chapters <621>, Chromatography; <467>, Residual Solvents, <1220> Analytical Procedure Lifecycle, The United States Pharmacopeia 49-NF 44. 2025. Available online: https://www.usp.org/ (accessed on 21 May 2025).
- Markevich, N.; Gertner, I. Comparison among methods for calculating FWHM. Nucl. Instrum. Methods Phys. Res. Sect. A 1989, 283, 72–77. [Google Scholar] [CrossRef]
- Felinger, A. Data Analysis and Signal Processing in Chromatography; Elsevier: Amsterdam, The Netherlands, 1998; pp. 19–39, 167–176. [Google Scholar]
- Wahab, M.F.; Patel, D.C.; Armstrong, D.W. Total peak shape analysis: Detection and quantitation of concurrent fronting, tailing, and their effect on asymmetry measurements. J. Chromatogr. A 2017, 1509, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Misra, S.; Wahab, M.F.; Patel, D.C.; Armstrong, D.W. The utility of statistical moments in chromatography using trapezoidal and Simpson’s rules of peak integration. J. Sep. Sci. 2019, 42, 1644–1657. [Google Scholar] [CrossRef] [PubMed]
- Burk, R.J.; Wahab, M.F.; Armstrong, D.W. Influence of theoretical and semi-empirical peak models on the efficiency calculation in chiral chromatography. Talanta 2024, 277, 126308. [Google Scholar] [CrossRef] [PubMed]
- Wahab, M.F.; Gritti, F.; O’Haver, T.C. Discrete Fourier transform techniques for noise reduction and digital enhancement of analytical signals. TrAC Trends Anal. Chem. 2021, 143, 116354. [Google Scholar] [CrossRef]
- Howell, K.B. Principles of Fourier Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 304–322, 359–363, 492–493. [Google Scholar]
- Kito, K. Digital Fourier Analysis: Advance Techniques; Springer: New York, NY, USA, 2015; pp. 105–119. [Google Scholar]
- Di Marco, V.B.; Bombi, G.G. Mathematical functions for the representation of chromatographic peaks. J. Chromatogr. A 2001, 931, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Torres-Lapasió, J.R.; Baeza-Baeza, J.J.; García-Alvarez-Coque, M.C. A model for the description, simulation, and deconvolution of skewed chromatographic peaks. Anal. Chem. 1997, 69, 3822–3831. [Google Scholar] [CrossRef]
- Baeza-Baeza, J.J.; Ortiz-Bolsico, C.; García-Álvarez-Coque, M.C. New approaches based on modified Gaussian models for the prediction of chromatographic peaks. Anal. Chim. Acta 2013, 758, 36–44. [Google Scholar] [CrossRef] [PubMed]
- Kotani, A.; Watanabe, R.; Hayashi, Y.; Machida, K.; Hakamata, H. Statistical reliability of a relative standard deviation of chromatographic peak area estimated by a chemometric tool based on the FUMI theory. J. Pharm. Biomed. Anal. 2024, 237, 115777. [Google Scholar] [CrossRef] [PubMed]
- Borman, P.J.; Guiraldelli, A.M.; Weitzel, J.; Thompson, S.; Ermer, J.; Roussel, J.M.; Marach, J.; Sproule, S.; Pappa, H.N. Ongoing analytical procedure performance verification using a risk-based approach to determine performance monitoring requirements. Anal. Chem. 2024, 96, 966–979. [Google Scholar] [CrossRef] [PubMed]
- Landers, J.P. (Ed.) Introduction to capillary electrophoresis. In Handbook of Capillary and Microchip Electrophoresis and Associated Microtechniques, 3rd ed.; CRC: Boca Raton, FL, USA, 2008; pp. 13–19. [Google Scholar]
- Gilmore, G.; Joss, D. Practical Gamma-Ray Spectrometry, 3rd ed.; Wiley: Chichester, UK, 2025; pp. 130–133, 425–428. [Google Scholar]
- Foley, J.P.; Dorsey, J.G. Equations for calculation of chromatographic figures of merit for ideal and skewed peaks. Anal. Chem. 1983, 55, 730–737. [Google Scholar] [CrossRef]
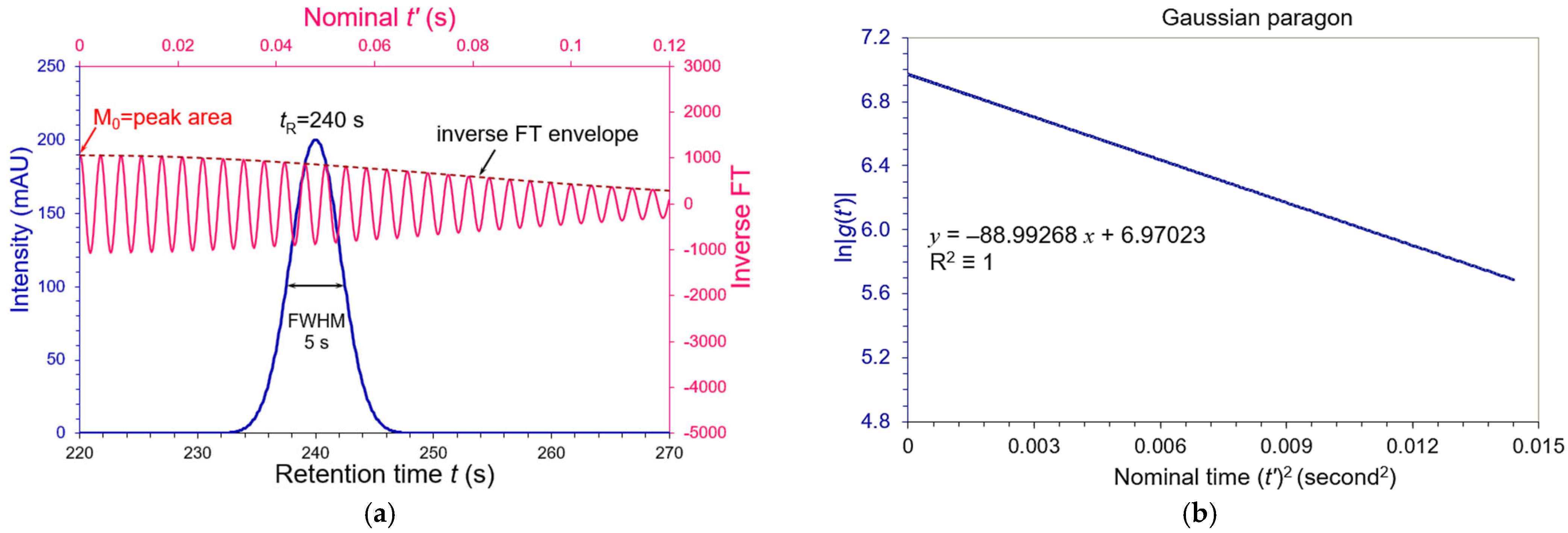
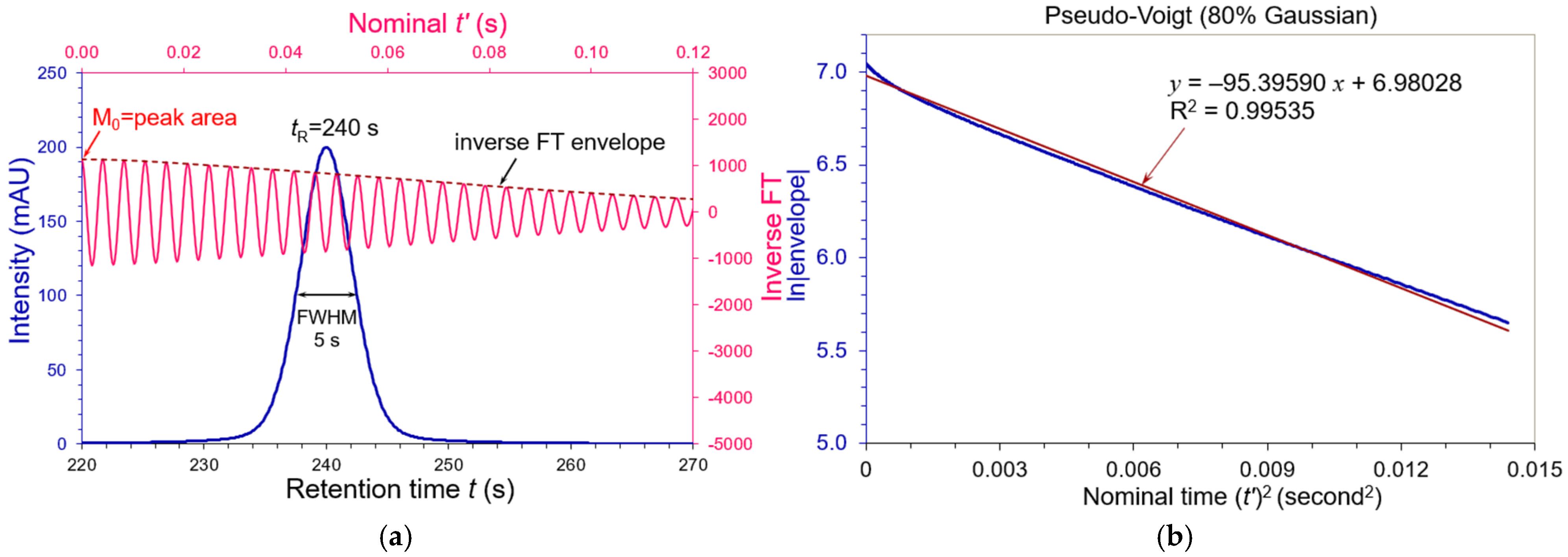
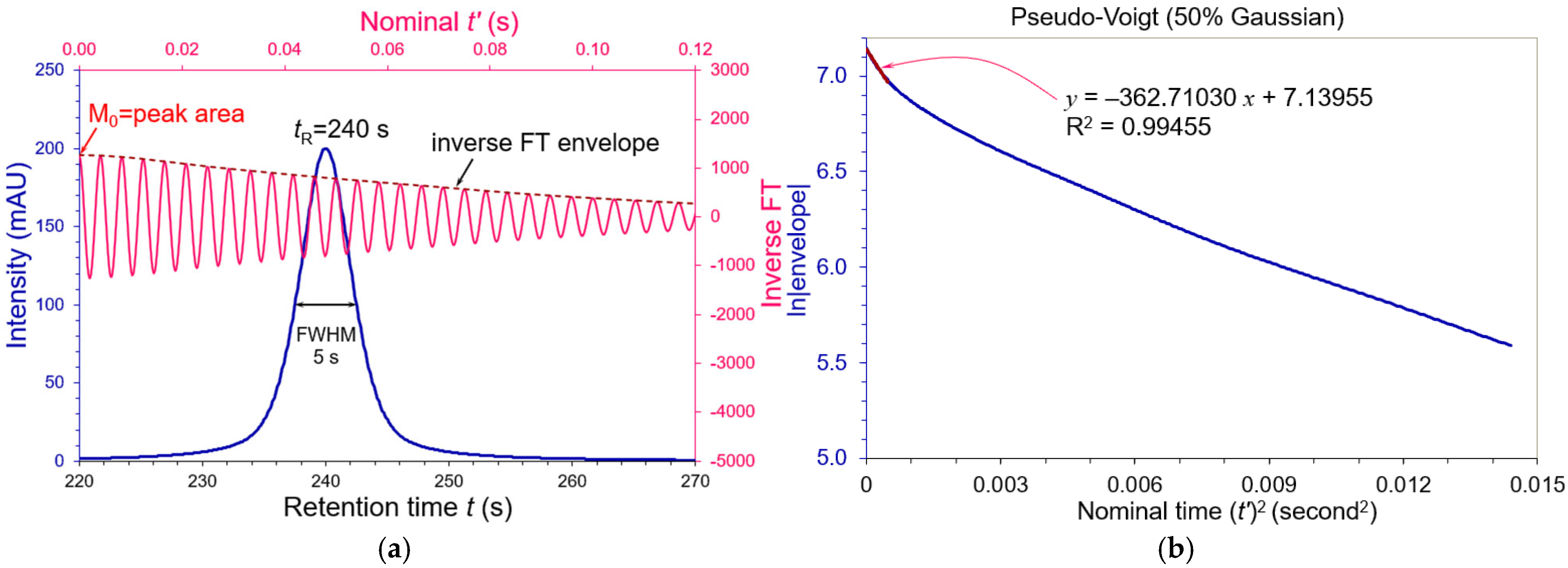
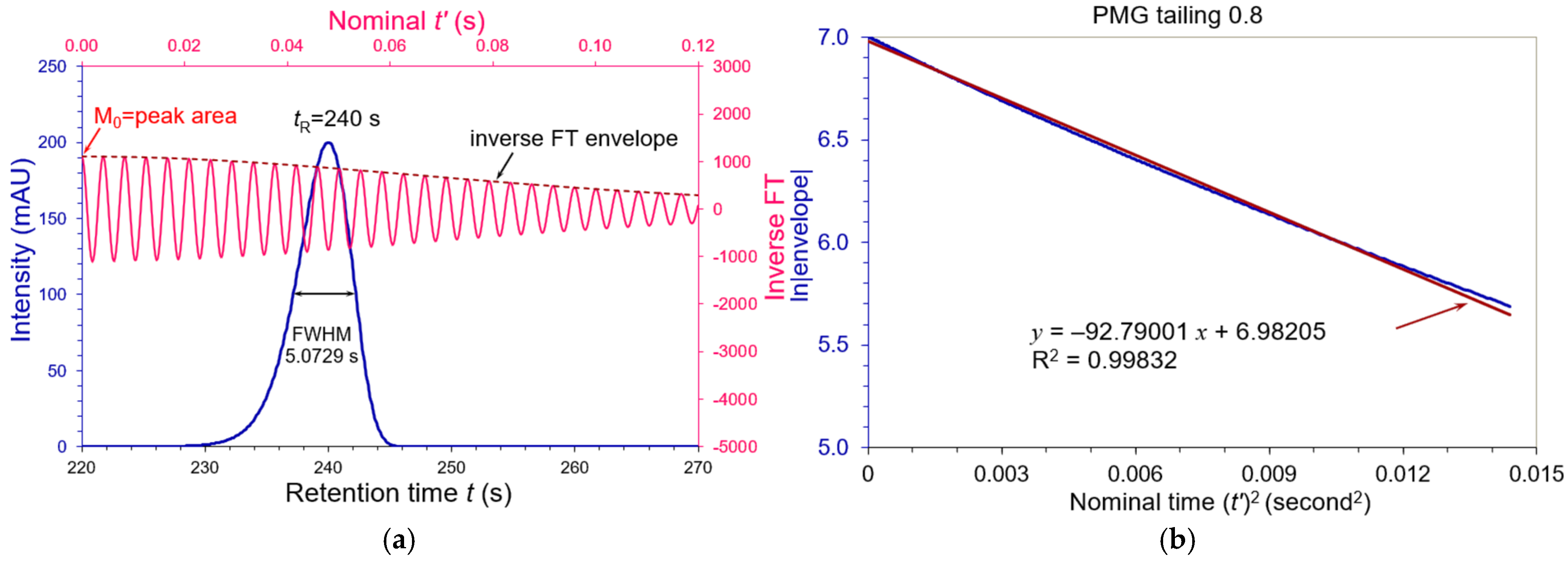
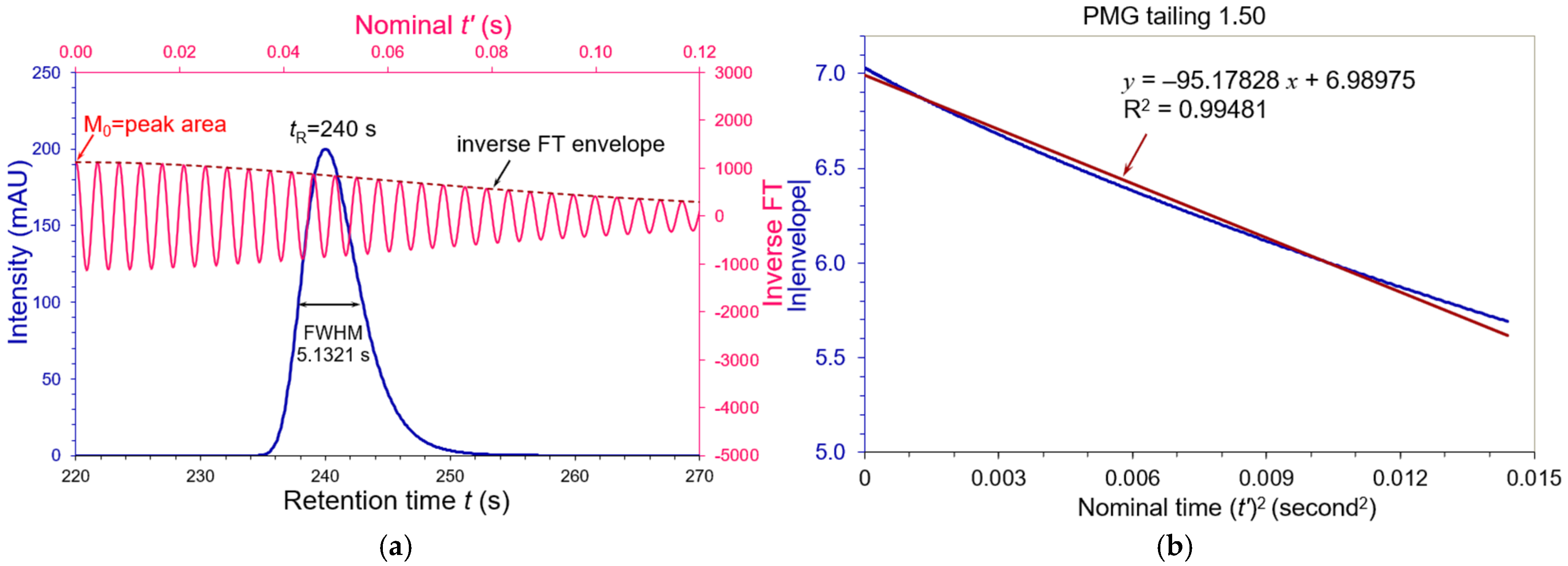
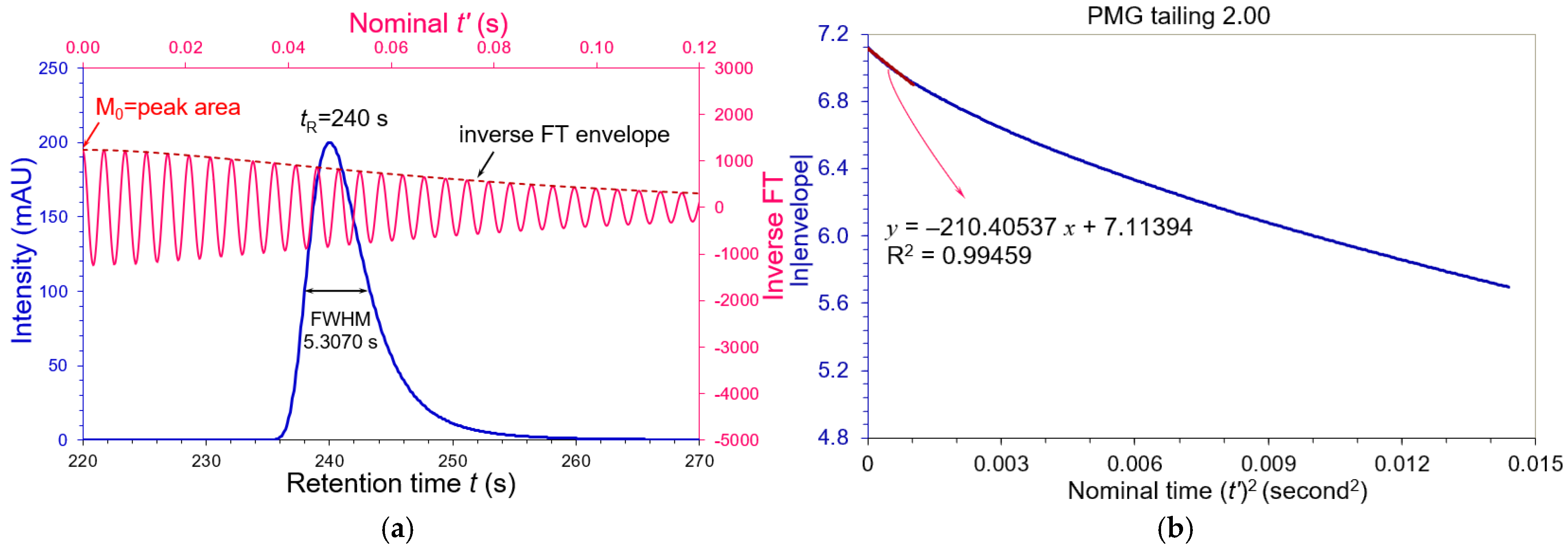
| Tailing AS | FWHM (s) | WeG (s) | N (USP) | N (WeG) | N (Moment) |
|---|---|---|---|---|---|
| 0.800 | 5.07291 | 5.10556 | 12,400 | 12,242 | 10,357 |
| 0.900 | 5.01433 | 5.02384 | 12,691 | 12,643 | 12,273 |
| 1.125 | 5.01433 | 5.02384 | 12,691 | 12,643 | 12,333 |
| 1.332 | 5.07291 | 5.10556 | 12,400 | 12,242 | 10,477 |
| 1.500 | 5.13209 | 5.17085 | 12,116 | 11,935 | 8639 |
| 1.533 | 5.14405 | 5.24825 | 12,059 | 11,585 | 8274 |
| 1.571 | 5.15766 | 5.37839 | 11,996 | 11,031 | 7864 |
| 1.600 | 5.16822 | 5.47332 | 11,947 | 10,652 | 7549 |
| 1.750 | 5.22190 | 6.12634 | 11,702 | 8502 | 6047 |
| 2.000 | 5.30702 | 7.68814 | 11,330 | 5399 | 4178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Zhu, W.; Huang, S.; Zheng, B. A Novel Linear Evaluation of Chromatographic Peak Features in Pharmacopoeias Using an Inverse Fourier Transform Algorithm. Biophysica 2025, 5, 21. https://doi.org/10.3390/biophysica5020021
Chen S, Zhu W, Huang S, Zheng B. A Novel Linear Evaluation of Chromatographic Peak Features in Pharmacopoeias Using an Inverse Fourier Transform Algorithm. Biophysica. 2025; 5(2):21. https://doi.org/10.3390/biophysica5020021
Chicago/Turabian StyleChen, Shuping, Weiyuan Zhu, Sai Huang, and Baoling Zheng. 2025. "A Novel Linear Evaluation of Chromatographic Peak Features in Pharmacopoeias Using an Inverse Fourier Transform Algorithm" Biophysica 5, no. 2: 21. https://doi.org/10.3390/biophysica5020021
APA StyleChen, S., Zhu, W., Huang, S., & Zheng, B. (2025). A Novel Linear Evaluation of Chromatographic Peak Features in Pharmacopoeias Using an Inverse Fourier Transform Algorithm. Biophysica, 5(2), 21. https://doi.org/10.3390/biophysica5020021






