Fractal Dimension Analyses to Detect Alzheimer’s and Parkinson’s Diseases Using Their Thin Brain Tissue Samples via Transmission Optical Microscopy

Abstract

Biological tissues in nature are fractal due to their self-similarity and porosity properties. These properties change with the progress of some diseases, including brain tissue in leading neurological disorders such as Alzheimer’s disease (AD) and Parkinson’s disease (PD). Thus, there is an unmet clinical need to develop a tool for accurate and early diagnosis of AD and PD conditions. Although the whole brain tissues in AD and PD have been extensively studied, their local structural alterations at the nano-to-submicron levels have not been explored. In this paper, we measure the local structural alterations in different brain regions of AD and PD patients by measuring their change in fractal dimensions via optical microscopy. Our results show an increase in the fractal dimension value of ~5–10% in the affected regions of the brain tissues relative to their respective controls. For AD cases, the structural alteration is attributed to the aberrant deposition of amyloid beta protein and neurofibrillary tangles in the brain, and for PD, the gradual loss of dopaminergic neurons and abnormal accumulation of α-synuclein in the brain. The work will enhance the further understanding of alterations in the brain structures in AD and PD and its detection.

1. Introduction

Fractals are defined as porous structures or variations in mass density that exhibit self-similarity such that in any scale, the form of the structures remains the same [1,2,3,4,5]. It has been described that most biological and non-biological systems maintain their self-similarity and are thus described as fractals; some examples include trees, clouds, coastlines, and biological cells/tissues [1,6,7,8,9]. Fractals can occur through random or deterministic processes. These fractals are quantified by their dimension at various length scales, known as the fractal dimension. Ideally, biological samples are heterogeneous in nature and show self-similarity in cell or tissue composition. It has been demonstrated in previous works that the fractal dimension serves as a potential biomarker for probing deformities in tissue samples [10,11,12,13,14,15,16,17,18,19], disease progressions, such as brain diseases and cancer, in tissues/cells, alternate the subcellular spatial structures of the building blocks, such as DNA, RNA, lipids, and protein in cells/tissue, leading to increased mass rearrangements [20,21,22,23]. Additionally, there are situations where additional masses are deposited inside the cells/tissues in the disease process, increasing the overall mass density and in turn the fractal dimension of the system [24]. Recent work has concentrated on detecting cancer and its various stages using the change in the fractal dimension as a biomarker using the tissue biopsy sample. In the case of two important brain diseases, in Alzheimer’s Disease (AD) and Parkinson’s Disease (PD), fractal dimension analyses have been used for bulk tissue micrographs using CT scans or MRI [25]; however, the local fractal dimension of different parts of the brain tissue samples has not been explored. This paper focuses on the local fractal dimension of AD and PD brain tissues samples at the micron-to-submicron level of different parts of the brain via optical transmission microscopy.

AD is a progressive neurodegenerative disorder that affects cognitive functions and causes memory loss [26,27,28]. AD is one leading cause of dementia; it has been estimated that nearly 55 million people worldwide have been affected by AD, and the numbers are expected to almost double every 20 years, reaching 78 million in 2030 and 139 million in 2050 [29,30]. The incidence of the disease is rising in line with the aging population. According to the WHO, the disease is predominantly diagnosed among older people (~60 years and above) even though it can happen in people in their early ages (~30 years) [31]. Currently, there are no therapeutic interventions that prevent or slow the progression of AD or AD-related dementia. AD is primarily linked to the formation and aggregation of abnormal proteins in the hippocampus and cerebral cortex; this is characterized by an upstream accumulation of amyloid-beta (Aβ) proteins and plaques and neurofibrillary tangles that could be used as a biomarker for diagnosis [29,32] by probing the increase in the fractal dimension.

PD, just like AD, is a progressive neurodegenerative disorder that causes both loss in motor and non-motor functions commonly found among older people (~65 years or above) [33,34,35,36,37] and is more likely among males than females for a given population of study [38]. PD is caused by the degeneration of dopaminergic neurons in the substantia nigra of the midbrain. This causes a deficiency in dopamine supply to the basal ganglia, thus resulting in motor disorders like tremor and rigidity [38,39]. Dopaminergic neurons are responsible for producing the neurotransmitter dopamine to send signals among the neurons. In most severe cases, PD patients tend to suffer from some non-motor symptoms (sleep apnea and sexual dysfunction), which is touted to occur decades before the onset of the loss of motor functions [38,39,40].

The accumulation of abnormal proteins in the brains of AD patients and degeneration of dopamine neurons in PD patients has become a major concern for many researchers, particularly regarding techniques for accurate and early detection of these brain diseases. Most techniques used to detect AD/PD are bulk imaging techniques, such as MRI, CT scan, etc. The scanning micrographs from these techniques provide macroscopic to sub-macroscopic views of the brain. As the brain is very complex in structure, other than cells and tissue structural complexity, it has also gyrification complexity. The local tissue level view at the nano-to-submicron level of AD or PD patients’ brains has not been studied in detail. It has become necessary for many researchers to investigate such brain abnormalities with light probing or light scattering experiments to investigate how the morphology of the different parts of the brain change with the progression of these brain diseases. Previous work has established that the refractive index of cellular/tissue constituents provides valuable information about the cell/tissue structure and their deformations in AD/PD [41]. In the existing literature, it has been established that many tissue disorders like brain abnormalities and cancer undergo fundamental alterations in the subcellular structures like DNA, protein, and lipids at the nano-to-subcellular scale level, which causes a fluctuation in the mass density distribution at these levels; thus the alteration in the refractive index can be used to quantify mass density alterations of the brain tissues [42,43,44,45]. Although light can interact with biological tissues to extract its structural information, most biological structures, including the organelles, are unresolved in conventional microscopy due to the diffraction limit (~200 nm), which is larger than the size of the fundamental building blocks of cells/tissues [42]. Current study on the brain tissues/cells requires pathologists to perform a biopsy on cells/tissues with staining chemicals, which is time-consuming and prone to human errors; as such, it has become pertinent for an easy and more reliable physics-based technique in analyzing these brain abnormalities. The fractal dimension analysis of the tissue sample using bright field images from scattered light will provide the needed information on the tissue structures and their alterations for quantifying the brain disorder.

In this work, we report using fractal dimensions in biological tissues for characterizing the different stages of AD/PD using paraffin-embedded brain tissue sections from different parts of the brain via transmission optical microscopy experiments. Tissue samples on glass slides containing multiple cores of tissue samples from the same bodily region of several human brain tissues samples for control and different stages of AD and PD with varying stages were used for the experiments. Our findings suggest that fractal dimensions could be a valuable tool for early and accurate diagnosis as well as for differentiating the disease stages.

2. Materials and Methods

2.1. Materials

Human brain tissue samples were obtained from two separate sources. Tissue samples were obtained commercially from Biochain Institute Inc. (Newark, CA, USA), which has collected tissue samples with legal procedures. The second tissue samples were obtained from Michigan Brain Bank, Ann Arbor, MI, USA and the University of Iowa (Iowa City, IA, USA) Deeded Body Program. All cases were consistent with neuropathological criteria for confirmed AD and PD. The study was approved (26 August 2020) by the University of Tennessee Health Science Center Institutional Review Board (IRB # 20-07595-NHSR), Memphis, TN, USA, and performed under standard ethical procedures. All the personal protection and safety procedures were followed to handle the human samples. The brain tissue samples were paraffin-embedded using a standard protocol; the microtome cut was performed for a thickness of 5 μm and placed on glass slides for optical microscopy experiments.

2.2. Mathematical Methods

2.2.1. Fractals and Fractal Dimensions

Structures that show self-similarity and porosity or variation in mass density at various length scales are said to be fractals [43,46,47]. Fractals are quantified by their dimensions, hence the fractal dimension, which is generally non-integer. There are two categories of fractals: random and deterministic. Random fractals are generated through a stochastic process. They are observed primarily in nature, whereas deterministic fractals are developed with a systematic algorithm to fill a space in a sample/structure [48]. Naturally occurring fractals like coastlines and biological tissues are random, and their dimensions are quantified by applying the box-counting technique. This technique covers the fractal figure with a grid of side length r. The number of boxes that cover the figure are represented as N_box(r) [1]. As such, for two different length scales, we can find the fractal dimension (D_f) by the equation.

$$N_1\left(r\right)\times r_1^{D_f}=N_2\left(r\right)\times r_2^{D_f}=K,$$

(1)

where K is a constant, a computer-based algorithm can measure the average fractal dimension even for many sizes. The algorithm uses the equation below to plot a curve of $ln\left(N\left(r\right)\right)$ vs. r, with the fractal dimension D_f being the line’s slope.

$$D_f=\frac{ln\left(N\left(r\right)\right)}{ln\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r$}\right.\right)}$$

(2)

2.2.2. Fractal Dimension Calculation from Microscopic Images

In this study, we report that we want to find the fractal dimension of paraffin-embedded brain tissues from different parts of the brain. Previous works have detailed the use of computer-based algorithms to find the fractal dimension of microscopic images by a series of steps [20,21]. In short, the images were first converted to a stacked binary grayscale image and a fractal box-counting method was used to calculate the fractal dimension (ImageJ, v1.53d, NIH). So far, there is not enough literature on the experimental analysis of multi-tissue brain disorders like AD and PD at the nano-to-submicron level. The report in this paper describes our experimental results and statistical analysis comparing normal brain tissues to AD/PD brain tissues in different parts of the brain, emphasizing the progression of the brain abnormalities in the hippocampus and other brain parts in AD/PD.

2.3. Experimental Setup

We obtained brain samples of AD and PD patients and their normal controls from Biochain Institute Inc. and UTHSC. For the tissue sample from Biochain, five slides of AD were commercially purchased, with eight cores of both normal/control and diseased tissue on each slide. Each slide was prepared from different brain tissue samples: precentral gyrus, postcentral gyrus, occipital lobe, and cerebellum. The PD sample from Biochain was made of two cores per slide for both regular and diseased tissue. The samples from UTHSC were sectioned into 5 μm thicknesses on a glass slide. They consisted of both standard and AD (hippocampus) and PD (substantial nigra) from the human brain.

We took microscopic images of the different tissue samples using an Olympus BX61 bright field Microscope (Tokyo, Japan) with the Amscope camera model MU1003 in transmission mode. Images of 20 spots per core were taken at a 50× magnification with proper focusing adjusted height.

As described in our previous work, we expect that the change in refractive index on a heterogeneous sample becomes apparent through its intensity. As discussed, the refractive index and transmission intensity are directly related, directly proportional to the mass density fluctuations [21]. That is, we can write:

$$I_t\left(x,y\right) \alpha n\left(x,y\right) \alpha \rho \left(x,y\right)$$

(3)

where I_t(x, y) is the transmission intensity at a spatial point (x, y), n(x, y) is the refractive index and ρ(x, y) is the mass density at that point.

Therefore, the microscope intensity is directly proportional to the mass density structure.

2.4. Analysis of Image Data

The thin tissue microscope images were converted to 8-bit gray binary images, and different areas were selected to analyze images taken at different depths. The images were cropped, and finally, the fractal box-counting tool was used to find the fractal dimensions using the ImageJ software. The obtained fractal dimension values were analyzed statistically by plotting the mean fractal values using Equation (2).

3. Results

Several (20–25) microscopic images are collected from each sample and converted into grayscale binary images. Then, images were analyzed by using the fractal box count to calculate the fractal dimension of AD and PD samples and their corresponding controls using ImageJ. The statistical analyses of the fractal dimension were carried out for different parts of the brain for AD and PD, namely AD: of the hippocampus of control, low, intermediate, and severe; precentral gyrus; postcentral gyrus; occipital lobe; and cerebellum. In the case of PD, normal and diseased samples were collected from the following parts of the brain: hippocampus and substantia nigra. The bar graphs detail the fractal dimension with the progression of diseased stages in AD.

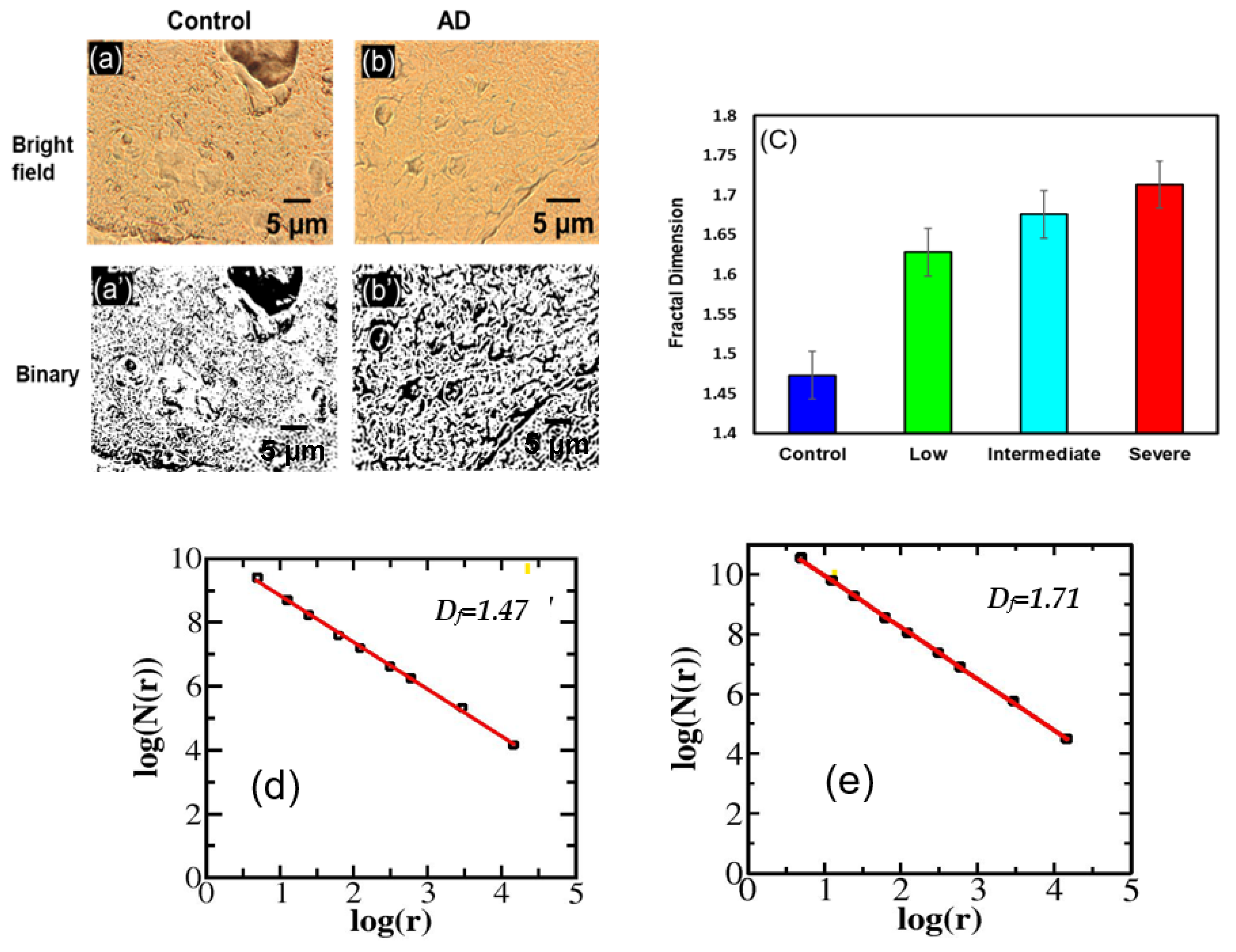
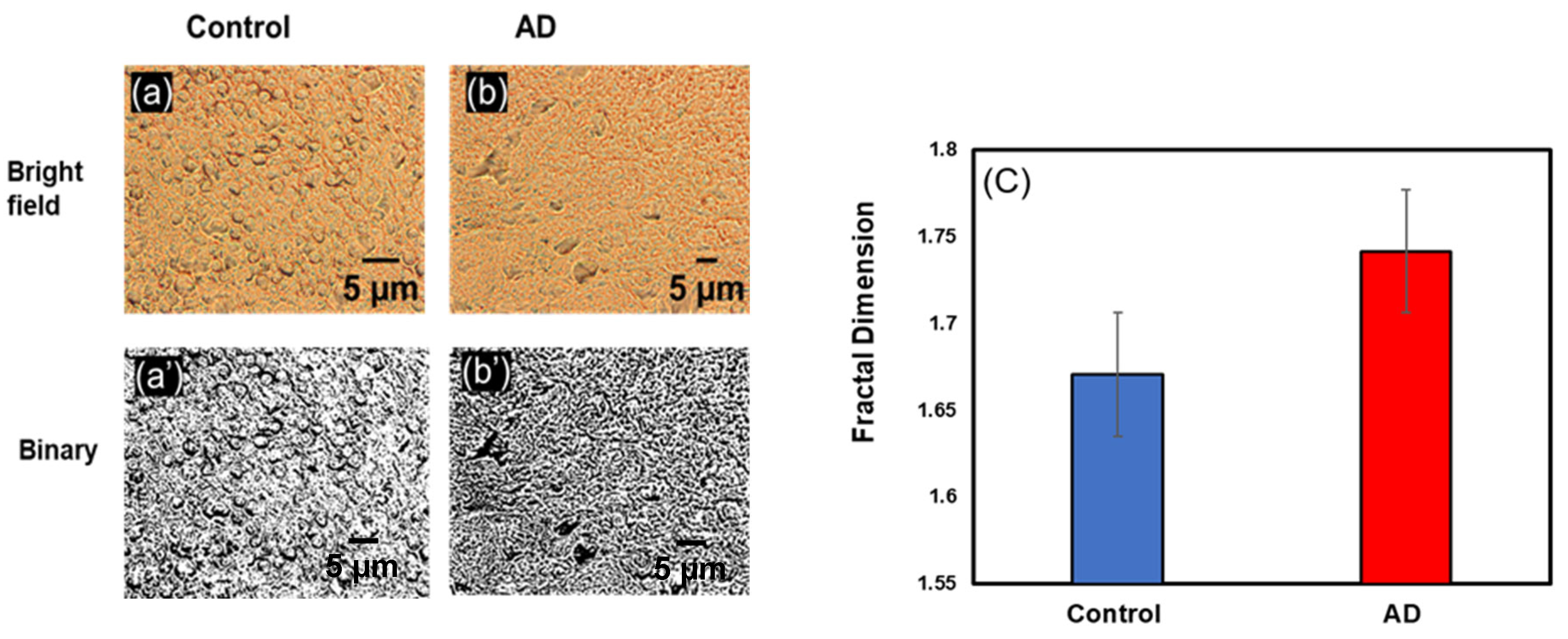
3.1. Change in Fractal Dimension (D_f) in Alzheimer’s Disease

In this section, we analyzed the fractal dimensions of normal and AD brain tissue samples for different brain parts with a focus on the various stages of AD in the hippocampus. The AD cases are categorized into low, intermediate, and severe AD stages based on Braak scores. Results from other brain parts, specifically the precentral gyrus, postcentral gyrus, occipital lobe, and cerebellum, are compared with their respective normal tissues. We observed a change in the fractal dimension value from normal tissue to AD tissue. The progression is directly related to the change in the spatial distribution in mass density, which becomes apparent in the transmission intensities due to the fluctuations within the refractive index, corroborating previous results [43,49,50,51].

3.1.1. Change in D_f in Hippocampus

Figure 1a,b shows the respective brightfield images of normal and different paraffin-embedded AD tissue stages. Figure 1a’,b’ shows the corresponding binary images of the paraffin imbedded AD sample. Figure 1c represents the bar graph of the mean fractal values for the various stages of AD tissue. In the binary images, there was space filling in tissue, resulting in an increase in mass density in tissue. The bar graph shows that the normal tissue has the lowest fractal value; however, as the AD progresses, there is an increasing order in magnitude for the fractal values of the respective stages. The fractal values were 1.4731 for normal brain tissue, 1.6283 for low AD, 1.6758 for intermediate AD, and 1.7133 for severe AD. The respective increases in the various stages were 10.5%, 13.8%, and 16.3% compared to the normal/control tissue samples. This is a significant percentage representation for the increment at various stages; this suggests that the fractal dimension is increasing with progression of AD. Figure 1d,e shows a graph of the ln(N(r)) against ln(r) for Control and Severe AD by applying the box-counting method. The slope of the plot is the fractal dimension.

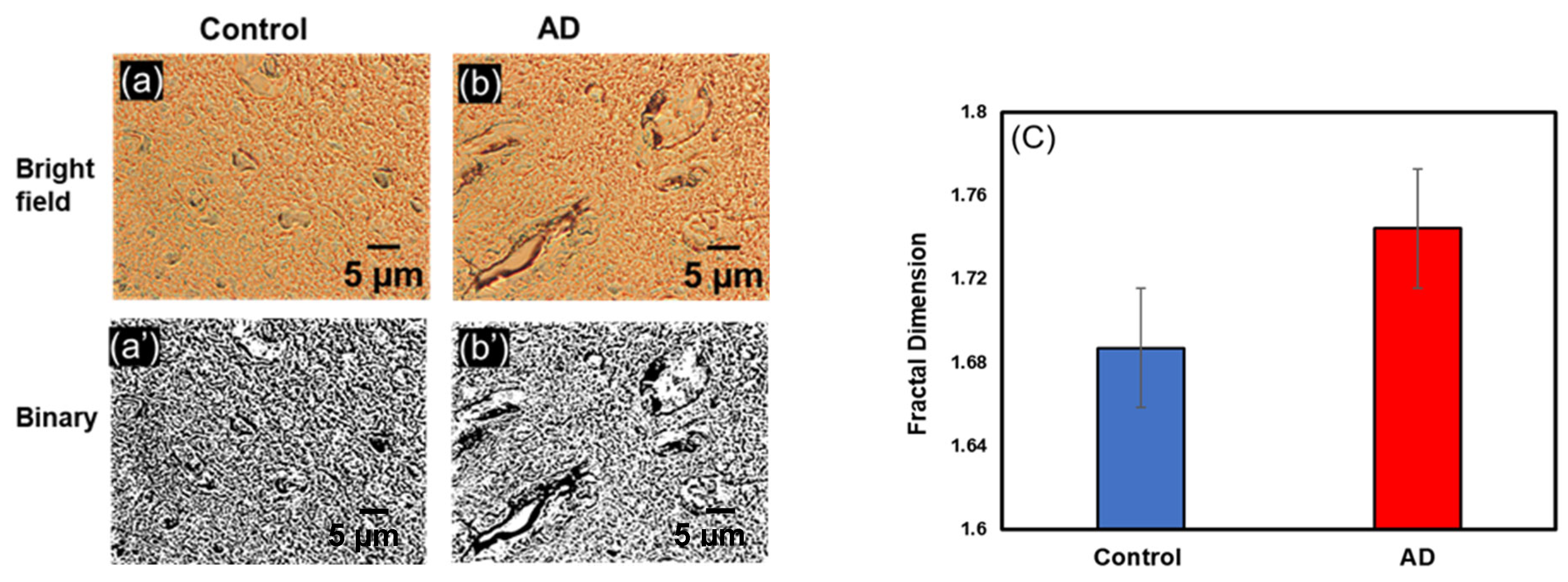
3.1.2. Change in D_f in Precentral Gyrus

Figure 2a,b shows the corresponding brightfield images of the normal brain tissue and AD brain tissue in the precentral gyrus. Figure 2a’,b’ represent the binary images of the respective brightfield images. The bar graph in Figure 2c compares the mean fractal value for normal and AD brain tissue. The actual values for normal and AD brain tissue are 1.687 and 1.744, respectively. As shown, the fractal value for the disorder marginally increased by 3.4% compared to the normal/control. This value is quite significant because, for extensive study on the various stages of the disease, the increment would be significantly larger in fractal value for progressing disorder. The binary image shows a distinctive space filling in the tissue suggesting an increase in the mass density of the tissue.

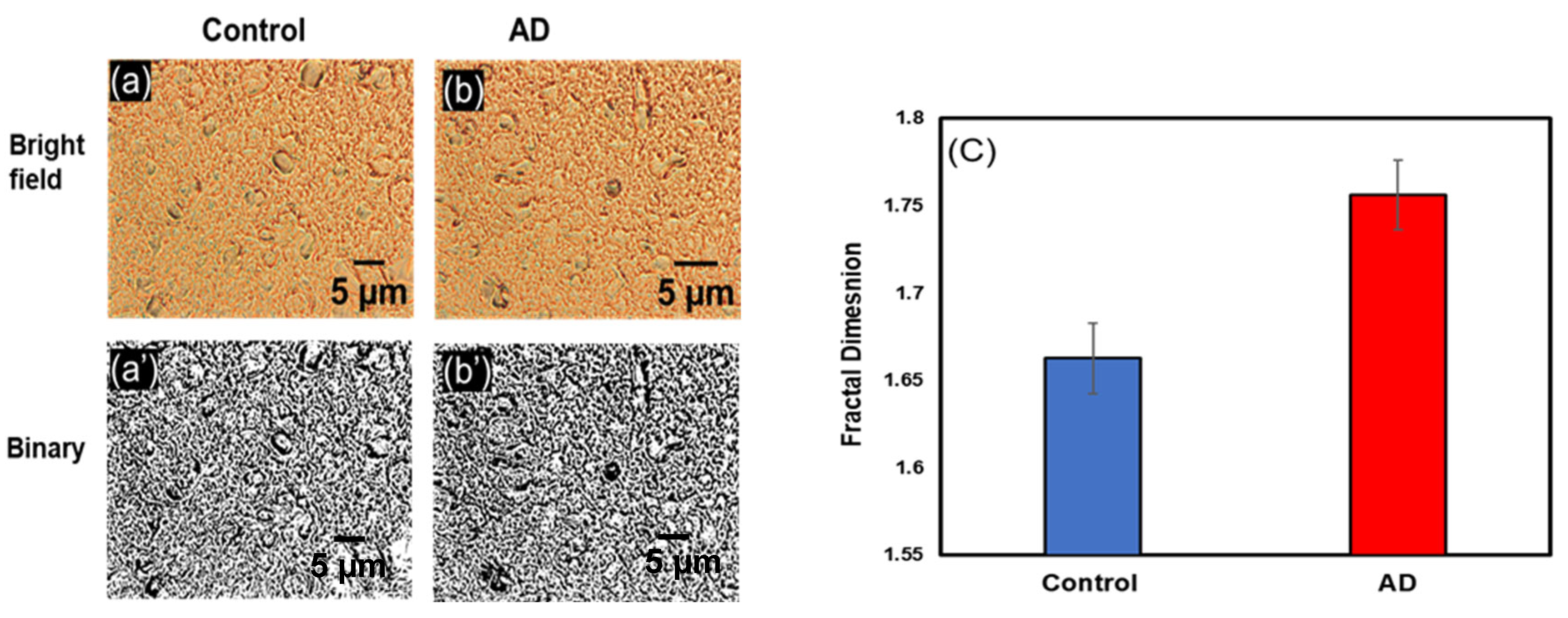
3.1.3. Change in D_f in Postcentral Gyrus

The brightfield images from normal and AD postcentral gyrus brain tissue are shown in Figure 3a and Figure 3b, respectively. Their binary analogs are shown in Figure 3a’,b’. Figure 3c shows the ensemble-averaged bar plots of the fractal dimensions of control/normal and AD tissue are 1.662 and 1.756, respectively. Figure 3c shows an increase in the fractal dimension value for AD by 5.63%.

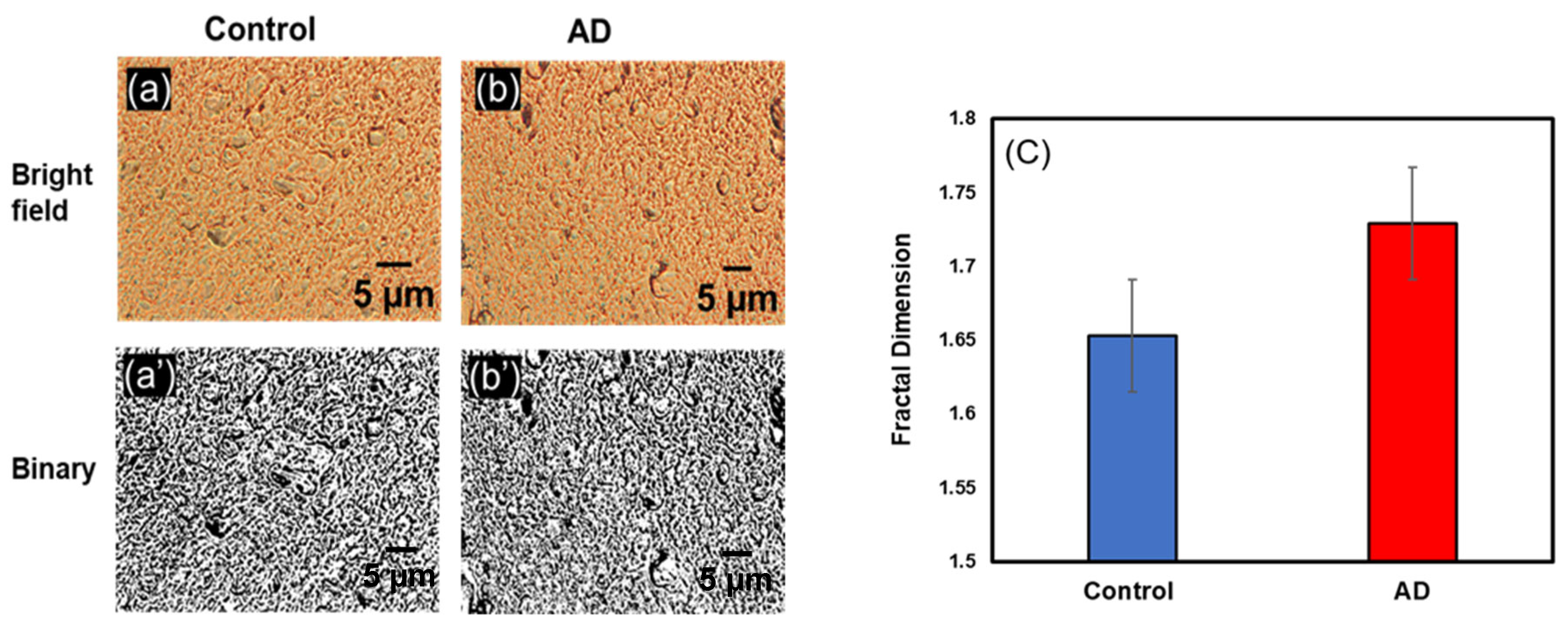
3.1.4. Change in D_f in Occipital Lobe

Representative brightfield images of normal and disordered brain tissue in the occipital lobe of the brain are shown in Figure 4a,b, respectively. Figure 4a’,b’ represents the binary images for the corresponding brightfield images obtained via ImageJ. The binary image shows that the mass density distribution in the tissue because of the molecule rearrangement increases compared to the normal brain tissue. Figure 4c shows the mean graph representation of the ordinary and AD brain tissue. The actual values obtained are 1.6530 and 1.729, respectively. The graph shows a progression in the fractal value of the disordered brain tissue by 4.6%. As stated earlier, the significant increase in the fractal dimension value is crucial because it could be helpful for future studies in different stages of AD in this part of the brain.

3.1.5. Change in D_f in Cerebellum

The brightfield images of normal and disordered paraffin-embedded AD brain tissue in the cerebellum are shown in Figure 5a,b. Figure 5a’,b’ shows the corresponding binary images and how the mass density distribution in the tissue sample increases from normal. The actual fractal values obtained are 1.67 and 1.74 for regular and AD brain tissue, respectively. The graph in Figure 5c shows a relative increase of 4.254% in the distribution as a comparison between the normal and AD. The mass density distribution in the sample increases and causes the tissues to be less porous causing mass density variation.

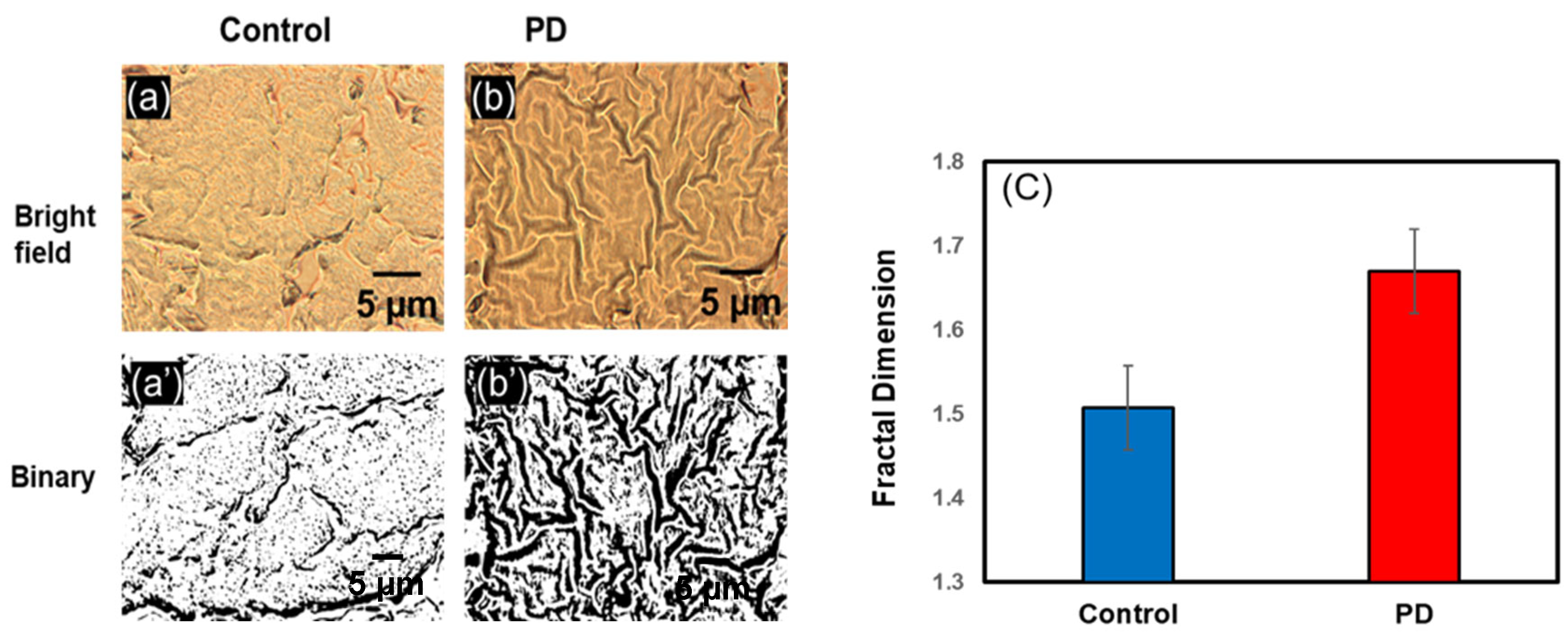
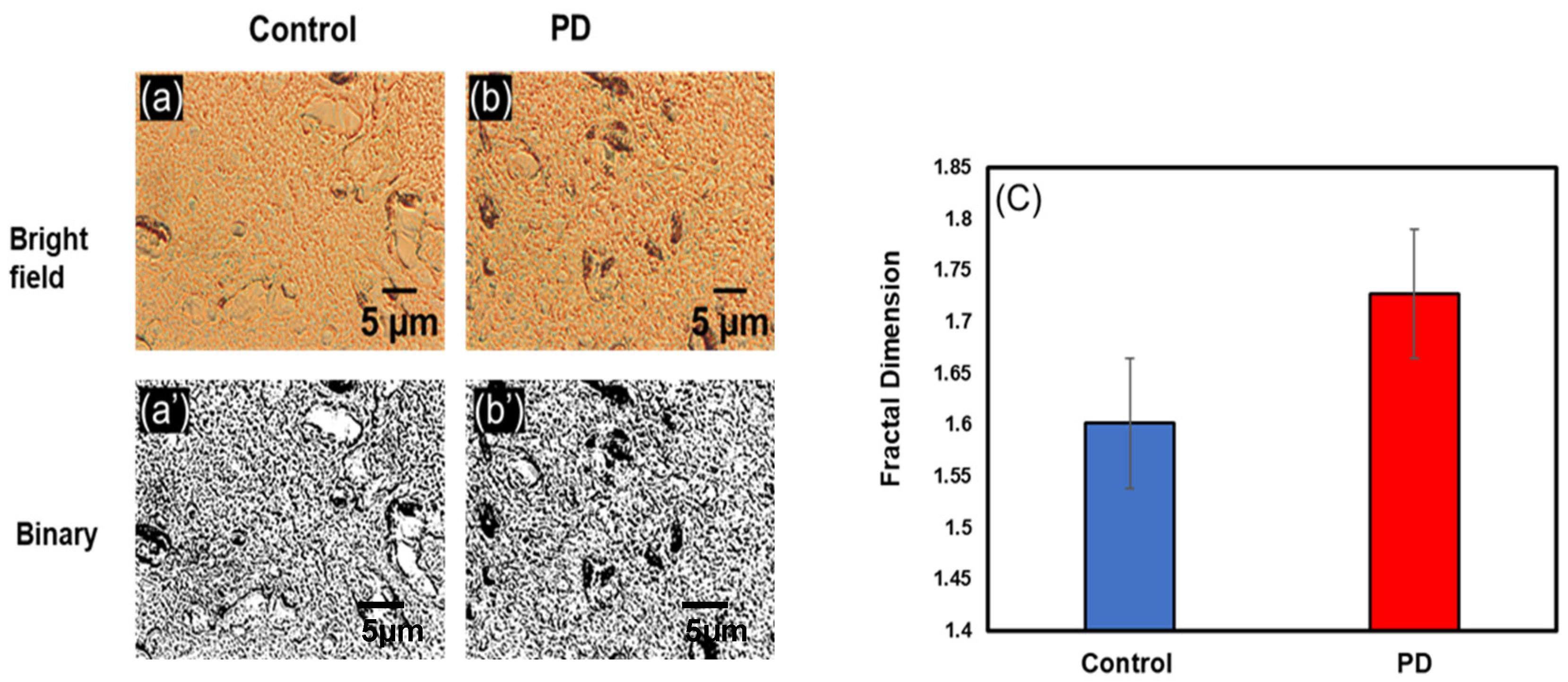
3.2. Change in Fractal Dimension (D_f) in Parkinson’s Disease

We studied the structural change and fractal dimension for PD-affected brain tissue samples for two brain regions: substantia nigra and hippocampus. The results show a significant increase in the fractal dimension of the affected tissues compared to the normal. These changes, as already discussed, are because of the redistribution due to mass density and space-filling within the tissues.

3.2.1. Change in D_f Substantia Nigra

Figure 6a,b below shows the representative brightfield images for paraffin-embedded PD brain tissue samples in the substantia nigra of the brain. The binary images are shown in Figure 6a’,b’ for regular and PD brain tissue, respectively. As per the literature, PD is mainly attributed to protein tangling, particularly α-synuclein in different brain parts. In this study, we investigate the dopamine deficiency in the substantia nigra. The binary images show a clear distinction in the structural pattern of the brain tissue between normal tissue and PD-affected tissue. The self-similarity of the tissue causes it to become less porous due to space-filling within the tissues. In previous work, it has been shown that mass density accumulations directly correlated with the increase in randomness within the tissue sample, leading to higher fluctuations in the mass density [20]. The mean bar graph in Figure 6c shows the actual values of normal and PD brain tissue as 1.507 and 1.67, respectively. This confirms a substantial increase of 10.78% between the normal tissue and disordered tissue.

3.2.2. Change in D_f in Hippocampus

The brightfield images of normal and PD brain tissue samples in the cerebellum are shown in Figure 7a,b. Figure 7a’,b’ shows the corresponding binary images and how the mass density distribution in the tissue sample increases from normal. The graph in Figure 7c shows a relative increase of 7.86% in the distribution as a comparison between the normal and PD. The actual fractal values obtained are 1.60 and 1.73 for normal and PD brain tissue, respectively. The mass density distribution in the sample increases due to the space filling within the tissue because of self-similarity, making the tissue less porous causing mass density fluctuations.

4. Discussion

In this paper, we analyzed the structural difference in normal controls and disordered brain tissues from AD and PD patients using fractal dimension analyses for various brain regions via brightfield transmission optical microscopy. As discussed, we have studied two different cases of neurodegenerative diseases, AD and PD.

In the AD tissue samples compared to their controls, we considered five main brain regions that have been implicated in AD pathogenesis: hippocampus, precentral gyrus, postcentral gyrus, occipital lobe, and cerebellum, particularly with more focus on the various stages of disease progression in the hippocampus. We took two different brain tissue samples for PD: a substantia nigra and hippocampus sections. Statistical analysis of the mean fractal values was performed for the various tissues using their binary images using ImageJ software. Our results show fractality in affected brain tissues compared with average brain tissues for both for AD and PD. Specifically, in the hippocampus of AD brains, we obtained very significant results in the increase in fractal values and percentages for the various stages of the PD disorder progression. Most importantly, there was a correlation regarding the increasing fractal dimension values from the normal tissues to the diseased AD and PD tissues. The increase in the fractal dimension could be attributed to the increase in the mass accumulation with space filling in the tissue [20], possibly due to the abnormal deposition of the amyloid beta or tau protein with the progression of AD. In previous studies, it was shown that a tissue sample’s fractal dimensions correlate well with the tissue’s mass density, which increases at various stages of cancer progression [20,21,45,49,52]. A study showed that an increase in the fractal dimension can be attributed to inflammatory response in the brain, a key feature of AD and PD [53]. Consistent with this notion, several studies documented changes in the fractal dimension in the brains of patients with neurodegenerative diseases including AD [25,54]. In fact, a strong association between the fractal dimension and clinical scores of diseases has been documented, indicating the potential of the fractal dimension as a marker to monitor brain changes during pathological conditions. This is quite apparent in our analysis because our results show a relative change in the transmission intensities due to mass density distribution within the tissue, which is due to the increase in irregularities in the structure of the AD tissues making them less porous. As previously stated, we can relate the fractal dimension to the spatial correlation length in mass density, which can be associated with the refractive index as well as the intensity of the light [20,55,56,57,58]. It is known that a change in the power of the image can be correlated to fluctuations in the refractive index, which is directly proportional to the local mass density in the brain tissue due to randomness. This is exhibited in the transmission intensities [52,58,59,60,61,62,63]. The increase for AD samples is around ~5–10% for the two types of samples used here, i.e., AD and PD, but is statistically significant.

Similarly, the changes in the fractal dimensions between the control tissue and affected tissues could be attributed to the increase in irregularity in the structure of these AD tissues, which caused the tissues to be less porous or less filled or exhibit fewer mass density fluctuations. These tissues are associated with space-filling, causing the self-similarity of the cells and tissues to increase. As the disease progresses, the fractal dimension will increase. Though different values, the increase shows how we can distinguish between normal tissues and diseased disordered tissues through their fractal values and the significance it plays in designing a physics-based prompt technique for early detection. As shown above in the results, the relative increase in fractal dimension values from the normal tissue to the disordered tissue further confirms that the quantification and effective use of the fractal dimension in biological samples, along with other simplified techniques for early detection, could become essential. Consistent with AD, the increase for PD samples is around ~5–10%, but statistically significant. This could help reduce the burden on the conventional analysis performed by pathologists through the qualitative analysis of microscopic tissue samples while reducing human errors and consuming too much time. It will become essential to compile a database for fractal data for all forms of disorder to assist clinicians in making efficient diagnoses.

5. Conclusions

As mentioned throughout, there is substantial amount of work required to detect the fractal dimension of the AD and PD patients’ brain through CT scans or MRI at the bulk level; but the local change in the fractal dimension of the tissue at the nano-to-submicron level in the brains of AD and PD patients is not described. Despite the paucity of the literature, our results provided evidence of local changes in the fractal dimension of the various parts of the brain tissues in AD and PD patients at the nano-to-submicron-to-micron scales. Due to the nature of the abnormalities, the changes in the fractal dimension of the tissue samples are finite and statistically significant, with an approximate increase of ~5–10%. Our results indicate that fractal dimension measures provide sensitive measures of structural changes in the brains of AD and PD patients and thereby may allow an early and more robust diagnosis of the disease. One potential limitation of the present study is that we did not correlate the fractal dimension with neuropathology associated with AD and PD. Therefore, further studies are warranted to determine the correlation of the fractal dimension with neuropathological hallmarks of AD and PD. Nevertheless, our findings strongly suggest the potential of fractal dimension in AD and PD research and could be used as a valuable tool for the diagnosis and prognosis of several neurodegenerative diseases.