Silica In Silico: A Molecular Dynamics Characterization of the Early Stages of Protein Embedding for Atom Probe Tomography
Abstract
1. Introduction
2. Materials and Methods
2.1. System Structures and Setup
2.2. MD Protocol and Force Field
2.3. Analysis Protocol
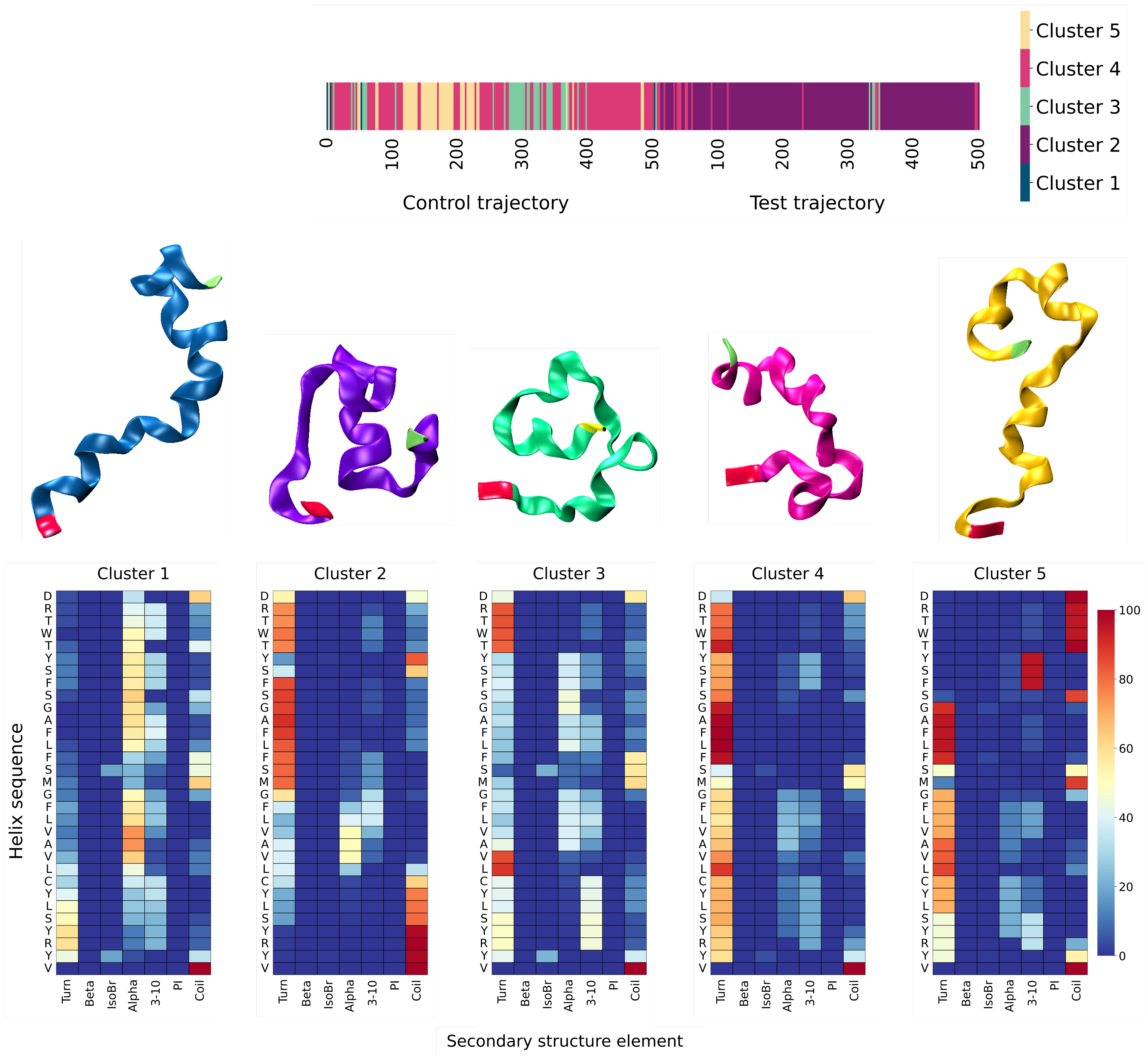
3. Results
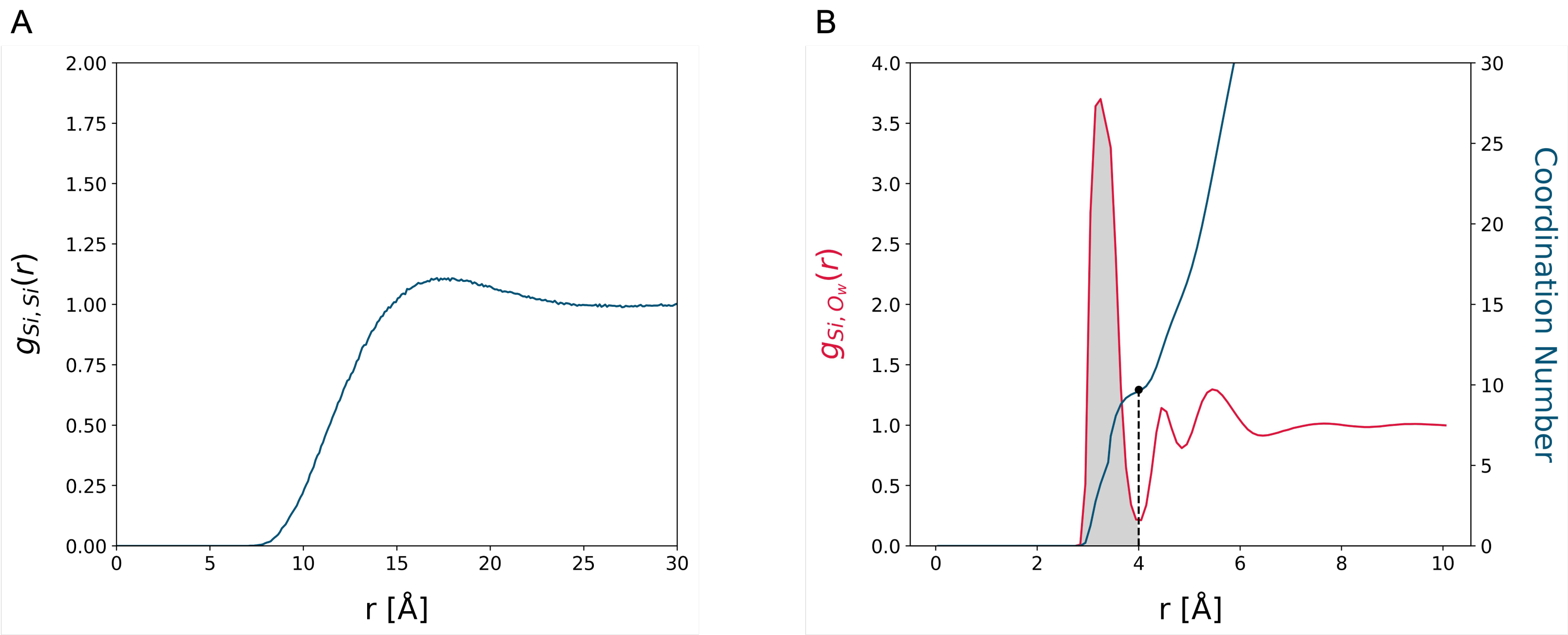
3.1. MD Assessment of the Water–Silica System
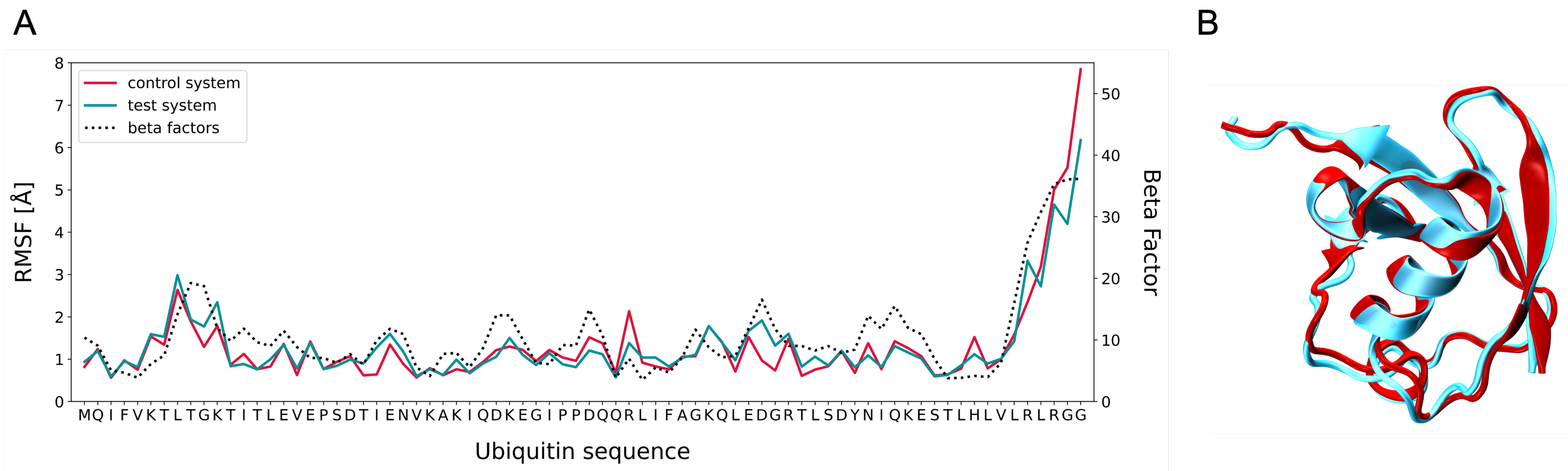
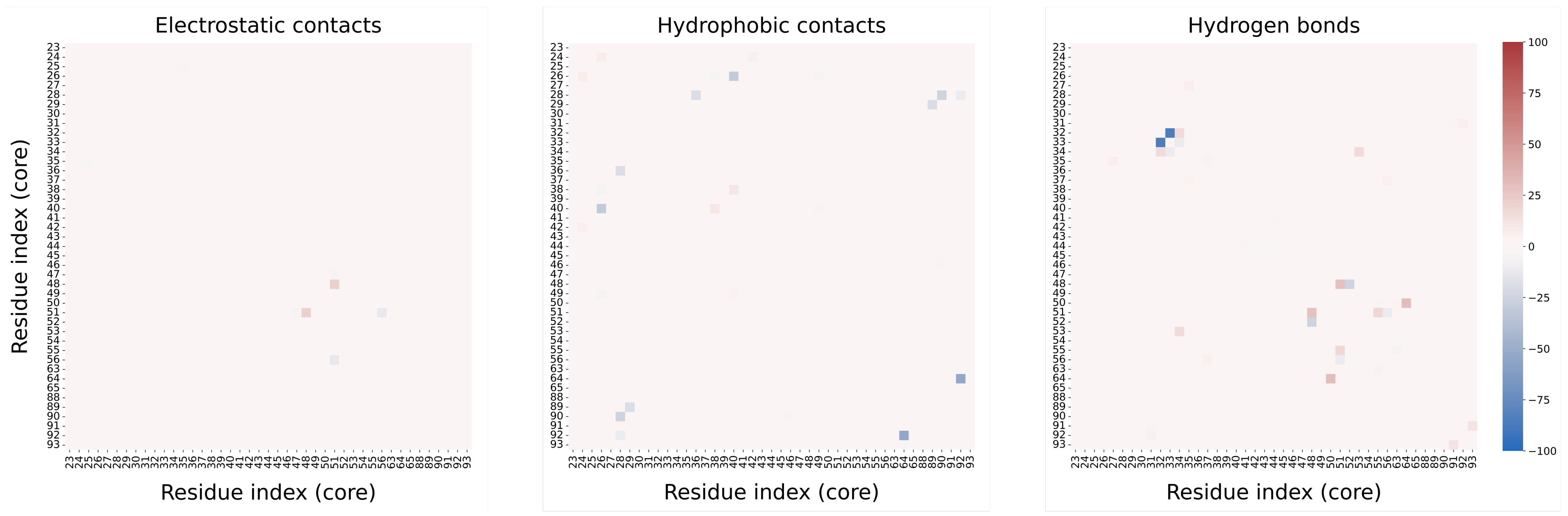
3.2. MD Assessment of Ubiquitin
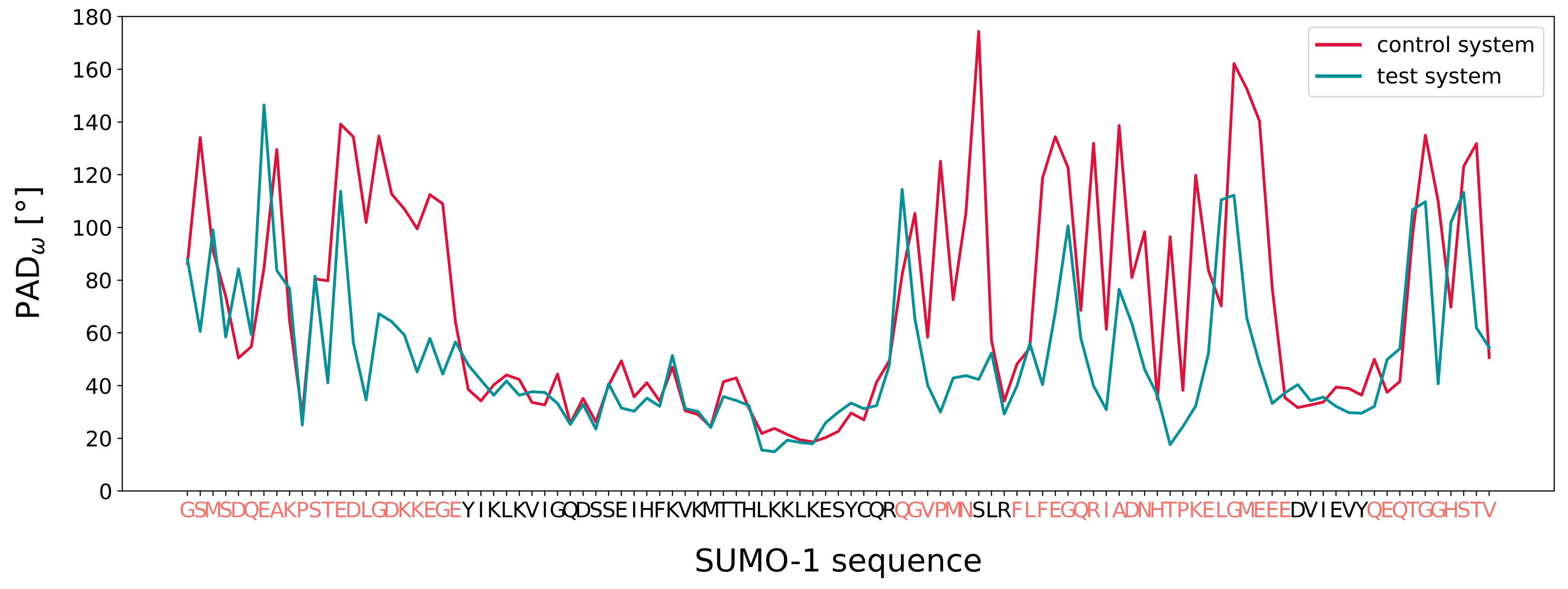
3.3. MD Assessment of the SUMO-1 Systems
3.4. MD Assessment of the IL22R1 System
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smyth, M.S.; Martin, J.H.J. X–ray crystallography. Clin. Pathol. Mol. Pathol. 2000, 53, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Geraets, J.A.; Pothula1, K.R.; Schröde, F.G.F. Integrating cryo–EM and NMR data. Curr. Opin. Struct. Biol. 2020, 61, 173–181. [Google Scholar] [CrossRef] [PubMed]
- Yip, K.M.; Fischer, N.; Paknia, E.; Chari, A.; Stark, H. Atomic-resolution protein structure determination by cryo-EM. Nature 2020, 587, 151–161. [Google Scholar] [CrossRef] [PubMed]
- McCarroll, I.E.; Bagot, P.A.J.; Devaraj, A.; Perea, D.E.; Cairney, J.M. New frontiers in atom probe tomography: A review of research enabled by cryo and/or vacuum transfer systems. Mater. Today Adv. 2020, 7, 100090. [Google Scholar] [CrossRef]
- Sundell, G.; Hulander, M.; Pihl, A.; Andersson, M. Atom Probe Tomography for 3D Structural and Chemical Analysis of Individual Proteins. Small 2019, 15, 24, 1900316. [Google Scholar] [CrossRef]
- Thompson, K.; Lawrence, D.; Larson, D.J.; Olson, J.D.; Kelly, T.F.; Gorman, B. In situ site–specific specimen preparation for atom probe tomography. Ultramicroscopy 2007, 107, 131–139. [Google Scholar] [CrossRef]
- Millera, M.K.; Russella, K.F.; Thompson, G.B. Strategies for fabricating atom probe specimens with a dual beam FIB. Ultramicroscopy 2005, 102, 287. [Google Scholar] [CrossRef]
- Belton, J.; Deschaume, O.; Perry, C.C. An overview of the fundamentals of the chemistry of silica with relevance to biosilicification and technological advances. FEBS J. 2012, 279, 1710. [Google Scholar] [CrossRef]
- Fragai, M.; Luchinat, C.; Martelli, T.; Ravera, E.; Sagi, I.; Solomonov, I.; Udi, Y. SSNMR of biosilica-entrapped enzymes permits an easy assessment of preservation of native conformation in atomic detail. Chem. Commun. 2014, 50, 421. [Google Scholar] [CrossRef]
- Karplus, M.; Petsko, G.A. Molecular dynamics simulations in biology. Nature 1990, 347, 631–639. [Google Scholar] [CrossRef]
- Fisher, M.; Bell, R.G. Influence of Zeolite Topology on CO2 N2 Separation Behavior: Force–Field Simulations Using a DFT–Derived Charge Model. J. Phys. Chem. C. 2012, 116, 26449–26463. [Google Scholar] [CrossRef]
- Vujic, B.; Lyubartsev, A.P. Transferable force–field for modeling of CO2, N2, Ar and O22 in all silica and Na+ exchanged zeolite. Modell. Simul. Mater. Sci. Eng. 2016, 24, 4, 045002. [Google Scholar] [CrossRef]
- Jorge, M.; Milne, A.W.; Barrera, M.C.; Gomes, J.R.B. New Force–Field for Organosilicon Molecules in the Liquid Phase. J. ACS Phys. Chem. Au 2021, 1, 54–9969. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open–source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm–conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Vijay-Kumar, S.; Bugg, C.E.; Cook, W.J. Structure of ubiquitin refined at 1.8 [Å] resolution. J. Mol. Biol. 1987, 3, 531–544. [Google Scholar] [CrossRef]
- Bayer, P.; Arndt, A.; Metzger, S.; Melchior, R.M.F.; Jaenicke, R.; Becker, J. Structure Determination of the Small Ubiquitin–related Modifier SUMO–1. J. Mol. Biol. 1998, 280, 275–286. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank Nucleic Acids Research. J. Mol. Biol. 2000, 28, 235–242. [Google Scholar]
- Full IL22Rα1 Sequence. Available online: https://www.uniprot.org/uniprotkb/Q8N6P7/entry (accessed on 10 December 2022).
- Coudert, E.; Gehant, S.; de Castro, E.; Pozzato, M.; Baratin, D.; Neto, T.; Sigrist, C.J.A.; Redaschi, N.; Bridge, A.; The UniProt Consortium. Annotation of biologically relevant ligands in UniProtKB using ChEBI. Bioinformatics 2023, 39, 1. [Google Scholar] [CrossRef] [PubMed]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- PyMOL Software. Available online: https://pymol.org/2/ (accessed on 10 December 2022).
- Mark, P.; Nilsson, L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindhal, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2018, 26, 1701–1718. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Eisenhaber, F.; Lijnzaad, P.; Argos, P.; Sander, C.; Scharf, M. The double cubic lattice method: Efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J. Comput. Chem. 1995, 16, 273–284. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Pyfferaph—PyPI. Available online: https://pypi.org/project/pyfferaph/ (accessed on 22 February 2023).
- Tiberti, M.; Invernizzi, G.; Lambrughi, M.; Yuval, I.; Schreiber, G.; Papaleo, E. PyInteraph: A Framework for the Analysis of Interaction Networks in Structural Ensembles of Proteins. Chem. Inf. Model. 2014, 54, 5, 1537–1551. [Google Scholar] [CrossRef]
- Caliandro, R.; Arndt, A.; Rossetti, G.; Carloni, P. Local Fluctuations and Conformational Transitions in Proteins. J. Chem. Theory Comput. 2012, 8, 4775–4785. [Google Scholar] [CrossRef]
- Fogarty, J.C.; Aktulga, H.M.; Grama, A.Y.; van Duin, A.C.T.; Pandit, S.A. A reactive molecular dynamics simulation of the silica-water interface. Chem. Phys. 2010, 132, 174704. [Google Scholar] [CrossRef]
- Dupuis, R.; Béland, L.K.; Roland, J.-M. Pellenq. Molecular simulation of silica gels: Formation, dilution, and drying. Phys. Rev. Mat. 2019, 3, 075603. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novi Inverardi, G.; Carnovale, F.; Petrolli, L.; Taioli, S.; Lattanzi, G. Silica In Silico: A Molecular Dynamics Characterization of the Early Stages of Protein Embedding for Atom Probe Tomography. Biophysica 2023, 3, 276-287. https://doi.org/10.3390/biophysica3020018
Novi Inverardi G, Carnovale F, Petrolli L, Taioli S, Lattanzi G. Silica In Silico: A Molecular Dynamics Characterization of the Early Stages of Protein Embedding for Atom Probe Tomography. Biophysica. 2023; 3(2):276-287. https://doi.org/10.3390/biophysica3020018
Chicago/Turabian StyleNovi Inverardi, Giovanni, Francesco Carnovale, Lorenzo Petrolli, Simone Taioli, and Gianluca Lattanzi. 2023. "Silica In Silico: A Molecular Dynamics Characterization of the Early Stages of Protein Embedding for Atom Probe Tomography" Biophysica 3, no. 2: 276-287. https://doi.org/10.3390/biophysica3020018
APA StyleNovi Inverardi, G., Carnovale, F., Petrolli, L., Taioli, S., & Lattanzi, G. (2023). Silica In Silico: A Molecular Dynamics Characterization of the Early Stages of Protein Embedding for Atom Probe Tomography. Biophysica, 3(2), 276-287. https://doi.org/10.3390/biophysica3020018







