Fibonacci Sequences, Symmetry and Order in Biological Patterns, Their Sources, Information Origin and the Landauer Principle
Abstract
1. Introduction
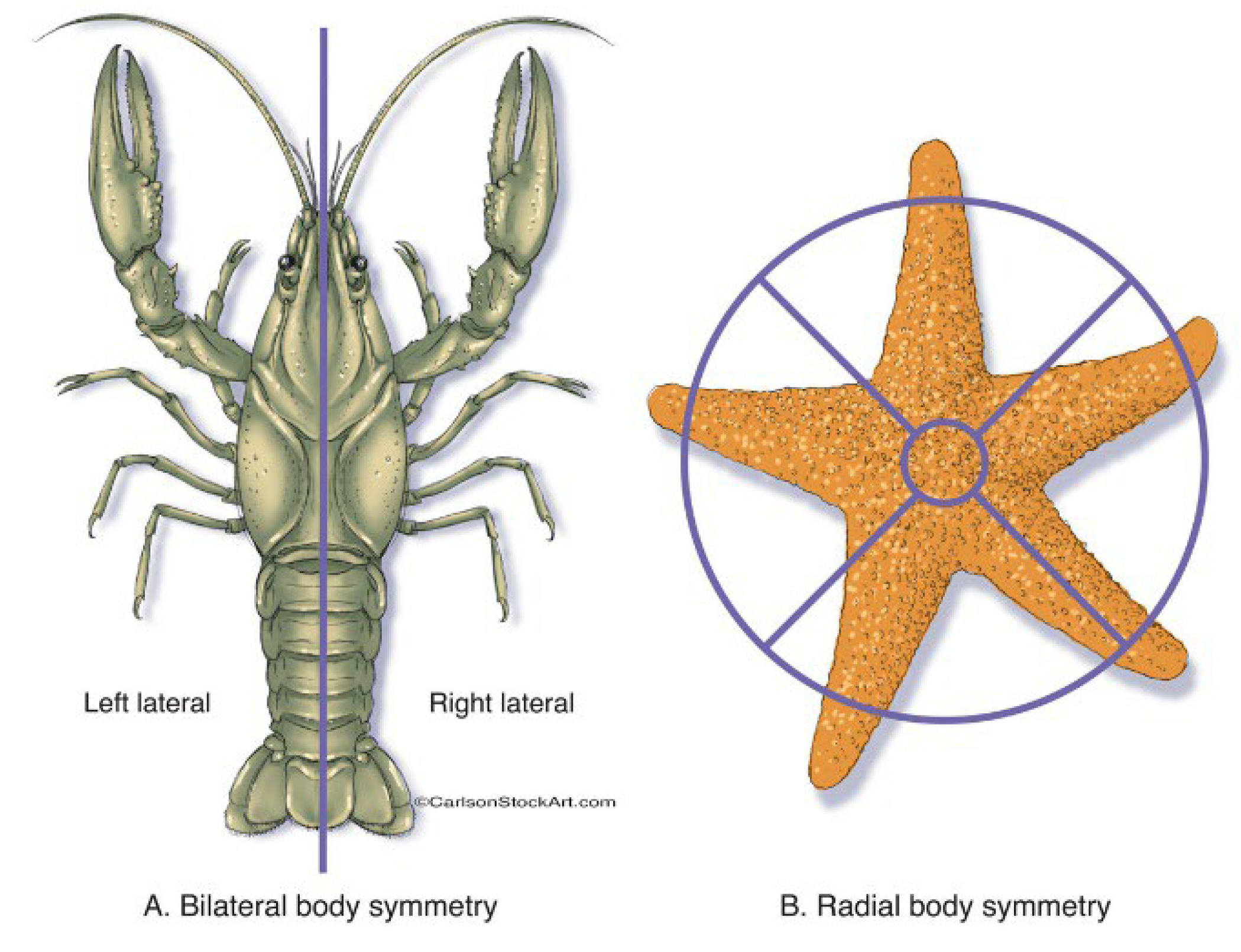
2. Physical Reasoning for the Abundant Symmetry of Biological Patterns
2.1. The “Top-Down” Approach to the Explanation of Symmetry in Organisms: Symmetry Is Dictated by the Properties of Media in Which the Organisms Act
- (i)
- The “top-down” approach, implying that the symmetry of the biological structure follows the symmetry of the media in which this structure is functioning;
- (ii)
- The “bottom-up” approach, assuming that the symmetry of biological structures emerges from the symmetry of molecules constituting the structure.
2.2. “Bottom-Up” Approach to the Symmetry of Biological Systems, Mathematical Measures of Order in Biological Patterns and the Curie-Neumann Principle
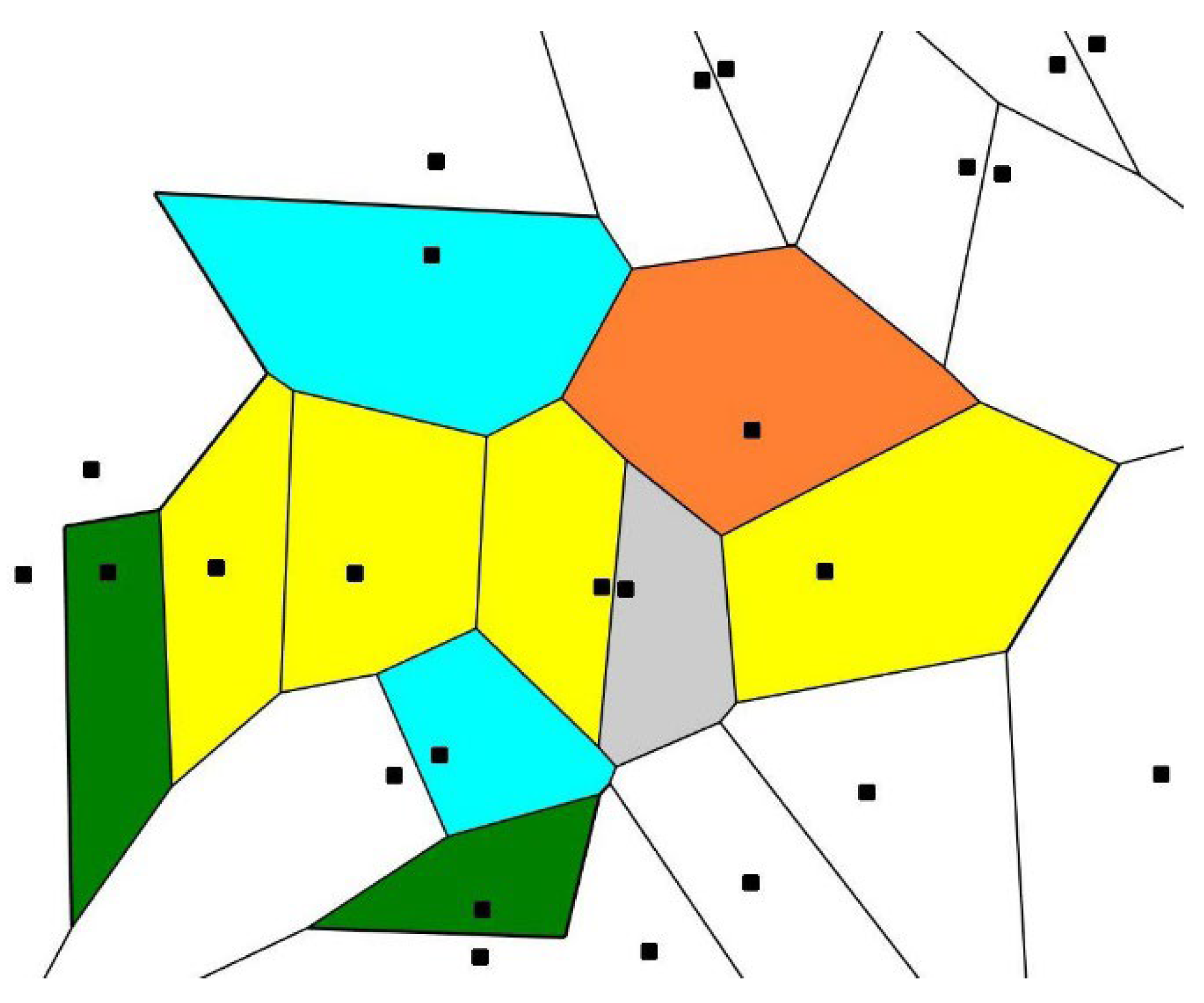
2.2.1. Mathematical Measures of Symmetry and Ordering in Biological Patterns
2.2.2. Bottom-Up Approach to the Symmetry of Biological Systems and the Curie–Neumann Principle
3. Informational Reasoning for Symmetry in Biological Systems
3.1. Symmetry and Order in Biological Systems Have Informational/Algorithmic Roots
3.2. Symmetry and Ordering in Biological Systems and the Landauer Principle: Informational Paradigm of Biology
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Finnerty, J.H. The origins of axial patterning in the metazoa: How old is bilateral symmetry? Int. J. Dev. Biol. 2003, 47, 523–529. [Google Scholar] [PubMed]
- Finnerty, J.H.; Pang, K.; Burton, P.; Paulson, D.; Martindale, M.Q. Origins of Bilateral Symmetry: Hox and Dpp Expression in a Sea Anemone. Science 2004, 304, 1335. [Google Scholar] [CrossRef] [PubMed]
- Longo, G.; Montévil, M. From Physics to Biology by Extending Criticality and Symmetry Breakings. In Perspectives on Organisms; Lecture Notes in Morphogenesis; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Yonekura, T.; Sugiyama, M. Symmetry and its transition in phyllotaxis. J. Plant. Res. 2021, 134, 417–430. [Google Scholar] [CrossRef] [PubMed]
- Dumais, J. Can mechanics control pattern formation in plants? Curr. Opin. Plant Biol. 2007, 10, 58–62. [Google Scholar] [CrossRef] [PubMed]
- Dengler, N.G. Anisophylly and dorsiventral shoot symmetry. Int. J. Plant Sci. 1999, 160, S67–S80. [Google Scholar] [CrossRef]
- Cannon, K.A.; Ochoa, J.M.; Yeates, T.O. High-symmetry protein assemblies: Patterns and emerging applications. Curr. Opin. Struct. Biol. 2019, 55, 77–84. [Google Scholar] [CrossRef]
- Wolynes, P.G. Symmetry and the energy landscapes of biomolecules. Proc. Natl. Acad. Sci. USA 1996, 93, 14249–14255. [Google Scholar] [CrossRef]
- Hollo, G. A new paradigm for animal symmetry. Interface Focus 2015, 5, 20150032. [Google Scholar] [CrossRef]
- Bormashenko, E. Entropy, Information, and Symmetry: Ordered is Symmetrical. Entropy 2020, 22, 11. [Google Scholar] [CrossRef]
- Bormashenko, E. Entropy, Information, and Symmetry; Ordered is Symmetrical, II: System of Spins in the Magnetic Field. Entropy 2020, 22, 235. [Google Scholar] [CrossRef]
- Macia, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2005, 68, 1–45. [Google Scholar] [CrossRef]
- Mitchison, G.J. Phyllotaxis and the Fibonacci series. Science 1977, 196, 270–275. [Google Scholar] [CrossRef] [PubMed]
- Adam, J.A. Mathematics in Nature: Modeling Patterns in the Natural World; Princeton University Press: Princeton, NJ, USA, 2003; Chapter 10; pp. 213–230. [Google Scholar]
- Nowlan, R.A. Rabbits & Patterns. In Masters of Mathematics; SensePublishers: Rotterdam, The Netherlands, 2017; Chapter 10; pp. 161–177. [Google Scholar]
- Posamentier, A.S.; Lehmann, I. The Fabulous Fibonacci Numbers; Prometheus Books: Amherst, NY, USA, 2007; Chapter 2; pp. 59–76. [Google Scholar]
- Swinton, J.; Ochu, E. Novel Fibonacci and non-Fibonacci structure in the sunflower: Results of a citizen science experiment. R. Soc. Open Sci. 2016, 3, 160091. [Google Scholar] [CrossRef]
- Li, R.; Bowerman, B. Symmetry Breaking in Biology. Cold Spring Harb. Perspect. Biol. 2010, 2, a003475. [Google Scholar] [CrossRef] [PubMed]
- Hollo, G. Demystification of animal symmetry: Symmetry is a response to mechanical forces. Biol. Direct. 2017, 12, 11. [Google Scholar] [CrossRef] [PubMed]
- Holló, G.; Novák, M. The manoeuvrability hypothesis to explain the maintenance of bilateral symmetry in animal evolution. Biol Direct. 2012, 7, 22. [Google Scholar] [CrossRef]
- Manuel, M. Early evolution of symmetry and polarity in metazoan body plans. Comptes Rendus Biol. 2009, 332, 184–209. [Google Scholar] [CrossRef]
- Van Workum, K.; Douglas, J.F. Schematic Models of Molecular Self-Organization. Macromol. Symp. 2005, 227, 1–16. [Google Scholar] [CrossRef]
- Van Workum, K.; Douglas, J.F. Symmetry, equivalence, and molecular self-assembly. Phys. Rev. E 2006, 73, 031502. [Google Scholar] [CrossRef]
- Williams, K.S.; Smith, K.G.; Stephen, F.M. Emergence of 13-Yr Periodical Cicadas (Cicadidae: Magicicada): Phenology, Mortality, and Predators Satiation. Ecology 1993, 74, 1143–1152. [Google Scholar] [CrossRef]
- Yoshimura, J. The Evolutionary Origins of Periodical Cicadas During Ice Ages. Am. Nat. 1997, 149, 112–124. [Google Scholar] [CrossRef]
- Cox, R.; Carlton, C.E. Paleoclimatic Influences in the Evolution of Periodical Cicadas. Am. Midl. Nat. 1988, 120, 183–193. [Google Scholar] [CrossRef]
- Cox, R.; Carlton, C.E. A Commentary on Prime Numbers and Life Cycles of Periodical Cicadas. Am. Nat. 1998, 152, 162–164. [Google Scholar] [CrossRef] [PubMed]
- Webb, G.F. The prime number periodical cicada problem. Am. Inst. Math. Sci. 2001, 1, 387–399. [Google Scholar] [CrossRef]
- Goles, E.; Schulz, A.B.; Markus, M. Prime number selection of cycles in a predator-prey model. Complexity 2001, 6, 33–38. [Google Scholar] [CrossRef]
- Baker, A. Are there Genuine Mathematical Explanations of Physical Phenomena? Mind 2005, 114, 223–238. [Google Scholar] [CrossRef]
- Swaddle, J.H. Reproductive success and symmetry in zebra finches. Anim. Behav. 1996, 51, 203–210. [Google Scholar] [CrossRef]
- Hansen, L.T.T.; Amundsen, T.; Forsgren, E. Symmetry: Attractive not only to females. Proc. R. Soc. Lond. B 1999, 266, 1235–1240. [Google Scholar] [CrossRef]
- Johnston, I.G.; Dinglee, K.; Greenbury, S.F.; Camargoh, Q.; Doyei, J.P.K.; Ahnert, S.E.; Louis, A.A. Symmetry and simplicity pontaneously emerge from the algorithmic nature of evolution. Proc. Natl. Acad. Sci. USA 2022, 119, e2113883119. [Google Scholar] [CrossRef]
- Ocklenburg, S.; Mundorf, A. Symmetry and asymmetry in biological structures. Proc. Natl. Acad. Sci. USA 2022, 119, e2204881119. [Google Scholar] [CrossRef]
- Landauer, R. Dissipation and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183. [Google Scholar] [CrossRef]
- Landauer, R. Information is physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Bormashenko, E. The Landauer Principle: Re-Formulation of the Second Thermodynamics Law or a Step to Great Unification? Entropy 2019, 21, 918. [Google Scholar] [CrossRef]
- Finnerty, J.H. Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals? Bioessays 2005, 27, 1174–1180. [Google Scholar] [CrossRef]
- Toxvaerd, S. The Emergence of the Bilateral Symmetry in Animals: A Review and a New Hypothesis. Symmetry 2021, 13, 261. [Google Scholar] [CrossRef]
- Weihs, D. Stability Versus Maneuverability in Aquatic Locomotion. Integr. Comp. Biol. 2002, 42, 127–134. [Google Scholar] [CrossRef]
- Lighthill, M.J. Aquatic animal propulsion of high hydromechanical efficiency. J. Fluid Mech. 1970, 44, 265–301. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Course of Theoretical Physics; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Kittel, C.H. Thermal Physics; John and Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Baierlein, R. Thermal Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Shroeder, D.V. An Introduction to Thermal Physics; Oxford University Press: Oxford, UK, 2021. [Google Scholar]
- van Hemmen, J.L. A Generalized Equipartition Theorem. Phys. Lett. A 1980, 79, 25–28. [Google Scholar] [CrossRef]
- Lawrence, E.; Turner, L.E., Jr. Generalized Classical Equipartition Theorem. Am. J. Phys. 1976, 44, 104–105. [Google Scholar]
- Landsberg, P.T. Generalized Equipartition. Am. J. Phys. 1978, 46, 296. [Google Scholar] [CrossRef]
- Landsberg, P.T. Equipartition for a Relativistic Gas. Am. J. Phys. 1992, 60, 561. [Google Scholar] [CrossRef]
- Lawless, W.N. Energy Equipartition: A Restatement. Am. J. Phys. 1964, 32, 686–687. [Google Scholar] [CrossRef]
- Bormashenko, E.; Gendelman, O. On the applicability of the equipartition theorem. Therm. Sci. 2010, 14, 855–858. [Google Scholar] [CrossRef]
- Stephen, M.J.; Straley, J.P. Physics of liquid crystals. Rev. Mod. Phys. 1974, 46, 617. [Google Scholar] [CrossRef]
- Mathur-De Vré, R. The NMR studies of water in biological systems. Prog. Biophys. Mol. Biol. 1980, 35, 103–134. [Google Scholar] [CrossRef]
- Tait, M.; Franks, F. Water in Biological Systems. Nature 1971, 230, 91–94. [Google Scholar] [CrossRef]
- Tortora, L.; Lavrentovich, O.D. Chiral symmetry breakingby spatial confinement in tactoidal droplets of lyotropic chromonic liquid rystals. Proc. Natl. Acad. Sci. USA 2011, 108, 5163–5168. [Google Scholar] [CrossRef]
- Strzelecka, T.E.; Davidson, M.W.; Rill, R.L. Multiple liquid crystal phases of DNA at high concentrations. Nature 1988, 331, 457–460. [Google Scholar] [CrossRef]
- Dierking, I. Chiral Liquid Crystals: Structures, Phases, Effects. Symmetry 2014, 6, 444–472. [Google Scholar] [CrossRef]
- Dierking, I.; Figueiredo Neto, A.M. Novel Trends in Lyotropic Liquid Crystals. Crystals 2020, 10, 604. [Google Scholar] [CrossRef]
- Bawden, F.C.; Pirie, N.W.; Bernal, J.D.; Fankuchen, I. Liquid Crystalline Substances from Virus-infected Plants. Nature 1936, 138, 1051–1052. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. 2. Symmetry groups and the tetrahedron. J. Am. Chem. Soc. 1993, 115, 8278–8828. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Avnir, D. Continuous Symmetry Measures. 4. Chirality. J. Am. Chem. Soc. 1995, 117, 462–473. [Google Scholar] [CrossRef]
- Pinsky, M.; Avnir, D. Continuous Symmetry Measures. 5. The Classical Polyhedra. Inorg. Chem. 1998, 37, 5575–5582. [Google Scholar] [CrossRef] [PubMed]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry as a continuous feature. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 1154–1166. [Google Scholar] [CrossRef]
- Grimme, S. Continuous symmetry measures for electronic wavefunctions. Chem. Phys. Lett. 1998, 297, 15–22. [Google Scholar] [CrossRef]
- Bormashenko, E.; Legchenkova, I.; Frenkel, M.; Shvalb, N.; Shoval, S. Voronoi Entropy vs. Continuous Measure of Symmetry of the Penrose Tiling: Part I. Analysis of the Voronoi Diagrams. Symmetry 2021, 13, 1659. [Google Scholar] [CrossRef]
- Pinsky, M.; Zait, A.; Bonjack, M.; Avnir, D. Continuous symmetry analyses: Cnv and Dn measures of molecules, complexes, and proteins. Comp. Chem. 2013, 34, 2–9. [Google Scholar] [CrossRef]
- Bonjack, M.; Avni, D. The near-symmetry of protein oligomers: NMR-derived structures. Sci. Rep. 2020, 10, 8367. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les paralléloèdres primitifs. Reine Angew. Math. 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Liebling, T.M.; Pournin, L. Voronoi diagrams and Delaunay triangulations: Ubiquitous Siamese Twins. Doc. Math. ISMP 2012, 419, 431. [Google Scholar]
- Suárez-Plasencia, L.; Herrera-Macías, J.A.; Legón-Pérez, C.M.; Socorro-LLanes, R.; Rojas, O.; Sosa-Gómez, G. Analysis of the Number of Sides of Voronoi Polygons in PassPoint. In Computer Science and Health Engineering in Health Services. COMPSE 2020; Marmolejo-Saucedo, J.A., Vasant, P., Litvinchev, I., Rodriguez-Aguilar, R., Martinez-Rios, F., Eds.; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Springer: Cham, Switzerland, 2021; Volume 359. [Google Scholar]
- Poupon, A. Voronoi and Voronoi-related tessellations in studies of protein structure and interaction. Curr. Opin. Struct. Biol. 2004, 14, 233–241. [Google Scholar] [CrossRef] [PubMed]
- Bock, M.; Tyagi, A.K.; Kreft, J.U.; Alt, W. Generalized Voronoi Tessellation as a Model of Two-dimensional Cell Tissue Dynamics. Bull. Math. Biol. 2010, 72, 1696–1731. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.T.; Tao, C.L.; Zhang, X. Mesophasic organization of GABAA receptors in hippocampal inhibitory synapses. Nat. Neurosci. 2020, 23, 1589–1596. [Google Scholar] [CrossRef]
- Railam, T.; Ambrulevičius, F.; Penkauskas, T.; Jankune, M.; Meškauskasm, T.; Vanderah, T.; Valincius, G. Clusters of protein pores in phospholipid bilayer membranes can be identified and characterized by electrochemical impedance spectroscopy. Electrochim. Acta 2020, 364, 137179. [Google Scholar] [CrossRef]
- Bormashenko, E.; Frenkel, M.; Vilk, A.; Legchenkova, I.; Fedorets, A.A.; Aktaev, N.; Dombrovsky, L.A.; Nosonovsky, M. Characterization of Self-Assembled 2D Patterns with Voronoi Entropy. Entropy 2018, 20, 956. [Google Scholar] [CrossRef]
- Frenkel, M.; Fedorets, A.A.; Dombrovsky, L.A.; Nosonovsky, M.; Legchenkova, I.; Bormashenko, E. Continuous Symmetry Measure vs Voronoi Entropy of Droplet Clusters. J. Phys. Chem. C 2021, 125, 2431–2436. [Google Scholar] [CrossRef]
- Larkin, T.J.; Canuto, H.C.; Kettunen, M.I.; Booth, T.S.; Hu, D.; Krishnan, A.S.; Bohndiek, S.E.; Neves, A.A.; McLachlan, C.; Hobson, M.P.; et al. Analysis of image heterogeneity using 2D Minkowski functionals detects tumor responses to treatment. Magn. Reson. Med. 2014, 71, 402–410. [Google Scholar] [CrossRef]
- Boehm, H.F.; Link, T.M.; Monetti, R.; Mueller, D.; Rummeny, E.J.; Newitt, D.; Majumdar, S.; Raeth, C. Application of the Minkowski functionals in 3D to high-resolution MR images of trabecular bone: Prediction of the biomechanical strength by nonlinear topological measures. Proc. SPIE 2004, 5370, 172–180. [Google Scholar]
- Bormashenko, E.; Legchenkova, I.; Frenkel, F.; Shvalb, N.; Shoval, S. Shannon (Information) Measures of Symmetry for 1D and 2D Shapes and Patterns. Appl. Sci. 2022, 12, 1127. [Google Scholar] [CrossRef]
- Curie, P. Sur la symetrie. Soc. Mineralog. France Bull. Paris 1884, 7, 418–457. [Google Scholar] [CrossRef]
- Brandmuller, J. An extension of the Neumann-Minnigerode-Curie Principle. Comp. Maths. Appl. 1986, 12, 97–100. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Yu, J.; Guo, Y.; Sun, Q. Symmetry-breaking induced large piezoelectricity in Janus tellurene materials. Phys. Chem. Chem. Phys. 2019, 21, 1207–1216. [Google Scholar] [CrossRef] [PubMed]
- Aizenberg, J.; Hanson, J.; Koetzle, T.F.; Leiserowitz, L.; Weiner, S.; Addadi, L. Biologically Induced Reduction in Symmetry: A Study of Crystal Texture of Calcitic Sponge Spicules. Chem. Eur. J. 1995, 1, 414–422. [Google Scholar] [CrossRef]
- Dingle, K.; Pérez, G.V.; Louis, A.A. Generic predictions of output probability based on complexities of inputs and outputs. Sci. Rep. 2020, 10, 4415. [Google Scholar] [CrossRef]
- Kong, X.-Z.; Mathias, S.R.; Guadalupe, T.; ENIGMA Laterality Working Group; Glahn, D.C.; Franke, B.; Crivello, F.; Tzourio-Mazoyer, N.; Fisher, S.E.; Thompson, P.M.; et al. Mapping cortical brain asymmetry in 17,141 healthy individuals worldwide via the ENIGMA Consortium. Proc. Natl. Acad. Sci. USA 2018, 115, E5154–E5163. [Google Scholar] [CrossRef]
- Boman, B.M.; Dinh, T.N.; Decker, K.; Emerick, B.; Raymond, C.; Schleiniger, G. Why do Fibonacci numbers appear in patterns of growth in nature? A model for tissue renewal based on asymmetric cell division. Fibonacci Q. 2017, 55, 30–41. [Google Scholar]
- Wheeler, J.A. Information, physics, quantum: The search for links. In Proceedings of the III International Symposium on Foundations of Quantum Mechanics, Tokyo, Japan, 28–31 August 1989. [Google Scholar]
- Bormashenko, E. Informational Reinterpretation of the Mechanics Notions and Laws. Entropy 2020, 22, 631. [Google Scholar] [CrossRef]
- Vopson, M.M. The mass-energy-information equivalence principle. AIP Adv. 2019, 9, 095206. [Google Scholar] [CrossRef]
- Vopson, M.M. Experimental protocol for testing the mass–energy–information equivalence principle. AIP Adv. 2022, 12, 035311. [Google Scholar] [CrossRef]
- Vopson, M.M. The information catastrophe. AIP Adv. 2020, 10, 085014. [Google Scholar] [CrossRef]
- Bérut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef]
- Jun, Y.; Gavrilov, Y.M.; Bechhoefer, J. High-precision test of Landauer’s principle in a feedback trap. Phys. Rev. Lett. 2014, 113, 190601. [Google Scholar] [CrossRef] [PubMed]
- Aydin, A.; Sisman, A.; Kosloff, R. Landauer’s Principle in a Quantum Szilard Engine without Maxwell’s Demon. Entropy 2020, 22, 294. [Google Scholar] [CrossRef] [PubMed]
- Herrera, L. Landauer Principle and General Relativity. Entropy 2020, 22, 340. [Google Scholar] [CrossRef]
- Müller, J.G. Observable and Unobservable Mechanical Motion. Entropy 2020, 22, 737. [Google Scholar] [CrossRef]
- Müller, J.G. Photon Detection as a Process of Information Gain. Entropy 2020, 22, 392. [Google Scholar] [CrossRef]
- Müller, J.G. Information Contained in Molecular Motion. Entropy 2019, 21, 1052. [Google Scholar] [CrossRef]
- Yolles, M.; Frieden, R. Viruses as Living Systems—A Metacybernetic View. Systems 2022, 10, 70. [Google Scholar] [CrossRef]
- Vopson, M.M. A Possible Information Entropic Law of Genetic Mutations. Appl. Sci. 2022, 12, 6912. [Google Scholar] [CrossRef]
- Bormashenko, E.; Voronel, A. Spatial scales of living cells and their energetic and informational capacity. Eur. Biophys. J. 2018, 47, 515–521. [Google Scholar] [CrossRef] [PubMed]
- Vellai, T.; Vida, G. The origin of eukaryotes: The difference between prokaryotic and eukaryotic cells. Proc. R. Soc. B 1999, 266, 1571–1577. [Google Scholar] [CrossRef] [PubMed]
- Lane, N.; Martin, W. The energetics of genome complexity. Nature 2010, 467, 929–934. [Google Scholar] [CrossRef]
- Goldman, N.; Bertone, P.; Chen, A.; Dessimoz, C.; LeProust, E.M.; Sipos, B.; Birney, B. Towards practical, high-capacity, low-maintenance information storage in synthesized DNA. Nature 2013, 494, 77–80. [Google Scholar] [CrossRef]
- Kempes, C.P.; Wolpert, D.; Cohen, Z.; Pérez-Mercader, J. The thermodynamic efficiency of computations made in cells across the range of life. Philos. Trans. R. Soc. A 2017, 375, 20160343. [Google Scholar] [CrossRef]
- Gillings, M.R.; Hilbert, M.; Kemp, D.J. Information in the Biosphere: Biological and Digital Worlds. Trends Biol. Evol. 2016, 31, 180–189. [Google Scholar] [CrossRef]
- Schrödinger, E. What is Life? The Physical Aspects of the Living Cell; Cambridge University Press: New York, NY, USA, 1944. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1989. [Google Scholar]
- Homblé, F.; Léonetti, M. Emergence of symmetry breaking in fucoid zygotes. Trends Plant. Sci. 2007, 12, 253–259. [Google Scholar] [CrossRef]
- Kaandorp, J.A.; de Kluijver, M.J. Verification of fractal growth models of the sponge Haliclona oculata (Porifera) with transplantation experiments. Mar. Biol. 1992, 113, 133–143. [Google Scholar] [CrossRef]
- Abrams, M.J.; Basinger, T.; Yuan, W.; Guo, C.-L.; Goentoro, L. Self-repairing symmetry in jellyfish through mechanically driven reorganization. Proc. Natl. Acad. Sci. USA 2015, 112, E3365–E3373. [Google Scholar] [CrossRef]
- Duarte, J.M.; Dutta, S.; Goodsell, D.S.; Burley, S.K. Exploring protein symmetry at the RCSB Protein Data Bank. Emerg. Top Life Sci. 2022, 6, 231–243. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating Asymmetry: Methods, Theory, and Applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef]
- Klingenberg, C.P. Analyzing Fluctuating Asymmetry with Geometric Morphometrics: Concepts, Methods, and Applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Hileman, L.C. Bilateral flower symmetry—How, when and why? Curr. Opin. Plant Biol. 2014, 17, 146–152. [Google Scholar] [CrossRef] [PubMed]
- Grabowsky, G.L. Symmetry, locomotion and the evolution of an anterior end: A lesson from sea urchins. Evolution 1994, 48, 1131–1146. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E. Fibonacci Sequences, Symmetry and Order in Biological Patterns, Their Sources, Information Origin and the Landauer Principle. Biophysica 2022, 2, 292-307. https://doi.org/10.3390/biophysica2030027
Bormashenko E. Fibonacci Sequences, Symmetry and Order in Biological Patterns, Their Sources, Information Origin and the Landauer Principle. Biophysica. 2022; 2(3):292-307. https://doi.org/10.3390/biophysica2030027
Chicago/Turabian StyleBormashenko, Edward. 2022. "Fibonacci Sequences, Symmetry and Order in Biological Patterns, Their Sources, Information Origin and the Landauer Principle" Biophysica 2, no. 3: 292-307. https://doi.org/10.3390/biophysica2030027
APA StyleBormashenko, E. (2022). Fibonacci Sequences, Symmetry and Order in Biological Patterns, Their Sources, Information Origin and the Landauer Principle. Biophysica, 2(3), 292-307. https://doi.org/10.3390/biophysica2030027





