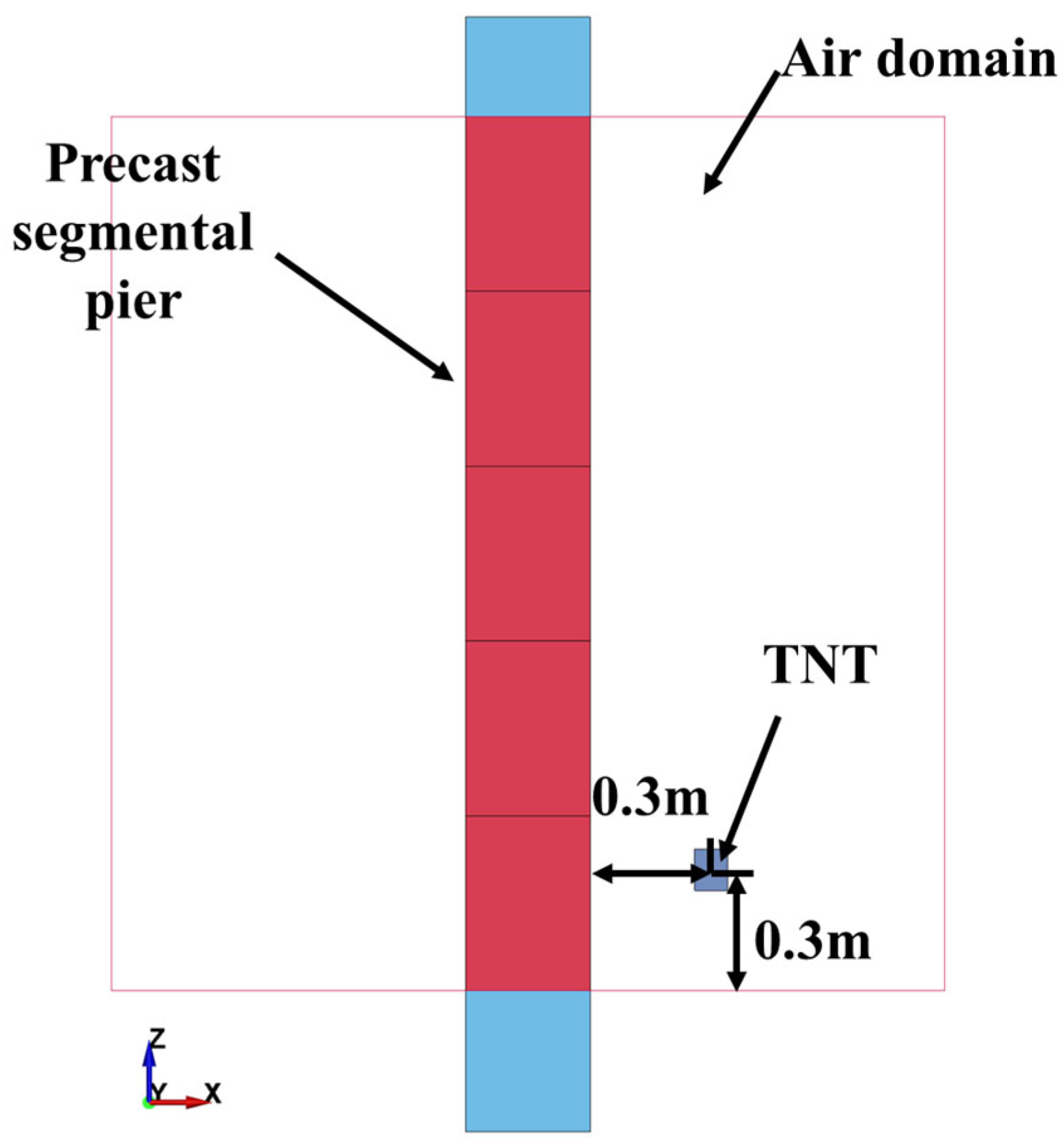
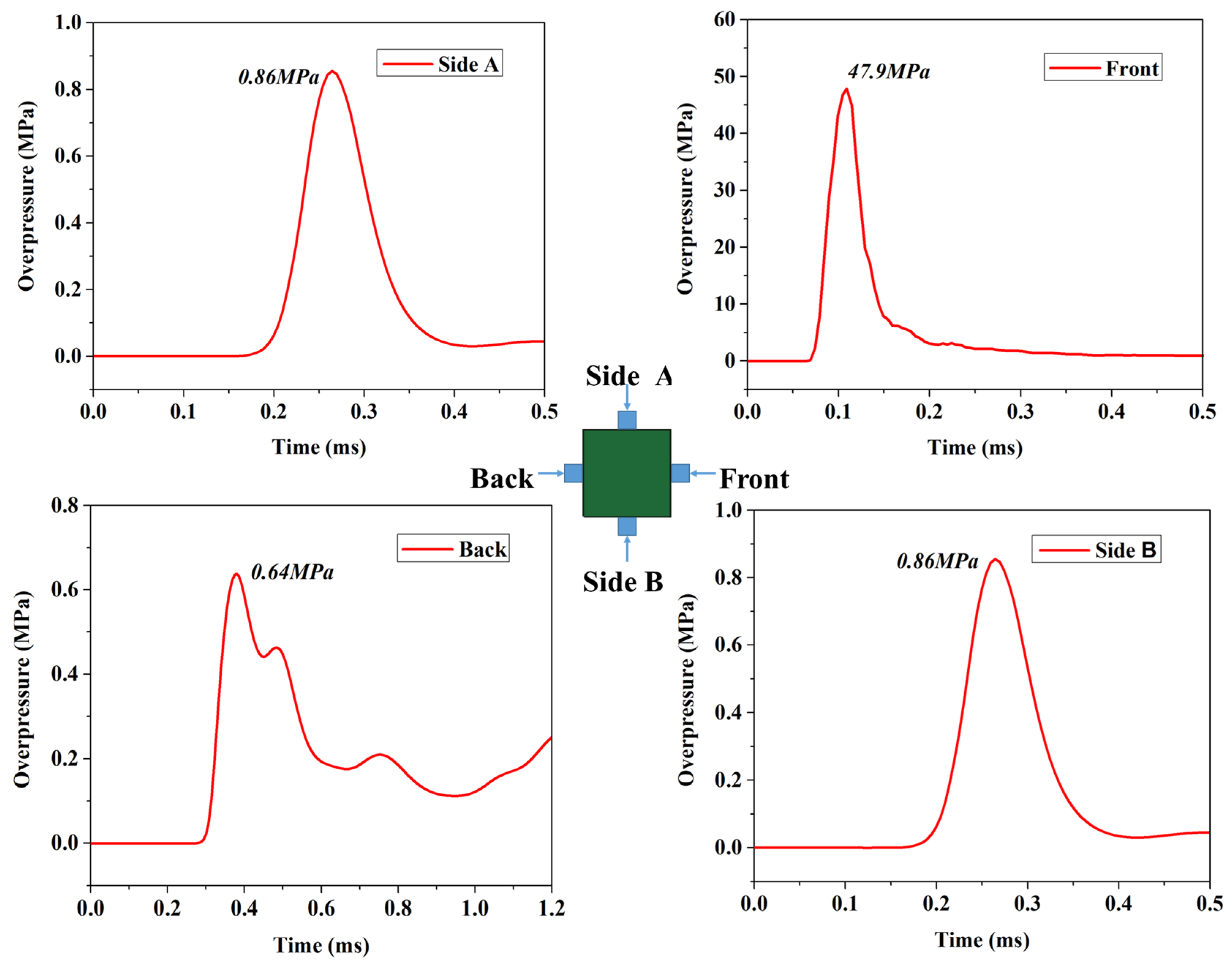
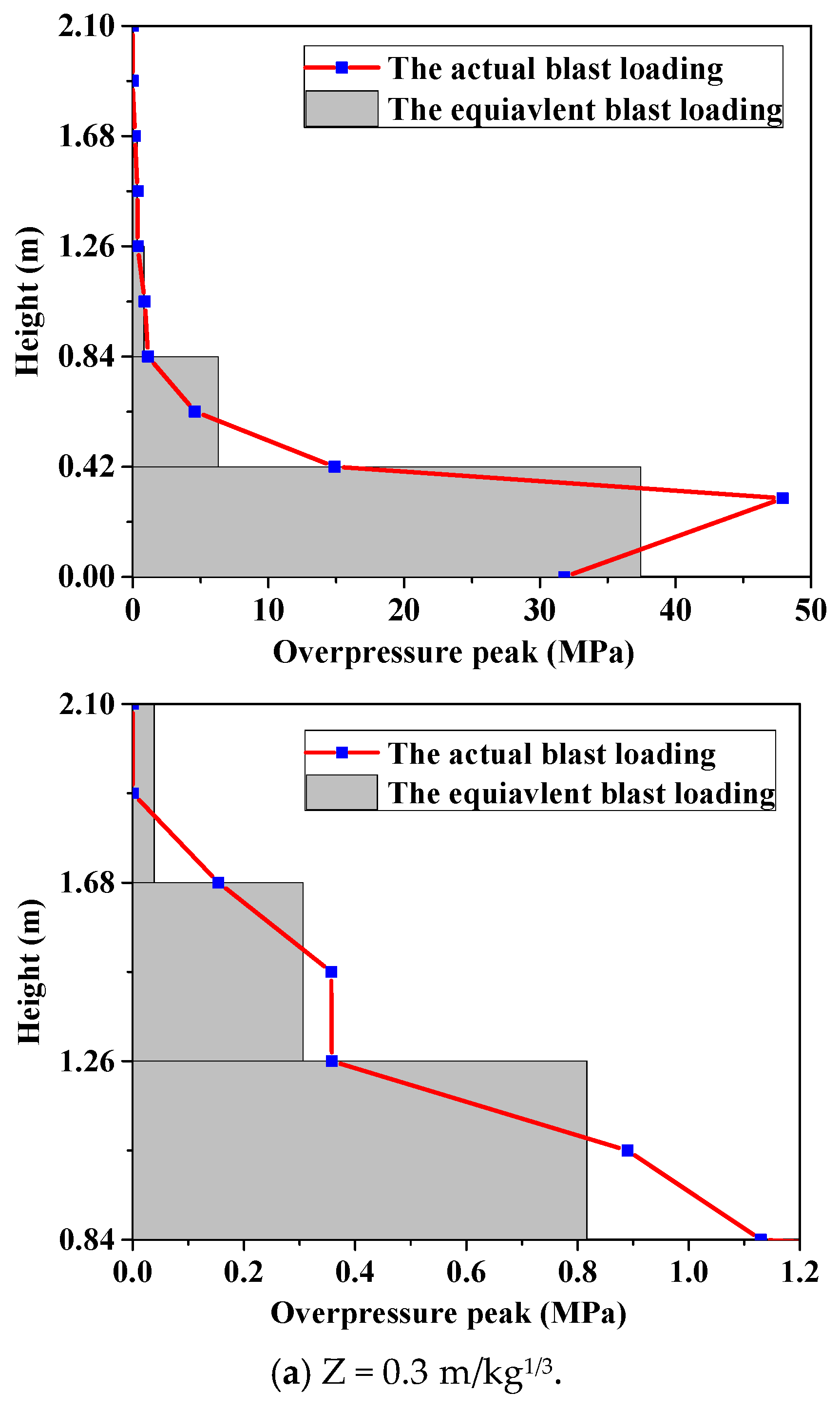
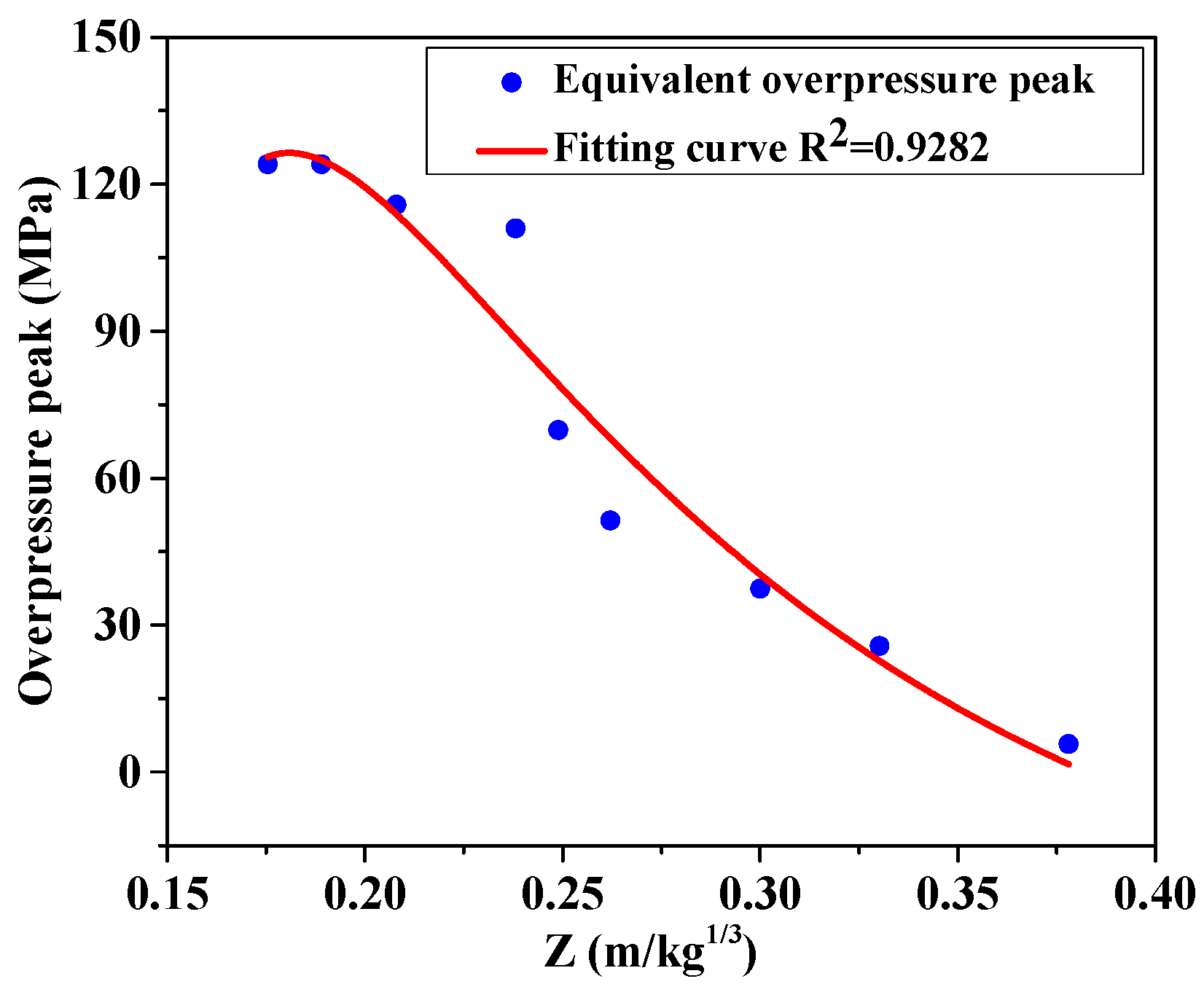
1. Introduction
Bridge structures are inevitably subjected to natural disasters and accidents during operation, including explosion threats. The main explosion threat comes from vehicle explosions, such as from car bombs during terrorist attacks or accidental explosions of hazardous chemical carriers. Explosions can cause partial damage or overall collapse of bridge structures. However, current domestic and international bridge design specifications [
1,
2] have not provided clear requirements for the blast-resistant design of bridge structures.
Thus far, researchers have investigated the explosion resistance of cast-in-place reinforced concrete (RC) bridge piers [
3,
4,
5,
6,
7,
8]. The U.S. Army Engineering Research and Development Center conducted experimental research on the explosion damage mechanisms and dynamic responses of highway bridge piers and proposed explosion protection measures for highway bridges [
9,
10,
11,
12]. Fujikura and Bruneau [
4,
13] conducted explosion tests on reinforced concrete bridge piers with earthquake resistance requirements. The results showed that the piers underwent base shear failure under explosion loads. Yi et al. [
14,
15,
16]. conducted numerical simulation studies of explosions under reinforced concrete bridges, and the results showed that there are six different failure mechanisms for bridge piers, namely, erosion and peeling of concrete at the bottom of the pier, shear failure at the base of the pier, steel bar cutting, overall failure of the pier column, surface concrete peeling, and plastic hinge formation. Zong et al. [
5,
6,
7,
17] conducted explosion tests on RC bridge piers and piers with different forms of protection. The results showed that contact explosion caused shear damage to the piers and that external steel plate and carbon fiber cloth reinforcement improved their explosion resistance. Echevarria et al. [
18] conducted explosion tests on FRP-reinforced pier columns, and the results showed that strengthening pier columns can reduce bending deformation and increase residual bearing capacity after explosions. Mutalib et al. [
19] simulated and analyzed the reinforcement of RC pier columns with FRP, considering parameters such as FRP thickness. The results showed that FRP effectively reduced the residual displacement and failure of transverse pier columns and could improve the blast resistance performance of RC pier columns. Remennikov et al. [
20] conducted near-field explosion tests and contact explosion tests on square steel reinforced concrete columns, and the results also showed that steel pipes can improve the blast resistance performance of pier columns. Zhang et al. [
21] conducted blast resistance research on hollow steel tube concrete cylinders and square columns, considering the effects of outer steel tube thickness, inner steel tube thickness, and hollow ratio on hollow steel tube concrete. The results showed that the influence of outer steel tubes was greater than that of inner steel tubes, and the blast resistance performance of pier columns was weakened when the hollow ratio was greater than 0.5.
Compared with cast-in-place piers, segmental piers [
22,
23,
24,
25] (
Figure 1) have garnered widespread attention owing to their precise factory production and rapid assembly-based construction [
20]. Based on the “multi-hazard” design concept [
26], segmental piers should not only have seismic performance but also good blast resistance. Hao et al. [
27,
28,
29] began to explore the blast resistance of precast segmental bridge piers under explosive loads. They analyzed precast segmental RC piers with square cross-sections using Ls-Dyna software and concluded that precast segmental piers could dissipate explosion energy through the openings and relative angles between segments. Zhang et al. [
30,
31,
32] conducted numerical simulations to analyze the blast resistance of RC segmental piers. They revealed the damage and failure mechanisms of segmental piers under explosion loads by changing the equivalent and distance of explosive loads. The research results showed that segmental bridge piers mainly exhibited shear failure and local failure. The large turning angles and displacements are generated between segments, causing lateral displacement of pier columns and weakening of segment sections. Pham and Do [
33] analyzed the dynamic response and damage mechanisms of steel tube segmental piers under explosive loads through numerical simulations. The steel tubes could effectively protect the concrete and improve the blast resistance of the segmental piers. This study found that stress waves propagated along the height direction in the pier, and the sections blocked the propagation of strain waves. The deformation of a segment consisted of two stages, which manifested as compression of stress waves in concrete and tension of reflected waves, with failure usually occurring during the tension stage of reflected waves. Due to the limiting effect of steel pipes in concrete segments, they could effectively protect the concrete from peeling off due to the reflected wave tension, further transferring the local failure of concrete segments to the overall bending deformation of the pier, accompanied by the fracture of post-tensioned prestress. The fragmentation of the segment near the explosive will cause the overall collapse of the pier. Liu et al. [
34,
35,
36] analyzed the effects of different parameters on the blast resistance of precast segmental RC piers through explosion experiments and numerical simulations. The local punching and cutting damage occurred in the bottom section of the segmental pier, and vertical cracks developed in the upper section when the explosive was detonated at the bottom of the column. The segmental pier experienced overall bending failure, characterized by typical bending deformation and detachment of the concrete protective layer in the middle section of the column, the development of vertical cracks in other sections, and concrete crushing when the explosive was detonated at the middle of the column. Meanwhile, increasing the number of segments could reduce the local residual deformation of the pier. The connection between rectangular shear keys and energy-absorbing steel bars between segments could reduce local residual deformation in the near-explosion zone of the pier, decrease concrete spalling, and reduce vertical cracks between segments. Increasing the initial axial pressure could reduce the overall residual deformation of segmental piers and alleviate vertical cracks between segments. Reducing the aspect ratio could improve the stiffness of the segmental piers and reduce the overall residual deformation of the pier. Ma et al. [
37] studied the influence of factors such as the segmental number, the initial prestress, the shear keys, the energy-absorbing steel bars, and the explosion distance on the blast resistance performance of precast reinforced concrete bridge piers.
The explosion loads experienced by segmental piers have significant randomness. The structural dynamic responses and failure modes vary under different explosion conditions. Currently, there is no unified design load standard for the blast resistance of bridges. An accurate application of explosion loads is a prerequisite for research on blast-resistant protection of bridge piers. In 1949, the US Army released the technical manual “TM5-855-1”, which established the basic calculation method for explosive shock waves [
38]. In 1969, the United States Navy, Army, and Air Force Command published the “Anti Accidental Explosion-Structural Design Manual” (TM5-1300), which detailed the selection of explosive loads, the dynamic response of components under explosive loads, and the basic methods of component anti-explosion design [
39]. In 2008, the US Department of Defense published a unified facility standard titled “Structural Resistance to Accidental Explosion Effects (UFC 3-340-02)” by integrating relevant regulations from the Navy and Army [
40]. Only the U.S. AASHTO LRFD [
1] bridge code incorporates blast resistance-related details based on the NCHRP 645 [
3] report. According to this code, blast design should consider factors such as the quantity of explosives and the distance of the explosion. However, there are no specific analysis methods. Henry et al. [
41], Brode [
42], Yang et al. [
43], Lin et al. [
44], and Zhang et al. [
45] proposed corresponding prediction formulae for the explosion loads. These load models are based on the assumption of an infinite reflective surface for the interaction between the shock wave and the structure. The uniform load on the large plane calculated simultaneously is obtained through fitting, and there is no unified calculation method for building structures. However, for slender components, such as bridge piers, explosion loads are affected by shock wave diffraction, reflection, and other factors. NCHRP 645 [
3] reported that the blast load could be used for the vertical distribution of triangles for blast design for a bridge pier when a vehicle bombing is at the bottom of the pier. This method is just for the integral poured pier, but it is definitely inappropriate and inaccurate for a precast segmental bridge pier, which requires consideration of its independence of segments. Hence, it is necessary to explore the distribution of explosion loads on the surface of bridge piers and develop engineering calculation methods for precast segmental bridge piers. Such efforts can help provide a basis for blast-resistant protection design of bridge piers.
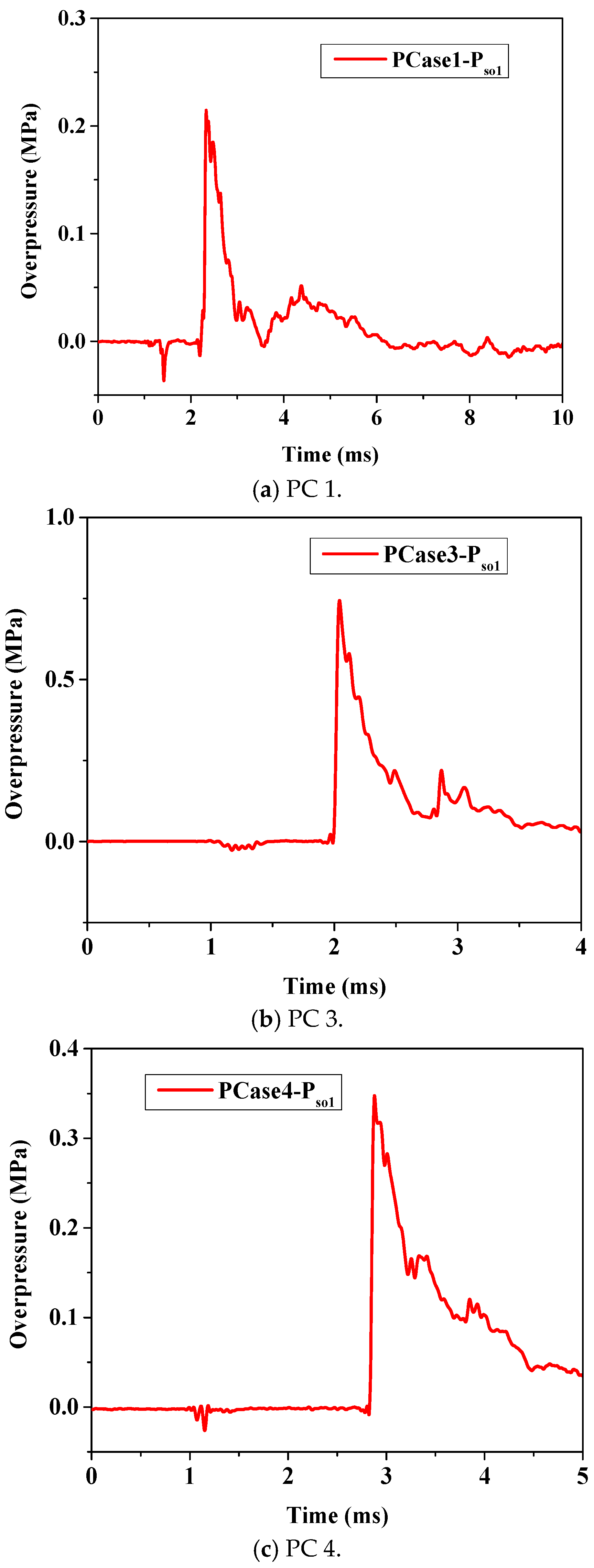
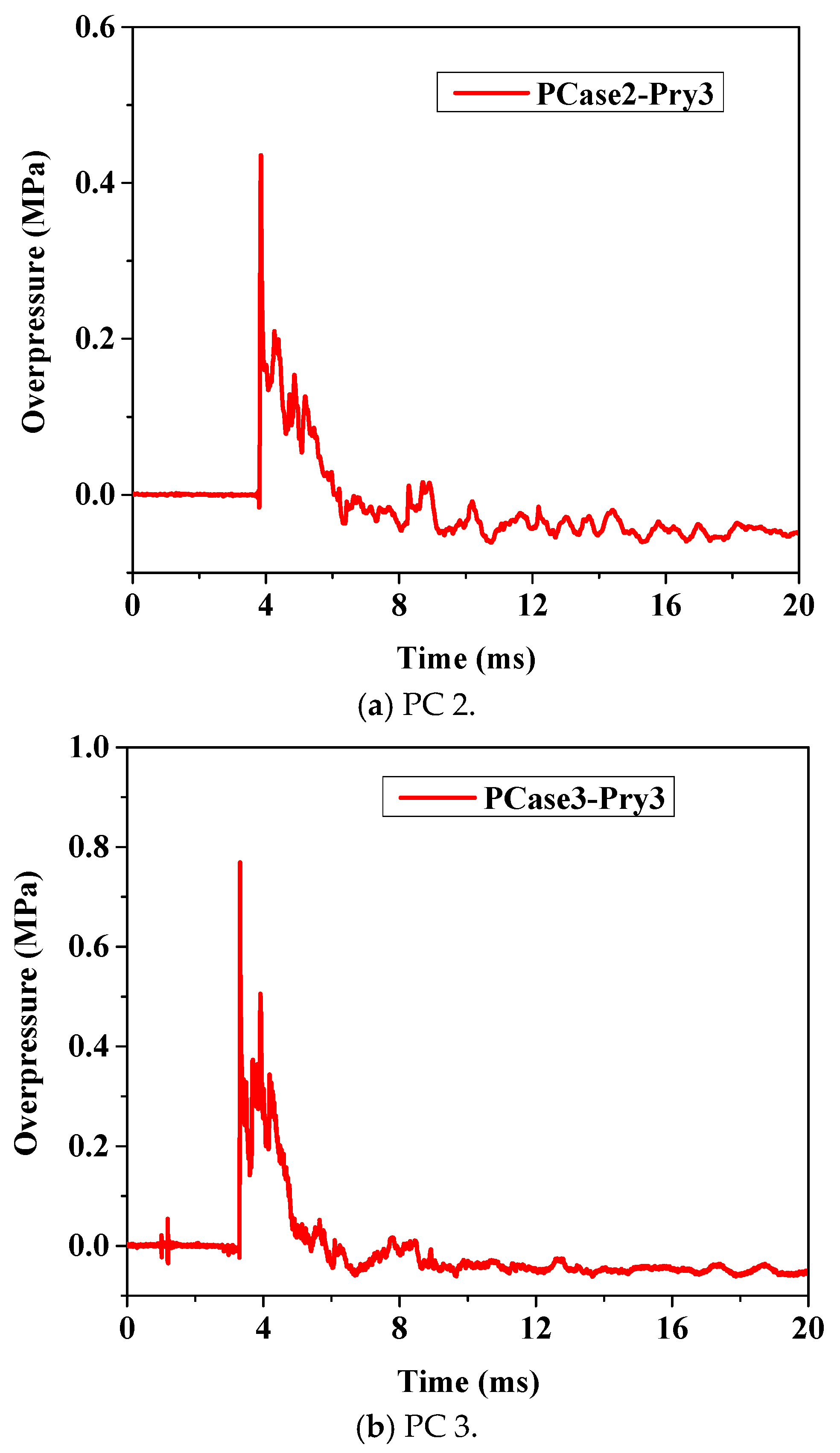
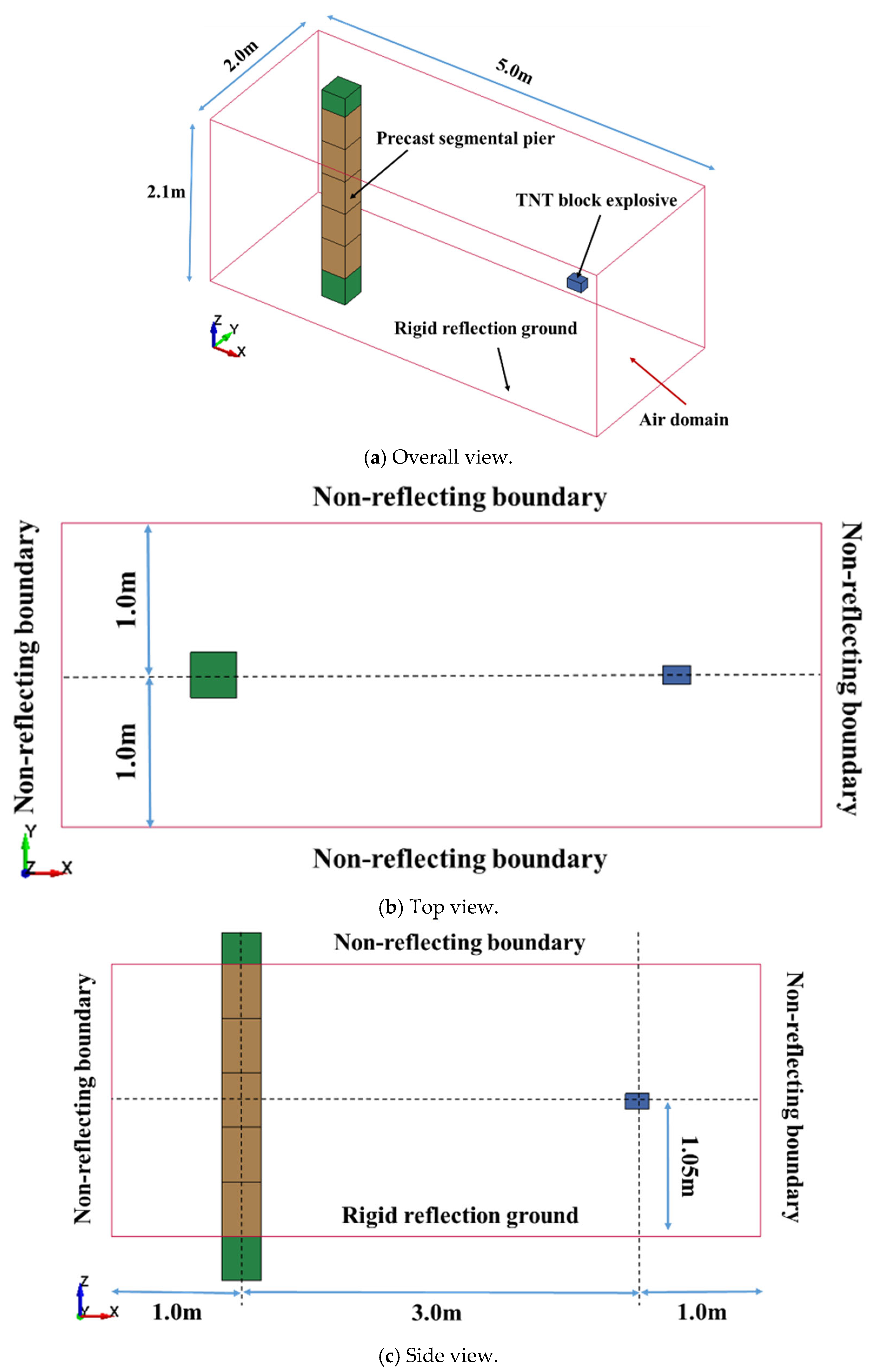
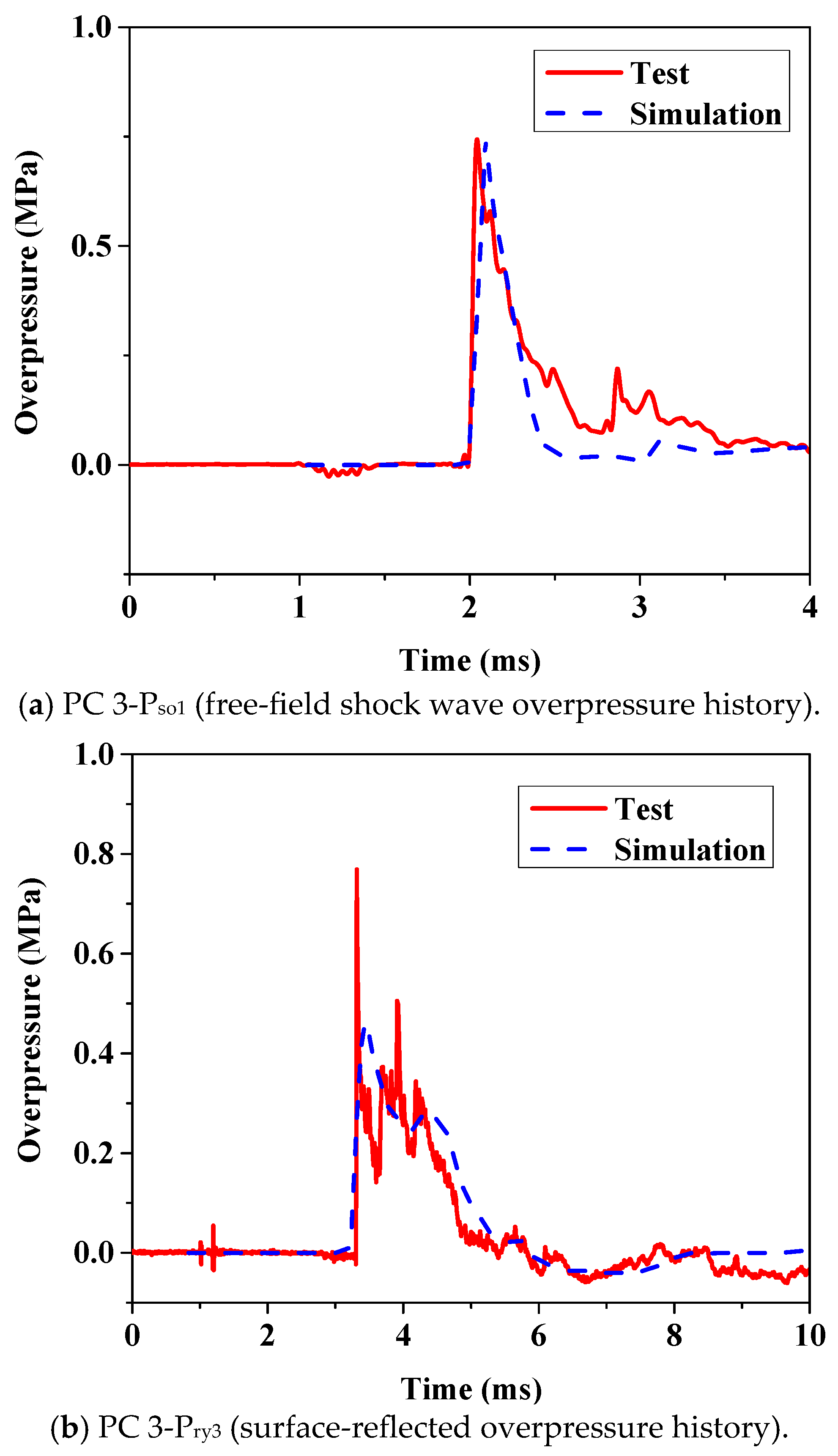
With this background, free field blast experiments and numerical simulations were conducted on segmental precast RC bridge piers in this study. The aim was to explore the interaction between shock waves and segmental precast RC bridge piers. Based on a reliable numerical model of the fluid–structure interaction, numerical simulations on segmental precast RC bridge piers subjected to near-field explosions were conducted. This study analyzed the blast load distribution patterns on the segmental precast RC bridge piers under near-field explosive conditions. With the results obtained, an engineering calculation method for blast loads acting on typical segmental RC piers during near-field explosions was developed.