Explainable Machine Learning to Predict the Construction Cost of Power Plant Based on Random Forest and Shapley Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Brief Overview of Research Methodology
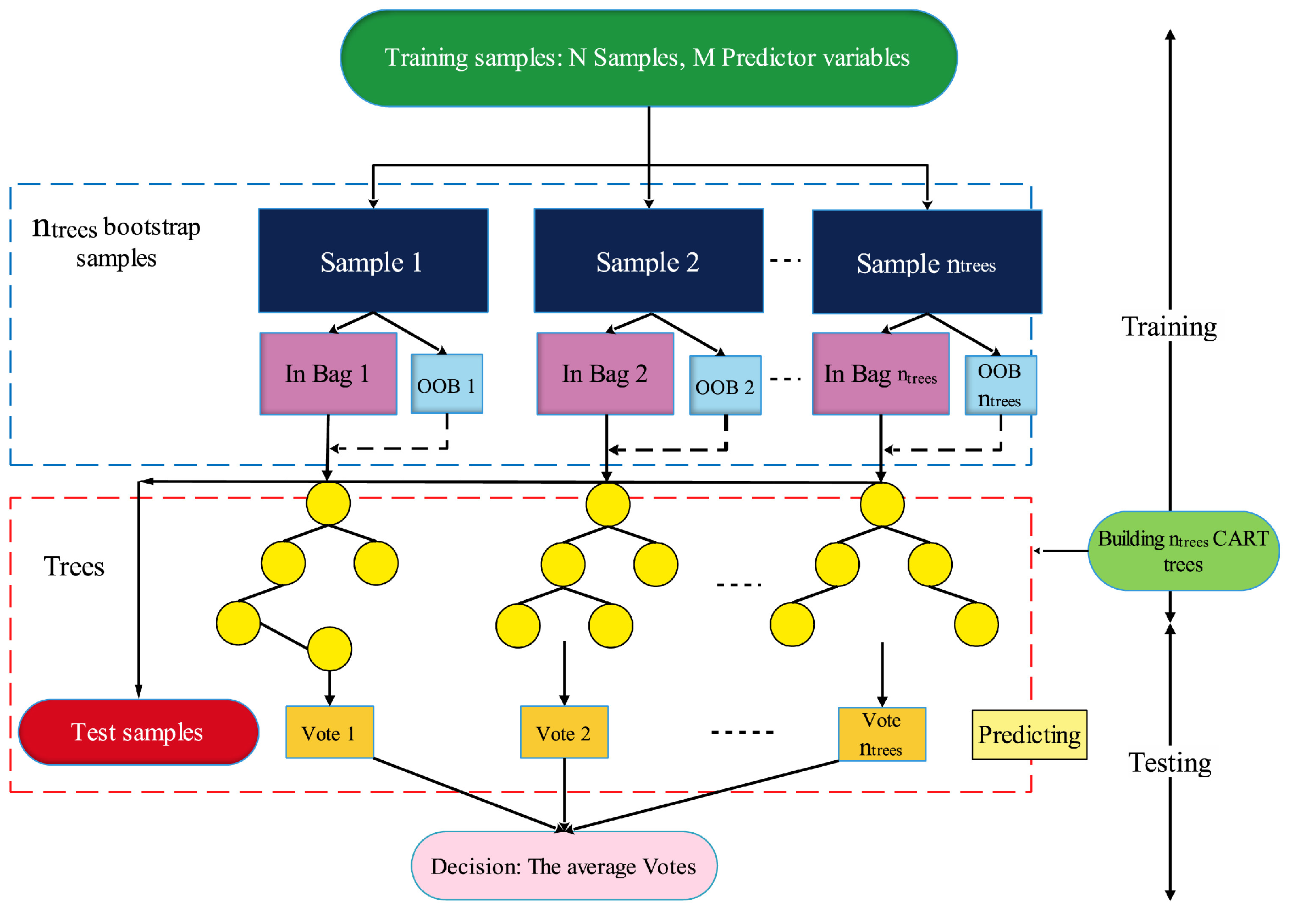
2.2. Random Forest (RF) Algorithm
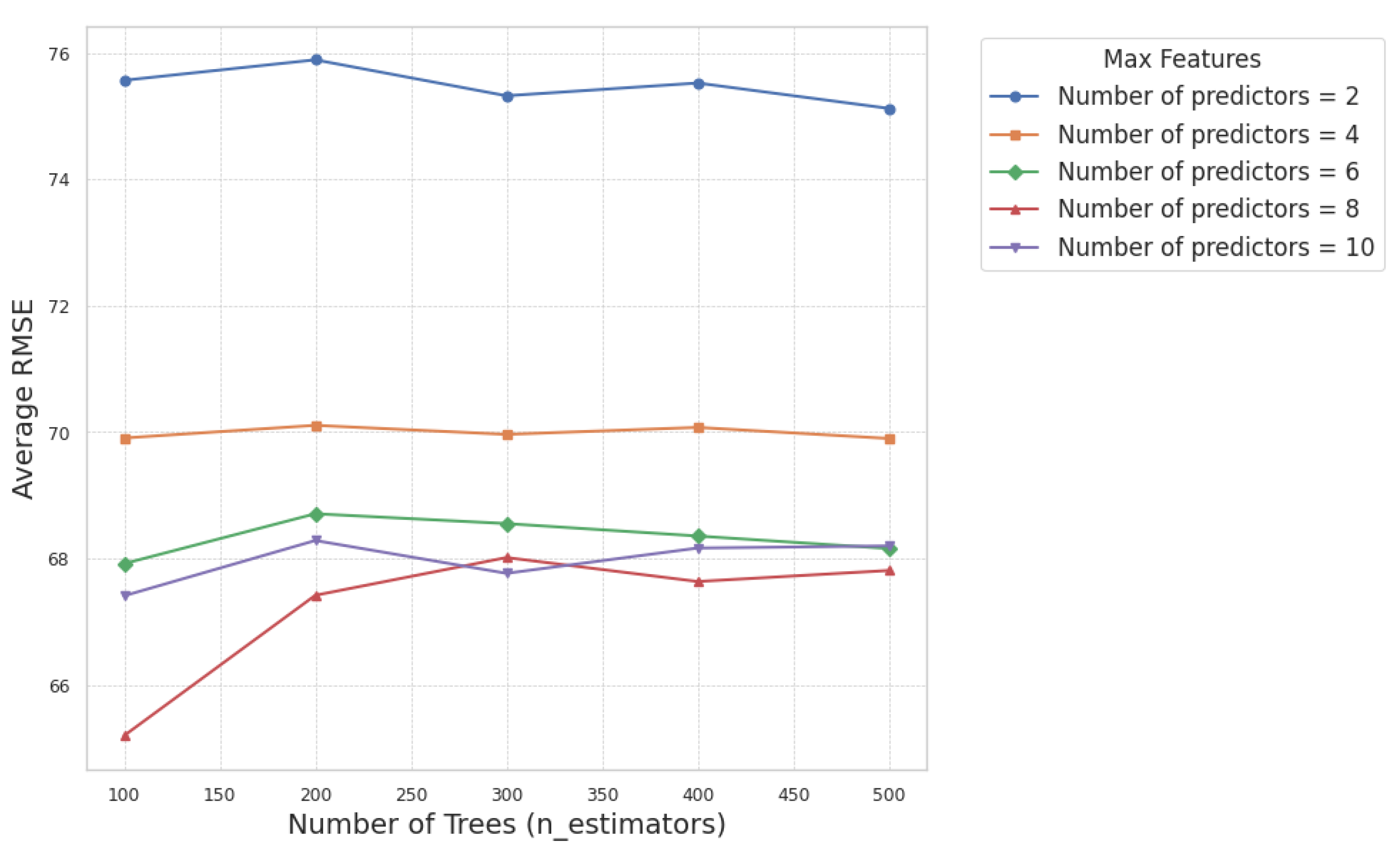
2.3. Hyperparameter Tunning Methodology
- Number of trees (n_estimators): This indicates the number of decision trees present in the forest. While increasing the number of trees can improve model performance, an excessively high value may lead to overfitting.
- Number of variables randomly selected at each split (Max_features): This determines how many features are considered when creating splits in the decision trees.
2.4. Feature Importance (Shapley Method)
2.5. Performance Metrics
3. Database Used
4. Model Results
4.1. Hyperparameter Tunning Results
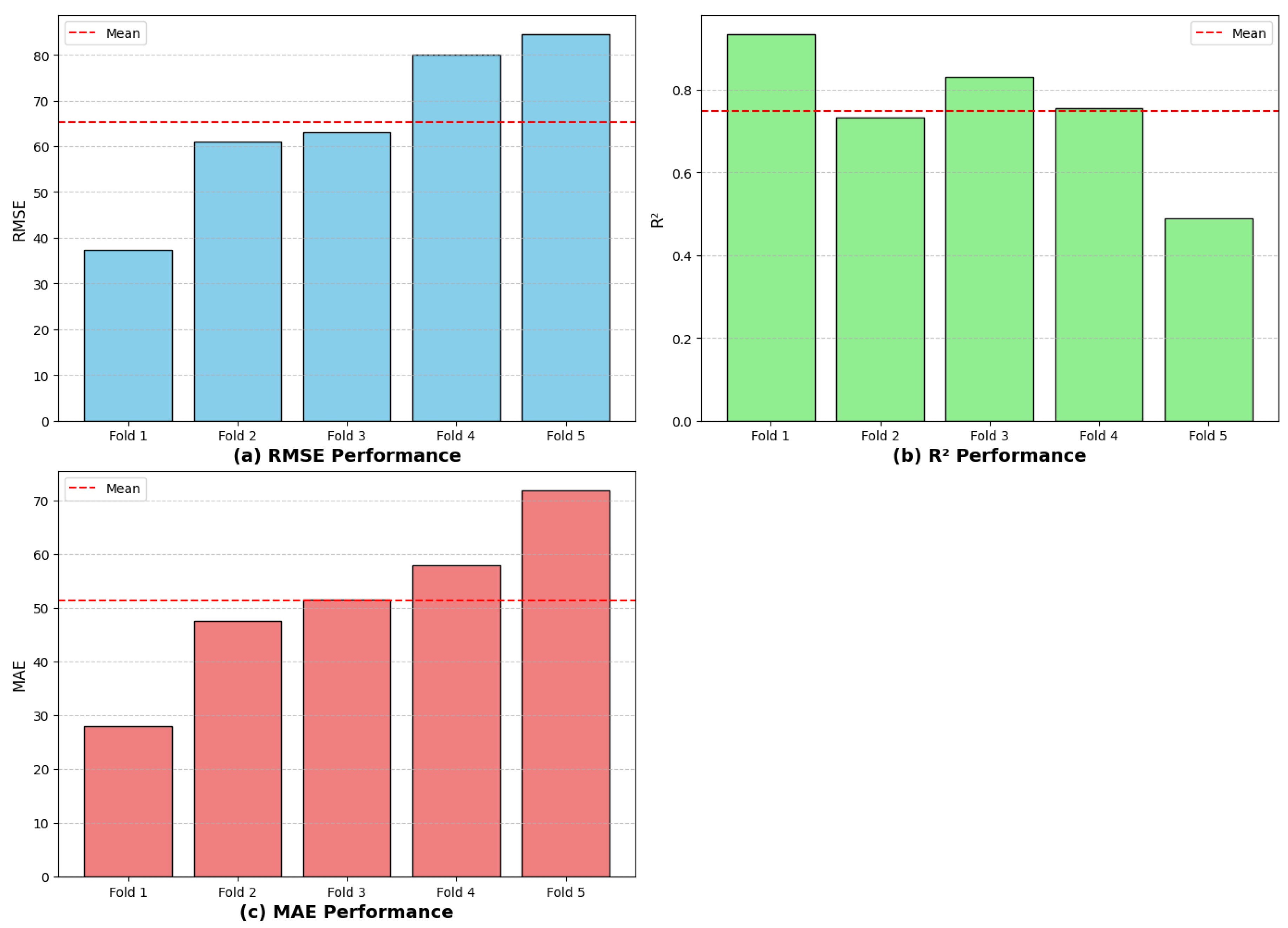
4.2. Optimal RF Model Five Fold Cross Validation Resutls
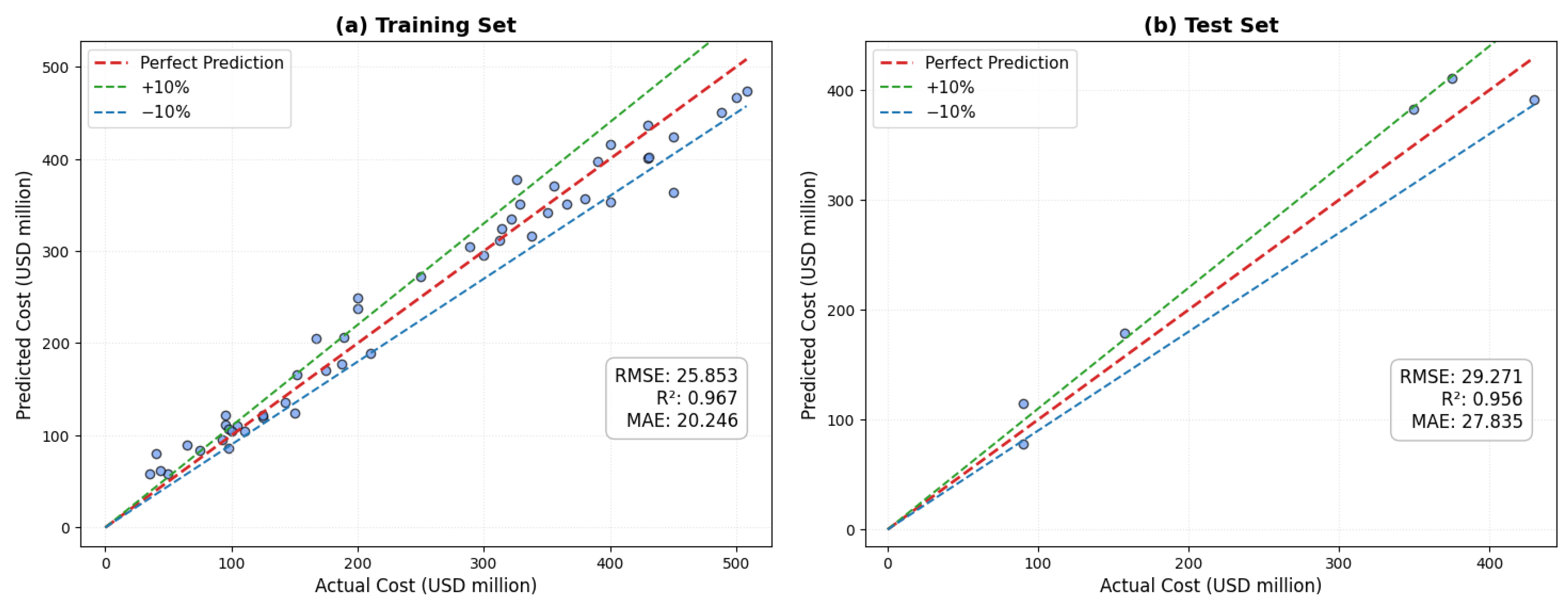
4.3. Model Performance Based on Training and Testing Sets
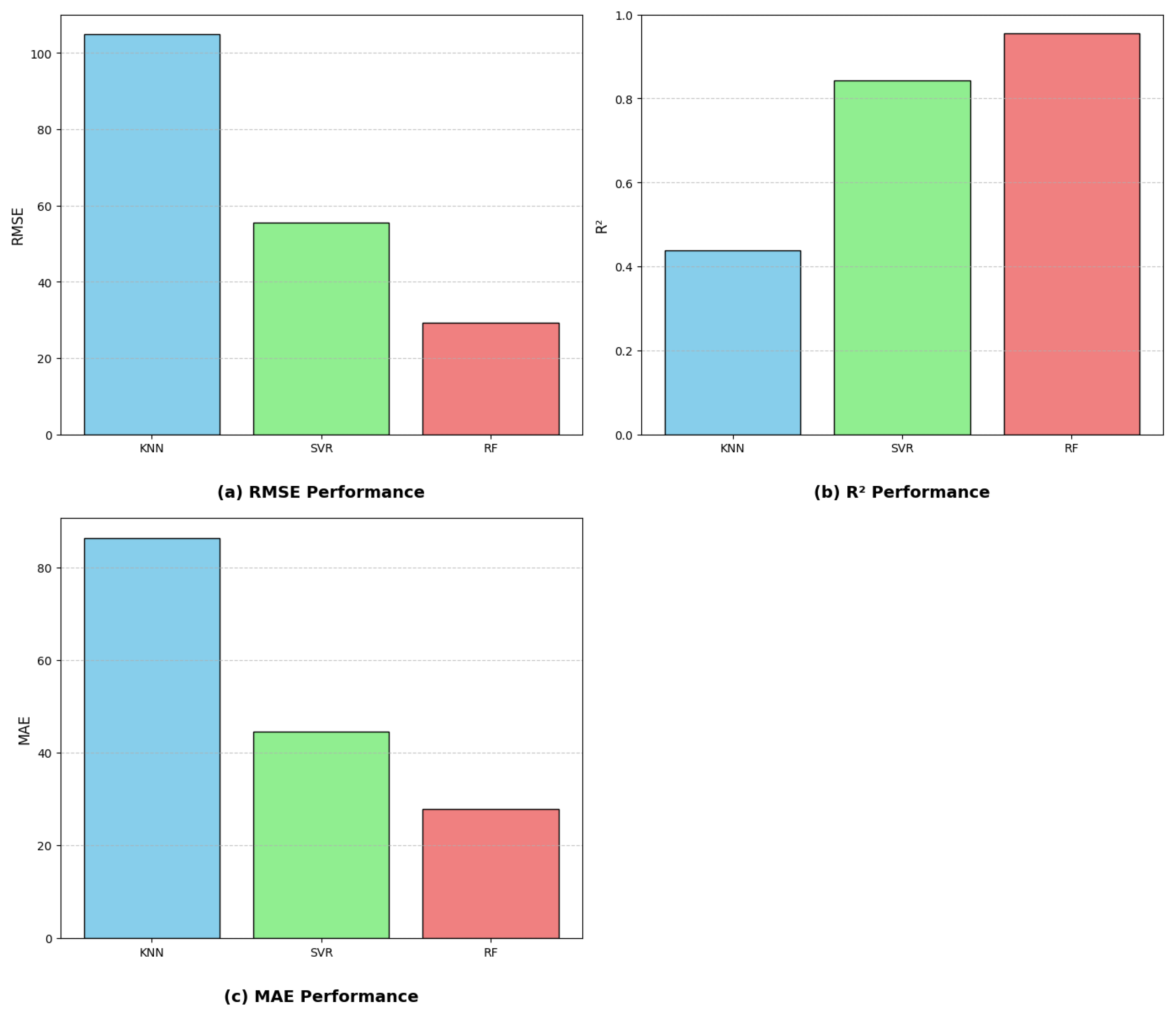
4.4. Performance Comparison with Single Learner ML Model
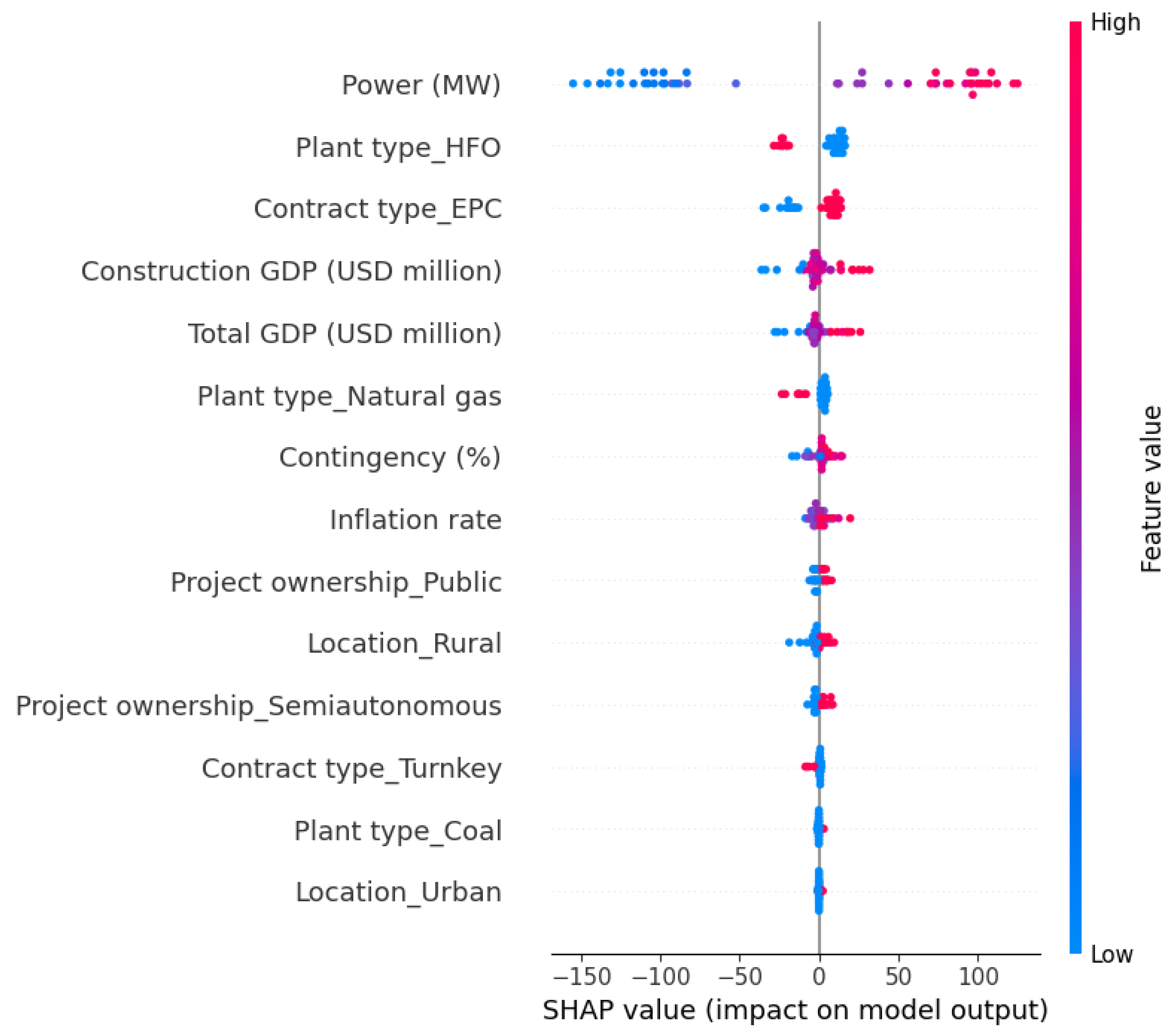
4.5. Feature Importance and SHAP Value
5. Conclusions
- The RF algorithm is closely aligned and adjacent to the perfect match line. In the RF model, most predictions are adjusted within the error margins ranging from +10% to −10%.
- In the research, three quantitative metrics are applied to measure the capability of models. The RF model demonstrated the highest outstanding R-square scores, about 0.967 and 0.956, respectively, at the train and test phases. In comparison, the KNN and SVR models exhibited approximately 0.438 and 0.842 in the testing stage. Notably, the remaining numerical metrics similarly behave superior for the RF model compared to the KNN and SVR models.
- The Shapley method implemented in this research revealed essential findings. The highly impactful attribute influencing overall construction cost estimates was determined as power (MW), followed by the heavy fuel oil (HFO) plant type, and the Contract type EPC. In particular, the study demonstrated that costs tend to increase when factors such as power (MW) and Contract type EPC increase, and decrease when the plant construction type is HFO.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sovacool, B.K.; Gilbert, A.; Nugent, D. An international comparative assessment of construction cost overruns for electricity infrastructure. Energy Res. Soc. Sci. 2014, 3, 152–160. [Google Scholar] [CrossRef]
- IHS. IHS Costs and Strategic Sourcing: Power Capital Costs Index and European Power Capital Costs Index. Available online: https://www.ihs.com/info/cera/ihsindexes/index.html (accessed on 1 April 2025).
- Sovacool, B.K.; Nugent, D.; Gilbert, A. Construction cost overruns and electricity infrastructure: An unavoidable risk? Electr. J. 2014, 27, 112–120. [Google Scholar] [CrossRef]
- Kagiri, D.; Wainaina, G. Time and Cost Overruns in Power Projects in Kenya: A Case Study of Kenya Electricity Generating Company Limited. Orsea J. 2013, 3. [Google Scholar]
- Bouayed, Z. Using Monte Carlo simulation to mitigate the risk of project cost overruns. Int. J. Saf. Secur. Eng. 2016, 6, 293–300. [Google Scholar] [CrossRef]
- Khodeir, L.M.; El Ghandour, A. Examining the role of value management in controlling cost overrun [application on residential construction projects in Egypt]. Ain Shams Eng. J. 2019, 10, 471–479. [Google Scholar] [CrossRef]
- Love, P.E.; Sing, C.P.; Carey, B.; Kim, J.T. Estimating construction contingency: Accommodating the potential for cost overruns in road construction projects. J. Infrastruct. Syst. 2015, 21, 04014035. [Google Scholar] [CrossRef]
- Lin, H. An artificial neural network model for data prediction. Adv. Mater. Res. 2014, 971, 1521–1524. [Google Scholar] [CrossRef]
- Arafa, M.; Alqedra, M. Early stage cost estimation of buildings construction projects using artificial neural networks. J. Artif. Intell. 2011, 4, 63–75. [Google Scholar] [CrossRef]
- Sodikov, J. Cost estimation of highway projects in developing countries: Artificial neural network approach. J. East. Asia Soc. Transp. Stud. 2005, 6, 1036–1047. [Google Scholar]
- Ahiaga-Dagbui, D.D.; Smith, S.D. Neural networks for modelling the final target cost of water projects. In Proceedings of the 28th Annual ARCOM Conference, Edinburgh, UK, 3–5 September 2012; Smith, S.D., Ed.; Association of Researchers in Construction Management: Edinburgh, UK, 2012; pp. 307–316. [Google Scholar]
- Khashei, M.; Bijari, M. An artificial neural network (p, d, q) model for timeseries forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Ali, Z.H.; Burhan, A.M. Hybrid machine learning approach for construction cost estimation: An evaluation of extreme gradient boosting model. Asian J. Civ. Eng. 2023, 24, 2427–2442. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elhegazy, H.; Elzarka, H.; Gutierrez, L. A novel construction cost prediction model using hybrid natural and light gradient boosting. Adv. Eng. Inform. 2020, 46, 101201. [Google Scholar] [CrossRef]
- Jin, R.; Cho, K.; Hyun, C.; Son, M. MRA-based revised CBR model for cost prediction in the early stage of construction projects. Expert Syst. Appl. 2012, 39, 5214–5222. [Google Scholar] [CrossRef]
- Lu, Y.; Luo, X.; Zhang, H. A gene expression programming algorithm for highway construction cost prediction problems. J. Transp. Syst. Eng. Inf. Technol. 2011, 11, 85–92. [Google Scholar] [CrossRef]
- Tayefeh Hashemi, S.; Ebadati, O.M.; Kaur, H. Cost estimation and prediction in construction projects: A systematic review on machine learning techniques. SN Appl. Sci. 2020, 2, 1703. [Google Scholar] [CrossRef]
- Wang, J.; Ashuri, B. Predicting ENR construction cost index using machine-learning algorithms. Int. J. Constr. Educ. Res. 2017, 13, 47–63. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, W.; Wang, W. Construction cost prediction based on genetic algorithm and BIM. Int. J. Pattern Recognit. Artif. Intell. 2020, 34, 2059026. [Google Scholar] [CrossRef]
- Tijanić, K.; Car-Pušić, D.; Šperac, M. Cost estimation in road construction using artificial neural network. Neural Comput. Appl. 2020, 32, 9343–9355. [Google Scholar] [CrossRef]
- Jiang, Q. Estimation of construction project building cost by back-propagation neural network. J. Eng. Des. Technol. 2020, 18, 601–609. [Google Scholar] [CrossRef]
- Wang, X. Application of fuzzy math in cost estimation of construction project. J. Discret. Math. Sci. Cryptogr. 2017, 20, 805–816. [Google Scholar] [CrossRef]
- Swei, O.; Gregory, J.; Kirchain, R. Construction cost estimation: A parametric approach for better estimates of expected cost and variation. Transp. Res. Part B Methodol. 2017, 101, 295–305. [Google Scholar]
- Coffie, G.; Cudjoe, S. Using extreme gradient boosting (XGBoost) machine learning to predict construction cost overruns. Int. J. Constr. Manag. 2024, 24, 1742–1750. [Google Scholar] [CrossRef]
- Yan, H.; He, Z.; Gao, C.; Xie, M.; Sheng, H.; Chen, H. Investment estimation of prefabricated concrete buildings based on XGBoost machine learning algorithm. Adv. Eng. Informatics 2022, 54, 101789. [Google Scholar]
- El-Sawalhi, N.I. Support vector machine cost estimation model for road projects. J. Civ. Eng. Archit. 2015, 9, 1115–1125. [Google Scholar]
- Hashemi, S.T.; Ebadati E, O.M.; Kaur, H. A hybrid conceptual cost estimating model using ANN and GA for power plant projects. Neural Comput. Appl. 2019, 31, 2143–2154. [Google Scholar]
- Lee, J.G.; Lee, H.S.; Park, M.; Seo, J. Early-stage cost estimation model for power generation project with limited historical data. Eng. Constr. Archit. Manag. 2022, 29, 2599–2614. [Google Scholar]
- Islam, M.S.; Mohandes, S.R.; Mahdiyar, A.; Fallahpour, A.; Olanipekun, A.O. A coupled genetic programming Monte Carlo simulation–based model for cost overrun prediction of thermal power plant projects. J. Constr. Eng. Manag. 2022, 148, 04022073. [Google Scholar]
- Arifuzzaman, M.; Gazder, U.; Islam, M.S.; Skitmore, M. Budget and cost contingency CART models for power plant projects. J. Civ. Eng. Manag. 2022, 28, 680–695. [Google Scholar]
- Wang, F.; Ma, S.; Wang, H.; Li, Y.; Qin, Z.; Zhang, J. A hybrid model integrating improved flower pollination algorithm-based feature selection and improved random forest for NOX emission estimation of coal-fired power plants. Measurement 2018, 125, 303–312. [Google Scholar]
- Janoušek, J.; Gajdoš, P.; Dohnálek, P.; Radeckỳ, M. Towards power plant output modelling and optimization using parallel Regression Random Forest. Swarm Evol. Comput. 2016, 26, 50–55. [Google Scholar] [CrossRef]
- Tohry, A.; Chelgani, S.C.; Matin, S.; Noormohammadi, M. Power-draw prediction by random forest based on operating parameters for an industrial ball mill. Adv. Powder Technol. 2020, 31, 967–972. [Google Scholar] [CrossRef]
- Sessa, V.; Assoumou, E.; Bossy, M.; Simões, S.G. Analyzing the applicability of random forest-based models for the forecast of run-of-river hydropower generation. Clean Technol. 2021, 3, 858–880. [Google Scholar] [CrossRef]
- Guo, J.; Zan, X.; Wang, L.; Lei, L.; Ou, C.; Bai, S. A random forest regression with Bayesian optimization-based method for fatigue strength prediction of ferrous alloys. Eng. Fract. Mech. 2023, 293, 109714. [Google Scholar]
- Gupta, A.; Gowda, S.; Tiwari, A.; Gupta, A.K. XGBoost-SHAP framework for asphalt pavement condition evaluation. Constr. Build. Mater. 2024, 426, 136182. [Google Scholar] [CrossRef]
- Arslan, Y.; Lebichot, B.; Allix, K.; Veiber, L.; Lefebvre, C.; Boytsov, A.; Goujon, A.; Bissyandé, T.F.; Klein, J. Towards refined classifications driven by shap explanations. In Proceedings of the International Cross-Domain Conference for Machine Learning and Knowledge Extraction, Vienna, Austria, 23–26 August 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 68–81. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 1, pp. 278–282. [Google Scholar]
- Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B. How can statistical models help to determine driving factors of landslides? Ecol. Model. 2012, 239, 27–39. [Google Scholar]
- Pourghasemi, H.R.; Kerle, N. Random forests and evidential belief function-based landslide susceptibility assessment in Western Mazandaran Province, Iran. Environ. Earth Sci. 2016, 75, 185. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar]
- Nicodemus, K.K.; Malley, J.D. Predictor correlation impacts machine learning algorithms: Implications for genomic studies. Bioinformatics 2009, 25, 1884–1890. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar]
- Lundberg, S. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Mangalathu, S.; Hwang, S.H.; Jeon, J.S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar]
- Somala, S.N.; Chanda, S.; Karthikeyan, K.; Mangalathu, S. Explainable Machine learning on New Zealand strong motion for PGV and PGA. Structures 2021, 34, 4977–4985. [Google Scholar]
- Jia, H.; Qiao, G.; Han, P. Machine learning algorithms in the environmental corrosion evaluation of reinforced concrete structures—A review. Cem. Concr. Compos. 2022, 133, 104725. [Google Scholar]



| Characteristic Type | Variable | Description | Type |
|---|---|---|---|
| Economic Variables | GDP | Total Bangladesh GDP during the construction year of the project. | Integer (USD million) |
| Const. GDP | GDP contribution of the construction sector in the construction year. | Integer (USD million) | |
| IR | Inflation rate in Bangladesh for the construction year. | Integer (percentage) | |
| Project Characteristics | Cost | Total construction cost of the project. | Integer (USD million) |
| Cont. | Estimated contingency as a percentage of the project cost. | Integer (percentage) | |
| Power | Power generation capacity of the project. | Integer (MW) | |
| Location Variables | Location | Location of the project (Urban, Rural, Peri-Urban). | Categorical (3 types) |
| Ownership Variables | Owner | Ownership type (Government, IPP, Semi-autonomous). | Categorical (3 types) |
| Plant Specifications | Plant | Type of power plant (CCPP, Coal, HFO, Natural Gas). | Categorical (4 types) |
| Contract Variables | Contract | Type of construction contract (EPC, BOO, Turnkey). | Categorical (3 types) |
| Fold | Root Mean Square Error (RMSE) | Mean Absolute Error (MAE) | |
|---|---|---|---|
| Fold 1 | 37.416 | 0.933 | 28.012 |
| Fold 2 | 61.001 | 0.732 | 47.587 |
| Fold 3 | 62.958 | 0.829 | 51.588 |
| Fold 4 | 80.127 | 0.755 | 57.951 |
| Fold 5 | 84.486 | 0.489 | 71.954 |
| Mean | 65.198 | 0.748 | 51.418 |
| Std Deviation | 16.670 | 0.147 | 14.331 |
| Model | RMSE (kN) | MAE (kN) | |
|---|---|---|---|
| KNN | 0.439 | 104.87 | 86.37 |
| SVR | 0.842 | 55.61 | 44.60 |
| RF | 0.956 | 29.27 | 27.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alazawy, S.F.M.; Ahmed, M.A.; Raheem, S.H.; Imran, H.; Bernardo, L.F.A.; Pinto, H.A.S. Explainable Machine Learning to Predict the Construction Cost of Power Plant Based on Random Forest and Shapley Method. CivilEng 2025, 6, 21. https://doi.org/10.3390/civileng6020021
Alazawy SFM, Ahmed MA, Raheem SH, Imran H, Bernardo LFA, Pinto HAS. Explainable Machine Learning to Predict the Construction Cost of Power Plant Based on Random Forest and Shapley Method. CivilEng. 2025; 6(2):21. https://doi.org/10.3390/civileng6020021
Chicago/Turabian StyleAlazawy, Suha Falih Mahdi, Mohammed Ali Ahmed, Saja Hadi Raheem, Hamza Imran, Luís Filipe Almeida Bernardo, and Hugo Alexandre Silva Pinto. 2025. "Explainable Machine Learning to Predict the Construction Cost of Power Plant Based on Random Forest and Shapley Method" CivilEng 6, no. 2: 21. https://doi.org/10.3390/civileng6020021
APA StyleAlazawy, S. F. M., Ahmed, M. A., Raheem, S. H., Imran, H., Bernardo, L. F. A., & Pinto, H. A. S. (2025). Explainable Machine Learning to Predict the Construction Cost of Power Plant Based on Random Forest and Shapley Method. CivilEng, 6(2), 21. https://doi.org/10.3390/civileng6020021


_Brownlee.png)







