Abstract
The rise in early-age temperature concrete structures, driven by the exothermic reactions during cement hydration, significantly increases the risk of thermal cracking. To address this issue, the construction industry employs several strategies, including the partial substitution of cement with ground granulated blast furnace slag (GGBS) due to its lower heat of hydration. Accurately predicting the hydration temperature of concrete is critical for preventing thermal cracking. This task becomes more complex, with fluctuating ambient temperatures influencing hydration kinetics and heat dissipation. Previous studies often assume adiabatic or isothermal conditions, thus overlooking the impact of ambient temperature variations. This paper presents an innovative finite element modelling (FEM) approach to simulate the hydration temperature progression in in situ concrete slabs, incorporating the effects of ambient temperature fluctuations. Isothermal calorimetry curves were adjusted using the Arrhenius-based approach to express the cement hydration rate as a function of ambient temperature. The FEM outcomes, validated with semi-adiabatic calorimetry tests, demonstrate the model’s capability to forecast temperature development in in situ concrete under varying ambient conditions. Additionally, the study examines the influence of partial cement replacement with GGBS on thermal behaviour, revealing that while GGBS effectively reduces thermal reactions at higher contents, its efficacy diminishes with rising ambient temperatures.
1. Introduction
The Portland cement hydration reactions lead to a significant temperature rise, particularly noticeable during mass concrete pouring. These exothermic hydration reactions encompass a series of complex multiphase processes. The hydration process of cement involves a series of exothermic chemical reactions between the anhydrous phases of cement and water. The main components of cement include tricalcium silicate (Ca3SiO5, Alite, C3S), dicalcium silicate (Ca2SiO4, Belite, C2S), tricalcium aluminate (Ca3Al2O6, Aluminate, C3A), and tetracalcium aluminoferrite (Ca2AlFeO5, Ferrite, C4AF). During hydration, these components react with water to form various hydration products such as calcium silicate hydrate (C-S-H), portlandite, gypsum, and ettringite [1,2,3,4,5]. These reactions release heat, which increases the internal temperature of the concrete. The rate of hydration and the amount of heat released are influenced by various factors, such as the type of cementitious materials used, the water-to-cement ratio, and the ambient curing conditions. For instance, a higher cement content or finer cement particles can accelerate the hydration process and increase heat generation. Similarly, a higher curing temperature or lower water-binder ratio can also enhance the reaction rate and result in a higher temperature rise [6,7]. The heat generated from these reactions not only influences the hydration process but also has significant implications for the structural integrity of the concrete, particularly in the form of thermal cracking.
A significant rise in temperature during hydration reactions can lead to substantial volume changes in concrete. The concrete will expand in volume during the temperature-rising process. The concrete begins to cool as it reaches its peak temperature, leading to volume contraction. Mass concrete’s large volume and low thermal conductivity make heat dissipation from the core challenging. The thermal properties of concrete, including thermal conductivity and specific heat capacity, play a crucial role in its temperature development. Thermal conductivity determines how efficiently heat is conducted through the concrete, while specific heat capacity indicates the amount of heat required to raise the temperature of the concrete by a given amount. These properties are affected by ambient temperature, as higher curing temperatures can accelerate the hydration process, leading to increased heat generation and faster temperature rise [8,9]. In direct contact with the air, the outer surface of mass concrete dissipates heat more efficiently, creating a temperature gradient from the surface to the core. This gradient results in differential thermal contraction, generating thermal tension stress, which can lead to thermal cracking on the concrete surface [10,11]. In addition to mass concrete, long-span concrete structures, especially thin-slab structures, face unique challenges. Despite the reduced temperature gradients due to efficient heat dissipation, these structures may experience significant stresses and cracking due to constrained temperature deformation. While these structures are less prone to internal restraint, their large spans and connections to vertical structures limit their deformation under temperature changes, resulting in compressive and tensile stresses during the heating and cooling phases separately. Due to the relatively lower tensile strength of concrete compared to its compressive strength, tensile stresses arising from constrained shrinkage are more prone to induce cracking in these structures [12,13,14,15,16,17]. Furthermore, very high hydration temperatures (over 70 °C) increase the risk of delayed ettringite formation and associated cracking [18,19]. For instance, the delayed ettringite formation can cause extensive cracking and even structural failure in severe cases [20,21].
Several engineering practices have been employed to mitigate thermal stresses in concrete and address these challenges. One such practice involves embedding water-cooling pipes within in situ concrete to control the temperature rise, effectively reducing the internal temperature rise [22,23]. For in situ concrete beams or slabs, an infill strip, often less than 1 m, is left to accommodate thermal expansion or contraction [13]. Furthermore, supplementary cementitious materials like ground granulated blast furnace slag (GGBS) and fly ash (FA) are frequently used to partially replace Portland cement, effectively lowering the cement hydration rate and the resultant concrete hydration temperature [12,24,25,26,27,28]. Replacing a portion of cement with GGBS impacts the hydration process and temperature development in concrete. GGBS has a lower heat of hydration compared to Portland cement, which helps reduce the overall temperature rise and mitigates the risk of thermal cracking. For example, Woo et al. [29] found that high-volume GGBS replacements (up to 80%) in mass concrete reduced the adiabatic temperature rise by up to 6.8 °C and the ultimate temperature by approximately 11 °C, further emphasising the efficacy of GGBS in controlling hydration heat and reducing thermal cracking risks. Additionally, Xu et al. [30] found that at 20 °C, a 40% replacement of Portland cement with GGBS reduced the cumulative heat release by approximately 32% over 72 h, while a 55% replacement resulted in a 44% reduction over the same period. The low early hydration rate of GGBS concrete is due to its two-stage hydration process: initially, GGBS reacts with alkali hydroxide from Portland cement, and subsequently, it reacts with calcium hydroxide produced during the hydration of Portland cement [14,31].
To accurately evaluate the risk of thermal cracking and implement suitable preventive measures, predicting the early-age hydration temperature of concrete is crucial. However, forecasting the hydration temperature of in situ concrete is challenging due to the variable on-site ambient temperatures, which influence the cement hydration rate, heat transfer, and heat dissipation within the concrete. The ambient temperature of the construction site, even for a short period (a day or a few days), constantly fluctuates up and down rather than being constant. These fluctuations can modify the hydration kinetics and thermal properties of the concrete, leading to varying temperature profiles and thermal stresses in in situ concrete. Consequently, it is imperative to consider the impact of ambient temperature variations on the hydration temperature of in situ concrete.
Temperature is a critical factor in determining the rate of hydration and subsequent temperature evolution within concrete. The correlation between the cement hydration rate and temperature is commonly represented by the Arrhenius equation [3,4,32,33,34] (as illustrated in Equation (1)). According to this equation, the cement hydration rate is proportional to the exponential function of the temperature. As the temperature increases, the hydration reaction accelerates, causing a rapid release of the heat of hydration. This temperature elevation, in turn, further hastens the hydration process. As depicted in Equation (1), it is important to note that the heat released during cement hydration does not have a linear relationship with temperature. Instead, it follows an exponential relationship, significantly amplifying the rate of the concrete temperature increase.
where k(T) is the rate constant at temperature T, T is the temperature (K), A is the rate constant, R is the universal gas constant = 8.314 (J/K·mol), and Ea is the apparent activation energy (J/mol).
The Arrhenius equation plays a crucial role in cement hydration, particularly in the concept of concrete maturity. This concept, representing the combined effects of age and temperature on concrete properties, is essential for predicting strength development [35]. The concrete equivalent age, as defined by Freiesleben Hansen and Pedersen [36], is a key metric in this relationship:
where te is the equivalent age of the concrete (h), T is the average temperature of the concrete during ∆t (°C), and Tr is the reference temperature (°C).
Reinhardt et al. [37] demonstrated that the normalised heat generation rate (Equation (3)) for the same cement mix remains constant at the same hydration degree (Equation (4)), regardless of ambient temperatures. They proposed an Arrhenius-form hydration rate equation based on the hydration degree and concrete temperature (Equation (5)). The reliability of Equation (5) as a heat source has been validated by several concrete temperature prediction FEM models [38,39,40], which show strong agreement with the site measurements.
The activation energy in Equations (1) and (5) represents the minimum energy necessary for chemical reactions, reflecting the temperature sensitivity of the hydration reaction [41]. Several methods are available for calculating the activation energy. The ASTM C1074 method [42], implemented via mortar strength tests or isothermal calorimetry tests, is well established and widely used [43,44]. Additionally, the activation energy can be determined based on the cement’s chemical composition [45].
And
And
where qv is the cement hydration rate (W/g), T is the concrete temperature (°C), qmax(T) is the peak hydration rate (W/g) at temperature T, f(α) is the normalised hydration heat rate, α is the hydration degree, Q(t) is the cumulative heat of hydration (J/g), Qmax is the ultimate hydration heat (J/g).
Adiabatic, semi-adiabatic, and isothermal calorimetry are the primary methods used to measure heat evolution during cement hydration. Adiabatic calorimetry minimises heat exchange with the environment, effectively simulating temperature progression in mass concrete [14]. Semi-adiabatic calorimetry, which allows some heat dissipation, offers a cost-effective method for simulating in situ concrete temperature evolution [14,46]. Isothermal calorimetry maintains constant temperatures, providing precise measurements of heat flow and hydration kinetics [14,25,47,48,49].
Despite the insights from calorimetry tests, predicting in situ concrete temperature development remains challenging due to variable ambient temperatures affecting hydration kinetics and heat dissipation. This necessitates a comprehensive approach that accounts for the dynamic and iterative nature of the in situ concrete temperature evolution. The Finite Element Method (FEM) has emerged as a powerful tool for modelling intricate heat transfer processes and predicting temperature evolution in concrete structures under varying ambient conditions.
Several researchers have explored the potential of the Finite Element Method (FEM) in predicting concrete temperature development. Tahersima and Tikalsky [50] used isothermal calorimetry data directly as the heat source in their FEM model. In their field study with ambient temperature variations of up to 20 °C, they observed a maximum discrepancy of 5 °C between the simulations and measurements. This discrepancy likely resulted from differences in the hydration heat between the actual concrete specimens and the isothermal calorimetry data. Tang et al. [14] noted that using isothermal calorimetry directly as a heat source might underestimate temperature development.
Jedrzejewska et al. [32] employed hydration kinetics equations to convert isothermal calorimetry data into actual concrete specimen data, achieving accurate temperature predictions through FEM modelling. However, their experiments were conducted under a constant ambient temperature (20 °C), not accounting for field conditions with fluctuating temperatures.
The impact of ambient temperature on concrete temperature varies with the sample size and monitoring point location. In large-volume concrete, the core temperature is minimally influenced by external temperatures due to slow heat dissipation, making adiabatic calorimetry a good approximation for the core’s maximum temperature increase. Conversely, thin concrete slabs efficiently dissipate heat from the top and bottom surfaces [12].
Huang et al. [36] simulated temperature development at various locations on concrete bridge piers using FEM. Their parameter analyses showed that ambient temperature fluctuations significantly affected points near the pier’s outer surface but had minimal impact on the core. However, their assumption of adiabatic conditions for all points in the mass concrete limited the model’s ability to quantify ambient temperature effects.
An examination of the current research underscores the complexity of accurately forecasting temperature changes in in situ concrete, particularly when considering fluctuating ambient temperatures. This challenge is paramount for maintaining the structural integrity of in situ concrete, as the thermal expansion caused by hydration reactions, followed by contraction, can be restricted by vertical support structures such as columns and shear walls.
This study aims to develop a finite element model to predict the early-age temperature development of a thin in situ concrete slab, emphasising the influence of ambient temperature fluctuations. A semi-adiabatic calorimetry test was used to monitor the temperature changes during hydration. The impact of varying ambient temperatures on cement hydration was investigated by adjusting the isothermal calorimetry data using the Arrhenius-based method. This time-dependent FEM model, utilising the adjusted calorimetry data as the heat source, simulated concrete temperature changes over the first three days.
This research also examines the effect of partially substituting Portland cement with ground granulated blast furnace slag (GGBS) on the thermal behaviour of concrete, incorporating experimental studies and FEM modelling. Semi-adiabatic calorimetry tests were performed to validate the FEM predictions.
2. Materials and Methods
2.1. Materials and Concrete Mixes
CEM I 42.5 Portland cement, meeting the standards of BS EN 197-1:2011 [51], with a specific surface area of 350 m2/kg, was used in this research. Ground granulated blast furnace slag (GGBS) with a specific surface area of 425 m2/kg complied with BS EN 15167-1:2006 [52]. Well-graded medium sand was used as the fine aggregate, featuring a particle density of 2450 kg/m3 and water absorption of 2.62%. For the coarse aggregate, 5–40 mm graded crushed gravel was chosen, with a particle density of 2680 kg/m3 and a water absorption of 0.88%.
Three distinct concrete mixes were prepared, as detailed in Table 1, incorporating varying amounts of GGBS to replace up to 70% of Portland cement to examine its effect on reducing early-age hydration temperatures. The target 28-day strength for the CEM-only concrete aimed to meet the C30/37 grade. To ensure proper workability, the water-binder ratio was adjusted according to BS 8500-1:2015 [53], which specifies a slump of over 100 mm for floor slab casting. The oxide contents of Portland cement and GGBS were measured by X-ray fluorescence, and the results are shown in Table 2.

Table 1.
Mix properties of concrete samples.

Table 2.
Oxide Compound of cement and GGBS.
2.2. Semi-Adiabatic Calorimetry
Semi-adiabatic calorimetry tests were performed to simulate the temperature development of in situ concrete slabs. CEM I 42.5 Portland cement was used as the binder, with 50% and 70% replaced by GGBS in separate mixes to investigate the reduction in hydration heat. Three different concrete mixes were prepared, as illustrated in Table 1. Concrete specimens, with dimensions of 660 × 460 × 300 mm, were cast in a timber box with 100 mm thickness. The four sides of each specimen were insulated with 20 mm thick expanded polystyrene. The bottom surface was in direct contact with a 50 mm thick timber board, while the top surface was exposed to air, allowing different heat dissipation rates at the top and bottom surfaces. Figure 1a,b show photographs of the concrete curing setup and the 3D model of the concrete mould for the semi-adiabatic calorimetry experiment, respectively.

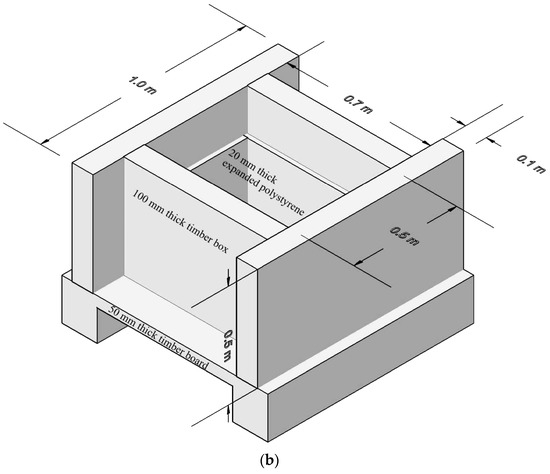
Figure 1.
Concrete curing setup: (a) Concrete curing chamber setup; (b) Insulation setup 3D mould.
The fresh concrete specimens were cured in an environmental chamber with the temperature maintained at 38 °C and fluctuations controlled within ±5 °C to simulate the hot summer climate of Shanghai, China. This setting reflects the typical summer conditions for concrete structures in the region. To monitor temperature development, a type-K thermocouple with an accuracy of ±0.1 °C was embedded in the core of each specimen, recording temperature data every 10 min for three days.
2.3. Isothermal Calorimetry
Isothermal calorimetry was employed to directly measure the hydration heat output rate of cementitious materials at constant temperatures for up to three days. This test utilised a TAM Air isothermal calorimeter equipped with eight channels, each designed to test one sample alongside an inert reference sample. To maintain isothermal conditions, the heat generated by the mortar sample was transferred to a heat sink inside the calorimeter. The resulting temperature gradient between the heat detector and the mortar sample produced a voltage proportional to the heat output.
Mortar samples (10 g) were used, with binder content and water-binder ratios matching those of the concrete specimens from the semi-adiabatic calorimetry test (as detailed in Table 1) to ensure similar hydration heat generation. The key assumption in the isothermal calorimetry test was that the heat production rate (per gram) of the mortar was equivalent to that of the binder in the concrete specimen under identical conditions. Each sample was placed in a 20 mL glass ampoule, and water was added to achieve the specified water-binder ratio. The ampoules were then sealed and transferred to a calorimeter for testing.
The test was conducted at 20 °C and 38 °C, representing the typical room temperature and summer construction conditions, respectively, to assess the impact of ambient temperature on the hydration rate. The isothermal calorimeter provided the heat output rate (W/g) and total hydration heat (J/g). The heat output rate data were recorded every 20 s for up to three days.
2.4. Finite Element Modelling
2.4.1. Concrete Heat Balance
The concrete temperature development was simulated using COMSOL Multiphysics. The heat balance within the concrete, considering the internal thermal gradients and heat exchange with the external environment, is described by a three-dimensional heat diffusion equation based on Fourier’s heat transfer principle [38,54]:
where q is the cement hydration heat generation rate (W/m3); X, Y, and Z are spatial coordinates; T is the concrete temperature (°C); k is the thermal conductivity of concrete (W/m·°C); ρ is the density of concrete (kg/m3); and Cp is the heat capacity of concrete (J/kg·°C).
2.4.2. Heat Source Definition
The temperature increase in concrete results from the hydration reactions of the cementitious materials. The FEM model defines the overall heat source as the concrete heat output rate (W/m3) derived from the adjusted isothermal calorimetry results (W/g) for these materials (Table 1).
The heat output rate data obtained through isothermal calorimetry were measured at a constant ambient temperature. To account for variable ambient temperatures, two applications of the Arrhenius equation (Equation (1)) were used to express the hydration rate of cementitious materials: the “hydration equation method” (Equation (5)) and the “two-step regression method”. The adjusted hydration rate curves, considering ambient temperature variations, were used as the heat output rates in the FEM model (q in Equation (6)).
The “hydration equation method” describes the temperature sensitivity of the Portland cement /GGBS blend via activation energy (Equation (5)). First, the activation energy was calculated based on the isothermal calorimetry results at 20 °C and 38 °C. Linear fitting was performed using Arrhenius equations (Equations (7) and (8)). The negative slope of Equation (8) corresponds to the ratio of the activation energy (E) to the universal gas constant (R). This calculation process followed the ASTM C1074 standard [42]. Second, the hydration degree α (Equation (4)) and normalised heat generation rate f(α) (Equation (3)) were determined from the isothermal calorimetry results.
And
where qmax is the peak hydration rate of isothermal calorimetry (W/g) and Ti is the test temperature of isothermal calorimetry (°C) (20 °C and 38 °C).
The “two-step regression method” is also based on the Arrhenius approach, assuming the cement hydration degree is proportional to the accumulated heat outputs. Initially, a 10th-order polynomial regression analysis was conducted between the hydration heat output rate q and accumulated heat output Q, expressing the heat output rate as a function of hydration heat, as described in Equation (9). Next, a linear regression analysis was conducted between the hydration heat output rate and ambient temperature to model the hydration rate under different ambient temperature conditions. This method facilitated the expression of the heat output rate at real-life ambient temperatures in terms of hydration heat. The regression analyses were developed using MATLAB, and the programming procedure flowchart is illustrated in Figure 2.
where the coefficient an in the polynomial represents the factor by which the variable term Hn is multiplied. In the context of a tenth-degree polynomial, is determined through data fitting procedures, ensuring that the polynomial approximates the experimental data as closely as possible. The value and sign of influence the magnitude and direction of term Hn, thereby affecting the shape and properties of the polynomial function.

Figure 2.
The “two-step regression method” (flowchart and MATLAB programming procedure).
2.4.3. Boundary Conditions and Concrete Heat Loss
In the FEM model, the thermal convection between the surfaces of the concrete (or insulation layer) and the surrounding air was accounted for using the convection coefficient (hc). Thermal convection can be expressed by the following equation:
where hc is the convection coefficient, which represents the heat transfer capacity between solids and air (W/m2 °C), Ts is the temperature of the surface (°C), and Ta is the ambient temperature (°C).
As depicted in Figure 1, the side and bottom surfaces of the semi-adiabatic calorimetry specimen were not directly exposed to air. Instead, an equivalent convection coefficient (heq) was used to represent the heat transfer through the insulation layer by Equation (11) [7,55]. The value of heq depends on the insulation layer’s properties, including its thickness and thermal conductivity.
The thermal properties of concrete and insulation materials were determined from the literature [10,56] and are summarised in Table 3. The top surface convection coefficient was set to 5.6 W/m2·°C. Equivalent convection coefficients for the sides and bottom were 0.86 W/m2·°C and 1.95 W/m2 °C, respectively.
where heq is the equivalent convection coefficient (W/m2 °C), hc is the convection coefficient between the concrete surface and air (W/m2·°C), Li represents the thickness of the i-th insulation layer (mm), and ki is the i-th insulation layer’s thermal conductivity (W/m·°C).

Table 3.
Thermal properties of the concrete and insulation layer.
2.4.4. Mesh and Solver Configuration
The FEM model employed a swept mesh approach due to the regular rectangular geometry of the concrete specimen. The mesh was discretised using hexahedral elements, which are well suited for such geometries. To enhance the computational accuracy, the “extra fine” meshing option in COMSOL Multiphysics was selected, resulting in 7540 hexahedral elements. The time-dependent solver with a time step size of 0.1 h was employed to simulate temperature development over 72 h. The FEM model’s accuracy was validated by comparing its results with semi-adiabatic calorimetry data.
3. Results and Discussion
3.1. Semi-Adiabatic Calorimetry Results
The temperatures inside the environmental chamber, representing the ambient curing temperatures for semi-adiabatic calorimetry, were monitored and are shown in Figure 3. The temperature development of the semi-adiabatic concrete specimens is presented in Figure 4.
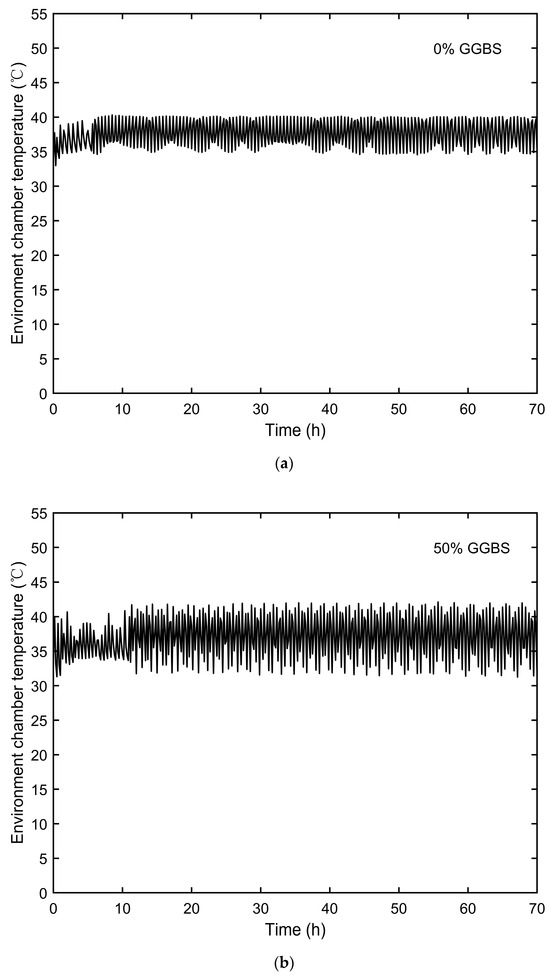
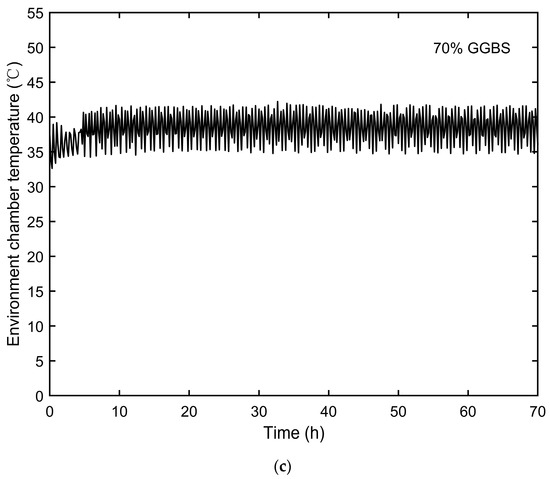
Figure 3.
Environmental chamber temperatures: (a) 0% GGBS, (b) 50% GGBS, and (c) 70% GGBS.
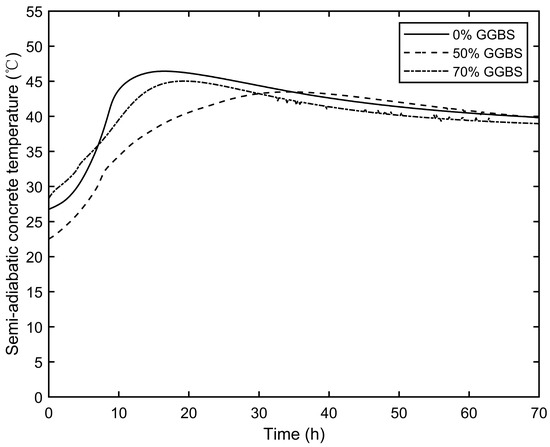
Figure 4.
Semi-adiabatic calorimetry concrete specimen temperatures for the three different mixes.
The monitoring results indicate that partially substituting Portland cement with GGBS significantly lowers the hydration temperature and delays the peak temperature. The 0% GGBS specimen reached a peak temperature of 46.4 °C after 16.2 h. In contrast, the 50% GGBS specimen took 33.2 h to reach a peak temperature of 43.5 °C, significantly lower than that of the cement-only mix. The 70% GGBS specimen reached a peak temperature of 45.0 °C after 19.0 h, which was only slightly lower than that of the cement-only mix. The reduction in temperature when using GGBS instead of Portland cement is due to the slower hydration process of GGBS, which generates less heat during the initial stages of hydration. This leads to a lower overall temperature rise and a delayed peak temperature compared to Portland cement. The subsequent isothermal calorimetry results further confirm this temperature reduction effect.
These findings contrast with Schindler and Folliard’s results [24], which indicate a positive correlation between GGBS content and temperature reduction. The discrepancy is due to the initial temperature differences, with the 50% GGBS concrete starting at 4.2 °C lower than the 0% GGBS concrete and 5.8 °C lower than the 70% GGBS concrete. Therefore, the results of this semi-adiabatic calorimetry test do not indicate a clear relationship between the GGBS content and the inhibition of the heat of hydration. Table 4 summarises the initial temperatures (°C), time required to reach peak temperatures (h), and peak temperatures (°C) for the three concrete mixes.

Table 4.
Concrete semi-adiabatic calorimetry initial and peak temperatures.
3.2. Isothermal Calorimetry Results
The isothermal calorimetry test results, including the heat output rate (W/g) and accumulated heat outputs (J/g), are displayed in Figure 5 and Figure 6. A comparison of the heat output rates for the same mix at different temperatures (20 °C and 38 °C) revealed that increasing the curing temperature from 20 °C to 38 °C led to peak hydration rate increases of 198.5%, 245.6%, and 239.6% for the 0% GGBS, 50% GGBS, and 70% GGBS mixes, respectively. Simultaneously, the time required to reach these peak values decreased by 39.7%, 63.5%, and 63.6%, respectively.
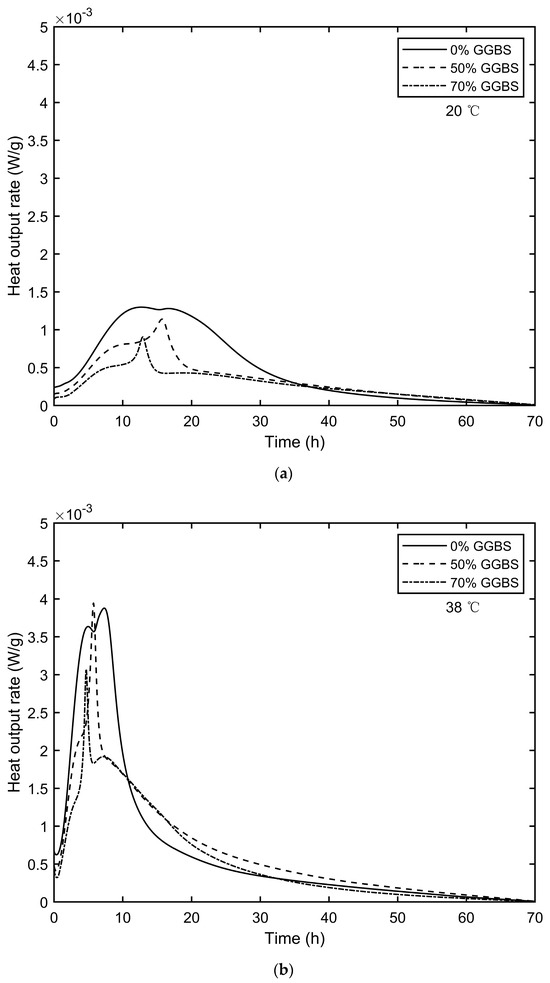
Figure 5.
Heat output rate of isothermal calorimetry: (a) 20 °C and (b) 38 °C.

Figure 6.
Accumulated heat outputs of isothermal calorimetry: (a) 20 °C and (b) 38 °C.
Additionally, increasing the ambient temperature significantly increased the 3-day accumulated heat output. Specifically, the 3-day accumulated heat outputs increased by 44.1%, 94.3%, and 112.7% for the 0% GGBS, 50% GGBS, and 70% GGBS mixes, respectively. These results indicate that GGBS concrete temperature development is more sensitive to ambient temperature variations compared to cement-only mixes, aligning with the findings of Wang et al. [31].
The hydration heat mitigation effect of GGBS varies at different temperatures. At 20 °C, the 3-day accumulated heat outputs were reduced by 33.9 J/g and 51.4 J/g when 50% and 70% Portland cement were replaced by GGBS, respectively. However, at 38 °C, the reductions were only 6.38 J/g and 34.36 J/g, respectively. This indicates that higher curing temperatures weaken the thermal mitigation effect of GGBS.
The hydration rate results at 38 °C show that adding GGBS decreased the time required to reach peak values. For the 50% GGBS mix, the peak hydration rate was 0.06 W/g higher than that of the 0% GGBS mix, and the time to peak was reduced by 1.6 h. The 3-day accumulated heat outputs for the 50% GGBS mix showed a slight reduction of 6.38 J/g compared to the 0% GGBS mix.
In contrast, the 70% GGBS mix had a peak hydration rate reduced by 0.81 W/g, with the time to peak advanced by 2.6 h compared to the 0% GGBS mix. The 3-day accumulated heat outputs for the 70% GGBS mix showed a significant reduction of 34.36 J/g compared to the 0% GGBS mix. These findings suggest that a higher GGBS content results in more substantial reductions in the peak hydration value, time to peak hydration, and 3-day accumulated heat outputs, consistent with Zheng et al. [25].
Table 5 summarises the peak hydration rates, the time required to reach these peak values, and the 3-day accumulated heat outputs for the three mixes at 38 °C.

Table 5.
The peak hydration rate and 3-d accumulated heat outputs of isothermal calorimetry (38 °C).
3.3. FEM Modelling Results
The accuracy of the model’s heat source, specifically the expression of cement hydration heat, directly determines the accuracy of the temperature prediction results. The activation energy values calculated for the 0% GGBS, 50% GGBS, and 70% GGBS mixes (with water-binder ratios of 0.49, 0.51, and 0.51, respectively, as per Table 1) were 46,023 J/mol, 55,286 J/mol, and 51,536 J/mol, respectively.
A literature review of activation energy calculations using a similar method (ASTM C1074 [42]) shows that Aleksandra and Elzbieta [44] calculated activation energies of 41,077 J/mol and 44,011 J/mol for CEM I 42.5 R Portland cement (water-binder ratio of 0.4). Barnett et al. [43] reported values of 54,600 J/mol and 58,800 J/mol for mixes of “50% Portland cement + 50% GGBS” (water-binder ratio of 0.61) and “30% Portland cement + 70% GGBS” (water-binder ratio of 0.52), respectively. While there is no direct comparison due to differences in cement composition and water-binder ratios, these studies indicate that the addition of GGBS increases the activation energy of cement, with a higher GGBS content leading to a higher activation energy.
However, the calculated activation energy for the 70% GGBS mix in this study was lower than that for the 50% GGBS mix, which contradicts the above conclusion. Several factors may have contributed to this discrepancy. Firstly, variations in the chemical composition and physical properties of the cement and GGBS used in different studies can significantly influence hydration kinetics and, consequently, activation energy calculations. Secondly, the disparities in water-to-binder ratios across studies may play a crucial role in modulating the hydration process and its energy requirements.
Figure 7 presents the 10th-order regression between the hydration heat output rate (q) and accumulated heat output (Q) at 20 °C and 38 °C. Figure 7a shows that the regression lines for the 0% GGBS mix closely match the experimental results. However, Figure 7b and c indicate that the regression lines for the 50% GGBS and 70% GGBS mixes do not accurately capture the “second peaks” observed in the isothermal calorimetry results (Figure 5 and Figure 6), especially at higher ambient temperatures (38 °C). These second peaks in the hydration reaction of the GGBS-blended samples are due to separate hydration events occurring at different times. To enhance the accuracy of the FEM model, further refinement of the polynomial regression method or additional experimental data points at various temperatures may be necessary. This could help better capture the complex hydration behaviour of GGBS-blended concretes under different thermal conditions.


Figure 7.
10th-order polynomial regression analyses between q and Q: (a) 0% GGBS, (b) 50% GGBS, and (c) 70% GGBS.
A comparison between the concrete semi-adiabatic calorimetry results and the FEM modelling results using the two methods (as described in Section 2.4) is shown in Figure 8. The accuracies of the two methods varied for the different mixes.
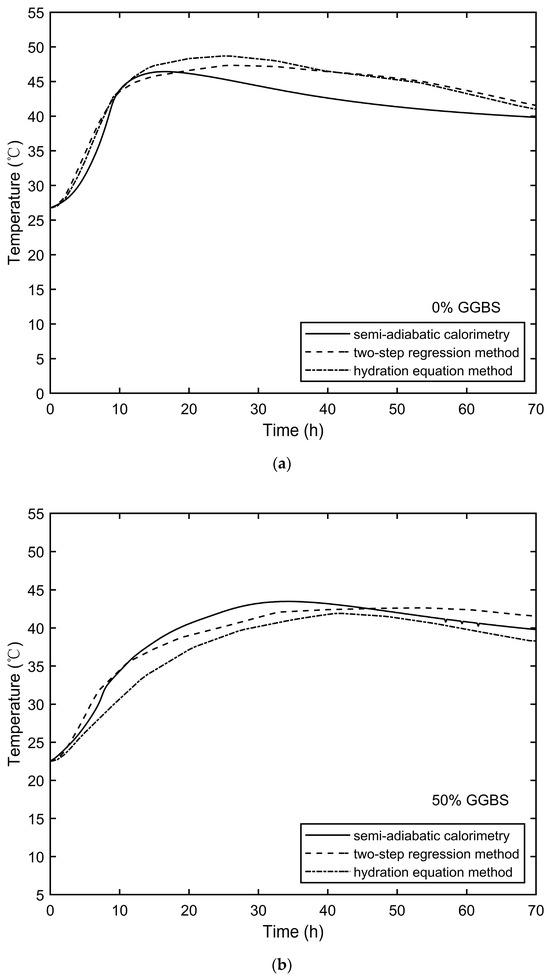

Figure 8.
FEM modelling results and semi-adiabatic calorimetry results comparison: (a) 0% GGBS, (b) 50% GGBS, and (c) 70% GGBS.
For the 0% GGBS concrete (Figure 8a), the FEM results were slightly higher than the semi-adiabatic calorimetry values after 20 h, with a maximum error of 4.2 °C occurring at 47 h using the “two-step regression method.” The prediction results for the 50% GGBS concrete (Figure 8b) were accurate for both methods, with a maximum error of 3.8 °C occurring at 12 h using the “hydration equation method”. However, for the 70% GGBS concrete (Figure 8c), the “two-step regression method” showed a significant error after 20 h, with a maximum error of 7.0 °C at 45 h. This discrepancy was due to the 10th-order regression for the 70% GGBS mix, which did not capture the second peak identified in Figure 7c. The verified FEM results demonstrate that the adjusted isothermal calorimetry results effectively quantify the impact of ambient temperature on the hydration process. These results provide a theoretical foundation for utilising the FEM to predict the temperature development in in situ concrete.
Figure 9 displays the temperature distribution diagram of the three sections parallel to the Y-Z plane of the 0% GGBS concrete at 16 h from the FEM results. The diagram indicates that when the Y and Z coordinates are the same, the middle slice has a higher temperature than the slices on either side, especially near the centre. For the same slice, the temperature gradually decreases from the centre to the edge, with the top edge having the lowest temperature due to the lack of insulation.

Figure 9.
Internal slice temperature distribution: 0% GGBS concrete via “two-step regression method” at 16 h.
The thermal profile of the specimen exhibits notable extrema. The peak temperature is observed at the geometric centre, while the minimum temperature occurs at the upper surface’s endpoint. This distribution pattern is attributed to the varying heat dissipation rates across the specimen. The central region retains heat most effectively due to its insulated position, whereas the upper surface, directly exposed to air, facilitates rapid heat loss. The gradual temperature transition from the core to the periphery, as depicted in Figure 9, demonstrates the FEM model’s capability to accurately simulate the thermal distribution within the concrete specimen, validating its effectiveness as a predictive tool for concrete thermal behaviour.
4. Conclusions and Future Work
The temperature rise in early-age concrete due to cement hydration heat poses a significant risk of thermal cracking, which can compromise the structural integrity of the concrete. Accurately predicting the concrete hydration temperature is essential for preventing such issues. A major challenge in predicting the in situ concrete temperature is the influence of variable ambient temperatures, which complicate the hydration rate and temperature development of concrete. This study established a finite element model (FEM) for predicting the temperature development of an in situ concrete slab over three days. The actual rise in the hydration temperature and hydration heat output rate of the concrete were determined separately using semi-adiabatic and isothermal calorimetry. The variable ambient temperature’s impact on the cement hydration rate was quantified by adjusting the isothermal calorimetry curves via the Arrhenius-based approach. These adjusted hydration curves were then input into the FEM model as the internal heat source. Ground granulated blast furnace slag (GGBS) was used to replace 50% and 70% of Portland cement in both the experiments and FEM modelling to study its mitigating effect on the concrete’s thermal action.
The key findings from the experimental and FEM results are summarised as follows:
- Semi-Adiabatic Calorimetry Results: Partial replacement of Portland cement with GGBS significantly reduced the early-age concrete hydration temperature. However, the temperature mitigation effect of the 70% GGBS specimens was not as effective as that of the 50% GGBS specimens, primarily due to the higher initial temperature of the 70% GGBS specimen by 5.8 °C compared to that of the 50% GGBS specimen.
- Isothermal Calorimetry Results: Higher ambient temperatures promoted the hydration reactions of both cement-only and GGBS cement blended mixes. GGBS was found to be more temperature-sensitive than Portland cement. The mitigating effect of GGBS on the hydration heat became more pronounced with a higher GGBS content but weakened as the ambient temperature increased.
- FEM Modelling Results: The FEM model results for 0% and 50% GGBS concrete closely matched the semi-adiabatic calorimetry results, with maximum errors of 4.2 °C and 3.8 °C, respectively. However, the model’s prediction accuracy decreased for the 70% GGBS mix, with a maximum error of 7.0 °C, due to the failure to capture secondary hydration peaks. The FEM modelling validated by semi-adiabatic calorimetry suggests that the adjusted isothermal calorimetry data effectively quantify the ambient temperature’s effect. Additionally, the FEM model successfully simulated the internal temperature distribution within the concrete.
Future research will focus on conducting additional isothermal calorimetry tests at various temperatures, enhancing activation energy calculations, and exploring different mix designs to improve the FEM model’s predictive accuracy and applicability.
Author Contributions
Conceptualisation, Y.T. and K.T.; methodology, Y.T. and K.T.; software, Y.T.; validation, Y.T.; formal analysis, Y.T. and K.T.; investigation, Y.T.; resources, Y.T. and K.T.; data curation, Y.T. and K.T.; writing—original draft preparation, Y.T.; writing—review and editing, Y.T. and K.T.; visualisation, Y.T.; supervision, K.T.; project administration, Y.T. and K.T.; funding acquisition, Y.T. and K.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data from the tests and simulations in this study are included in this published article.
Acknowledgments
The author expresses sincere gratitude to Brunel University London for providing research licences for the Finite Element software COMSOL 5.5 and the Mathematical software MATLAB R2020b, which were essential for this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Notation
| T | Temperature of the concrete in degrees Celsius (°C). |
| α | Degree of hydration |
| Cp | Specific heat capacity of concrete (J/kg·K) |
| ρ | Density of concrete (kg/m3) |
| k | Thermal conductivity of concrete (W/m·K) |
| q | Heat generation rate of hydration (W/g). |
| Q | Cumulative heat of hydration (J/g) |
| f(α) | Normalised heat generation rate |
| k(T) | Rate constant at temperature T |
| A | Pre-exponential factor in the Arrhenius equation |
| Ea | Apparent activation energy (J/mol) |
| R | Constant universal gas constant (8.314 J/K·mol) |
| Tr | Reference temperature (°C) |
| te | Equivalent age of the concrete (h) |
References
- Young, J.F. Portland Cements. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 7768–7773. [Google Scholar]
- Mindess, S.; Young, J.F.; Darwin, D. Concrete; Prentice Hall: Hoboken, NJ, USA, 2003. [Google Scholar]
- Neville, A.M. Properties of Concrete, 5th ed.; Longman: London, UK, 2011; Volume 4. [Google Scholar]
- Hewlett, P.C.; Liska, M. Lea’s Chemistry of Cement and Concrete; Butterworth-Heinemann: Oxford, UK, 2019; pp. 1–858. [Google Scholar]
- Lu, Z.; Haist, M.; Ivanov, D.; Jakob, C.; Jansen, D.; Leinitz, S.; Link, J.; Mechtcherine, V.; Neubauer, J.; Plank, J.; et al. Characterization data of reference cement CEM I 42.5 R used for priority program DFG SPP 2005 “Opus Fluidum Futurum—Rheology of reactive, multiscale, multiphase construction materials”. Data Brief 2019, 27, 104699. [Google Scholar] [CrossRef]
- Ge, Z. Predicting Temperature and Strength Development of the Field Concrete. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2005. [Google Scholar]
- Hatzitheodorou, A. In-Situ Strength Development of Concretes with Supplementary Cementitious Materials. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2007. [Google Scholar]
- Mydin, M.A.O. Assessment of thermal conductivity, thermal diffusivity and specific heat capacity of lightweight aggregate foamed concrete. J. Teknol. 2016, 78, 477–482. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Sultan, M.A. Effect of Temperature on Thermal Properties of High-Strength Concrete. J. Mater. Civ. Eng. 2003, 15, 101–107. [Google Scholar] [CrossRef]
- Lawrence, A.M.; Tia, M.; Ferraro, C.C.; Bergin, M. Effect of Early Age Strength on Cracking in Mass Concrete Containing Different Supplementary Cementitious Materials: Experimental and Finite-Element Investigation. J. Mater. Civ. Eng. 2012, 24, 362–372. [Google Scholar] [CrossRef]
- Bilčík, J.; Sonnenschein, R.; Gažovičová, N. Causes of Early-Age Thermal Cracking of Concrete Foundation Slabs and their Reinforcement to Control the Cracking. Slovak J. Civ. Eng. 2017, 25, 8–14. [Google Scholar] [CrossRef]
- Tang, K.; Millard, S.; Beattie, G. Early-age heat development in GGBS concrete structures. Proc. Inst. Civ. Eng. Struct. Build. 2015, 168, 541–553. [Google Scholar] [CrossRef]
- Tang, K.; Millard, S.; Beattie, G. Technical and economical feasibility of using GGBS in long-span concrete structures. Adv. Concr. Constr. 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Tang, K.; Khatib, J.; Beattie, G.; Sato, T.; Beaudoin, J.J.; Kong, X.-M.; Lu, Z.-B.; Liu, H.; Wang, D.-M.; Barbhuiya, S.A.; et al. Effect of partial replacement of cement with slag on the early-age strength of concrete. Proc. Inst. Civ. Eng. Struct. Build. 2017, 170, 451–461. [Google Scholar] [CrossRef]
- Tiwari, S.; Mondal, G.; Dash, S.R.; Roy, K. Experimental investigation of unbonded reinforced concrete PT shear wall under lateral loading: A state-of-the-art review. J. Build. Eng. 2023, 78, 107504. [Google Scholar] [CrossRef]
- Philip, R.E.; Andrushia, A.D.; Nammalvar, A.; Gurupatham, B.G.A.; Roy, K. A Comparative Study on Crack Detection in Concrete Walls Using Transfer Learning Techniques. J. Compos. Sci. 2023, 7, 169. [Google Scholar] [CrossRef]
- Lowe, D.; Roy, K.; Das, R.; Clifton, C.G.; Lim, J.B. Full scale experiments on splitting behaviour of concrete slabs in steel concrete composite beams with shear stud connection. Structures 2020, 23, 126–138. [Google Scholar] [CrossRef]
- Bamforth, P.B. Early-Age Thermal Crack Control in Concrete; CIRIA: London, UK, 2007. [Google Scholar]
- Brunetaud, X.; Divet, L.; Damidot, D. Impact of unrestrained Delayed Ettringite Formation-induced expansion on concrete mechanical properties. Cem. Concr. Res. 2008, 38, 1343–1348. [Google Scholar] [CrossRef]
- Sellier, A.; Multon, S. Chemical modelling of Delayed Ettringite Formation for assessment of affected concrete structures. Cem. Concr. Res. 2018, 108, 72–86. [Google Scholar] [CrossRef]
- Taylor, H.; Famy, C.; Scrivener, K.J. Delayed ettringite formation. Cem. Concr. Res. 2001, 31, 683–693. [Google Scholar] [CrossRef]
- Hong, Y.-X.; Chen, W.; Lin, J.; Gong, J.; Cheng, H.-D. Thermal field in water pipe cooling concrete hydrostructures simulated with singular boundary method. Water Sci. Eng. 2017, 10, 107–114. [Google Scholar] [CrossRef]
- Singh, P.R.; Rai, D.C. Effect of Piped Water Cooling on Thermal Stress in Mass Concrete at Early Ages. J. Eng. Mech. 2018, 144, 04017183. [Google Scholar] [CrossRef]
- Schindler, A.; Folliard, K. Influence of supplementary cementing materials on the heat of hydration of concrete. In Proceedings of the Advances in Cement and Concrete IX Conference, Copper Mountain Conference Resort in Colorado, Denver, CO, USA, 10–14 August 2003. [Google Scholar]
- Zheng, L.; Paine, K.; Dhir, R. Heat evolution and hydration modelling of GGBS cement. In Proceedings of the International Symposium on Role of Cement Science in Sustainable Development, Scotland, UK, 3–4 September 2003. [Google Scholar]
- Klemczak, B.; Batog, M. Heat of hydration of low-clinker cements. J. Therm. Anal. Calorim. 2015, 123, 1351–1360. [Google Scholar] [CrossRef]
- Roy, K.; Ananthi, G.B.G. Sustainable Composite Construction Materials; MDPI—Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2023. [Google Scholar]
- Özkılıç, Y.O.; Zeybek, O.; Bahrami, A.; Çelik, A.I.; Mydin, A.O.; Karalar, M.; Hakeem, I.Y.; Roy, K.; Jagadesh, P. Optimum usage of waste marble powder to reduce use of cement toward eco-friendly concrete. J. Mater. Res. Technol. 2023, 25, 4799–4819. [Google Scholar] [CrossRef]
- Woo, H.-M.; Kim, C.-Y.; Yeon, J.H. Heat of hydration and mechanical properties of mass concrete with high-volume GGBFS replacements. J. Therm. Anal. Calorim. 2018, 132, 599–609. [Google Scholar] [CrossRef]
- Xu, G.; Tian, Q.; Miao, J.; Liu, J. Early-age hydration and mechanical properties of high volume slag and fly ash concrete at different curing temperatures. Constr. Build. Mater. 2017, 149, 367–377. [Google Scholar] [CrossRef]
- Wang, Q.; Miao, M.; Feng, J.; Yan, P. The influence of high-temperature curing on the hydration characteristics of a cement–GGBS binder. Adv. Cem. Res. 2012, 24, 33–40. [Google Scholar] [CrossRef]
- Jędrzejewska, A.; Benboudjema, F.; Lacarrière, L.; Azenha, M.; Schlicke, D.; Pont, S.D.; Delaplace, A.; Granja, J.; Hájková, K.; Heinrich, P.J.; et al. COST TU1404 benchmark on macroscopic modelling of concrete and concrete structures at early age: Proof-of-concept stage. Constr. Build. Mater. 2018, 174, 173–189. [Google Scholar] [CrossRef]
- Jeong, D.J.; Kim, T.; Ryu, J.-H.; Kim, J.H. Analytical model to parameterize the adiabatic temperature rise of concrete. Constr. Build. Mater. 2020, 268, 121656. [Google Scholar] [CrossRef]
- Kiernożycki, W.; Błyszko, J. The Influence of Temperature on the Hydration Rate of Cements Based on Calorimetric Measurements. Materials 2021, 14, 3025. [Google Scholar] [CrossRef] [PubMed]
- Soutsos, M.; Hatzitheodorou, A.; Kwasny, J.; Kanavaris, F. Effect of in situ temperature on the early age strength development of concretes with supplementary cementitious materials. Constr. Build. Mater. 2016, 103, 105–116. [Google Scholar] [CrossRef]
- Hansen, P.F.; Pedersen, E.J. Maturity Computer for Controlled Curing and Hardening of Concrete. Nordisk Betong 1977, 21, 19–34. [Google Scholar]
- Reinhardt, J.B.H.; Jongedijk, J. Temperature development in concrete structures taking account of state dependent properties. In Proceedings of the International Conference of Concrete at Early Ages, Paris, France, 14–16 September 1982. [Google Scholar]
- Azenha, M. Numerical Simulation of the Structural Behaviour of Concrete Since Its Early Ages. Ph.D. Thesis, University of Porto, Porto, Protugal, 2009. [Google Scholar]
- Azenha, M.; Faria, R.; Ferreira, D. Identification of early-age concrete temperatures and strains: Monitoring and numerical simulation. Cem. Concr. Compos. 2009, 31, 369–378. [Google Scholar] [CrossRef]
- Matthieu, B.; Farid, B.; Jean-Michel, T.; Georges, N. Analysis of semi-adiabiatic tests for the prediction of early-age behavior of massive concrete structures. Cem. Concr. Compos. 2012, 34, 634–641. [Google Scholar] [CrossRef]
- Poole, J.; Riding, K.; Folliard, K.; Juenger, M.; Schindler, A. Methods for Calculating Activation Energy for Portland Cement. ACI Mater. J. 2007, 104, 303–311. [Google Scholar]
- ASTM C1074-19e1; Standard Practice for Estimating Concrete Strength by the Maturity Method. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- Barnett, S.; Soutsos, M.; Millard, S.; Bungey, J. Strength development of mortars containing ground granulated blast-furnace slag: Effect of curing temperature and determination of apparent activation energies. Cem. Concr. Res. 2006, 36, 434–440. [Google Scholar] [CrossRef]
- Kuryłowicz-Cudowska, A.; Haustein, E. Isothermal Calorimetry and Compressive Strength Tests of Mortar Specimens for Determination of Apparent Activation Energy. J. Mater. Civ. Eng. 2021, 33, 04021035. [Google Scholar] [CrossRef]
- Kevin, J.; Folliard, M.J.; Schindler, A.; Riding, K.; Poole, J.; Kallivokas, L.F.; Slatnick, S.; Whigham, J.; Meadows, J.L. Prediction Model for Concrete Behavior—Final Report; Technical report; Report No. 0-5483-1; The University of Texas at Austin: Austin, TX, USA, 2008. [Google Scholar]
- Kanagaraj, B.; Kiran, T.; Gunasekaran, J.; Nammalvar, A.; Arulraj, P.; Gurupatham, B.G.A.; Roy, K. Performance of Sustainable Insulated Wall Panels with Geopolymer Concrete. Materials 2022, 15, 8801. [Google Scholar] [CrossRef]
- Wadsö, L. An Experimental Comparison between Isothermal Calorimetry, Semi-Adiabatic Calorimetry and Solution Calorimetry for the Study of Cement Hydration; Final Report, NORDTEST Project 1534-01; NORDTEST: Espoo, Finland, 2002. [Google Scholar]
- Wadsö, L. Applications of an eight-channel isothermal conduction calorimeter for cement hydration studies. Cem. Int. 2005, 5, 94–101. [Google Scholar]
- Xu, Q.; Hu, J.; Ruiz, J.M.; Wang, K.; Ge, Z. Isothermal calorimetry tests and modeling of cement hydration parameters. Thermochim. Acta 2010, 499, 91–99. [Google Scholar] [CrossRef]
- Tahersima, M.; Tikalsky, P. Finite element modeling of hydration heat in a concrete slab-on-grade floor with limestone blended cement. Constr. Build. Mater. 2017, 154, 44–50. [Google Scholar] [CrossRef]
- BS EN 197-1:2011; Cement. Composition, Specifications and Conformity Criteria for Common Cements. BSI: London, UK, 2011.
- BS EN 15167-1:2006; Ground Granulated Blast Furnace Slag for Use in Concrete, Mortar and Grout. Part 1–Definitions, Specifications and Conformity Criteria. BSI: London, UK, 2006.
- BS 8500-1:2015; Concrete. Complementary British Standard to BS EN 206. Method of Specifying and Guidance for the Specifier. BSI: London, UK, 2015.
- Huang, Y.; Liu, G.; Huang, S.; Rao, R.; Hu, C. Experimental and finite element investigations on the temperature field of a massive bridge pier caused by the hydration heat of concrete. Constr. Build. Mater. 2018, 192, 240–252. [Google Scholar] [CrossRef]
- Azenha, M.; Faria, R.; Figueiras, H. Thermography as a technique for monitoring early age temperatures of hardening concrete. Constr. Build. Mater. 2011, 25, 4232–4240. [Google Scholar] [CrossRef]
- Bamforth, P.; Chisholm, D.; Gibbs, J.; Harrison, T. Properties of Concrete for Use in Eurocode 2; The Concrete Centre: Camberley, UK, 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).