Separation of Floodplain Flow and Bankfull Discharge: Application of 1D Momentum Equation Solver and MIKE 21C

Abstract

A floodplain is an area of low-lying land adjacent to a river, stream, or other water body that is regularly inundated by water during periods of high flow. Floodplains typically have relatively flat terrain and are composed of sediments deposited by the river over time. Floodplain flow refers to the movement of water across the surface of the floodplain during periods of high flow. This flow can occur as a result of water spilling over the river banks or seeping into the ground and then re-emerging on the surface of the floodplain. Bankfull discharge is the flow of water that just fills the channel of a river or stream to the top of its banks. It is the point at which the river or stream is at its maximum capacity without overflowing onto the floodplain. Bankfull discharge is often used as a reference point for assessing flood risk and planning floodplain management strategies. To examine the bank-to-bank hydro-morphodynamics of a river, it is necessary to comprehend the flow distribution throughout the main stream and floodplain. Along with river hydraulics, bankfull discharge is a crucial parameter for estimating river bank erosion. For evaluating the distribution and generation of river flow over the floodplain and main stream, a variety of modeling tools and approaches are available. This study investigates methods for separating floodplain flow and bankfull discharge from observed discharge data using the one-dimensional momentum equation. A two-dimensional modeling tool (MIKE 21C) was also employed to investigate the usefulness of the proposed method in a region with an enormous floodplain.

1. Introduction

A floodplain is a low-lying area that is frequently inundated by water from an adjacent river [1] or from the river network [2,3,4] within a watershed. Most floodplains are formed by the deposition within river meanders and overbank flow [1]. On the other hand, the maximum discharge the channel can convey without overflowing onto the floodplain is commonly referred to as bankfull discharge ($Q_{bf}$) [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The $Q_{bf}$ corresponds to an abrupt change in the rating curve’s slope [28]. Therefore, there is a close relationship between floodplain flow ($Q_{fp}$) and $Q_{bf}$ in a river system. $Q_{bf}$ represents the maximum amount of water that a river channel can contain without overflowing onto the floodplain. When the water level in a river reaches $Q_{bf}$, water begins to spill over the banks and onto the floodplain, creating $Q_{fp}$.

The amount of water that flows into the floodplain during a flood event depends not only on the $Q_{bf}$ but also on the characteristics of the floodplain itself. Factors such as the slope of the floodplain, the presence of vegetation, and the soil type can all affect the speed and amount of $Q_{fp}$.

$Q_{fp}$ can be an important natural process, as it can redistribute sediment, nutrients, and organic matter throughout the floodplain, creating an important habitat for aquatic and terrestrial species. However, if $Q_{fp}$ is excessive, it can cause significant damage to human communities and infrastructure. Therefore, understanding the relationship between $Q_{bf}$ and $Q_{fp}$ is important for managing the risks associated with flooding, and for preserving the ecological health of river systems.

When a river flows at $Q_{bf}$, the water exerts a shear stress on the bed and banks, which can cause erosion and the transport of sediment. Over time, this can lead to the formation of riffles, pools, bars, and other features in the river channel. $Q_{bf}$ also plays a role in determining the width, depth, and slope of the channel. By studying the relationship between $Q_{bf}$ and channel morphology, scientists and engineers can better understand how rivers respond to changes in flow conditions, such as changes in precipitation or land use. This information can be used to develop more accurate models for predicting river behavior and managing river resources [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].

The observed discharge is, therefore, the sum of $Q_{bf}$ and the $Q_{fp}$. There are gaps in our understanding of the hydraulics of overbank flows. The majority of studies regarding water flow in floodplains are experimental or statistical in nature. Using a stage-discharge rating curve constructed from collected discharge data, $Q_{\mathit{bf}}$ may be calculated. When the floodplain conveyance is significant relative to the channel conveyance, the stage-discharge rating curve will exhibit a distinct break at the bankfull stage [29,30,31,32]. This implementation emerges since the stage is a unique function of the discharge in alluvial streams [33,34,35]. Although, estimating a rating curve is significantly easier. However, due to the sporadic and unexpected occurrence of floods, especially large ones, the brief duration of overbank flows, and the inherent hazards associated with taking measurements during flood discharges, complicated scenarios frequently arise. Due to the complexity of the flow conditions, the discharge measurements may fluctuate during extreme events. Although calculating the hydraulics of flood flows on a real river is extremely complex, it is essential for practical purposes, such as determining the channel’s and floodplain’s conveyance capacity and predicting the flood route.

A number of studies have investigated the relationship between $Q_{bf}$ and $Q_{fp}$. A study by Schumm found that the frequency and magnitude of floods are related to the size and shape of the drainage basin and that $Q_{bf}$ is a useful parameter for predicting the potential for flooding [36,37]. Another study by Montgomery and Buffington found that $Q_{bf}$ is closely related to the width and depth of the channel and that the width and depth of the channel are in turn related to the sediment transport capacity of the river [38,39]. They also found that the vegetation on the floodplain can have a significant impact on $Q_{fp}$ by influencing the resistance to flow. More recent studies have used computer models to simulate $Q_{fp}$ and investigate the role of $Q_{bf}$. For example, a study by Dutta et al. used a two-dimensional hydrodynamic model for flood inundation simulation on the lower Mekong River basin [40]. They found that $Q_{bf}$ was a key parameter in determining the extent and duration of flooding on the floodplain. Overall, the literature suggests that $Q_{bf}$ is an important parameter in $Q_{fp}$ and can be used to predict the potential for flooding. The relationship between $Q_{bf}$ and $Q_{fp}$ is complex and is affected by a number of factors, including river morphology, sediment transport, vegetation, and land use. Computer models can be used to simulate $Q_{fp}$ and investigate the role of $Q_{bf}$ in more detail.

The purpose of this article is to provide a practical, accurate, and predictable tool for separating $Q_{fp}$ and $Q_{bf}$ based on the one-dimensional momentum equation and its usefulness for predicting two-dimensional river morphology [41] in order to protect riparian areas from exploitation.

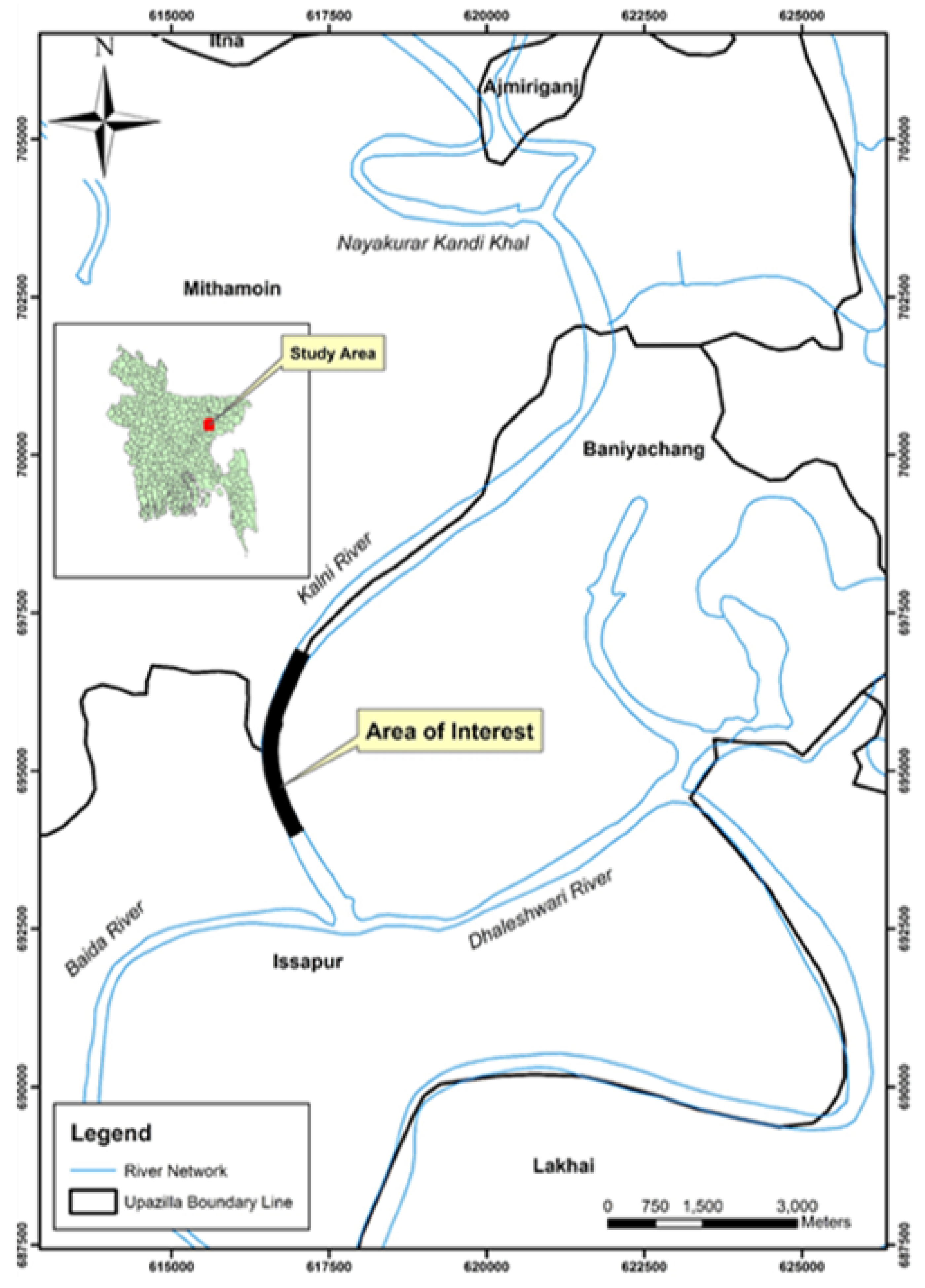
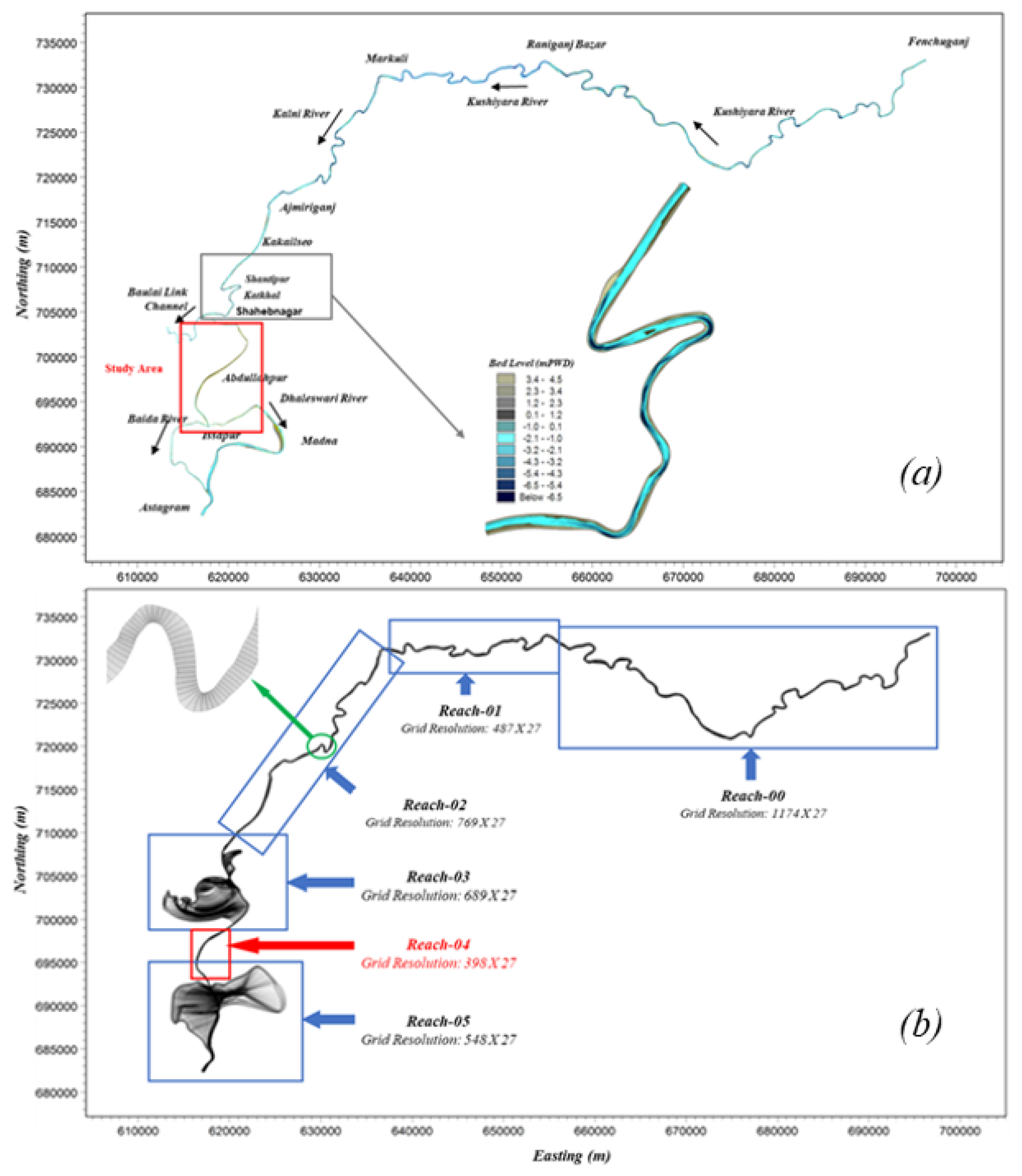
2. Study Area

Originating on the banks of the Barak River in India, the Kalni-Kushiyara River system is a transboundary river system. The system includes the Kalni and Kushiyara rivers. Through the Indian provinces of Assam, Manipur, and Mizoram, the Barak River flows. The river then enters Bangladesh in the vicinity of Amalshid, where it meets the south-flowing Kushiyara River. After Markuli, the river’s name changes to Kalni. The Kalni River is approximately 160 km long, while the Kushiyara River is about 230 km long. The combined length of the Kalni-Kushiyara River system is approximately 390 km. The river system is an important source of water for irrigation, transportation, and fisheries for the people living in the region. However, the Kalni-Kushiyara River system is facing several environmental challenges, including pollution, erosion, and sedimentation. In addition, there have been disputes between India and Bangladesh over the sharing of water from the river system, which has led to tensions between the two countries. The governments of both India and Bangladesh are working together to address these challenges and to ensure the sustainable management of the river system.

The Kalni River has an extensive floodplain, and suitable bathymetric data are available for our techniques. In a small section of the Kalni River (see Figure 1), the 1D and 2D $MIKE21C$ models are employed. The Kalni-Kushiyara River Management Project ($KKRMP$) from $IWM$ (https://www.iwmbd.org/, accessed on 3 November 2021) provided all the information for this Kalni River segment. Afterward, the applicability of our techniques for predicting two-dimensional river morphology in the context of protecting areas from exploitation is discussed, and the 1D and 2D $MIKE21C$ models are compared.

3. Methods

In this section, we discuss and formulate our suggested 1D technique and governing equation, which has been modified to generate the discharge for a small reach using only the water level, cross-sectional area, and roughness inputs. This method utilized convective acceleration and a change in the water surface slope. The governing equation was numerically solved by discretizing the water-level cross-sections (see details in [42]). The numerical solution and data processing of the formulation were carried out in VBA [42]. In conjunction with the Kalni-Kushiyara River Management project, a 2D model was also modified using a $MIKE21C$ model gathered from the $IWM$ (https://www.iwmbd.org/, accessed on 3 November 2021) collection. Eventually, the extracted $Q_{bf}$ was calibrated relative to the 2D $MIKE21C$ model reproduced $Q_{bf}$ of the corresponding study area.

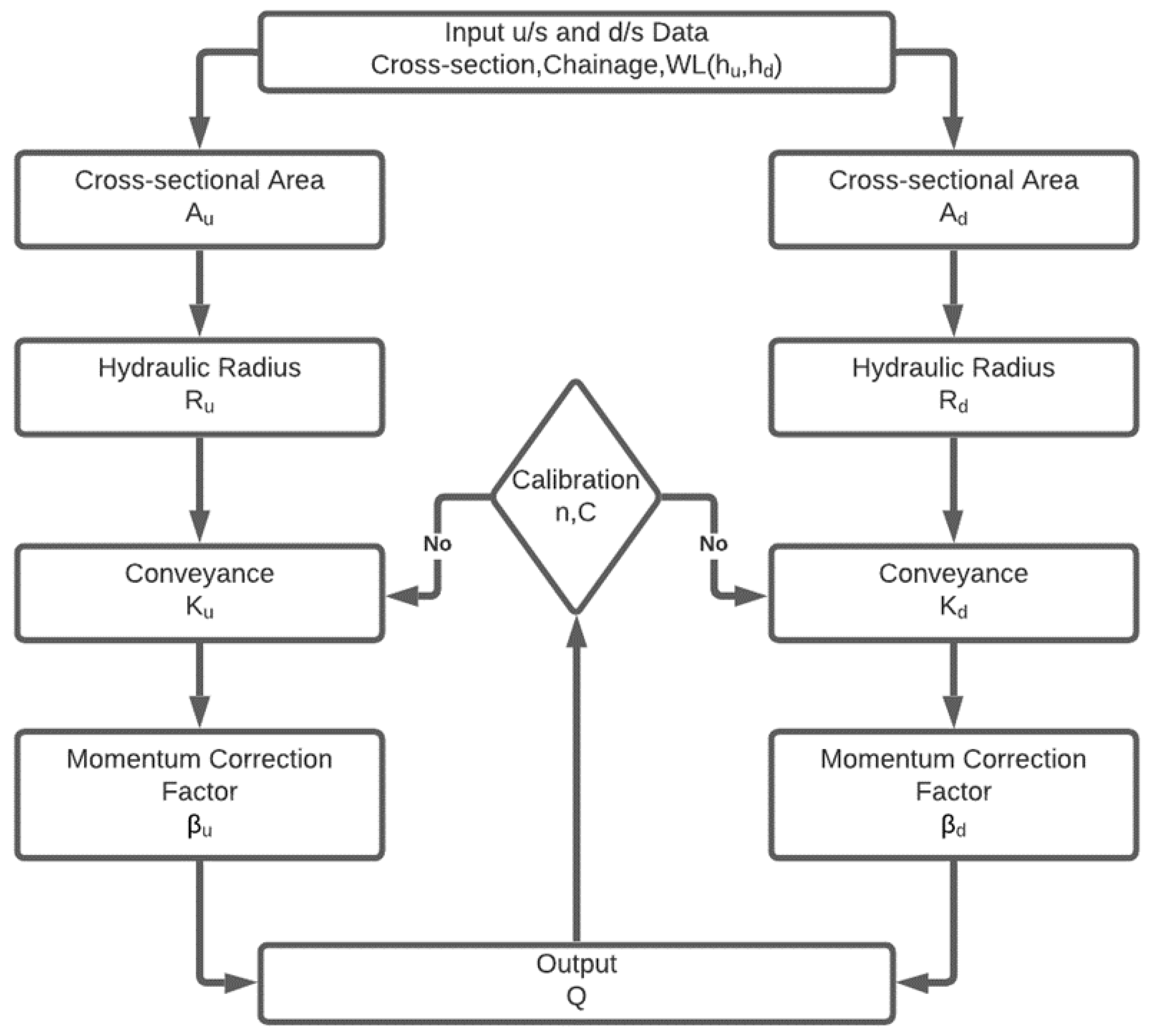
3.1. One-Dimensional Governing Equation

This technique adopted the differential form of the 1D momentum equation (see Equation (1)), which can be simplified for a small channel segment. Equation (1) is composed of pressure, gravity, and friction forces (see details in [34,42,43]), each of which produces convective and local acceleration (see details in [34]). Therefore, the 1D momentum equation can be simplified as the following:

$$\frac{\partial Q}{\partial t}+\frac{\partial }{\partial t}\left(\frac{Q^2}{A}\right)+gA\frac{\partial h}{\partial x}-gA(S-S_f)=0$$

(1)

Utilizing the momentum correction factor, water surface slope, discharge and cross-section, Equation (1) can be further written as the following:

$$\frac{\partial z}{\partial x}+\frac{1}{2g}\frac{\partial }{\partial x}\left(\frac{\beta Q^2}{A^2}\right)+\frac{1}{g}\frac{\partial \left(\frac{Q}{A}\right)}{\partial t}+\frac{Q^2}{K^2}=0$$

(2)

where $x=$ the distance along the reach, $t=$ time, $z=z_0+h$ water level, $z_0=$ bed level from the datum, $\beta =$ momentum correction factor, $A=$ cross-sectional area, and $K=$ conveyance of the section.

This computation is nearly accurate when the water level fluctuates significantly over time. The $\beta$ depends on the entire cross-sectional conveyance. Each cross-section contains a large number of small elements:

$$K=\sum _{j=1}^N{K}_j=\frac{1}{N}\sum _{j=1}^N{A}_j{R}_j^{\frac{2}{3}}$$

(3)

where $K_j=$ the cross-sectional conveyance, $A_j=$ area of the segment, $R_j=$ hydraulic radius of the segment, and $n=$ Manning’s roughness, and $\beta$ can be calculated as the following:

$$\beta =\frac{1}{U^{2}A}{\int }_0^A{u}^{2}dA\cong \frac{A}{K^2}\sum _{j=1}^N\frac{K_j^2}{A_j}$$

(4)

3.2. Solution of the 1D Governing Equation

It is presumed that there is no discernible discharge entering or exiting the segment between the two adjacent cross-sections. Consequently, the cross-sections for a straight stretch remain straight and near enough together. Thus, the fluctuation in the discharge results solely from the longitudinal discharge variation (see Equation (2) [29,42]):

$$(h_u-h_d)+\frac{Q^2}{2g}\left(\frac{{\beta }_u}{A_u^2}-\frac{{\beta }_d}{A_d^2}\right)+\frac{x_u-x_d}{2}\left(\frac{1}{K_u^2}+\frac{1}{K_d^2}\right)Q^2+(x_u-x_d)\frac{\partial \frac{Q}{A}}{\partial t}=0$$

(5)

When the local acceleration from Equation (5) is disregarded, the solution can be reduced to a single unknown quadratic equation as shown in Equation (6):

$$\left(h_u-h_d\right)+\frac{Q^2}{2g}\left(\frac{{\beta }_u}{A_u^2}-\frac{{\beta }_d}{A_d^2}\right)+\frac{(x_u-x_d)}{2}\left(\frac{1}{K_u^2}+\frac{1}{K_d^2}\right)Q^2=0$$

(6)

Figure 2 shows the solution algorithm. The solutions are used to numerically solve these equations for various changes in the water level, and calibrate the Chezy’s C [42]. The extracted $Q_{bf}$ using the above procedure is further evaluated on a morphodynamic river with an enormous floodplain. In this consequence, a morphological model was constructed using MIKE 21C.

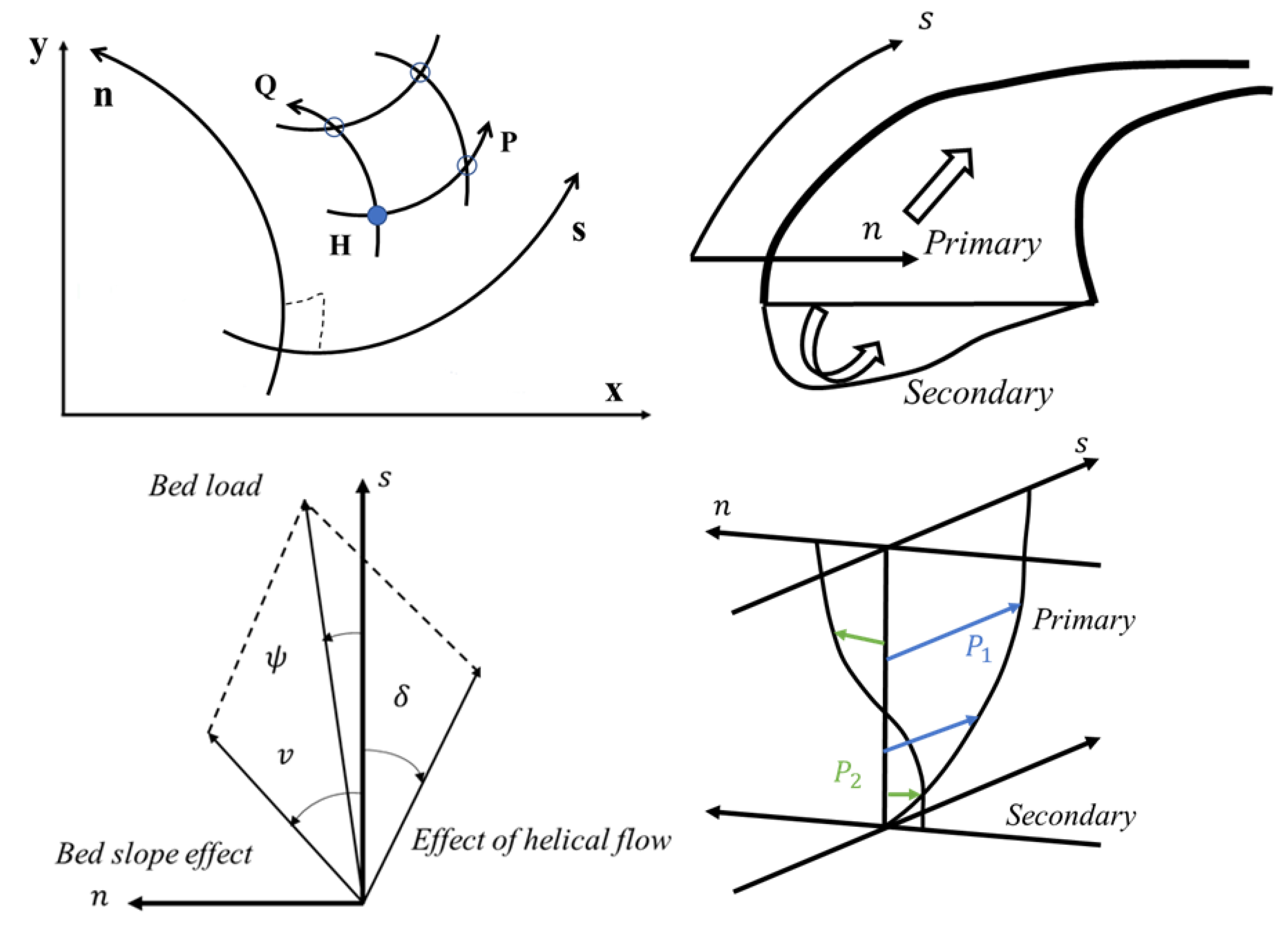
3.3. MIKE 21C Curvilinear Model

MIKE 21C predicts two-dimensional river bed and channel platform development using curvilinear finite difference grids ($CFDG$). $CFDG$ is adept in simulating construction, dredging, seasonal flow changes, and other events that cause bank erosion, scouring, and shoaling [44].

3.3.1. Curvilinear Grid Generator

The Curvilinear Grid Generator ($CGG$) consists of discretization, the solution, initial conditions, smoothing techniques, and residual evaluation. The $CGG$ of MIKE 21C consisted of two primary $PDE$s [44,45]:

$$\frac{\partial }{\partial \zeta }\left(w\frac{\partial x}{\partial \zeta }\right)+\frac{\partial }{\partial \eta }\left(w\frac{\partial x}{\partial \eta }\right)=0$$

(7)

$$\frac{\partial }{\partial \zeta }\left(w\frac{\partial y}{\partial \zeta }\right)+\frac{\partial }{\partial \eta }\left(w\frac{\partial y}{\partial \eta }\right)=0$$

(8)

where x and y are Cartesian coordinates, and w denotes a weight factor (see Equation (9)):

$$w=\sqrt{\frac{x_{\zeta }^2+y_{\zeta }^2}{x_{\eta }^2+y_{\eta }^2}}$$

(9)

For this system, the boundary condition ($BC$) is nonlinear orthogonality, mathematically $x_{\zeta }{x}_{\eta }+x_{\zeta }{x}_{\eta }=0$. This described system generates an orthogonal grid containing streamlines ($\zeta$ lines) and potential lines ($\eta$ line) and the $BC$ is equivalent to the kinematic $BC$, in which the streamlines are parallel to a boundary [34,44]. When $w=1$, the system is said to be conformal [44,45]. For the $BC$, Equations (7) and (8) are solved using the Newton–Raphson method and Stone’s implicit elliptic solution approach [44,45]. Therefore, the discretization of the grid can be stated as Equation (10):

$$\begin{array}{c}\hfill x_p=C_N{x}_N+C_E{x}_E+C_S{x}_S+C_W{x}_W\\ \hfill y_p=C_N{y}_N+C_E{y}_E+C_S{y}_S+C_W{y}_W\end{array}$$

(10)

where N, E, S, and W indicate a four-directional grid around $x_p$ and $y_p$.

3.3.2. Two-Dimensional Hydrodynamic Model

In this model, the Navier–Stokes equations are simplified and reduced to conservation equations for mass and momentum in two horizontal dimensions. Introducing a helical flow component and presuming vertical flow velocities allows the depth-averaged model to retain secondary flow [44,45]. Two parallel horizontal axes can be coupled to create a curvilinear orthogonal coordinate system, which provides a more precise description of the flow field near the boundary during bank erosion computations [44,45]. Equations (11)–(14) define the transformation from the Cartesian ($CarCS$) to curvilinear ($CurCS$) coordinate systems (shown in Figure 3):

$$h=H\mathrm{and}\frac{\partial h}{\partial x}=\frac{\partial H}{\partial s}\mathrm{and}\frac{\partial h}{\partial y}=\frac{\partial H}{\partial n}$$

(11)

$$u=U\mathrm{and}v=V$$

(12)

$$\frac{\partial u}{\partial x}=\frac{\partial U}{\partial s}-\frac{V}{R_s}\mathrm{and}\frac{\partial u}{\partial y}=\frac{\partial U}{\partial n}-\frac{V}{R_n}$$

(13)

$$\frac{\partial v}{\partial x}=\frac{\partial V}{\partial s}+\frac{U}{R_s}\mathrm{and}\frac{\partial v}{\partial y}=\frac{\partial V}{\partial n}+\frac{U}{R_n}$$

(14)

where s and n are two horizontal axes that intersect at a right angle, h and H are the depth, $(u,v)$ and $(U,V)$ are the velocity components in the $CarCS$ and $CurCS$, respectively, and $R_s$ and $R_n$ denote the radius of the curvature of the s-lines and the n-lines, respectively. Under shallow water, hydrostatic pressure distribution, and rigid lid approximation, the hydrodynamic model resolves the vertically integrated Saint Venant equations in two directions [44,45]. This flow model is applicable to shallow, slightly undulating topography, gently curved, and vast river channels with low Froude numbers [44,45]. Thus, the governing equations can be written as Equations (15)–(17):

$$\frac{\partial H}{\partial t}+\frac{\partial p}{\partial s}+\frac{\partial q}{\partial n}-\frac{q}{R_s}+\frac{p}{R_n}$$

(15)

$$\frac{\partial p}{\partial t}+\frac{\partial }{\partial s}\left(\frac{p^2}{h}\right)+\frac{\partial }{\partial n}\left(\frac{pq}{h}\right)-2\frac{pq}{h{R}_n}+\frac{p^2-q^2}{h{R}_s}+gh\frac{\partial H}{\partial s}+\frac{g}{C^2}\frac{p\sqrt{p^2+q^2}}{h^2}=RS$$

(16)

$$\frac{\partial q}{\partial t}+\frac{\partial }{\partial s}\left(\frac{pq}{h}\right)+\frac{\partial }{\partial n}\left(\frac{q^2}{h}\right)+2\frac{pq}{h{R}_s}-\frac{q^2-p^2}{h{R}_n}+gh\frac{\partial H}{\partial n}+\frac{g}{C^2}\frac{q\sqrt{p^2+q^2}}{h^2}=RS$$

(17)

where p, q are the mass fluxes in the s- and n-direction, respectively, and $RS$ is the force balance terms, such as Reynolds stress, Coriolis force, and atmospheric pressure, which can be described in a $CGG$ for the p and q-direction as the following:

$$\frac{\partial }{\partial x}\left(E\frac{\partial P}{\partial x}\right)+\frac{\partial }{\partial y}\left(E\frac{\partial P}{\partial y}\right)=\frac{\partial }{\partial s}\left(E\frac{\partial p}{\partial s}\right)+\frac{\partial }{\partial n}\left(E\frac{\partial p}{\partial n}\right)-\frac{2E}{R_s}\frac{\partial q}{\partial s}-\frac{\partial E}{\partial s}\frac{q}{R_s}-\frac{2E}{R_n}\frac{\partial q}{\partial n}-\frac{\partial E}{\partial n}\frac{q}{R_n}$$

(18)

$$\frac{\partial }{\partial x}\left(E\frac{\partial Q}{\partial x}\right)+\frac{\partial }{\partial y}\left(E\frac{\partial Q}{\partial y}\right)=\frac{\partial }{\partial s}\left(E\frac{\partial q}{\partial s}\right)+\frac{\partial }{\partial n}\left(E\frac{\partial q}{\partial n}\right)+\frac{2E}{R_s}\frac{\partial p}{\partial s}+\frac{\partial E}{\partial s}\frac{p}{R_s}+\frac{2E}{R_n}\frac{\partial p}{\partial n}+\frac{\partial E}{\partial n}\frac{p}{R_n}$$

(19)

where $(P,Q)$ are the fluxes described in $CarCS$ and $(p,q)$ are the fluxes described in $CurCS$ [44,45]. This conventional analytical solution predicts a single helical vortex that transports fluids downstream along spiral paths and generates a lateral free surface slope to maintain the equilibrium between the lateral pressure force, centripetal force, and lateral shear force generated by friction along the bed. This helical flow pattern has both a longitudinal and a perpendicular component [44,45]. The intensity of the helical flow ($i_s$) may be defined as Equation (20):

$$i_s=u\frac{h}{R_s}$$

(20)

where u and $R_s$ are the longitudinal flow and radius of the curvature of the streamlines, respectively. Due to the importance of the bed shear stress direction in a curved flow field within a bed topography model for the river bends, the logarithmic technique (see [44,45]) provides the bed shear stress direction as follows:

$$tan{\partial }_s=-\alpha \frac{2}{{\kappa }^2}\left(1-\frac{\sqrt{g}}{\kappa C}\right)\frac{h}{R_s}$$

(21)

where ${\partial }_s=$ the angle between bed shear stress and flow, $\kappa =0.4$ is Von Kárman’s constant, and $\alpha =$ the calibration constant [44,45]. In addition, the secondary flow profile adapts significantly faster as it approaches the bed, which complicates secondary flow adaptation. Therefore, the adaptation length is dependent on water depth and friction [44,45], and the model uses the differential length scale as in Equation (22):

$${\lambda }_{sf}=\frac{1.2hC}{\sqrt{g}}$$

(22)

Therefore, the direction of bed shear stress can be written as follows:

$${\lambda }_{sf}\frac{\partial \left(tan{\partial }_s\right)}{\partial S_s}+tan{\partial }_s=-\beta \frac{h}{R_s}$$

(23)

For the $(s,n)$ coordinate system, Equation (23) can be written as follows:

$$\frac{\partial s}{\partial S_s}\frac{\partial \left(tan{\partial }_s\right)}{\partial s}+\frac{\partial n}{\partial S_s}\frac{\partial \left(tan{\partial }_s\right)}{\partial n}+\frac{tan{\partial }_s+\beta \frac{h}{R_s}}{{\lambda }_{sf}}=0$$

(24)

This yields the advection-dispersion equation, which can be numerically solved in the hydrodynamic model:

$$u\frac{\partial \left(tan{\partial }_s\right)}{\partial s}+v\frac{\partial \left(tan{\partial }_s\right)}{\partial n}+\frac{\sqrt{p^2+q^2}}{h{\lambda }_{sf}}\left(tan{\partial }_s+\beta \frac{h}{R_s}\right)=0$$

(25)

where $\frac{\partial s}{\partial S_s}=\frac{p}{\sqrt{p^2+q^2}}$ and $\frac{\partial n}{\partial S_s}=\frac{q}{\sqrt{p^2+q^2}}$.

3.3.3. Sediment Transport

The sediment transport model uses a combination of empirical and physical models to simulate the sediment transport processes. The model includes algorithms for calculating bed shear stress, sediment concentration, sediment flux, and sediment transport rates. The model also includes features for modeling sedimentation and erosion, bed load and suspended load transport, and cohesive sediment transport. Typically, sediment movement is divided into three categories: bed load, suspended load, and wash load.

This model focuses on the transport of the bed material and the proportion of the suspended load that originates from the bed material. Due to the interaction between bed bathymetry and hydrodynamics, only bed material transport influences the morphological development of alluvial rivers. In simulations of sediment movement, the suspended load behaves substantially differently than the bed load, which can be modeled. The governing Equation (26) is used as the basis for the model of suspended sediment transport:

$$\frac{\partial \mathcal{C}}{\partial t}+u\frac{\partial \mathcal{C}}{\partial x}+v\frac{\partial \mathcal{C}}{\partial y}+w\frac{\partial \mathcal{C}}{\partial z}={\omega }_s\frac{\partial \mathcal{C}}{\partial z}+\frac{\partial }{\partial x}\left(ϵ\frac{\partial \mathcal{C}}{\partial x}\right)+\frac{\partial }{\partial y}\left(ϵ\frac{\partial \mathcal{C}}{\partial y}\right)+\frac{\partial }{\partial z}\left(ϵ\frac{\partial \mathcal{C}}{\partial z}\right)$$

(26)

where $\mathcal{C}=$ the suspended sediment concentration, $ϵ=$ the turbulent diffusion coefficient, and ${\omega }_s=$ the fall velocity of the suspended sediment particles. Considering only the vertical diffusion term, the equation along a streamline can be written as follows:

$$\frac{\partial \mathcal{C}}{\partial t}+u\frac{\partial \mathcal{C}}{\partial s}+v\frac{\partial \mathcal{C}}{\partial n}+w\frac{\partial \mathcal{C}}{\partial z}={\omega }_s\frac{\partial \mathcal{C}}{\partial z}+\frac{\partial }{\partial z}\left(ϵ\frac{\partial \mathcal{C}}{\partial z}\right)$$

(27)

The velocities are represented in the following way:

$$\begin{array}{c}\hfill u\left(z\right)=U_h{p}_1\left(\eta \right)\\ \hfill v\left(z\right)=\frac{U_{h}H}{R_s}{p}_2\left(\eta \right)\end{array}$$

(28)

where $U_h=$ the depth-averaged flow velocity, $\eta =$ the vertical coordinate $\frac{z}{H}$, $p_1=$ longitudinal, and $p_2=$ the transverse velocity profile. The effect of a sloping river bed must be considered; as a result, modeling the helical flow must be distinct from modeling the bed load [44,45]:

$${\theta }_c={\theta }_{C0}\left(1+\frac{\partial z_b}{\partial s}\right)$$

(29)

where ${\theta }_c=$ the modified critical shields parameter and ${\theta }_{C0}=$ the critical shields parameter [44,45]. If a model does not assume zero bed load transfer at critical shear stress, the following bed load modification can be applied:

$$S_s=S_{bl}\left(1-\alpha \frac{\partial z^{\ast }}{\partial s}\right)$$

(30)

where $S_{bl}=$ the bed load as calculated from the sediment transport formula and $\alpha =$ the model calibration parameter that has to be specified. River engineers recommended Equation (31) as a possible solution of transverse depth distributions:

$$S_n=\left(tan{\delta }_s-G{\theta }^{-\alpha }\frac{\partial z^{\ast }}{\partial n}\right)S_{bl}$$

(31)

where $G=$ the transverse bed slope factor (calibration coefficient) and $tan{\delta }_s=$ the bed shear direction change due to helical flow strength. In a fixed ($x,y$) coordinate system, the bed slopes are calculated as in Equation (32):

$$\frac{\partial z^{\ast }}{\partial s}=\frac{\partial z}{\partial x}cos\varphi +\frac{\partial z}{\partial y}sin\varphi$$

(32)

Hence, the bed slope in the transverse direction will be as follows:

$$\frac{\partial z^{\ast }}{\partial n}=\frac{\partial z}{\partial y}cos\varphi -\frac{\partial z}{\partial x}sin\varphi$$

(33)

where $\varphi =$ the angle of the streamline compared to the fixed ($x,y$) coordinate system. The transformation from the streamline coordinates to fixed coordinates can be written as in Equation (34):

$$\begin{array}{c}\hfill S_x=S_{s}cos\varphi +S_{n}sin\varphi \\ \hfill S_y=S_{n}cos\varphi -S_{s}sin\varphi \end{array}$$

(34)

The model uses a finite volume method to solve the transport equation and also includes a variety of sediment transport models, including the Meyer-Peter and Müller bed load transport formula, the Engelund and Hansen suspended sediment transport formula, and the Van Rijn transport formula. These models can be calibrated to match the characteristics of the sediment being transported and the flow conditions in the river or coastal environment (see details in [33,45]).

3.3.4. Morphology

The morphology model is based on the concept of morphological equilibrium. The morphological model combines the hydrodynamic and sediment transport models. As the bathymetry of the bed varies, the flow field is continuously adjusted. Additional sub-models, including bank erosion, bank line updates, alluvial bed resistance, bed morphologies, and graded sediment, may be incorporated. Equation (35) is used to compute the change in the bed level after computing the sediment transport of the bed material (i.e., bed load and suspended load):

$$(1-n)\frac{\partial z}{\partial t}+\frac{\partial S_x}{\partial x}+\frac{\partial S_y}{\partial y}=\Delta S_e$$

(35)

where $S_e=$ the lateral sediment supply from bank erosion, $n=$ bed porosity, and $S_x$ and $S_y$ is the total sediment transport in the x and y direction. A space-centered-time-forwarded method was used and the time step is constrained by the Courant criteria [34]. The sediment transport model can include bank erosion in continuity as in Equation (36):

$$E_b=-\alpha \frac{\partial z}{\partial t}+\beta \frac{S}{h}+\gamma$$

(36)

where $E_b=$ the bank erosion rate, $S=$ near bank sediment transport, $h=$ local water depth, $z=$ local bed level, and $\alpha ,\beta ,\gamma$ are the calibration coefficients specified in the model.

This morphology model also includes a range of sub-models, such as bed load transport, suspended sediment transport, and erosion and deposition due to currents and waves. The sub-models can be calibrated based on the characteristics of the sediment being transported and the flow conditions. Using the included visualization and analysis tools, the results of this model can be used to investigate the evolution of the bed and bank geometry of a river.

3.4. MIKE 21C Curvilinear Model Setup

This study’s river reach is located between E610,000 m and E700,000 m and N680,000 m and N735,000 m ($BTM$ coordinates) within the Greater Sylhet and Mymenshing districts (see details in Figure 4a). The Kalni-Kushiyara River system includes a variety of branches, tributaries, and floodplains. The 2D model also considers these features as transverse boundaries. In contrast, the discharge and water level hydrographs vary considerably at these boundary locations due to the significant floodplain flow. The model domain is, therefore, subdivided into the six reaches depicted in Figure 4b. In addition, the trend and amplitude of the hydrographs within each reach display less variation. Therefore, the model is broken into six subdivided reaches. Reach 0 spans approximately 63 km along the Kushiyara River, from Fenchuganj to Raniganj Bazar. From Raniganj Bazar to Markuli, Reach 1 spans approximately 23 km of the Kushiyara River. From Markuli to Kakailseo, Reach 2 spans approximately 34 km of the Kalni River. Reach 3 encompasses roughly 12 km of the Kalni River (from Kakailseo to the offtake of the Baulai Link channel). Reach 4 encompasses roughly 18 km of the Kalni River (from the Baulai Link channel’s outflow to Issapur). From Issapur to Astagram, Reach 5 consists of approximately 27 km of the Dhaleswari River and 17 km of the Baida River. In this study, we only intend to present the results of the Reach 4 morphological model to validate our method for separating $Q_{bf}$ and $Q_{fp}$ from the observed flow.

A computational grid was adopted to import the bathymetry into the model to compute the various hydraulic variables, such as velocity, water surface profile, water depth, bed level, erosion/deposition, etc. The model variables are computed at each grid point. Each grid resolution is displayed in the six consecutive reaches. Figure 4b depicts the model’s curvilinear computational grid, which is subdivided into six reaches with their respective grid resolutions. In May 2012, the bank lines along the area of interest that are used for grid generation from Raniganj to Astagram were surveyed. For the reach of Fenchuganj up to Raniganj, the pre-monsoon 2013 bank lines were implemented. The grid’s boundary lines are determined by three main criteria: the grid should be aligned with the natural streamlines; the grid line should follow the bank lines; and the grid should be orthogonal (see details in [44]).

The model bathymetry includes cross-sectional dimensions, such as the bed level of a river or low-lying area, which represent the field condition. In the present instance, the model bathymetry was derived from survey data collected between May 2012 and June 2012. The bathymetric survey of the Kalni-Kushiyara River was conducted at 100 m intervals from u/s of Raniganj Bazar to Astagram, and the bathymetry from Raniganj Bazar to Fenchuganj was derived from pre-monsoon 2013 survey data. The bathymetry was also produced for an 8 km stretch of the Baulai Link channel based on survey data from 2011. Figure 4a,b depicts the model domain (extent) and bathymetry used in this current study. The upstream discharge and downstream water level boundary was collected from the 1D North-East regional model of $IWM$ (https://www.iwmbd.org/, accessed on 3 November 2021). The simulation period has been considered from 1 January 2011 to 31 December 2011.

Prior to the application of the model with the average and design flood events, it is necessary to check the performance of the model so that the improved model shows satisfactory agreement between the model output and observation through calibration to improve the parameterization of the model. In this case, a few trials have been made to tune the model parameters for the calibration year of 2011. The calibration was performed in several locations throughout the model domain in respect of recent $IWM$ (https://www.iwmbd.org/, accessed on 3 November 2021) collected water level and discharge, sediment concentration, and velocity data.

4. Input Data

In order to investigate the applicability of the proposed tool for the separation of $Q_{bf}$ and $Q_{fp}$ from the observed discharge, we have picked a short reach (see Figure 1) that will allow us to test it. We have chosen one u/s cross-section (Figure 5a) and one d/s cross-section (Figure 5b) within that reach. The corresponding cross-sectional water level hydrograph can be seen in Figure 6.

5. Results and Discussion

Figure 7 demonstrates the separation of $Q_{bf}$ and the corresponding $Q_{fp}$ from the observed discharge. The simulation of $Q_{bf}$ using our proposed method was also compared to the bank-to-bank discharge from the MIKE 21C. In addition, through sediment calibration using this proposed method in the morphological model of the aforementioned study area, a consistent model output was observed. It is important to note that the parameterization of this morphological model depicts reliability and is able to simulate morphological prediction for average and designed flood events (see details in Figure 8). In addition, calibrated morphological parameters were used in conjunction with MIKE 21C to reproduce $Q_{bf}$ (see details in Figure 7).

In addition to a visual comparison between the reproduced $Q_{bf}$ from MIKE 21C and $Q_{bf}$ simulated using our proposed method, a statistical comparison is presented in

Table 1. Statistical comparison between MIKE 21C $Q_{bf}$ and simulated $Q_{bf}$.

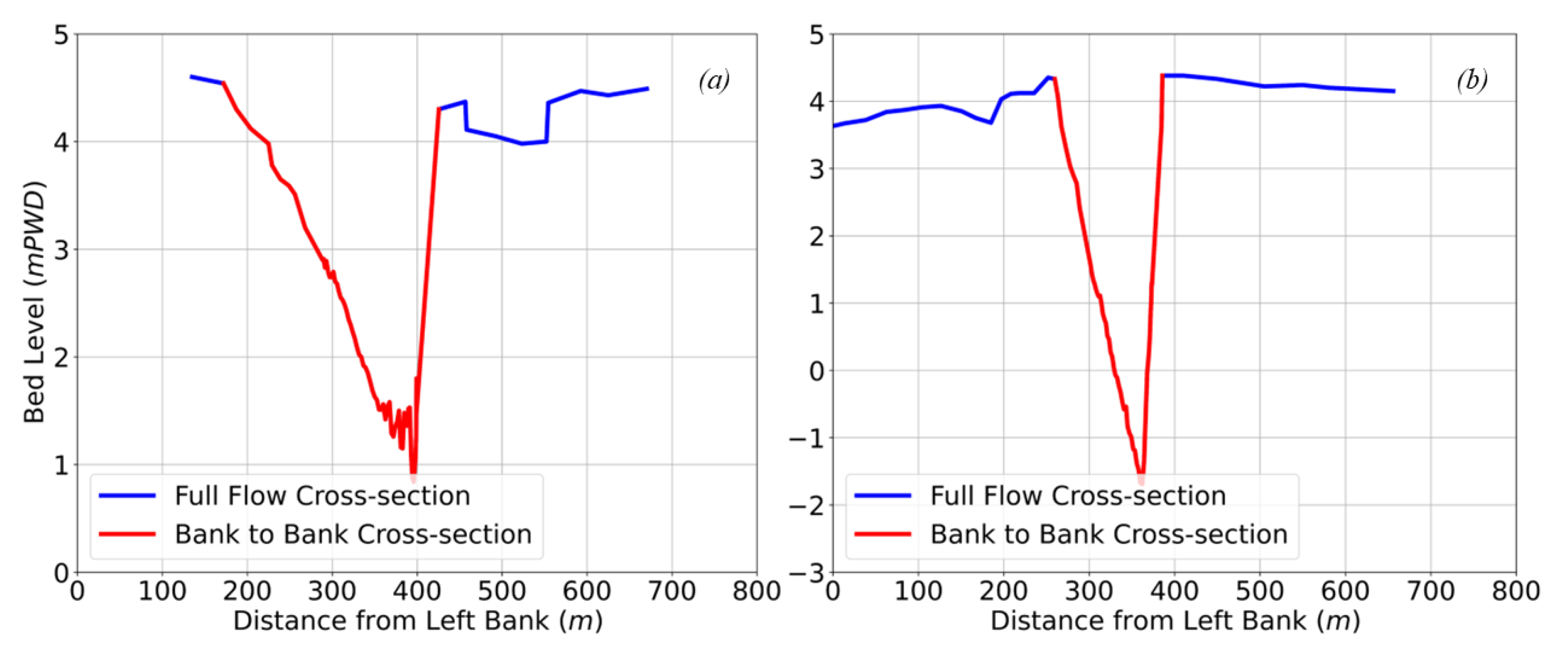
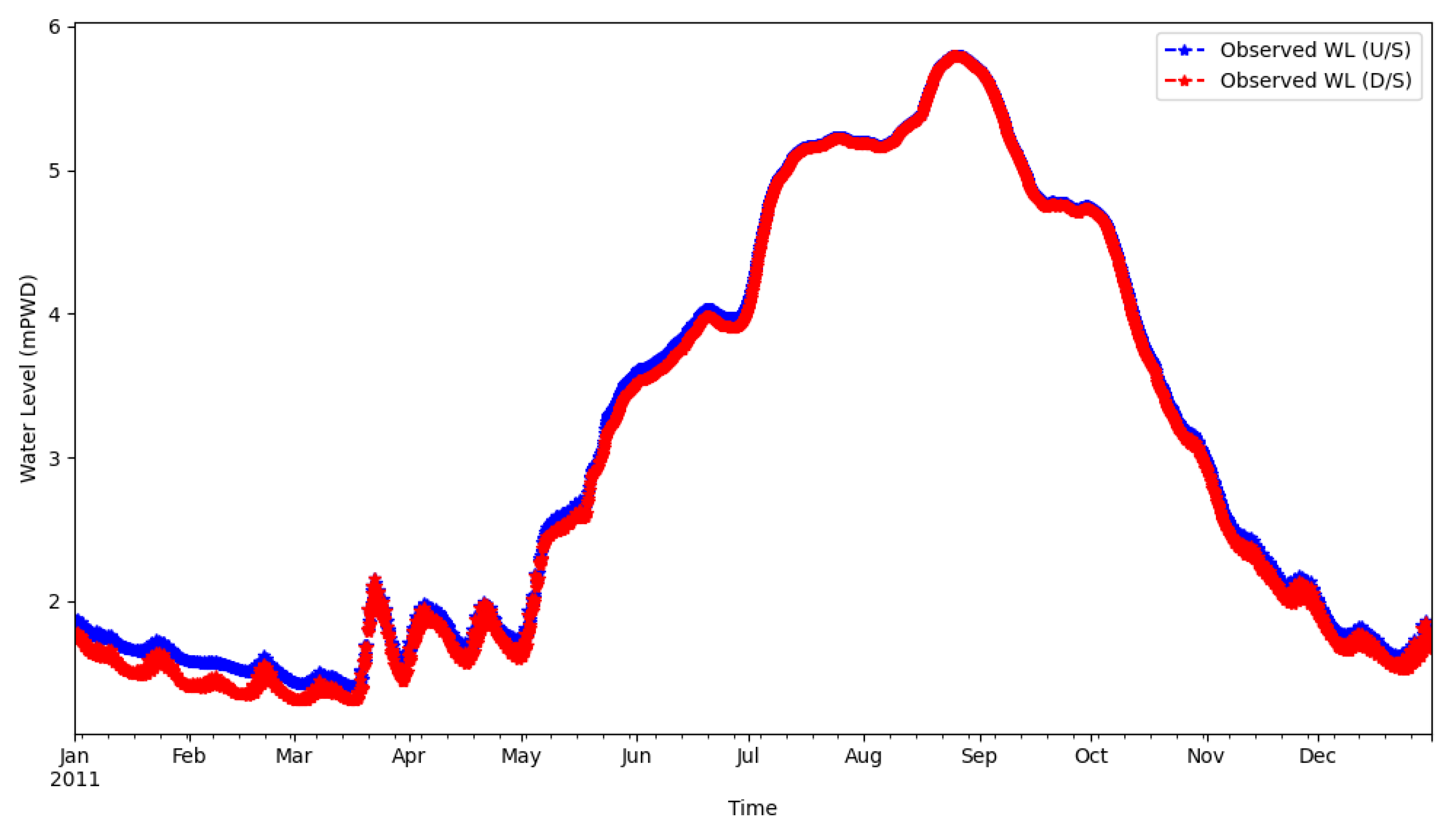
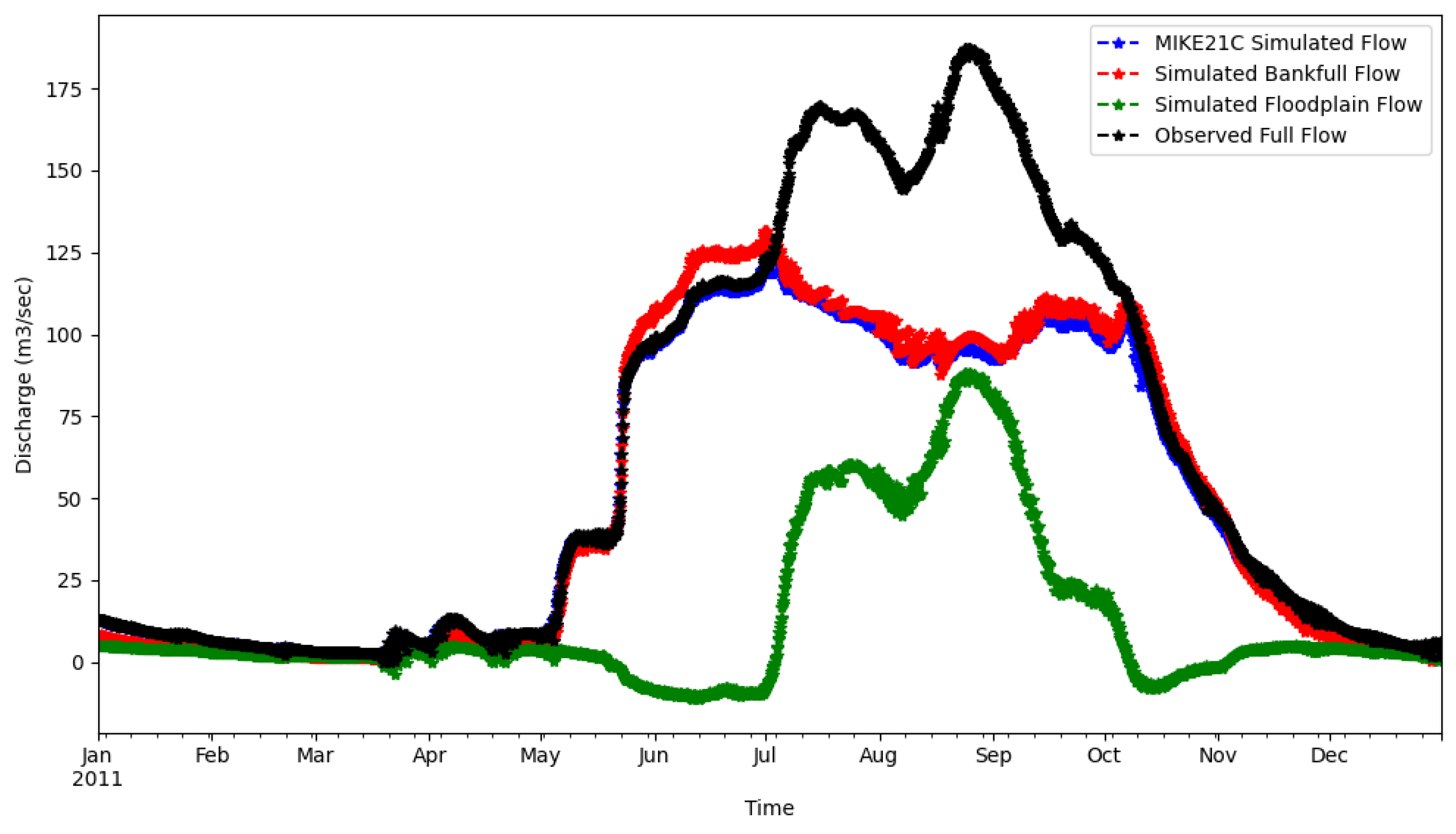
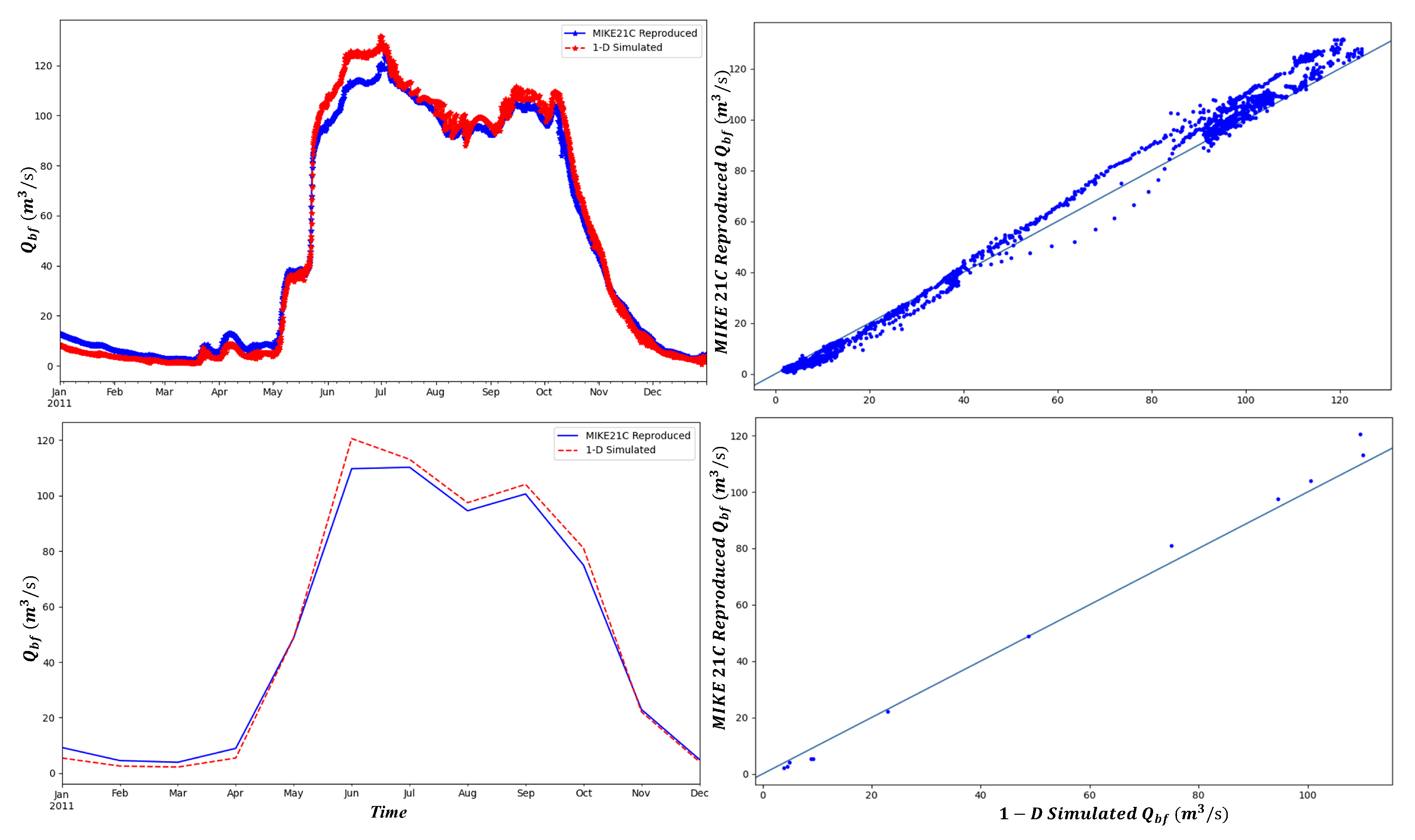
Statistic	MIKE 21C (Daily)	Simulated (Daily)	MIKE 21C (Monthly)	Simulated (Monthly)
Count	2913	2916	12	12
Mean	49.79	50.88	49.44	50.56
Std	44.82	48.54	45.38	49.07
Min	1.56	0.52	3.91	2.17
25%	7.06	4.48	7.93	5.10
50%	32.37	30.88	35.87	35.42
75%	97.92	103.36	96.05	99.09
Max	124.67	131.67	110.21	120.55
Statistic Comparison	Daily Comparison		Monthly Comparison
Mean error or bias	1.14		1.12
Percent bias	2.29		2.27
Absolute percent bias	7.39		6.55
Root-mean-square error (RMSE)	4.77		4.26
Centered RMSD (CRMSD)	4.64		4.12
Pearson correlation coefficient (r)	0.99		0.99
Coefficient of determination ($r^2$)	0.99		0.99
Skill score (Murphy)	0.98		0.99
Nash–Sutcliffe efficiency	0.98		0.99
Kling–Gupta efficiency (2009)	0.91		0.91
Kling–Gupta efficiency (2012)	0.93		0.93
Index of agreement	0.99		0.99
Brier’s score	3772.54		15.10
Mean absolute error	3.68		3.23
Common count	2913		12
Count of NaNs	3		0
Mean	49.79		49.43
Standard deviation	44.826		45.38

. It is important to point out that a significant linear relationship (slope $=1.08$) was observed from their comparison, with an $R^2$ value of $0.99$; in addition, t test results [3] show a significant correlation, with a $95\%$ confidence interval (see details in Figure 9). In addition to this, an almost perfect $NSE$ value was observed from the calibration. Hence, one can separate $Q_{bf}$ and $Q_{fp}$ from the observed discharge depicted in Figure 7. Therefore, our proposed technique can be used where $Q_{bf}$ and $Q_{fp}$ separation is necessary due to hydrologic or morphological purposes.

6. Conclusions and Recommendation

By measuring $Q_{bf}$ and $Q_{fp}$, one can gain a profound understanding of the morphological processes of a river bank caused by hydrological extreme flow from the catchment. Consequently, this program has considerable potential in the context of river morphology under extreme watershed hydrology due to climate change [46]. With the inclusion of local acceleration and a new numerical scheme, it is possible to precisely simulate the separation of $Q_{bf}$ and $Q_{fp}$ from the observed discharges. Furthermore, this proposed extraction method could aid the comprehension of the morphodynamic properties of a complex river, such as the Brahmaputra in the context of the protection and exploitation of riparian areas [41] and the nature of the inundation on them, which could be the subject of further research.