Feasibility Study on the Effect of FRP Shear Reinforcements on the Behaviour of FRP-Reinforced Concrete Deep Beams
Abstract
1. Introduction
2. Literature Review
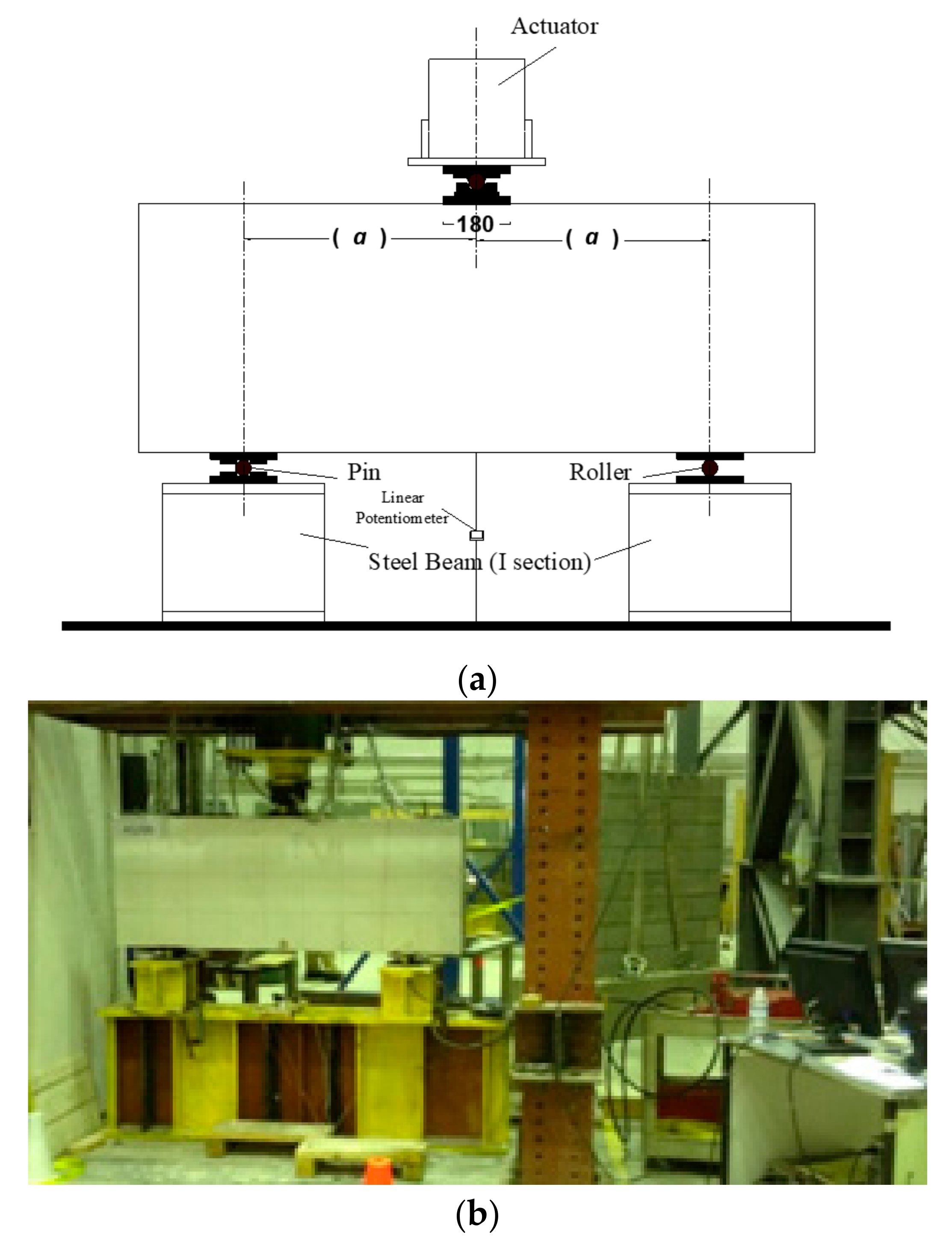
3. Experimental Program
3.1. Material Properties
3.2. Testing Procedure
4. Results and Discussion
4.1. Finite Element Modelling
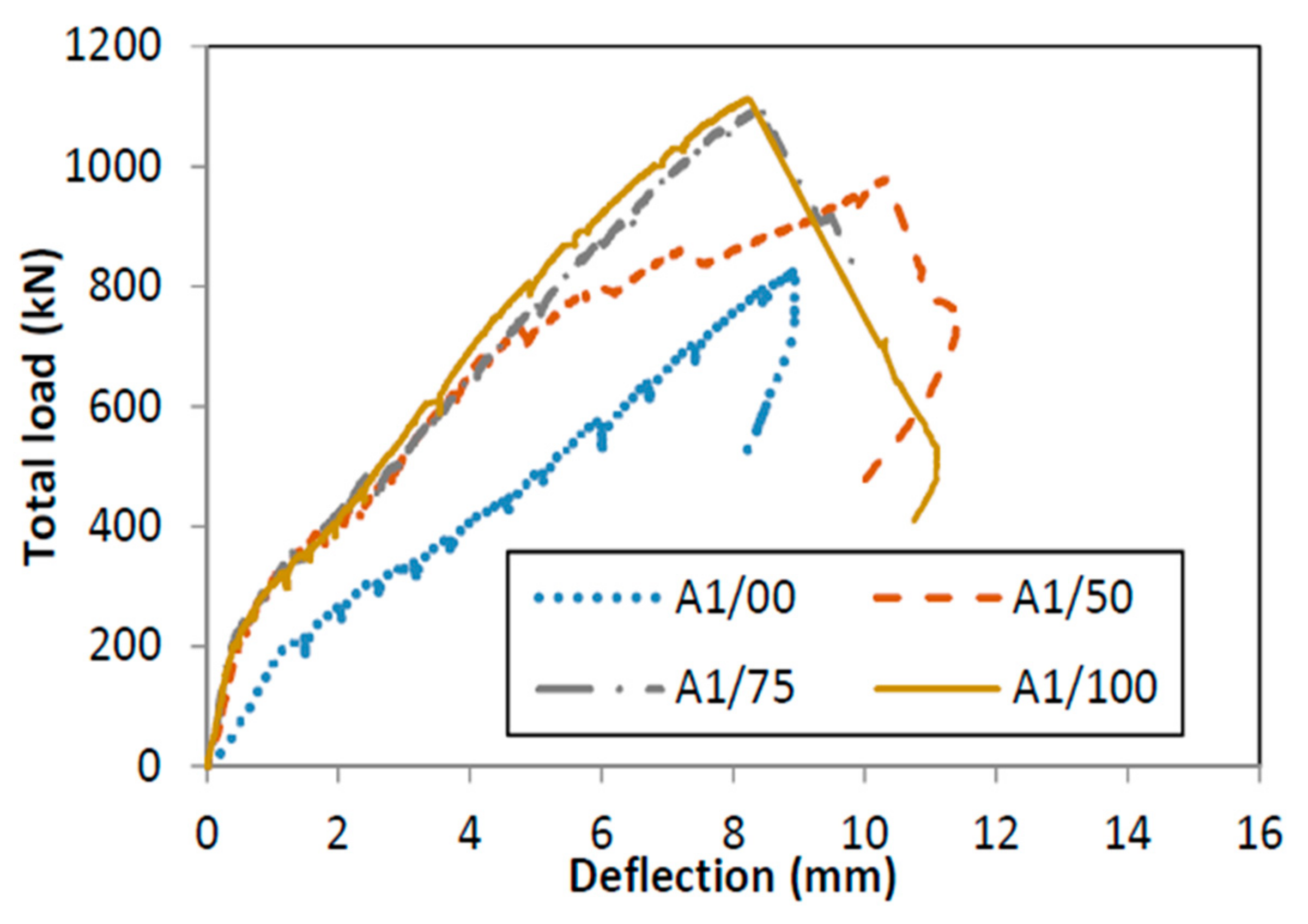
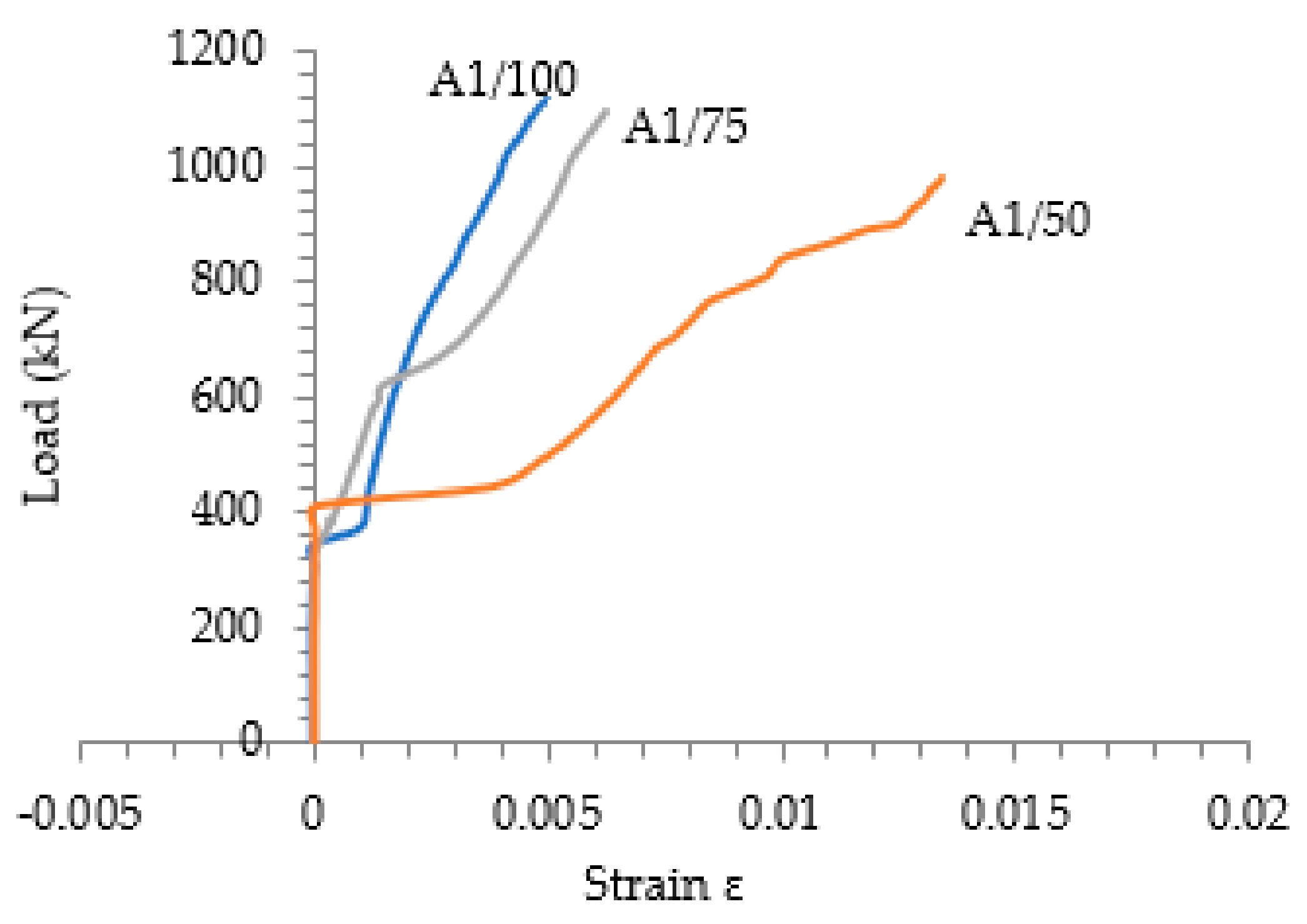
4.2. Experimental Results
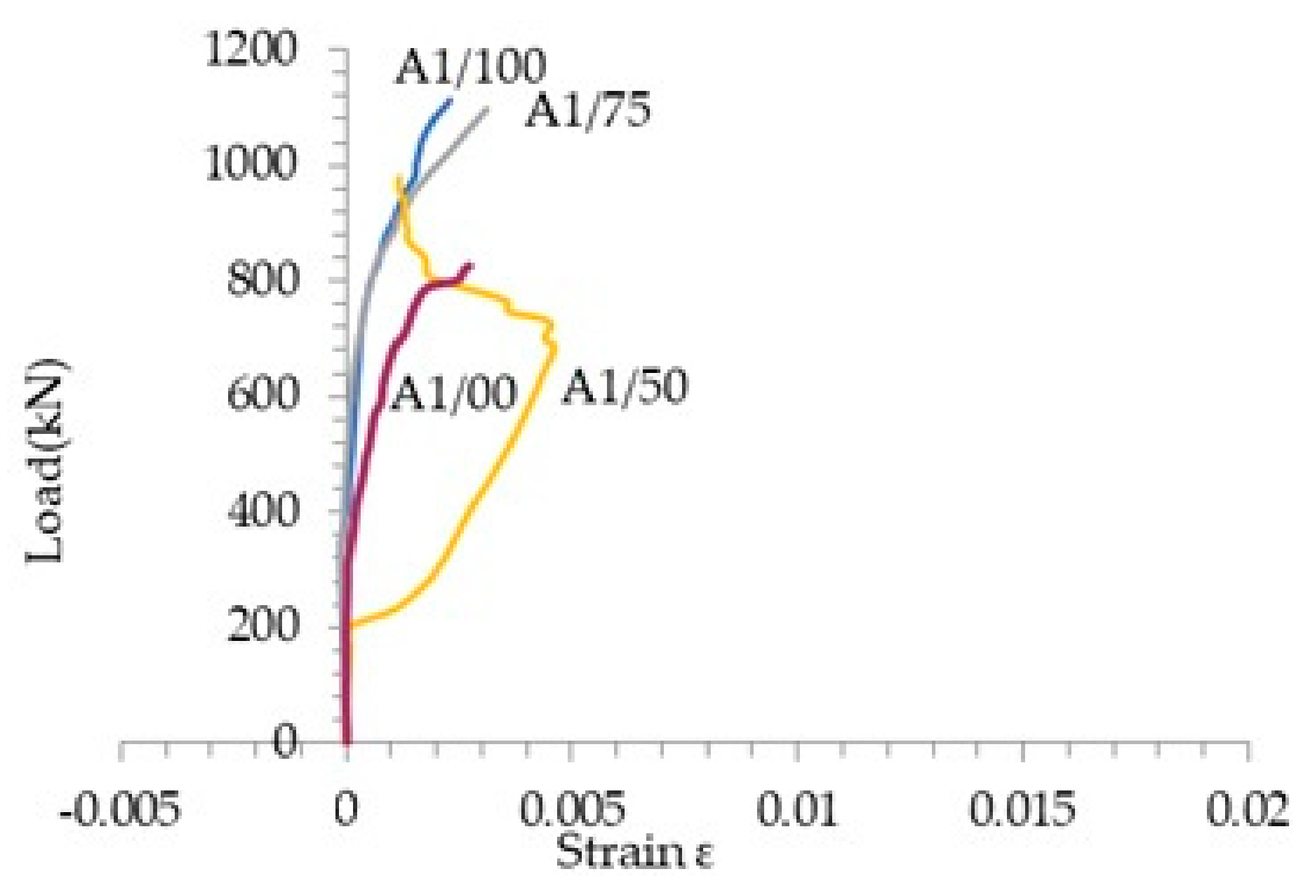
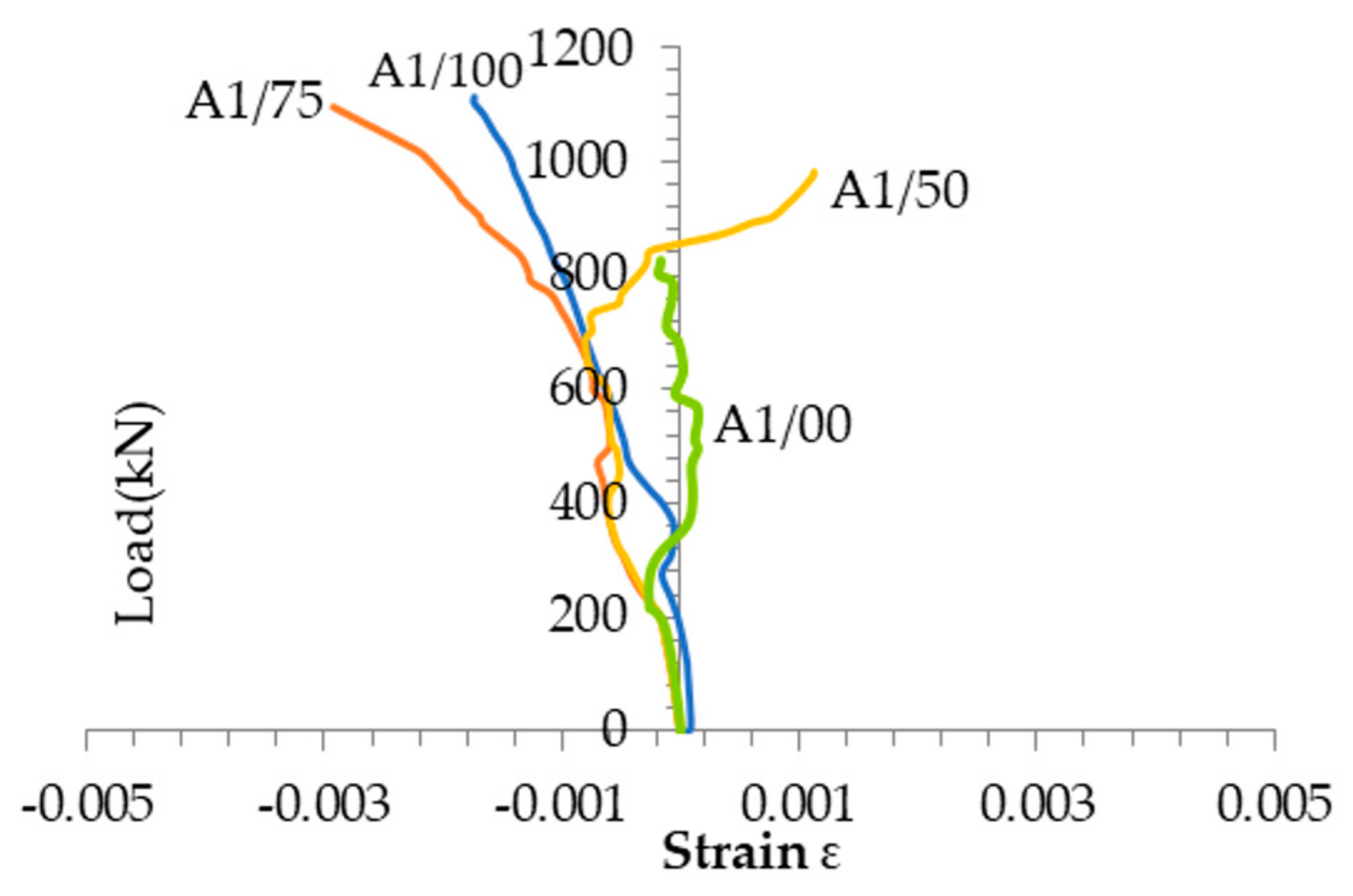
4.3. Load-Strain in FRP Response
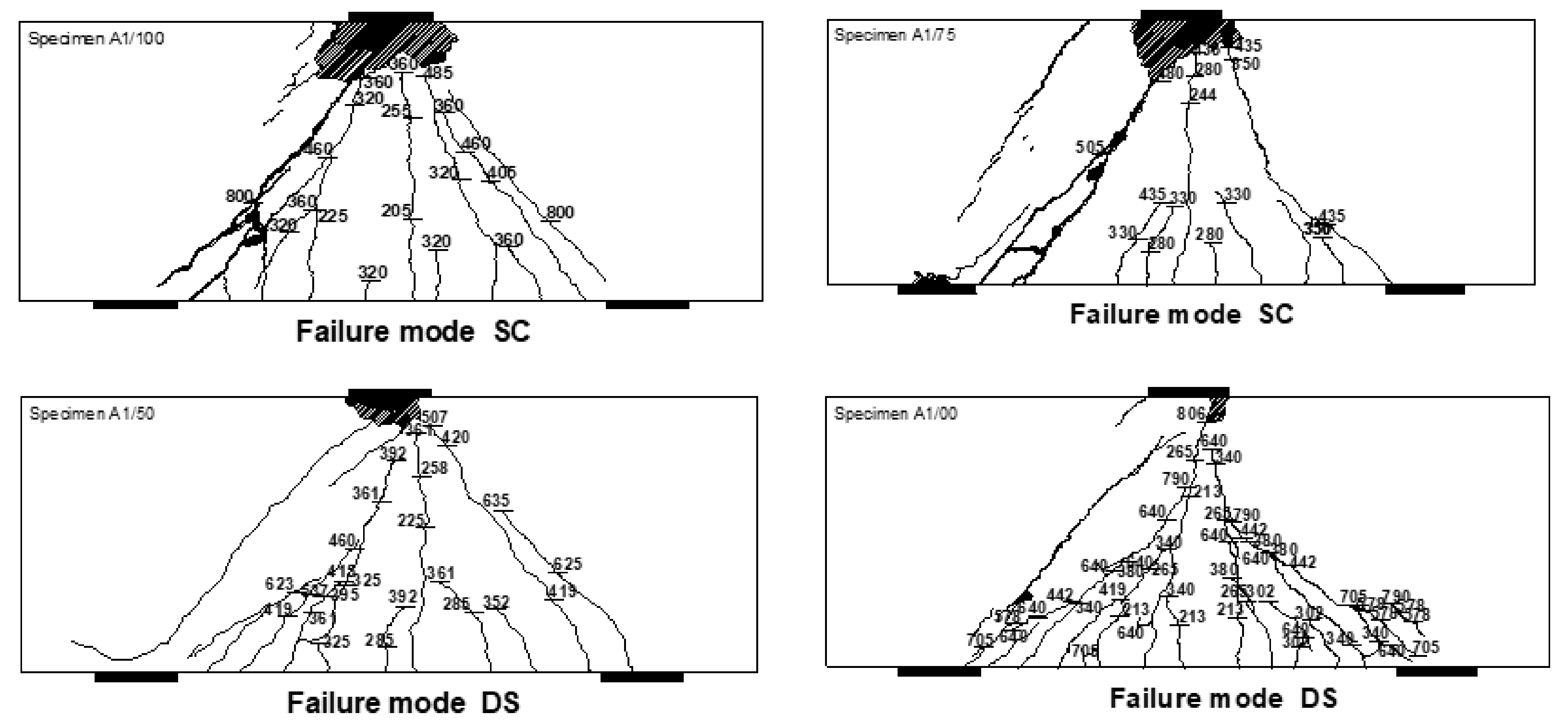
4.4. Crack Developments
4.5. Failure Modes
5. Conclusions
- The experimental results indicated that the FRP web reinforcement had a noticeable yet minor influence on the beam stiffness. Specifically, the deflection of the beams with web reinforcement exhibited a gradual increase.
- In comparison to the experimental investigations, the Finite Element model produces comparable, but slightly conservative, estimates of the ultimate shear strength.
- The strain in the FRP web reinforcements were found to be lower than the percentage of the manufacturer-specified ultimate tensile strength Fu as recommended in Clause 8.5.3.1 of the CAN/CSA-S806-12 code and was adequate in accordance with the results.
- The increase in the tensile strains in the region of the assumed direction of the main struts and in the main longitudinal FRP rebars located in two different layers exhibited mostly the same stress.
- Web reinforcement has a significant effect on crack control, propagation, and distribution. The deep beams without or with less web reinforcement exhibited more damaging failure modes (e.g., diagonal splitting) compared to those with adequate web reinforcements.
- The presence of web reinforcement resulted in an increase in the ultimate shear strength of the tested beams.
- The failure modes were found to be affected by the amount of web reinforcements. An increased amount of web reinforcements helps prevent diagonal splitting failures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nawy, E.G. Reinforced Concrete: A Fundamental Approach, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2005; 824p. [Google Scholar]
- CAN/CSA S806-02; Design and Construction of Building Components with Fiber-Reinforced Polymers. Canadian Standards Association: Mississauga, ON, Canada, 2002; 218p.
- ACI Committee 440. Guide for the Design and Construction of Concrete Reinforced with FRP Bars; American Concrete Institute: Farmington Hills, MI, USA, 2015; 206p. [Google Scholar]
- ISIS Canada Research Network. Design Manual No. 3: Reinforcing Concrete Structures with Fibre-Reinforced Polymers; University of Manitoba: Winnipeg, MB, Canada, 2007; Volume 2, 151p. [Google Scholar]
- CAN/CSA S806-12; Design and Construction of Building Components with Fiber-Reinforced Polymers. Canadian Standards Association: Mississauga, ON, Canada, 2012; 206p.
- ACI Committee 440. Guide for the Design and Construction of Concrete Reinforced with FRP Bars; American Concrete Institute: Farmington Hills, MI, USA, 2006; 88p. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014; 524p. [Google Scholar]
- European Standard EN1992-1-1; Euro Code 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization: Luxembourg, 2004.
- CAN/CSA CAN3-A23.3-04; Design of Concrete Structures for Buildings with Explanatory Notes. Canadian Standards Association: Rexdale, ON, Canada, 2004.
- Nehdi, M.; Omeman, Z.; El-Chabib, H. Optimal efficiency factor in strut-and-tie model for FRP-reinforced concrete short beams with (1.5\a/d\2.5). Mater. Struct. 2008, 41, 1713–1727. [Google Scholar] [CrossRef]
- El-Sayed, A.K.; El-Salakawy, E.F.; Benmokrane, B. Shear strength of fibre-reinforced polymer reinforced concrete deep beams without web reinforcement. Civ. Eng. Can. J. 2012, 39, 546–555. [Google Scholar] [CrossRef]
- Andermatt, M.; Lubell, A. Behavior of concrete deep beams reinforced with internal fiber-reinforced polymer—Experimental study. ACI Struct. J. 2013, 110, 585–594. [Google Scholar]
- Farghaly, S.A.; Benmokrane, B. Shear Behavior of FRP-Reinforced Concrete Deep Beams without Web Reinforcement. J. Compos. Constr. 2013, 17, 04013015. [Google Scholar] [CrossRef]
- Kim, D.J.; Lee, J.; Lee, Y.H. Effectiveness factor of strut-and-tie model for concrete deep beams reinforced with FRP bars. Compos. Part B 2014, 56, 117–125. [Google Scholar] [CrossRef]
- Mohamed, K.; Farghaly, S.A.; Benmokrane, B. Effect of Vertical and Horizontal Web Reinforcement on the Strength and Deformation of Concrete Deep Beams Reinforced with GFRP Bars. J. Struct. Eng. 2017, 143, 04017079, Erratum in Struct. J. 2017, 41, 1713–1727. [Google Scholar] [CrossRef]
- Latosh, F. Structural Behaviour of Conventional and FRP- Reinforced Concrete Deep Beams. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2014. [Google Scholar]
- Smith, K.N.; Vantsiotis, A.S. Shear strength of deep beams. ACI Struct. J. 1983, 79, 201–213. [Google Scholar]
- Tan, K.H.; Kong, F.K.; Teng, S.; Weng, L.W. Effect of Web Reinforcement on High Strength Concrete Deep Beams. ACI Struct. J. 1997, 94, 572–581. [Google Scholar]
- Shin, S.W.; Lee, K.S.; Moon, J.; Ghosh, S.K. Shear strength of reinforced high-strength concrete beams with shear span-to-depth ratios between 1.5 and 2.5. ACI Struct. J. 1999, 96, 549–556. [Google Scholar]
- Kong, F.K.; Robins, P.J.; Cole, D.F. Web Reinforcement Effects on Deep Beams. ACI Struct. J. 1970, 67, 1010–1018. [Google Scholar]
- Rogowsky, D.M.; MacGregor, J.G.; Ong, S.Y. Tests of Reinforced Concrete Deep Beams. ACI Struct. J. 1986, 83, 614–623. [Google Scholar]
- AlHamaydeh, M.; Markou, G.; Bakas, N.; Papadrakakis, M. AI-based shear capacity of FRP-reinforced concrete deep beams without stirrups. Eng. Struct. 2022, 264, 114441. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Ashour, A. A feasibility study of BBP for predicting shear capacity of FRP reinforced concrete beams without stirrups. Adv. Eng. Softw. 2016, 97, 29–39. [Google Scholar] [CrossRef]
- Dhahir, M.K. Strut and tie modeling of deep beams shear strengthened with FRP laminates. Compos. Struct. 2018, 193, 247–259. [Google Scholar] [CrossRef]
- Jin, L.; Lei, Y.; Song, B.; Jiang, X.A.; Xiuli, D.U. Meso-scale modelling of size effect on shear behavior of basalt fiber reinforced concrete deep beams. Compos. Struct. 2022, 304, 116440. [Google Scholar] [CrossRef]
- Alam, M.S.; Sultana, N.; Hossain, S.Z. Bayesian optimization algorithm based support vector regression analysis for estimation of shear capacity of FRP reinforced concrete members. Appl. Soft Comput. 2021, 105, 107281. [Google Scholar] [CrossRef]
- Albidah, A.; Abadel, A.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Experimental and analytical study of strengthening schemes for shear deficient RC deep beams. Constr. Build. Mater. 2019, 216, 673–686. [Google Scholar] [CrossRef]
- Zinkaah, O.H.; Alridha, Z.; Alhawat, M. Numerical and theoretical analysis of FRP reinforced geopolymer concrete beams. Case Stud. Constr. Mater. 2022, 16, e01052. [Google Scholar] [CrossRef]
- Zhang, G.; Ali, Z.H.; Aldlemy, M.S.; Mussa, M.H.; Salih, S.Q.; Hameed, M.M.; Al-Khafaji, Z.S.; Yaseen, Z.M. Reinforced concrete deep beam shear strength capacity modelling using an integrative bio-inspired algorithm with an artificial intelligence model. Eng. Comput. 2020, 38, 15–28. [Google Scholar] [CrossRef]
- Algamati, M.; Al-Sakkaf, A.; Mohammed Abdelkader, E.; Bagchi, A. Studying and Analyzing the Seismic Performance of Concrete Moment-Resisting Frame Buildings. CivilEng 2023, 4, 34–54. [Google Scholar] [CrossRef]
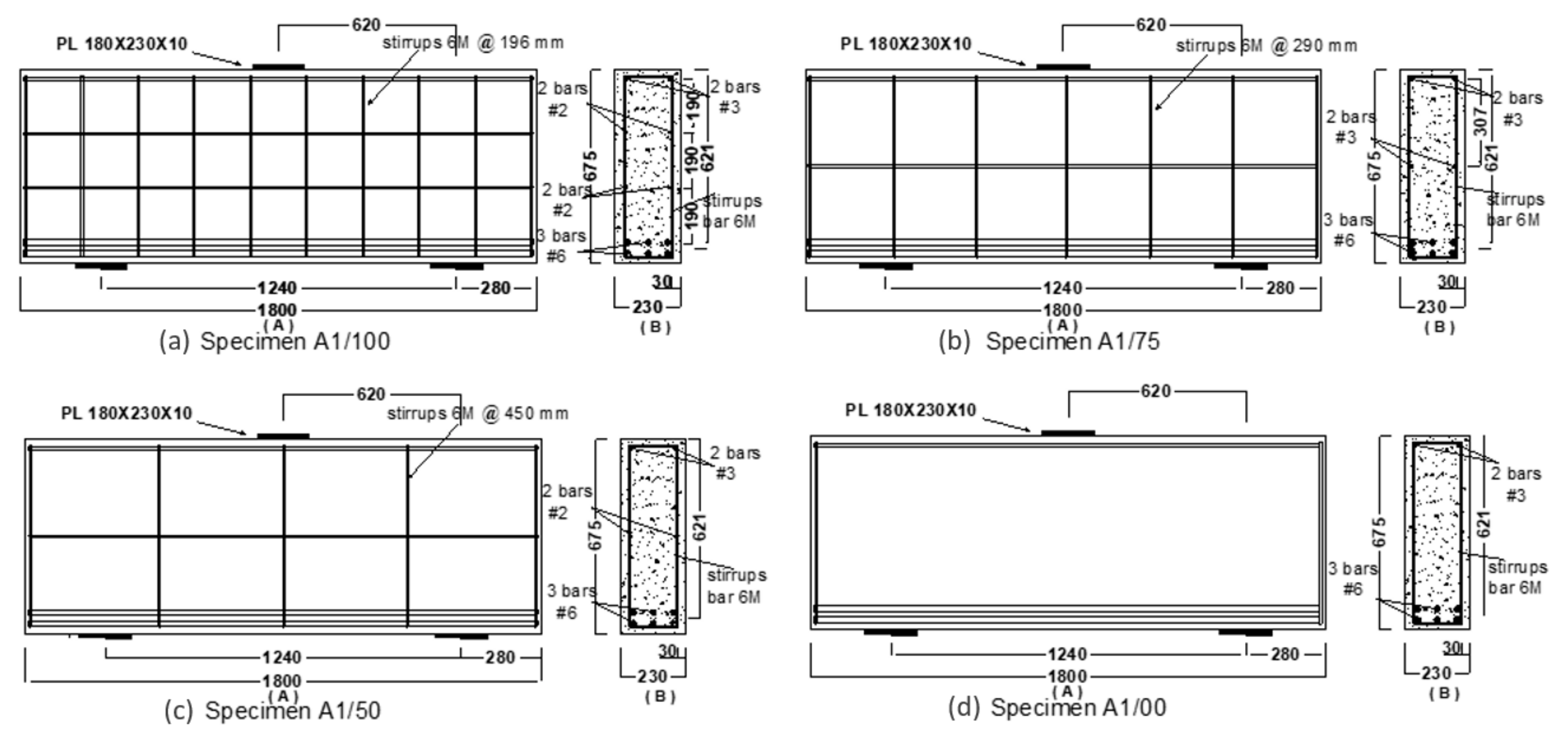



| Specimen No | fc (MPa) | b (mm) | d (mm) | Le (mm) | a/d | Main Reinforcement | ffu (MPa) | εfu | Vertical & Horizontal Reinforcement | Ρ (%) | Ρw (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1/100 | 49.8 | 230 | 621 | 1240 | 1 | 3 # 6(19 mm) 3# 6 (19 mm) | 656 | 0.0153 | 6 M@196 mm 6 M@190 mm | 1.197 | 0.131 |
| A1/75 | 52.2 | 230 | 621 | 1240 | 1 | 3 # 6(19 mm) 3# 6 (19 mm) | 656 | 0.0153 | 6 M@290 mm 10 M@300 mm | 1.197 | 0.095 |
| A1/50 | 52.5 | 230 | 621 | 1240 | 1 | 3 # 6(19 mm) 3# 6 (19 mm) | 656 | 0.0153 | 6 M@450 mm 6 M@300 mm | 1.197 | 0.061 |
| A1/00 | 52.7 | 230 | 621 | 1240 | 1 | 3 # 6(19 mm) 3# 6 (19 mm) | 656 | 0.0153 | N/A | 1.197 | N/A |
| Soft Metric Size | Diameter (mm) | Area (mm2) | Tensile Modulus of Elasticity Et (GPa) | Ultimate Tensile Strength Fu (MPa) | Ultimate Strain in Tension εFu (%) | Poisson’s Ratio μ |
|---|---|---|---|---|---|---|
| #6 | 6.35 | 31.7 | 46.1 | 874 | 1.90 | 0.25 |
| #10 | 9.52 | 71.3 | 45.4 | 856 | 1.89 | 0.21 |
| #13 | 12.70 | 126.7 | 46.3 | 708 | 1.70 | 0.26 |
| #19 | 19.05 | 285 | 47.6 | 656 | 1.53 | 0.25 |
| Specimen No. | PuEXP (kN) | Δ (mm) | VuEXP (kN) | PuFEM (kN) | PuEXP/PuFEM | Mode of Failure |
|---|---|---|---|---|---|---|
| A1/100 | 1113.80 | 8.22 | 560.25 | 1118.78 | 0.99 | Shear Compression |
| A1/75 | 1098.07 | 8.43 | 552.39 | 1120.63 | 0.98 | Shear Compression |
| A1/50 | 980.68 | 10.33 | 493.69 | 1040.49 | 0.94 | Diagonal Splitting |
| A1/00 | 827.07 | 8.91 | 416.89 | 800.56 | 1.03 | Diagonal Splitting |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latosh, F.; Al-Sakkaf, A.; Bagchi, A. Feasibility Study on the Effect of FRP Shear Reinforcements on the Behaviour of FRP-Reinforced Concrete Deep Beams. CivilEng 2023, 4, 522-537. https://doi.org/10.3390/civileng4020030
Latosh F, Al-Sakkaf A, Bagchi A. Feasibility Study on the Effect of FRP Shear Reinforcements on the Behaviour of FRP-Reinforced Concrete Deep Beams. CivilEng. 2023; 4(2):522-537. https://doi.org/10.3390/civileng4020030
Chicago/Turabian StyleLatosh, Fawzi, Abobakr Al-Sakkaf, and Ashutosh Bagchi. 2023. "Feasibility Study on the Effect of FRP Shear Reinforcements on the Behaviour of FRP-Reinforced Concrete Deep Beams" CivilEng 4, no. 2: 522-537. https://doi.org/10.3390/civileng4020030
APA StyleLatosh, F., Al-Sakkaf, A., & Bagchi, A. (2023). Feasibility Study on the Effect of FRP Shear Reinforcements on the Behaviour of FRP-Reinforced Concrete Deep Beams. CivilEng, 4(2), 522-537. https://doi.org/10.3390/civileng4020030








