Investigation of Resonant Signal Timing Plans through Comprehensive Evaluation of Various Optimization Approaches
Abstract
1. Introduction
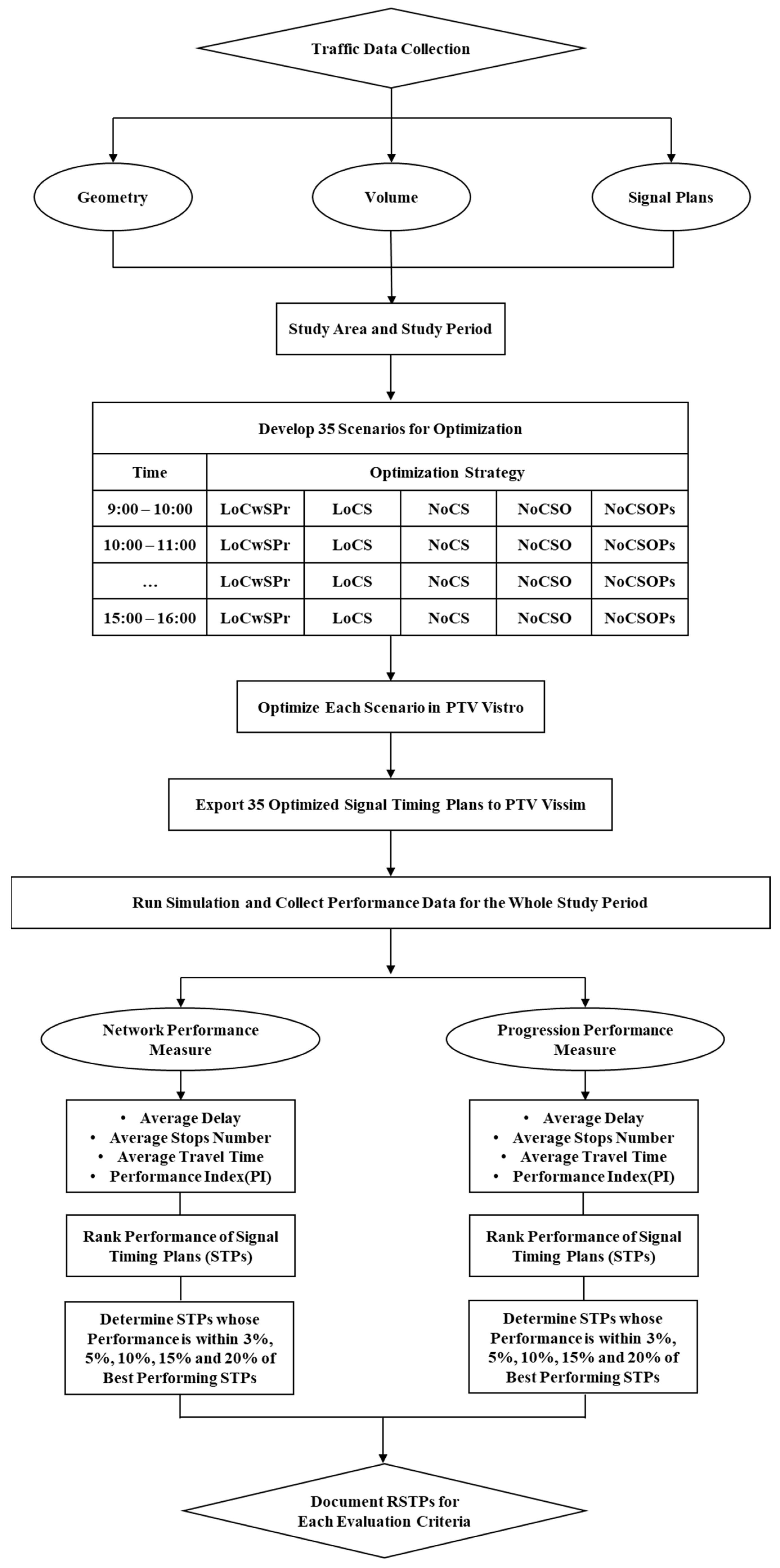
2. Research Methodology
- Combination of signal timing parameters—In our study, we optimized all basic signal timing parameters, including the cycle length, offsets, splits and phase sequences. Thus, once an optimization was performed and an optimal signal timing plan was found, which was used without alterations in the testing of all other scenarios. This approach required that experimentation was conducted for alike traffic conditions (e.g., midday balanced flows in each direction, without major shifts of directional traffic demand), but a different approach could be used for different circumstances (e.g., one could consider a RSTP with a fixed cycle length, phasing sequence and splits, while the offsets could be adjusted for the morning and afternoon peaks).
- Acceptable performance—We introduced multiple threshold levels to describe if a RSTP performed similarly to the best signal timing plan (STP) for the given conditions. It is logical that an optimal STP would be the best for conditions for which it was optimized. However, what makes a RSTP distinctive is the fact that a RSTP may be close to the best STPs for many scenarios for which it was not originally designed. In order to classify if a STP can be a candidate for a RSTP, we observed whether its performance was within a threshold (e.g., 5%) of the performance of the best STP. For example, if the best STP for the given conditions could yield a delay of X hours, another STP would be a candidate for the RSTP, for the same conditions, if its performance was within 1.05× hours of delay. Thus, this concept does not recognize only a single RTSP, but a family of RSTPs relevant for the given thresholds, all representing different levels of acceptable performance.
- Variety of traffic conditions—We observed the performance of various STPs over a midday period of several hours when directional traffic flows were balanced to stay truthful to the original idea presented by Shelby et al. [14], where the RCL was defined in such a way.
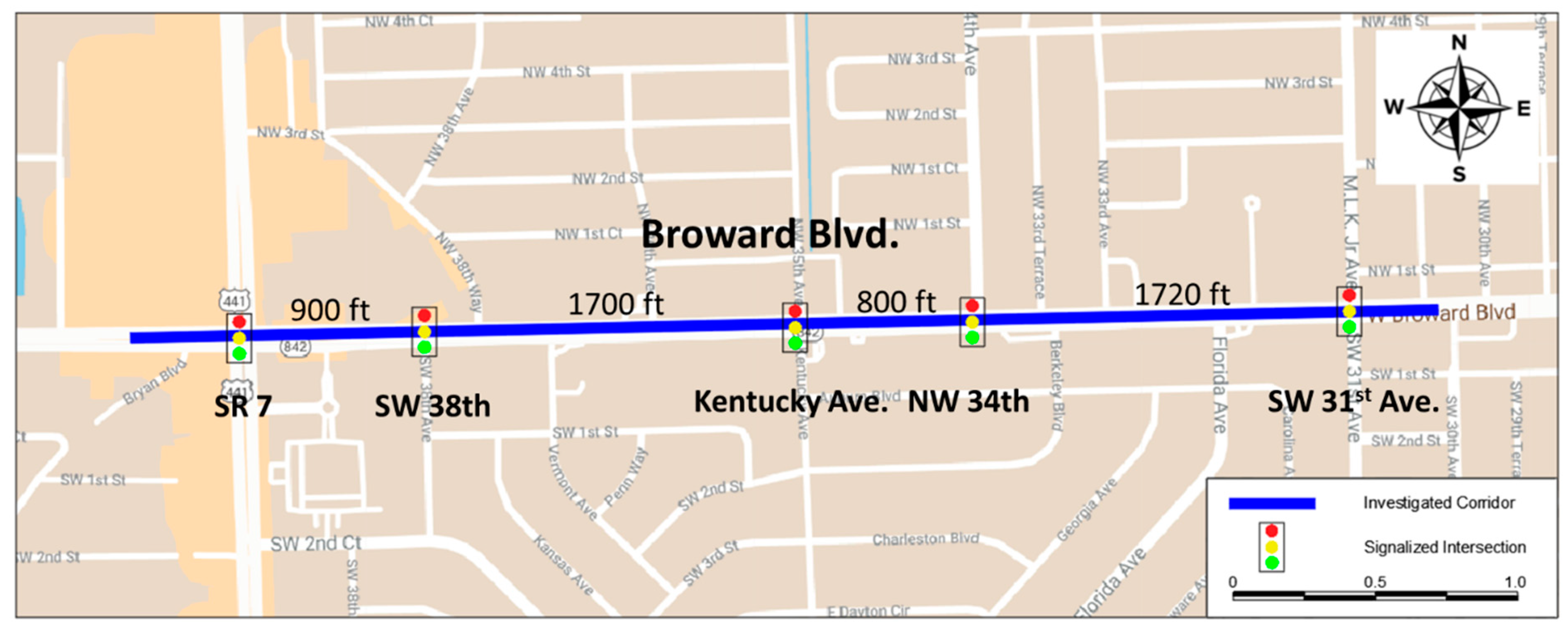
2.1. Study Network
- (a)
- Pattern 1: from 6:00 to 9:00—morning peak period;
- (b)
- Pattern 2: from 9:00 to 16:00—off-peak period;
- (c)
- Pattern 3: from 16:00 to 20:00—evening peak period.
2.2. Simulation Model Development
2.3. Experimental Design
- Local cycle length optimization with splits proportionally (LoCwSPt) distributed: After Local optimization of splits and cycle times for each intersection, the longest cycle length was selected for the entire network, and the intersections’ splits were adjusted proportionally. This optimization strategy aimed to find the optimal cycle length (between 30 and 200 s) for each intersection by using the local optimization function in PTV Vistro. The largest cycle length of those five was chosen as the cycle length of the whole network and the intersection splits were increased proportionally. The optimization objective function was to minimize the critical movement delay.
- Local cycle length and splits (LoCSs) optimization: After the local optimization of splits and cycle times for each intersection, the longest cycle length was selected for the entire network and the intersections’ splits were again optimized with Vistro.
- Network cycle length and splits (NoCSs) optimization: In this scenario, Vistro’s network optimization was used to find the optimal cycle length and splits. The performance index (PI) was used as an objective function with a stop penalty of 8, the same value as used in the study of Shelby et al. [14]. Hill climbing was chosen as a search mechanism and the number of starting solutions was set to 20.
- Network cycle length, splits and offsets (NoCSOs) optimization: This scenario was similar to NoCS, but the offset optimization was added to the options for network optimization, which meant that the cycle length, splits and offsets were all optimized on the network level.
- Network cycle length, splits, offsets and phase sequences (NoCSOPs) optimization: In this scenario, phase sequence optimization was added to the optimization options. All other settings remained the same as in NoCSO.
2.4. Evaluation Procedure
3. Results and Discussion
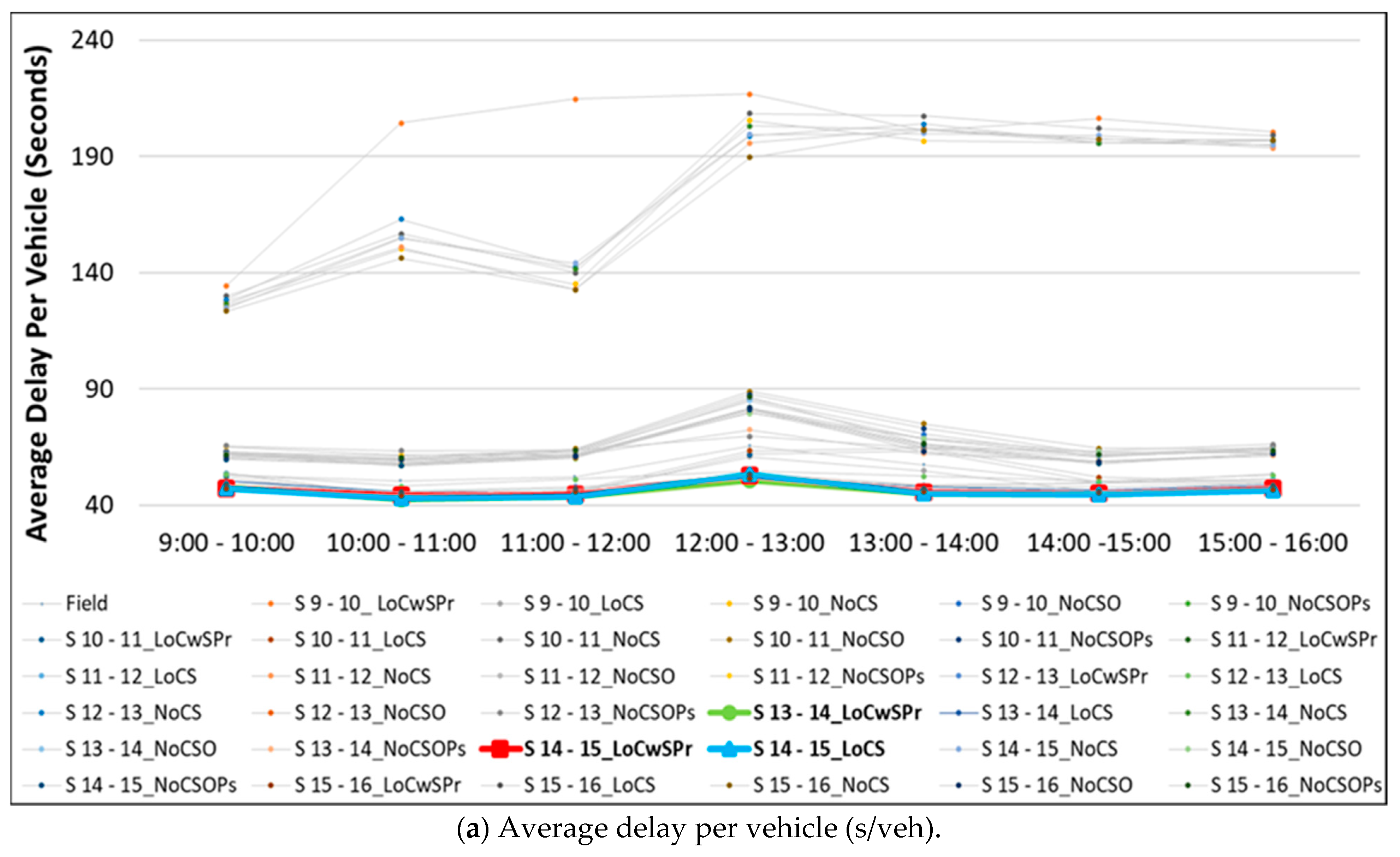
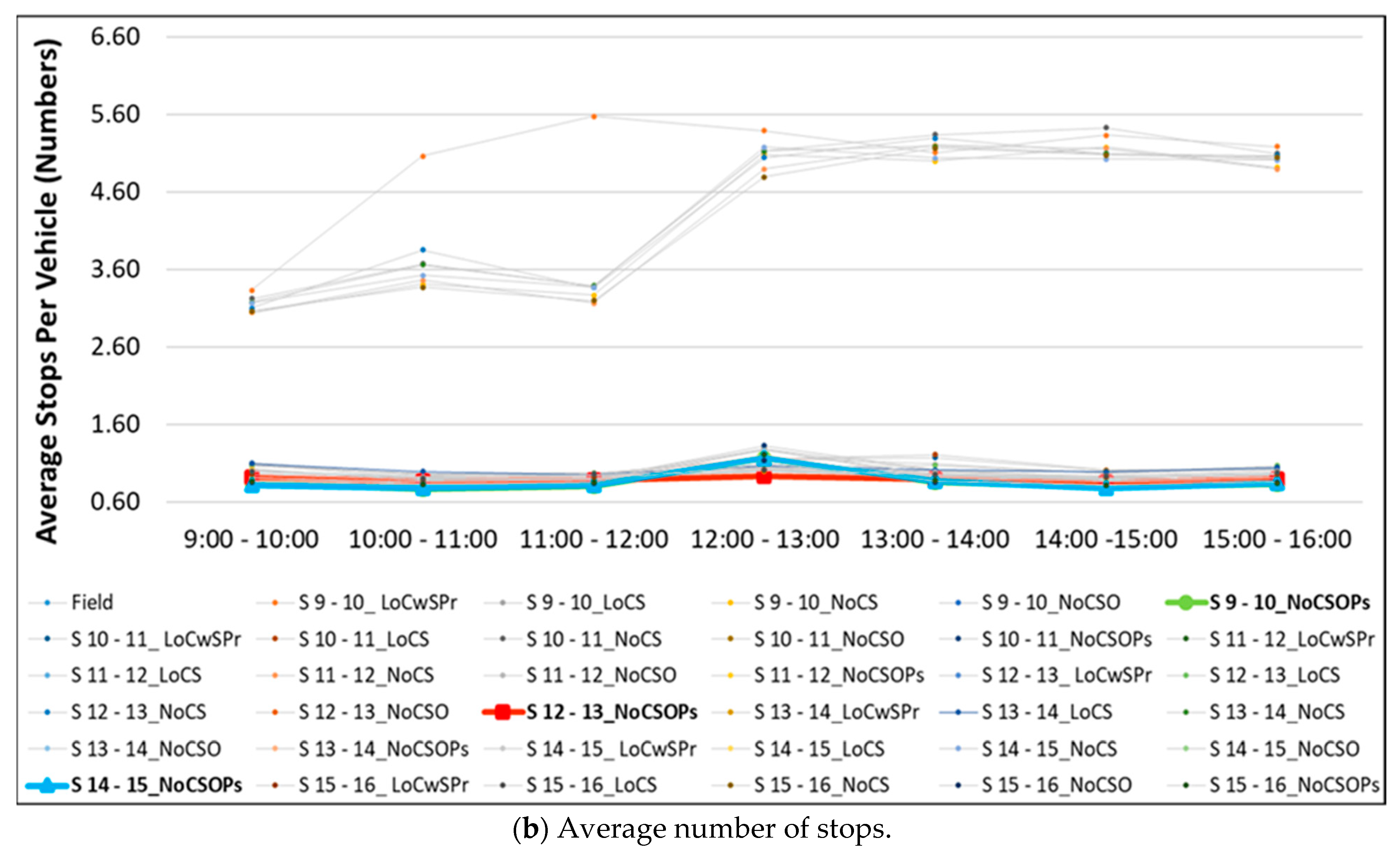
3.1. Network Evaluation
3.2. Progression Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gartner, N.; Little, J.D.; Gabbay, H. Optimization of traffic signal settings in network by mixed-integer linear programming. Transp. Sci. 1974, 9, 344–363. [Google Scholar] [CrossRef]
- Foy, M.D.; Benekohal, R.F.; Goldberg, D.E. Signal timing determination using genetic algorithms. Transp. Res. Rec. 1992, 108. [Google Scholar]
- Hu, P.; Tian, Z.Z. A new approach to variable-bandwidth progression optimization. In Proceedings of the Transportation Research Board 89th Annual Meeting, Washington, DC, USA, 10–14 January 2010. No. 10-1140. [Google Scholar]
- Stevanovic, J.; Stevanovic, A.; Martin, P.T.; Bauer, T. Stochastic optimization of traffic control and transit priority settings in VISSIM. Transp. Res. Part C Emerg. Technol. 2008, 16, 332–349. [Google Scholar] [CrossRef]
- Shayeb, S.A.; Dobrota, N.; Stevanovic, A.; Mitrovic, N. Assessment of arterial signal timings based on various operational policies and optimization tools. Transp. Res. Rec. 2021, 2675, 195–210. [Google Scholar] [CrossRef]
- Shirke, C.; Sabar, N.; Chung, E.; Bhaskar, A. Metaheuristic approach for designing robust traffic signal timings to effectively serve varying traffic demand. J. Intell. Transp. Syst. 2022, 26, 343–355. [Google Scholar] [CrossRef]
- Dobrota, N.; Mitrovic, N.; Gavric, S.; Stevanovic, A. Comprehensive Data Analysis Approach for Appropriate Scheduling of Signal Timing Plans. Future Transp. 2022, 2, 27. [Google Scholar] [CrossRef]
- Korosec, K. Ford, VW-backed Argo AI is Shutting Down. TechCrunch+. 26 October 2022. Available online: https://techcrunch.com/2022/10/26/ford-vw-backed-argo-ai-is-shutting-down/ (accessed on 19 December 2022).
- Gordon, R.L. Traffic Signal Retiming Practices in the United States; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar]
- Urbanik, T.; Tanaka, A.; Lozner, B.; Lindstrom, E.; Lee, K.; Quayle, S.; Beaird, S.; Tsoi, S.; Ryus, P.; Gettman, D.; et al. Signal Timing Manual; Transportation Research Board: Washington, DC, USA, 2015. [Google Scholar]
- Dobrota, N.; Stevanovic, A.; Mitrovic, N. Development of assessment tool and overview of adaptive traffic control deployments in the US. Transp. Res. Rec. 2020, 2674, 464–480. [Google Scholar] [CrossRef]
- ITE. Traffic Signal Benchmarking and State of the Practice Report; ITE: Washington, DC, USA, 2020; pp. 39–43. [Google Scholar]
- Henry, R.D. Signal Timing on a Shoestring; U.S. Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2005. [Google Scholar]
- Shelby, S.G.; Bullock, D.M.; Gettman, D. Resonant Cycles in Traffic Signal Control. Transp. Res. Rec. J. Transp. Res. Board 2005, 1925, 215–226. [Google Scholar] [CrossRef]
- Guevara, F.L.; Hickman, M.; Head, L. Resonant Cycles under Various Intersection Spacing, Speeds, and Traffic Signal Operational Treatments. Transp. Res. Rec. J. Transp. Res. Board 2015, 2488, 87–96. [Google Scholar] [CrossRef]
- Guevara, F.L. Resonant Cycles and Traffic Signal Performance; The University of Arizona: Tucson, AZ, USA, 2013. [Google Scholar]
- Day, C.M.; Emtenan, A.M.T. Impact of Phase Sequence on Cycle Length Resonance. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 398–408. [Google Scholar] [CrossRef]
- Li, H.; Day, C.; Hainen, A.; Stevens, A.; Lavrenze, S.; Smith, B.; Summers, H.; Freije, R.; Sturdevant, J.; Bullock, D. Field Cycle Length Sweep to Evaluate Resonant Cycle Sensitivity. JTRP Other Publications and Reports. Paper 8. 2014. Available online: https://docs.lib.purdue.edu/jtrpdocs/8/ (accessed on 19 December 2022). [CrossRef]
- PTV-Vision, PTV Vistro 2020 User Manual. 2019. Available online: https://www.ptvgroup.com/en/solutionsproducts/ptv-vistro/ (accessed on 3 April 2019).
- PTV-Vision, PTV Vissim 2020 User Manual. 2019. Available online: https://www.ptvgroup.com/en/solutionsproducts/ptv-vissim/ (accessed on 5 March 2019).
- So, J.; Ostojic, M.; Jolovic, D.; Stevanovic, A. Building, Calibrating, and Validating a Large-scale High Fidelity Microscopic Traffic Simulation Model-A Manual Approach. In Proceedings of the 95th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 10–14 January 2016. [Google Scholar]
- Dobrota, N.; Stevanovic, A.; Mitrovic, N. Modifying signal retiming procedures and policies by utilizing high-fidelity modeling with medium-resolution traffic data. Transp. Res. Rec. 2022, 2676, 660–684. [Google Scholar] [CrossRef]
- Gavric, S.; Dobrota, N.; Erdagi, I.; Stevanovic, A.; Osman, O. Estimation of Arrivals on Green at Signalized Intersections Using Stop-Bar Video Detection. Transp. Res. Rec. 2023. [Google Scholar] [CrossRef]
- Erdağı, İ.G.; Silgu, M.A.; Çelikoğlu, H.B. Emission effects of cooperative adaptive cruise control: A simulation case using SUMO. EPiC Ser. Comput. 2019, 62, 92–100. [Google Scholar]
- Silgu, M.A.; Erdağı, İ.G.; Çelikoğlu, H.B. Network-wide emission effects of cooperative adaptive cruise control with signal control at intersections. Transp. Res. Procedia 2020, 47, 545–552. [Google Scholar] [CrossRef]
- Alshayeb, S.; Stevanovic, A.; Effinger, J.R. Investigating impacts of various operational conditions on fuel consumption and stop penalty at signalized intersections. Int. J. Transp. Sci. Technol. 2022, 11, 690–710. [Google Scholar] [CrossRef]
- Sharafeldin, M.; Farid, A.; Ksaibati, K. Examining the Risk Factors of Rear-End Crashes at Signalized Intersections. J. Transp. Technol. 2022, 12, 635–650. [Google Scholar] [CrossRef]
- Sharafeldin, M.; Farid, A.; Ksaibati, K. Injury Severity Analysis of Rear-End Crashes at Signalized Intersections. Sustainability 2022, 14, 13858. [Google Scholar] [CrossRef]
- Sharafeldin, M.; Farid, A.; Ksaibati, K. A Random Parameters Approach to Investigate Injury Severity of Two-Vehicle Crashes at Intersections. Sustainability 2022, 14, 13821. [Google Scholar] [CrossRef]
- Iqbal, S.; Ardalan, T.; Hadi, M.; Kaisar, E. Developing Guidelines for Implementing Transit Signal Priority and Freight Signal Priority Using Simulation Modeling and a Decision Tree Algorithm. Transp. Res. Rec. 2022, 2676, 133–144. [Google Scholar] [CrossRef]
- Gavric, S.; Sarazhinsky, D.; Stevanovic, A.; Dobrota, N. Development and evaluation of non-traditional pedestrian timing treatments for coordinated signalized intersections. Transp. Res. Rec. 2023, 2677, 460–474. [Google Scholar] [CrossRef]
- Arafat, M.; Hadi, M.; Raihan, M.A.; Iqbal, M.S.; Tariq, M.T. Benefits of connected vehicle signalized left-turn assist: Simulation-based study. Transp. Eng. 2021, 4, 100065. [Google Scholar] [CrossRef]

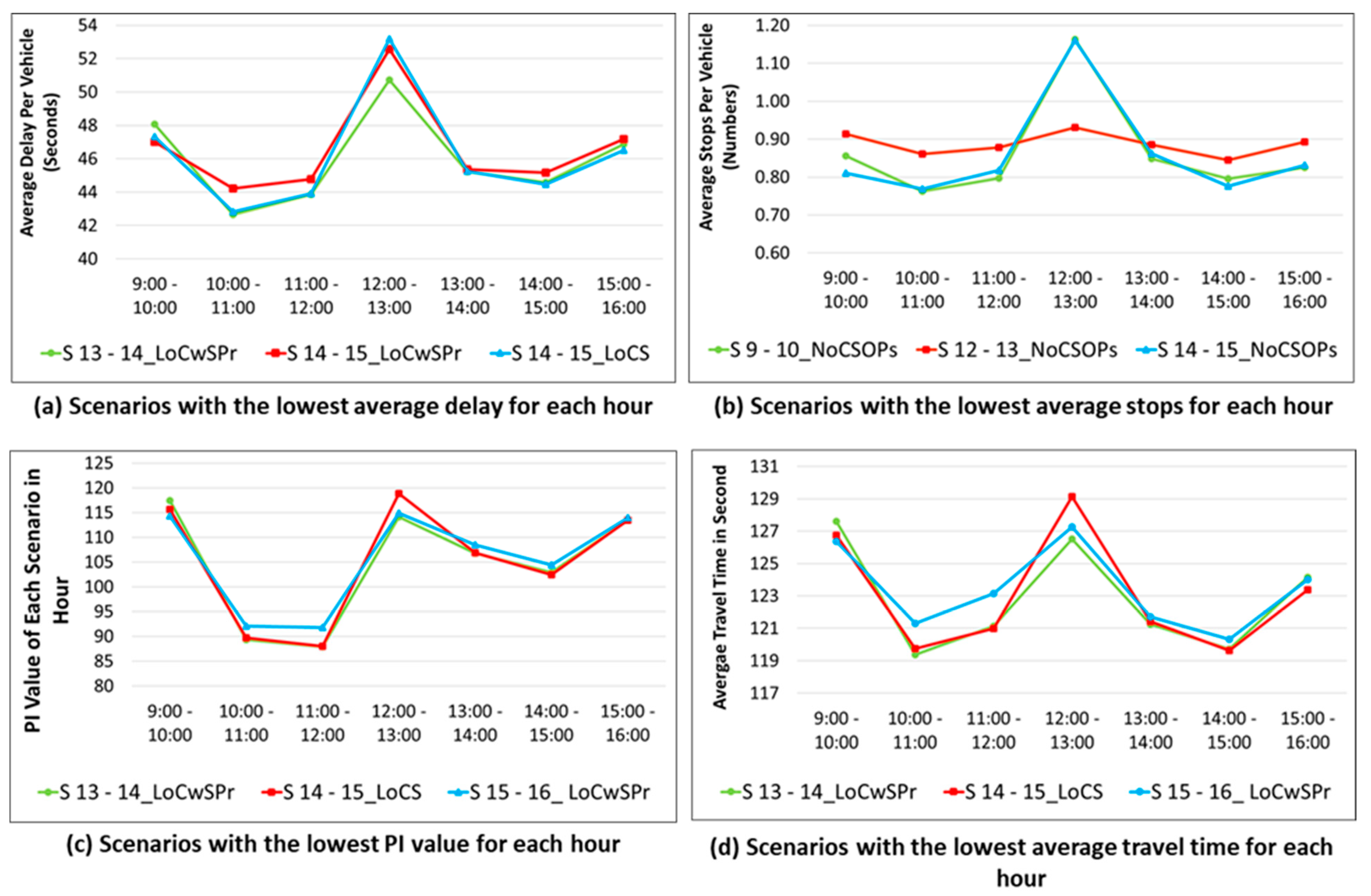
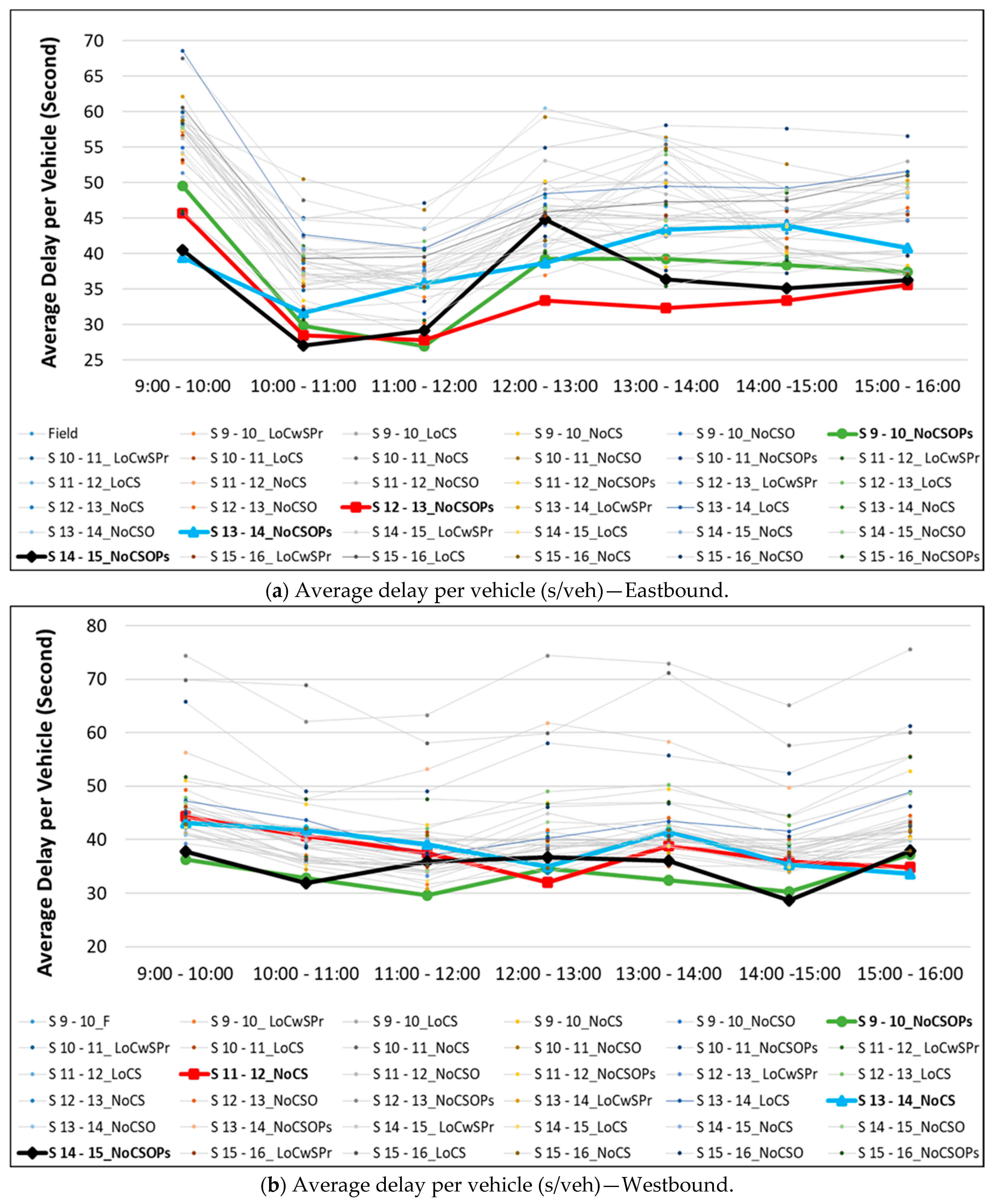
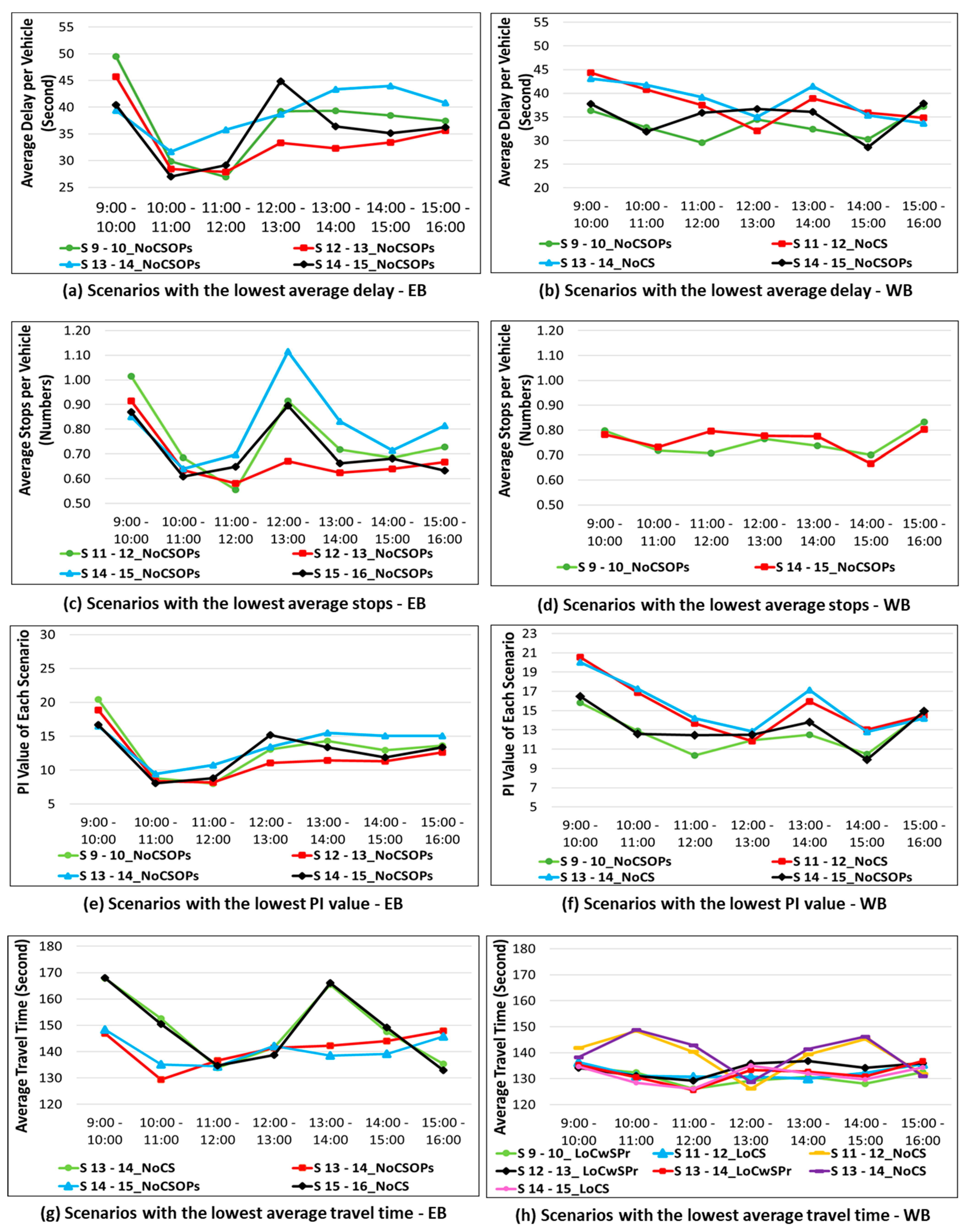
| Scenario | Optimization Mode | Cycle Length | Split | Offsets | Phase Sequence |
|---|---|---|---|---|---|
| LoCwSPr | Locally | Yes | No | No | No |
| LoCS | Locally | Yes | Yes | No | No |
| NoCS | Network | Yes | Yes | No | No |
| NoCSO | Network | Yes | Yes | Yes | No |
| NoCSOPs | Network | Yes | Yes | Yes | Yes |
| Threshold | Scenario | ||||
|---|---|---|---|---|---|
| 3% | S 13-14 LoCwSPr | ||||
| 5% | S 13-14 LoCwSPr | S 14-15 LoCS | S 14-15 LoCwSPr | S 15-16 LoCwSPr | |
| 10% | S 13-14 LoCwSPr | S 14-15 LoCS | S 14-15 LoCwSPr | S 15-16 LoCwSPr | S 13-14 LoCS |
| S 15-16 LoCS | S 12-13 LoCwSPr | ||||
| 15% | S 13-14 LoCwSPr | S 14-15 LoCS | S 14-15 LoCwSPr | S 15-16 LoCwSPr | S 15-16 LoCS |
| S 12-13 LoCwSPr | S 13-14 LoCS | S 11-12 LoCwSPr | |||
| 20% | S 13-14 LoCwSPr | S 14-15 LoCS | S 14-15 LoCwSPr | S 15-16 LoCwSPr | S 13-14 LoCS |
| S 15-16 LoCS | S 12-13 LoCwSPr | S 11-12 LoCwSPr | S 11-12 LoCS | S 12-13 LoCS | |
| Threshold | Scenario | ||
|---|---|---|---|
| Eastbound | Westbound | ||
| 3% | NA 1 | NA | |
| 5% | NA | NA | |
| 10% | NA | NA | |
| 15% | S 12-13_NoCSOPs | S 9-10_NoCSOPs | |
| 20% | S 12-13_NoCSOPs | S 9-10_NoCSOPs | S 12-13_NoCSOPs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobrota, N.; Stevanovic, A.; Yang, Y.; Alshayeb, S. Investigation of Resonant Signal Timing Plans through Comprehensive Evaluation of Various Optimization Approaches. CivilEng 2023, 4, 416-432. https://doi.org/10.3390/civileng4020024
Dobrota N, Stevanovic A, Yang Y, Alshayeb S. Investigation of Resonant Signal Timing Plans through Comprehensive Evaluation of Various Optimization Approaches. CivilEng. 2023; 4(2):416-432. https://doi.org/10.3390/civileng4020024
Chicago/Turabian StyleDobrota, Nemanja, Aleksandar Stevanovic, Yifei Yang, and Suhaib Alshayeb. 2023. "Investigation of Resonant Signal Timing Plans through Comprehensive Evaluation of Various Optimization Approaches" CivilEng 4, no. 2: 416-432. https://doi.org/10.3390/civileng4020024
APA StyleDobrota, N., Stevanovic, A., Yang, Y., & Alshayeb, S. (2023). Investigation of Resonant Signal Timing Plans through Comprehensive Evaluation of Various Optimization Approaches. CivilEng, 4(2), 416-432. https://doi.org/10.3390/civileng4020024







