Finite Element Analysis of Heavy Duty Riveted Steel Grating Bridge Deck

Abstract

Heavy duty riveted gratings are a good alternative for applications that often employ other deck systems, if they are carefully analyzed under static and fatigue loads. Understanding the static behavior of a riveted steel deck under tire patch loads will aid in establishing a design model based on an effective beam width. In addition, use of a riveted system avoids welded details that may lead to fatigue cracking, thereby improving design life. In this study, analysis of a typical riveted steel deck under a standard AASHTO fatigue truck with a 15% impact factor was conducted. Hand calculations were compared with the results of a finite element model using SAP2000 v19.2.1. Bending moments and stresses were evaluated and compared. Stresses at the rivet hole for the most highly loaded bearing bar were evaluated. A model for fatigue cracking around a rivet hole is discussed.

1. Introduction

Structural system integrity relies on the connections through which load transfers. Connection types are based on the use of the structure, the cross section of the member that is to be connected, and the fabrication cost. Structural connections may use mechanical fasteners such as rivets or bolts, or welds. In general, mechanically fastened joints are classified according to the type of forces transferred, and they include shear, tension, and combined tension/shear to which the fasteners are subjected [1].

One performance issue in bridges is fatigue cracking induced by repeated cyclic loads. Field experience has demonstrated that connections under such conditions may eventually fail from fatigue or stable crack growth, even though the maximum applied stress is less than the yield stress. In addition, fatigue failures often occur with small deformation, making fatigue cracks difficult to detect until sufficient growth has occurred [2].

In the 19th and the 20th centuries, hot riveting was used in many steel bridge structures as a means to assemble the structural members. The behavior of riveted connections has drawn attention from researchers, given their wide use in steel bridges and other metal structures. In fact, even with increased traffic load, many riveted bridges have provided reliable service over a long period of time [3,4].

Riveting is a method to fasten two or more steel sheets or plates as well as a means of connecting steel members. The riveting operation consists of inserting the rivet into a matching hole. The rivet head is formed by rapid forging or by continuous squeezing of the protruding end of the shank. It is worth noting that hole’s diameter should be at least 1 mm greater than the rivet diameter [1,2].

It is important to note that riveted grating has been used in various applications. One particular use is on bridges, which require light weight, either for rating or to meet the equipment requirements of movable spans. Indeed, some of the most replaced systems on movable bridges include the deck. For this reason, lighter weight reduces the dead load on the bridge, which affects the size of the counterweights and the overall size of the structural members. Furthermore, heavy-duty riveted grating continues to be the choice of many engineers due to its reliability and durability [5,6]. The focus of this study is on heavy duty riveted decks. In particular, the 37R5 L series is a popular choice, which is a modified form of the 37R5 series that employs angle sections instead of flat stock for bearing bars. This product has a wider spacing between full-size bearing bars to decrease the weight per sq. ft., while still meeting design requirements. In addition, riveted connections provide improved fatigue resistance over some other joining methods and connecting bars that help spread the load and add strength, and flexibility in bar sizes [6].

Finite Element Analysis (FEA) is a numerical method for solving engineering problems to obtain approximate solutions. It is useful for problems with complicated geometries, loading, and/or material properties, where analytical solutions cannot easily be obtained [7]. Szymczyk and others (2009) studied the residual stress and strain fields associated with solid mushroom rivets around the hole due to the riveting process. They used a local model developed with MSC Nastran and Marc software codes [8]. Rans and others (2007) sought to better understand the rivet installation process, the resulting residual stress field and the implications on the fatigue performance of riveted joints. A three-dimensional FE model was developed using ETA/FEMB and LS-DYNA [9]. Correia and others (2021) used ANSYS to evaluate the fatigue behavior of riveted joints. Two small-scale riveted specimens were modelled and fatigue life predicted [4].

Several finite element (FE) studies have been undertaken in order to enhance the understanding of the effect of the rivet installation process on fatigue behavior by modeling the load–unload cycle. However, it is limited to evaluating the riveting process in an individual case without taking into consideration the entire member. Ensuring the safety of bridges is essential, and developing models with respect to fatigue is needed.

The focus of the current study is the behavior of heavy duty riveted steel decks under simulated fatigue load, as given by AASHTO HL truck loading. SAP2000 v19.2.1 and Abaqus/CAE 6.14-5 have been used to examine the behavior of riveted steel angle grating through three-dimensional analysis. As part of this work, a 3D finite element model using SAP2000 was built in order to analyze a typical riveted steel deck under a standard AASHTO fatigue truck. Results were compared with hand calculations. Bending moments and stresses were evaluated and compared. Stresses for the most highly loaded bearing bar were evaluated. A more refined analysis of the stresses around a rivet hole were determined and a fracture mechanics model has been used to predict fatigue life.

2. Finite Element Modeling

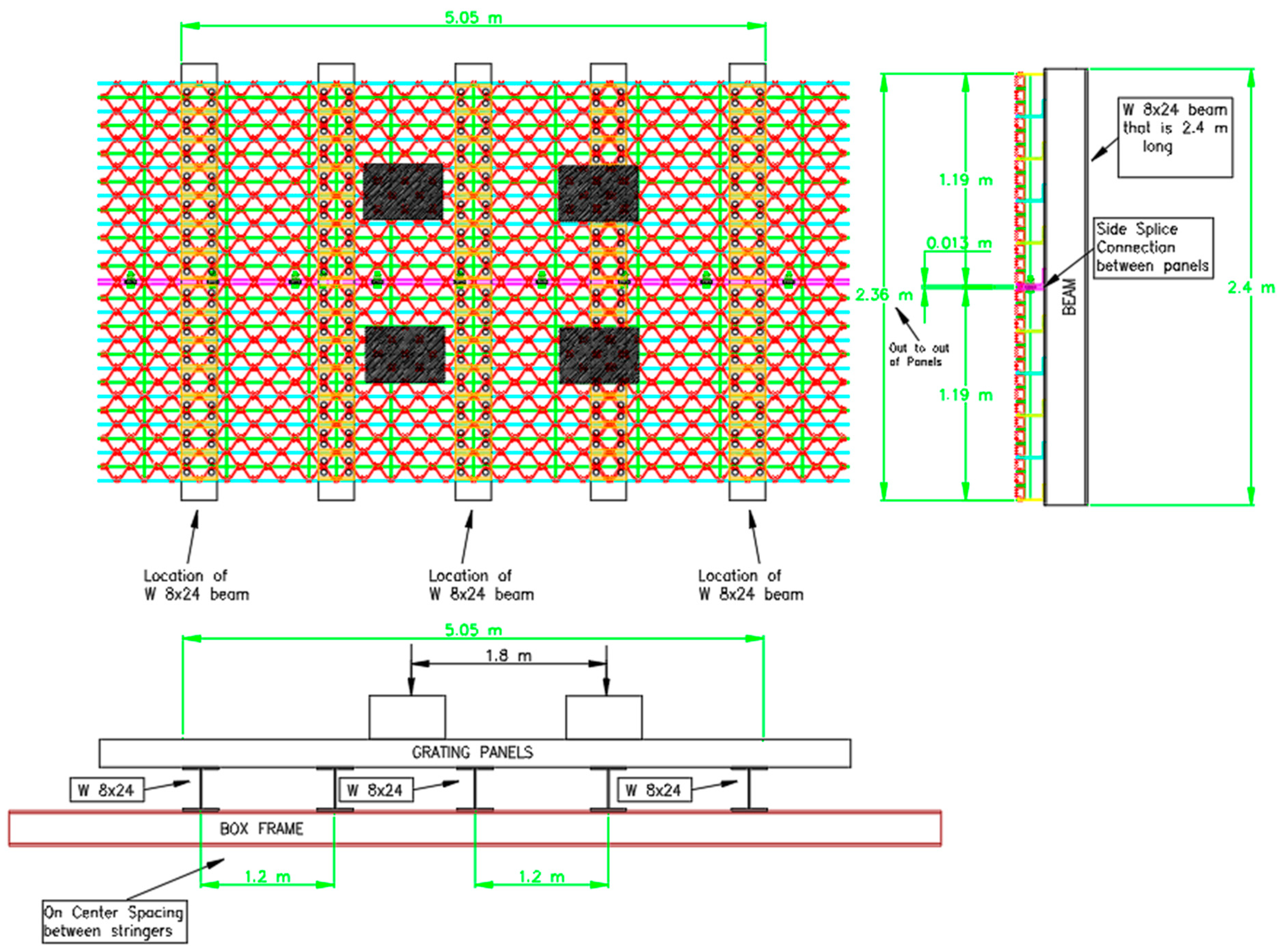
2.1. Building the Model: A Heavy Duty Riveted Grating

A four span 37R5 L-Series panel with dimensions as shown in Figure 1 has been modeled using SAP2000.

Three-dimensional shell elements were used to model the main bearing bars, intermediate bars and reticuline bars. The model was created in an X–Y plane. It is noteworthy that the model used half of the panel, taking into consideration symmetry (Figure 2). Both bearing bars and intermediate bars were created with the right spacing that corresponds to the physical geometry of the deck. Consequently, the bearing and intermediate bars were assembled using reticuline (connecting) bars through the joint linking (master/slave) feature to simulate the deck rigidity.

Also, a convenient mesh size of 12.7 mm (0.5 inches) was taken for the combined parts, which leads to more accurate results and reasonable analysis run times. This model corresponds to the physical geometry, which simplifies the visualization and helps with the analysis process [10].

2.2. Elastic Properties, Boundary Conditions and Loading

A linear elastic steel model with a Young’s modulus of 199,948 MPa (29,000 ksi) and a Poisson’s ratio of 0.3 is used. The boundary conditions were assigned as roller supports at joints A, B, C and D, which will restrict movement in the vertical direction, Z. However, A, B, C and D will have free movement in the horizontal direction, X, as well as a free rotation about the Y-axis. In addition, a pinned support was assigned to joint E which will restrict movements in both X and Z directions, but allows rotation about the Y-axis (Figure 3a).

In addition, boundary conditions are used to represent the continuous behavior of the panel as shown in Figure 3b. The analysis considers an AASHTO HL-93 (2014) truck loading with a 15% impact factor. This load was applied through a plate measuring 508 mm × 254 mm (20 in × 10 in), which represents the dimension for a typical dual tire. In addition, the tire patch is assumed to behave as a rigid body and is tied to the model during the analysis, making it work with the entire panel [10].

2.3. Results of Finite-Element Analysis

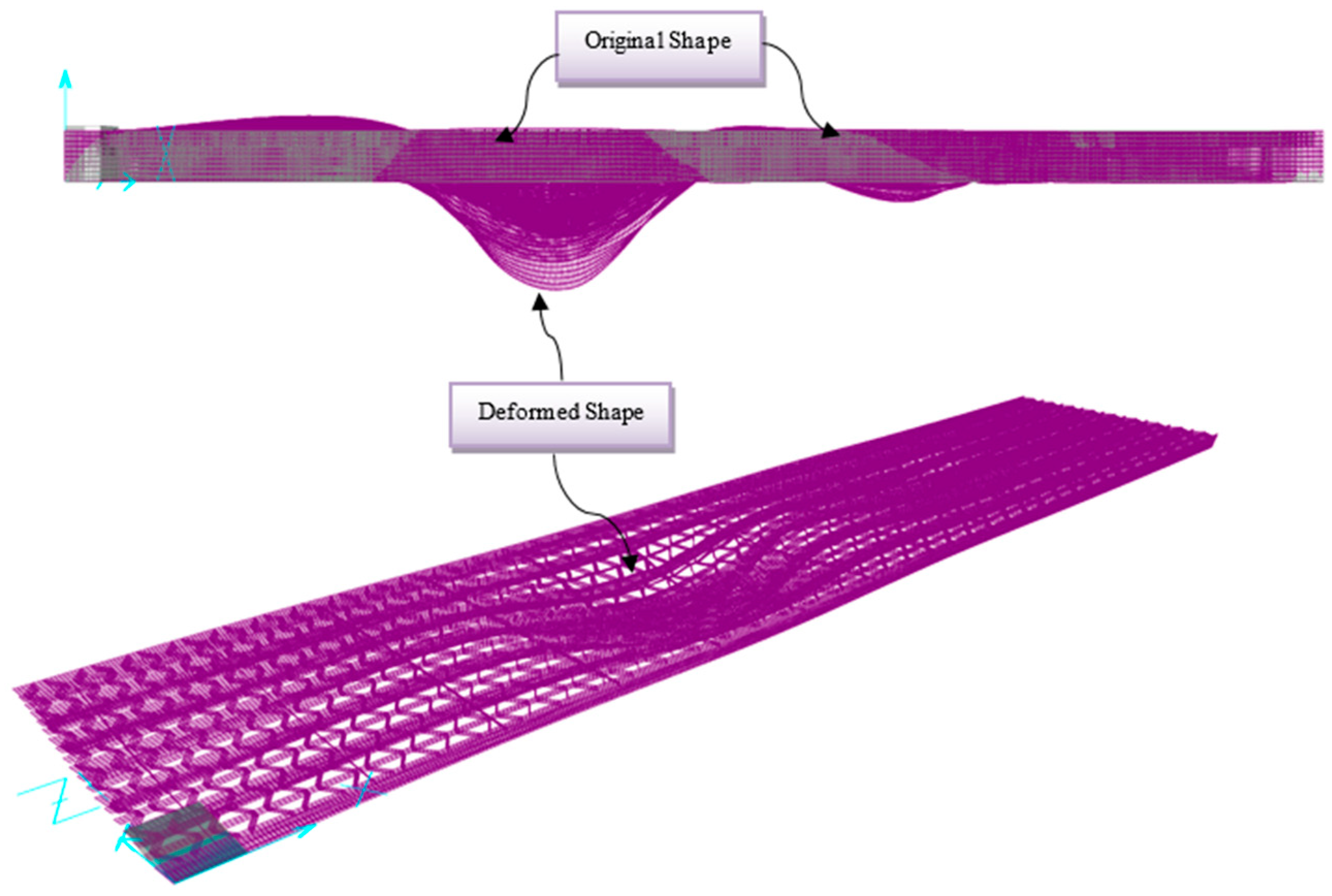
2.3.1. Static Results of the Entire Panel Model

Displacement, Deformation, Stress, Strain and Moment

One significant aspect of the analysis relates to the deformation caused by the loads applied to the structure. It is worth noting that deformation may prevent the structure from achieving its desired purpose. Displacements induced by the applied loads are essentially movement of individual points on the structural system due to various external loads. As a result, displacements cause the size and/or shape to be altered, and individual points move relative to one another. This relative change of dimension is referred to as the deformation [11].

Displacements have been obtained through the analysis using the SAP2000 model. Figure 4a shows the relationship between the applied load of 95.15 MPa (13.8 kips) and the resultant displacement (Δz) of the main and intermediate bars under tire#1 at the midspan. Displacement (Δz) ranges from near “zero” to −0.762 mm (“zero” to −0.030 in) with the highest values of −0.508, −0.762 mm (−0.020, −0.030 in) experienced by the two main bearing bars directly under the load. Figure 4b for tire#2 located close to, but not touching, the support, shows the same variables as Figure 4a. However, the range of Δz displacements are near “zero” to −0.102 mm (“zero” to −0.004 in) with the highest values of −0.102 mm (−0.004 in).

Figure 5 presents an isometric as well as a front view of the deformation of the heavy duty riveted grating using the wire shadow feature in SAP to highlight the differences between the original and the deformed shape. It is worthwhile to note that the maximum deflection occurs around the midspan of the loaded panel. Figure 6 shows the L shape cross-section of the bearing bar at the midspan from which it may be seen that the highest displacement and deformation occurs under the load.

There are higher tensile stresses directly under the load with the largest value equal to 71 MPa (10.3 ksi) at 6.35 mm (0.25 in) from the bottom fiber of the fourth main bearing bar at the midspan (Figure 7). Note that the fourth bearing bar is directly beneath a tire patch. However, the highest tensile stress value at 6.35 mm (0.25 in) from the bottom fiber close to the interior support was 16 MPa (2.3 ksi). In addition, there are compressive stresses at the top fibers for the midspan and the interior support of −31 and −7 MPa (−4.5 and −1 ksi), respectively.

Table 1. Stresses located 6.35 mm (0.25 in) from the top and bottom fibers.

Bar#	At 6.35 mm (0.25 in)	Midspan Stress/MPa (ksi)	Bar#	At 6.35 mm (0.25 in)	Midspan Stress/MPa (ksi)
Mb3	[01] T	−26 (−3.8)	Mb4	[08] B	71(10.3)
Mb3	[02] B	45.5 (6.6)	I7	[09] T	−24.8 (−3.6)
I5	[03] T	−21 (−3.1)	I7	[10] B	−18 (−2.6)
I5	[04] B	7.5 (1.1)	I8	[11] T	−23 (−3.4)
I6	[05] T	−22.7 (−3.3)	I8	[12] B	−5.5 (−0.8)
I6	[06] B	16.5 (2.4)	Mb5	[13] T	−27.6 (−4)
Mb4	[07] T	−31 (−4.5)	Mb5	[14] B	38 (5.5)
T = Top	B = Bottom	M = Main Bar		I = Intermediate Bar

provides a summary of the stresses located 6.35 mm (0.25 in) from the top and bottom of the main bearing and intermediate bars along the midspan of the grate, for the span loaded by Tire Patch 1. The location for reporting tensile stresses corresponds to strain gage measurements taken during an earlier experimental study [12].

Furthermore, data taken from the SAP analysis includes strains in both tension and compression at 6.35 mm (0.25 in) from the top and bottom fibers of the main bearing and intermediate bars located at the midspan and over the interior support. Figure 8 shows the strain distribution at the bottom fibers for a tire patch load of 95.15 MPa (13.8 kips): (a) along the positive moment region at the midspan and (b) along the negative moment region over the interior support.

To be more specific, Figure 8 focuses on critical components which are the three main bearing bars and four intermediate bars in between, both under the tire patch and over the continuous support. In general, the main load carrying members are the bearing bars which provide load resistance for the panel. According to the strain distribution, the resistance of the heavy-duty riveted grating is provided primarily by the bearing bars under the load and the two bearing bars adjacent to these main bearing bars on each side.

A comparison between the midspan and interior support strain distribution in: (a) tension and (b) compression is seen in Figure 9. The strain distribution is primarily concentrated at the midspan.

Another significant observation from the analysis is the moment distribution across the width of the panel. In this portion of the study, we determined the moment distribution across the width of the panel using several methods. It is noteworthy that there are steps through which the bending moment was calculated. Those calculations are as follows:

• Moment of inertia has been calculated from the thickness of the member and location of the centroid.
• Bending stresses for each bearing bar were determined from the model.
• Moments were calculated using the stress distribution and the following expression.

  $$M=\frac{\sigma I}{C}$$

  (1)

  where M = moment at the end; σ = bending stress; C = distance to extreme fiber; and I = moment of inertia of the cross section.

The moment distribution along the midspan was determined and plotted against the width of the grating (Figure 10). It can be seen that the highest value was 3.07 kN-m (27 kips-in) which is from the bearing bar directly under the load. The overall positive moment carried by the bearing bars of the panel is 9 kN-m (78 kips-in). About 8 kN-m (69 kips-in) of moment, or about 88% is carried by the three bearing bars closest to the load.

In addition, we calculated and plotted the negative moments over the interior support B and C, as shown in Figure 11 and Figure 12, and they are about −7 and −6 kN-m (−63 and −54 kips-in) in total, respectively. The majority of moments are carried by bearing bars 3, 4 and 5.

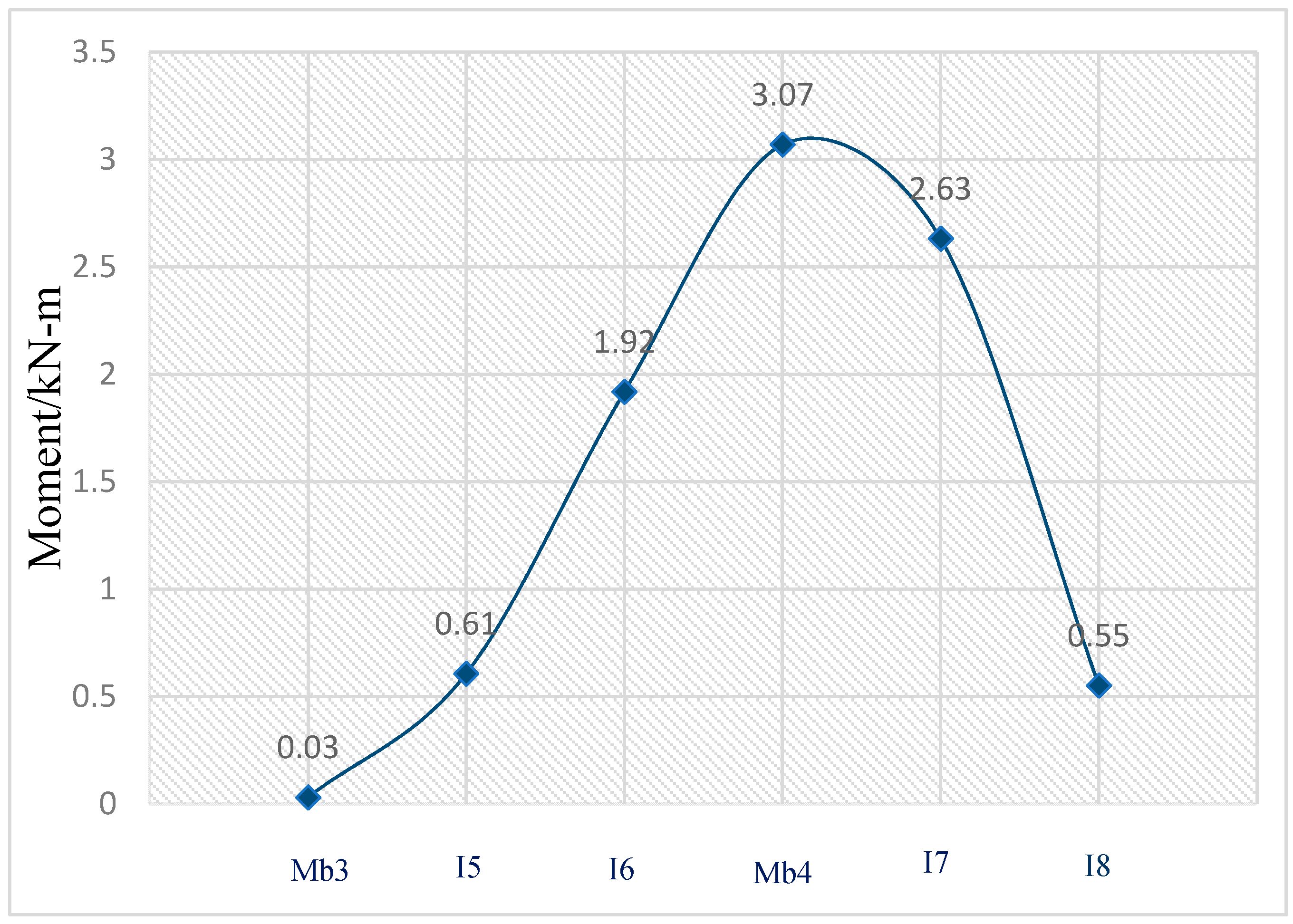
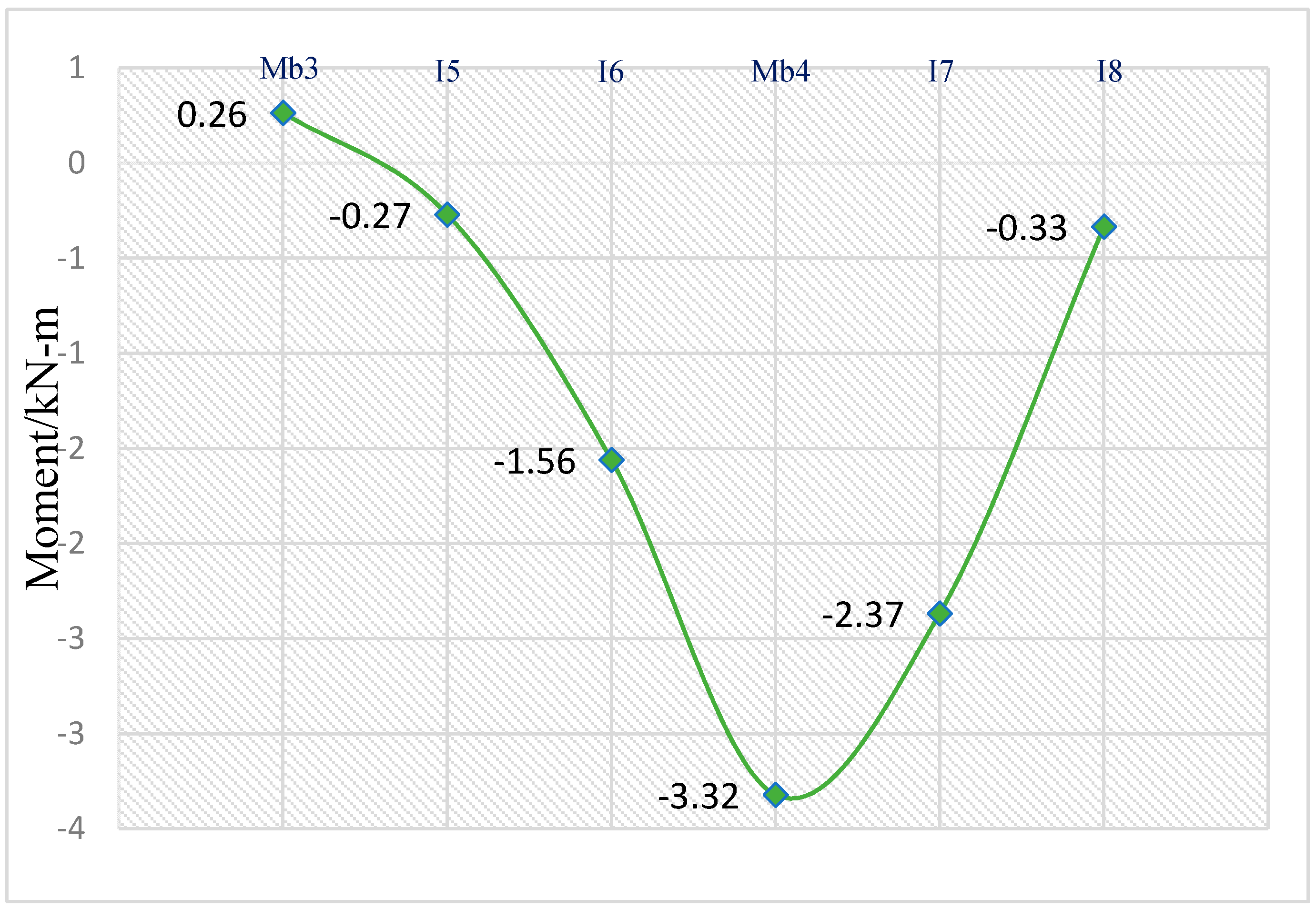
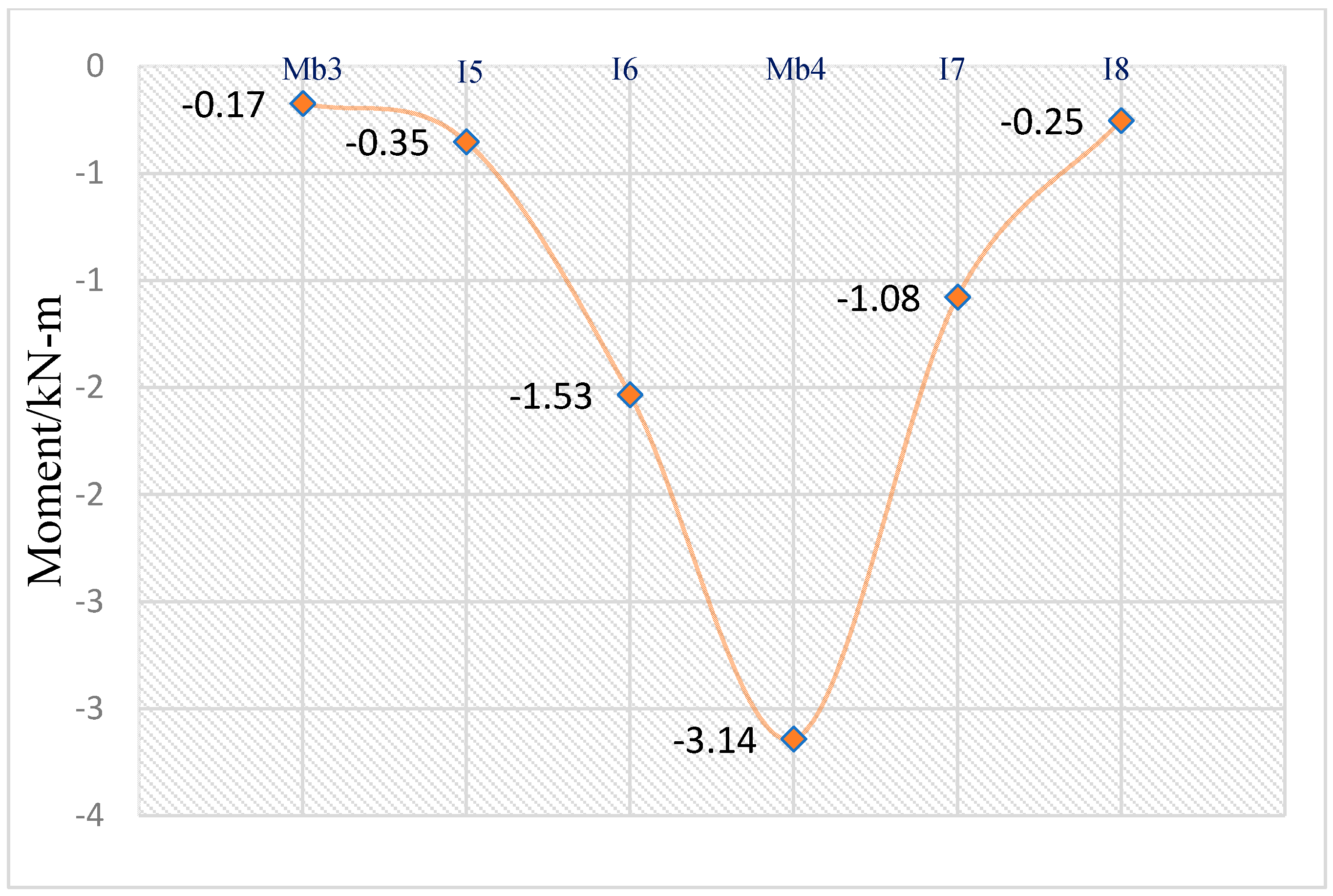
Moment Results Comparison

In addition to the FEA model, several other methods were used to obtain the moment distribution across the panel width and compared.

a.

Continuous beam analysis using SAP2000

In this analysis, the heavy-duty grating panel was modeled as a continuous beam. The positive moment distribution along the panel midspan was calculated to be about 9.3 kN-m (83 kips-in) and the negative moment over supports were about −5, −5.5 kN-m (−44, −49 kips-in), respectively (Figure 13).

b.

Influence lines in the continuous beam

Hand calculations were made for negative moments at supports B and C using influence lines, and resulted in about −5 and −5.6 kN-m (−45 and −50 kips-in), respectively. The positive moment at the midspan was found to be 9.3 kN-m (82 kips-in). A comparison of the moments for each method is given in

Table 2. Moment results comparison in kN-m (kips-in).

Location@	FEA Model kN-m (kips-in)	Continuous Beam Analysis kN-m (kips-in)	Hand Calculation kN-m (kips-in)
Support (B)	−7 (−63)	−5 (−44)	−5 (−45)
Midspan	9 (78)	9.3 (83)	9.3 (82)
Support (C)	−6 (−54)	−5.5 (−49)	−5.6 (−50)

.

3. Fatigue Results from the Fracture Mechanics Model

3.1. S-N Curves

Background

Fatigue damage occurs when components subjected to nominal elastic stress cycles have regions of localized stress that exceed the yield strength of the material. Damage accumulates due to cyclic plasticity and results in the initiation and subsequent propagation of a crack or cracks that may lead to the failure of the component(s). In particular, stress concentrations occur as a result of the changes in cross-section of the structural member, such as connections, cutouts, keyways and weldments. It is worth noting that the more intense the stress concentration, the shorter the fatigue life, given that other conditions are equal. In addition, the total fatigue life is the sum number of cycles of the initiation and propagation of lives. In general, the fatigue life of a structure or component is considered to consist of three stages: crack initiation, propagation, and fracture. In addition, fatigue performance is affected by many parameters which are related to stress (load), geometry and properties of the component, as well as the external environment. However, the main factor that affects the fatigue is the variation in localized stress or strain. Accordingly, S-N curves that represent the classification or ranking of the stress concentration should be derived [13,14].

Our goal from the detailed analysis of the bearing bar with a rivet hole is to predict fatigue life and obtain S-N curves using a fracture mechanics model. Therefore, the procedure included the following:

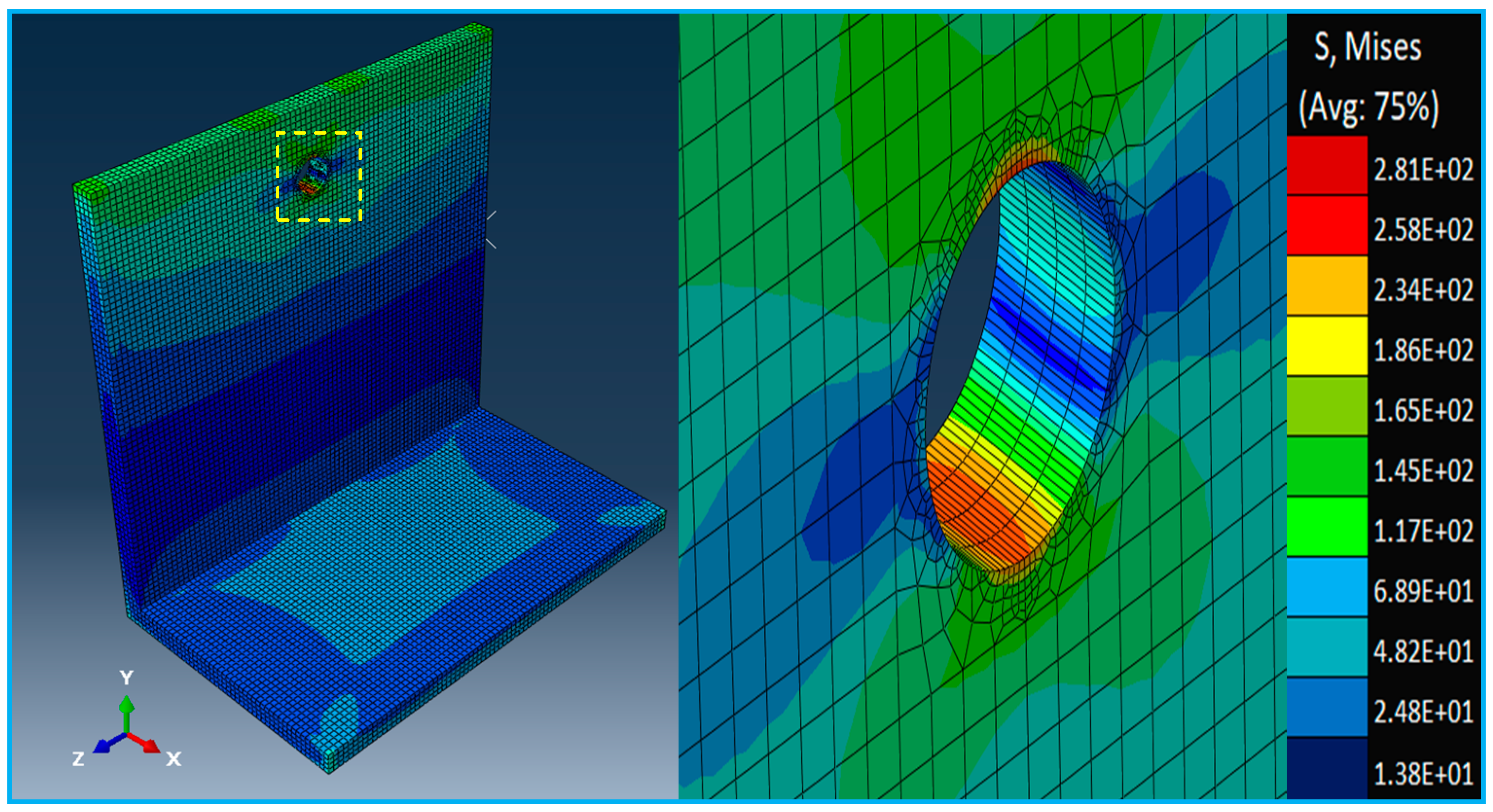
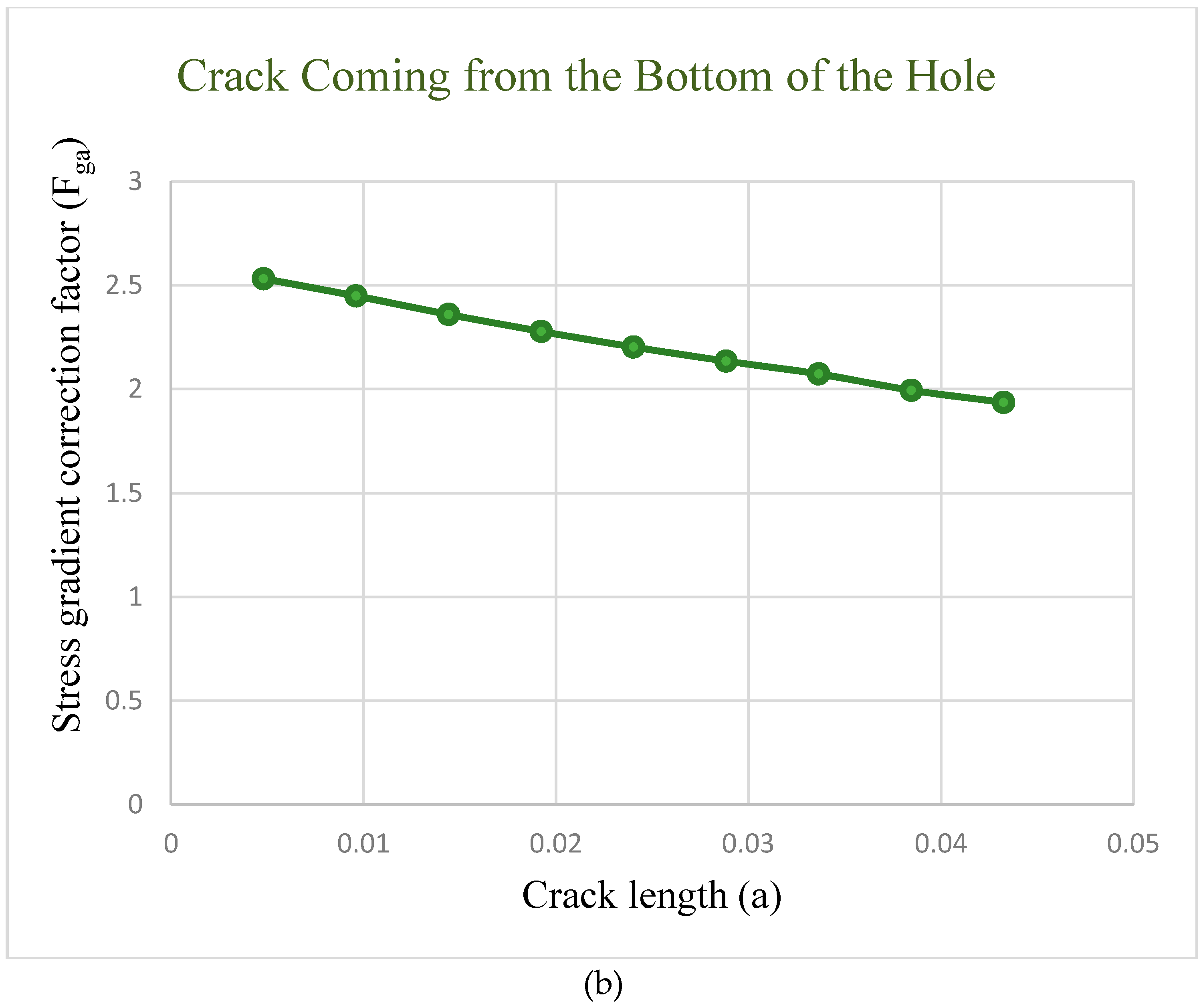
• The calculation of the stress gradient correction factor F_ga using the following expression [3]:

  $$F_{\mathrm{ga}}=\frac{2}{\pi }{\sum }_{j=1}^m{k}_{tj}[{\sin }^{-1}(\frac{l_j+1}{a})-{\sin }^{-1}(\frac{l_j}{a})]$$

  (2)

  where k_tj = stress concentration factor in element j of the finite element, lj = distance from the crack origin to the near and far, lj + 1 = sides of finite element j, and m = the number of elements to crack length a. After applying a moment of 2.8 kN-m (25 kips-in), we obtained the stress gradient around the rivet hole. Figure 14 shows the deformed shape and stress concentration due to a circular hole in the structure.

In order to calculate the stress concentration factor k_tj, we use the following formula:

$$k_{tj}=\frac{{\sigma }_{max}}{{\sigma }_{nom}}$$

(3)

The maximum stress σ_max for each element of the top and bottom along the assumed crack length was determined. In addition, the nominal stress was obtained by the use of the following formula.

$${\sigma }_{nom}=\frac{MC}{I}$$

(4)

where σ_nom = nominal bending stress; M = moment at the free end; c = distance to extreme fiber; and I = moment of inertia of the cross section.

By assuming the crack path from the model, we calculated F_ga using Equation (2). The relationship between the crack length and stress gradient correction factor was plotted and given in Figure 15a,b.

2.

Accounting for the effect of a free surface on some finite length of crack, $F_w$ was calculated using five formulas [16]:

$$F_w=\sqrt{Sec\frac{\pi a_i}{W}}$$

(5)

where $a_i$= crack length for each element, and W = crack width for the top and bottom.

3.

The range of stress intensity factor ΔK was calculated as [3]:

$$\Delta K=F_{ga}{F}_w{S}_r\sqrt{\pi a_i}$$

(6)

where Sr = stress range. Other notations are as previously noted.

4.

Fourth, the calculation of fatigue crack growth per cycle by the use of Paris’s equation [11]:

$$\frac{da}{dN}=C{\left(\Delta K\right)}^n \mathrm{in}/\mathrm{cycle}$$

(7)

where a = length of the crack, N = number of cycles to failure, ΔK = the range of the stress intensity factor, and C and n are constants based on material properties, which, in our case for structural steel, C = 3.6 × 10⁻¹⁰, n = 3.

5.

Finally, by rearranging Equation (7) and integrating between the initial and final crack sizes the number of cycles, N, can be predicted as [17]:

$$\mathrm{N}=\frac{1}{C}{\int }_{a_i}^{a_f}\frac{1}{{\left(\Delta K\right)}^n} \mathrm{da}$$

(8)

where $a_i$ and $a_f$ represent initial crack size and the critical crack length respectively.

As a result of this equation, the number of cycles (N) was predicted. In addition, based on a regression analysis of fatigue data from previous tests of the heavy-duty riveted grating, Equation (9) was obtained as the line of best fit [12].

LogN = 10.3 − 3.16 logS_r

(9)

Figure 16 shows a graph of the predicted S-N curve versus the best fit line.

Also, in order to compare with the fatigue requirements of the AASHTO manual, the mean line is specified by Equation (10) [12].

LogN = 10.02 − 3 LogS_r

(10)

Figure 17 presents a graph of the AASHTO S-N curve versus the best fit line.

4. Conclusions

The main conclusions of this study are as follows:

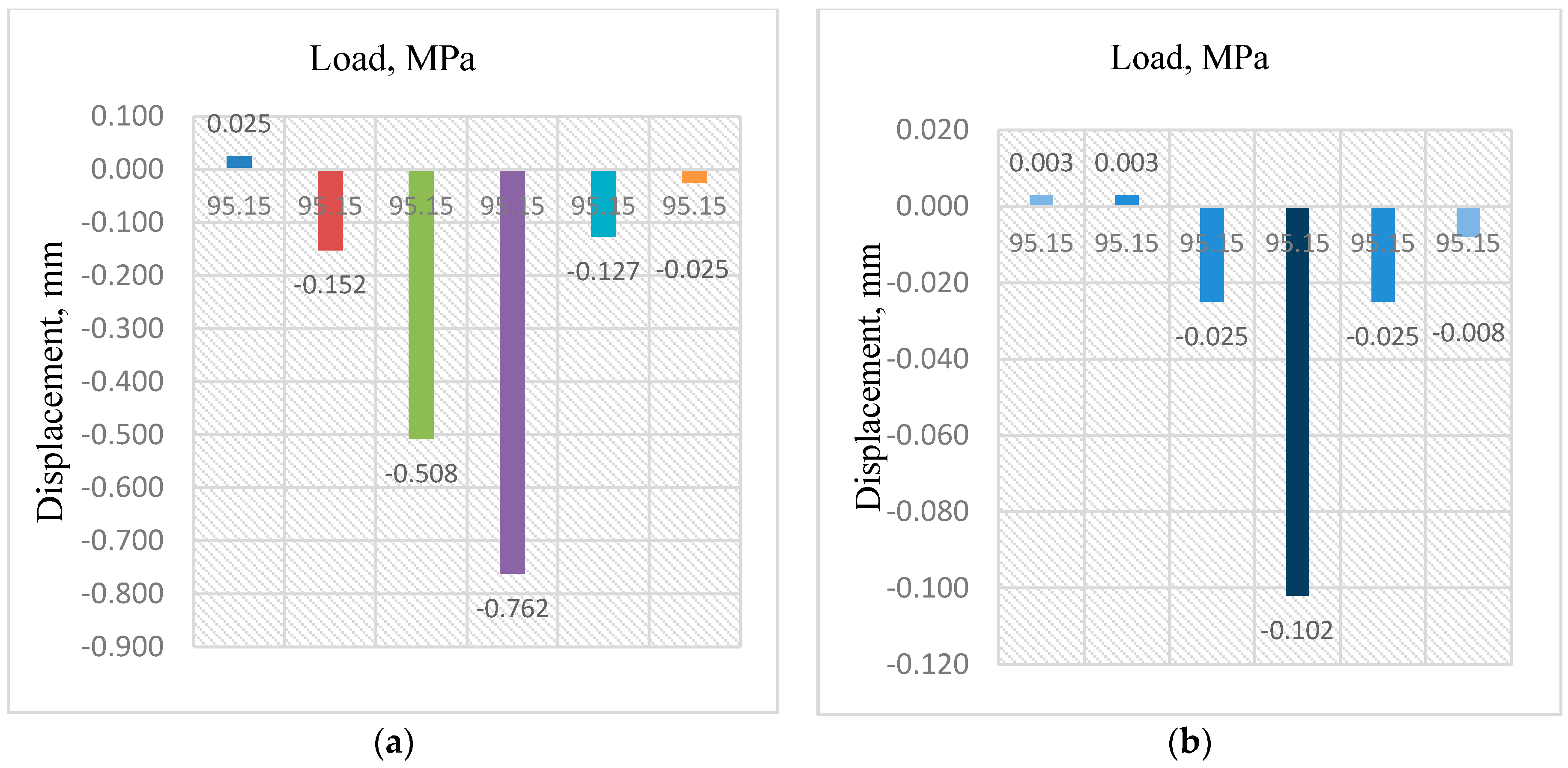
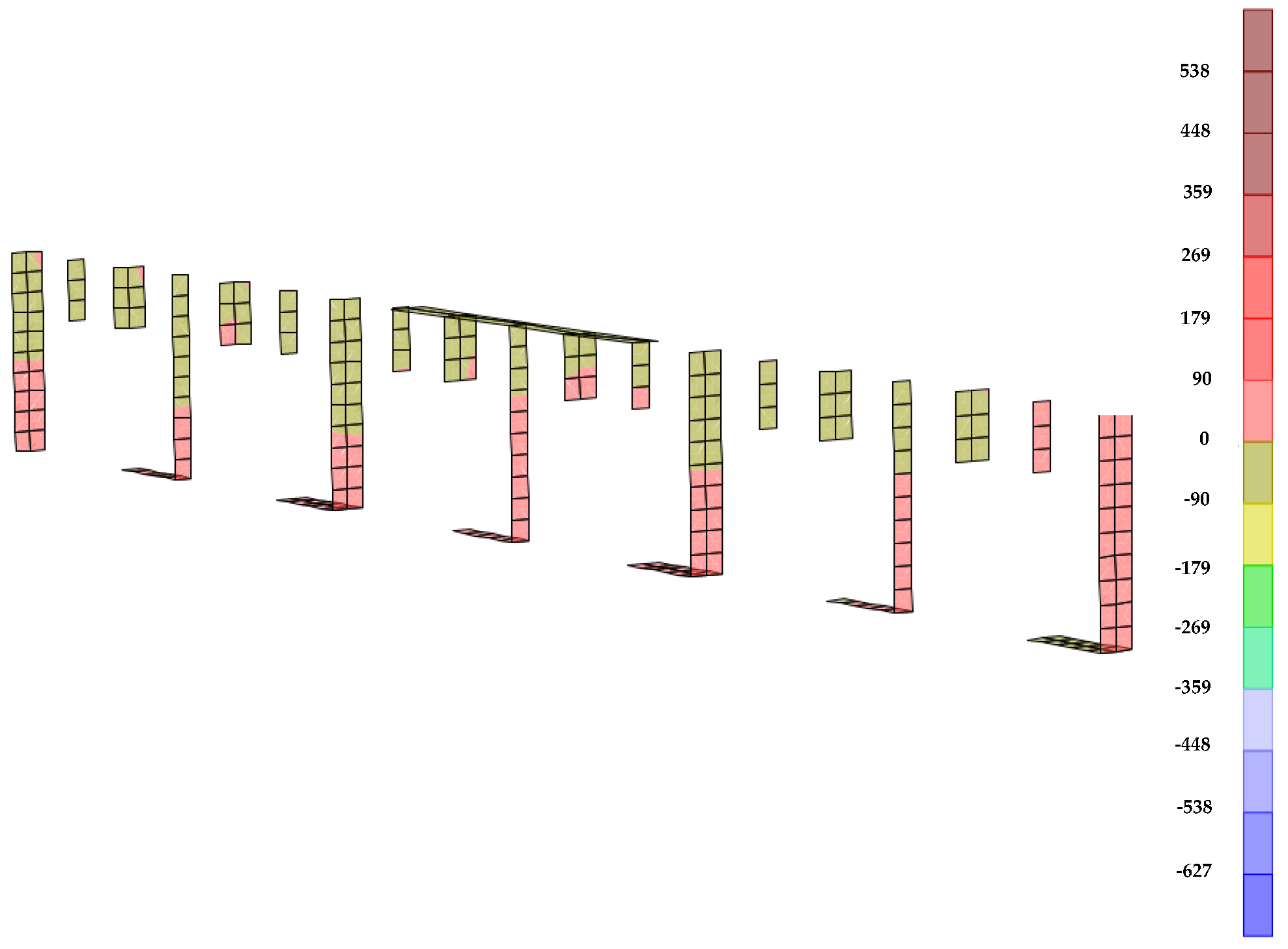
• The displacement for midspan ranges from near “zero” to −0.762 mm (“zero” to −0.030 in), with the largest value of −0.762 mm (−0.030 in) for the main bar directly under the tire patch load. However, the displacement is extremely small near the interior support for the main bar, as expected. The displacement average for the midspan was −0.254 mm (−0.010 in), and for the support it was near zero.
• The stress distribution was calculated for the bearing bar directly under the tire contact area as well as the adjacent bearing bars at a location 6.35 mm (0.25 in) from the top and bottom fiber of the bars. The highest value of tensile stress was 71 MPa (10.3 ksi) for the main bearing bar at the midspan; however, it was only 16 MPa (2.3 ksi) for the main bearing bar at the support, which is about 22% of the midspan value.
• Also, the compressive stresses at midspan and over the interior support were −31 and −7 MPa (−4.5 ksi and −1 ksi), respectively. In general, gratings had a total of six bearing bars and three actively participated in resisting the applied load.
• The manner of strain distribution was studied both in tension and in compression. The load is resisted mainly by the bearing bars located directly under the tire patch. In addition, the adjacent two intermediate bars provide some level of resistance, which was about 24% of the main bar directly under the load. A comparison was made between the midspan and interior support strain distributions, which demonstrated that it is concentrated at the midspan near the applied load. In general, the moment regions closest to the area of the applied load have larger strains compared to other regions.
• The largest positive bending moment for a single bearing bar was 3 kN-m (27 kips-in) which was recorded directly under the load at midspan.
• In addition, the maximum negative bending moment for a bearing bar was 3.3 kN-m (−29 kips-in) near the interior support B. The bending moment results obtained from the finite element analysis were compared to those obtained from different methods. The values were relatively close to each other.
• Fatigue analysis using fracture mechanics focusing on crack propagation around the rivet hole was used to predict the fatigue life of the heavy duty riveted grating. In fact, at a peak alternating stress of 69 MPa (10 ksi), we could expect that the structural components survive about 1,250,000 cycles.
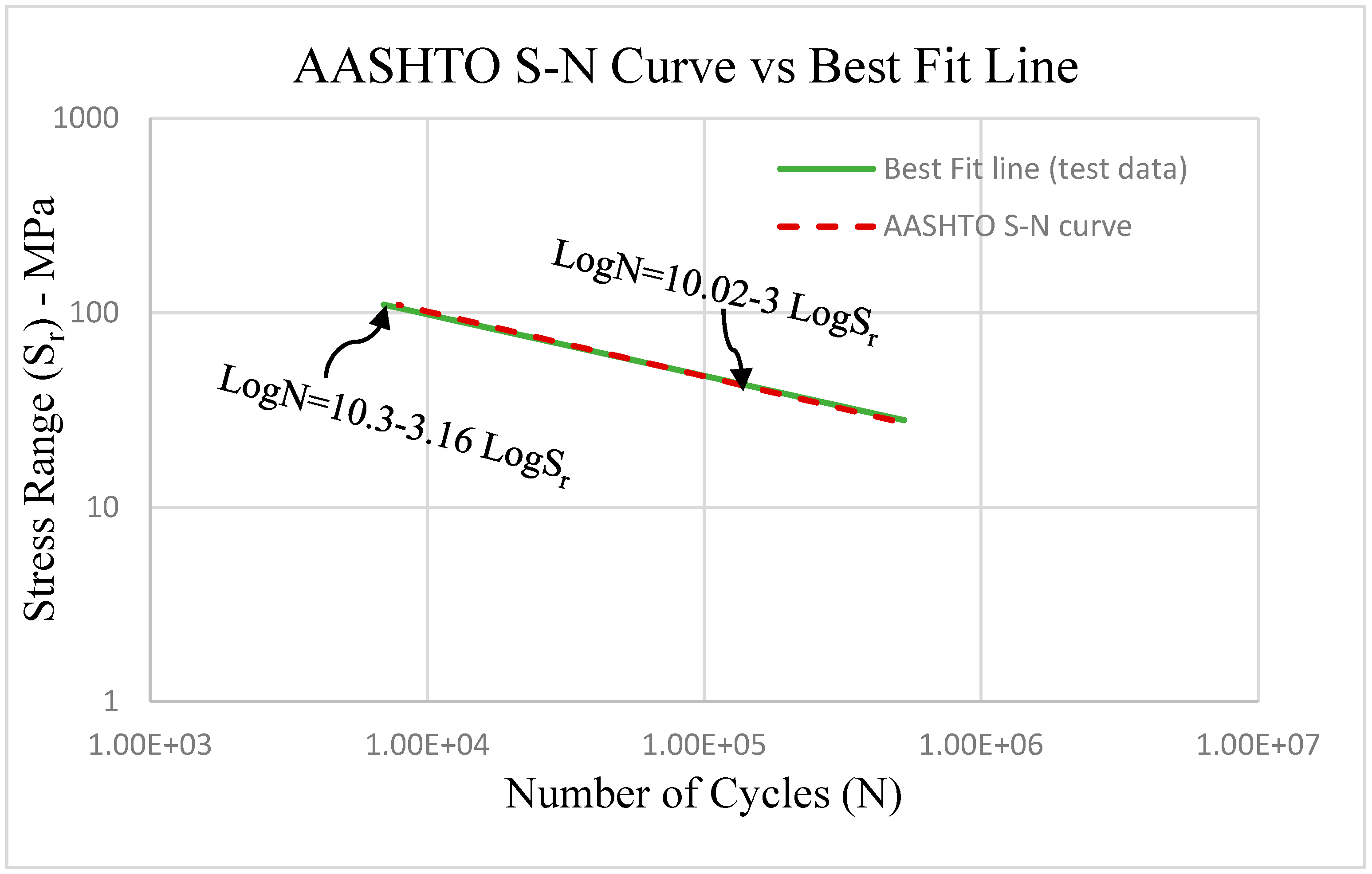
• The line of best fit was close to the required AASHTO S-N curve.