Material-Dependent Shear Capacity of Threaded Rods
Abstract
:1. Introduction
- performing at least five shear tests with the fastening elements in concrete;
- calculating shear tensile strength using Equation (1).
2. Materials and Methods
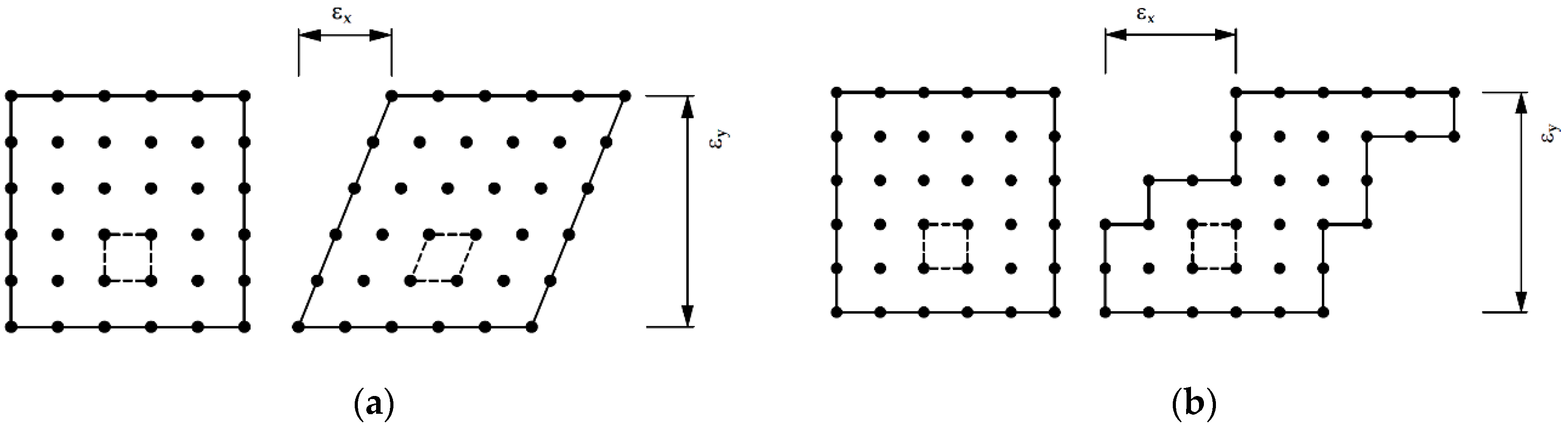
2.1. Method—Plasticity Module
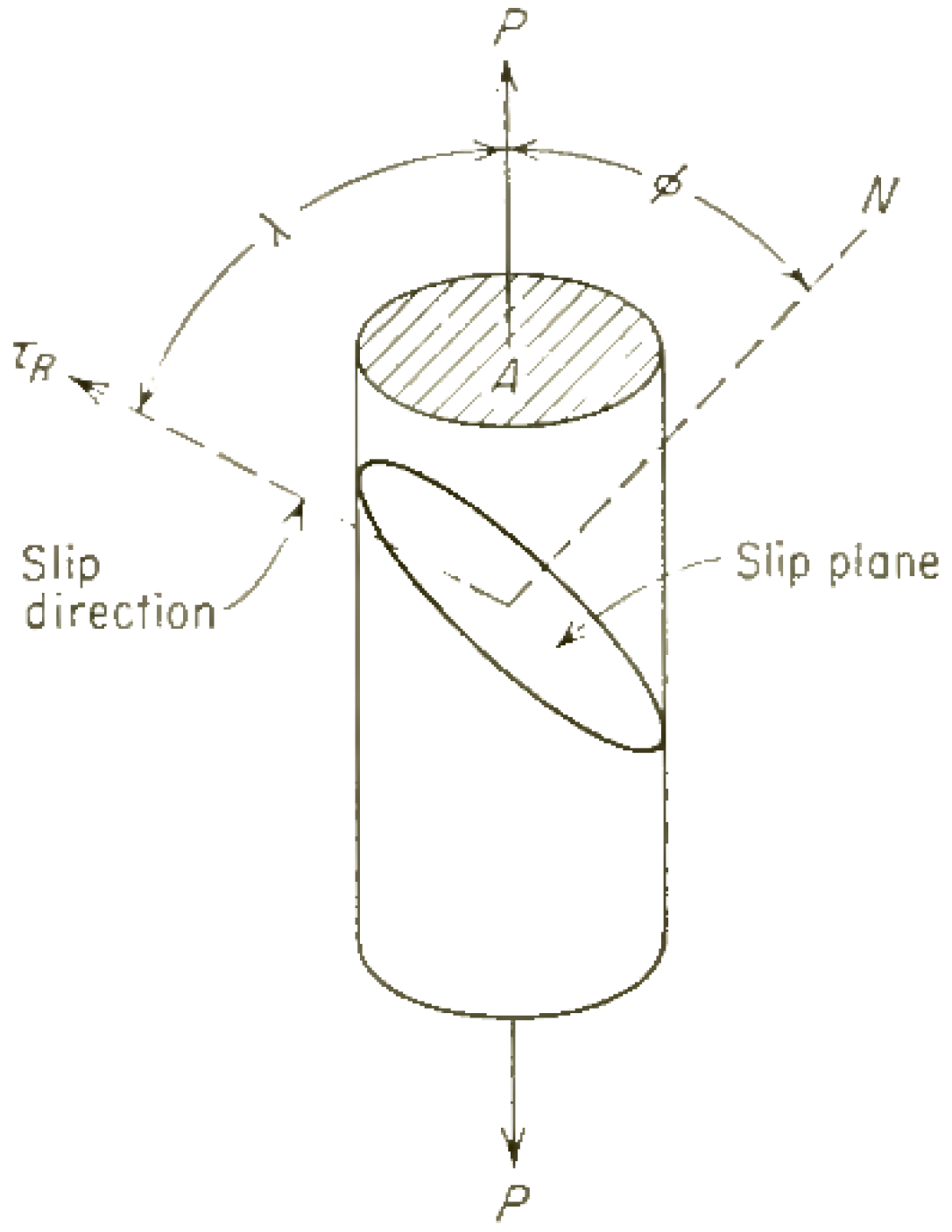
2.2. Tensile Tests
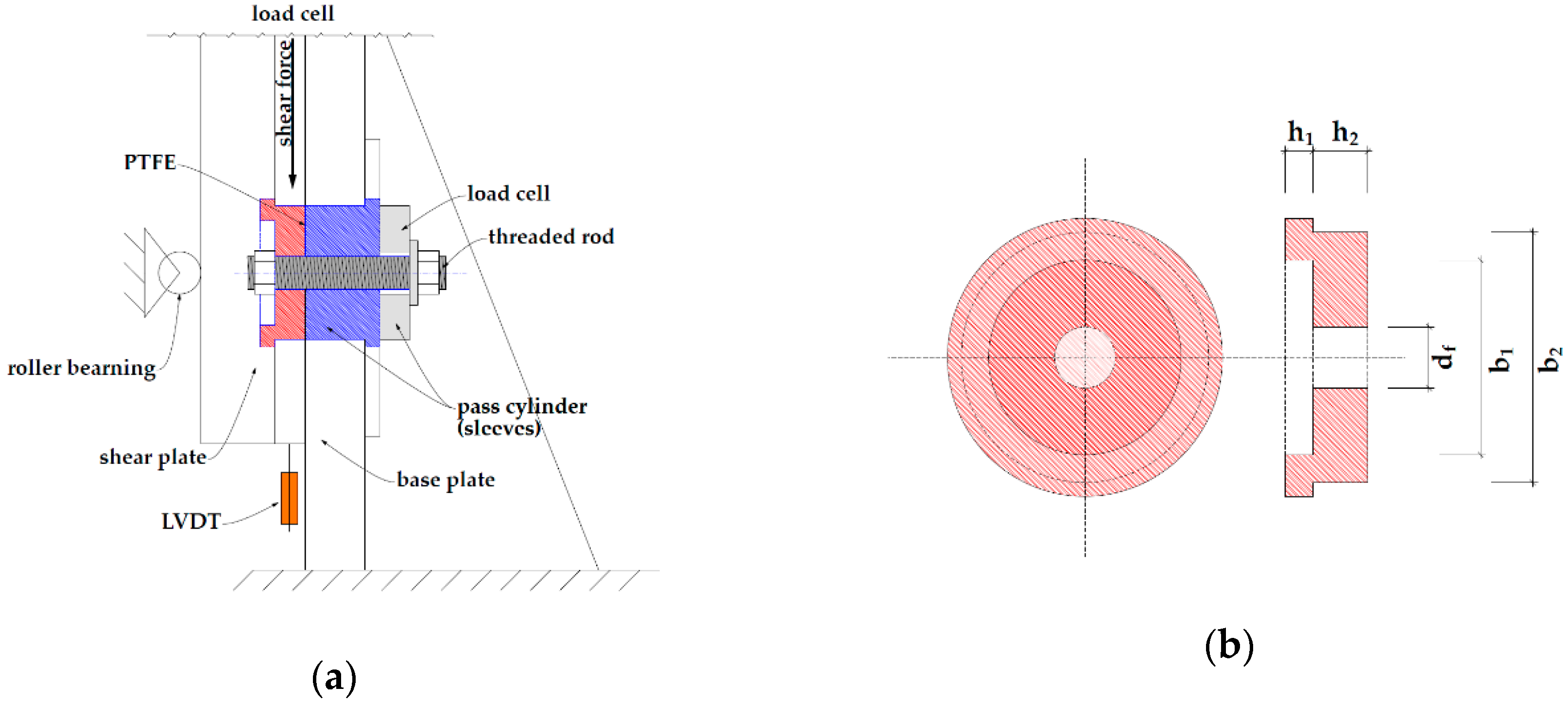
2.3. Shear Tests
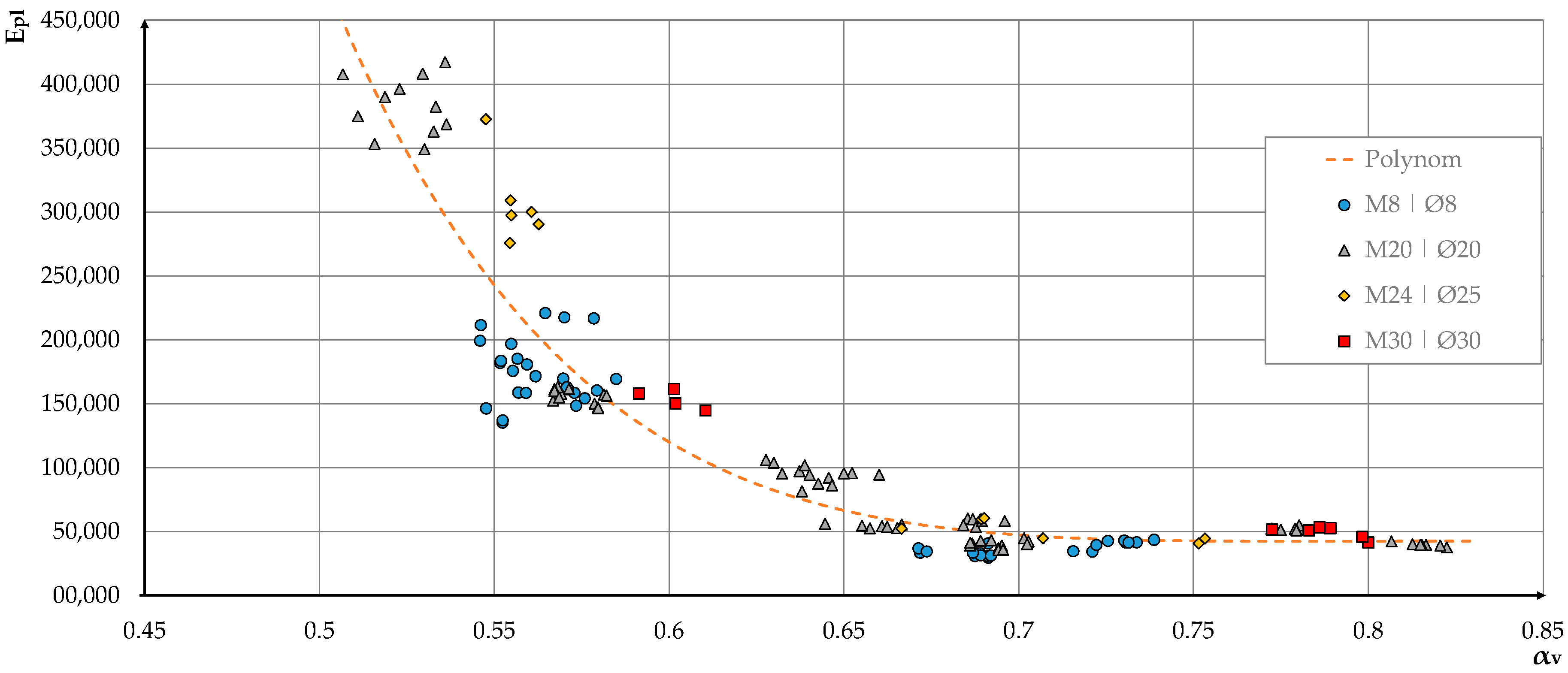
3. Results
- Results from the tensile tests were used as individual results;
- Results from the shear tests were used as average values.
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
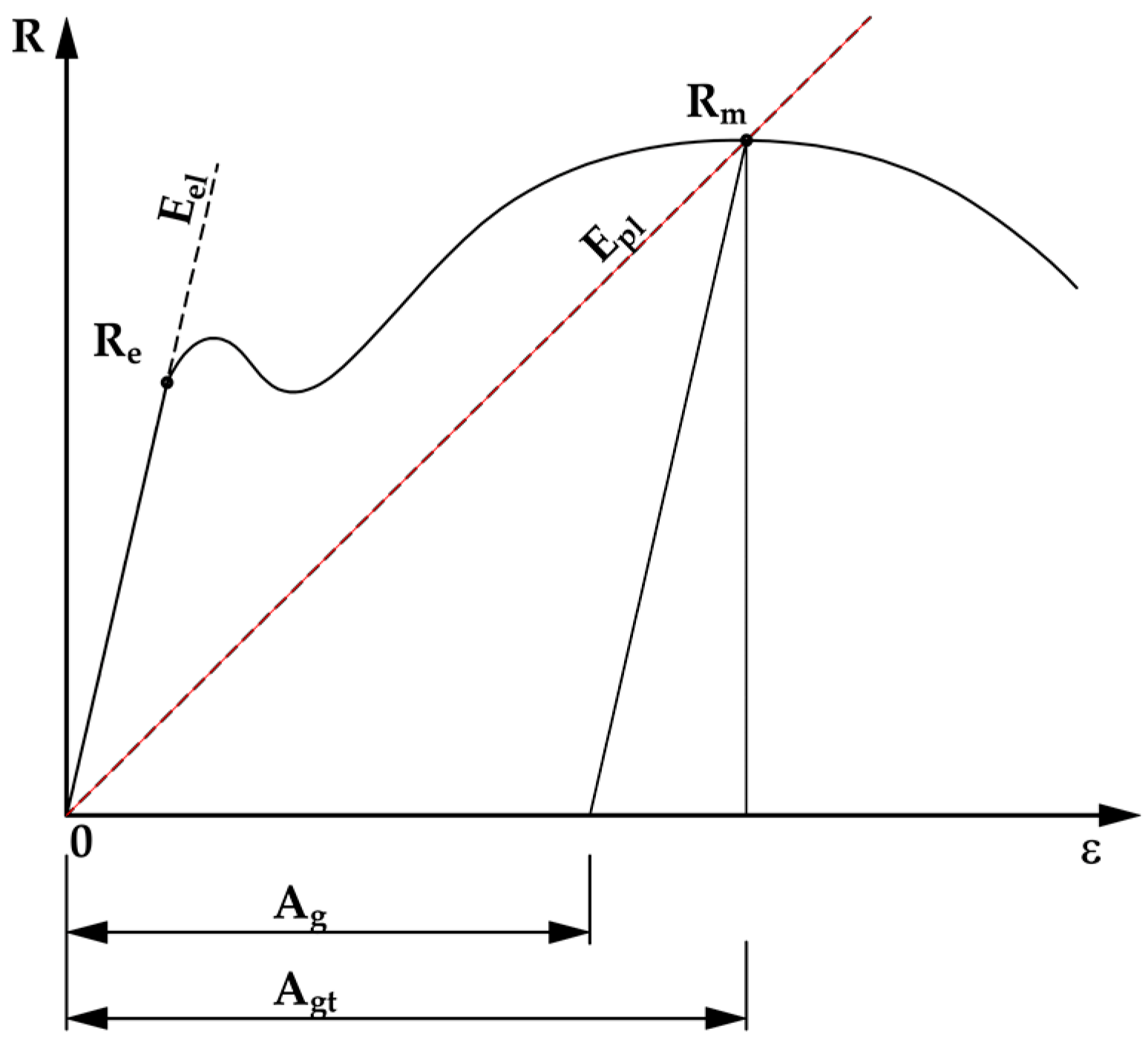
| % | plastic extension at maximum force | |
| % | total extension at maximum force | |
| mm2 | effective stressed cross-sectional area of steel element | |
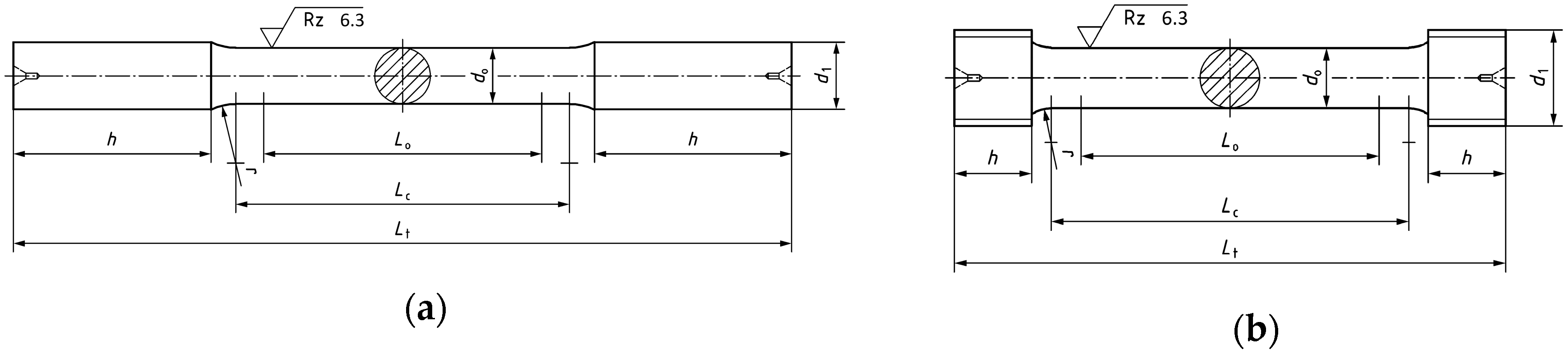
| mm | test piece diameter | |
| mm | diameter of gripped ends | |
| mm | diameter of clearance hole | |
| mm | nominal diameter | |
| mm | distance from lever arm | |
| mm | distance from lever arm | |
| N/mm2 | elastic modulus | |
| N/mm2 | plastic modulus | |
| N/mm2 | characteristic steel ultimate tensile strength | |
| mm | length of gripped ends | |
| mm | height of the bracket of the sleeves | |
| mm | height of the sleeves | |
| mm | inside diameter of the sleeves | |
| mm | outside diameter of the sleeves | |
| ° | angle between tension direction and slip plane | |
| mm | original gauge length | |
| mm | parallel length | |
| mm | total length of test piece | |
| kNm | secondary bending moment | |
| kN | ultimate tension load | |
| mm | radius | |
| N/mm2 | stress | |
| N/mm2 | yield strength | |
| N/mm2 | ultimate tensile stress | |
| kN | characteristic steel shear resistance for static loading | |
| kN | characteristic steel shear resistance for seismic loading | |
| - | reduction factor | |
| s−1 | strain rate | |
| % | extension | |
| % | total extension (include elastic and plastic extensions) | |
| % | dislocation motion in X direction | |
| % | dislocation motion in Y direction | |
| N/mm2 | compressive stress | |
| N/mm2 | tensile stress (tensile component from shear force) | |
| N/mm2 | ultimate tensile stress | |
| N/mm2 | ultimate shear stress | |
| ° | angle between tension direction and sliding direction | |
| N/mm2 | average value of the ultimate tensile stress | |
| N/mm2 | average value of the tensile stress (tensile component from shear force) | |
| N/mm2 | average value of the ultimate shear stress |
Appendix A
| Nr. | Size | Material | |||||
|---|---|---|---|---|---|---|---|
| (-) | (-) | (-) | (mm2) | (N/mm2) | (%) | (N/mm2) | (-) |
| 1 | M20 | 8.8 | 113.10 | 1050 | 2.58 | 407641 | 0.51 ** |
| 2 | M20 | 8.8 | 113.10 | 1031 | 2.92 | 353339 | 0.52 ** |
| 3 | M20 | 8.8 | 113.10 | 1017 | 2.57 | 396335 | 0.52 ** |
| 4 | M20 | 8.8 | 113.10 | 1004 | 2.87 | 349181 | 0.53 ** |
| 5 | M20 | 8.8 | 113.10 | 1025 | 2.63 | 390016 | 0.52 ** |
| 1 | Ø20 | B500B | 113.10 | 635 | 11.49 | 55265 | 0.78 |
| 2 | Ø20 | B500B | 113.10 | 636 | 12.15 | 52348 | 0.78 |
| 3 | Ø20 | B500B | 113.10 | 635 | 12.44 | 51082 | 0.78 |
| 4 | Ø20 | B500B | 113.10 | 641 | 12.23 | 52445 | 0.77 |
| 5 | Ø20 | B500B | 113.10 | 636 | 12.45 | 51038 | 0.78 |
| 6 | Ø20 | B500B | 113.10 | 639 | 12.39 | 51611 | 0.77 |
| 1 | M24 | 8.8 | 153.94 | 953 | 2.56 | 372491 | 0.55 |
| 2 | M24 | 8.8 | 153.94 | 941 | 3.04 | 309174 | 0.55 |
| 3 | M24 | 8.8 | 153.94 | 940 | 3.16 | 297617 | 0.55 |
| 4 | M24 | 8.8 | 153.94 | 941 | 3.41 | 275879 | 0.55 |
| 5 | M24 | 8.8 | 153.94 | 927 | 3.19 | 290572 | 0.56 |
| 6 | M24 | 8.8 | 153.94 | 930 | 3.10 | 300172 | 0.56 |
| 1 | Ø25 | B500B | 153.94 | 591 | 13.22 | 44714 | 0.75 |
| 2 | Ø25 | B500B | 153.94 | 593 | 14.44 | 41044 | 0.75 |
| 3 | Ø25 | B500B | 153.94 | 646 | 10.81 | 59761 | 0.69 |
| 4 | Ø25 | B500B | 153.94 | 668 | 12.75 | 52426 | 0.67 |
| 5 | Ø25 | B500B | 153.94 | 630 | 14.05 | 44827 | 0.71 |
| 6 | Ø25 | B500B | 153.94 | 645 | 10.64 | 60651 | 0.69 |
| 1 | M30 | 8.8 | 314.16 | 1049 | 6.63 | 158174 | 0.59 |
| 2 | M30 | 8.8 | 314.16 | 1032 | 6.38 | 161785 | 0.60 |
| 3 | M30 | 8.8 | 314.16 | 1031 | 6.86 | 150338 | 0.60 |
| 4 | M30 | 8.8 | 314.16 | 1017 | 7.01 | 144935 | 0.61 |
| 1 | Ø32 | B500B | 314.16 | 600 | 14.40 | 41690 | 0.80 |
| 2 | Ø32 | B500B | 314.16 | 613 | 12.01 | 51061 | 0.78 |
| 3 | Ø32 | B500B | 314.16 | 622 | 11.99 | 51878 | 0.77 |
| 4 | Ø32 | B500B | 314.16 | 611 | 11.40 | 53599 | 0.79 |
| 5 | Ø32 | B500B | 314.16 | 602 | 13.05 | 46111 | 0.80 |
| 6 | Ø32 | B500B | 314.16 | 609 | 11.49 | 52971 | 0.79 |
| Nr. | Size | Material | |||||
|---|---|---|---|---|---|---|---|
| (-) | (-) | (-) | (mm2) | (N/mm2) | (%) | (N/mm2) | (-) |
| 1 | M8 | 4.8 | 19.63 | 531 | 3.57 | 148711 | 0.57 |
| 2 | M8 | 4.8 | 19.63 | 544 | 3.01 | 181014 | 0.56 |
| 3 | M8 | 4.8 | 19.63 | 547 | 3.44 | 158952 | 0.56 |
| 4 | M8 | 4.8 | 19.63 | 532 | 3.35 | 158693 | 0.57 |
| 5 | M8 | 4.8 | 19.63 | 556 | 3.79 | 146581 | 0.55 |
| 6 | M8 | 4.8 | 19.63 | 551 | 4.07 | 135411 | 0.55 |
| 7 | M8 | 4.8 | 19.63 | 551 | 4.02 | 137157 | 0.55 |
| 8 | M8 | 4.8 | 19.63 | 552 | 3.03 | 182140 | 0.55 |
| 9 | M8 | 4.8 | 19.63 | 534 | 3.15 | 169863 | 0.57 |
| 10 | M8 | 4.8 | 19.63 | 542 | 3.16 | 171768 | 0.56 |
| 1 | M8 | 8.8 | 19.63 | 987 | 5.32 | 185467 | 0.56 |
| 2 | M8 | 8.8 | 19.63 | 973 | 4.40 | 221146 | 0.56 |
| 3 | M8 | 8.8 | 19.63 | 961 | 5.95 | 161478 | 0.57 |
| 4 | M8 | 8.8 | 19.63 | 949 | 4.37 | 217058 | 0.58 |
| 5 | M8 | 8.8 | 19.63 | 963 | 4.42 | 217789 | 0.57 |
| 6 | M8 | 8.8 | 19.63 | 990 | 5.02 | 197049 | 0.55 |
| 7 | M8 | 8.8 | 19.63 | 1005 | 4.75 | 211710 | 0.55 |
| 8 | M8 | 8.8 | 19.63 | 989 | 5.62 | 175877 | 0.56 |
| 9 | M8 | 8.8 | 19.63 | 948 | 5.90 | 160665 | 0.58 |
| 10 | M8 | 8.8 | 19.63 | 1006 | 5.04 | 199452 | 0.55 |
| 11 | M8 | 8.8 | 19.63 | 982 | 6.19 | 158722 | 0.56 |
| 12 | M8 | 8.8 | 19.63 | 995 | 5.42 | 183726 | 0.55 |
| 13 | M8 | 8.8 | 19.63 | 939 | 5.53 | 169633 | 0.58 |
| 14 | M8 | 8.8 | 19.63 | 962 | 5.90 | 163139 | 0.57 |
| 15 | M8 | 8.8 | 19.63 | 953 | 6.18 | 154383 | 0.58 |
| 1 | M8 | A4 | 19.63 | 797 | 23.60 | 33791 | 0.67 |
| 2 | M8 | A4 | 19.63 | 798 | 21.45 | 37202 | 0.67 |
| 3 | M8 | A4 | 19.63 | 743 | 21.50 | 34557 | 0.72 |
| 4 | M8 | A4 | 19.63 | 795 | 22.91 | 34710 | 0.67 |
| 5 | M8 | A4 | 19.63 | 775 | 18.86 | 41091 | 0.69 |
| 6 | M8 | A4 | 19.63 | 749 | 21.50 | 34822 | 0.72 |
| 7 | M8 | A4 | 19.63 | 779 | 25.07 | 31079 | 0.69 |
| 8 | M8 | A4 | 19.63 | 778 | 23.28 | 33408 | 0.69 |
| 9 | M8 | A4 | 19.63 | 775 | 25.95 | 29861 | 0.69 |
| 10 | M8 | A4 | 19.63 | 775 | 24.82 | 31246 | 0.69 |
| 11 | M8 | A4 | 19.63 | 777 | 24.50 | 31730 | 0.69 |
| 12 | M8 | A4 | 19.63 | 774 | 24.63 | 31431 | 0.69 |
| 13 | M8 | A4 | 19.63 | 780 | 23.08 | 33787 | 0.69 |
| 1 | Ø8 | B500B | 19.63 | 609 | 14.61 | 41671 | 0.71 |
| 2 | Ø8 | B500B | 19.63 | 609 | 14.08 | 43273 | 0.71 |
| 3 | Ø8 | B500B | 19.63 | 606 | 14.51 | 41788 | 0.72 |
| 4 | Ø8 | B500B | 19.63 | 602 | 13.72 | 43871 | 0.72 |
| 5 | Ø8 | B500B | 19.63 | 616 | 15.46 | 39820 | 0.70 |
| 6 | Ø8 | B500B | 19.63 | 613 | 14.28 | 42929 | 0.71 |
| 7 | Ø8 | B500B | 19.63 | 608 | 14.59 | 41684 | 0.71 |
| 1 | M20 | 4.8 | 153.94 | 429 | 7.90 | 54309 | 0.66 |
| 2 | M20 | 4.8 | 153.94 | 413 | 6.85 | 60318 | 0.69 |
| 3 | M20 | 4.8 | 153.94 | 413 | 6.90 | 59827 | 0.69 |
| 4 | M20 | 4.8 | 153.94 | 407 | 6.97 | 58384 | 0.70 |
| 5 | M20 | 4.8 | 153.94 | 412 | 7.66 | 53826 | 0.69 |
| 6 | M20 | 4.8 | 153.94 | 414 | 7.48 | 55403 | 0.68 |
| 7 | M20 | 4.8 | 153.94 | 425 | 7.64 | 55648 | 0.67 |
| 8 | M20 | 4.8 | 153.94 | 426 | 8.04 | 52970 | 0.67 |
| 9 | M20 | 4.8 | 153.94 | 440 | 7.79 | 56420 | 0.64 |
| 10 | M20 | 4.8 | 153.94 | 431 | 8.17 | 52747 | 0.66 |
| 11 | M20 | 4.8 | 153.94 | 433 | 7.88 | 54883 | 0.66 |
| 12 | M20 | 4.8 | 153.94 | 428 | 7.95 | 53835 | 0.66 |
| 1 | M20 | 5.6 | 153.94 | 563 | 5.95 | 94686 | 0.66 |
| 2 | M20 | 5.6 | 153.94 | 575 | 6.23 | 92323 | 0.65 |
| 3 | M20 | 5.6 | 153.94 | 580 | 6.13 | 94617 | 0.64 |
| 4 | M20 | 5.6 | 153.94 | 570 | 5.94 | 95891 | 0.65 |
| 5 | M20 | 5.6 | 153.94 | 572 | 5.97 | 95723 | 0.65 |
| 6 | M20 | 5.6 | 153.94 | 575 | 6.66 | 86350 | 0.65 |
| 7 | M20 | 5.6 | 153.94 | 578 | 6.59 | 87709 | 0.64 |
| 8 | M20 | 5.6 | 153.94 | 583 | 5.99 | 97370 | 0.64 |
| 9 | M20 | 5.6 | 153.94 | 582 | 5.70 | 102051 | 0.64 |
| 10 | M20 | 5.6 | 153.94 | 592 | 5.58 | 106141 | 0.63 |
| 11 | M20 | 5.6 | 153.94 | 590 | 5.67 | 104012 | 0.63 |
| 12 | M20 | 5.6 | 153.94 | 588 | 6.15 | 95607 | 0.63 |
| 13 | M20 | 5.6 | 153.94 | 582 | 7.13 | 81680 | 0.64 |
| 1 | M20 | 8.8 | 153.94 | 958 | 6.07 | 157970 | 0.57 |
| 2 | M20 | 8.8 | 153.94 | 942 | 6.28 | 150136 | 0.58 |
| 3 | M20 | 8.8 | 153.94 | 941 | 6.38 | 147339 | 0.58 |
| 4 | M20 | 8.8 | 153.94 | 938 | 5.96 | 157316 | 0.58 |
| 5 | M20 | 8.8 | 153.94 | 941 | 6.41 | 146732 | 0.58 |
| 6 | M20 | 8.8 | 153.94 | 937 | 5.99 | 156473 | 0.58 |
| 7 | M20 | 8.8 | 153.94 | 960 | 6.18 | 155400 | 0.58 |
| 8 | M20 | 8.8 | 153.94 | 960 | 5.88 | 163124 | 0.57 |
| 9 | M20 | 8.8 | 153.94 | 954 | 5.90 | 151756 | 0.57 |
| 10 | M20 | 8.8 | 153.94 | 961 | 5.95 | 161683 | 0.57 |
| 11 | M20 | 8.8 | 153.94 | 962 | 6.31 | 152534 | 0.57 |
| 12 | M20 | 8.8 | 153.94 | 961 | 5.99 | 160396 | 0.57 |
| 13 | M20 | 8.8 | 153.94 | 959 | 6.19 | 154952 | 0.57 |
| 14 | M20 | 8.8 | 153.94 | 992 | 2.69 | 368417 | 0.54 ** |
| 15 | M20 | 8.8 | 153.94 | 998 | 2.61 | 382472 | 0.53 ** |
| 16 | M20 | 8.8 | 153.94 | 1005 | 2.46 | 408331 | 0.53 ** |
| 17 | M20 | 8.8 | 153.94 | 993 | 2.38 | 417149 | 0.54 ** |
| 18 | M20 | 8.8 | 153.94 | 999 | 2.75 | 363023 | 0.53 ** |
| 19 | M20 | 8.8 | 153.94 | 1041 | 2.78 | 374964 | 0.51 ** |
| 1 | M20 | A4 | 153.94 | 777 | 17.89 | 43402 | 0.69 |
| 2 | M20 | A4 | 153.94 | 783 | 19.14 | 40902 | 0.69 |
| 3 | M20 | A4 | 153.94 | 765 | 18.05 | 42374 | 0.70 |
| 4 | M20 | A4 | 153.94 | 766 | 17.06 | 44924 | 0.70 |
| 5 | M20 | A4 | 153.94 | 765 | 18.91 | 40477 | 0.70 |
| 6 | M20 | A4 | 153.94 | 780 | 13.33 | 58495 | 0.69 |
| 7 | M20 | A4 | 153.94 | 773 | 19.72 | 39210 | 0.70 |
| 8 | M20 | A4 | 153.94 | 783 | 19.95 | 39269 | 0.69 |
| 9 | M20 | A4 | 153.94 | 774 | 20.87 | 37093 | 0.69 |
| 10 | M20 | A4 | 153.94 | 780 | 18.13 | 43025 | 0.69 |
| 11 | M20 | A4 | 153.94 | 783 | 18.88 | 41502 | 0.69 |
| 12 | M20 | A4 | 153.94 | 774 | 21.69 | 35703 | 0.69 |
| 13 | M20 | A4 | 153.94 | 773 | 21.48 | 35981 | 0.70 |
| 1 | Ø20 | B500B | 153.94 | 602 | 15.94 | 37800 | 0.80 |
| 2 | Ø20 | B500B | 153.94 | 607 | 15.26 | 39766 | 0.80 |
| 3 | Ø20 | B500B | 153.94 | 608 | 15.30 | 39702 | 0.80 |
| 4 | Ø20 | B500B | 153.94 | 614 | 14.46 | 42484 | 0.79 |
| 5 | Ø20 | B500B | 153.94 | 604 | 15.40 | 39199 | 0.80 |
| 6 | Ø20 | B500B | 153.94 | 610 | 15.18 | 40176 | 0.80 |
| 7 | Ø20 | B500B | 153.94 | 608 | 15.23 | 39913 | 0.80 |
| Nr. | Size | Material | |||
|---|---|---|---|---|---|
| (-) | (-) | (-) | (mm2) | (N/mm2) | (N/mm2) |
| 1 | M8 | 4.8 | 36.6 | 298 | 62.6 |
| 2 | M8 | 4.8 | 36.6 | 299 | 71.8 |
| 3 | M8 | 4.8 | 36.6 | 317 | 70.4 |
| 4 | M8 | 4.8 | 36.6 | 328 | 72.1 |
| 5 | M8 | 4.8 | 36.6 | 327 | 69.1 |
| 6 | M8 | 4.8 | 36.6 | 314 | 41.3 |
| 1 | M8 | 8.8 | 36.6 | 542 | 103.4 |
| 2 | M8 | 8.8 | 36.6 | 540 | 75.8 |
| 3 | M8 | 8.8 | 36.6 | 538 | 81.2 |
| 4 | M8 | 8.8 | 36.6 | 558 | 60.3 |
| 5 | M8 | 8.8 | 36.6 | 554 | 80.0 |
| 6 | M8 | 8.8 | 36.6 | 563 | 64.0 |
| 1 | M8 | A4 | 36.6 | 525 | 56.6 |
| 2 | M8 | A4 | 36.6 | 521 | 60.7 |
| 3 | M8 | A4 | 36.6 | 529 | - |
| 4 | M8 | A4 | 36.6 | 550 | 61.4 |
| 5 | M8 | A4 | 36.6 | 542 | 63.8 |
| 6 | M8 | A4 | 36.6 | 547 | 63.9 |
| 1 | Ø8 | B500B | 50.3 | 452 | 49.5 |
| 2 | Ø8 | B500B | 50.3 | 450 | 50.6 |
| 3 | Ø8 | B500B | 50.3 | 442 | 36.6 |
| 4 | Ø8 | B500B | 50.3 | 437 | 38.3 |
| 5 | Ø8 | B500B | 50.3 | 434 | 41.6 |
| 6 | Ø8 | B500B | 50.3 | 453 | - |
| 1 | M20 | 4.8 | 245.0 | 282 | 17.9 |
| 2 | M20 | 4.8 | 245.0 | 283 | 17.7 |
| 3 | M20 | 4.8 | 245.0 | 281 | 22.8 |
| 4 | M20 | 4.8 | 245.0 | 288 | 20.2 |
| 5 | M20 | 4.8 | 245.0 | 281 | 16.4 |
| 6 | M20 | 4.8 | 245.0 | 286 | 20.7 |
| 1 | M20 | 5.6 | 245.0 | 374 | 23.0 |
| 2 | M20 | 5.6 | 245.0 | 365 | 32.0 |
| 3 | M20 | 5.6 | 245.0 | 372 | 25.6 |
| 4 | M20 | 5.6 | 245.0 | 374 | 14.0 |
| 5 | M20 | 5.6 | 245.0 | 373 | 16.8 |
| 6 | M20 | 5.6 | 245.0 | 371 | 21.0 |
| 1 | M20 | 8.8 | 245.0 | 548 | 37.2 |
| 2 | M20 | 8.8 | 245.0 | 554 | 42.6 |
| 3 | M20 | 8.8 | 245.0 | 532 | 36.8 |
| 4 | M20 | 8.8 | 245.0 | 550 | 27.7 |
| 5 | M20 | 8.8 | 245.0 | 545 | 22.6 |
| 6 | M20 | 8.8 | 245.0 | 542 | 25.0 |
| 1 | M20 | A4 | 245.0 | 550 | 29.8 |
| 2 | M20 | A4 | 245.0 | 540 | 35.5 |
| 3 | M20 | A4 | 245.0 | 554 | 43.4 |
| 4 | M20 | A4 | 245.0 | 530 | 39.4 |
| 5 | M20 | A4 | 245.0 | 527 | 13.0 |
| 6 | M20 | A4 | 245.0 | 524 | 14.1 |
| 1 | Ø20 | B500B | 314.2 | 501 | 24.1 |
| 2 | Ø20 | B500B | 314.2 | 500 | 31.3 |
| 3 | Ø20 | B500B | 314.2 | 503 | 37.1 |
| 4 | Ø20 | B500B | 314.2 | 485 | 20.9 |
| 5 | Ø20 | B500B | 314.2 | 492 | 17.3 |
| 6 | Ø20 | B500B | 314.2 | 493 | 8.6 |
| 1 | M24 | 8.8 | 352.5 | 530 | 28.3 |
| 2 | M24 | 8.8 | 352.5 | 519 | 25.9 |
| 3 | M24 | 8.8 | 352.5 | 527 | 47.2 |
| 4 | M24 | 8.8 | 352.5 | 514 | 39.3 |
| 5 | M24 | 8.8 | 352.5 | 517 | 44.9 |
| 6 | M24 | 8.8 | 352.5 | 523 | 45.8 |
| 1 | Ø25 | B500B | 490.9 | 447 | 57.0 |
| 2 | Ø25 | B500B | 490.9 | 448 | 50.6 |
| 3 | Ø25 | B500B | 490.9 | 441 | - |
| 1 | M30 | 8.8 | 561.0 | 618 | 51.9 |
| 2 | M30 | 8.8 | 561.0 | 619 | 66.1 |
| 3 | M30 | 8.8 | 561.0 | 628 | 56.3 |
| 4 | M30 | 8.8 | 561.0 | 626 | 36.6 |
| 5 | M30 | 8.8 | 561.0 | 615 | 68.2 |
| 6 | M30 | 8.8 | 561.0 | 617 | 39.4 |
| 1 | Ø32 | B500B | 804.2 | 491 | 25.6 |
| 2 | Ø32 | B500B | 804.2 | 478 | 47.2 |
| 3 | Ø32 | B500B | 804.2 | 472 | 38.5 |
References
- DIN EN 1992-4. Eurocode 2—Design of Concrete Structures—Part 4: Design of Fastenings for Use in Concrete; Deutsches Institut für Normung: Berlin, Germany, 2019. [Google Scholar]
- EAD 330499-00-0601. Bonded Fasteners for Use in Concrete; European Organisation for Technical Assessment (EOTA): Brussels, Belgium, 2017. [Google Scholar]
- Friberg, B.F. Design of Dowels in Transverse Joints of Concrete Pavements. Am. Soc. Civ. Eng. 1938, 64, 1809–1828. [Google Scholar]
- Friberg, B.F. Load and deflection characteristics of dowles in transverse joints of concrete pavements. In Proceedings of the Eighteenth Annual Meeting of the Highway Research Board Held at Washington, Washington, DC, USA, 28 November–2 December 1938; Volume 18, pp. 140–161. [Google Scholar]
- Paulay, T.; Park, R.; Phillips, M.H. Horizontal Construction Joints in Cast-In-Place Reinforced Concrete. J. Am. Concr. Inst. 1974, 42, 599–616. [Google Scholar]
- Rasmussen, B.H. The Carrying Capacity of Transversely Loaded Bolts and Dowles Embded in Concrete. Bygn. Medd. 1963, 34, 39–55. [Google Scholar]
- Vintzeleou, E.N.; Tassios, T. Behavior of Dowels under Cyclic Deformations. ACI Struct. J. 1987, 84, 18–30. [Google Scholar]
- DAfStb 346. Tragfähigkeit Geschweißter Verbindungen im Betonfertigteilbau; Deutscher Ausschuss für Stahlbeton: Berlin-München, Germany, 1983. [Google Scholar]
- DAfStb 424. Tragverhalten von Befestigungen unter Querlasten in ungerissenem Beton; Deutscher Ausschuss für Stahlbeton: Berlin, Germany, 1992. [Google Scholar]
- Kim, Y.H.; Trejo, D. Large-Diameter Shear Connector Systems for Full-Depth Precast Overhang Panels: Evaluation and Design. ACI Struct. J. 2015, 112, 439–449. [Google Scholar] [CrossRef]
- Kim, Y.H.; Trejo, D. Shear-Transfer Mechanism and Design of Shear Connectors for Full-Depth Precast Deck Panel System. ACI Struct. J. 2014, 111, 935–944. [Google Scholar] [CrossRef]
- Welz, G.; Eligehausen, R. Tragverhalten und Bemessung von Injektionsdübeln unter Quer- und Schrägzugbelastung im Mauerwerk. Ph.D. Thesis, University of Stuttgart, Germany, Stuttgart, 12 July 2011. [Google Scholar]
- Lungerhausen, H. Zur Schubtragfähigkeit von Kopfbolzendübeln. Rep. Tech. 1988, Notification Nr. 88-7, 10–26. [Google Scholar]
- Eligehausen, R. Befestigungstechnik im Beton- und Mauerwerksbau; Ernst und Sohn: Berlin, Germany, 2000; pp. 100–180. [Google Scholar]
- Grosser, P.R.; Eligehausen, R. Load-Bearing Behavior and Design of Anchorages Subjected to Shear and Torsion Loading in Uncracked Concrete. Ph.D. Thesis, University of Stuttgart, Germany, Stuttgart, 31 July 2012. [Google Scholar]
- Sklarov, N. Contribution to Load Bearing Behaviour of Bonded Anchors under Seismic Loads. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 2021. (Unpublished). [Google Scholar]
- DIN EN 1993-1-4. Eurocode 3: Design of Steel Structures—Part 1-4: General Rules—Supplementary Rules for Stainless Steels; Deutsches Institut für Normung: Berlin, Germany, 2015. [Google Scholar]
- DIN EN 1993-1-8. Eurocode 3: Design of Steel Structures—Part 1-8: Design of Joints; Deutsches Institut für Normung: Berlin, Germany, 2010. [Google Scholar]
- DIN EN ISO 898-1. Mechanical Properties of Fasteners Made of Carbon Steel and Alloy Steel—Part 1: Bolts, Screws and Studs with Specified Property Classes—Coarse Thread and Fine Pitch Thread (ISO 898-1:2013); Deutsches Institut für Normung: Berlin, Germany, 2013. [Google Scholar]
- VDI 2230 Part 1. Systematic Calculation of Highly Stressed Bolted Joints Joints with One Cylindrical Bolt; Verein Deutscher Ingenieuere (VDI): Düsseldorf, Germany, 2015. [Google Scholar]
- DIN EN ISO 3506-1. Mechanical Properties of Corrosion-Resistant Stainless Steel Fasteners—Part 1: Bolts, Screws and Studs (ISO 3506-1:2020); Deutsches Institut für Normung: Berlin, Germany, 2020. [Google Scholar]
- DIN 18800-1. Steel Structures—Part 1: Design and Construction; Deutsches Institut für Normung: Berlin, Germany, 2008. [Google Scholar]
- Mises, V.R. Mechanics of solid bodies in the plastically-deformable state. Nachr. Ges. Wiss. Göttingen 1913, 4, 582–592. [Google Scholar]
- Gottstein, G. Mechanical properties. In Materialwissenschaft und Werkstofftechnik, 4th ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2014; pp. 207–272. [Google Scholar]
- Gottstein, G. Physikalische Grundlagen der Materialkunde, 3rd ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2007; pp. 210–239. [Google Scholar]
- Dieter, G.E. Mechanical Metallurgy, 1st ed.; Mehl, R.F., Bever, M.B., Eds.; Indian Edition; McGraw-Hill: New York, NY, USA, 1961; pp. 81–111. [Google Scholar]
- Roos, E.; Maile, K.; Seidenfuß, M. Werkstoffkunde für Ingenieure, 6th ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2017; pp. 114–119. [Google Scholar]
- DIN 50125. Testing of Metallic Materials—Tensile Test Pieces; Deutsches Institut für Normung: Berlin, Germany, 2016. [Google Scholar]
- RTSS Videoextensometer: Limess Messtechnik und Software GmbH. Available online: https://www.limess.com/de/produkte/rtss-videoextensometer (accessed on 28 September 2020).
- DIN EN ISO 6892-1. Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature (ISO 6892-1:2019); Deutsches Institut für Normung: Berlin, Germany, 2020. [Google Scholar]
- DIN EN 28749. Pins and Grooved Pins; Shear test; (ISO 8749: 1986); Deutsches Institut für Normung: Berlin, Germany, 1992. [Google Scholar]
- TR 048. Details of Test for Post-Installed Fasteners in Concrete; European Organisation for Technical Assessment (EOTA): Brussels, Belgium, 2016. [Google Scholar]
- TR 049. Post-Installed Fasteners in Concrete under Seismic Action; European Organisation for Technical Assessment (EOTA): Brussels, Belgium, 2016. [Google Scholar]
- EAD 330232-00-0601. Mechanical Fasterners for Use in Concrete; European Organisation for Technical Assessment (EOTA): Brussels, Belgium, 2016. [Google Scholar]

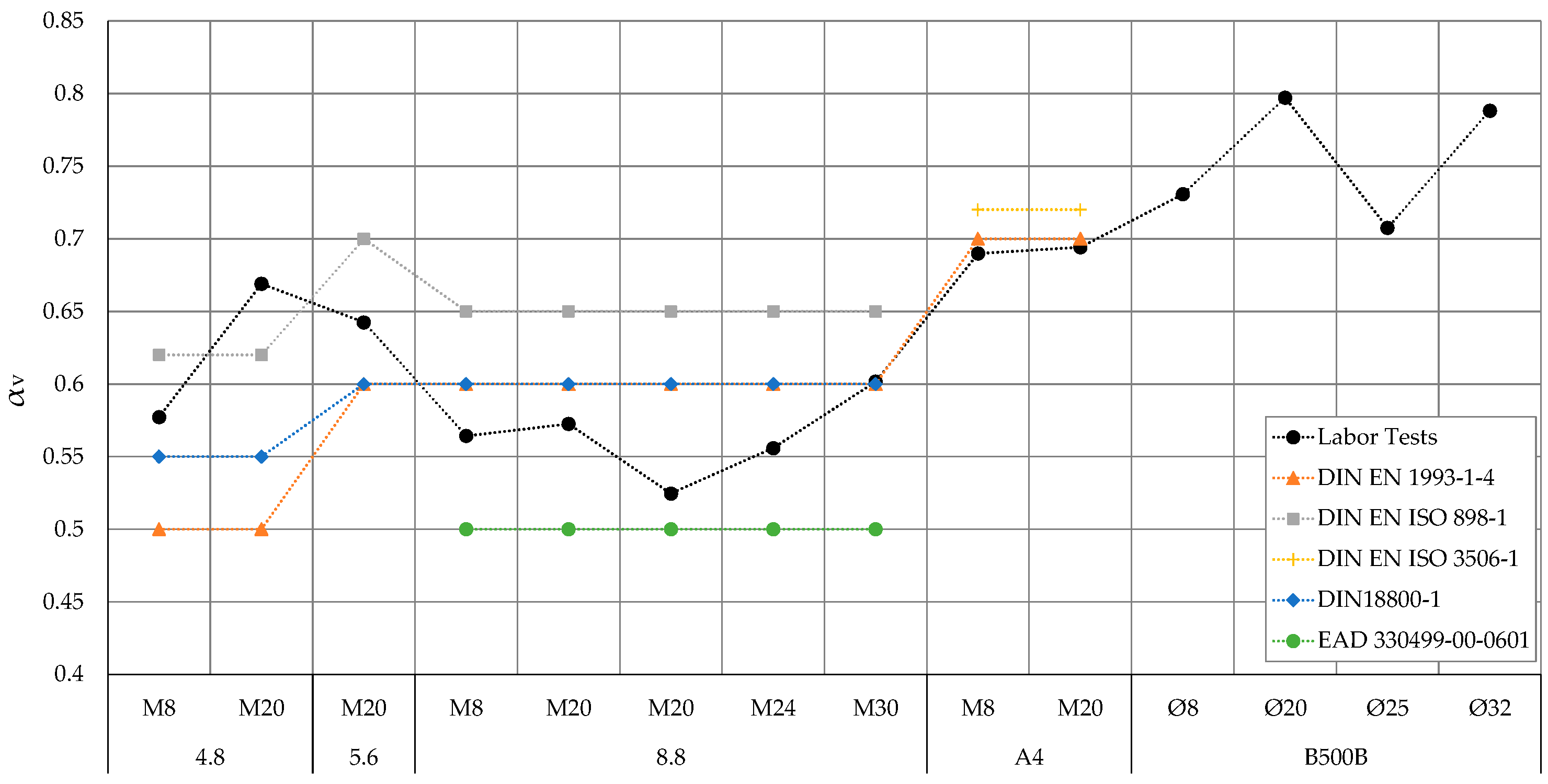

| Standard | 4.8 | 5.6 | 8.8 | A4/70 |
|---|---|---|---|---|
| DIN EN 1993-1-4 [17] DIN EN 1993-1-8 [18] | 0.50 | 0.60 | 0.60 | 0.70 |
| VDI 2230 [19,20,21] | 0.62 | 0.70 | 0.65 | 0.72 |
| DIN18800-1 [22] | 0.55 | 0.60 | 0.60 | - |
| EAD 330499-00-0601 [2] | - | - | 0.50 | - |
| Size | Steel Grade | |
|---|---|---|
| (-) | (mm) | (-) |
| M8 M20 | 8 20 | 4.8 8.8 A4/70 |
| M20 | 20 | 5.6 |
| M24 | 24 | 8.8 |
| M30 | 30 | |
| Ø8 | 8 | B500 B |
| Ø20 | 20 | |
| Ø25 | 25 | |
| Ø32 | 32 |
| Form | Size | d0 | L0 | d1 | r | h | Lc | Lt |
|---|---|---|---|---|---|---|---|---|
| A | M20|Ø20 | 12 | 60 | 15 | 9 | 150 | 72 | 382 |
| A | M24|Ø25 | 14 | 70 | 17 | 11 | 150 | 84 | 396 |
| A | M30|Ø32 | 20 | 100 | 24 | 15 | 150 | 120 | 435 |
| B | M8|Ø8 | 5 | 25 | M8 | 4 | 20 | 30 | 77 |
| B | M20|Ø20 | 14 | 70 | M20 | 11 | 40 | 95 | 180 |
| Shear Plate | Base Plate | ||||||
|---|---|---|---|---|---|---|---|
| Size | df | h1 | h2 | b1 | h1 | h2 | b1 |
| (-) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) |
| M8 | 8 | 5 | 8 | 90 | 5 | 50 | 90 |
| M20 | 20 | 5 | 20 | 90 | 5 | 50 | 90 |
| M24 | 24 | 5 | 24 | 90 | 5 | 50 | 90 |
| M30 | 30 | 5 | 30 | 90 | 5 | 50 | 90 |
| Ø8 | 9 | 5 | 8 | 90 | 5 | 50 | 90 |
| Ø20 | 22 | 5 | 20 | 90 | 5 | 50 | 90 |
| Ø25 | 29 | 5 | 25 | 90 | 5 | 50 | 90 |
| Ø32 | 35 | 5 | 32 | 90 | 5 | 50 | 90 |
| Size | Material | |||
|---|---|---|---|---|
| (-) | (-) | (N/mm2) | (N/mm2) | (-) |
| M8 | 4.8 | 544 | 314 | 0.58 |
| M8 | 8.8 | 973 | 549 | 0.56 |
| M8 | A4 | 777 | 536 | 0.69 |
| Ø8 | B500B | 609 | 445 | 0.73 |
| M20 | 4.8 | 423 | 283 | 0.67 |
| M20 | 5.6 | 579 | 372 | 0.64 |
| M20 | 8.8 | 952 | 545 | 0.57 |
| M20 | 8.8 | 1014 | 532 ** | 0.52 |
| M20 | A4 | 775 | 538 | 0.69 |
| Ø20 | B500B | 621 | 495 | 0.80 |
| M24 | 8.8 | 939 | 522 | 0.56 |
| Ø25 | B500B | 629 | 445 | 0.71 |
| M30 | 8.8 | 1032 | 621 | 0.60 |
| Ø32 | B500B | 609 | 480 | 0.79 |
| Size | Material | |||
|---|---|---|---|---|
| (-) | (-) | (N/mm2) | (N/mm2) | (-) |
| M8 | 4.8 | 314 | 65 | 0.21 |
| M8 | 8.8 | 549 | 77 | 0.14 |
| M8 | A4 | 536 | 61 | 0.11 |
| Ø8 | B500B | 445 | 43 * | 0.07 |
| M20 | 4.8 | 283 | 19 | 0.07 |
| M20 | 5.6 | 372 | 22 | 0.06 |
| M20 | 8.8 | 545 | 32 | 0.06 |
| M20 | A4 | 538 | 29 | 0.05 |
| Ø20 | B500B | 495 | 23 * | 0.05 |
| M24 | 8.8 | 522 | 38 | 0.07 |
| Ø25 | B500B | 445 | 44 * | 0.10 |
| M30 | 8.8 | 621 | 53 | 0.09 |
| Ø32 | B500B | 480 | 38 * | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sklarov, N.; Thiele, C. Material-Dependent Shear Capacity of Threaded Rods. CivilEng 2020, 1, 351-367. https://doi.org/10.3390/civileng1030022
Sklarov N, Thiele C. Material-Dependent Shear Capacity of Threaded Rods. CivilEng. 2020; 1(3):351-367. https://doi.org/10.3390/civileng1030022
Chicago/Turabian StyleSklarov, Nikolai, and Catherina Thiele. 2020. "Material-Dependent Shear Capacity of Threaded Rods" CivilEng 1, no. 3: 351-367. https://doi.org/10.3390/civileng1030022
APA StyleSklarov, N., & Thiele, C. (2020). Material-Dependent Shear Capacity of Threaded Rods. CivilEng, 1(3), 351-367. https://doi.org/10.3390/civileng1030022






