Effect of Frequency Content of Earthquake on the Seismic Response of Interconnected Electrical Equipment
Abstract
1. Introduction
2. Analytical Model for Cabinet Assembly
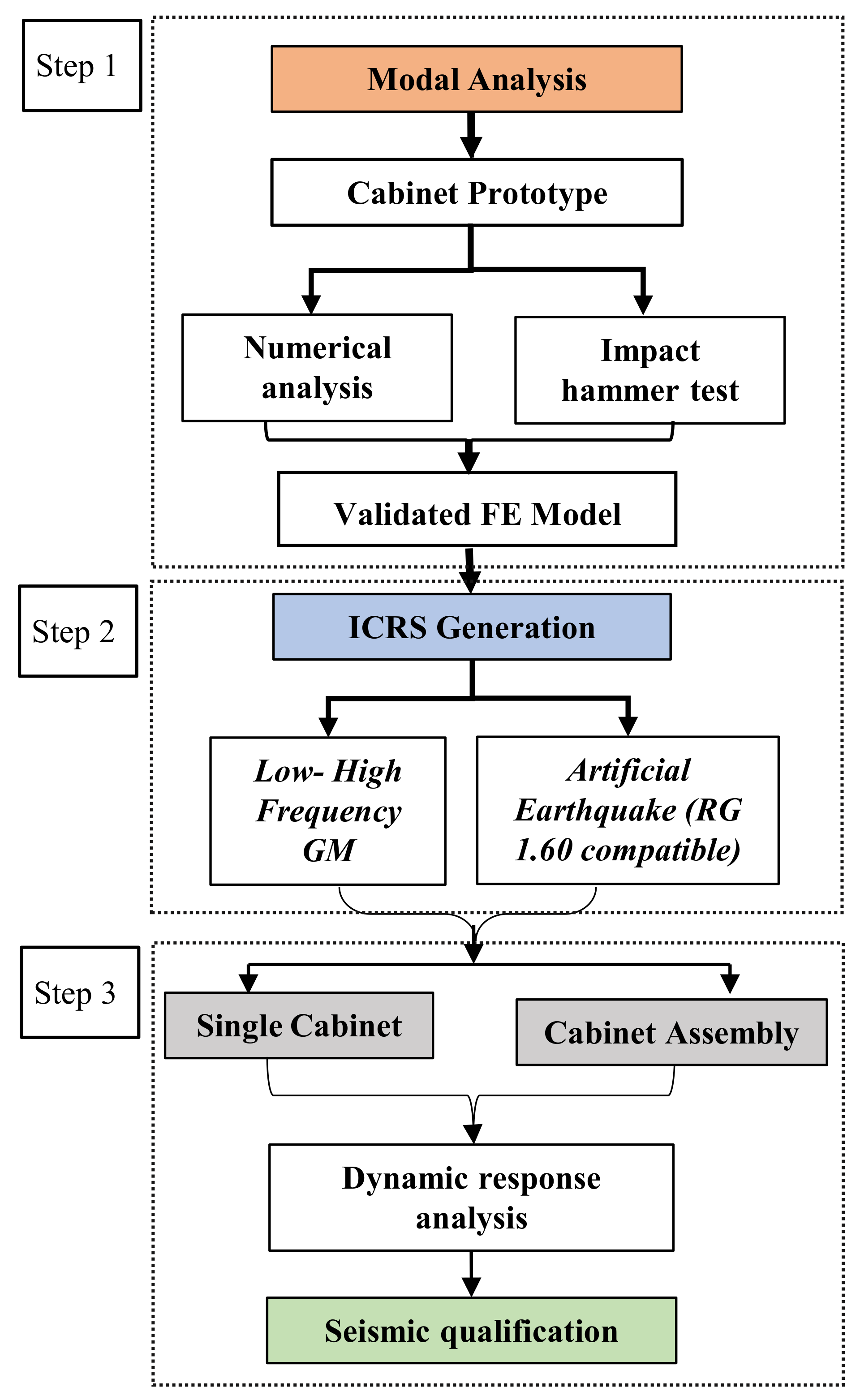
2.1. Development Steps
2.2. Modal Testing
2.3. Numerical Modeling
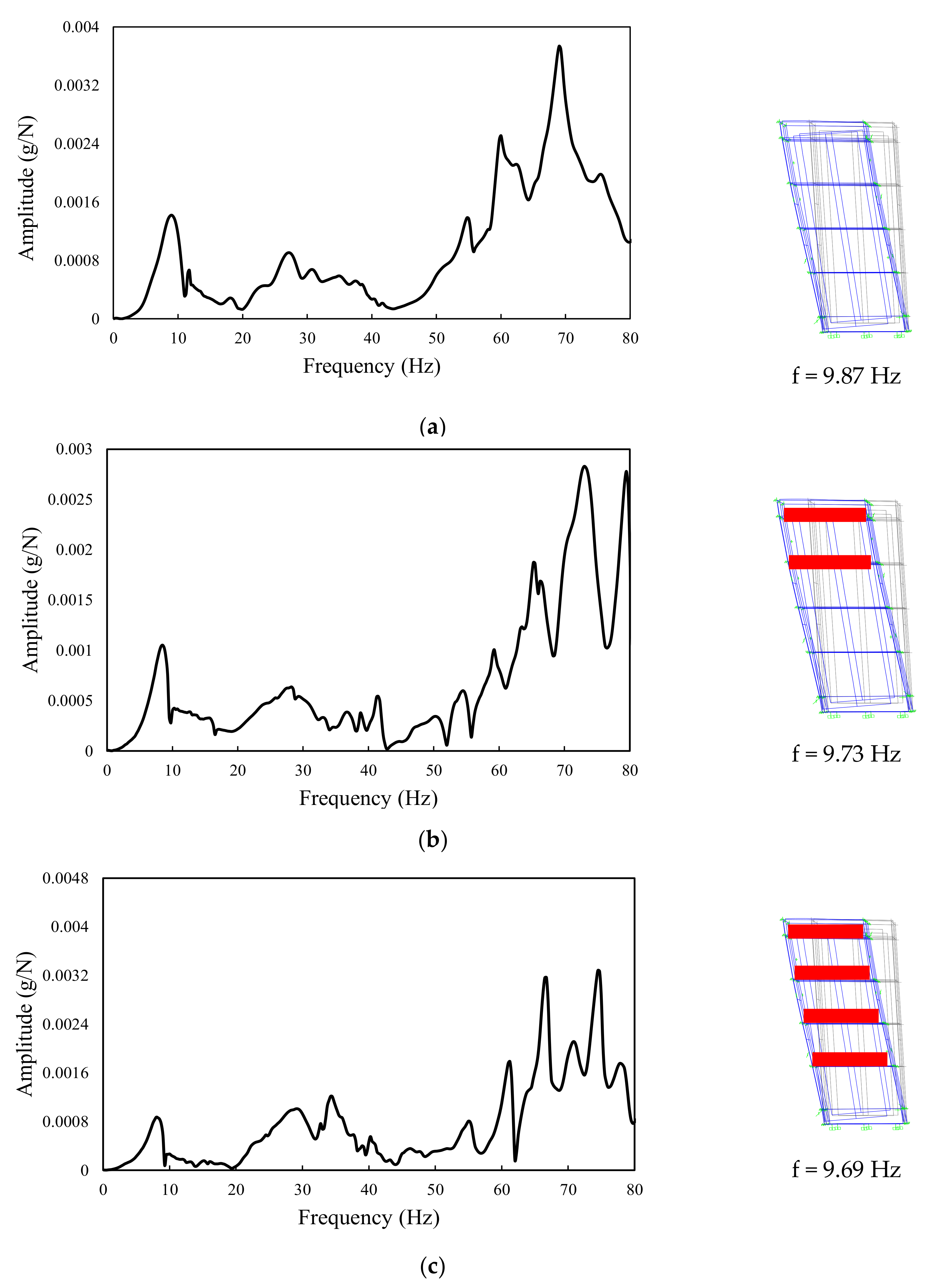
2.4. Validation of FE Models
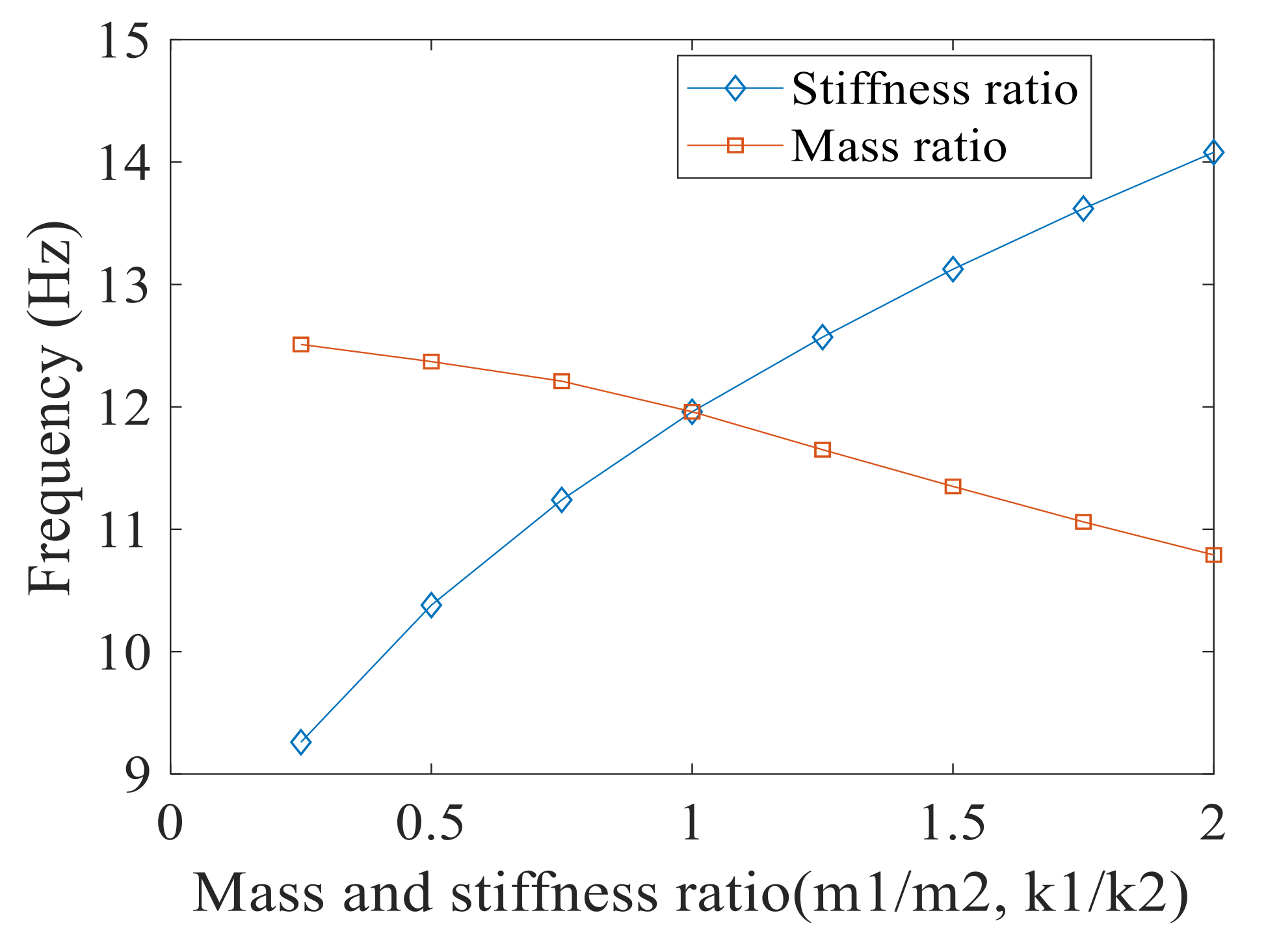
3. Mathematical Model for Interconnected Cabinets
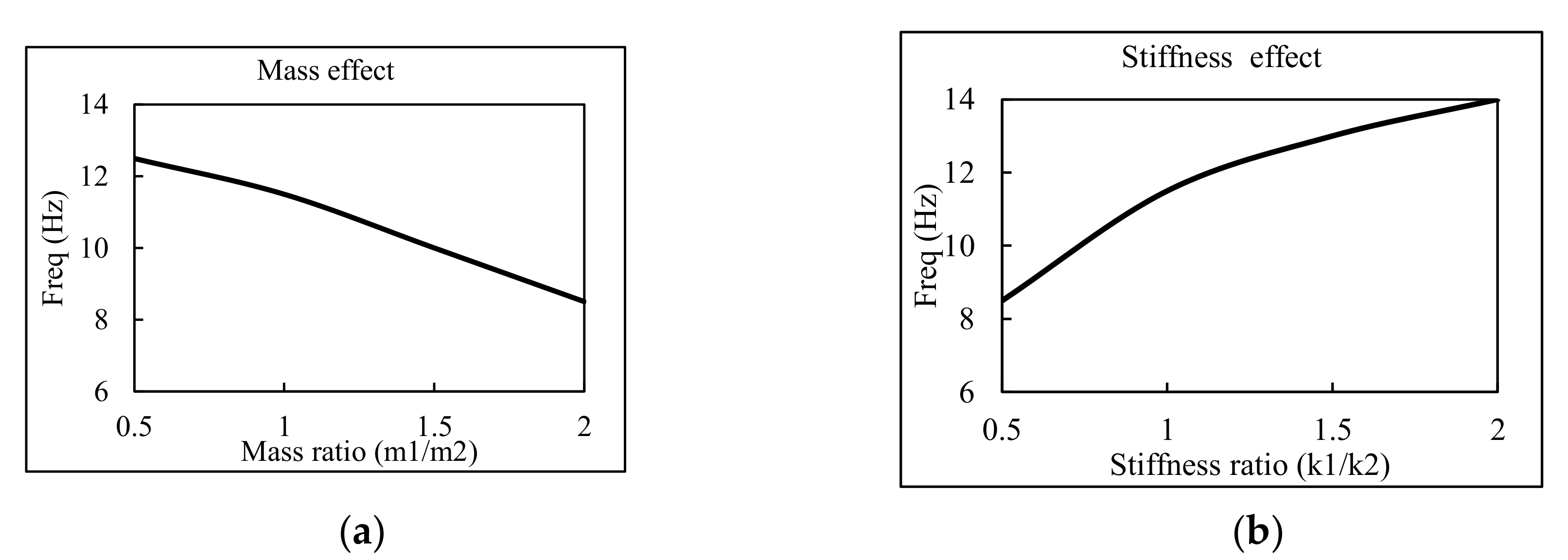
4. Uncertainties in In-Cabinet Response Generation
4.1. Grouping Effects of the Cabinet
4.2. Effect of the In-Cabinet Component Load
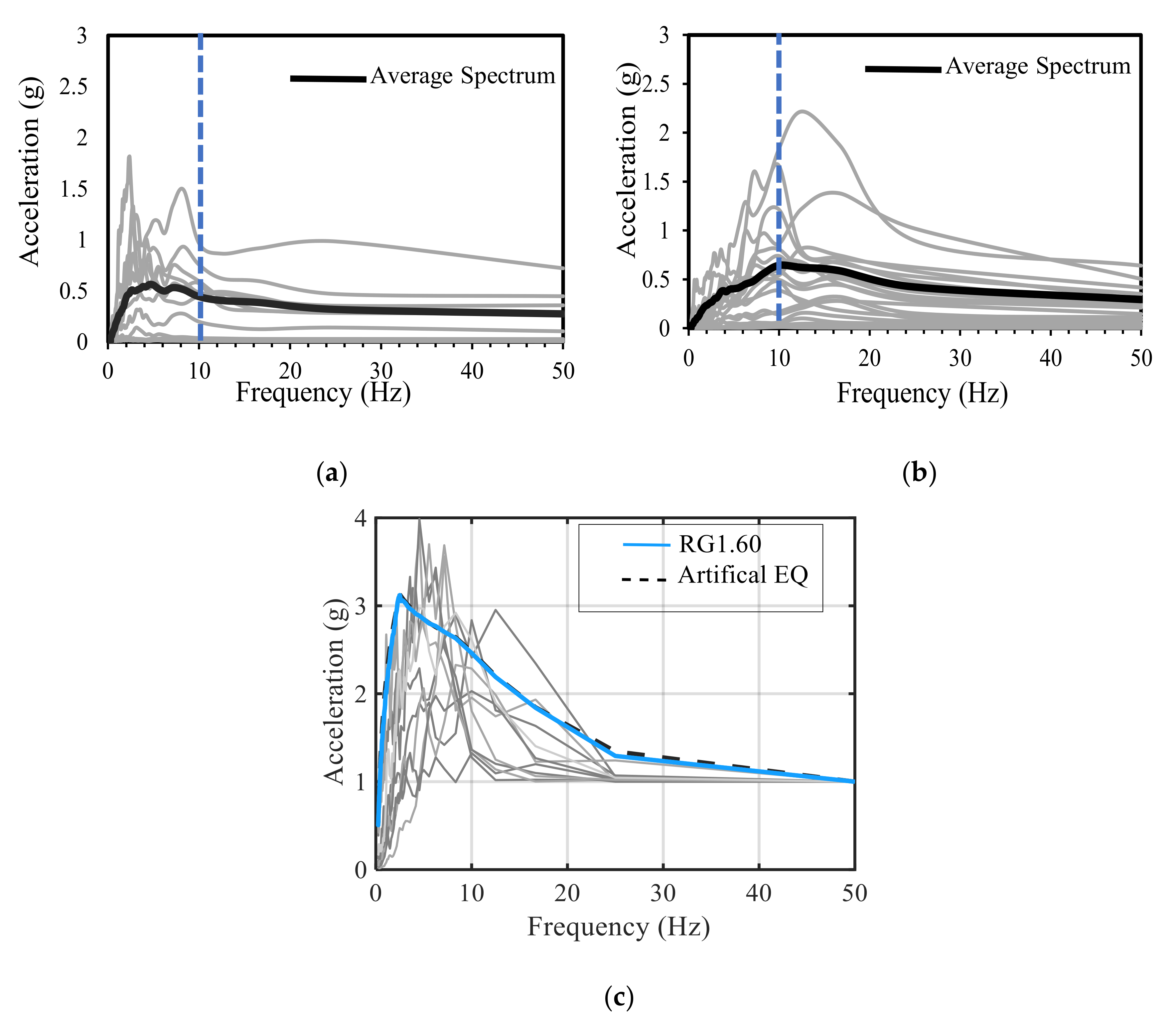
4.3. Influence on ICRS due to Input Protocol
5. Result and Discussion
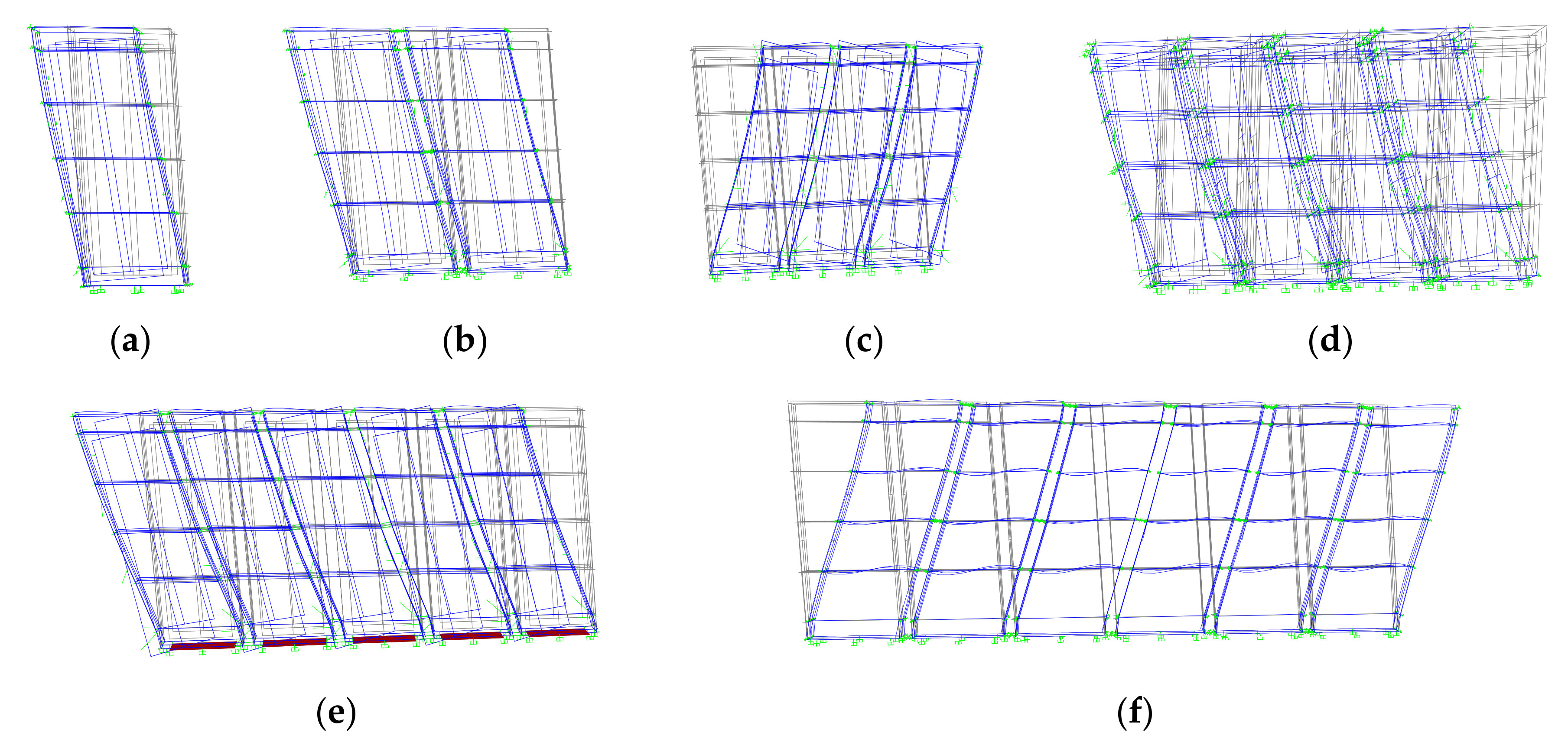
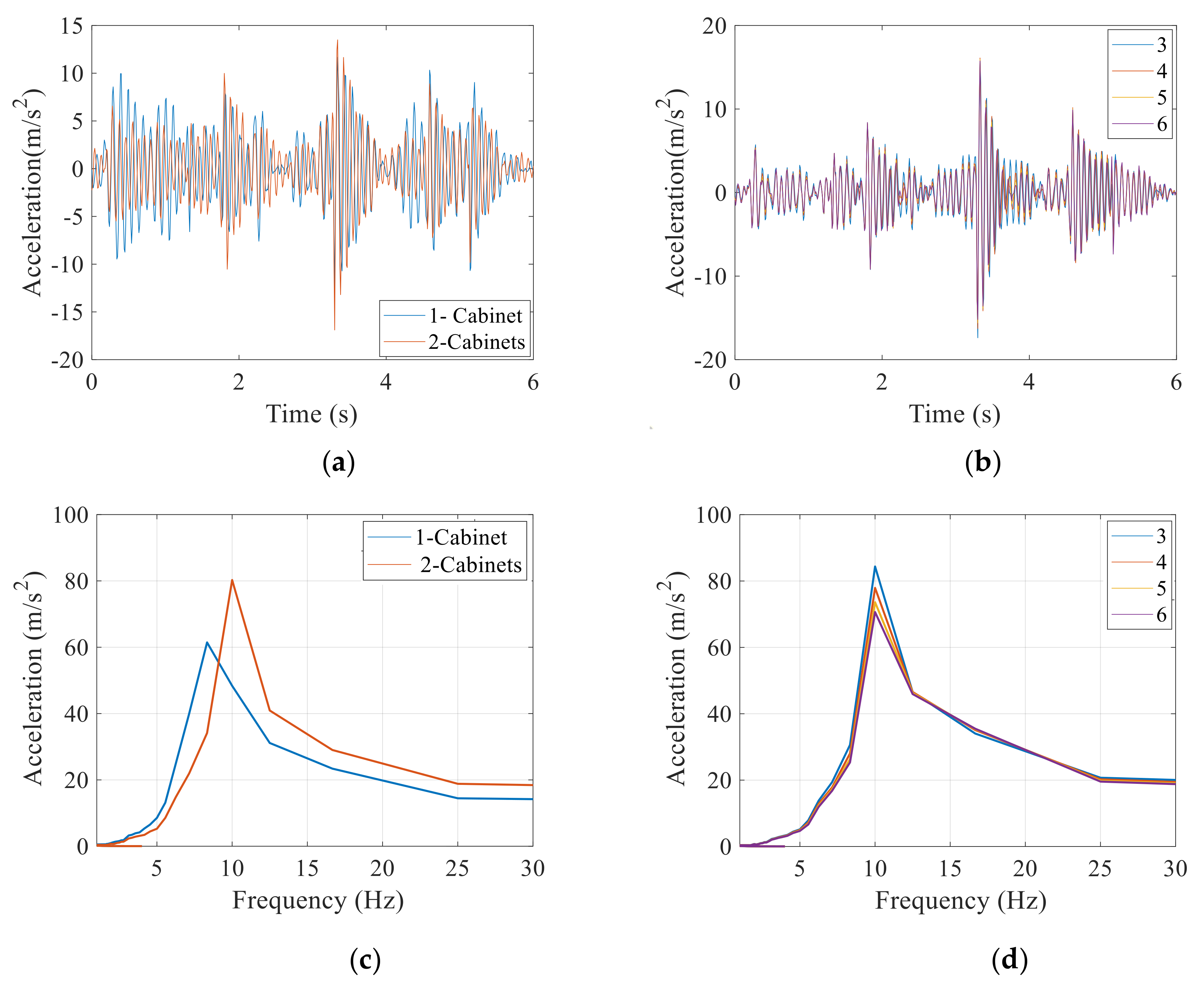
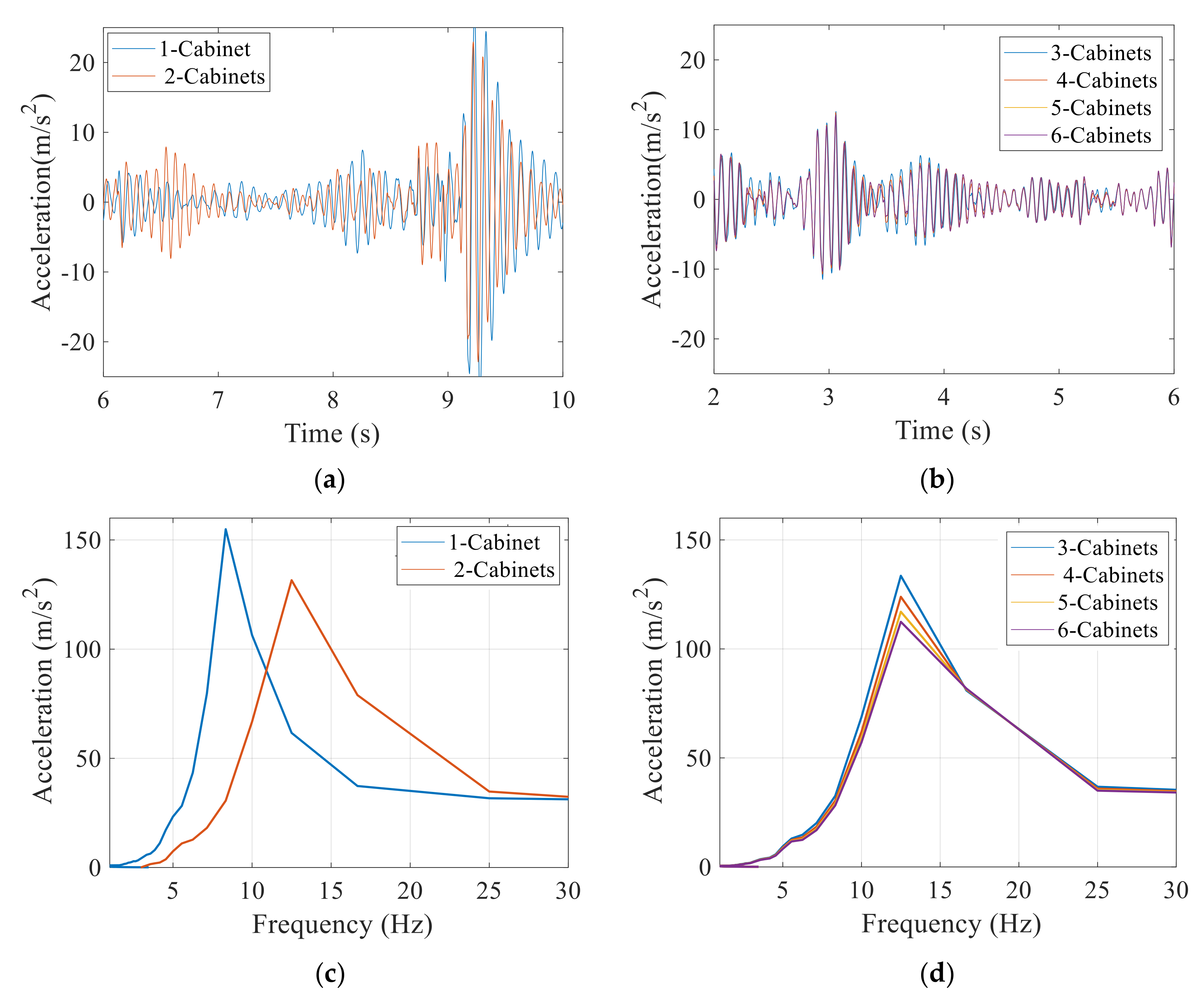
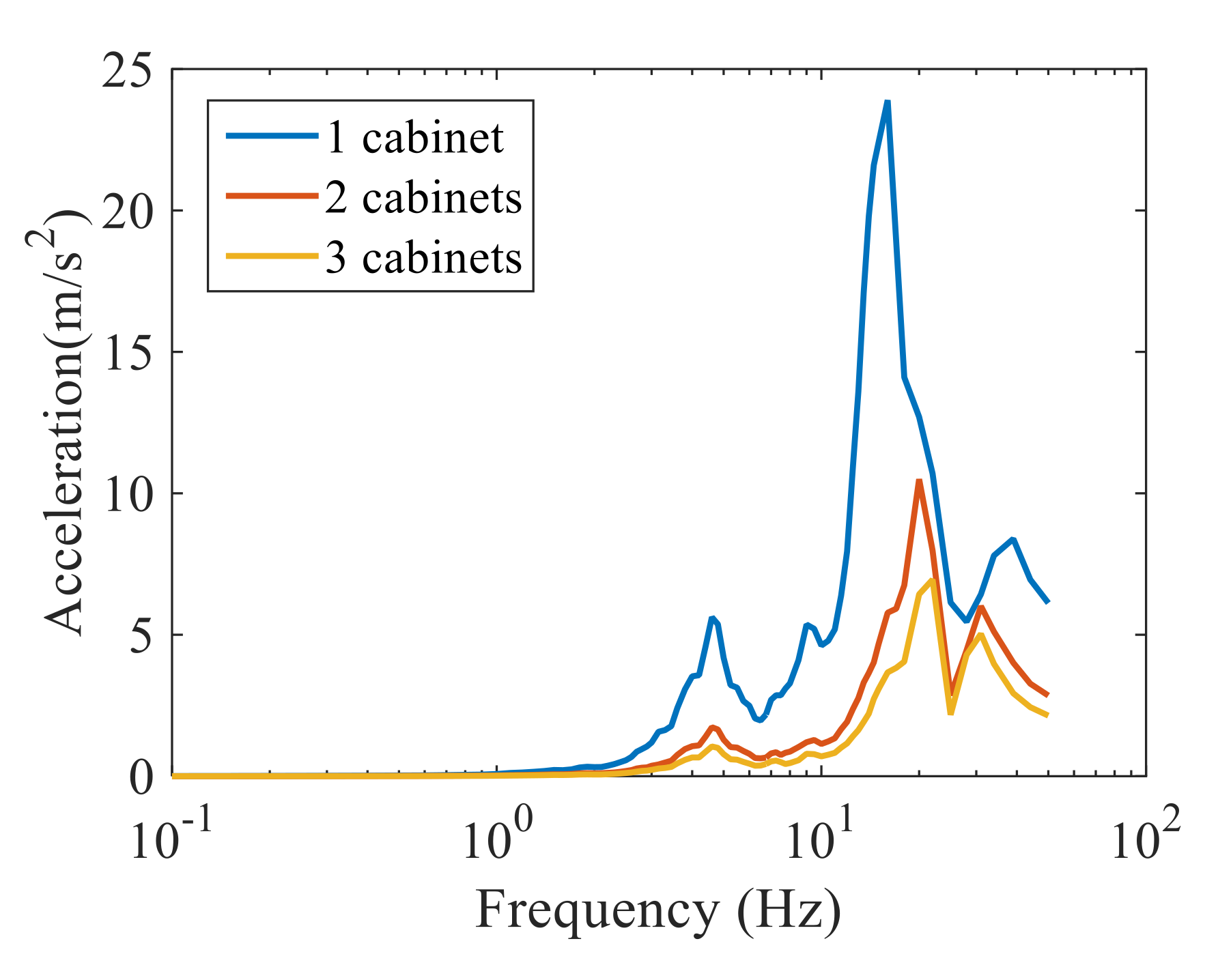
5.1. In-Cabinet Components and Grouping Effect of the Cabinets
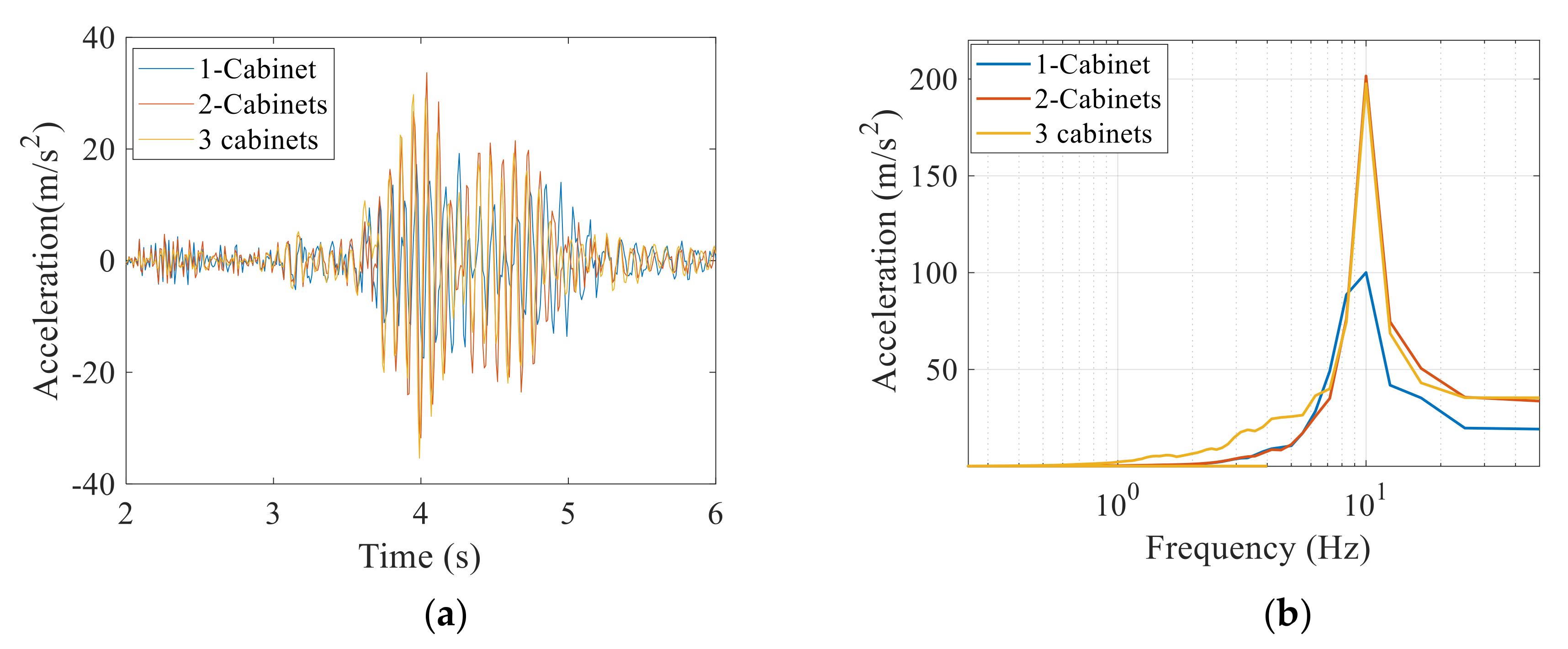
5.2. Seismic Response of the Inter-Connected Cabinet Assemblies
ICRS under the Low and High Frequency Pluses
6. Effect on the Seismic Qualification
7. Conclusions
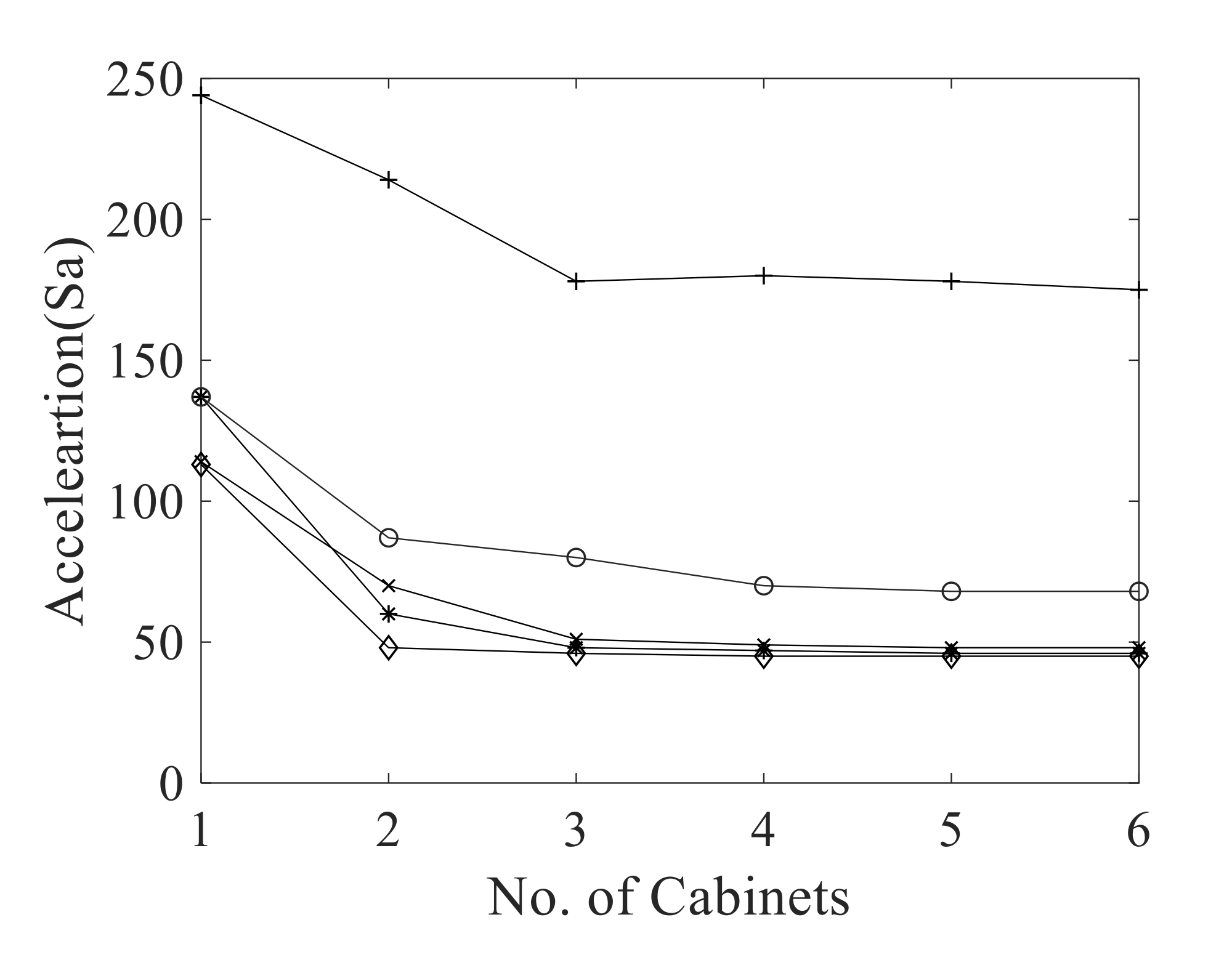
- Grouping effect of the cabinets considering the internal equipment reduces the seismic response on one hand, but it can considerably amplify the response due to inherent ground motion parameters.
- Grouping effect under the low-frequency input motion has a constant de-amplification almost (50%) in the in-cabinet response that corresponds to the higher stiffness provided by the number of cabinets as shown in Figure 18. Meanwhile, under the high frequency of ground motion, the response is dramatically amplified. High frequency of ground motion usually above 10 Hz can cause the interconnected cabinets to resonate as the natural frequency of this equipment lies in this range.
- High frequency of the multi-cabinets manifests the higher stiffness, however the energy of the strong motion can amplify the response of the cabinets as compared to a single cabinet.
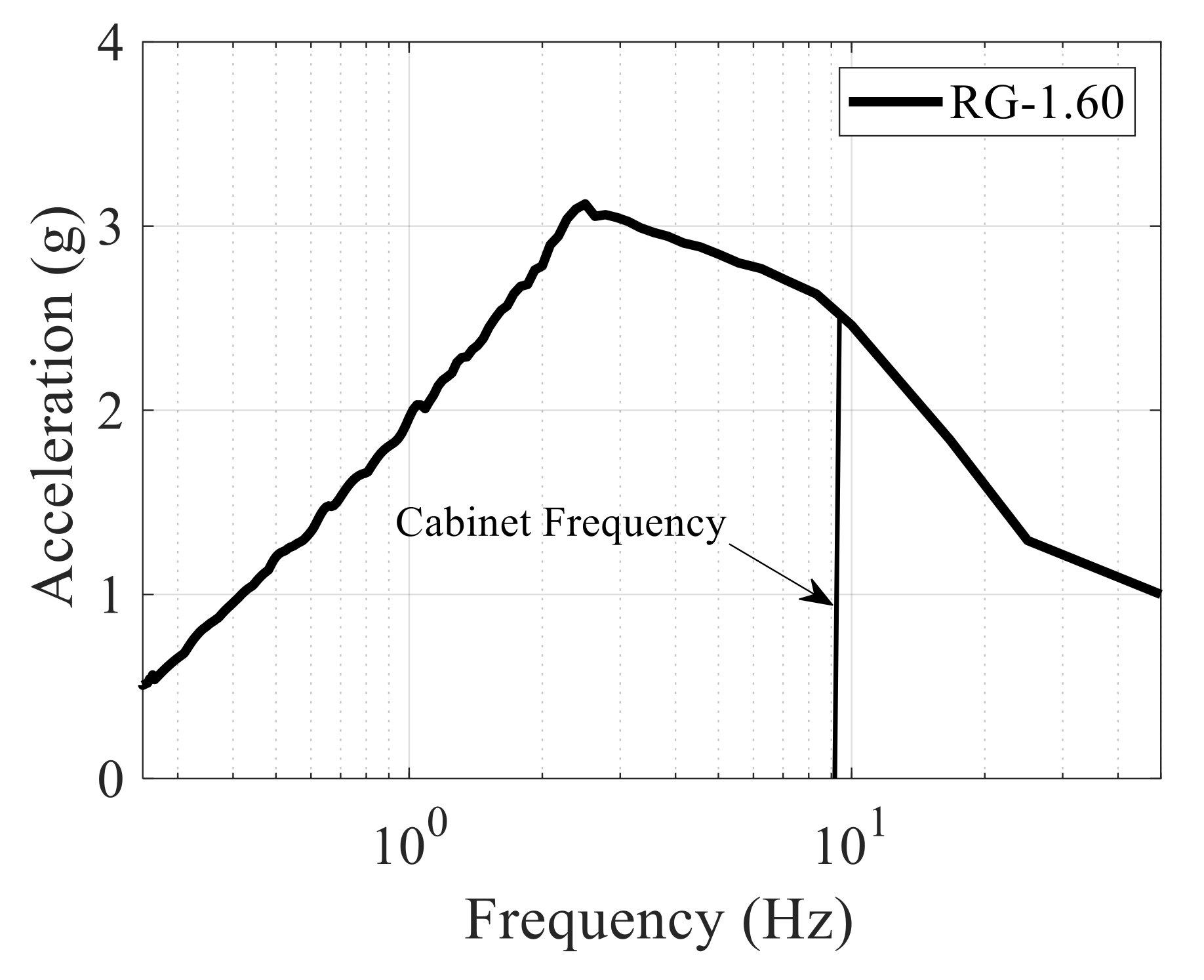
- Using the standard design spectra (RG 1.60) the comparative response of the cabinets represents no potential difference on the ICRS while it is significantly amplified by the seismic inputs having high frequency pulses.
- Cabinets connected in series may have high integral stiffness, but due to their sensitivity to the input motion parameters, they can be more vulnerable than a stand-alone cabinet. This analysis is based on a cabinet prototype that has less stiffness than the available NPP cabinets, in this regards the grouping effect for the cabinets having higher stiffness can be more effective.
- Future extension in this domain can be considered by investigating the nonlinear dynamic interaction of the cabinets having different dynamic characteristics as in this study the cabinet was considered to have the same dynamic properties.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Electric Power Research Institute. High Frequency Program: Application Guidance for Functional Confirmation and Fragility Evaluation; EPRI: Palo Alto, CA, USA, 2015. [Google Scholar]
- Goodno, B.J.; Gould, N.C.; Caldwell, P.; Gould, P.L. Effects of the January 2010 haitian earthquake on selected electrical equipment. Earthq. Spectra 2011, 27, 251–276. [Google Scholar] [CrossRef]
- Tran, T.T.; Cao, A.T.; Nguyen, T.H.X.; Kim, D. Fragility assessment for electric cabinet in nuclear power plant using response surface methodology. Nucl. Eng. Technol. 2019, 51, 894–903. [Google Scholar] [CrossRef]
- Hur, J. Seismic Performance Evaluation of Switchboard Cabinets Using Nonlinear Numerical Models. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2012. [Google Scholar]
- Salman, K.; Tran, T.T.; Kim, D. Grouping effect on the seismic response of cabinet facility considering primary-secondary structure interaction. Nucl. Eng. Technol. 2019, 52, 1318–1326. [Google Scholar] [CrossRef]
- Salman, K.; Tran, T.T.; Kim, D. Seismic capacity evaluation of NPP electrical cabinet facility considering grouping effects. J. Nucl. Sci. Technol. 2020, 57, 1–13. [Google Scholar] [CrossRef]
- Gupta, A.; Yang, J. Modified Ritz vector approach for dynamic properties of electrical cabinets and control panels. Nucl. Eng. Des. 2002, 217, 49–62. [Google Scholar] [CrossRef]
- Gupta, A.; Rustogi, S.; Gupta, A. Ritz vector approach for evaluating incabinet response spectra. Nucl. Eng. Des. 1999, 190, 255–272. [Google Scholar] [CrossRef]
- Lim, E. A Method for Generating Simplified Finite Element Models for Electrical Cabinets. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2016. [Google Scholar]
- Djordjevic, W.; O’Sullivan, J. Guidelines for Development of In-Cabinet Amplified Response Spectra for Electrical Benchboards and Panels; Electric Power Research Institute: Palo Alto, CA, USA; Stevenson and Associates, Inc.: Woburn, MA, USA, 1990. [Google Scholar]
- Di Sarno, L.; Petrone, C.; Magliulo, G. Dynamic properties of typical consultation room medical components. Eng. Struct. 2015, 100, 442–454. [Google Scholar] [CrossRef]
- Cho, S.G.; Kim, D.; Chaudhary, S. A simplified model for nonlinear seismic response analysis of equipment cabinets in nuclear power plants. Nucl. Eng. Des. 2011, 8, 2750–2757. [Google Scholar] [CrossRef]
- Zentner, I. Numerical computation of fragility curves for NPP equipment. Nucl. Eng. Des. 2010, 6, 1614–1621. [Google Scholar] [CrossRef]
- Bandyopadhyay, K.K.; Hofmayer, C.H.; Kassir, M.K. Seismic Fragility of Nuclear Power Plant Components: Phase 2, Motor Control Center, Switchboard, Panel Board and Power Supply; Department of Nuclear Energy, Brookhaven National Laboratory: Long Island, NY, USA, 1987. [Google Scholar]
- Institute of Electrical and Electronics Engineers. IEEE Recommended Practice for Seismic Design of Substations; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2005. [Google Scholar]
- U.S. Nuclear Regulatory Commission. Regulatory Guide 1.60, Revision 2; Nuclear Regulatory Commission: Rockville, MD, USA, 2014. [Google Scholar]
- Computers and Structures Inc. SAP2000, CSI; Computers and Structures Inc.: Berkeley, CA, USA, 2013. [Google Scholar]
- Lin, F.R.; Chai, J.F.; Lai, Z.Y.; Chang, K.C.; Liao, W.I.; Chou, P.F.; Huang, C.C. Experimental Study of Seismic Qualification of Incabinet Equipment in NPP. In Proceedings of the 15th World Conference on Earthquake Engineering LISBON, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Richards, J.; Merz, K.; Hardy, G. High Frequency Seismic Testing of Potentially Sensitivity Components. In Proceedings of the 23rd Conference on Structural Mechanics in Reactor Technology, Manchester, UK, 10–14 August 2015. [Google Scholar]
- Gupta, A.; Cho, S.G.; Hong, K.J.; Han, M. Current state of in-cabinet response spectra for seismic qualification of equipment in nuclear power plants. Nucl. Eng. Des. 2019, 269–275. [Google Scholar] [CrossRef]
- Short, S.; Hardy, G.; Merz, K.; Johnson, J. Effect of Seismic Wave Incoherence on Foundation and Building Response; DOE EPRI—EPRI: Palo Alto, CA, USA; The US Department of Energy: Washington, DC, USA, 2005. [Google Scholar]
- Maniyar, M.M.; Khare, R.K. Selection of ground motion for performing incremental dynamic analysis of existing reinforced concrete buildings in India. Curr. Sci. 2011, 701–713. [Google Scholar]
- Özer, E.; Soyöz, S.; Çelebi, M. Effect of strong ground motion duration on structural damage. In Proceedings of the 15th World Conference on Earthquake Engineering LISBON, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
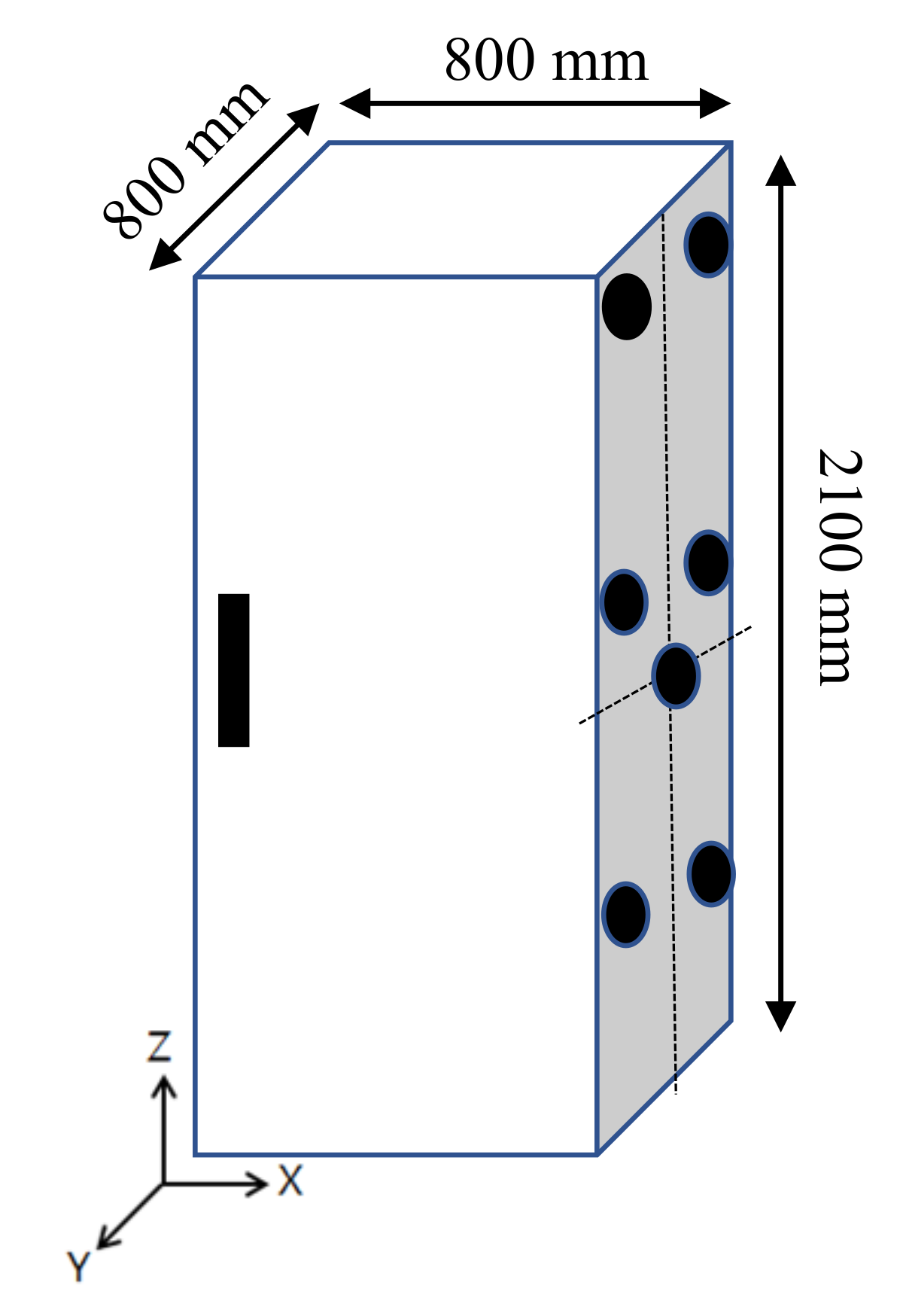


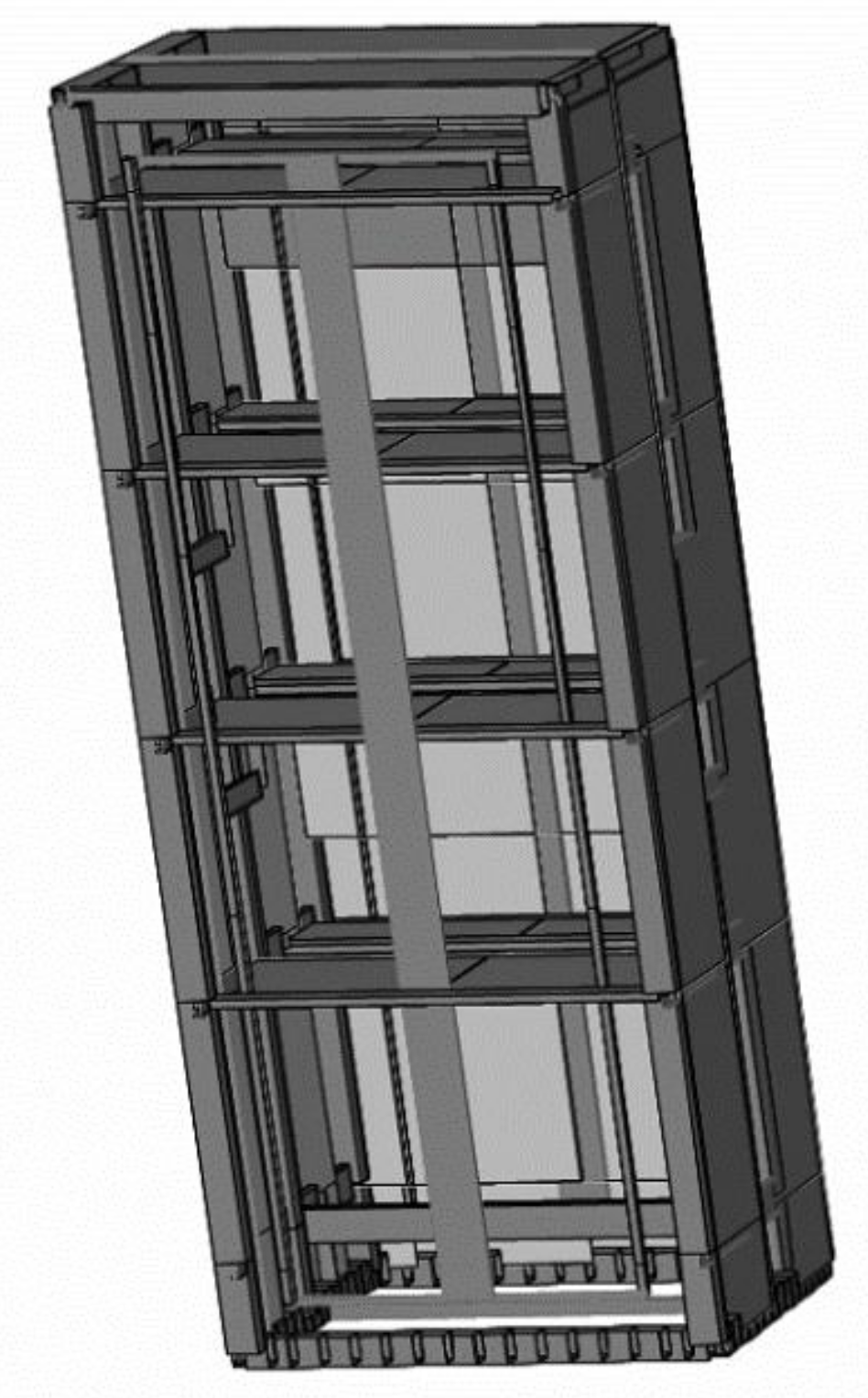
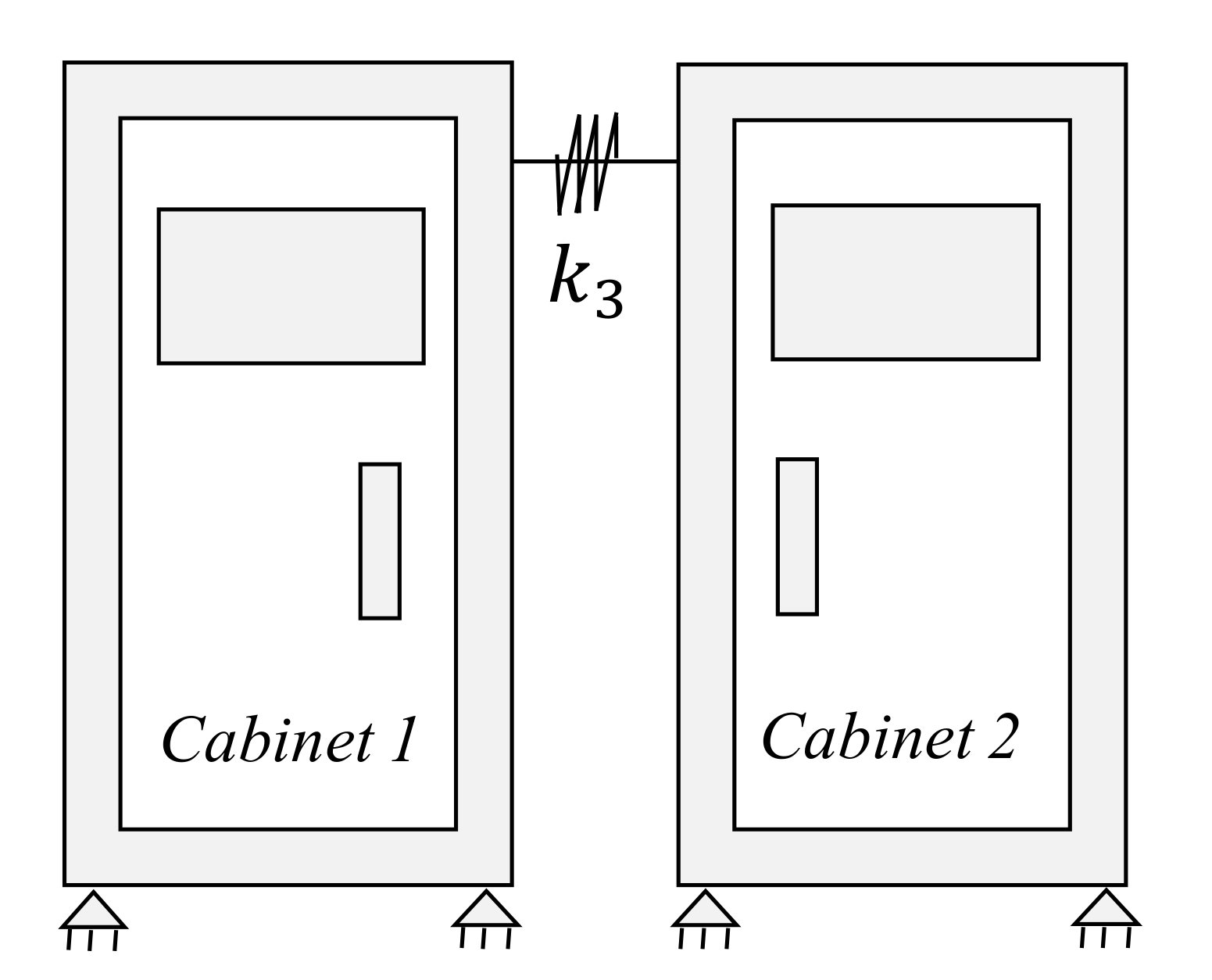
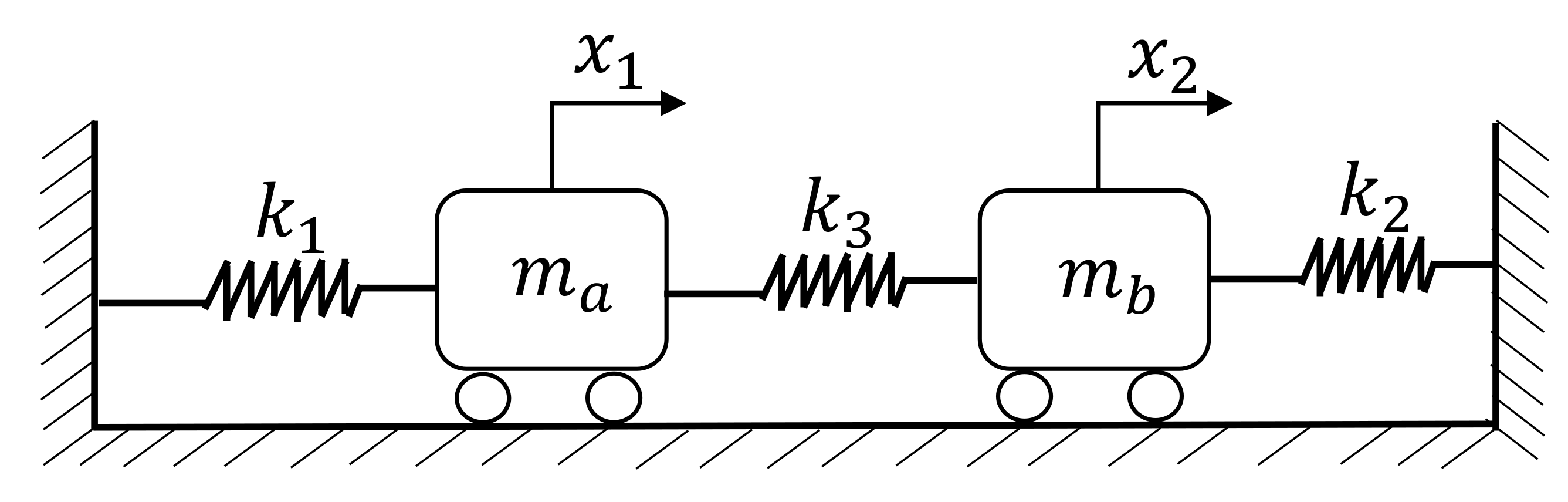


| Size | 2100 (H) × 800 (W) × 800 (D) mm |
| Weight | 290 kg |
| Internal Dead Load (Assumed) | 200 kg per cabinet |
| Elastic Modulus, Density, and Poisson’s Ratio | 200 GPa, 7850 kg/m3, and 0.3 |
| Bolt Size | M14 × 80 |
| No | Earthquake Name | Year | Magnitude | ||
|---|---|---|---|---|---|
| 1 | Victoria_Mexico | 1980 | 6.33 | 14.37 | 471.53 |
| 2 | Nahanni_Canada | 1985 | 6.76 | 9.6 | 605.04 |
| 3 | Cape Mendocino | 1992 | 7.01 | 6.96 | 567.78 |
| 4 | Landers | 1992 | 7.28 | 69.21 | 382.93 |
| 5 | Northridge-01 | 1994 | 6.69 | 68.93 | 501.75 |
| 6 | Northridge-01 | 1994 | 6.69 | 47.98 | 544.68 |
| 7 | Hector Mine | 1999 | 7.13 | 43.05 | 382.93 |
| 8 | El Mayor-Cucapah_Mexico | 2010 | 7.2 | 45.47 | 523.99 |
| 9 | Goungju_South Korea | 2016 | 5.7 | 14 | 550.60 |
| Number of Cabinets | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Frequency (Hz) | Empty Cabinet | 9.87 | 13.60 | 15.46 | 15.87 | 15.90 | 16.02 |
| Loaded Cabinet | 9.69 | 11.95 | 12.55 | 12.83 | 12.96 | 12.98 | |
| Stiffness Ratio | Mass Ratio | Modal Characteristic | ||||
|---|---|---|---|---|---|---|
| No. of Cabinets | Modal Stiffness (kN/m) | Difference | Modal Mass (kg) (Active/Total) | Difference | Modal Frequency (Hz) | Modal Mass Participation % |
| 1 | 4403 | ----- | 365/480 | ------ | (9.8) | 77.11 |
| 2 | 7262 | 40% | 672/960 | 50% | (11.95) | 77.18 |
| 3 | 7851 | 8% | 1008/1440 | 34% | (12.55) | 77.80 |
| 4 | 8294 | 5.3% | 1344/1920 | 25% | (12.87) | 77.84 |
| 5 | 8561 | 4% | 1680/2400 | 18% | (12.96) | 77.88 |
| 6 | 8739 | 2% | 2016/2880 | 16.65% | (12.98) | 77.88 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salman, K.; Gook Cho, S. Effect of Frequency Content of Earthquake on the Seismic Response of Interconnected Electrical Equipment. CivilEng 2020, 1, 198-215. https://doi.org/10.3390/civileng1030012
Salman K, Gook Cho S. Effect of Frequency Content of Earthquake on the Seismic Response of Interconnected Electrical Equipment. CivilEng. 2020; 1(3):198-215. https://doi.org/10.3390/civileng1030012
Chicago/Turabian StyleSalman, Kashif, and Sung Gook Cho. 2020. "Effect of Frequency Content of Earthquake on the Seismic Response of Interconnected Electrical Equipment" CivilEng 1, no. 3: 198-215. https://doi.org/10.3390/civileng1030012
APA StyleSalman, K., & Gook Cho, S. (2020). Effect of Frequency Content of Earthquake on the Seismic Response of Interconnected Electrical Equipment. CivilEng, 1(3), 198-215. https://doi.org/10.3390/civileng1030012




