Bond Modelling for the Assessment of Transmission Length in Prestressed-Concrete Members
Abstract
1. Introduction
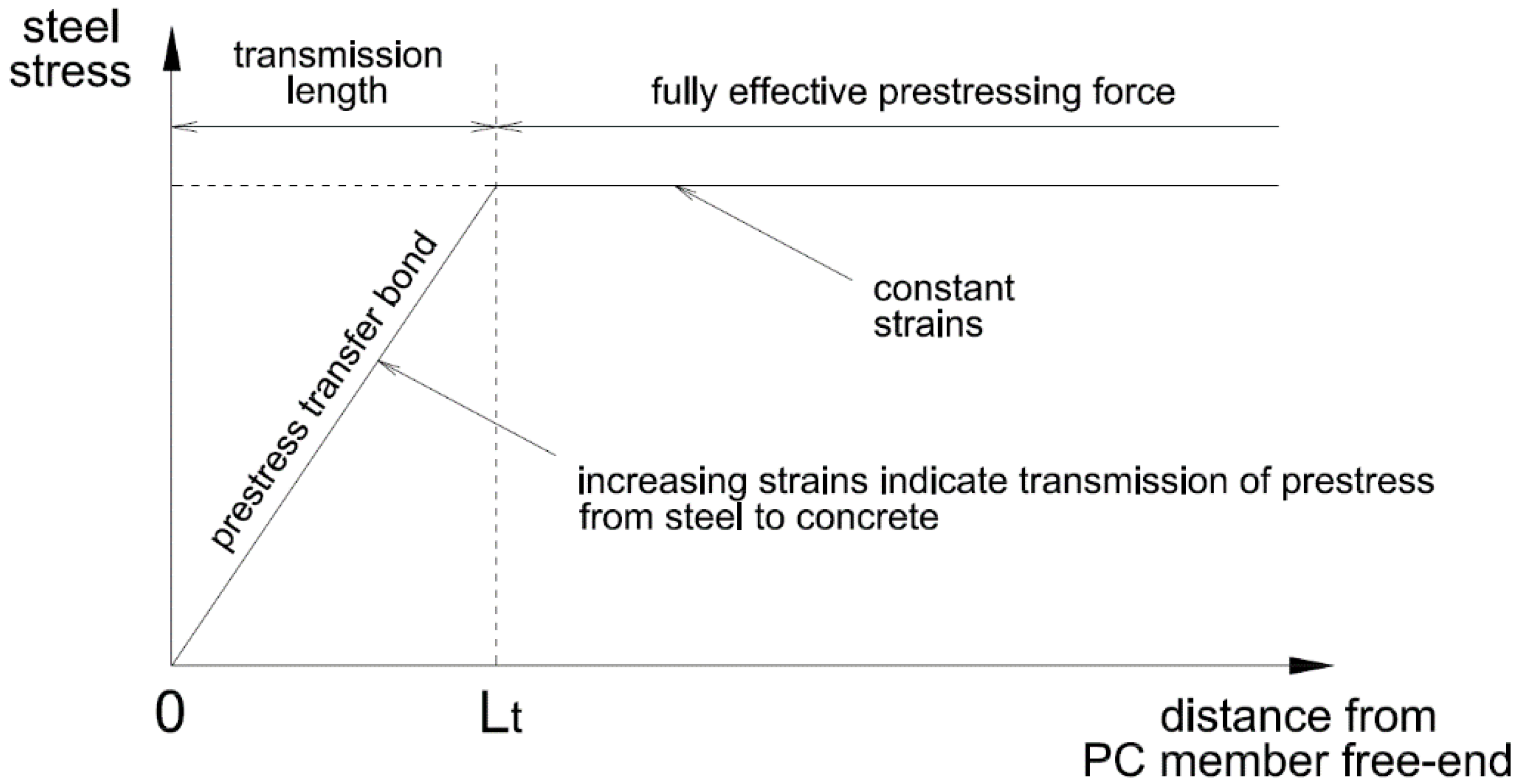
2. Roles of the Major Parameters Affecting the Transmission Length
3. Analytical Modelling of the Transmission Length
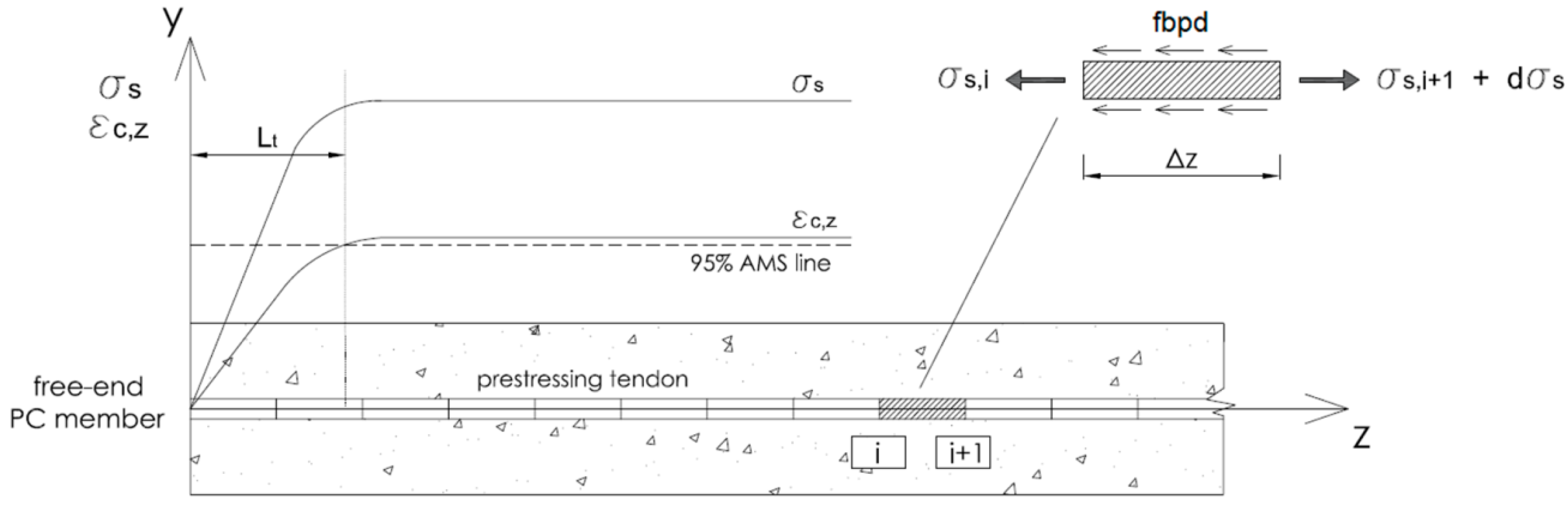
3.1. General Calculation Procedure
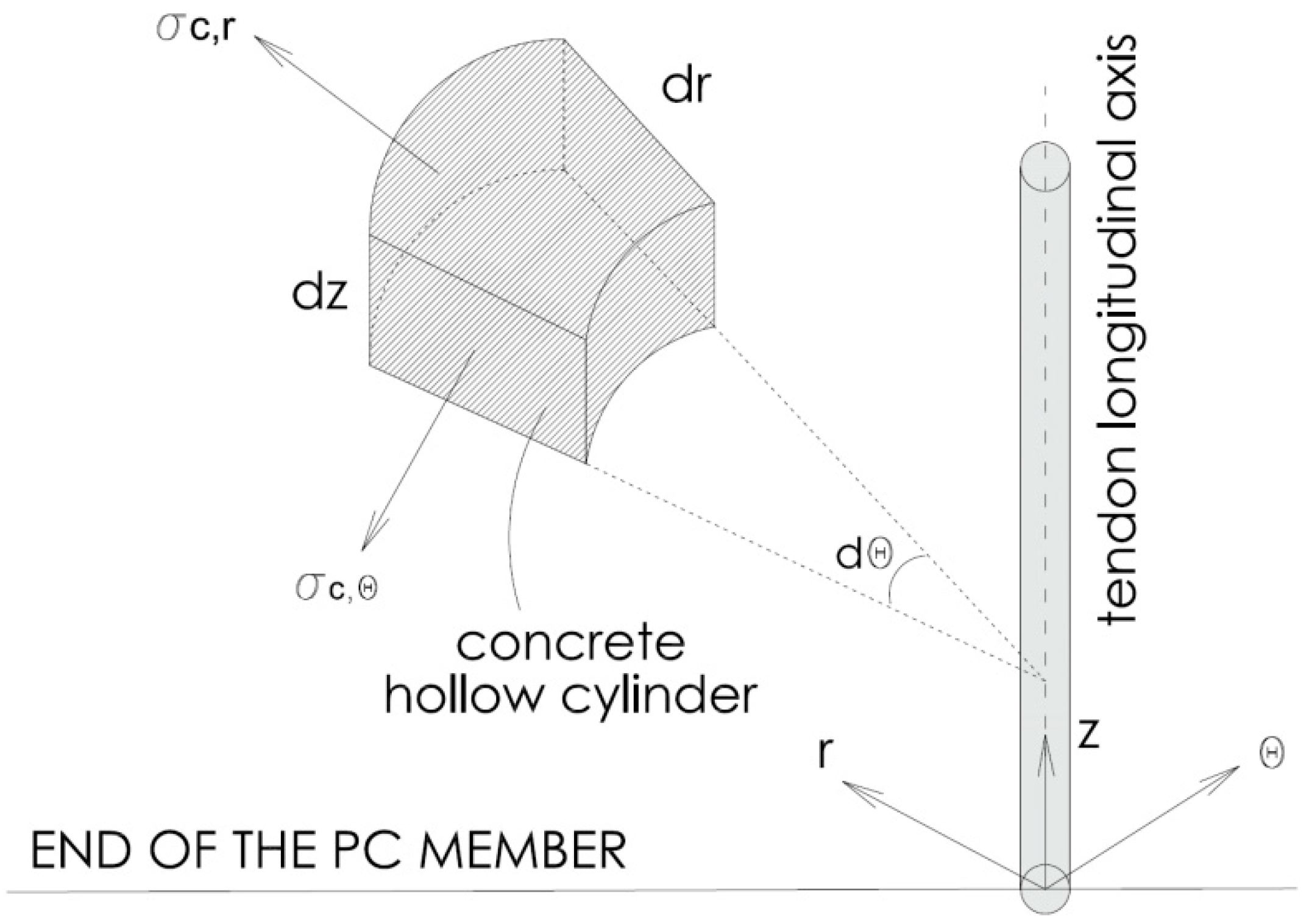
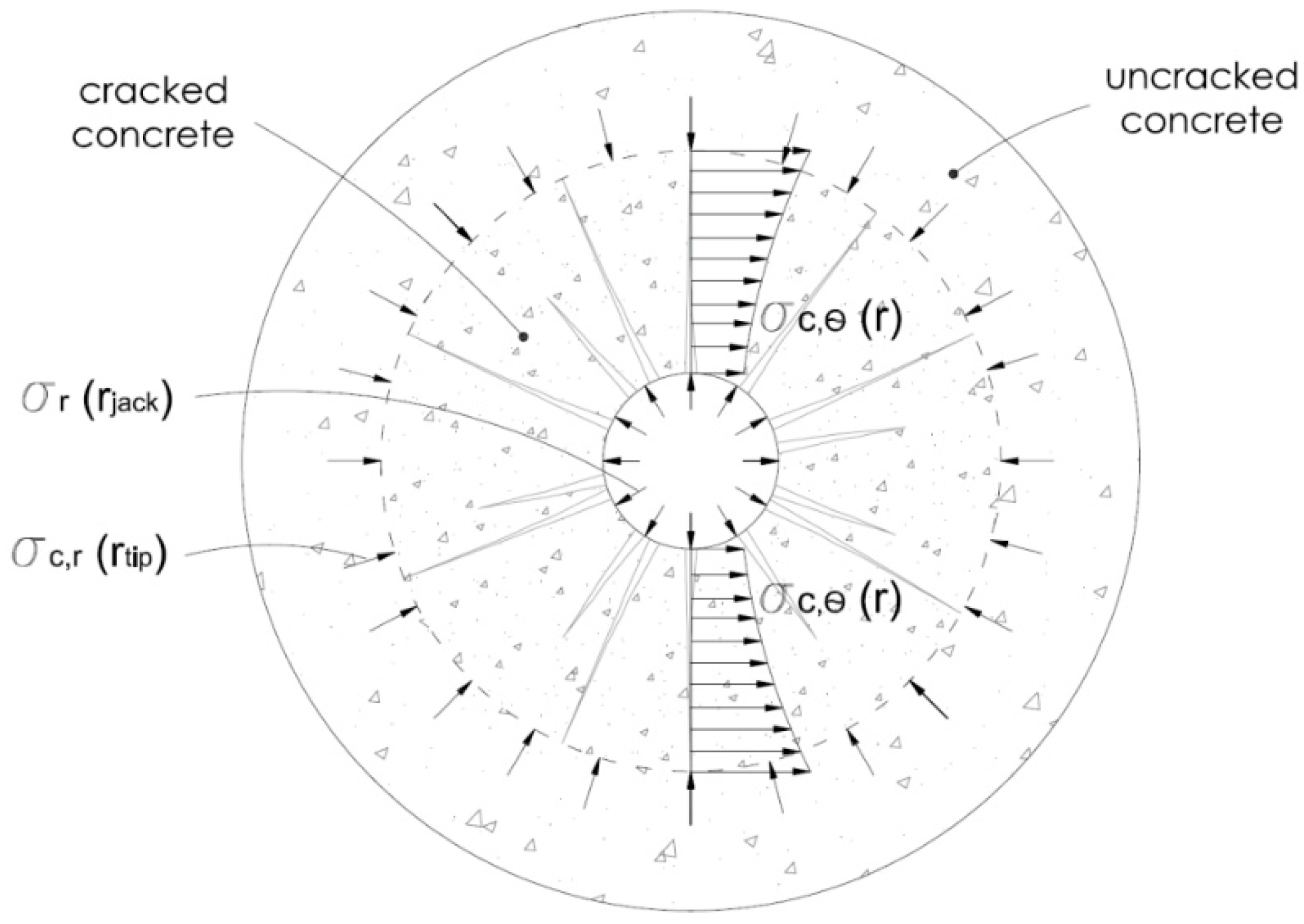
3.2. Elastic Analysis Based on the Thick-walled Cylinders Theory
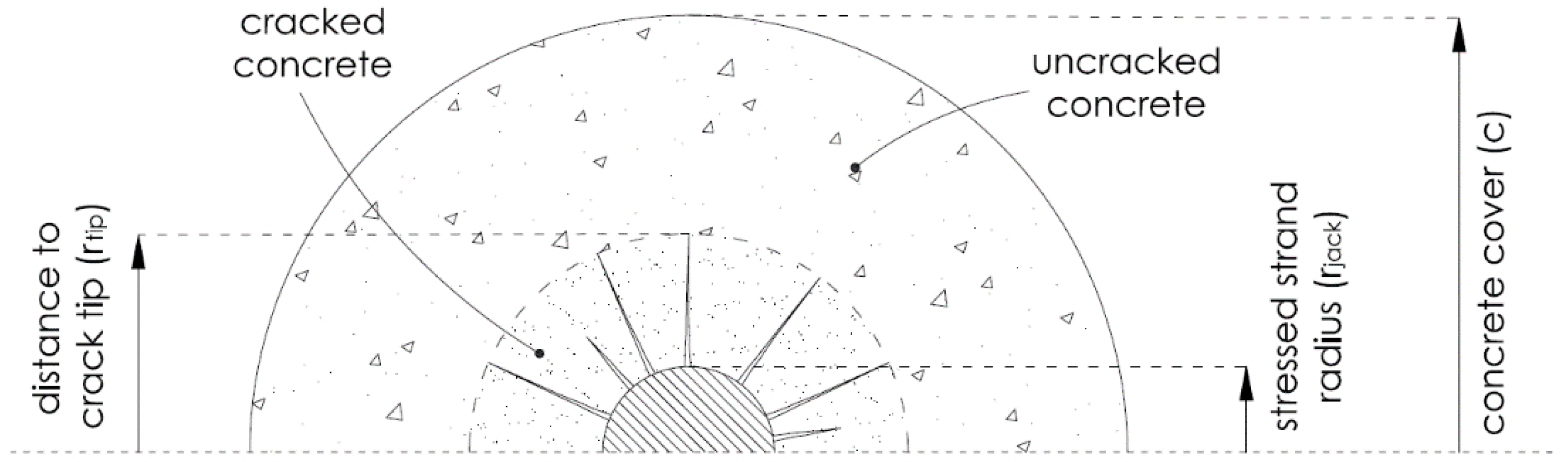
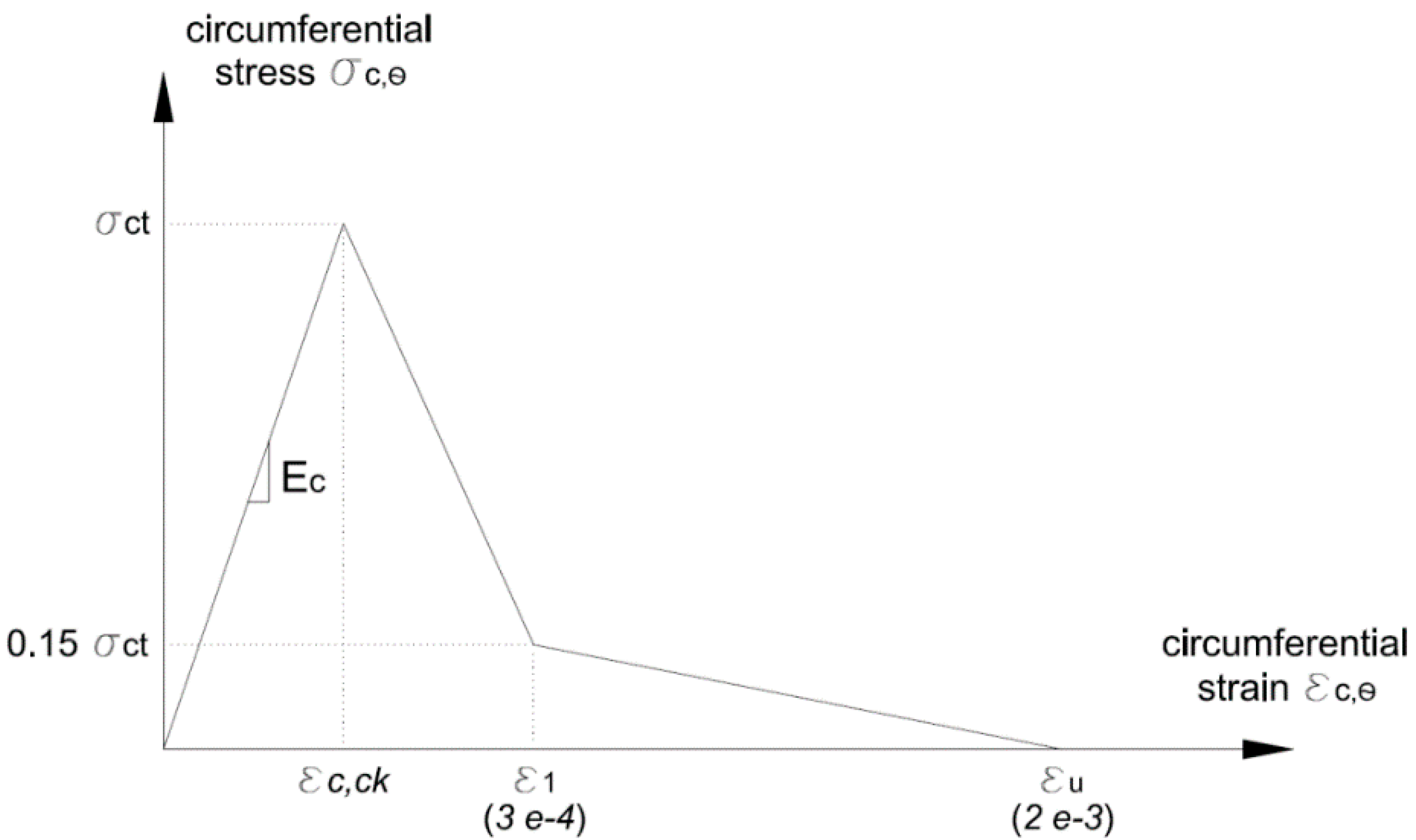
3.3. Anisotropic Analysis for Cracked Concrete
4. Model Calibration and Results
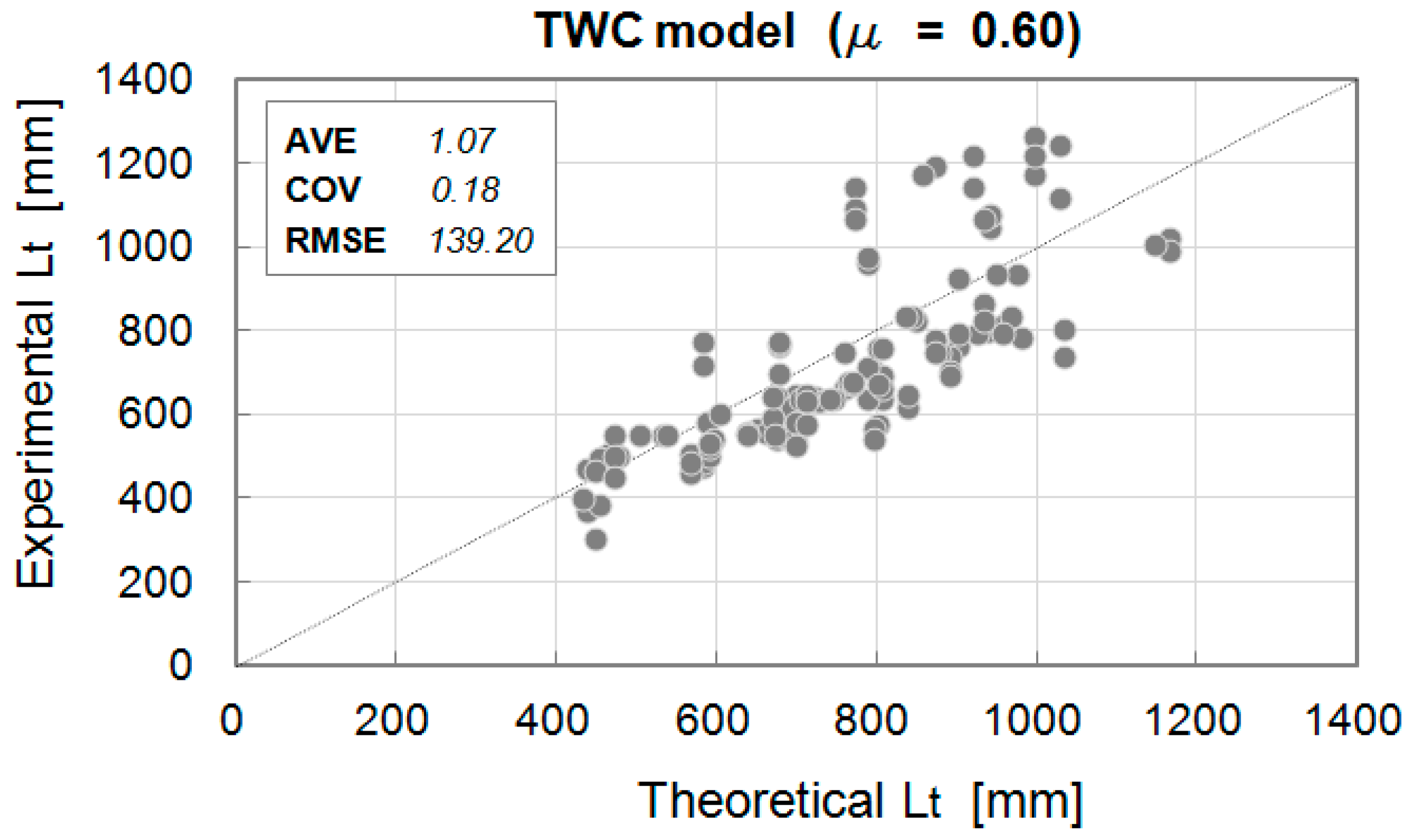
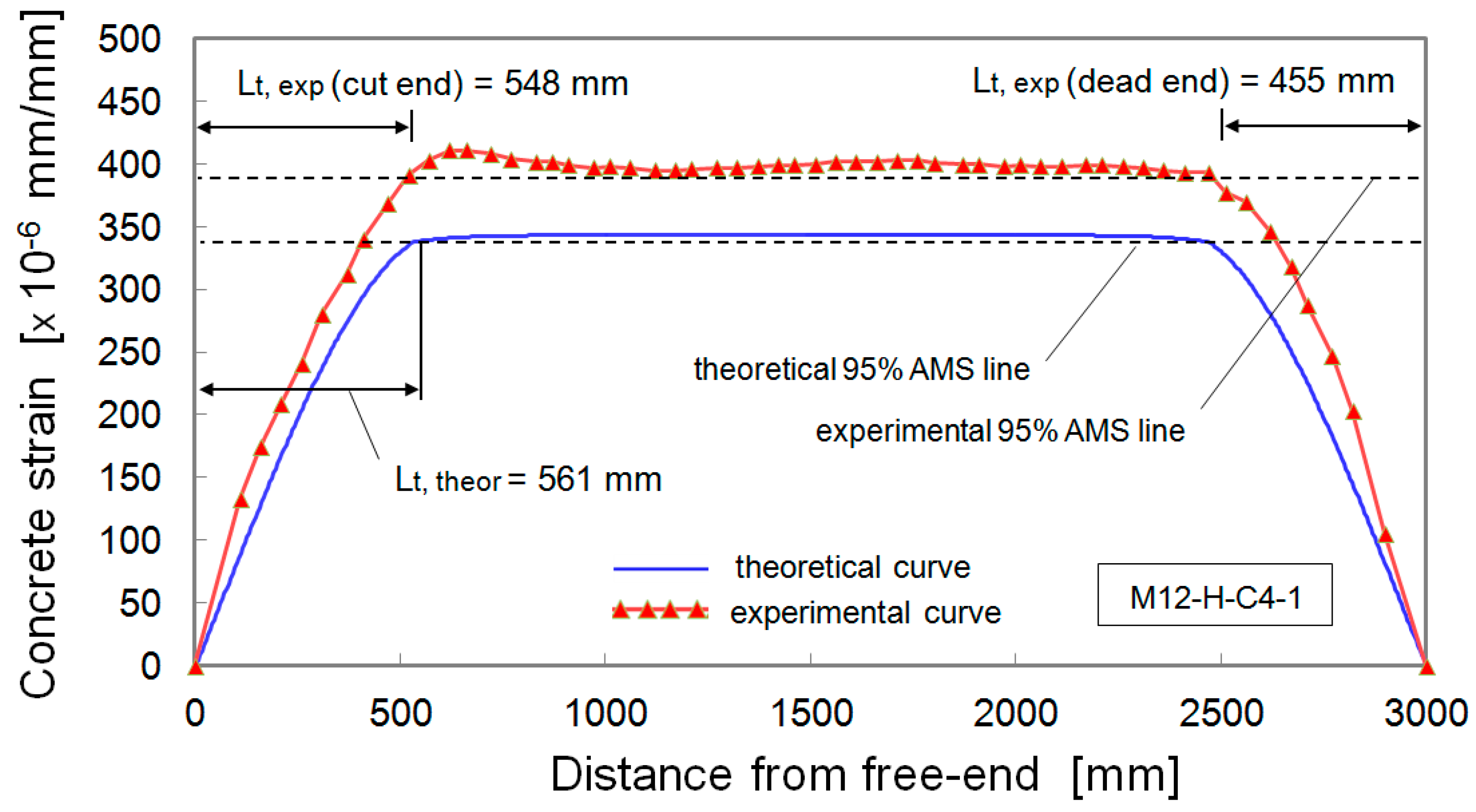
4.1. Global Behaviour: Transmission Length Assessment
4.2. Local Behaviour: Radial Cracking and Bond Stress Development
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Statement of Data Availability
Nomenclature
| Ac | Cross-sectional area of concrete |
| Asp | Cross-sectional area of prestressing tendon |
| b | Width of the concrete section |
| c | Concrete cover thickness |
| , | Constants of integration for the solution of u |
| Ec | Elastic modulus of concrete |
| Eps | Elastic modulus of prestressing steel |
| e | Vertical eccentricity of the considered tendon with respect to the centre of gravity of the concrete section |
| h | Height of the concrete section |
| Jx | Moment of inertia of the concrete section |
| Lt | Transmission length of the prestressing tendon |
| Lt, experimental | Experimental value of the transmission length |
| Lt, theoretical | Theoretical value of the transmission length |
| lbp | Basic anchorage length according to fib MC2010 |
| P | Initial prestressing-force in the tendon |
| r | Radial distance from the tendon centroid |
| rjack | Radius of the tendon after release |
| rps | Radius of the unstressed tendon |
| rtip | Distance from the tendon centroid to the crack tip |
| u | Radial displacement |
| uc | Radial displacement of the concrete |
| ups | Radial displacement of the tendon outer surface |
| y | Vertical distance from the centre of gravity of the concrete section |
| z | Length of the single finite element in which the prestressing tendon is subdivided |
| z | Longitudinal distance from the free-end of the PC member |
| αp1 | Coefficient which takes into account the prestress release method, according to fib MC2010 |
| αp2 | Coefficient which takes into account the action effect to be verified, according to fib MC2010 |
| αp3 | Coefficient which takes into account the influence of bond situation, according to fib MC2010 |
| αrel | Coefficient which takes into account the prestress release method, according to the findings proposed by the authors |
| Concrete strain (assumed as 0.0003) corresponding to concrete tensile stress equal to 0.15 , according to Han’s softening model | |
| Cracking strain of concrete | |
| Concrete strain in the radial direction | |
| Concrete strain in the circumferential direction | |
| Concrete axial strain at the level of the tendon centroid | |
| Ultimate concrete strain (assumed as 0.002) corresponding to concrete tensile stress equal to zero, according to Han’s softening model | |
| ηp1 | Coefficient which takes into account the type of tendon, according to fib MC2010 |
| ηp2 | Coefficient which takes into account the position of the tendon, according to fib MC2010 |
| Overall friction coefficient between the tendon and the surrounding concrete, combining actual frictional and mechanical bond | |
| Poisson’s ratio of the concrete | |
| Poisson’s ratio of the prestressing steel | |
| Prestress transfer bond at the interface tendon-concrete | |
| Concrete radial stress | |
| Concrete circumferential stress | |
| Concrete axial stress | |
| Tensile strength of concrete | |
| Design tensile strength of the prestressing steel | |
| Tendon radial stress | |
| (rjack) | Radial compressive stress at the interface between steel and concrete, arising from the Hoyer effect |
| Increment in tendon stress resulting from the development of bond stress along the finite element | |
| Tendon stress at the considered point along the length of the member | |
| Jacking stress of the tendon at prestressing-force release | |
| φ | Nominal tendon diameter |
References
- fib Model Code 2010. fib Model Code for Concrete Structures; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2013. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Janney, J.R. Nature of bond in pretensioned prestressed concrete. ACI J. 1954, 50, 717–736. [Google Scholar]
- Hanson, N.W.; Kaar, P.H. Flexural bond of pretensioned prestressed beams. ACI J. 1959, 55, 783–802. [Google Scholar]
- Metelli, G.; Plizzari, G.A. Influence of the relative rib area on bond behaviour. Mag. Concr. Res. 2014, 66, 277–294. [Google Scholar] [CrossRef]
- Pellegrino, C.; Zanini, M.A.; Faleschini, F.; Corain, L. Predicting bond formulations for prestressed concrete elements. Eng. Struct. 2015, 97, 105–117. [Google Scholar] [CrossRef]
- Mohandoss, P.; Pillai, R.G.; Sengupta, A.K. Transmission length of pretensioned concrete systems - comparison of codes and test data. Mag. Concr. Res. 2018, 71, 1–13. [Google Scholar] [CrossRef]
- Abdelatif, A.O.; Owen, J.S.; Hussein, M.F. Modelling the prestress transfer in pre-tensioned concrete elements. Finite Elem. Anal. Des. 2015, 94, 47–63. [Google Scholar] [CrossRef]
- Ramirez-Garcia, A.T.; Dang, C.N.; Hale, W.M.; Martí-Vargas, J.R. A higher-order equation for modeling strand bond in pretensioned concrete beams. Eng. Struct. 2017, 131, 345–361. [Google Scholar] [CrossRef]
- Eurocode 2. Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings; Comitè Europèen de Normalisation: Brussels, Belgium, 2004. [Google Scholar]
- Oh, B.H.; Kim, E.S. Realistic evaluation of transfer lengths in pretensioned prestressed concrete members. ACI Struct. J. 2000, 97, 821–830. [Google Scholar]
- Dang, C.N.; Hale, W.M.; Martì-Vargas, J.R. Quantification of bond performance of 18-mm prestressing steel. Constr. Build. Mater. 2018, 159, 451–462. [Google Scholar] [CrossRef]
- Zia, P.; Mostafa, T. Development length of prestressing strands. PCI J. 1977, 22, 54–65. [Google Scholar]
- Martí-Vargas, J.R.; Serna-Ros, P.; Navarro-Gregori, J.; Bonet, J.L. Effects of concrete composition on transmission length of prestressing strands. Constr. Build. Mater. 2012, 27, 350–356. [Google Scholar] [CrossRef]
- Mitchell, D.; Cook, W.D.; Kahn, A.A.; Tham, T. Influence of High-Strength concrete on transfer and development length of pretensioning strand. PCI J. 1993, 38, 52–66. [Google Scholar] [CrossRef]
- Oh, B.H.; Kim, E.S.; Choi, Y.C. Theoretical analysis of transfer lengths in pretensioned prestressed concrete members. J. Eng. Mech. 2006, 132, 1057–1066. [Google Scholar]
- Base, G.D. An Investigation of Transmission Length in Pretensioned Concrete. In Proceedings of the Third Congress of FIP-Session III, Brussels, Belgium, 1958; pp. 603–623. [Google Scholar]
- Holmberg, A.; Lindgren, S. Anchorage and Prestress Transmission; Document D1; National Swedish Institute for Building Research: Stockholm, Sweden, 1970. [Google Scholar]
- Kaar, P.H.; Hanson, N.W. Bond fatigue tests of beams simulating pretensioned concrete crossties. J. Prestress. Concr. Inst. 1975, 20, 65–80. [Google Scholar] [CrossRef]
- Cousins, T.E.; Johnston, D.W.; Zia, P. Transfer and development length of epoxy-coated and uncoated prestressing strand. PCI J. 1990, 35, 92–103. [Google Scholar] [CrossRef]
- Pellegrino, C.; Faleschini, F.; Fabris, N.; Zanini, M.A. Bond of Prestressing Tendons; Internal report, Submitted to: Fib Bulletin on “Advances on Bond in Concrete”; University of Padova: Padua, Italy, 2018. [Google Scholar]
- Deatherage, J.H.; Burdette, E.G.; Chew, C.K. Development length and lateral spacing requirements of prestressing strand for prestress concrete bridge girders. PCI J. 1994, 39, 70–83. [Google Scholar] [CrossRef]
- Barnes, R.W.; Groove, J.W.; Burns, N.H. Experimental assessment of factors affecting transfer length. ACI Struct. J. 2003, 100, 740–748. [Google Scholar]
- Russell, B.W.; Burns, N.H. Measured transfer lengths of 0.5 and 0.6 in. Strands in pretensioned concrete. J. Struct. Eng. 1996, 123, 44–65. [Google Scholar] [CrossRef]
- Tepfers, R. Cracking of concrete cover along anchored deformed reinforcing bars. Mag. Concr. Res. 1979, 31, 3–12. [Google Scholar] [CrossRef]
- Han, S.J.; Lee, D.H.; Cho, S.H.; Ka, S.B.; Kim, K.S. Estimation of transfer lengths in precast pretensioned concrete members based on a modified thick-walled cylinder model. Struct. Concr. 2016, 17, 52–62. [Google Scholar] [CrossRef]
- Han, S.J.; Lee, D.H.; Kim, K.S.; Seo, S.Y.; Moon, J.; Monteiro, P.J. Degradation of flexural strength in reinforced concrete members caused by steel corrosion. Constr. Build. Mater. 2014, 54, 572–583. [Google Scholar] [CrossRef]
- Russell, B.W.; Burns, N.H. Measurement of transfer lengths on pretensioned concrete elements. PCI J. 1997, 41, 541–549. [Google Scholar] [CrossRef]
- Martì-Vargas, J.R.; Arbeláez, C.A.; Serna-Ros, P.; Castro-Bugallo, C. Reliability of transfer length estimation from strand end slip. ACI Struct. J. 2007, 104, 487–494. [Google Scholar]
- Dang, C.N.; Hale, W.M.; Martì-Vargas, J.R. Assessment of transmission length of prestressing strands according to fib Model Code 2010. Eng. Struct. 2017, 147, 425–433. [Google Scholar] [CrossRef]
- Martins, J.A.C.; Oden, J.T. Interface models, variational principles and numerical solutions for dynamic friction problems. In Mechanics of Material Interfaces, Proceedings of ASCE/ASME Mechanics Conference, Albuquerque, NM, USA, 23–26 June 1985; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Olofsson, U.; Holmgren, M. Friction Measurement at Low Sliding Speed Using a Servo-Hydraulic Tension-Torsion Machine; Report SP AR 1992:51; Swedish National Testing Institute-Building Structures Section: Stockholm, Sweden, 1992. [Google Scholar]
- den Uijl, J.A. Bond modelling of prestressing strand. ACI Spec. Publ. 1998, 180, 145–170. [Google Scholar]


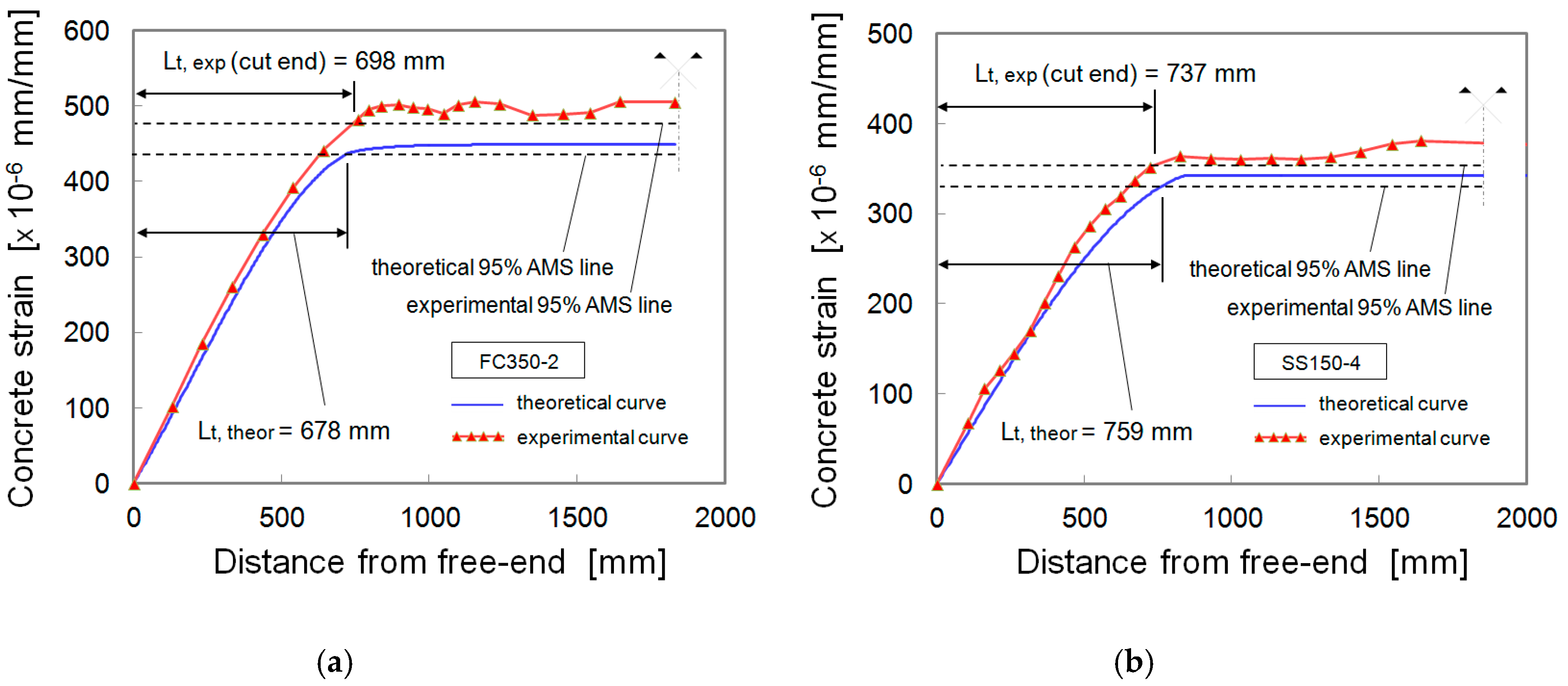
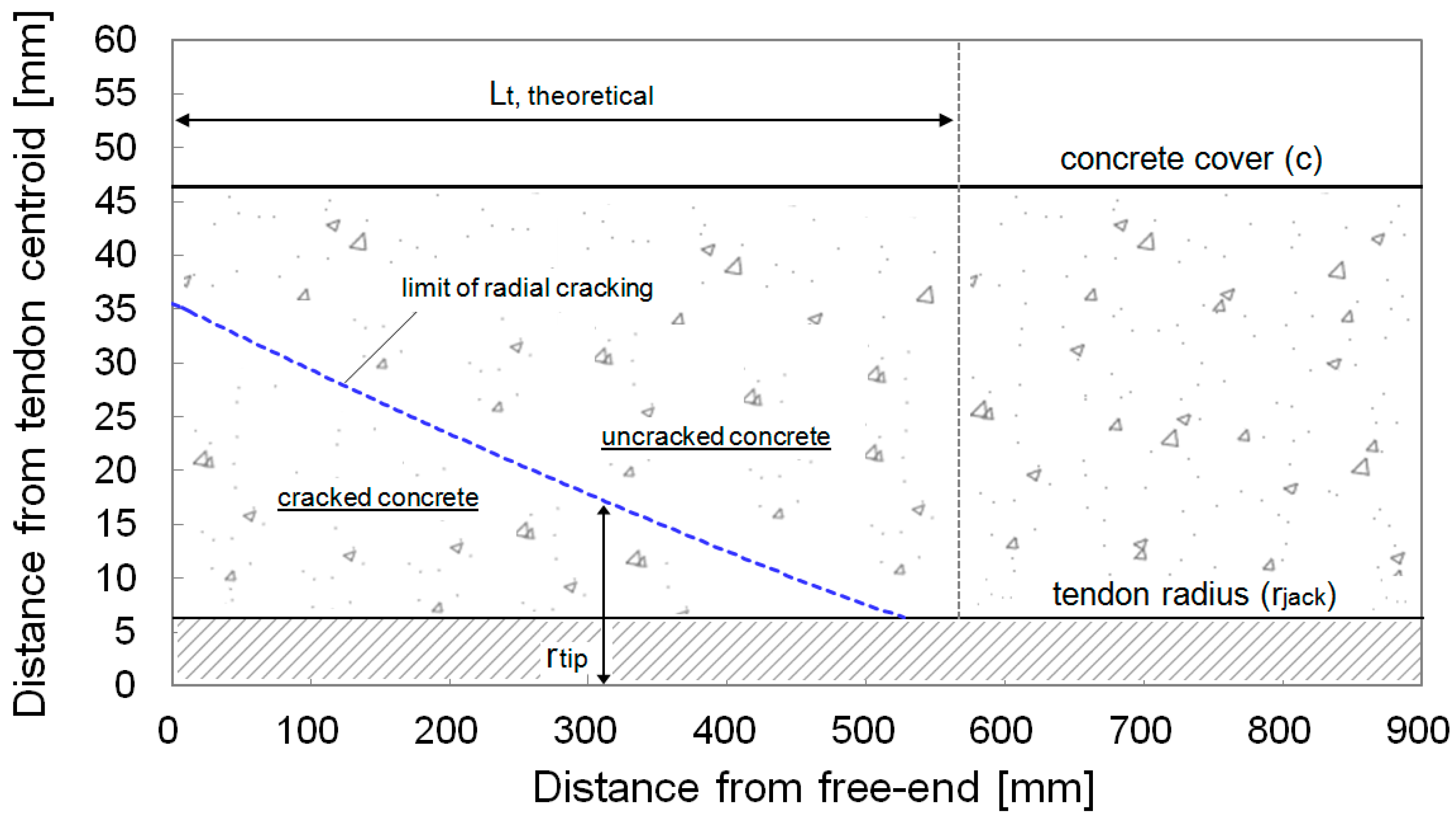
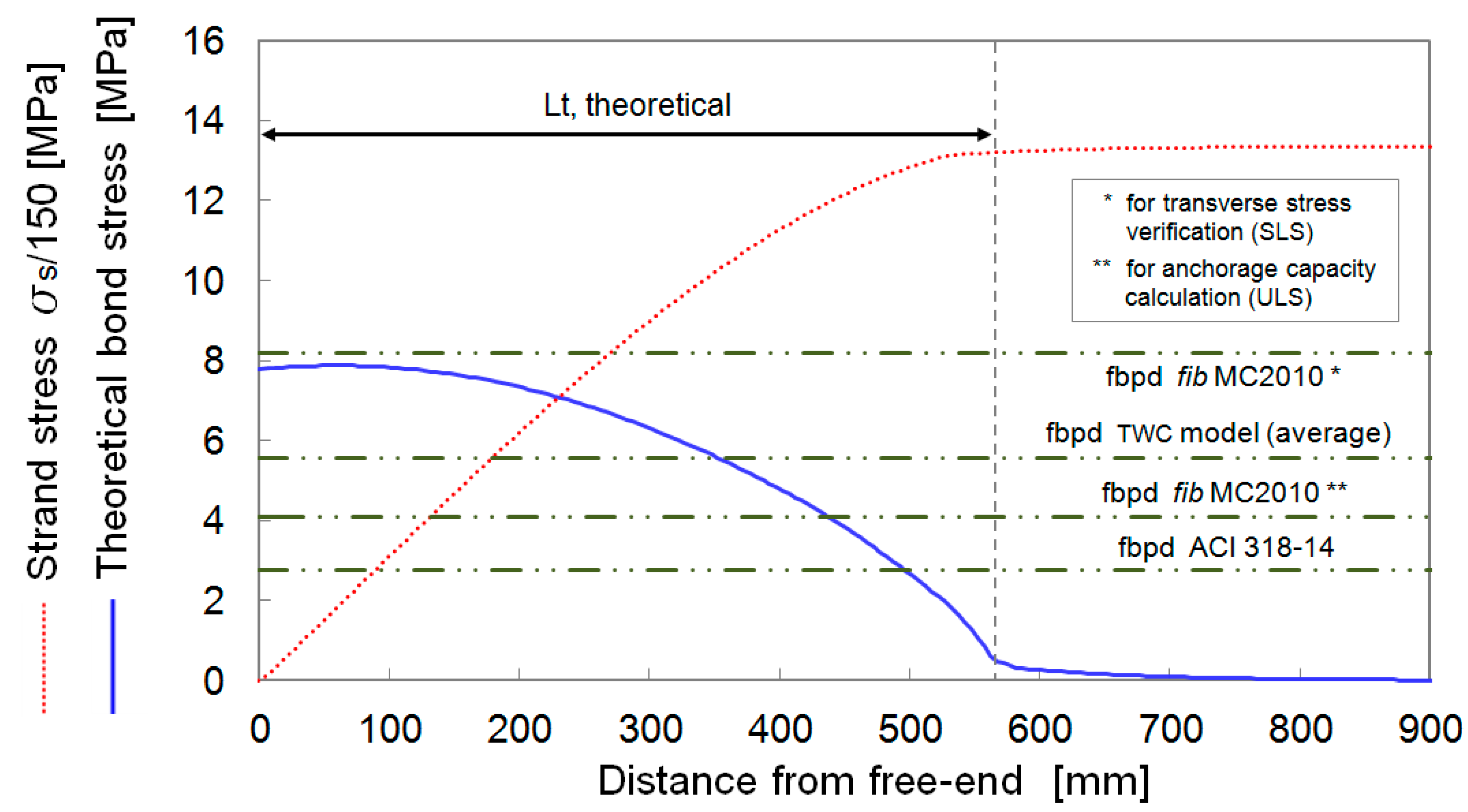
| Reference Citation | No. of Experimental Tests |
|---|---|
| Mitchell et al. (1993) [15] | 14 |
| Russell and Burns (1996) [24] | 20 |
| Russell and Burns (1997) [28] | 12 |
| Oh and Kim (2000) [11] | 36 |
| Oh et al. (2006) [16] | 24 |
| Martì-Vargas et al. (2007) [29] | 12 |
| Dang et al. (2017) [30] | 12 |
| Friction Coefficient | AVE | COV | RMSE |
|---|---|---|---|
| = 0.3 | 2.10 | 1.15 | 755.57 |
| = 0.4 | 1.62 | 0.67 | 439.31 |
| = 0.5 | 1.30 | 0.36 | 232.72 |
| = 0.6 | 1.07 | 0.18 | 139.20 |
| = 0.7 | 0.92 | 0.16 | 154.16 |
| = 0.8 | 0.81 | 0.23 | 207.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabris, N.; Faleschini, F.; Pellegrino, C. Bond Modelling for the Assessment of Transmission Length in Prestressed-Concrete Members. CivilEng 2020, 1, 75-92. https://doi.org/10.3390/civileng1020006
Fabris N, Faleschini F, Pellegrino C. Bond Modelling for the Assessment of Transmission Length in Prestressed-Concrete Members. CivilEng. 2020; 1(2):75-92. https://doi.org/10.3390/civileng1020006
Chicago/Turabian StyleFabris, Nicola, Flora Faleschini, and Carlo Pellegrino. 2020. "Bond Modelling for the Assessment of Transmission Length in Prestressed-Concrete Members" CivilEng 1, no. 2: 75-92. https://doi.org/10.3390/civileng1020006
APA StyleFabris, N., Faleschini, F., & Pellegrino, C. (2020). Bond Modelling for the Assessment of Transmission Length in Prestressed-Concrete Members. CivilEng, 1(2), 75-92. https://doi.org/10.3390/civileng1020006





