Eco-Efficiency of Agriculture in the Amazon Biome: Robust Indices and Determinants
Abstract
1. Introduction
2. Materials and Methods
2.1. DEA Models
2.2. Statistical Inference of Bootstrap DEA Estimators
2.3. Detection of Influent Observations in Eco-Efficiency Calculations
2.4. The Bootstrap to Estimate the Bias and the Confidence Interval
- For each DMU (xi, yi) ∈ Sn, compute the efficiency using the DEA model chosen—CRS (3) or VRS (5)—and transforming the Farrell efficiency into Shephard efficiency;
- Generate a random sample of size n of using a density function of kernel smoothing and the reflection method to obtain , where is the bootstrap score of the DMUi. It is done as follows:
- Extract a sample with replacement of (,…, ) and call the results (,…, );
- Calculate the bandwidth h and generate independent random numbers of standard-normal distribution: ,…, ;
- Compute
- 3.
- Extract a new sample data whose elements, Y* = [, …, ] and X* = [, …, ], are given by e . That way, will continue in the same radius as ;
- 4.
- Use the DEA model chosen—(3) or (5)—to calculate the estimation of new indices de ;
- 5.
- Repeat the steps 2, 3 and 4 B times to obtain the set of estimations [ ] to b = 1… B.
2.5. Testing for Return-to-Scale Types
2.6. Eco-Efficiency Dependency of External Factors: Second-Stage Analysis
- Estimate the corrected efficiency to all DMUs (i = 1, …, n) using the DEA-CRS or DEA-BCC model oriented to outputs;
- Regress , using a tobit regression using maximum likelihood estimation, aiming to obtain estimations , and its standard deviation, ;
- Repeat the next three steps (a, b, c) L times to produce a set of bootstrap estimators :
- For each DMUi, with the estimated in stage 2, extract random values of of a normal distribution N(0,) truncated to left in (1 − );
- For each DMUi estimate , where is the estimator found in stage 2;
- Following the maximum likelihood estimation, estimate the truncated regression of in obtaining the estimations ;
- Use the L values of the set to construct the confidence intervals of and .
2.7. Object of the Study and Variables
3. Results and Discussion
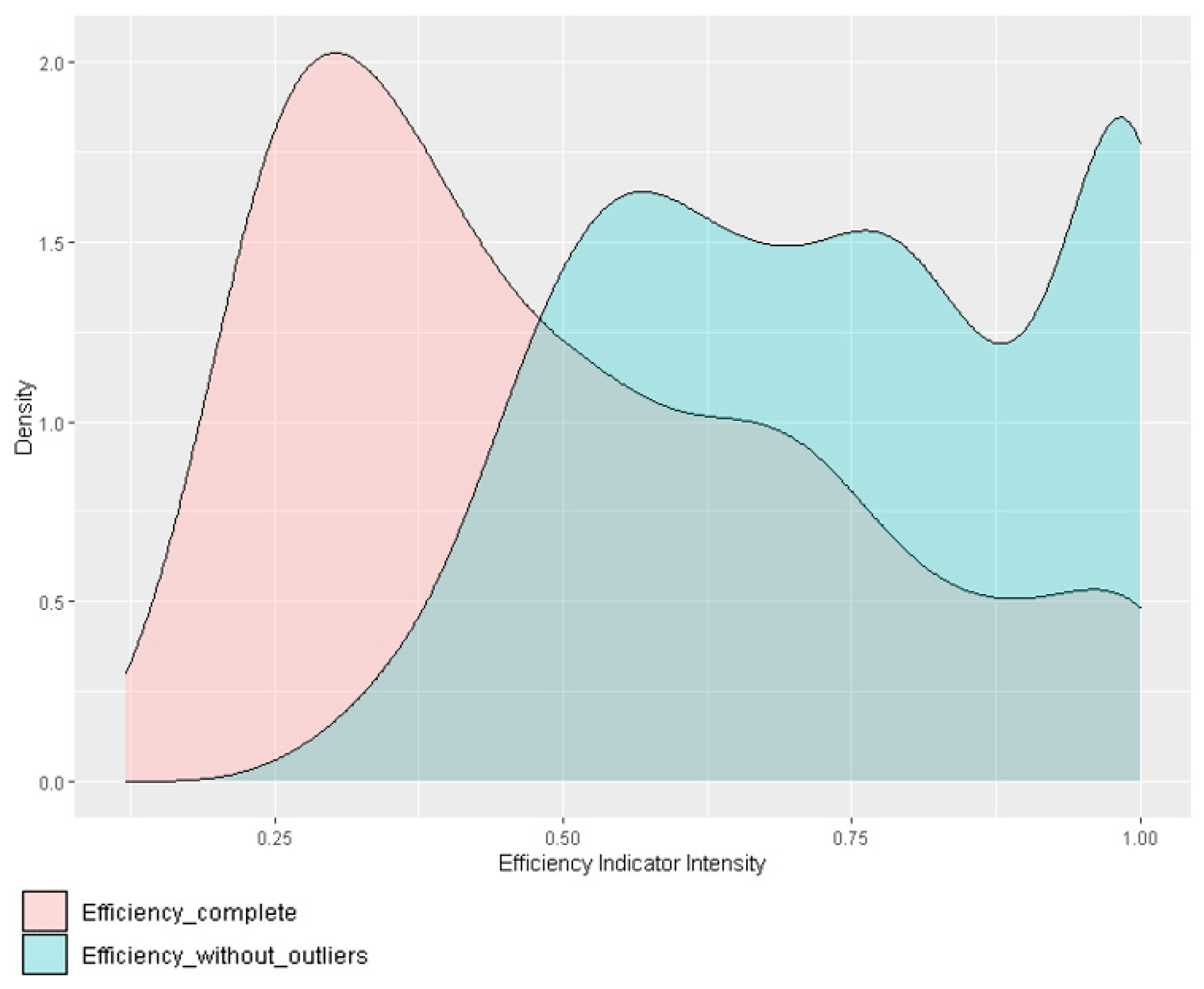
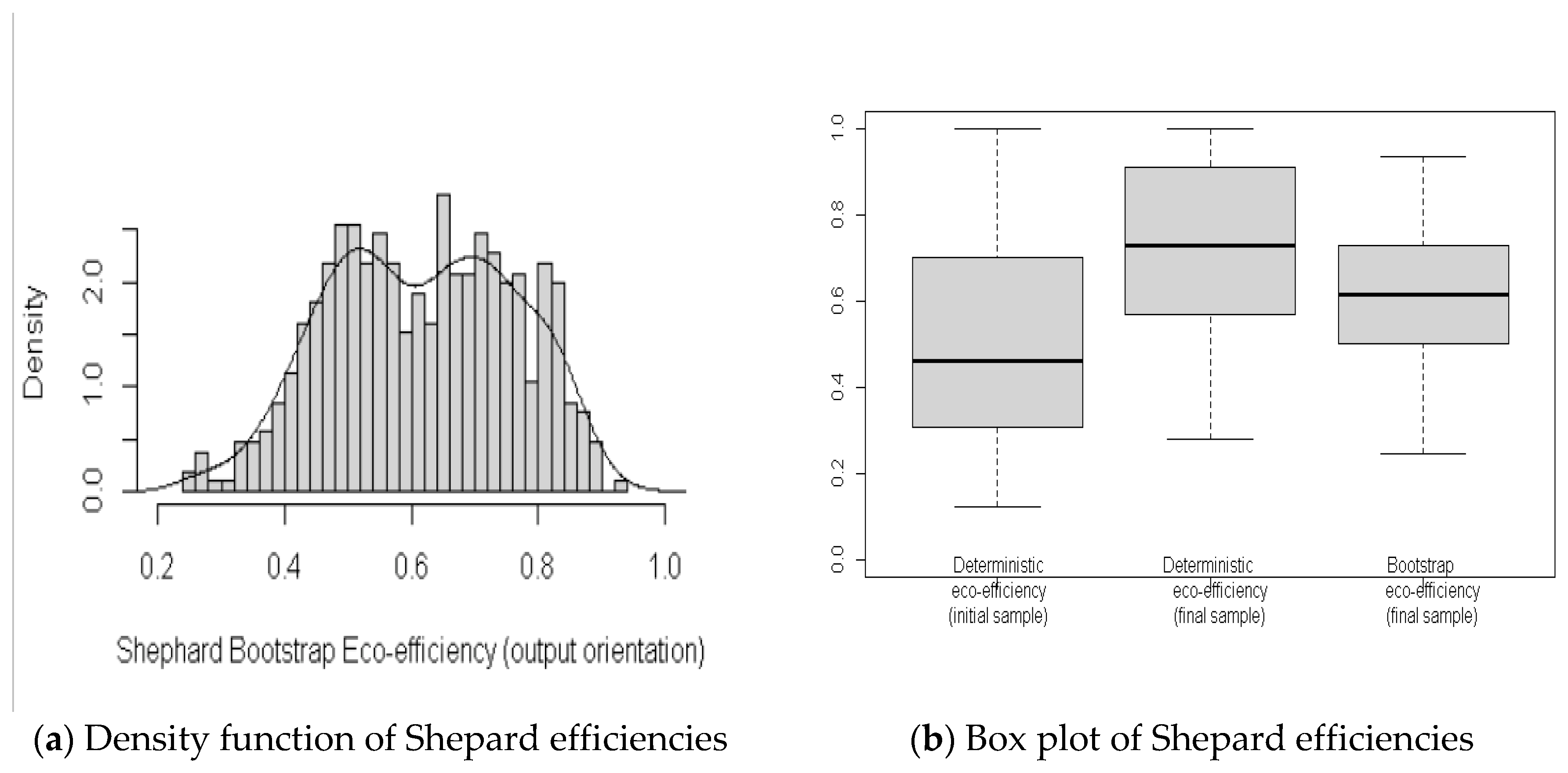
3.1. Descriptive Analysis, Outlier Detection and Final Sample
3.2. Statistical Inference of the DEA Indices
3.3. Impact of the Contextual Variables into Eco-Efficiency Indicators
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Araujo, R.D.C.; Ponte, M.X. Agronegócios na Amazônia: Ameaças e oportunidades para o desenvolvimento sustentável da região. Rev. Ciênc. Agroambient. 2015, 13, 101–114. [Google Scholar] [CrossRef]
- Fishlow, A.; Filho, J.E.R.V. Agriculture and Industry in Brazil; Columbia University Press: Chichester, NY, USA, 2019. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G.-L. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Meeusen, W.; van den Broeck, J. Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.A.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econ. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Coelli, T.; Rao, D.S.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis; Kluwer Academic Publishers: New York, NY, USA, 1998. [Google Scholar]
- Simar, L. Estimating Efficiencies from Frontier Models with Panel Data: A Comparison of Parametric, Non-Parametric and Semi-Parametric Methods with Bootstrapping. In International Applications of Productivity and Efficiency Analysis; Springer: Dordrecht, The Netherlands, 1992; pp. 167–199. [Google Scholar] [CrossRef]
- Wilson, P.W. Detecting Outliers in Deterministic Nonparametric Frontier Models with Multiple Outputs. J. Bus. Econ. Stat. 1993, 11, 319. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimation and inference in two-stage, semi-parametric models of production processes. J. Econ. 2007, 136, 31–64. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P. Estimation and Inference in Two-Stage, Semi-Parametric Models of Production Processes. STAT Discussion Papers; 0307 (2003) 36 Pages. Available online: http://hdl.handle.net/2078.1/122906 (accessed on 25 June 2020).
- Caiado, R.G.G.; De Freitas Dias, R.; Mattos, L.V.; Quelhas, O.L.G.; Filho, W.L. Towards sustainable development through the perspective of eco-efficiency—A systematic literature review. J. Clean. Prod. 2017, 165, 890–904. [Google Scholar] [CrossRef]
- Coluccia, B.; Valente, D.; Fusco, G.; De Leo, F.; Porrini, D. Assessing agricultural eco-efficiency in Italian Regions. Ecol. Indic. 2020, 116, 106483. [Google Scholar] [CrossRef]
- Souza, G.S.; Gomes, E.G. Métodos alternativos para análise de regressão em dois estágios com resposta DEA: Uma aplicação para a agricultura brasileira. In Proceedings of the Simpósio de Pesquisa Operacional e Logística da Marinha, Rio de Janeiro, Brazil, 6–8 November 2019; pp. 1644–1657. [Google Scholar]
- Barros, E.D.S.; Xavier, L.F.; Fonseca, H.V.D.P.; Costa, E.D.F. Eficiência na produção agrícola do Vale São Francisco: Mensuração de escores e análise de fatores correlacionados. Rev. Econ. Agríc. 2016, 63, 35–50. [Google Scholar]
- Grassauer, F.; Herndl, M.; Nemecek, T.; Guggenberger, T.; Fritz, C.; Steinwidder, A.; Zollitsch, W. Eco-efficiency of farms considering multiple functions of agriculture: Concept and results from Austrian farms. J. Clean. Prod. 2021, 297, 126662. [Google Scholar] [CrossRef]
- Guo, S.; Hu, Z.; Ma, H.; Xu, D.; He, R. Spatial and Temporal Variations in the Ecological Efficiency and Ecosystem Service Value of Agricultural Land in China. Agriculture 2022, 12, 803. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Bin, P. Agriculture carbon-emission reduction and changing factors behind agricultural eco-efficiency growth in China. J. Clean. Prod. 2021, 334, 130193. [Google Scholar] [CrossRef]
- IPEA; Instituto Brasileiro de Geografia e Estatística. Censo Agropecuário 2017: Resultados Definitivos; IBGE: Rio de Janeiro, Brazil, 2019; Available online: https://censoagro2017.ibge.gov.br/ (accessed on 1 May 2019).
- Roll, Y.; Golany, B.; Seroussy, D. Measuring the efficiency of maintenance units in the Israeli Air Force. Eur. J. Oper. Res. 1989, 43, 136–142. [Google Scholar] [CrossRef]
- Picazo-Tadeo, A.J.; Gómez-Limón, J.A.; Reig-Martínez, E. Assessing farming eco-efficiency: A Data Envelopment Analysis approach. J. Environ. Manag. 2011, 92, 1154–1164. [Google Scholar] [CrossRef]
- Pyatt, G.; Shephard, R.W. Theory of Cost and Production Functions. Econ. J. 1972, 82, 1059. [Google Scholar] [CrossRef]
- Färe, R. Representing the Technology by Functions. In Fundamentals of Production Theory; Springer: Berlin/Heidelberg, Germany, 1988; pp. 22–42. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Pasurka, C.A., Jr. Environmental production functions and environmental directional distance functions. Energy 2007, 32, 1055–1066. [Google Scholar] [CrossRef]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. Ser. A Gen. 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Gusarov, S.; Dmitriev, Y. Extended Koopmans’ Approximation for CASDFT Exchange-Correlation Functional. J. Appl. Math. Phys. 2018, 6, 1242–1246. [Google Scholar] [CrossRef][Green Version]
- WBCSD. World Business Council for Sustainable Development Eco-Efficiency Creating More Value with Less Impact; WBCSD: Geneva, Switzerland, 2006. [Google Scholar]
- Debreu, G. The Coefficient of Resource Utilization. Econometrica 1951, 19, 273–292. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Korostelev, A.P.; Simar, L.; Tsybakov, A.B. Efficient Estimation of Monotone Boundaries. Ann. Stat. 1995, 23, 476–489. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. In Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 569–593. [Google Scholar]
- Simar, L.; Wilson, P.W. Sensitivity Analysis of Efficiency Scores: How to Bootstrap in Nonparametric Frontier Models. Manag. Sci. 1998, 44, 49–61. [Google Scholar] [CrossRef]
- Bogetoft, P.; Otto, L. Benchmarking with dea, sfa, and r; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 157. [Google Scholar]
- Sousa, M.D.C.S.D.; Stosic, B. Technical Efficiency of the Brazilian Municipalities: Correcting Nonparametric Frontier Measurements for Outliers. J. Prod. Anal. 2005, 24, 157–181. [Google Scholar] [CrossRef]
- Wilson, P.W. FEAR: A software package for frontier efficiency analysis with R. Socio-Econ. Plan. Sci. 2008, 42, 247–254. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Non-parametric tests of returns to scale. Eur. J. Oper. Res. 2002, 139, 115–132. [Google Scholar] [CrossRef]
- Lovell, C.K. Production frontiers and productive efficiency. Meas. Product. Effic. Tech. Appl. 1993, 3, 67. [Google Scholar]
- Xue, M.; Harker, P.T. Overcoming the Inherent Dependency of DEA Efficiency Scores: A Bootstrap Approach; Unpublished Working Paper; Wharton Financial Institutions Center, University of Pennsylvania: Philadelphia, PA, USA, 1999. [Google Scholar]
- Miranda, E.; de Carvalho, C.A.; Martinho, P.R.R.; Oshiro, O.T. Contribuições do geoprocessamento à compreensão do mundo rural e do desmatamento no bioma Amazônia. COLÓQUIO-Rev. Desenvolv. Reg. 2020, 17, 16–34. [Google Scholar] [CrossRef][Green Version]
- Suzigan, L.H.; Peña, C.R.; Guarnieri, P. Eco-efficiency Assessment in Agriculture: A Literature Review Focused on Methods and Indicators. J. Agric. Sci. 2020, 12, 118. [Google Scholar] [CrossRef]
- Beltrán-Esteve, M.; Reig-Martínez, E.; Estruch-Guitart, V. Assessing eco-efficiency: A metafrontier directional distance function approach using life cycle analysis. Environ. Impact Assess. Rev. 2017, 63, 116–127. [Google Scholar] [CrossRef]
- Bravo-Ureta, B.E.; Pinheiro, A.E. Efficiency Analysis of Developing Country Agriculture: A Review of the Frontier Function Literature. Agric. Resour. Econ. Rev. 1993, 22, 88–101. [Google Scholar] [CrossRef]
- Sousa, K.M.; Sousa, M.D.C.S.; Monte, P.A.D. Package Jackstrap. 2020. Available online: https://CRAN.R-project.org/package=jackstrap (accessed on 28 May 2021).
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Freitas, C.O.; Teixeira, E.C.; Braga, M.J.; de Souza Schuntzemberger, A.M. Technical efficiency and farm size: An analysis based on the Brazilian agriculture and livestock census. Ital. Rev. Agric. Econ. 2019, 74, 33–48. [Google Scholar] [CrossRef]
- Alves, E. Retornos à escala e mercado competitivo: Teoria e evidências empíricas. Rev. Econ. Agronegócio 2004, 2, 311–334. [Google Scholar] [CrossRef]
- Hoffmann Rodolfo. A distribuição da posse de terra no brasil (1985–2017). In Uma Jornada Pelos Contrastes do Brasil: Cem Anos de Censo Agropecuário; Vieira Filho, J.E.R., Gasques, J.G., Eds.; Ipea: Brasília, Brazil, 2020; Volume 1, pp. 77–90. [Google Scholar]
- Souza, G.S.; Gomes, E.G.; Alves, E.R.A. Imperfeições de Mercado e Concentração de Renda na Produção Revista de Política Agrícola, Brasília, DF, Abr./Maio/Jun. 2018, 27, pp. 31–38. Available online: http://www.alice.cnptia.embrapa.br/alice/handle/doc/1102920 (accessed on 1 May 2020).
- Caves, R.E.; Porter, M.E. From Entry Barriers to Mobility Barriers: Conjectural Decisions and Contrived Deterrence to New Competition. Q. J. Econ. 1977, 91, 241–261. [Google Scholar] [CrossRef]
- Porter, M.E. The Structure within Industries and Companies’ Performance. Rev. Econ. Stat. 1979, 61, 214. [Google Scholar] [CrossRef]
- Taylor, T.G.; Drummond, H.E.; Gomes, A.T. Agricultural Credit Programs and Production Efficiency: An Analysis of Traditional Farming in Southeastern Minas Gerais, Brazil. Am. J. Agric. Econ. 1986, 68, 110–119. [Google Scholar] [CrossRef]
- Fernandes de Oliveira, L.A.; Pascual, U. Análise da eficiência da agricultura familiar agroecologista. Revibec Rev. De La Red Iberoam. Econ. Ecol. 2015, 24, 221–233. Available online: https://raco.cat/index.php/Revibec/article/view/298652 (accessed on 19 May 2020).
- Araújo, J.A.; Vieira Filho, J.E.R. Análise dos Impactos do PRONAF na Agricultura do Brasil no Período de 2007 a 2016; Discussion Paper, 2412; Ipea: Brasília, Brazil, 2018; Available online: http://hdl.handle.net/10419/211361 (accessed on 20 September 2021).
- Gasson, R. Educational qualifications of UK farmers: A review. J. Rural Stud. 1998, 14, 487–498. [Google Scholar] [CrossRef]
- Ondersteijn, C.; Giesen, G.; Huirne, R. Perceived environmental uncertainty in Dutch dairy farming: The effect of external farm context on strategic choice. Agric. Syst. 2006, 88, 205–226. [Google Scholar] [CrossRef]
- Gomes, A.P.; Ervilha, G.T.; Freitas, L.F.D.; Nascif, C. Assistência técnica, eficiência e rentabilidade na produção de leite. Rev. Polít. Agríc. 2018, 27, 79. [Google Scholar]
- Braga, M.J.; Vieira Filho, J.E.R.; Freitas, C.O. Impactos da extensão rural na renda produtiva. In Diagnóstico e Desafios da Agricultura Brasileira; Vieira Filho, J.E.R., Ed.; IPEA: Brasília, Brazil, 2019; Volume 5, pp. 137–160. [Google Scholar]
- Ramos, E.B.T.; Vieira Filho, J.E.R. Cooperativismo e Associativismo na Produção Agropecuária de Menor Porte no Brasil; Discussion Paper, 2693; Ipea: Brasília, Brazil, 2021. [Google Scholar] [CrossRef]
- Araújo, R.; Benatti, J.E.; Pena, S. Grilagem de Terras Públicas na Amazônia Brasileira; MMA: Brasília, Brazil, 2006. [Google Scholar]
| Mean | Median | Standard Deviation | Minimum | 1° Quartile | 3° Quartile | Maximum | |
|---|---|---|---|---|---|---|---|
| x1 | 176,913 | 89,392.5 | 250,039.1 | 72 | 29,453 | 220,394 | 2,462,092 |
| x2 | 5947.399 | 2280 | 11,922.16 | 1 | 663.8 | 6217.8 | 122,958 |
| x3 | 27,865.48 | 5704.5 | 82,192.97 | 32 | 1132 | 18,530 | 1,004,087 |
| x4 | 4500.781 | 3338.5 | 4337.971 | 105 | 1825 | 5774 | 48,246 |
| x5 | 37,807.83 | 11,388 | 97,494.70 | 23 | 2542 | 32,924 | 1,320,992 |
| y1 | 12.39416 | 4.83375 | 26.95020 | 0.0857 | 1.65 | 11.16 | 306.1954 |
| y2 | 6.772156 | 2.4825 | 11.13849 | 0.00001 | 0.650 | 7.785 | 96.2598 |
| y3 | 2.320974 | 1.64081 | 1.728685 | 1.00084 | 1.180 | 2.862 | 13.99893 |
| y4 | 83.67418 | 7.29497 | 384.8253 | 0.23926 | 2.697 | 35.992 | 6681.91 |
| z1 | 0.798722 | 0.814445 | 0.1154 | 0.27478 | 0.740 | 0.8725 | 0.980769 |
| z2 | 0.130973 | 0.090833 | 0.1290 | 0 | 0.040 | 0.170 | 0.898204 |
| z3 | 0.047284 | 0.020535 | 0.0691 | 0 | 0.010 | 0.060 | 0.562325 |
| z4 | 0.216148 | 0.200064 | 0.0935 | 0.02521 | 0.140 | 0.270 | 0.65 |
| z5 | 0.795039 | 0.859133 | 0.1927 | 0.055172 | 0.710 | 0.930 | 1 |
| z6 | 0.113395 | 0.091004 | 0.0884 | 0.002396 | 0.050 | 0.160 | 0.754491 |
| z7 | 31.71617 | 6.799077 | 163.2888 | 0.031568 | 2.345 | 18.942 | 2803.911 |
| z8 | −5.9986 | −4.40389 | 4.7996 | −26.7836 | −9.987 | −2.245 | 4.595012 |
| z9 | −53.6487 | −51.2433 | 7.4920 | −72.8958 | −59.70 | −47.61 | −36.4 |
| DMU | Without the Outliers and with Bias Correction | Confidence Interval | Without the Outliers and without Bias Correction | With the Initial Sample | |
|---|---|---|---|---|---|
| Lower Limit | Upper Limit | ||||
| Parauapebas (PA) | 0.936 | 0.910 | 0.983 | 0.998 | 0.450 |
| Novo Airão (AM) | 0.897 | 0.861 | 0.973 | 0.985 | 0.847 |
| Medicilândia (PA) | 0.891 | 0.869 | 0.938 | 0.953 | 0.506 |
| Presidente Figueiredo (AM) | 0.885 | 0.856 | 0.971 | 0.977 | 0.852 |
| Rio Preto da Eva (AM) | 0.880 | 0.858 | 0.985 | 1.000 | 0.849 |
| Santa L. do Paruá (MA) | 0.274 | 0.259 | 0.304 | 0.308 | 0.178 |
| Garrafão do Norte (PA) | 0.268 | 0.255 | 0.330 | 0.334 | 0.215 |
| Anajatuba (MA) | 0.267 | 0.261 | 0.299 | 0.303 | 0.121 |
| Governador Nunes F. (MA) | 0.255 | 0.244 | 0.288 | 0.291 | 0.128 |
| Itapecuru Mirim (MA) | 0.247 | 0.238 | 0.275 | 0.278 | 0.137 |
| Average | 0.615 | 0.601 | 0.720 | 0.730 | 0.519 |
| Environmental Variables | Beta Coefficient | Confidence Interval of 95% | Average Marginal Effect | |
|---|---|---|---|---|
| Lower Limit | Upper Limit | |||
| Y-intercept | 2.2547 | 2.25 | 2.26 | |
| z1—familiar farming | 0.1219 | 0.11 | 0.13 | 0.12185 |
| z2—technical assistance | −0.4800 | −0.49 | −0.47 | −0.48002 |
| z3—cooperative | −0.0892 | −0.10 | −0.08 | −0.08918 |
| z4—high school | −0.6851 | −0.69 | −0.68 | −0.68505 |
| z5—landlord | −0.0340 | −0.04 | −0.03 | −0.03400 |
| z6—financing | 1.1557 | 1.15 | 1.17 | 1.15569 |
| z7—density | 0.00004 | 0.00003 | 0.00004 | 0.00004 |
| z8—latitude | 0.00024 | 0.00007 | 0.00042 | 0.00024 |
| z9—longitude | 0.0084 | 0.00830 | 0.00850 | 0.00840 |
| Error variance | 0.398 | 0.398 | 0.398 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosano-Peña, C.; Silva, J.V.B.; Serrano, A.L.M.; Vieira Filho, J.E.R.; Kimura, H. Eco-Efficiency of Agriculture in the Amazon Biome: Robust Indices and Determinants. World 2022, 3, 753-771. https://doi.org/10.3390/world3040042
Rosano-Peña C, Silva JVB, Serrano ALM, Vieira Filho JER, Kimura H. Eco-Efficiency of Agriculture in the Amazon Biome: Robust Indices and Determinants. World. 2022; 3(4):753-771. https://doi.org/10.3390/world3040042
Chicago/Turabian StyleRosano-Peña, Carlos, João Vitor Borges Silva, André Luiz Marques Serrano, José Eustáquio Ribeiro Vieira Filho, and Herbert Kimura. 2022. "Eco-Efficiency of Agriculture in the Amazon Biome: Robust Indices and Determinants" World 3, no. 4: 753-771. https://doi.org/10.3390/world3040042
APA StyleRosano-Peña, C., Silva, J. V. B., Serrano, A. L. M., Vieira Filho, J. E. R., & Kimura, H. (2022). Eco-Efficiency of Agriculture in the Amazon Biome: Robust Indices and Determinants. World, 3(4), 753-771. https://doi.org/10.3390/world3040042






