MPC-Based Sensor Fault-Tolerant Control: Application to a Heat Exchanger with Measurement Noise
Abstract
1. Introduction
1.1. Related Work
1.1.1. Heat Exchanger
1.1.2. Fault-Tolerant Control Applied to Heat Exchangers
1.1.3. MPC-Based Fault-Tolerant Control
1.2. Original Contributions
2. Fault-Tolerant Control
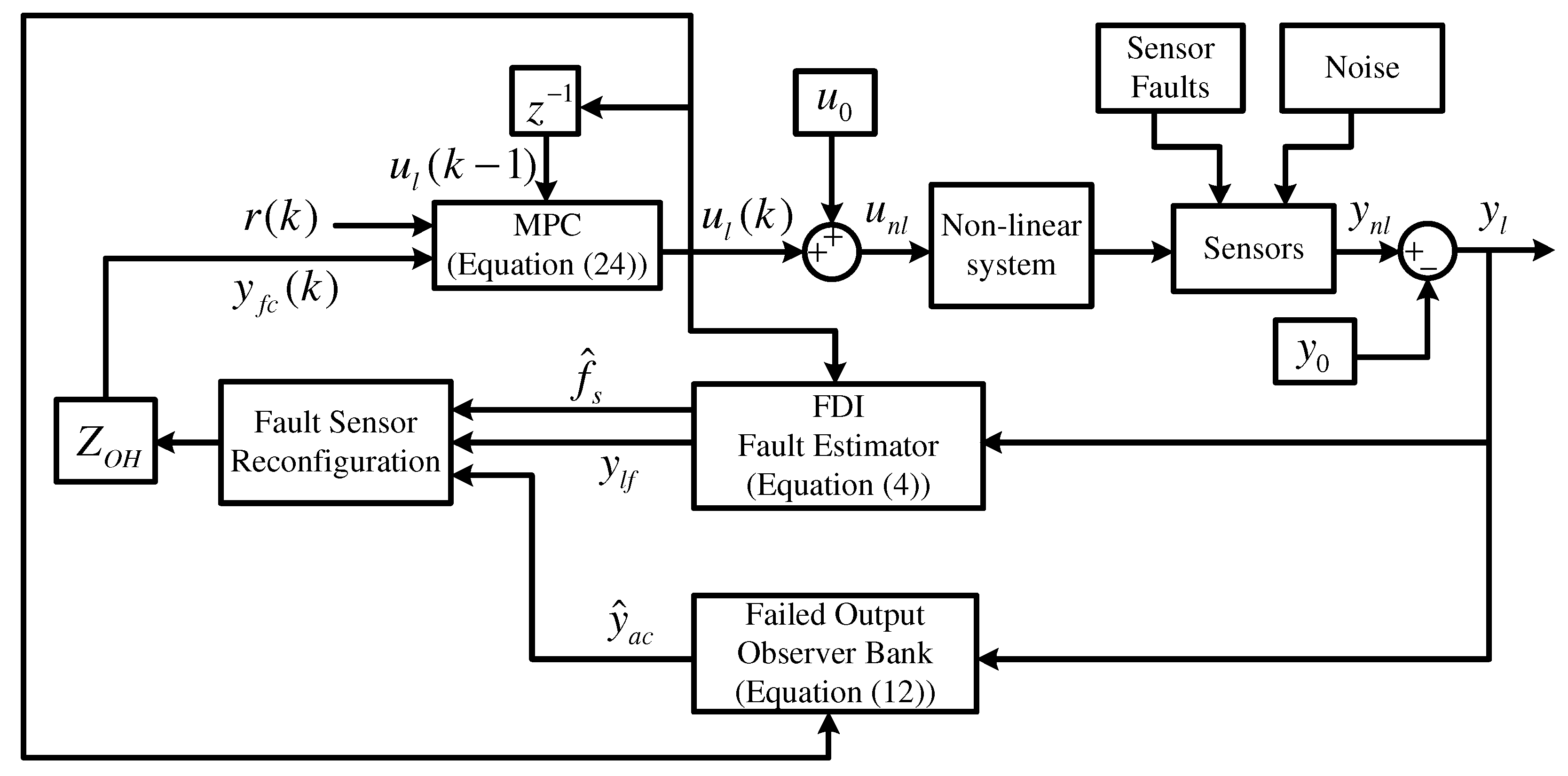
2.1. General Description
- A model predictive control, tracking desired references for the output of the system.
- A fault estimation observer that includes a filter acting on the outputs with noise, providing the estimations for the faults at each sensor.
- A set of observers providing the faulty output reconstruction, driven by the fault-free output.
- A sensor fault reconfiguration unit, in charge of making decisions to provide fault-free outputs in the case of fault occurrence in the control system or, in the fault-free case, the filtered system outputs.
2.1.1. Fault-Free Case
2.1.2. Faulty System Case
2.2. Fault-Tolerant Control Design
2.2.1. Fault Estimator Design
2.2.2. Observer Design for Fault Reconfiguration
2.2.3. MPC Control Design
2.2.4. Sensor Fault Reconfiguration Unit
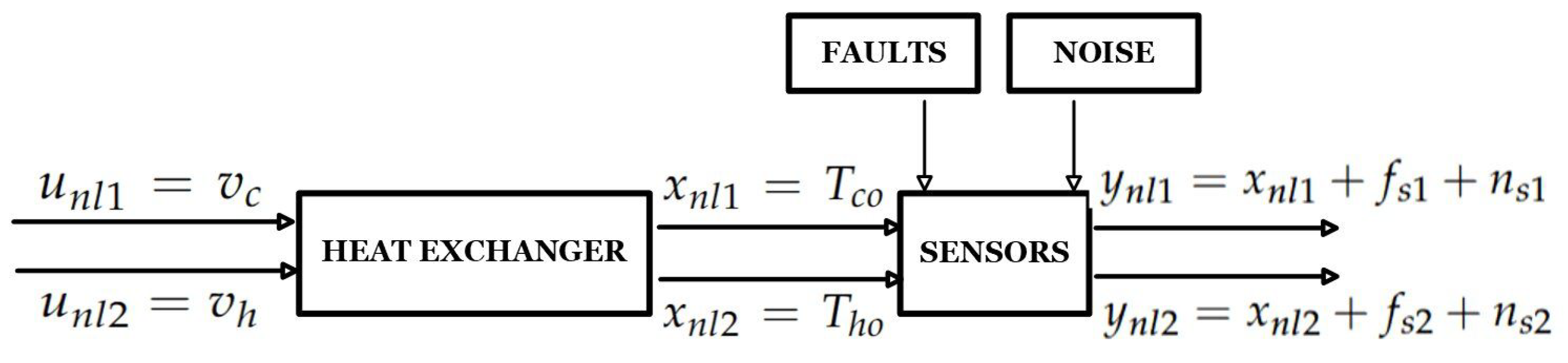
3. Case Study Description: Heat Exchanger Dynamics
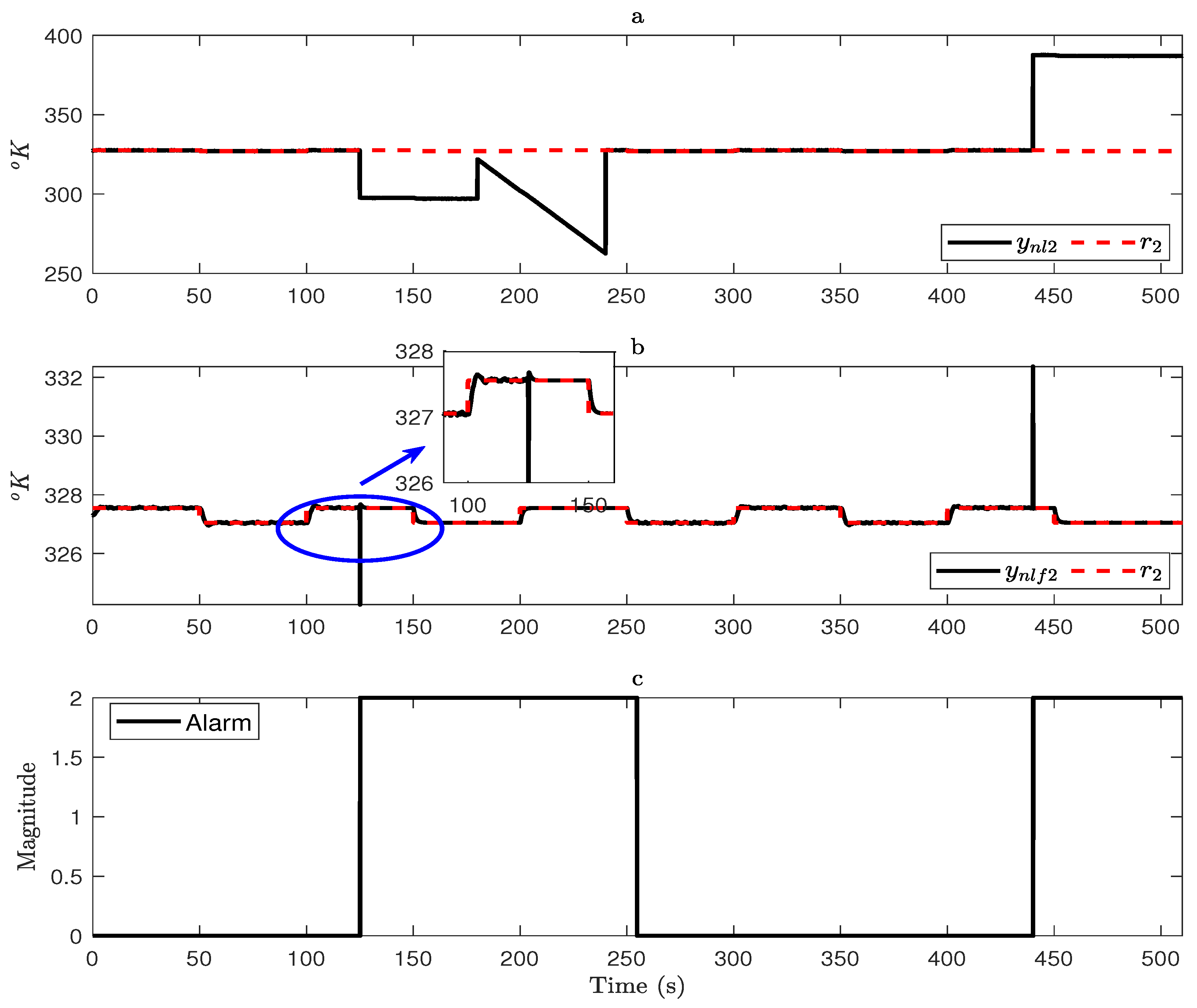
4. Results
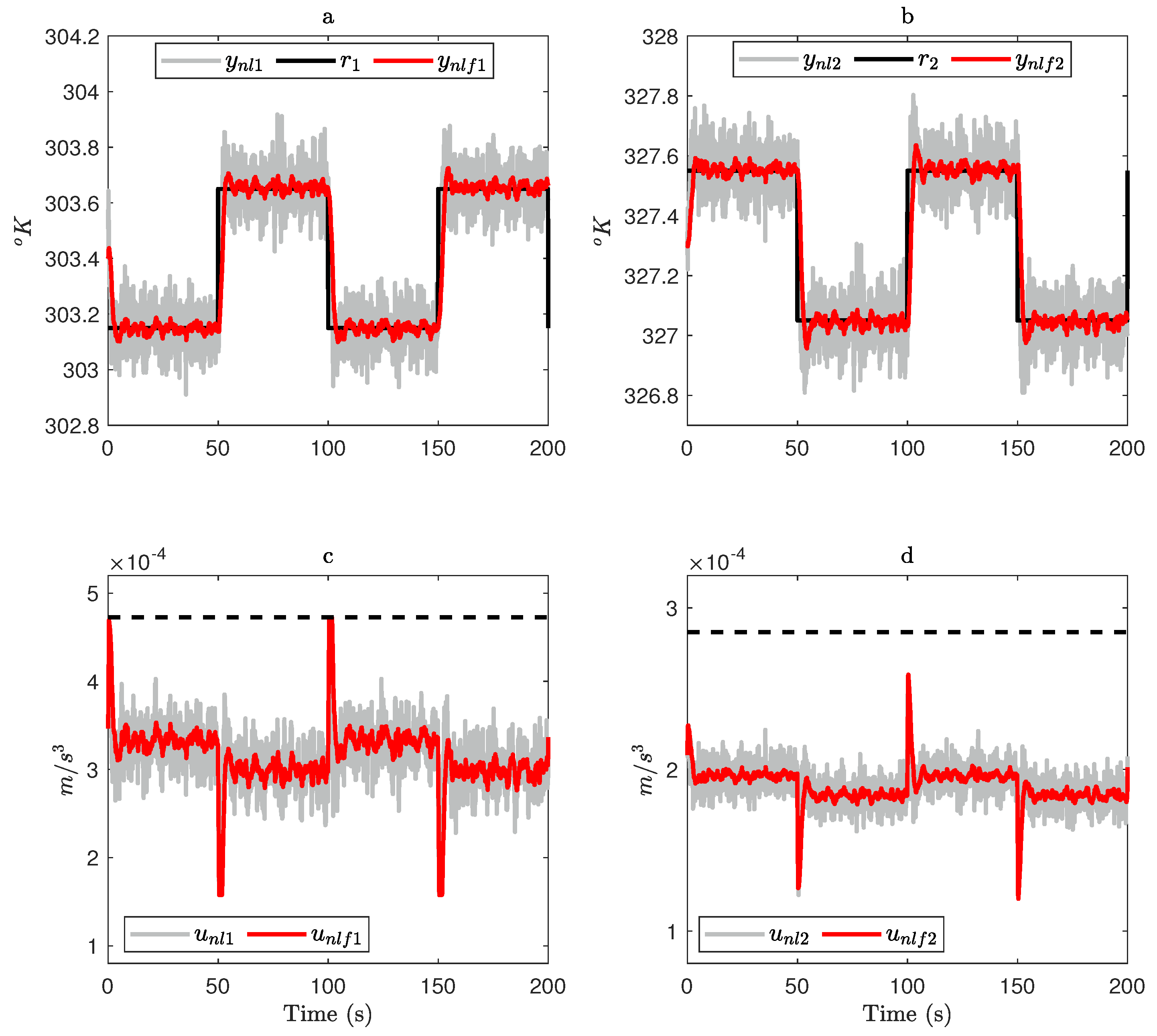
4.1. Fault-Free Case
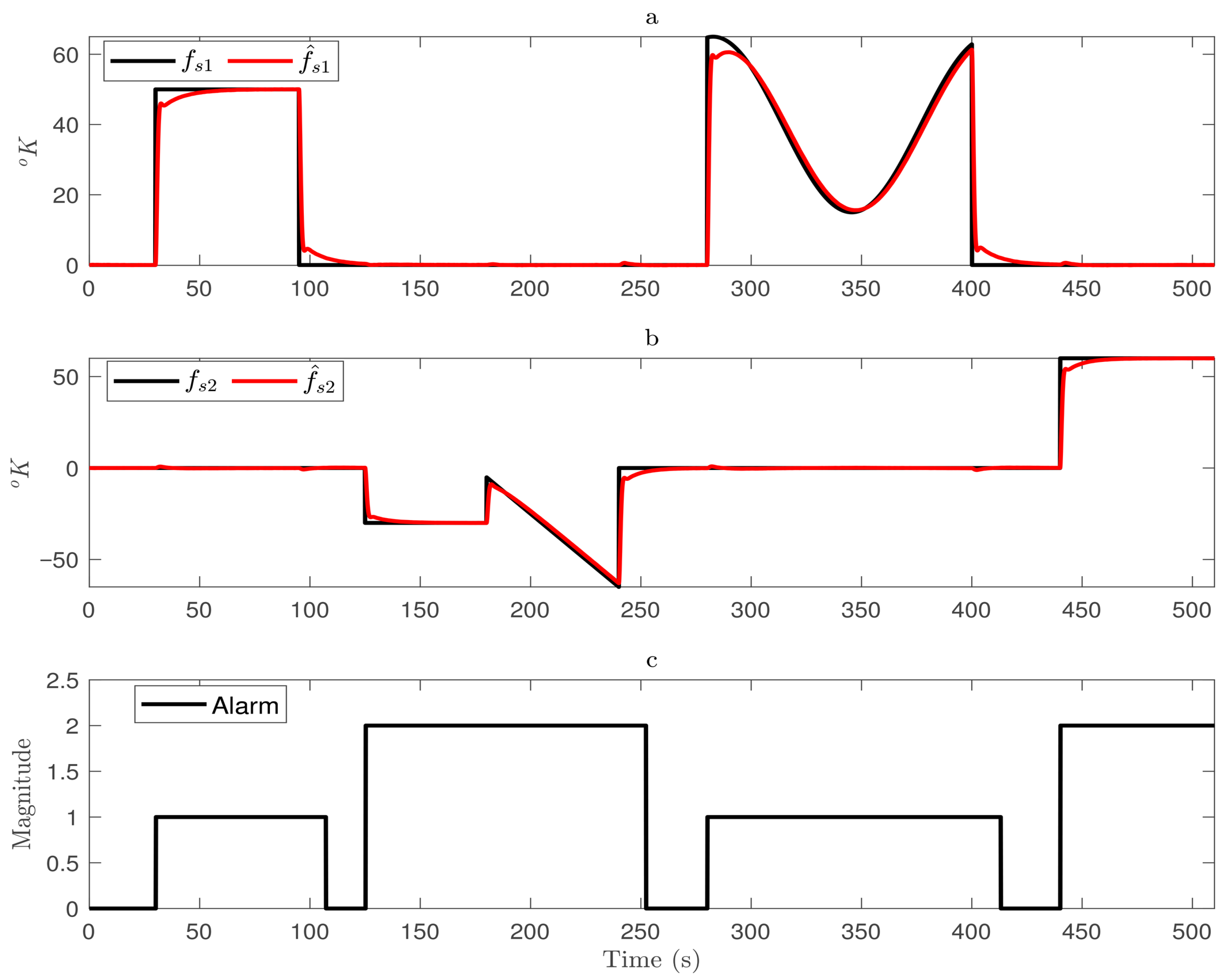
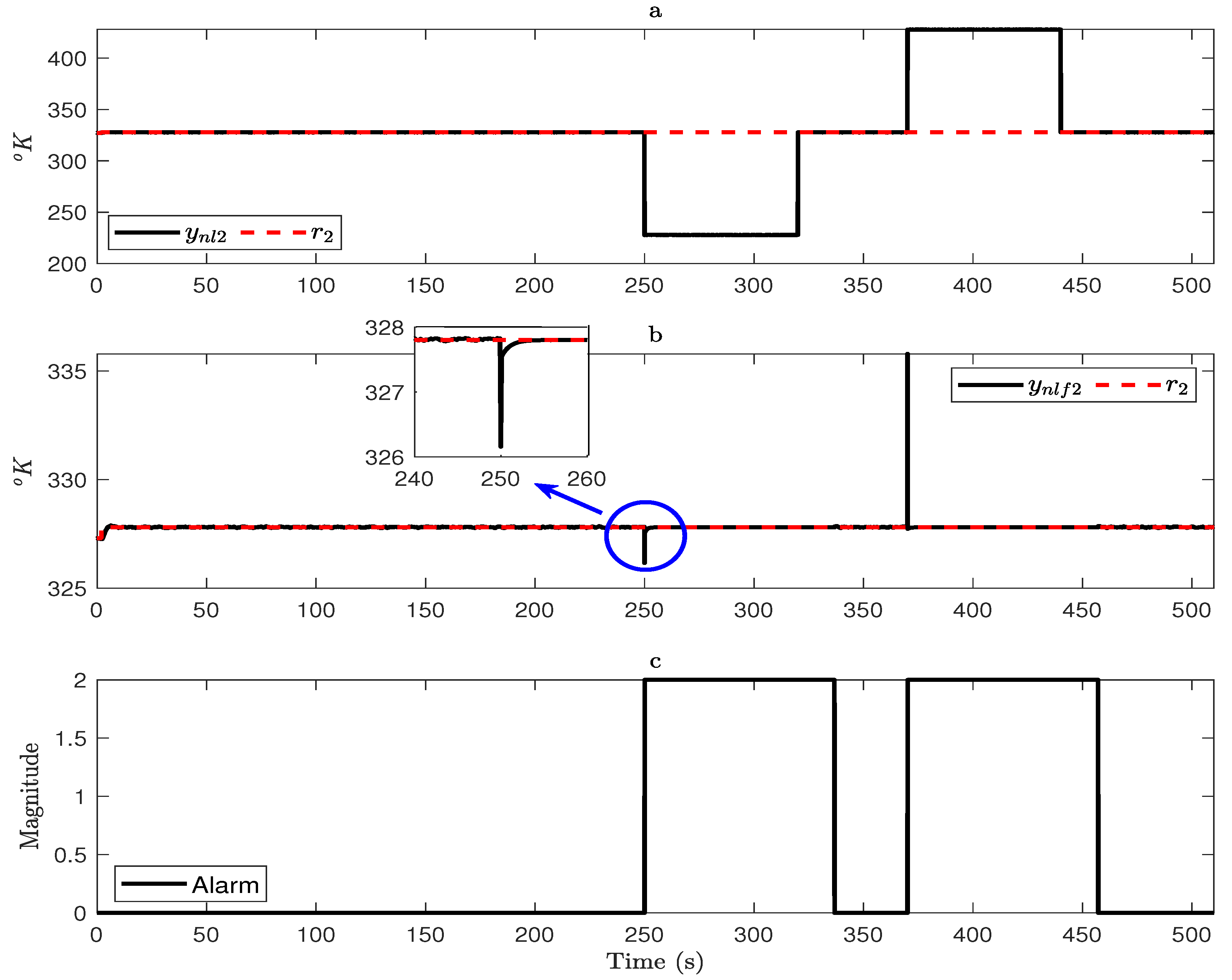
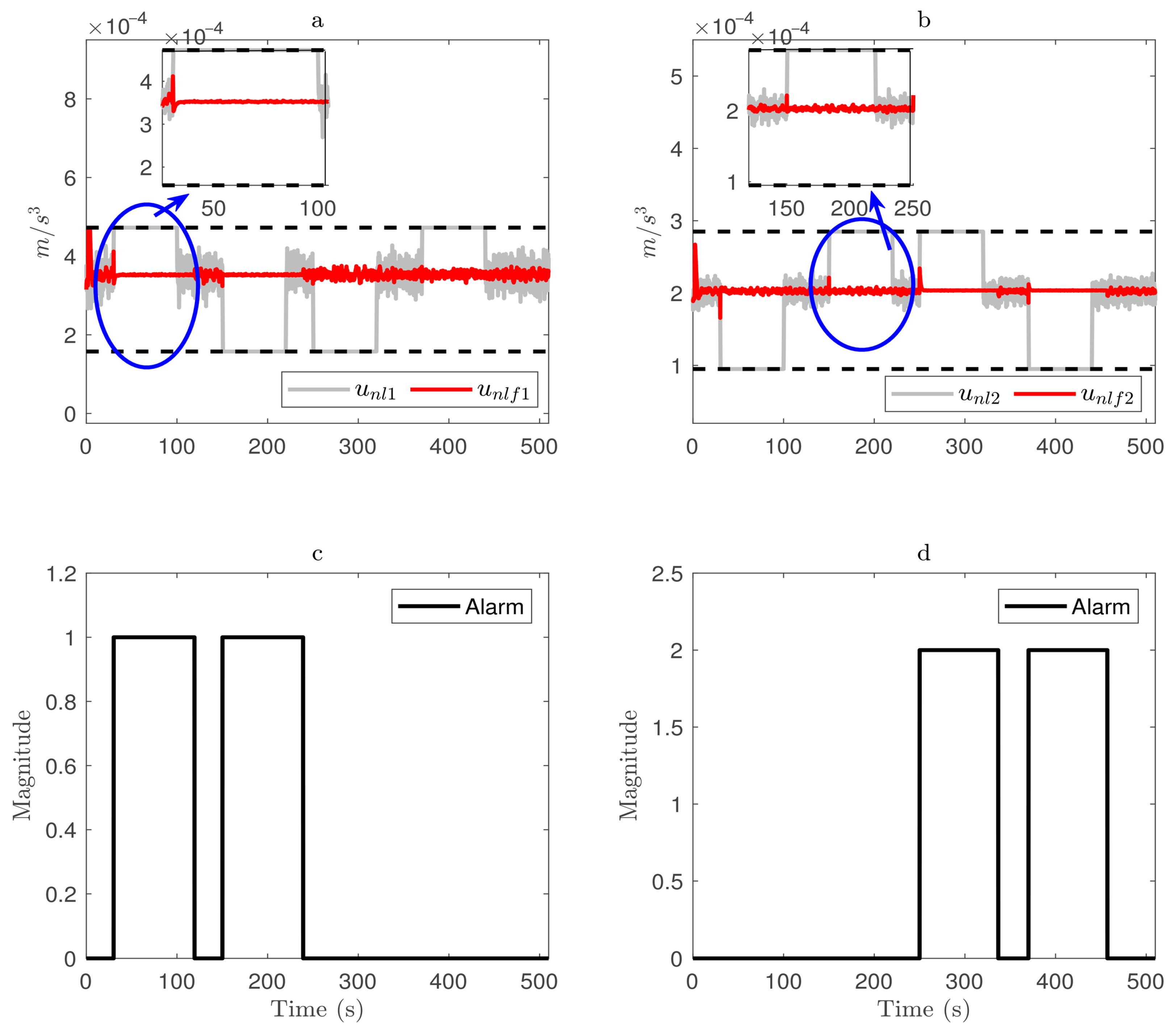
4.2. Faulty Case
5. Discussion
- Regarding the measured noise in the proposed FTC scheme, it is important to note that the FTC considers its representation in the system dynamics analytically, giving rise to the FTC element design. The proposed FTC scheme includes these elements to deal with the measurement noise, defining the main contribution of the present paper.
- In addressing the proposed FTC scheme for the control law, it is relevant to note that the MPC controller cannot attenuate the sensor fault effect, which makes the proposed FTC scheme suitable. Besides this condition, let us point out that its design, from the results shown throughout this paper, presents the achievement of the boundary conditions correctly, included within its analytical design. In this sense, note that the system outputs exhibit a saturation evolution over time in the faulty case, from which the correct controller performance can be defined. As a concluding comment, let us mention that the designer can choose the design parameters to reach specific transient responses and boundary conditions, depending on the addressed dynamical system.
- Regarding the observer for fault estimation and observers for fault reconfiguration, it is essential to point out that they contribute to mitigating/reducing the effect of the measurement noise on their corresponding estimations. These elements include specific terms in charge of having this effect on their results, which in the present paper refers to the control law computation aiming at achieving the control objectives with a noise reduction within the closed-loop system dynamics.
- Let us focus on the faulty case. It is important to note that under faulty sensor operation, physically, the corresponding element will continue providing a measurement that does not accurately reflect the real variable value. However, the output of the system will remain at the desired values due to the FTC system operation as a consequence of the fault reconfiguration process. The real value for the output will be provided by the observer (virtual sensor), which does not consider the faulty output for its estimation.
- On the other hand, an important issue is related to the threshold involved in triggering the fault alarm. Note that its value depends on how fast the fault must be detected and isolated. In the present paper, this condition refers to the selection considering the remaining noise presented in the fault estimations. A threshold defined close to the remaining noise in the fault estimation could lead to an unnecessary reconfiguration process and thus to an unnecessary switching behavior between the observers for fault reconfiguration. As a result, its selection depends on the measurement noise presented in the system, from which the fault occurrence is defined.
- Following with the threshold and aiming at explicitly mentioning its importance, in the present paper, the selected value is defined in such a way that the result of the proposed method can be generated. The authors consider that further analysis is necessary in real scenarios to ensure the optimal value, possibly an optimization process from data provided by the real system instrumentation. This condition will generate more accurate results when handling real systems.
- It is worth mentioning the motivation behind this paper in contrast with existing methods handling the measurement noise within dynamical systems. Although several works have been reported regarding sensor noise, as an example, those presented in [39,40], the results presented in this paper consider functional observers to provide fault recovery in the case of faulty conditions in the system outputs. The authors mention that future research directions could utilize more complex schemes regarding the elements in charge of providing fault and state reconstruction, dealing with measurement noise, in the context of FCT systems.
- In addressing the second result shown in the corresponding section, it is essential to mention that faults with values are considered the worst case that the proposed FTC scheme can deal with. In the simulation, the authors applied fault magnitudes beyond this value, making the system unsolvable. Notice that despite this fact, the proposed FTC deals with BIAS or loss of effectiveness in the sensor around 30% regarding the operating point considered in the linearization process for FTC design. Along with this consideration, the observer for fault estimation and the MPC controller can provide information for the operation of the reconfiguration unit, giving accurate results. Note that the MPC controller bounds the control signals. As long as the solution to the optimization problem is feasible, the system maintains stability by having the inputs bounded under defined fault conditions. These issues can define that linear approaches can be considered for dealing with non-linear systems.
- Regarding the heat exchanger’s non-linear dynamics, the condition related to is worth mentioning. Notice that this condition involves the quotient between the difference of temperatures and a natural logarithm. It is well known that this function is not defined in 0, giving rise to an undefined and, consequently, unsolvable dynamics. This consideration is a limitation and a challenging problem when dealing with the heat exchanger approximated by the model addressed in this paper.
- As a concluding comment, the present study allows us to define extensions of FTC towards linear systems by considering possible actuator faults or simultaneous sensor and actuator faults in a dynamical system affected by measurement noise. Also, different controllers can be implemented within this FTC scheme to ensure defined control objectives, allowing, as a result, the proposed FTC control system extension. These issues are future research directions regarding FTC in dynamical systems with outputs measured with noise.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Fault Estimator Design
Appendix A.2. Observer Design for Fault Reconfiguration
References
- Abbaspour, A.; Mokhtari, S.; Sargolzaei, A.; Yen, K.K. A Survey on Active Fault-Tolerant Control Systems. Electronics 2020, 9, 1513. [Google Scholar] [CrossRef]
- Brizuela-Mendoza, J.A.; Sorcia-Vázquez, F.D.J.; Rumbo-Morales, J.Y.; Lozoya-Ponce, R.E.; Rodríguez-Cerda, J.C. Active fault tolerant control based on eigenstructure assignment applied to a 3-DOF helicopter. Asian J. Control 2021, 23, 673–684. [Google Scholar] [CrossRef]
- Ortiz-Torres, G.; Rumbo-Morales, J.; Sorcia-Vázquez, F.; Pérez-Vidal, A.; Cruz-Rojas, A.; Brizuela-Mendoza, J.; Oceguera-Contreras, E. Concentration estimation and fault tolerant control in a CSTR modelled as a quasi linear parameter varying system. Rev. Mex. Ing. Química 2021, 20, 51–66. [Google Scholar] [CrossRef]
- Zhu, F.; Fu, Y.; Dinh, T.N. Asymptotic convergence unknown input observer design via interval observer. Automatica 2023, 147, 110744. [Google Scholar] [CrossRef]
- Zhu, F.; Li, M. Distributed Interval Observer and Distributed Unknown Input Observer Designs. IEEE Trans. Autom. Control 2024, 69, 8868–8875. [Google Scholar] [CrossRef]
- Hanif, O.; Deshpande, N.G.; Chatterjee, M. Identification and Control of a Heat Exchanger. In Proceedings of the 2021 International Symposium of Asian Control Association on Intelligent Robotics and Industrial Automation (IRIA), Goa, India, 20–22 September 2021; pp. 259–264. [Google Scholar]
- Jin, Y.; Sun, L.; Hua, Q.; Chen, S. Experimental Research on Heat Exchanger Control Based on Hybrid Time and Frequency Domain Identification. Sustainability 2018, 10, 2667. [Google Scholar] [CrossRef]
- Miao, W.; Xu, B. Application of Feedforward Cascade Compound Control Based on Improved Predictive Functional Control in Heat Exchanger Outlet Temperature System. Appl. Sci. 2023, 13, 7132. [Google Scholar] [CrossRef]
- Al-Dhaifallah, M. Fuzzy fractional-order PID control for heat exchanger. Alex. Eng. J. 2023, 63, 11–16. [Google Scholar] [CrossRef]
- Fürst, Y.; Brandt, S.; Kriegel, M. Introducing a new nonlinear approach to model heat exchangers designed for control engineering applications. Eur. J. Control 2024, 79, 101072. [Google Scholar] [CrossRef]
- Amin, A.A.; Hasan, K.M. A review of Fault Tolerant Control Systems: Advancements and applications. Measurement 2019, 143, 58–68. [Google Scholar] [CrossRef]
- Ortiz-Torres, G.; Valdez-Resendiz, J.E.; Torres-Cantero, C.A.; Rumbo-Morales, J.Y.; Ramos-Martinez, M.B.; Valdez-Martinez, J.S. Actuator and Sensor Fault Detection and Isolation System Applied to a Distillation Column. IEEE Access 2023, 11, 48548–48558. [Google Scholar] [CrossRef]
- Ortiz Torres, G.; Rumbo Morales, J.Y.; Ramos Martinez, M.; Valdez-Martínez, J.S.; Calixto-Rodriguez, M.; Sarmiento-Bustos, E.; Torres Cantero, C.A.; Buenabad-Arias, H.M. Active Fault-Tolerant Control Applied to a Pressure Swing Adsorption Process for the Production of Bio-Hydrogen. Mathematics 2023, 11, 1129. [Google Scholar] [CrossRef]
- Escobar-Jimenez, R.F.; Carbot-Rojas, D.A.; Gómez-Aguilar, J.F.; Alvarado-Martínez, V.M.; Téllez-Anguiano, A.C.; Hernandez-Perez, J.A. Actuator Fault Tolerant Control Based on a MIMO-MPC: Application in a Double-Pipe Heat Exchanger. Chem. Eng. Commun. 2017, 204, 86–96. [Google Scholar] [CrossRef]
- Carbot-Rojas, D.; Escobar, R.; Gómez-Aguilar, J.; López-López, G.; Olivares-Peregrino, V. Experimental validation of an actuator fault tolerant control system using virtual sensor: Application in a double pipe heat exchanger. Chem. Eng. Res. Des. 2015, 104, 400–408. [Google Scholar] [CrossRef]
- Escobar, R.; Astorga-Zaragoza, C.; Téllez-Anguiano, A.; Juárez-Romero, D.; Hernández, J.; Guerrero-Ramírez, G. Sensor fault detection and isolation via high-gain observers: Application to a double-pipe heat exchanger. ISA Trans. 2011, 50, 480–486. [Google Scholar] [CrossRef] [PubMed]
- Alegría-Zamudio, M.; Escobar-Jiménez, R.; Gómez-Aguilar, J. Fault tolerant system based on non-integers order observers: Application in a heat exchanger. ISA Trans. 2018, 80, 286–296. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Rammal, R.; Li, Z.; Cabassud, M.; Dahhou, B. Interval Observer-Based Active Fault Tolerant Control for an Intensified Heat Exchanger/Reactor. In Proceedings of the 2021 9th International Conference on Systems and Control (ICSC), Caen, France, 24–26 November 2021; pp. 133–138. [Google Scholar]
- Wang, J.; Sun, J.; Ge, W.; Zhang, F.; Gao, R.X. Virtual Sensing for Online Fault Diagnosis of Heat Exchangers. IEEE Trans. Instrum. Meas. 2022, 71, 1–8. [Google Scholar] [CrossRef]
- Han, X.; Rammal, R.; He, M.; Li, Z.; Cabassud, M.; Dahhou, B. Dynamic and sensor fault tolerant control for an intensified heat-exchanger/reactor. Eur. J. Control 2023, 69, 100736. [Google Scholar] [CrossRef]
- Morato, M.M.; Felix, M.S. Data Science and Model Predictive Control: A survey of recent advances on data-driven MPC algorithms. J. Process Control 2024, 144, 103327. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Siza, J.; Llanos, J.; Velasco, P.; Moya, A.P.; Sumba, H. Model Predictive Control (MPC) of a Countercurrent Flow Plate Heat Exchanger in a Virtual Environment. Sensors 2024, 24, 4511. [Google Scholar] [CrossRef] [PubMed]
- Dyrska, R.; Horváthová, M.; Bakaráč, P.; Mönnigmann, M.; Oravec, J. Heat exchanger control using model predictive control with constraint removal. Appl. Therm. Eng. 2023, 227, 120366. [Google Scholar] [CrossRef]
- Liu, R.; Li, Y. A review of fault tolerant control based on Model Predictive Control. In Proceedings of the 2022 37th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Beijing, China, 19–20 November 2022; pp. 818–823. [Google Scholar]
- Bavili, R.E.; Mohammadzadeh, A.; Tavoosi, J.; Mobayen, S.; Assawinchaichote, W.; Asad, J.H.; Mosavi, A.H. A New Active Fault Tolerant Control System: Predictive Online Fault Estimation. IEEE Access 2021, 9, 118461–118471. [Google Scholar] [CrossRef]
- Feng, X.; Patton, R. Active Fault Tolerant Control of a Wind Turbine via Fuzzy MPC and Moving Horizon Estimation. In Proceedings of the 19th IFAC World Congress, Cape Town, South Africa, 24–29 August 2014; Volume 47, pp. 3633–3638. [Google Scholar]
- Ranjan, R.; Kravaris, C. Model-predictive fault-tolerant control of safety-critical processes based on dynamic safe set. J. Process Control 2024, 144, 103329. [Google Scholar] [CrossRef]
- Xiao, G.; Liu, F. Distributed fault-tolerant model predictive control for intermittent fault: A cooperative way. ISA Trans. 2019, 89, 113–121. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Li, H.; Shi, H.; Sun, Q.; Li, P. Dynamic output feedback robust MPC hybrid fault-tolerant control for discrete uncertain systems: A switching control strategy. Int. J. Control 2025, 98, 1518–1531. [Google Scholar] [CrossRef]
- He, M.; Li, Z.; Han, X.; Dahhou, B.; Cabassud, M. Study on Fault Tolerant Control of an Intensified Heat-Exchanger/Reactor Using Two-Layer Multiple Model Structure, Proceedings of the 15th European Workshop on Advanced Control and Diagnosis (ACD 2019), Bologna, Italy, 21–22 November 2019; Zattoni, E., Simani, S., Conte, G., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 295–312. [Google Scholar]
- Zhang, B.; Sun, X.; Liu, S.; Deng, X. Distributed fault tolerant model predictive control for multi-unmanned aerial vehicle system. Asian J. Control 2022, 24, 1273–1292. [Google Scholar] [CrossRef]
- Oh, S.; Song, T.; Kim, M.; Oh, K.S. Adaptive Model Predictive Fault-Tolerant Control for Four-Wheel Independent Steering Vehicles with Sensitivity Estimation. Int. J. Automot. Technol. 2023, 24, 829–850. [Google Scholar] [CrossRef]
- Bakhtiaridoust, M.; Yadegar, M.; Jahangiri, F. Koopman fault-tolerant model predictive control. IET Control Theory Appl. 2024, 18, 939–950. [Google Scholar] [CrossRef]
- Khedher, A.; Benothman, K.; Maquin, D.; Benrejeb, M. State and sensor faults estimation via a proportional integral observer. In Proceedings of the 2009 6th International Multi-Conference on Systems, Signals and Devices, Djerba, Tunisia, 23–26 March 2009; pp. 1–6. [Google Scholar]
- Rossiter, J.A. Model-Based Predictive Control: A Practical Approach; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Astorga-Zaragoza, C.M.; Zavala-Río, A.; Alvarado, V.; Méndez, R.M.; Reyes-Reyes, J. Performance monitoring of heat exchangers via adaptive observers. Measurement 2007, 40, 392–405. [Google Scholar] [CrossRef]
- Zhang, S.; Qi, X.; Yang, S. An Extended State Observer with Adjustable Bandwidth for Measurement Noise. J. Syst. Eng. Electron. 2024, 35, 233–241. [Google Scholar] [CrossRef]
- Battilotti, S. Robust observer design under measurement noise with gain adaptation and saturated estimates. Automatica 2017, 81, 75–86. [Google Scholar] [CrossRef]




| Parameter | Description | Value | Unit |
|---|---|---|---|
| Inlet temperature on the cold side | 298 | K | |
| Inlet temperature on the hot side | 338 | K | |
| U | Heat transfer coefficient | 160 | J/(m2K s) |
| A | Heat transfer surface area | m2 | |
| Specific heat on the cold side | 1910 | J/(Kg K) | |
| Specific heat on the hot side | 1519 | J/(Kg K) | |
| Density of the cold side | 1000 | kg/m3 | |
| Density of the hot side | 1000 | kg/m3 | |
| Volume on the cold side | m3 | ||
| Volume on the hot side | m3 |
| Symbol | Parameter | Value |
|---|---|---|
| Prediction Horizon | 50 | |
| Control Horizon | 15 | |
| Error Tracking Weight | ||
| Input Increment Weight |
| Observer | Parameter Design | Observer Gain | |
|---|---|---|---|
| Alarm | Meaning | Observer | To Compute | for Control |
|---|---|---|---|---|
| 0 | Fault-free | - | - | = |
| 1 | Fault in | with | = | |
| 2 | Fault in | with | = |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brizuela-Mendoza, J.A.; Sorcia-Vázquez, F.D.J.; Ortiz-Torres, G.; Rumbo-Morales, J.Y.; Torres-Cantero, C.A.; Ramos-Martinez, M.; Pérez-Vidal, A.F. MPC-Based Sensor Fault-Tolerant Control: Application to a Heat Exchanger with Measurement Noise. Automation 2025, 6, 48. https://doi.org/10.3390/automation6030048
Brizuela-Mendoza JA, Sorcia-Vázquez FDJ, Ortiz-Torres G, Rumbo-Morales JY, Torres-Cantero CA, Ramos-Martinez M, Pérez-Vidal AF. MPC-Based Sensor Fault-Tolerant Control: Application to a Heat Exchanger with Measurement Noise. Automation. 2025; 6(3):48. https://doi.org/10.3390/automation6030048
Chicago/Turabian StyleBrizuela-Mendoza, Jorge A., Felipe D. J. Sorcia-Vázquez, Gerardo Ortiz-Torres, Jesse Y. Rumbo-Morales, Carlos A. Torres-Cantero, Moises Ramos-Martinez, and Alan F. Pérez-Vidal. 2025. "MPC-Based Sensor Fault-Tolerant Control: Application to a Heat Exchanger with Measurement Noise" Automation 6, no. 3: 48. https://doi.org/10.3390/automation6030048
APA StyleBrizuela-Mendoza, J. A., Sorcia-Vázquez, F. D. J., Ortiz-Torres, G., Rumbo-Morales, J. Y., Torres-Cantero, C. A., Ramos-Martinez, M., & Pérez-Vidal, A. F. (2025). MPC-Based Sensor Fault-Tolerant Control: Application to a Heat Exchanger with Measurement Noise. Automation, 6(3), 48. https://doi.org/10.3390/automation6030048









