Pre-Routing Slack Prediction Based on Graph Attention Network
Abstract
1. Introduction
- We present an end-to-end graph learning framework for predicting pre-routing arrival time and slack values at timing endpoints with no need to invoke additional STA tools.
- We leverage an attention mechanism to capture the importance of interactions between nodes, thereby enhancing the prediction accuracy of net delay.
- Inspired by the Nonlinear Delay Model (NLDM) computation process, our method incorporates the lookup table as a cell feature, addressing the model’s tendency to fall into local optima and improving operational efficiency.
- Results on the 21 real-world circuit benchmarks demonstrate that our method achieves a 16.62% improvement in of slack while reducing runtime by 15.55% compare to the previous state-of-the-art (SOTA) method [7].
2. Literature Survey
2.1. Graph Attention Network Applied to Electronic Design Automation
2.2. Machine Learning Applied to Static Timing Analysis
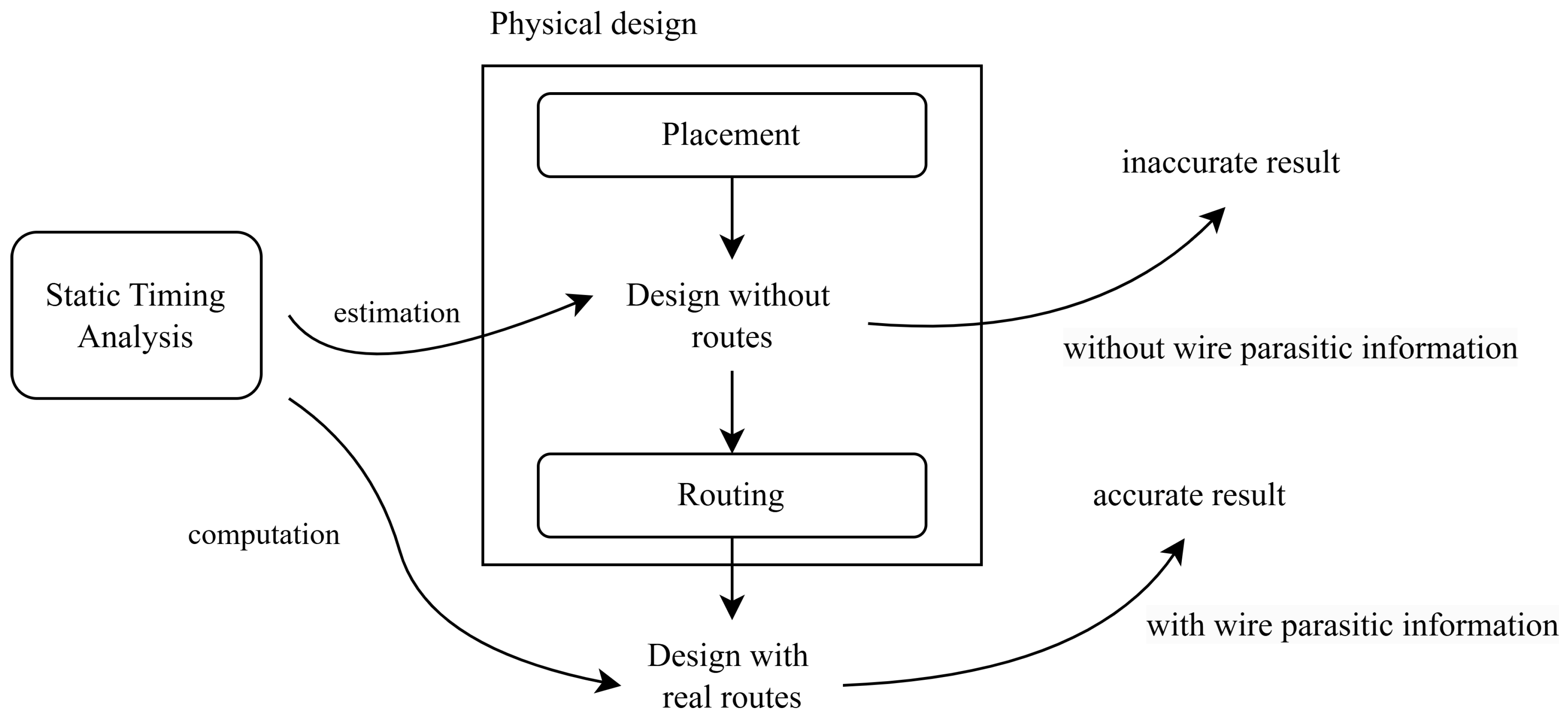
3. Proposed Methods
3.1. Overall Flow
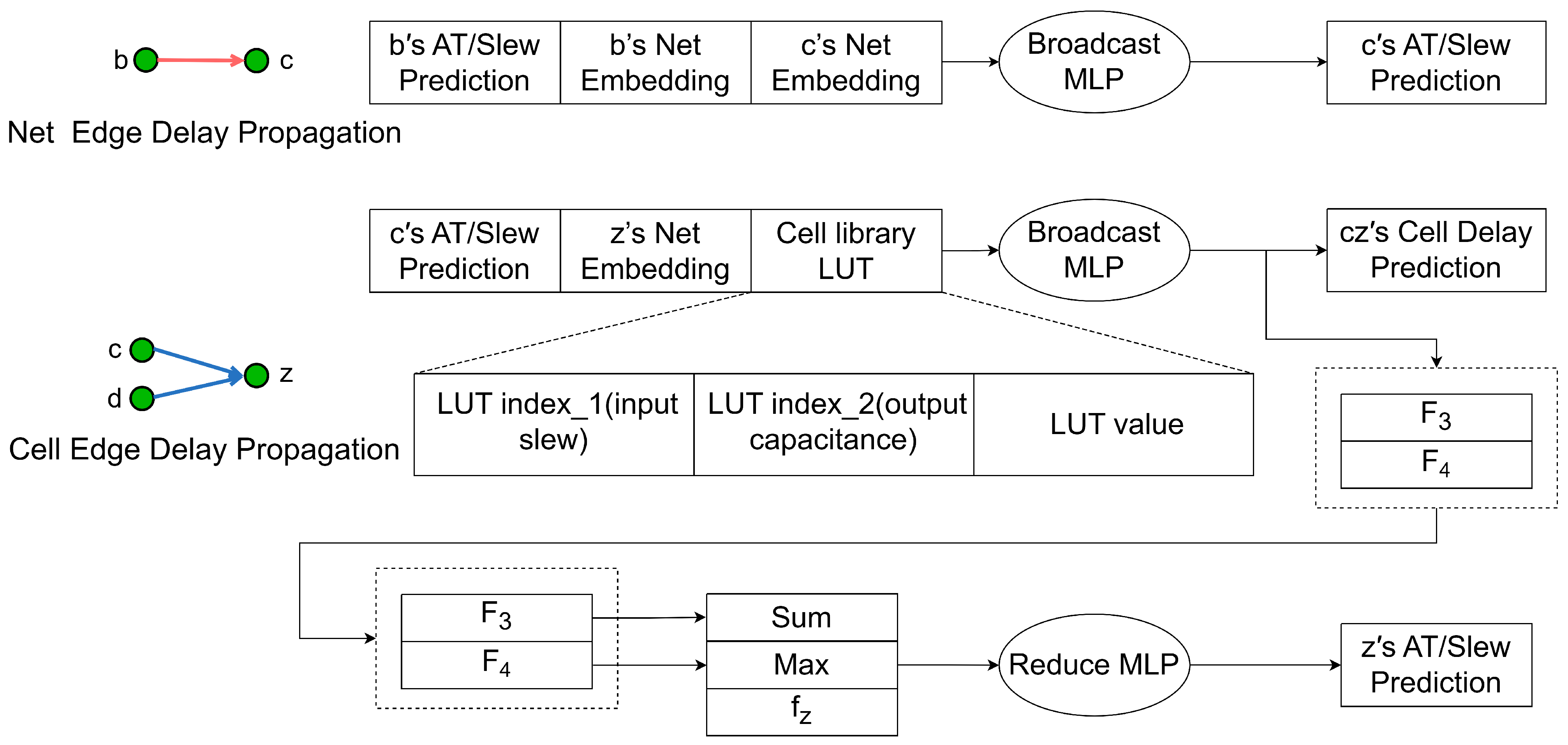
- Lines 4 to 10 outline the process of updating sink node features: The driver node feature , the sink node feature , and the edge feature are weighted by the weight matrix , concatenated and passed through the MLP to obtain the new feature of the sink node.
- Lines 11 through 20 outline the process of updating the driver node features: The driver node feature , the sink node feature , and the edge feature from the sink node to the driver node are weighted by the weight matrix , and concatenated to obtain the new features and by MLP. Then, weighting it again with the driver node feature , concatenating it and passing it through the MLP, we obtain the new feature of the driver node.
- Lines 21 to 23 describe the prediction process for arrival times and slew along net edges: By concatenating the arrival time of the driver node, the slew , the new feature of the driver node, and the new feature of the sink node and passing it through the MLP, we obtain the arrival time and slew of the sink node.
- Lines 24 to 30 outline the prediction process for arrival times and turns along cell edges: Firstly, the LUT value is found by cell slew and capacitance, and then the three are concatenated to obtain the cell edge feature . Then, the arrival time of the driver node, the slew , the new feature of the sink node , and the cell edge feature are concatenated and passed through the MLP to obtain the new features , and the cell delay. Finally, is summed up, takes the maximum value and concatenates the features of the sink node and passes it through MLP. We can obtain the arrival time and slew of the sink node.
| Algorithm 1 Graph-based delay prediction with attention and LUT | ||
| 1: | Input: Circuit Graph , Netlist N, Cell Library | |
| 2: | Output: Arrival time/slew Prediction for sink Nodes | |
| 3: | Initialization: Initialize node features for each | |
| 4: | for each sink node do | ▹ Graph Broadcast Phase |
| 5: | for each diver node do | |
| 6: | ||
| 7: | ||
| 8: | ||
| 9: | end for | |
| 10: | end for | |
| 11: | for each diver node do | ▹ Graph Reduction Phase |
| 12: | for each sink node do | |
| 13: | ||
| 14: | ||
| 15: | ||
| 16: | ||
| 17: | ||
| 18: | ||
| 19: | end for | |
| 20: | end for | |
| 21: | for each net edge do | ▹ Net Edge Delay Propagation |
| 22: | ||
| 23: | end for | |
| 24: | for each cell edge do | ▹ Cell Edge Delay Propagation |
| 25: | ||
| 26: | ||
| 27: | ||
| 28: | ||
| 29: | end for | |
| 30: | Return | |
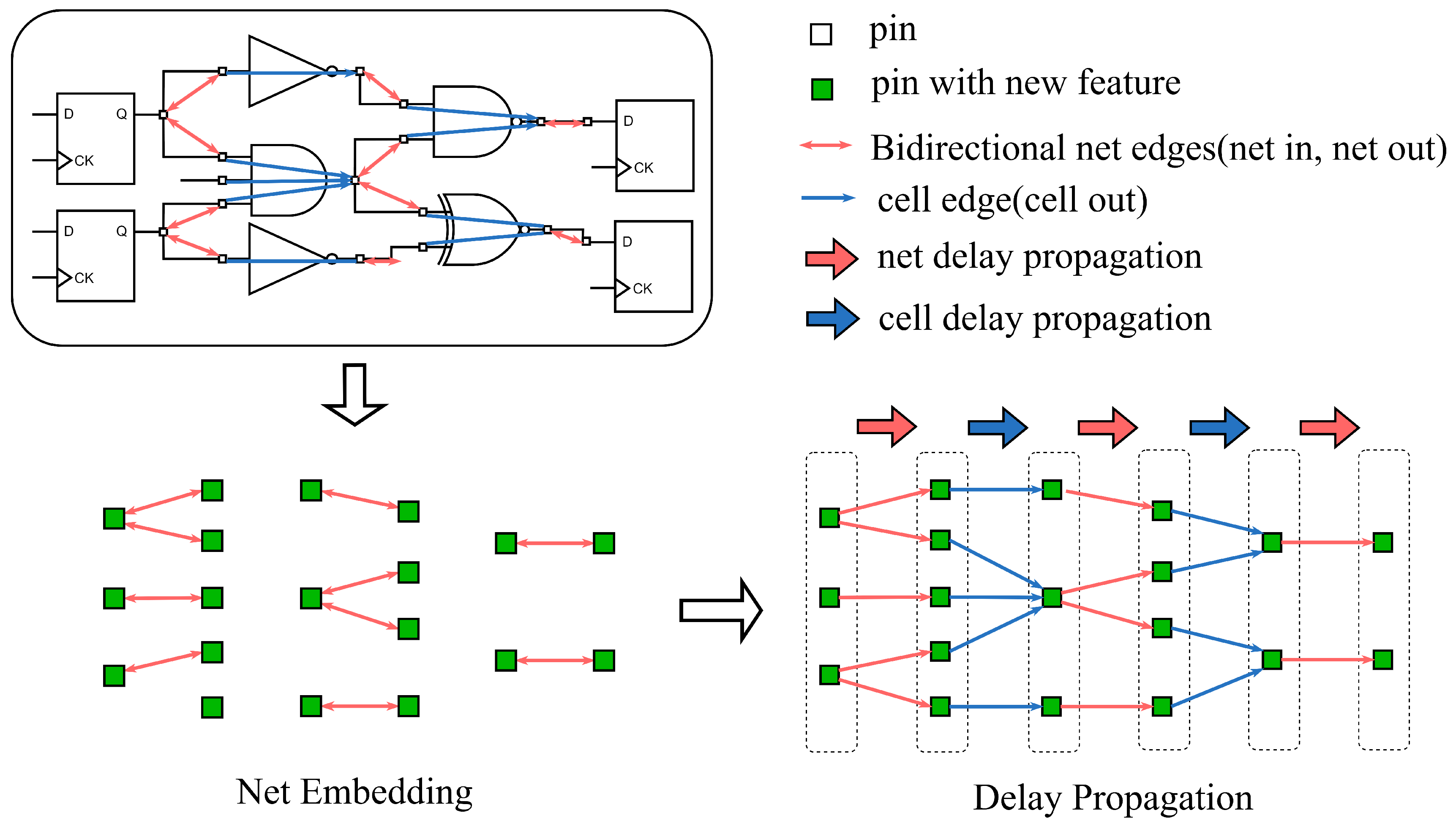
3.2. Net Embedding Model
3.3. Delay Propagation Model
4. Results
4.1. Experimental Setup
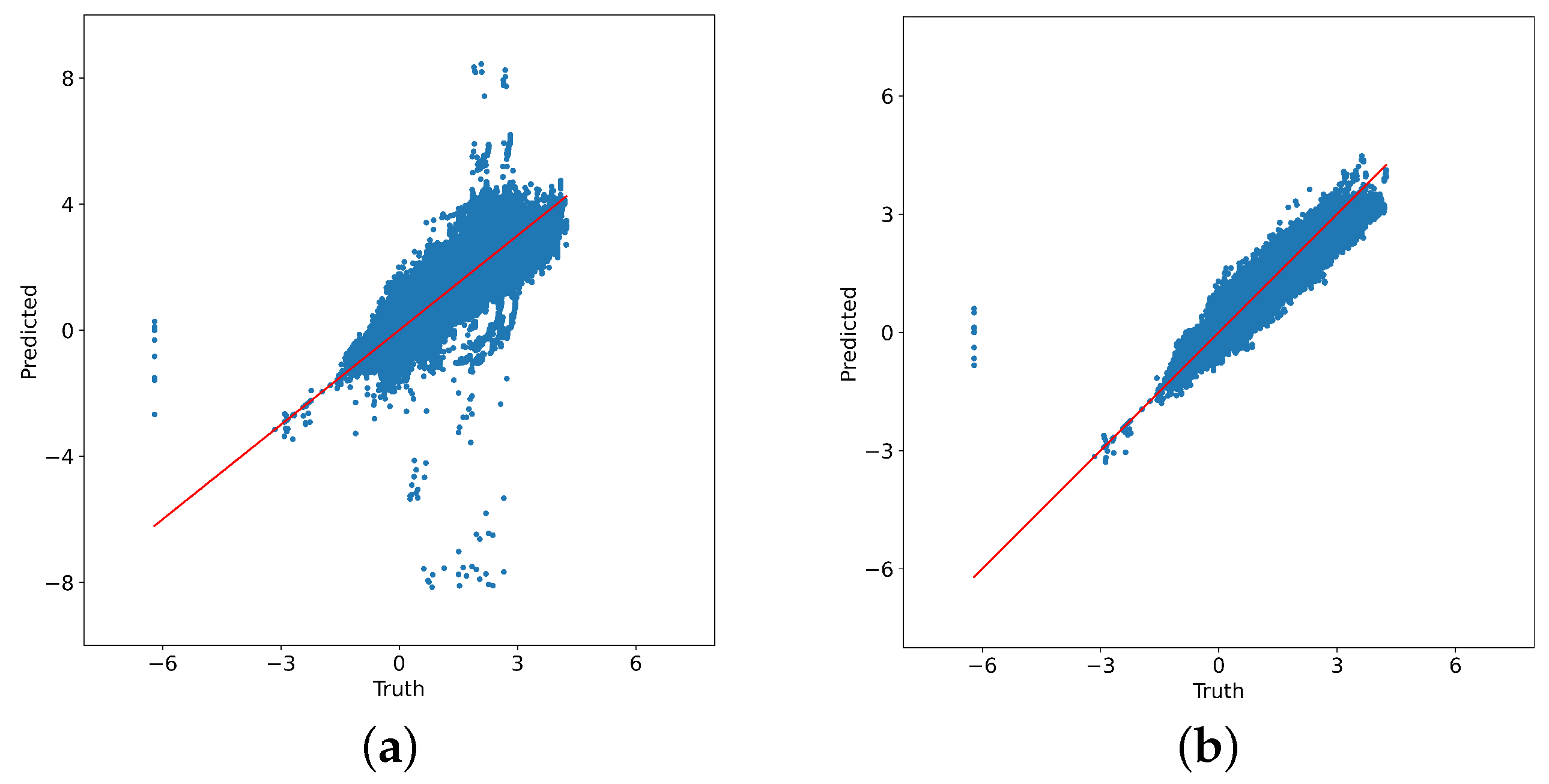
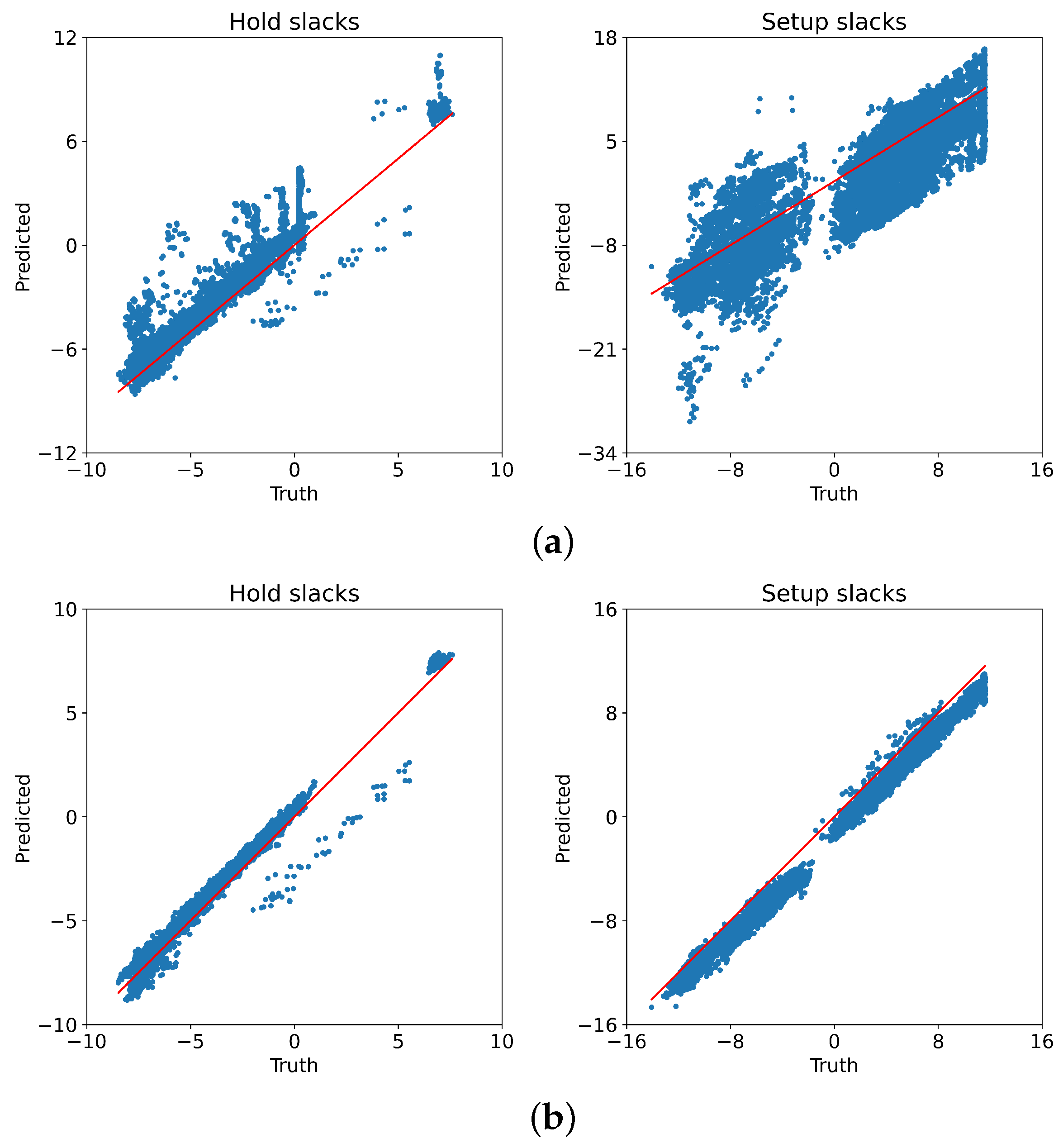
4.2. Timing Prediction Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, H.; Nath, S.; Zhang, Y.; Chen, H.; Liu, M. Why are graph neural networks effective for eda problems? In Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design, San Diego, CA, USA, 30 October–3 November 2022; pp. 1–8. [Google Scholar]
- Chang, H.; Sapatnekar, S.S. Statistical timing analysis considering spatial correlations using a single PERT-like traversal. In Proceedings of the ICCAD-2003. International Conference on Computer Aided Design (IEEE Cat. No. 03CH37486), San Jose, CA, USA, 9–13 November 2003; pp. 621–625. [Google Scholar]
- Barboza, E.C.; Shukla, N.; Chen, Y.; Hu, J. Machine learning-based pre-routing timing prediction with reduced pessimism. In Proceedings of the 56th Annual Design Automation Conference 2019, Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- He, X.; Fu, Z.; Wang, Y.; Liu, C.; Guo, Y. Accurate timing prediction at placement stage with look-ahead rc network. In Proceedings of the 59th ACM/IEEE Design Automation Conference, San Jose, CA, USA, 10–14 July 2022; pp. 1213–1218. [Google Scholar]
- Ye, Y.; Chen, T.; Gao, Y.; Yan, H.; Yu, B.; Shi, L. Fast and accurate wire timing estimation based on graph learning. In Proceedings of the 2023 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 17–19 April 2023; pp. 1–6. [Google Scholar]
- Lopera, D.S.; Ecker, W. Applying gnns to timing estimation at rtl. In Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design, San Diego, CA, USA, 29 October–3 November 2022; pp. 1–8. [Google Scholar]
- Guo, Z.; Liu, M.; Gu, J.; Zhang, S.; Pan, D.Z.; Lin, Y. A timing engine inspired graph neural network model for pre-routing slack prediction. In Proceedings of the 59th ACM/IEEE Design Automation Conference, San Jose, CA, USA, 10–14 July 2022; pp. 1207–1212. [Google Scholar]
- Zhong, R.; Ye, J.; Tang, Z.; Kai, S.; Yuan, M.; Hao, J.; Yan, J. Preroutgnn for timing prediction with order preserving partition: Global circuit pre-training, local delay learning and attentional cell modeling. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; Volume 38, pp. 17087–17095. [Google Scholar]
- Cao, P.; He, G.; Yang, T. Tf-predictor: Transformer-based prerouting path delay prediction framework. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 42, 2227–2237. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, S.; Pu, Y.; Chen, S.; Ho, T.Y.; Yu, B. Restructure-tolerant timing prediction via multimodal fusion. In Proceedings of the 2023 60th ACM/IEEE Design Automation Conference (DAC), San Jose, CA, USA, 9–13 July 2023; pp. 1–6. [Google Scholar]
- He, G.; Ding, W.; Ye, Y.; Cheng, X.; Song, Q.; Cao, P. An Optimization-aware Pre-Routing Timing Prediction Framework Based on Heterogeneous Graph Learning. In Proceedings of the 2024 29th Asia and South Pacific Design Automation Conference (ASP-DAC), Incheon, Republic of Korea, 22–25 January 2024; pp. 177–182. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Agiza, A.; Roy, R.; Ene, T.D.; Godil, S.; Reda, S.; Catanzaro, B. GraPhSyM: Graph Physical Synthesis Model. In Proceedings of the 2023 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Francisco, CA, USA, 28 October–2 November 2023; pp. 1–9. [Google Scholar]
- Xie, Z.; Liang, R.; Xu, X.; Hu, J.; Duan, Y.; Chen, Y. Net2: A graph attention network method customized for pre-placement net length estimation. In Proceedings of the 26th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 18–21 January 2021; pp. 671–677. [Google Scholar]
- Saibodalov, M.; Karandashev, I.; Sokhova, Z.; Kocheva, E.; Zheludkov, N. Routing Congestion Prediction in VLSI Design Using Graph Neural Networks. In Proceedings of the 2024 26th International Conference on Digital Signal Processing and its Applications (DSPA), Moscow, Russia, 27–29 March 2024; pp. 1–4. [Google Scholar]
- Kirby, R.; Godil, S.; Roy, R.; Catanzaro, B. Congestionnet: Routing congestion prediction using deep graph neural networks. In Proceedings of the 2019 IFIP/IEEE 27th International Conference on Very Large Scale Integration (VLSI-SoC), Cuzco, Peru, 6–9 October 2019. [Google Scholar]
- Ren, H.; Kokai, G.F.; Turner, W.J.; Ku, T.S. ParaGraph: Layout parasitics and device parameter prediction using graph neural networks. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar]
- Li, Y.; Lin, Y.; Madhusudan, M.; Sharma, A.; Xu, W.; Sapatnekar, S.S.; Harjani, R.; Hu, J. A customized graph neural network model for guiding analog IC placement. In Proceedings of the 39th International Conference on Computer-Aided Design, Virtual Conference, 2–5 November 2020; pp. 1–9. [Google Scholar]
- Bhasker, J.; Chadha, R. Static Timing Analysis for Nanometer Designs: A Practical Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Li, D.; Tan, S.; Zhang, Y.; Jin, M.; Pan, S.; Okumura, M.; Jiang, R. DyG-Mamba: Continuous State Space Modeling on Dynamic Graphs. arXiv 2024, arXiv:2408.06966. [Google Scholar]
- Tan, S.; Li, D.; Jiang, R.; Zhang, Y.; Okumura, M. Community-invariant graph contrastive learning. arXiv 2024, arXiv:2405.01350. [Google Scholar]
- Su, Y.; Zeng, S.; Wu, X.; Huang, Y.; Chen, J. Physics-informed graph neural network for electromagnetic simulations. In Proceedings of the 2023 XXXVth General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Hokkaido, Japan, 19–26 August 2023; pp. 1–3. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Huang, G.; Hu, J.; He, Y.; Liu, J.; Ma, M.; Shen, Z.; Wu, J.; Xu, Y.; Zhang, H.; Zhong, K.; et al. Machine learning for electronic design automation: A survey. ACM Trans. Des. Autom. Electron. Syst. (TODAES) 2021, 26, 1–46. [Google Scholar] [CrossRef]
- Weste, N.H.; Harris, D. CMOS VLSI Design: A Circuits and Systems Perspective; Pearson Education India: Noida, India, 2015. [Google Scholar]
- Domingos, P. A few useful things to know about machine learning. Commun. ACM 2012, 55, 78–87. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch; OpenReview: Amherst, MA, USA, 2017. [Google Scholar]
- Wang, M.; Zheng, D.; Ye, Z.; Gan, Q.; Li, M.; Song, X.; Zhou, J.; Ma, C.; Yu, L.; Gai, Y.; et al. Deep graph library: A graph-centric, highly-performant package for graph neural networks. arXiv 2019, arXiv:1909.01315. [Google Scholar]


| Name | Nodes | Nets | Cells | Endpoints | |
|---|---|---|---|---|---|
| Train | blabla | 55,568 | 39,853 | 35,689 | 1614 |
| usb_cdc_core | 7406 | 5200 | 4869 | 630 | |
| BM64 | 38,458 | 27,843 | 25,334 | 1800 | |
| salsa20 | 78,486 | 57,737 | 52,895 | 3710 | |
| aes128 | 211,045 | 148,997 | 138,457 | 5696 | |
| wbqspiflash | 9672 | 6798 | 6454 | 323 | |
| cic_decimator | 3131 | 2232 | 2102 | 130 | |
| aes256 | 290,955 | 207,414 | 189,262 | 11,200 | |
| des | 60,541 | 44,478 | 41,845 | 2048 | |
| aes_cipher | 59,777 | 42,671 | 41,411 | 660 | |
| picorv32a | 58,676 | 43,047 | 40,208 | 1920 | |
| zipdiv | 4398 | 3102 | 2913 | 181 | |
| genericfir | 38,827 | 28,845 | 25,013 | 3811 | |
| usb | 3361 | 2406 | 2189 | 344 | |
| Test | jpeg_encoder | 23,8216 | 17,6737 | 16,7960 | 4422 |
| usbf_device | 66,345 | 46,241 | 42,226 | 4404 | |
| aes192 | 234,211 | 165,350 | 152,910 | 8096 | |
| xtea | 10,213 | 7151 | 6882 | 423 | |
| spm | 1121 | 765 | 700 | 129 | |
| y_huff | 48,216 | 33,689 | 30,612 | 2391 | |
| synth_ram | 25,910 | 19,024 | 16,782 | 2112 |
| Benchmark | Net Delay ( Score) | Cell Delay ( Score) | |||||
|---|---|---|---|---|---|---|---|
| TimingGCN | Our Method | Improve | TimingGCN | Our Method | Improve | ||
| test | jpeg_encoder | 0.973 | 0.978 | 0.45% | 0.607 | 0.976 | 60.89% |
| usbf_device | 0.968 | 0.969 | 0.01% | 0.956 | 0.972 | 1.67% | |
| aes192 | 0.967 | 0.968 | 0.09% | 0.954 | 0.979 | 2.57% | |
| xtea | 0.949 | 0.960 | 1.08% | 0.754 | 0.981 | 30.12% | |
| spm | 0.903 | 0.928 | 2.77% | 0.941 | 0.965 | 2.56% | |
| y_huff | 0.967 | 0.971 | 0.47% | 0.852 | 0.941 | 10.39% | |
| synth_ram | 0.955 | 0.986 | 3.17% | 0.890 | 0.925 | 3.93% | |
| Avg.train | 0.987 | 0.978 | −0.91% | 0.978 | 0.989 | 1.17% | |
| Avg.test | 0.955 | 0.966 | 1.13% | 0.851 | 0.963 | 13.18% | |
| Benchmark | Slack ( Score) | Inference Time (s) | |||||
|---|---|---|---|---|---|---|---|
| TimingGCN | Our Method | Improve | TimingGCN | Our Method | Improve | ||
| train | blabla | 0.985 | 0.995 | 1.11% | 1.711 | 1.355 | 20.78% |
| usb_cdc_core | 0.992 | 0.997 | 0.52% | 0.788 | 0.600 | 23.93% | |
| BM64 | 0.988 | 0.996 | 0.83% | 1.352 | 0.903 | 33.18% | |
| salsa20 | 0.988 | 0.991 | 0.26% | 1.851 | 1.476 | 20.26% | |
| aes128 | 0.484 | 0.961 | 98.36% | 1.390 | 1.187 | 14.54% | |
| wbqspiflash | 0.991 | 0.992 | 0.07% | 1.183 | 0.874 | 26.12% | |
| cic_decimator | 0.983 | 0.994 | 1.07% | 0.458 | 0.341 | 25.52% | |
| aes256 | 0.784 | 0.987 | 25.98% | 1.423 | 1.227 | 13.75% | |
| des | 0.992 | 0.997 | 0.46% | 1.423 | 0.442 | 68.93% | |
| aes_cipher | 0.969 | 0.989 | 2.04% | 0.852 | 0.602 | 29.41% | |
| picorv32a | 0.941 | 0.995 | 5.76% | 2.022 | 1.478 | 26.88% | |
| zipdiv | 0.984 | 0.998 | 1.42% | 0.856 | 0.668 | 21.98% | |
| genericfir | 0.978 | 0.998 | 2.09% | 0.401 | 0.317 | 20.78% | |
| usb | 0.990 | 0.993 | 0.32% | 0.408 | 0.334 | 18.13% | |
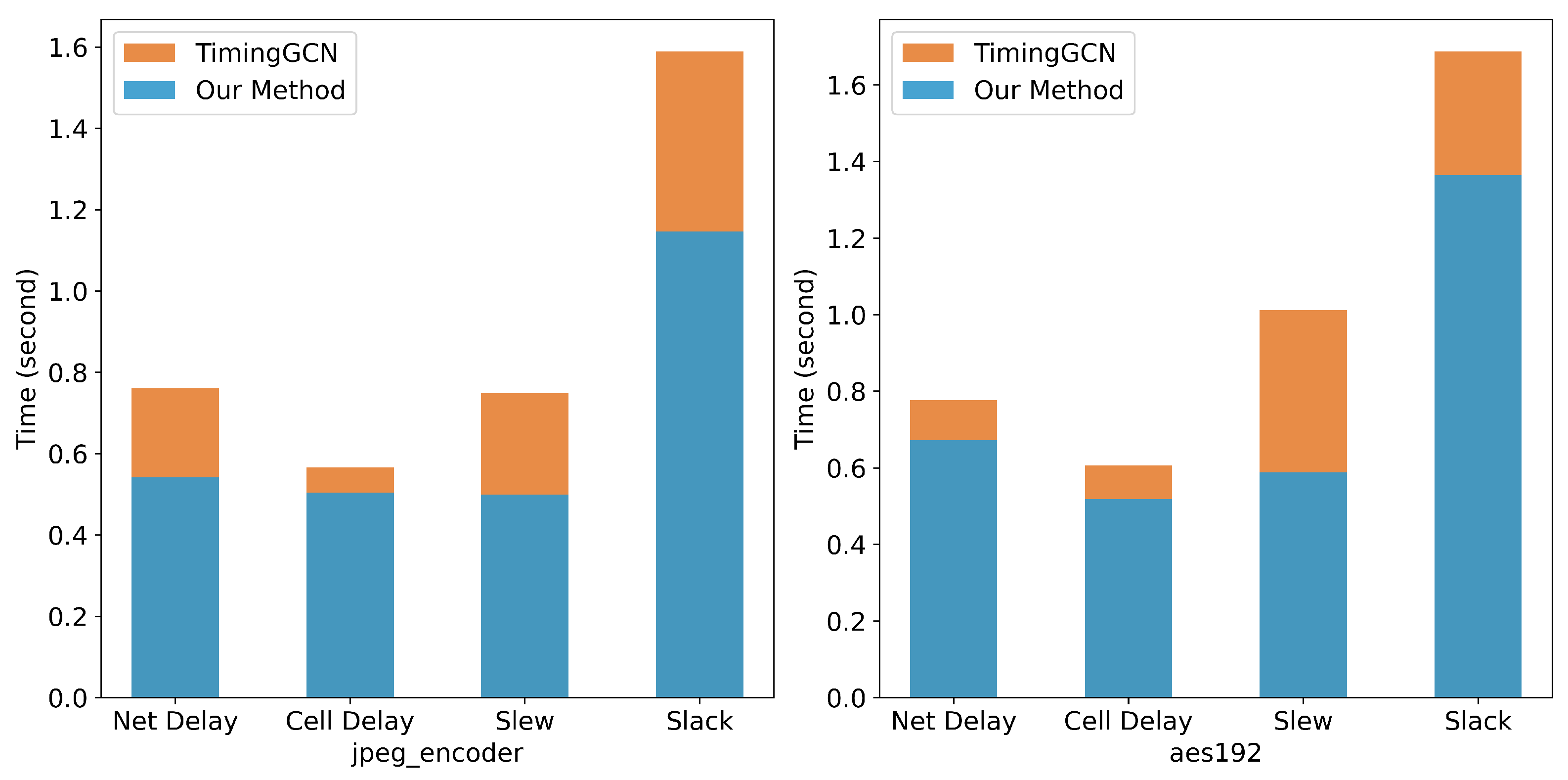
| test | jpeg_encoder | 0.351 | 0.971 | 176.71% | 1.589 | 1.146 | 27.86% |
| usbf_device | 0.926 | 0.973 | 5.08% | 1.333 | 1.143 | 14.23% | |
| aes192 | 0.765 | 0.971 | 26.92% | 1.687 | 1.365 | 19.08% | |
| xtea | 0.931 | 0.991 | 6.46% | 1.361 | 1.295 | 4.86% | |
| spm | 0.954 | 0.994 | 4.27% | 0.223 | 0.216 | 3.21% | |
| y_huff | 0.984 | 0.992 | 0.81% | 0.710 | 0.642 | 9.52% | |
| synth_ram | 0.998 | 0.998 | 0.01% | 0.302 | 0.277 | 8.32% | |
| Avg.train | 0.932 | 0.992 | 6.39% | 1.151 | 0.843 | 26.75% | |
| Avg.test | 0.844 | 0.984 | 16.62% | 1.029 | 0.869 | 15.55% | |
| Benchmark | MSE Net Delay | MSE Cell Delay | MSE Slack | ||||
|---|---|---|---|---|---|---|---|
| TimingGCN | Our Method | TimingGCN | Our Method | TimingGCN | Our Method | ||
| test | jpeg_encoder | 0.076 | 0.063 | 0.019 | 0.001 | 15.100 | 0.671 |
| usbf_device | 0.055 | 0.055 | 0.002 | 0.001 | 1.310 | 0.476 | |
| aes192 | 0.058 | 0.056 | 0.002 | 0.001 | 8.270 | 1.030 | |
| xtea | 0.086 | 0.069 | 0.014 | 0.001 | 4.750 | 0.628 | |
| spm | 0.081 | 0.060 | 0.002 | 0.001 | 0.458 | 0.056 | |
| y_huff | 0.116 | 0.100 | 0.010 | 0.004 | 0.163 | 0.081 | |
| synth_ram | 0.169 | 0.055 | 0.011 | 0.008 | 0.575 | 0.561 | |
| Avg.train | 0.028 | 0.048 | 0.001 | 0.001 | 2.780 | 0.496 | |
| Avg.test | 0.092 | 0.065 | 0.009 | 0.003 | 4.375 | 0.500 | |
| Benchmark | Slack ( Score) | ||||||
|---|---|---|---|---|---|---|---|
| Our Method with 1 Head | Our Method with 3 Layers | ||||||
| 3 Layers | 4 Layers | 8 Layers | 1 Head | 2 Heads | 4 Heads | ||
| test | jpeg_encoder | 0.971 | 0.905 | 0.757 | 0.971 | 0.803 | 0.869 |
| usbf_device | 0.973 | 0.943 | 0.956 | 0.973 | 0.963 | 0.958 | |
| aes192 | 0.971 | 0.887 | 0.640 | 0.971 | 0.913 | 0.938 | |
| xtea | 0.991 | 0.952 | 0.968 | 0.991 | 0.972 | 0.979 | |
| spm | 0.994 | 0.994 | 0.975 | 0.994 | 0.996 | 0.994 | |
| y_huff | 0.992 | 0.945 | 0.775 | 0.992 | 0.942 | 0.986 | |
| synth_ram | 0.998 | 0.997 | 0.990 | 0.998 | 0.978 | 0.986 | |
| Avg.train | 0.992 | 0.959 | 0.919 | 0.992 | 0.969 | 0.979 | |
| Avg.test | 0.984 | 0.946 | 0.866 | 0.984 | 0.938 | 0.959 | |
| Benchmark | Slack ( Score) | ||||
|---|---|---|---|---|---|
| TimingGCN | AT Only | LUT Only | Our GNN | ||
| test | jpeg_encoder | 0.351 | 0.940 | 0.788 | 0.971 |
| usbf_device | 0.926 | 0.987 | 0.927 | 0.973 | |
| aes192 | 0.765 | 0.955 | 0.908 | 0.971 | |
| xtea | 0.931 | 0.986 | 0.977 | 0.991 | |
| spm | 0.954 | 0.993 | 0.991 | 0.994 | |
| y_huff | 0.984 | 0.891 | 0.975 | 0.992 | |
| synth_ram | 0.998 | 0.999 | 0.984 | 0.998 | |
| Avg.train | 0.932 | 0.984 | 0.978 | 0.992 | |
| Avg.test | 0.844 | 0.964 | 0.936 | 0.984 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Hu, J.; Wu, Y.; Yang, X. Pre-Routing Slack Prediction Based on Graph Attention Network. Automation 2025, 6, 20. https://doi.org/10.3390/automation6020020
Li J, Hu J, Wu Y, Yang X. Pre-Routing Slack Prediction Based on Graph Attention Network. Automation. 2025; 6(2):20. https://doi.org/10.3390/automation6020020
Chicago/Turabian StyleLi, Jinke, Jiahui Hu, Yue Wu, and Xiaoyan Yang. 2025. "Pre-Routing Slack Prediction Based on Graph Attention Network" Automation 6, no. 2: 20. https://doi.org/10.3390/automation6020020
APA StyleLi, J., Hu, J., Wu, Y., & Yang, X. (2025). Pre-Routing Slack Prediction Based on Graph Attention Network. Automation, 6(2), 20. https://doi.org/10.3390/automation6020020






