Next Article in Journal / Special Issue
Modified Medial Meniscectomy (MMM) Model to Assess Post-Traumatic Knee Osteoarthritis in Mouse
Previous Article in Journal / Special Issue
Development of a Clinical Guideline for Managing Knee Osteoarthritis in Portugal: A Physiotherapist-Centered Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Osteology
Volume 5
Issue 3
10.3390/osteology5030024
osteology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation of the Stress-Shielding Effect of a PEEK Knee Prosthesis. A Finite Element Study

by
Mario Ceddia
1,*,
Arcangelo Morizio
1,
Giuseppe Solarino
2 and
Bartolomeo Trentadue
1
1
Department of Mechanics, Mathematics and Management, Polytechnic of Bari University, 70125 Bari, Italy
2
Department of Translational Biomedicine and Neuroscience, University of Bari, 70124 Bari, Italy
*
Author to whom correspondence should be addressed.
Osteology 2025, 5(3), 24; https://doi.org/10.3390/osteology5030024
Submission received: 22 May 2025 / Revised: 25 June 2025 / Accepted: 4 August 2025 / Published: 5 August 2025
(This article belongs to the Special Issue Advances in Bone and Cartilage Diseases)
Browse Figures
Versions Notes

Abstract

Background: The long-term success of total knee arthroplasty (TKA) is often compromised by stress shielding, which can lead to bone resorption and even implant loosening. This study employs finite element analysis (FEA) to compare the stress-shielding effects of a knee prosthesis made from polyether ether ketone (PEEK) with a traditional titanium Ti6Al4V implant on an osteoporotic tibial bone model. Methods: Stress distribution and the stress-shielding factor (SSF) were evaluated at seven critical points in the proximal tibia under physiological loading conditions. Results: Results indicate that the PEEK prosthesis yields a more uniform stress transmission, with von Mises stress levels within the optimal 2–3 MPa range for bone maintenance and consistently negative or near-zero SSF values, implying minimal stress shielding. Conversely, titanium implants exhibited significant stress shielding with high positive SSF values across all points. Additionally, stress concentrations on the polyethylene liner were lower and more evenly distributed in the PEEK model, suggesting reduced wear potential. Conclusions: These findings highlight the biomechanical advantages of PEEK in reducing stress shielding and preserving bone integrity, supporting its potential use to improve implant longevity in TKA. Further experimental and clinical validation are warranted.

1. Introduction

Total knee arthroplasty (TKA) is currently the most effective treatment for advanced knee osteoarthritis [1,2]. Among the various surgical techniques, kinematic alignment has shown potential biomechanical benefits. However, recent evidence suggests that these advantages do not always translate into clinically significant improvements in functional outcomes [3,4,5].
Over the past decade, the number of TKA procedures has increased substantially and is expected to exceed 3 million per year in the United States by 2030 [6]. Parallel to this trend, there has also been an increase in the rate of revision surgeries, primarily due to prosthetic failure. Several studies have investigated factors that contribute to such failures, including both pre- and postoperative conditions as well as implant design [7,8,9,10]. The main causes of revision include infection, instability, aseptic loosening, polyethylene wear, stiffness, and periprosthetic fractures [11,12,13]. Additionally, patient-related factors such as sex, age, body mass index (BMI) [14], comorbidities, socioeconomic status, and surgical variables like implant alignment and positioning play a critical role in the success of TKA [15,16,17].
One of the most relevant biomechanical challenges in TKA is stress shielding, a phenomenon that can significantly compromise the longevity of the implant and the quality of the surrounding bone tissue [18,19,20,21]. Stress shielding arises due to the high Young’s modulus of the metallic components, which alters the physiological distribution of mechanical loads. This leads to reduced mechanical stimulation of the peri-prosthetic bone compared to healthy conditions [22,23].
According to Wolff’s Law, bone remodels in response to mechanical stress. Therefore, the reduction of stress caused by stress shielding induces local bone resorption and structural weakening [24,25,26]. In the case of the tibial component, which is typically rigid, a large portion of the load is transferred through the implant, bypassing adjacent bone regions—particularly the proximal tibial metaphysis. This load imbalance can lead to periprosthetic osteoporosis, compromising both the primary and long-term stability of the implant, especially in osteoporotic patients [27,28,29].
Stress shielding may also result in morphological changes in the tibia and femur, complicating future revision surgeries due to the reduced quality and quantity of residual bone [30]. Several factors influence the extent of stress shielding, including the material and geometry of the prosthetic components, the method of fixation (cemented or uncemented), and the accuracy of their alignment [31]. For instance, tibial components with high Young’s modulus may exacerbate load deviation, while misalignment may increase localized underloading or overloading, further worsening the effects of stress shielding [32,33].
To address these issues, polyether ether ketone (PEEK) has recently emerged as a promising alternative material for knee prostheses. Thanks to its biomechanical properties, which more closely resemble those of natural bone, PEEK offers a potential solution to reduce stress shielding [34]. Its lower elastic modulus compared to metals such as cobalt-chromium or titanium enables better load transmission to the surrounding bone and helps preserve bone density, promoting long-term implant stability [35,36,37,38].
Biomechanical studies and finite element simulations have demonstrated that PEEK components reduce the overall stiffness of the bone–implant system, decreasing abnormal stress concentrations beneath the implant [39,40,41,42]. For example, Yu et al. [43] observed a significant reduction in stress shielding when using PEEK tibial components compared to traditional metallic ones. Similarly, Zhang et al. [36], in a cadaveric study, reported improved preservation of bone microarchitecture. Zhao et al. [44] confirmed the clinical viability of PEEK prostheses, showing comparable short-term outcomes to those of cobalt-chromium alloys.
The finite element method (FEM) is widely used to assess stress shielding in preclinical stages by simulating biomechanical responses under physiological loading conditions [18,45]. Wilczyński et al. [46] highlighted how using elastic materials and uncemented fixation in FEM models can promote more physiological load transfer and protect peri-prosthetic bone.
Despite growing interest in PEEK, the literature lacks well-validated FEM studies specifically focused on modeling its mechanical interaction with osteoporotic bone in TKA. To fill this gap, it is necessary to combine numerical simulations with experimental data to evaluate the actual effectiveness of PEEK in reducing stress shielding and enhancing implant performance.
The objective of this study is to numerically investigate the effects of using PEEK as a material for the tibial component in total knee arthroplasty. Specifically, we aim to evaluate the extent to which PEEK can reduce stress shielding compared to traditional metallic materials in osteoporotic bone conditions. To this end, a finite element model of the proximal tibia with an implanted prosthesis was developed. The model includes both metallic (Ti6Al4V) and polymeric (PEEK) tibial components, and simulations were carried out under physiological loading conditions. Stress and strain distributions within the periprosthetic bone were then analyzed to quantify the impact of different material properties on stress shielding.

2. Materials and Methods

The study focuses on comparing a knee prosthetic component made of titanium Ti6Al4V with one made of PEEK. To evaluate the influence of these materials on the transmission of stress to the proximal part of the tibia, a finite element model was developed based on previously validated works [46,47,48,49,50]. The model analyzes bone stress after implantation and loading of the Ti6Al4V component compared to the PEEK component. Hypothetically, the PEEK component can transfer more load to the bone, resulting in higher bone stresses due to the less stiff mechanical properties of PEEK compared to titanium (lower Young’s modulus).

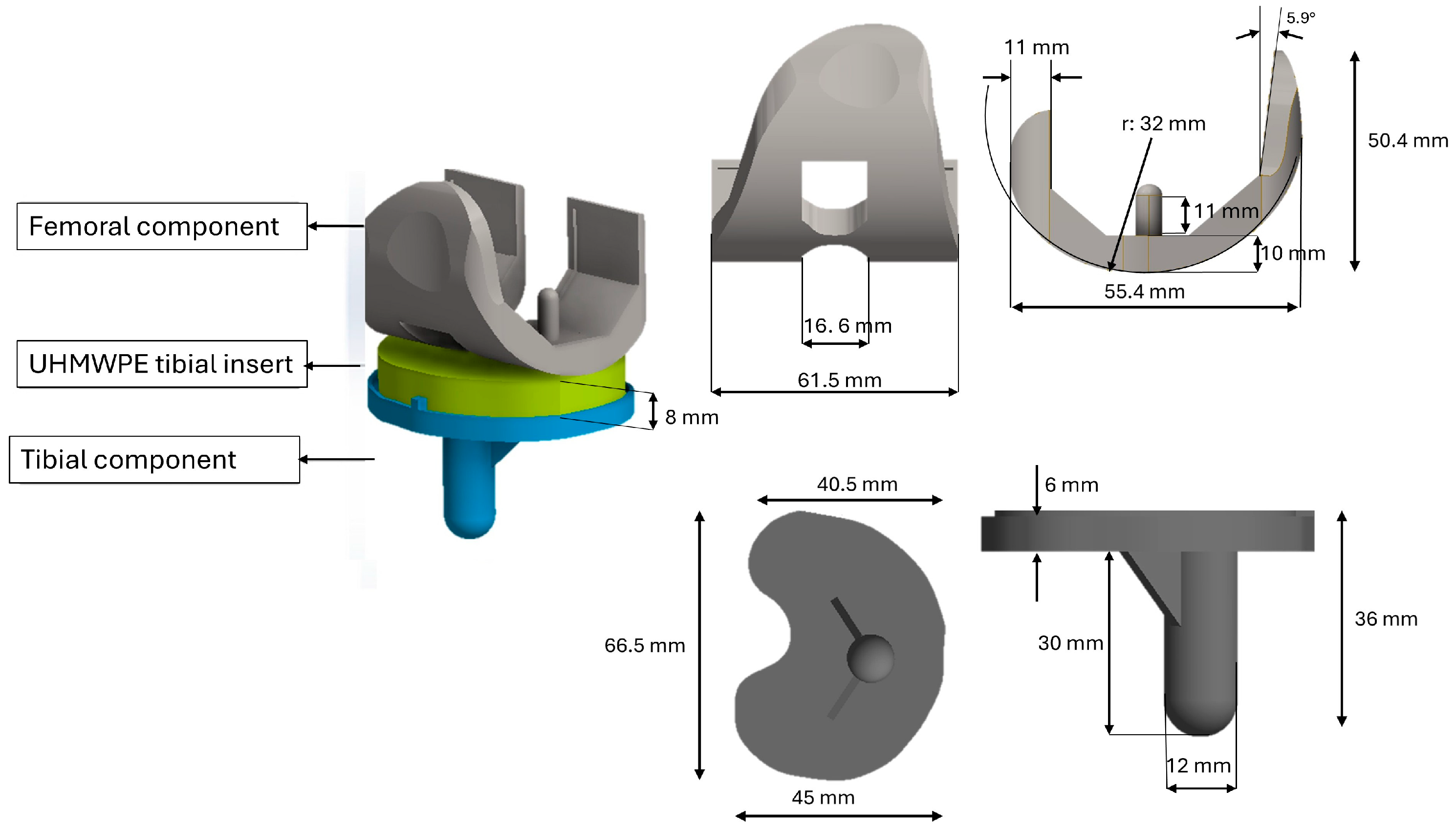
2.1. Geometries

The study examined two femoral prostheses with fixed tibial platforms, identical in design, but differing in materials and manufacturing technologies. The experimental device includes a femoral and tibial component, both entirely made with 3D printing in PEEK and using titanium alloy casting, respectively, along with a polymer insert positioned between the two components (see Figure 1).
The simulation of total knee arthroplasty (TKA) was performed based on the anatomical dimensions of the tibial bone of a male individual, taking as reference the study conducted by Carman et al. [45].
The average cortical bone thickness was 3 mm. A simplification was made regarding the 3D model of the tibia by referencing the study conducted by Wliczyński et al. [46], which allowed for a reduced complexity of the tibial geometry while preserving essential anatomical features relevant for the simulation. All 3D models were created using the Autodesk Inventor 2024 software Figure 2.

2.2. Materials

Bone is generally composed of cortical bone on the outer part and trabecular bone on the inner part [50], both characterized by anisotropic behavior. By definition, a material with anisotropic behavior has 21 elastic constants describing its elastic properties. However, it has been demonstrated that bone exhibits transverse isotropy in the YZ and XZ planes Figure 2. Consequently, it can be modeled as an orthotropic material with 9 elastic constants. To model osteoporotic bone, the Young’s modulus of cortical bone was reduced by 32%, and that of trabecular bone was reduced by 66%. According to the study by Galas et al. [51], the mechanical properties of bone considered are reported in Table 1 [50,51,52].
In the case of prosthetic materials of the tibial component, the insert, femoral component, isotropic and linearly elastic mechanical properties have been considered, as reported in Table 2 [49,50,51,52].

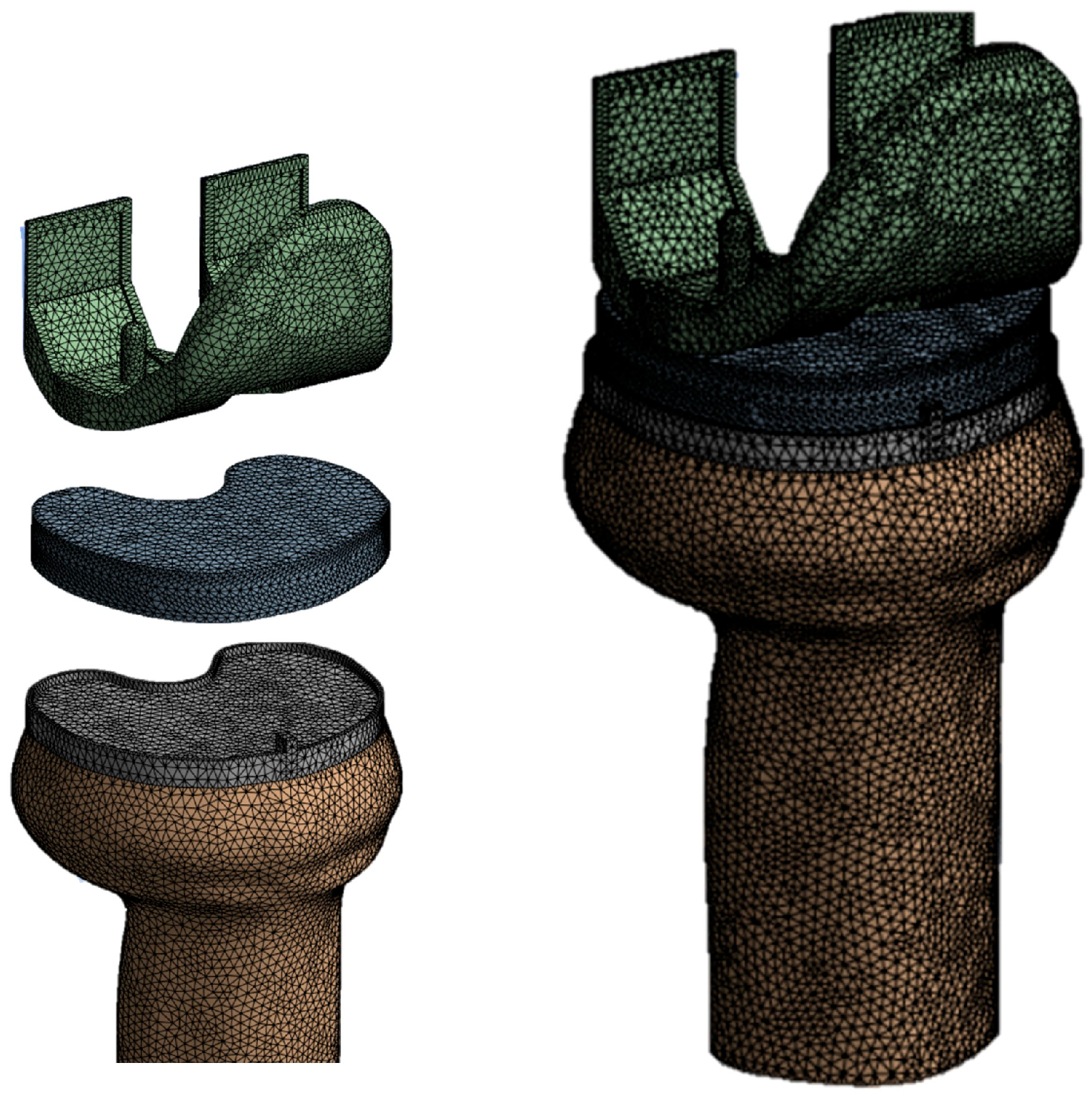
2.3. Finite Element Model

Two finite element models were created using Ansys Workbench R 2023 (Southpointe 2600 Ansys Drive, Canonsburg, PA 15317, USA) software, one for each material of the tibial and femoral components. A mesh sensitivity analysis was performed with the aim of defining the optimal element size in terms of computational cost and result accuracy. Meshes with element sizes ranging from 1.8 mm to 3 mm were tested. The main results of the analysis are summarized in the following Table 3:
As can be observed, the variation in results between the 2 mm mesh and the 1.8 mm mesh is negligible (<0.2%), while the computational time increases significantly. Therefore, a mesh with an element size of 2 mm was chosen as the optimal compromise between accuracy and computational cost. The total number of elements was 36,326 for the tibial component, 45,369 for the insert, and 231,123 for the tibial bone (Figure 3).

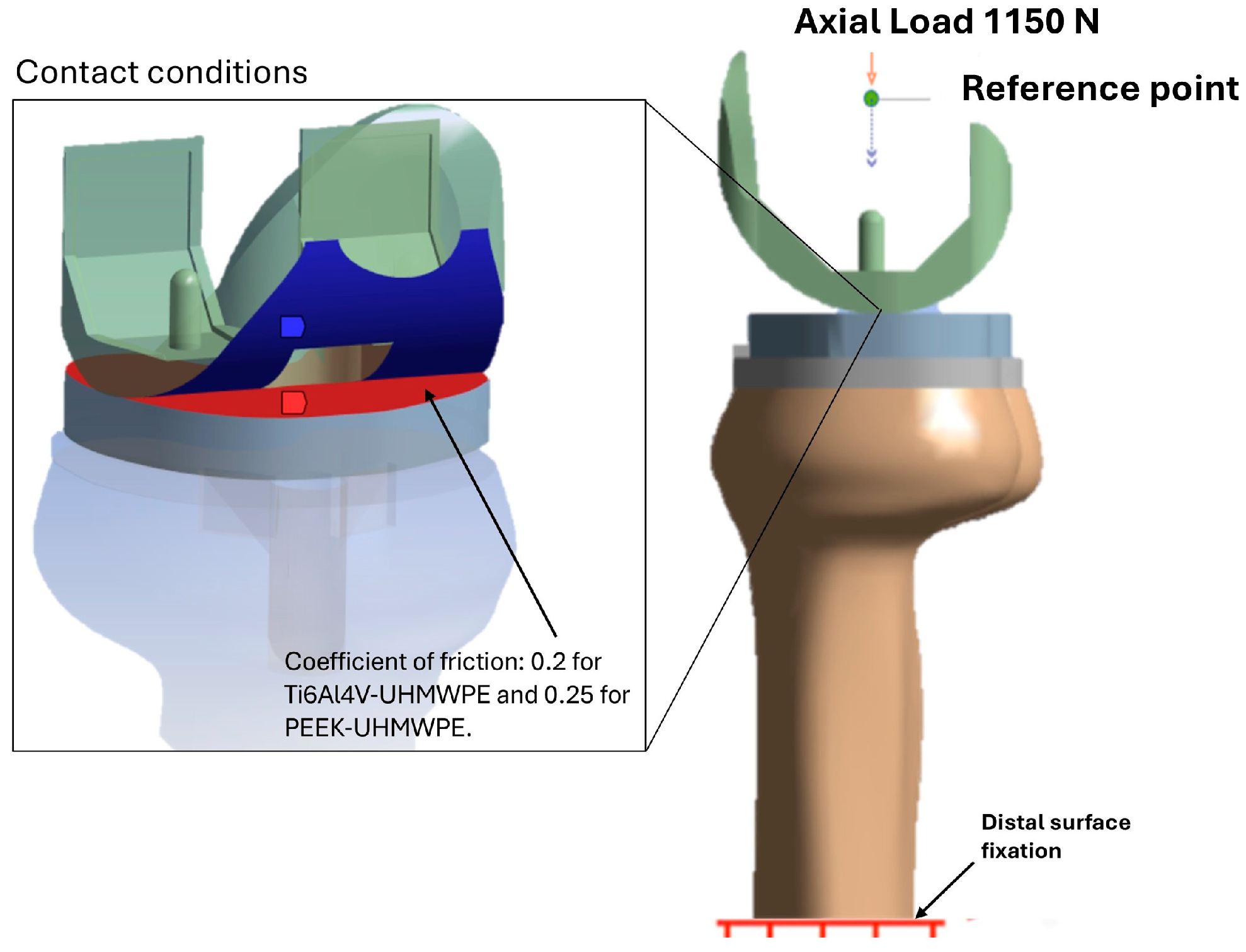
2.4. Contact, Loading, and Boundary Conditions

The interactions between the implant, bone, and implant components were modeled using a “surface–surface” contact formulation, applying specific friction coefficients based on the materials involved: 0.2 for Ti6Al4V-UHMWPE and 0.25 for PEEK-UHMWPE [51]. A fixed contact type was used between the bone and the tibial component through the sharing of contact elements. Subsequently, a vertical compressive load of 1150 N (along the Z axis, approximately twice the body weight; Figure 4) was applied to the midpoint of the transepicondylar axis of the femur to simulate the load during the gait cycle with the knee in a straight position at 0° of flexion [51]. This load condition represents the most severe condition a patient who has undergone TKA could encounter.
Meanwhile, the lower part of the tibia was constrained in all directions.
To evaluate the phenomenon of stress shielding, we analyzed the contact stress distribution between the tibial component and the surrounding bone using the von Mises criterion. This stress measure, derived from plasticity theory, provides a scalar value that integrates the principal stresses into an equivalent state of stress. It is particularly useful for assessing complex, multidirectional loading patterns acting on bone tissue, which is inherently anisotropic and heterogeneous. As established in the literature, stress shielding occurs when the mechanical stimuli applied to the bone fall below a critical threshold, leading to bone resorption. This bone loss compromises implant fixation, reduces mechanical stability, and increases the risk of early or late loosening. In addition, it may complicate revision surgeries due to the diminished quality and quantity of residual bone. Numerous studies indicate that a threshold stress of approximately 2 MPa is critical: below this value, bone tends to undergo resorption, while stresses between 2 and 5 MPa are generally considered necessary to maintain bone mass—often referred to as maintenance stress [50,53,54,55,56,57]. Therefore, in this study, von Mises stress values in the peri-prosthetic bone were interpreted with respect to these thresholds to evaluate the potential of alternative materials to mitigate stress-shielding effects [58,59,60,61]. Furthermore, to quantify stress shielding, we calculated the stress-shielding factor (SSF) using Equation (1), which compares the stress in the peri-prosthetic bone with and without the implant. This approach follows the methodology proposed by Ceddia et al. [62] whose FEA-based procedure has been validated for simulating orthopedic implant–bone interactions. By applying this method to prosthetic components made from materials with different elastic moduli, we were able to assess the degree of mechanical stimulus reduction and its correlation with the stiffness of the tibial component.
S t r e s s   s h i e l d i n g   f a c t o r = σ b o n e r e f − σ b o n e w i t h   i m p l a n t σ b o n e r e f

3. Results

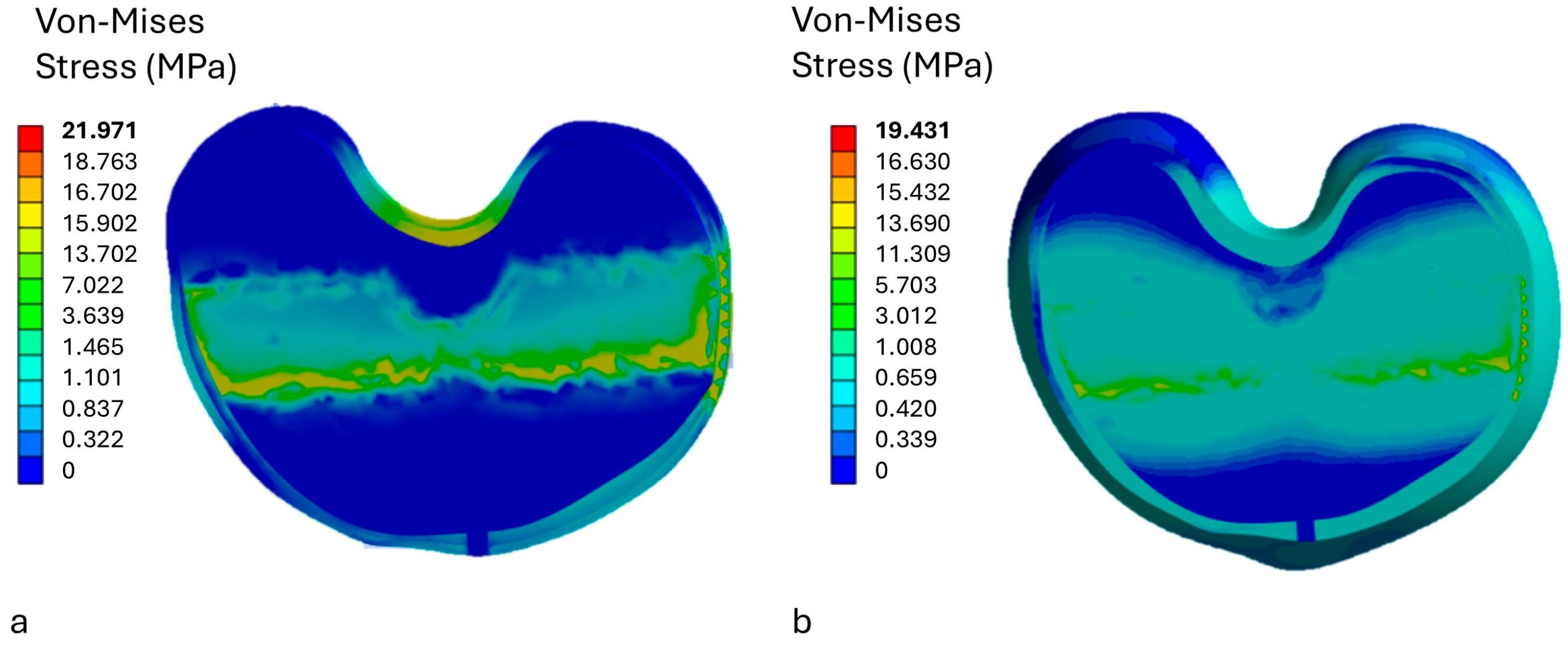
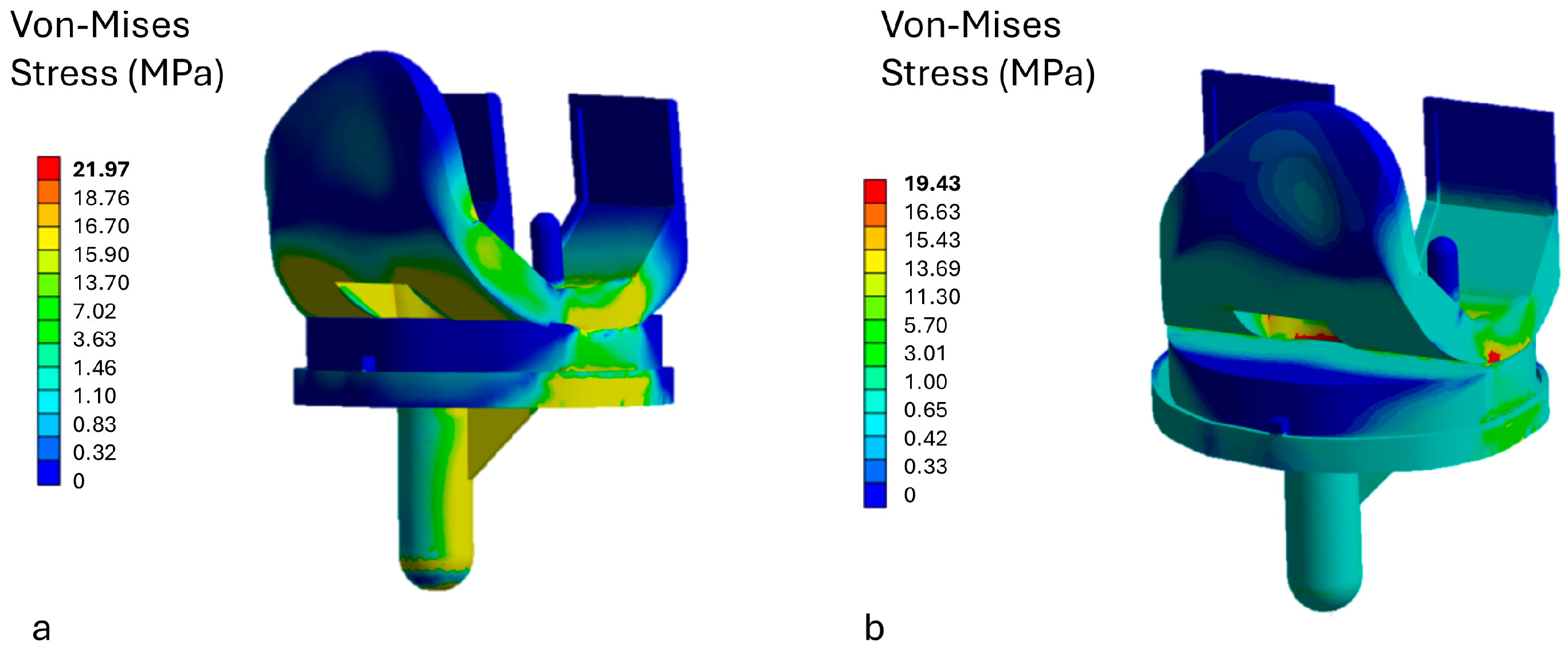
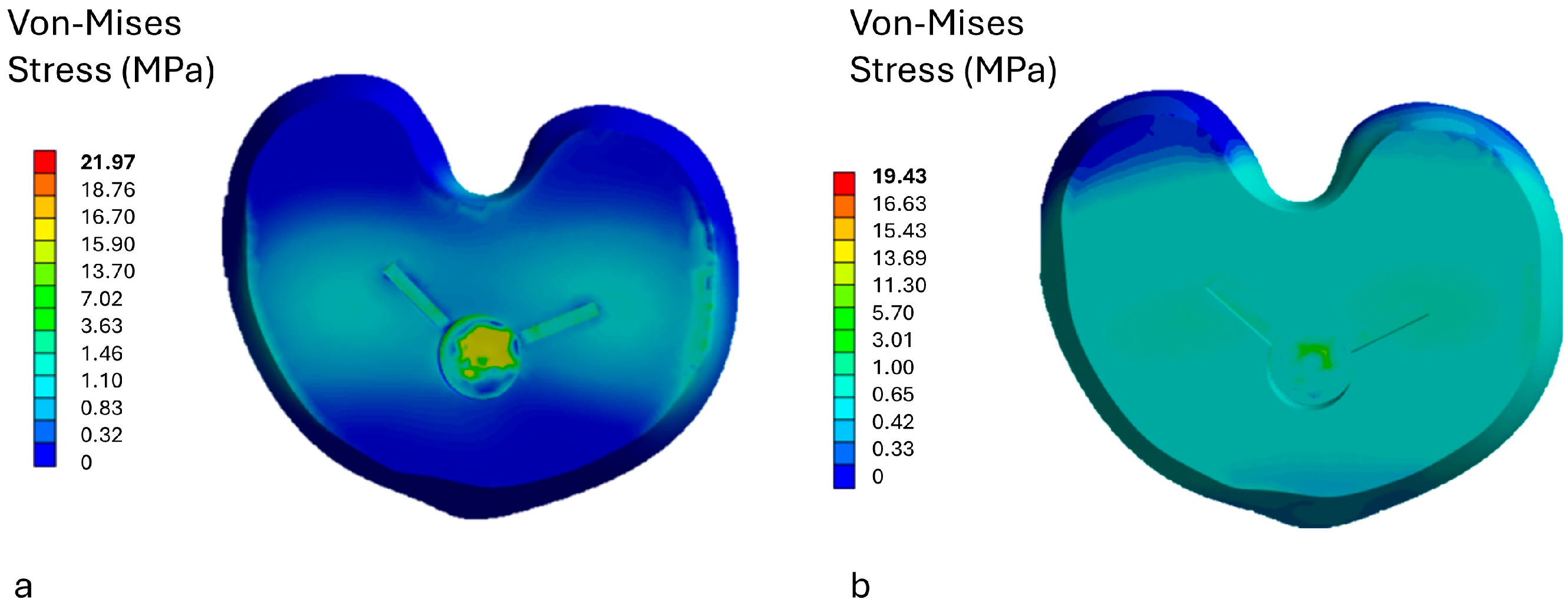
3.1. Stress Analysis on the Insert

The finite element analysis allowed the evaluation of the von Mises stress on the upper surface of the polyethylene liner in model a, with femoral and tibial components made of titanium, and in model b, with both femoral and tibial components made of PEEK (Figure 5). It can be observed that the highest stress value was 16.324 MPa for model a and 7.412 MPa for model b.
The reduction of contact stress on the polyethylene liner surface is essential to limit material wear and extend the lifespan of the prosthetic implant. High pressure peaks cause localized stress concentrations, leading to plastic deformations and micro-damage, which promote the formation of micro-cracks and the release of wear particles. A more uniform and lower stress distribution, as shown in the model with PEEK components (Figure 5, model b), reduces overload areas, thereby limiting the risk of mechanical damage and friction between the joint surfaces. From a tribological perspective, lower stress values help reduce both abrasion and fatigue from cyclic loading, which are the main causes of polyethylene surface degradation. Controlling the level of contact stress thus helps preserve the integrity of the liner, decreasing the generation of debris and improving the overall durability of the implant.

3.2. Stress Analysis on Prosthetic Components

The highest stress concentrations are mainly observed in the prosthesis made of titanium (model a, Figure 6). This is due to the significantly higher Young’s modulus of titanium compared to the surrounding tibial bone, causing the prosthesis to absorb most of the applied loads, thereby shielding the bone from stress. However, from a mechanical strength standpoint, these stress levels are not critical, remaining well below the yield strength of titanium. In contrast, the model with the PEEK prosthesis shows a more uniform stress distribution, with loads spread over a larger surface area. Thanks to its lower Young’s modulus compared to titanium, PEEK promotes better stress transfer to the surrounding bone, encouraging a more physiological load distribution. Even in this case, the stress values in the PEEK prosthesis are below its yield strength, confirming its mechanical safety under the applied loading conditions.

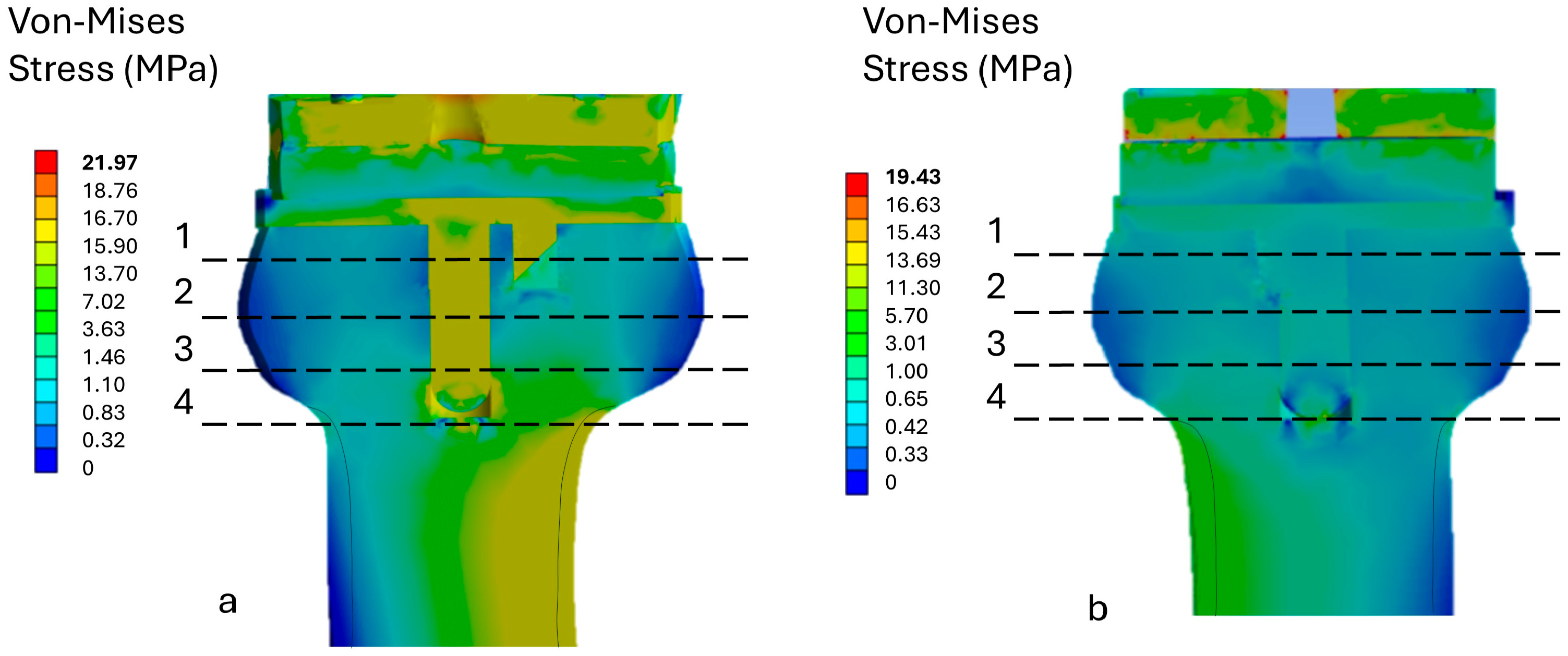
3.3. Stress Analysis on Bone

The analysis of stress transmitted to the tibial bone in the two prosthesis configurations, one made of titanium and the other of PEEK, shows significant differences related to the mechanical properties of the materials. The stiffness of titanium, with a Young’s modulus significantly higher than that of bone, causes a phenomenon known as “stress shielding,” which is the protection of the bone from mechanical load. In practice, most of the load is absorbed by the prosthesis itself, resulting in reduced stress transfer to the surrounding bone. Consequently, the stress values in the bone under the titanium tibial insert lower, with a maximum of 1.532 MPa. This low level of stress can lead to decreased mechanical stimulation necessary to maintain bone mass and health, increasing the risk of bone atrophy and long-term compromise of stability. On the contrary, the PEEK prosthesis, characterized by lower Young’s modulus, allows greater transmission of mechanical forces to the bone. This results in a more uniform stress distribution on the bone, with higher stress values reaching a maximum of 3.176 MPa (Figure 7). This stress range is consistent with that favorable for bone maintenance and formation (2–3 MPa), suggesting that the PEEK prosthesis promotes more physiological and beneficial mechanical stimulation for the bone. The increased transmission of stress helps maintain bone remodeling and density, reducing the risk of bone loss associated with stress shielding.

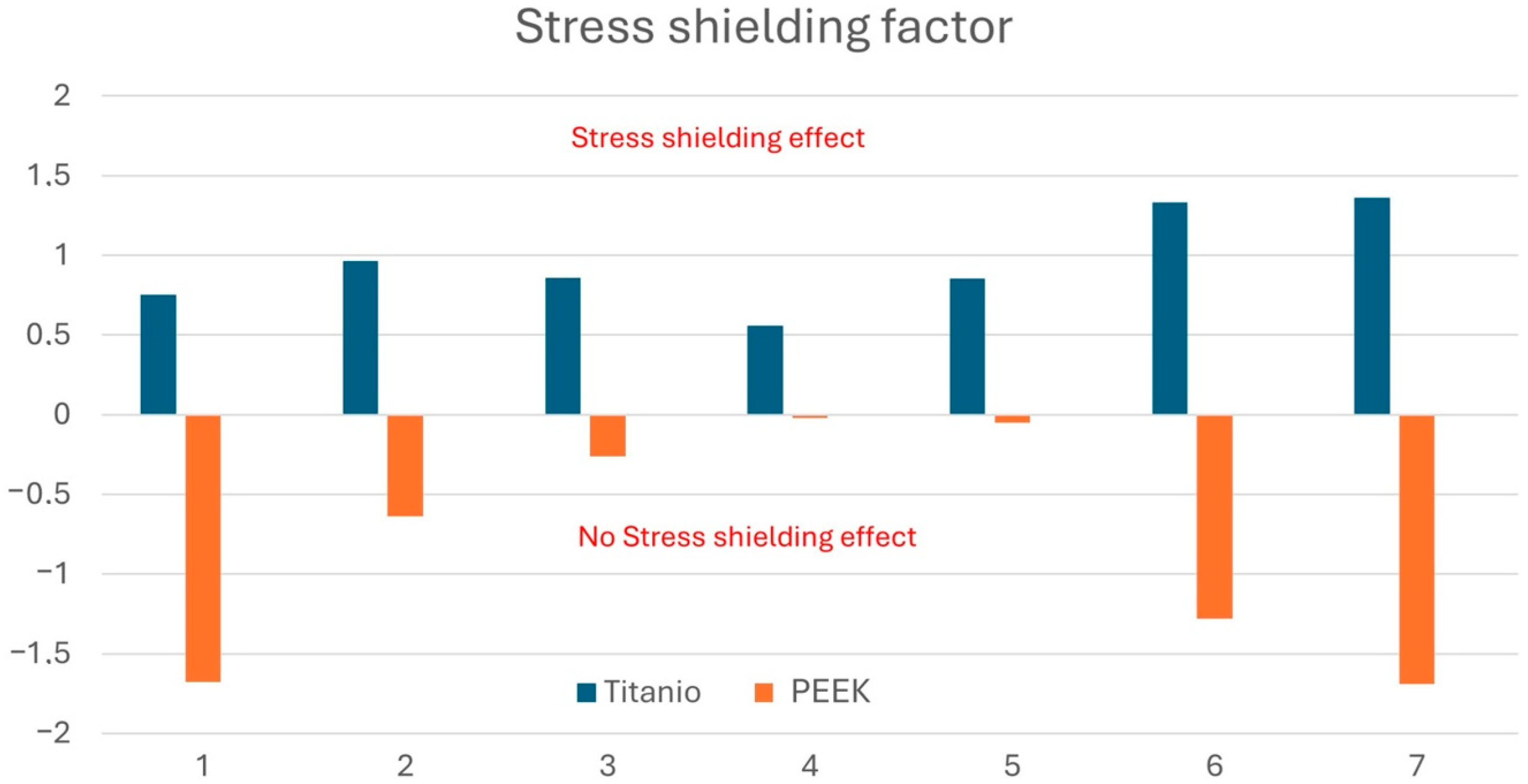
3.4. Stress Shielding Evaluation

Four cross sections (labeled 1–4 in Figure 8) were examined for the stress-shielding analysis. For each section, we calculated the average stress in the bone at 1 mm from the implant and presented it in Table 4.
From Table 4, it can be observed that the lowest stress in the bone occurs in section 1 for model A, with an average value of 0.965 MPa, and in section 2 for model B, with 1.136 MPa. Conversely, the highest stress is recorded in the lower part of the implant (section 4), measuring 2.046 MPa for model A and 2.663 MPa for model B. Overall, the PEEK model (model B) exhibits higher stress values compared to the titanium model.
By applying Equation (1) to calculate the stress-shielding factor (SSF), the results presented in Figure 9 were obtained. A positive SSF value indicates a reduction in stress levels within the bone following prosthesis implantation, a condition that may lead to bone loss. At all investigated sections, the SSF values for the PEEK prosthesis were significantly lower. Conversely, for the Ti6Al4V titanium alloy, negative stress-shielding factor values were observed. These findings allow us to conclude that the PEEK prosthesis for TKA shows no clear evidence of stress shielding at any of the seven analyzed sections.
The analysis of the results clearly shows that the titanium prosthesis induces a stress-shielding effect at all analyzed points, with stress-shielding-factor values consistently positive and particularly high at points 2, 6, and 7. In contrast, PEEK systematically exhibits negative or near-zero values, indicating a substantial absence of stress shielding throughout the entire examined tibial area. The differences are especially pronounced at points 1, 6, and 7, where PEEK presents significantly negative values (up to −1.7), compared to the correspondingly high values observed for titanium (up to +1.3). This behavior suggests that PEEK is capable of transferring load more homogeneously and physiologically to the surrounding bone, thereby reducing the risk of pathological bone remodeling and potential long-term bone resorption. In summary, the results highlight that the use of PEEK for TKA prosthesis fabrication effectively minimizes the stress-shielding effect, indicating a greater biomechanical compatibility with bone tissue compared to titanium.

4. Discussion

The loosening of the tibial prosthesis after total knee arthroplasty (TKA) remains an unresolved issue in knee surgery [56]. Several hypotheses have been proposed to explain early loosening, including insufficient fixation, inadequate cementation technique, the phenomenon of stress shielding, or incorrect implant positioning [58,59,60]. Additionally, implant design factors such as the presence of a cement pocket under the tibial plate and surface roughness have prompted design modifications aimed at reducing failure rates. Despite these improvements, tibial loosening continues to be frequently reported in clinical practice.
A study by Chaiyaki et al. [61] highlighted how prostheses with a thicker tibial base (≥4 mm), especially when made of materials with high elastic modulus such as cobalt-chromium (CoCr), are associated with increased bone resorption in the proximal tibial region. The greater stiffness and thickness of these components reduce load transmission to the bone, particularly in the metaphyseal region, promoting stress shielding. In line with Wolff’s Law, this insufficient mechanical stimulation leads to bone resorption and decreased bone density, thereby compromising implant stability.
In this context, optimizing the prosthesis design to mitigate stress shielding is crucial. Eltlhawy et al. [62] investigated porous tibial stems based on triply periodic minimal surfaces (TPMS), such as Schwarz, diamond, and gyroid structures, made of Ti6Al4V. Finite element analyses under static and dynamic loading showed that TPMS stems increased von Mises stress on the bone surface beneath the tibial plate by 14–24% and 15–36%, respectively, when compared to solid stems. This increase is considered beneficial as it stimulates the bone and reduces the risk of resorption. Moreover, TPMS stems reduced stress concentrations at the stem tip by up to 21.3%, improving overall biomechanical integration and decreasing potential complications.
Garabano et al. [19], in a 10-year follow-up study, found a significantly higher incidence of medial tibial bone resorption with titanium tibial bases (24.41%) compared to all-polyethylene bases (1.25%). These findings support the idea that the Young’s modulus of the implant material plays a major role in stress shielding. Materials like titanium or cobalt-chromium, due to their high elastic modulus, are associated with more pronounced bone loss in the proximal tibia.
Recently, the use of polymeric materials such as PEEK (polyether ether ketone), which have mechanical properties closer to those of native bone, has emerged as a promising solution. PEEK reduces the stiffness mismatch between the implant and bone, resulting in improved load transfer and reduced stress shielding [49,63,64,65,66]. Zhao et al. [44] reported that PEEK tibial components led to increased stress transmission to the tibial tray and proximal tibia while reducing the area affected by stress shielding. Similar benefits were observed in osteoporotic bone models, confirming the potential of PEEK in complex clinical cases.
Our findings corroborate these results. The finite element analysis conducted in this study demonstrated that PEEK prosthetic components significantly reduce stress shielding compared to titanium Ti6Al4V. The von Mises stress values in the proximal tibial region with PEEK remained within the 2–3 MPa range—favorable for maintaining bone mass—while titanium components led to a more pronounced reduction in local mechanical stimulus. The calculated stress-shielding factor (SSF) in PEEK-based models was consistently close to zero or negative, indicating effective stress transmission, while titanium-based models showed high SSF values, especially in the metaphyseal region.
These results align with the existing literature and reinforce the notion that PEEK components promote more physiological stress distribution, enhance osseointegration, and may ultimately improve implant longevity. Additionally, PEEK may represent a viable alternative for patients with metal allergies, offering improved biocompatibility and reduced risk of hypersensitivity reactions [49,67,68,69,70,71].

Limitations

Despite the promising results, this study has several limitations. First, the finite element model is based on idealized boundary conditions and material properties, and it assumes perfect bonding between the implant and the bone, which may not fully reflect the complex biomechanical environment of the human knee. A fundamental limitation in applying realistic loads in finite element analysis (FEA) of knee prostheses lies in the variability of patient-specific factors, such as gait patterns, muscle strength, and joint kinematics. Moreover, replicating dynamic and multidirectional loading in simplified static or dynamic simulations can lead to oversimplification. Future studies should consider a wider range of load cycles to improve modeling accuracy.
Second, the model does not account for patient-specific anatomical variations and biological responses, which may affect the generalizability of the findings. Third, the analysis focuses solely on the proximal tibial region and does not consider long-term bone remodeling or fatigue effects over time. Future work should include experimental validation and in vivo data to better replicate physiological conditions and strengthen the reliability of numerical predictions. Finally, the effects of micromotions at the bone–implant interface, as well as the differences between cemented and uncemented fixation methods, were not evaluated in this study.

5. Conclusions

This finite element analysis study demonstrates that PEEK (polyetheretherketone) knee prosthetic components substantially reduce the stress-shielding effect compared to conventional titanium Ti6Al4V implants in total knee arthroplasty. The PEEK prosthesis provides a more uniform and physiological transmission of mechanical stresses to the proximal tibial bone, with von Mises stress values maintained within the favorable range for bone maintenance and formation (2–3 MPa). The calculated stress-shielding factor (SSF) for PEEK components consistently showed negative or near-zero values at all evaluated points, indicating minimal risk of bone resorption and pathological remodeling, in contrast to the titanium model which exhibited a pronounced stress-shielding effect. Moreover, stress concentrations on the polyethylene liner were lower and more evenly distributed with the PEEK model, suggesting potential improvements in implant longevity through reduced wear. These findings support the superior biomechanical compatibility of PEEK material for tibial components in knee prostheses, with potential clinical benefits including better preservation of bone microarchitecture and enhanced implant durability, even in osteoporotic patients. Further experimental validation and long-term clinical studies are recommended to corroborate these promising computational results.

Author Contributions

Conceptualization, M.C. and B.T.; Methodology, M.C.; Software, M.C.; Validation, B.T., G.S. and A.M.; Formal analysis, M.C.; Investigation, M.C., B.T. and G.S.; Resources, M.C.; Data curation, M.C.; Writing—original draft preparation, M.C.; Writing—review and editing, M.C. and B.T.; Visualization, M.C.; Supervision, M.C.; Project administration, G.S.; Funding acquisition, G.S. and B.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Konnyu, K.J.; Thoma, L.M.; Cao, W.; Aaron, R.K.; Panagiotou, O.A.; Bhuma, M.R.; Adam, G.P.; Balk, E.M.; Pinto, D. Rehabilitation for total knee arthroplasty: A systematic review. Am. J. Phys. Med. Rehabil. 2023, 102, 19–33. [Google Scholar] [CrossRef]
  2. Alrawashdeh, W.; Eschweiler, J.; Migliorini, F.; El Mansy, Y.; Tingart, M.; Rath, B. Effectiveness of total knee arthroplasty rehabilitation programmes: A systematic review and meta-analysis. J. Rehabil. Med. 2021, 53, 2784. [Google Scholar] [CrossRef] [PubMed]
  3. Karasavvidis, T.; Moldenhauer, C.A.P.; Haddad, F.S.; Hirschmann, M.T.; Pagnano, M.W.; Vigdorchik, J.M. Current concepts in alignment in total knee arthroplasty. J. Arthroplast. 2023, 38, S29–S37. [Google Scholar] [CrossRef] [PubMed]
  4. Lustig, S.; Sappey-Marinier, E.; Fary, C.; Servien, E.; Parratte, S.; Batailler, C. Personalized alignment in total knee arthroplasty: Current concepts. SICOT-J 2021, 7, 19. [Google Scholar] [CrossRef] [PubMed]
  5. Minoda, Y. Alignment techniques in total knee arthroplasty. J. Jt. Surg. Res. 2023, 1, 108–116. [Google Scholar] [CrossRef]
  6. Rullán, P.J.; Xu, J.R.; Emara, A.K.; Molloy, R.M.; Krebs, V.E.; Mont, M.A.; Piuzzi, N.S. Major national shifts to outpatient total knee arthroplasties in the United States: A 10-year trends analysis of procedure volumes, complications, and healthcare utilizations (2010 to 2020). J. Arthroplast. 2023, 38, 1209–1216. [Google Scholar] [CrossRef]
  7. Carender, C.N.; Glass, N.A.; DeMik, D.E.; Elkins, J.M.; Brown, T.S.; Bedard, N.A. Projected prevalence of obesity in primary total knee arthroplasty: How big will the problem get? J. Arthroplast. 2022, 37, 1289–1295. [Google Scholar] [CrossRef]
  8. Huitema, G.C.; de Vries, L.M.; Verboom, T.W.; Spekenbrink–Spooren, A.; Steens, J. Patella related problems as common reason for revision of NexGen PS® total knee arthroplasty without patella resurfacing: An analysis of 5911 primary total knee arthroplasties registered in the Dutch Arthroplasty Register. Knee 2022, 34, 217–222. [Google Scholar] [CrossRef]
  9. Liang, S.; Xing, M.; Jiang, S.; Zou, W. Effect of intravenous dexamethasone on postoperative pain in patients undergoing total knee arthroplasty: A systematic review and meta-analysis. Pain Physician 2022, 25, E169. [Google Scholar]
  10. Sabah, S.A.; Alvand, A.; Knight, R.; Beard, D.J.; Price, A.J. Patient-reported function and quality of life after revision total knee arthroplasty: An analysis of 10,727 patients from the NHS PROMs program. J. Arthroplast. 2021, 36, 2887–2895. [Google Scholar] [CrossRef]
  11. Haslhofer, D.J.; Kraml, N.; Winkler, P.W.; Gotterbarm, T.; Klasan, A. Risk for total knee arthroplasty after tibial plateau fractures: A systematic review. Knee Surg. Sports Traumatol. Arthrosc. 2023, 31, 5145–5153. [Google Scholar] [CrossRef]
  12. Pander, P.; Fransen, B.L.; Hagemans, F.J.A.; Keijser, L.C.M. Functional outcome of total knee arthroplasty following tibial plateau fractures: A systematic review. Arch. Orthop. Trauma Surg. 2023, 143, 1265–1274. [Google Scholar] [CrossRef]
  13. Mohammad, H.R.; Judge, A.; Murray, D.W. A comparison of the periprosthetic fracture rate of cemented and cementless total knee arthroplasties: An analysis of data from the national joint registry. J. Arthroplast. 2024, 39, 1505–1511. [Google Scholar] [CrossRef]
  14. Başdelioğlu, K. Effects of body mass index on outcomes of total knee arthroplasty. Eur. J. Orthop. Surg. Traumatol. 2021, 31, 595–600. [Google Scholar] [CrossRef]
  15. Shen, T.S.; Rodriguez, S.; LeBrun, D.G.; Yu, J.S.; Della Valle, A.G.; Ast, M.P.; Rodriguez, J.A. Reasons and risk factors for failed same-day discharge after primary total knee arthroplasty. J. Arthroplast. 2023, 38, 668–672. [Google Scholar] [CrossRef] [PubMed]
  16. Lewis, P.L.; Campbell, D.G.; Lorimer, M.F.; Requicha, F.; W-Dahl, A.; Robertsson, O. Primary total knee arthroplasty revised for instability: A detailed registry analysis. J. Arthroplast. 2022, 37, 286–297. [Google Scholar] [CrossRef] [PubMed]
  17. Nogalo, C.; Meena, A.; Abermann, E.; Fink, C. Complications and downsides of the robotic total knee arthroplasty: A systematic review. Knee Surg. Sports Traumatol. Arthrosc. 2023, 31, 736–750. [Google Scholar] [CrossRef]
  18. Safavi, S.; Yu, Y.; Robinson, D.L.; Gray, H.A.; Ackland, D.C.; Lee, P.V. Additively manufactured controlled porous orthopedic joint replacement designs to reduce bone stress shielding: A systematic review. J. Orthop. Surg. Res. 2023, 18, 42. [Google Scholar] [CrossRef] [PubMed]
  19. Garabano, G.; Rodriguez, J.; Alamino, L.P.; Pesciallo, C.A.; Del Sel, H.; Lopreite, F. Stress shielding in total knee replacements: Comparative analysis between titanium and all-polyethylene bases at 10 years follow-up. J. Orthop. 2022, 34, 276–281. [Google Scholar] [CrossRef]
  20. de Ruiter, L.; Rankin, K.; Browne, M.; Briscoe, A.; Janssen, D.; Verdonschot, N. Decreased stress shielding with a PEEK femoral total knee prosthesis measured in validated computational models. J. Biomech. 2021, 118, 110270. [Google Scholar] [CrossRef]
  21. Cho, B.W.; Kang, K.T.; Kwon, H.M.; Lee, W.S.; Yang, I.H.; Nam, J.H.; Koh, Y.G.; Park, K.K. Biomechanical effect of anatomical tibial component design on load distribution of medial proximal tibial bone in total knee arthroplasty: Finite element analysis indicating anatomical design prevents stress-shielding. Bone Jt. Res. 2022, 11, 252–259. [Google Scholar] [CrossRef]
  22. Ceddia, M.; Trentadue, B. Evaluation of rotational stability and stress shielding of a stem optimized for hip replacements—A finite element study. Prosthesis 2023, 5, 678–693. [Google Scholar] [CrossRef]
  23. Ceddia, M.; Trentadue, B.; De Giosa, G.; Solarino, G. Topology optimization of a femoral stem in titanium and carbon to reduce stress shielding with the FEM method. J. Compos. Sci. 2023, 7, 298. [Google Scholar] [CrossRef]
  24. Ceddia, M.; Solarino, G.; Giannini, G.; De Giosa, G.; Tucci, M.; Trentadue, B. A Finite Element Analysis Study of Influence of Femoral Stem Material in Stress Shielding in a Model of Uncemented Total Hip Arthroplasty: Ti-6Al-4V versus Carbon Fibre-Reinforced PEEK Composite. J. Compos. Sci. 2024, 8, 254. [Google Scholar] [CrossRef]
  25. Nizlan, M.; Kiat, R.Y.D.; Rashid, A.H. The Fate of Coracoid Graft after Latarjet Procedure: Arthroscopic and Open Findings of Graft Union and Glenoid Remodelling. J. Coll. Physicians Surg.-Pak. JCPSP 2022, 32, 1356–1359. [Google Scholar]
  26. Tverier, V.M.; Chikova, T.N. Modelling of bone tissue adaptation in Ilyushin’s spaces. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2317, p. 012009. [Google Scholar]
  27. Forlenza, E.M.; Serino, J., III; Terhune, E.B.; Weintraub, M.T.; Nam, D.; Della Valle, C.J. Cementless total knee arthroplasty is associated with early aseptic loosening in a large national database. J. Arthroplast. 2023, 38, S215–S220. [Google Scholar] [CrossRef]
  28. Yao, K.; Chen, Y. Comprehensive evaluation of risk factors for aseptic loosening in cemented total knee arthroplasty: A systematic review and meta-analysis. J. Exp. Orthop. 2024, 11, e12095. [Google Scholar] [CrossRef]
  29. Levent, A.; Suero, E.M.; Gehrke, T.; Citak, M. Risk factors for aseptic loosening after total knee arthroplasty with a rotating-hinge implant: A case-control study. J. Bone Jt. Surg. 2021, 103, 517–523. [Google Scholar] [CrossRef]
  30. Savio, D.; Bagno, A. When the total hip replacement fails: A review on the stress-shielding effect. Processes 2022, 10, 612. [Google Scholar] [CrossRef]
  31. Seechaipat, T.; Rooppakhun, S.; Phombut, C. Finite Element Analysis of Contact Stress Distribution on Insert Conformity Design of Total Knee Arthroplasty. Int. J. Online Biomed. Eng. 2022, 18. [Google Scholar] [CrossRef]
  32. Shahjavan, Y.; Naserkhaki, S.; Farahmand, F. A Parametric Study on the Geometrical Design of Augmented Cones for Revision Total Knee Arthroplasty. In Proceedings of the 2024 31st National and 9th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 28–29 November 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 372–379. [Google Scholar]
  33. Bendich, I.; Lawrie, C.M.; Riegler, V.; Barrack, R.L.; Nunley, R.M. The impact of component design and fixation on stress shielding after modern total knee arthroplasty. J. Arthroplast. 2022, 37, S221–S225. [Google Scholar] [CrossRef]
  34. Mbogori, M.; Vaish, A.; Vaishya, R.; Haleem, A.; Javaid, M. Poly-Ether-Ether-Ketone (PEEK) in orthopaedic practice-A current concept review. J. Orthop. Rep. 2022, 1, 3–7. [Google Scholar] [CrossRef]
  35. Naghavi, S.A.; Lin, C.; Sun, C.; Tamaddon, M.; Basiouny, M.; Garcia-Souto, P.; Taylor, S.; Hua, J.; Li, D.; Wang, L.; et al. Stress shielding and bone resorption of press-fit polyether–ether–ketone (PEEK) hip prosthesis: A sawbone model study. Polymers 2022, 14, 4600. [Google Scholar] [CrossRef] [PubMed]
  36. Zheng, Z.; Liu, P.; Zhang, X.; Zou, X.; Mei, X.; Zhang, S.; Zhang, S. Strategies to improve bioactive and antibacterial properties of polyetheretherketone (PEEK) for use as orthopedic implants. Mater. Today Bio 2022, 16, 100402. [Google Scholar] [CrossRef] [PubMed]
  37. Zheng, W.; Wu, D.; Zhang, Y.; Luo, Y.; Yang, L.; Xu, X.; Luo, F. Multifunctional modifications of polyetheretherketone implants for bone repair: A comprehensive review. Biomater. Adv. 2023, 154, 213607. [Google Scholar] [CrossRef]
  38. Naghavi, S.A.; Lin, C.; Sun, C.; Tamaddon, M.; Basiouny, M.; Garcia-Souto, P.; Taylor, S.; Hua, J.; Li, D.; Wang, L.; et al. Enhancing distraction osteogenesis with carbon fiber reinforced polyether ether ketone bone pins and a three-dimensional printed transfer device to permit artifact-free three-dimensional magnetic resonance imaging. J. Craniofacial Surg. 2021, 32, 360–364. [Google Scholar]
  39. Fabris, D.; Moura, J.P.; Fredel, M.C.; Souza, J.C.; Silva, F.S.; Henriques, B. Biomechanical analyses of one-piece dental implants composed of titanium, zirconia, PEEK, CFR-PEEK, or GFR-PEEK: Stresses, strains, and bone remodeling prediction by the finite element method. J. Biomed. Mater. Res. Part B Appl. Biomater. 2022, 110, 79–88. [Google Scholar] [CrossRef]
  40. Shash, Y.H.; El-Wakad, M.T.; El-Dosoky, M.A.; Dohiem, M.M. Evaluation of stresses on mandible bone and prosthetic parts in fixed prosthesis by utilizing CFR-PEEK, PEKK and PEEK frameworks. Sci. Rep. 2023, 13, 11542. [Google Scholar] [CrossRef]
  41. Oladapo, B.I.; Zahedi, S.A. Improving bioactivity and strength of PEEK composite polymer for bone application. Mater. Chem. Phys. 2021, 266, 124485. [Google Scholar] [CrossRef]
  42. Li, S.; Li, M.; Hu, J.; Li, G.; Wang, B.; Zhou, Z. A new strategy for PEEK-based biocomposites to achieve porous surface for bioactivity and adjustable mechanical properties for orthopedic stress matching. Compos. Part A Appl. Sci. Manuf. 2024, 177, 107909. [Google Scholar] [CrossRef]
  43. Yu, J.; Zhao, D.; Chen, W.M.; Chu, P.; Wang, S.; Zhang, C.; Huang, J.; Wang, X.; Ma, X. Finite element stress analysis of the bearing component and bone resected surfaces for total ankle replacement with different implant material combinations. BMC Musculoskelet. Disord. 2022, 23, 70. [Google Scholar] [CrossRef]
  44. Zheng, J.; Zhao, H.; Dong, E.; Kang, J.; Liu, C.; Sun, C.; Li, D.; Wang, L. Additively-manufactured PEEK/HA porous scaffolds with highly-controllable mechanical properties and excellent biocompatibility. Mater. Sci. Eng. C 2021, 128, 112333. [Google Scholar] [CrossRef]
  45. Carman, L.; Besier, T.; Stott, N.S.; Choisne, J. Sex differences in linear bone measurements occur following puberty but do not influence femoral or tibial torsion. Sci. Rep. 2023, 13, 11733. [Google Scholar] [CrossRef] [PubMed]
  46. Wilczyński, M.; Bieniek, M.; Krakowski, P.; Karpiński, R. Cemented vs. cementless fixation in primary knee replacement: A narrative review. Materials 2024, 17, 1136. [Google Scholar] [CrossRef] [PubMed]
  47. Dagneaux, L.; Canovas, F.; Jourdan, F. Finite element analysis in the optimization of posterior-stabilized total knee arthroplasty. Orthop. Traumatol. Surg. Res. 2024, 110, 103765. [Google Scholar] [CrossRef] [PubMed]
  48. Sun, H.; Zhang, H.; Wang, T.; Zheng, K.; Zhang, W.; Li, W.; Zhang, W.; Xu, Y.; Geng, D. Biomechanical and finite-element analysis of femoral pin-site fractures following navigation-assisted total knee arthroplasty. J. Bone Jt. Surg. 2022, 104, 1738–1749. [Google Scholar] [CrossRef]
  49. Ficarella, E.; Minooei, M.; Santoro, L.; Toma, E.; Trentadue, B.; De Spirito, M.; Papi, M.; Pruncu, C.I.; Lamberti, L. Visco-Hyperelastic Characterization of the Equine Immature Zona Pellucida. Materials 2021, 14, 1223. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
  50. Ceddia, M.; Solarino, G.; Tucci, M.; Lamberti, L.; Trentadue, B. Stress analysis of tibial bone using three different materials for bone fixation plates. J. Compos. Sci. 2024, 8, 334. [Google Scholar] [CrossRef]
  51. Galas, A.; Banci, L.; Innocenti, B. The effects of different femoral component materials on bone and implant response in total knee arthroplasty: A finite element analysis. Materials 2023, 16, 5605. [Google Scholar] [CrossRef]
  52. Gefen, A. Computational simulations of stress shielding and bone resorption around existing and computer-designed orthopaedic screws. Med. Biol. Eng. Comput. 2002, 40, 311–322. [Google Scholar] [CrossRef]
  53. Huiskes, R.I.K.; Weinans, H.; Van Rietbergen, B. The relationship between stress shielding and bone resorption around total hip stems and the effects of flexible materials. Clin. Orthop. Relat. Res. 1992, 274, 124–134. [Google Scholar] [CrossRef]
  54. Scheuren, A.C.; Vallaster, P.; Kuhn, G.A.; Paul, G.R.; Malhotra, A.; Kameo, Y.; Müller, R. Mechano-regulation of trabecular bone adaptation is controlled by the local in vivo environment and logarithmically dependent on loading frequency. Front. Bioeng. Biotechnol. 2020, 8, 566346. [Google Scholar] [CrossRef] [PubMed]
  55. Gong, H.; Zhu, D.; Gao, J.; Lv, L.; Zhang, X. An adaptation model for trabecular bone at different mechanical levels. Biomed. Eng. Online 2010, 9, 32. [Google Scholar] [CrossRef] [PubMed]
  56. Jain, T.; Sharma, G.K.; Ghosh, R. Design of functionally graded porous lattice structure tibial implant for TAR. Int. J. Mech. Sci. 2024, 281, 109671. [Google Scholar] [CrossRef]
  57. Ducheyne, P.A.U.L.; Kagan, A., 2nd; Lacey, J.A. Failure of total knee arthroplasty due to loosening and deformation of the tibial component. J. Bone Jt. Surg. 1978, 60, 384–391. [Google Scholar] [CrossRef]
  58. Chen, Z.; Han, J.; Zhang, J.; Peng, Y.; Guo, L.; Chen, S.; Jin, Z. Tibial post loading increases the risk of aseptic loosening of posterior-stabilized tibial prosthesis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2024, 238, 886–896. [Google Scholar] [CrossRef]
  59. Vasudevan, B.; Megaraj, M.; Palanivel, A.; Durvasulu, R.; Manjunathan, K.; Dillibabu, S.P. Analysis of bone prosthesis for cementless tibal prosthesis fixation and the influence of loading condition. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2023; Volume 2766. [Google Scholar]
  60. Linke, P.; Wilhelm, P.; Levent, A.; Gehrke, T.; Salber, J.; Akkaya, M.; Suero, E.M.; Citak, M. Anatomical risk factors for aseptic loosening of full hinge knee prosthesis in primary and revision TKAs. Arch. Orthop. Trauma Surg. 2023, 143, 4299–4307. [Google Scholar] [CrossRef]
  61. Chaiyakit, P.; Ompornnuwat, K. Stress Shielding in the Proximal Tibia after Total Knee Arthroplasty: A Finite Element Analysis of 2-and 4-mm-thick Tibia Prosthesis Models. Vajira Med. J. J. Urban Med. 2022, 66, 397–406. [Google Scholar] [CrossRef]
  62. Ceddia, M.; Solarino, G.; Dramisino, P.; De Giosa, G.; Rizzo, S.; Trentadue, B. Comparison of Stress between Three Different Functionally Graded Hip Stem Implants Made of Different Titanium Alloys and Composite Materials. J. Compos. Sci. 2024, 8, 449. [Google Scholar] [CrossRef]
  63. Azbari, Z.S.; Rad, M.R.; Nahvinejad, A.; Gilakjani, H.A.; Khorsandi, M. Biomechanical Analysis of Hip Replacement Stem Design: A Finite Element Analysis. In Proceedings of the 2022 29th National and 7th International Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 21–22 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 305–309. [Google Scholar]
  64. Joshi, M.G.; Advani, S.G.; Miller, F.; Santare, M.H. Analysis of a femoral hip prosthesis designed to reduce stress shielding. J. Biomech. 2000, 33, 1655–1662. [Google Scholar] [CrossRef]
  65. Glassman, A.H.; Bobyn, J.D.; Tanzer, M. New femoral designs: Do they influence stress shielding? Clin. Orthop. Relat. Res. 2006, 453, 64–74. [Google Scholar] [CrossRef] [PubMed]
  66. Kang, K.T.; Chun, H.J.; Kim, H.J.; Yeom, J.S.; Park, K.M.; Hwang, I.H.; Lee, K.I. Finite element analysis of instrumented posterior lumbar interbody fusion cages for reducing stress shielding effects: Comparison of the CFRP cage and titanium cage. Compos. Res. 2012, 25, 98–104. [Google Scholar]
  67. Roberts, T.T.; Haines, C.M.; Uhl, R.L. Allergic or hypersensitivity reactions to orthopaedic implants. JAAOS-J. Am. Acad. Orthop. Surg. 2017, 25, 693–702. [Google Scholar] [CrossRef]
  68. Benakatti, V.B.; Sajjanar, J.A.; Acharya, A. Polyetheretherketone (PEEK) in dentistry. J. Clin. Diagn. Res. 2019, 13, e46485. [Google Scholar] [CrossRef]
  69. Mishra, S.; Chowdhary, R. PEEK materials as an alternative to titanium in dental implants: A systematic review. Clin. Implant Dent. Relat. Res. 2019, 21, 208–222. [Google Scholar] [CrossRef]
  70. Luo, C.; Liu, Y.; Peng, B.; Chen, M.; Liu, Z.; Li, Z.; Kuang, H.; Gong, B.; Li, Z.; Sun, H. PEEK for oral applications: Recent advances in mechanical and adhesive properties. Polymers 2023, 15, 386. [Google Scholar] [CrossRef]
  71. Ortega-Martínez, J.; Farré-Lladós, M.; Cano-Batalla, J.; Cabratosa-Termes, J. Polyetheretherketone (PEEK) as a medical and dental material. A literature review. Med. Res. Arch. 2017, 5, 4. [Google Scholar]
Osteology 05 00024 g001
Figure 1. Components of TKA knee implant model with the geometrical details.
Figure 1. Components of TKA knee implant model with the geometrical details.
Osteology 05 00024 g001
Osteology 05 00024 g002
Figure 2. Details of the tibia modeled using Autodesk Inventor 2024 CAD software.
Figure 2. Details of the tibia modeled using Autodesk Inventor 2024 CAD software.
Osteology 05 00024 g002
Osteology 05 00024 g003
Figure 3. Finite Element Model of the Knee Prosthesis and Tibial Bone.
Figure 3. Finite Element Model of the Knee Prosthesis and Tibial Bone.
Osteology 05 00024 g003
Osteology 05 00024 g004
Figure 4. Representation of contact, boundary, and loading conditions.
Figure 4. Representation of contact, boundary, and loading conditions.
Osteology 05 00024 g004
Osteology 05 00024 g005
Figure 5. von Mises stress on the insert: model (a) femoral and tibial components in titanium; model (b) femoral and tibial components in PEEK.
Figure 5. von Mises stress on the insert: model (a) femoral and tibial components in titanium; model (b) femoral and tibial components in PEEK.
Osteology 05 00024 g005
Osteology 05 00024 g006
Figure 6. von Mises stress on femoral and tibial component: model (a) titanium prosthesis; model (b) PEEK prosthesis.
Figure 6. von Mises stress on femoral and tibial component: model (a) titanium prosthesis; model (b) PEEK prosthesis.
Osteology 05 00024 g006
Osteology 05 00024 g007
Figure 7. von Mises stress in the tibial epiphyseal region: model (a) titanium prosthesis; model (b) PEEK prosthesis.
Figure 7. von Mises stress in the tibial epiphyseal region: model (a) titanium prosthesis; model (b) PEEK prosthesis.
Osteology 05 00024 g007
Osteology 05 00024 g008
Figure 8. Representation of the cross sections (1–4) used for von Mises stress analysis: model (a) titanium prosthesis; model (b) PEEK prosthesis.
Figure 8. Representation of the cross sections (1–4) used for von Mises stress analysis: model (a) titanium prosthesis; model (b) PEEK prosthesis.
Osteology 05 00024 g008
Osteology 05 00024 g009
Figure 9. Stress-shielding factor for titanium and PEEK model.
Figure 9. Stress-shielding factor for titanium and PEEK model.
Osteology 05 00024 g009
Table 1. Mechanical properties of osteoporotic bone; the subscripts x and y refer to the orthogonal directions of the tibia, while the subscript z represents the direction parallel to the length of the tibia.
Table 1. Mechanical properties of osteoporotic bone; the subscripts x and y refer to the orthogonal directions of the tibia, while the subscript z represents the direction parallel to the length of the tibia.
Material PropertiesCortical Osteoporotic BoneCancellous Osteoporotic Bone
Young’s modulus (MPa)Ex = 7820Ex = 6252
Ey = 7820Ey = 2.380
Ez = 11,560Ez = 2.890
Poisson’s ratio ν x y = 0.12 ν x z = 0.3
ν y z = 0.37 ν y z = 0.27
ν x z = 0.14 ν x z = 0.19
Table 2. Mechanical properties of prosthetic materials.
Table 2. Mechanical properties of prosthetic materials.
Material PropertiesTi6Al4VPEEKUHMWPE
Young’s modulus (MPa)E = 110,000E = 18,000E = 920
Poisson’s ratioν = 0.3ν = 0.3ν = 0.3
Table 3. Sensitivity analysis of the mesh.
Table 3. Sensitivity analysis of the mesh.
Mesh Element Size
(mm)		von Mises StressComputation Time (min)
3.015 MPa5
2.518 MPa8
2.022 MPa14
1.822.3 MPa22
Table 4. Bone stress values measured in the four sections for models a and b.
Table 4. Bone stress values measured in the four sections for models a and b.
Sectionsvon Mises Stress (MPa)
Model A		von Mises Stress (MPa)
Model B
10.9651.243
21.0651.136
31.7642.269
42.0462.663
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ceddia, M.; Morizio, A.; Solarino, G.; Trentadue, B. Evaluation of the Stress-Shielding Effect of a PEEK Knee Prosthesis. A Finite Element Study. Osteology 2025, 5, 24. https://doi.org/10.3390/osteology5030024

AMA Style

Ceddia M, Morizio A, Solarino G, Trentadue B. Evaluation of the Stress-Shielding Effect of a PEEK Knee Prosthesis. A Finite Element Study. Osteology. 2025; 5(3):24. https://doi.org/10.3390/osteology5030024

Chicago/Turabian Style

Ceddia, Mario, Arcangelo Morizio, Giuseppe Solarino, and Bartolomeo Trentadue. 2025. "Evaluation of the Stress-Shielding Effect of a PEEK Knee Prosthesis. A Finite Element Study" Osteology 5, no. 3: 24. https://doi.org/10.3390/osteology5030024

APA Style

Ceddia, M., Morizio, A., Solarino, G., & Trentadue, B. (2025). Evaluation of the Stress-Shielding Effect of a PEEK Knee Prosthesis. A Finite Element Study. Osteology, 5(3), 24. https://doi.org/10.3390/osteology5030024

Article Metrics

Back to TopTop