Enabling Intelligent 6G Communications: A Scalable Deep Learning Framework for MIMO Detection
Abstract
1. Introduction
- We developed a DL-driven signal detection method known as the MIMONet detector for signal detection in a MIMO system and explored the study under diverse channel conditions.
- We developed a customized FFNN network architecture through selective feature-based network settings, which helped MIMONet to achieve optimal performance compared to benchmark MIMO detectors.
- MIMONet was analyzed through the bit error rate (BER) and complexity against both traditional MIMO detectors (MMSE, ZF, MLD, GS, CG, OCDBOX, and ADMIN) and AI-based detectors (AIDETECT, AMP-DNN, OAMP-Net, OAMP-Net2, and DetNet), highlighting its relative performance and efficiency.
2. Related Work
3. MIMO Detection: A System Model
3.1. Conventional MIMO Detection
3.1.1. Maximum Likelihood Detector
3.1.2. Zero-Forcing Detector
3.1.3. Minimum Mean Square Error Detector
3.2. Gauss–Seidel Detector
3.3. Conjugate Gradient Detector
3.4. Optimized Coordinate Descent Detector
3.5. DL-Based MIMO Detection
3.6. AIDETECT MIMO Detector
4. Problem Formulation and Data Preparation
4.1. Problem Formulation
4.2. Data Generation and Preprocessing
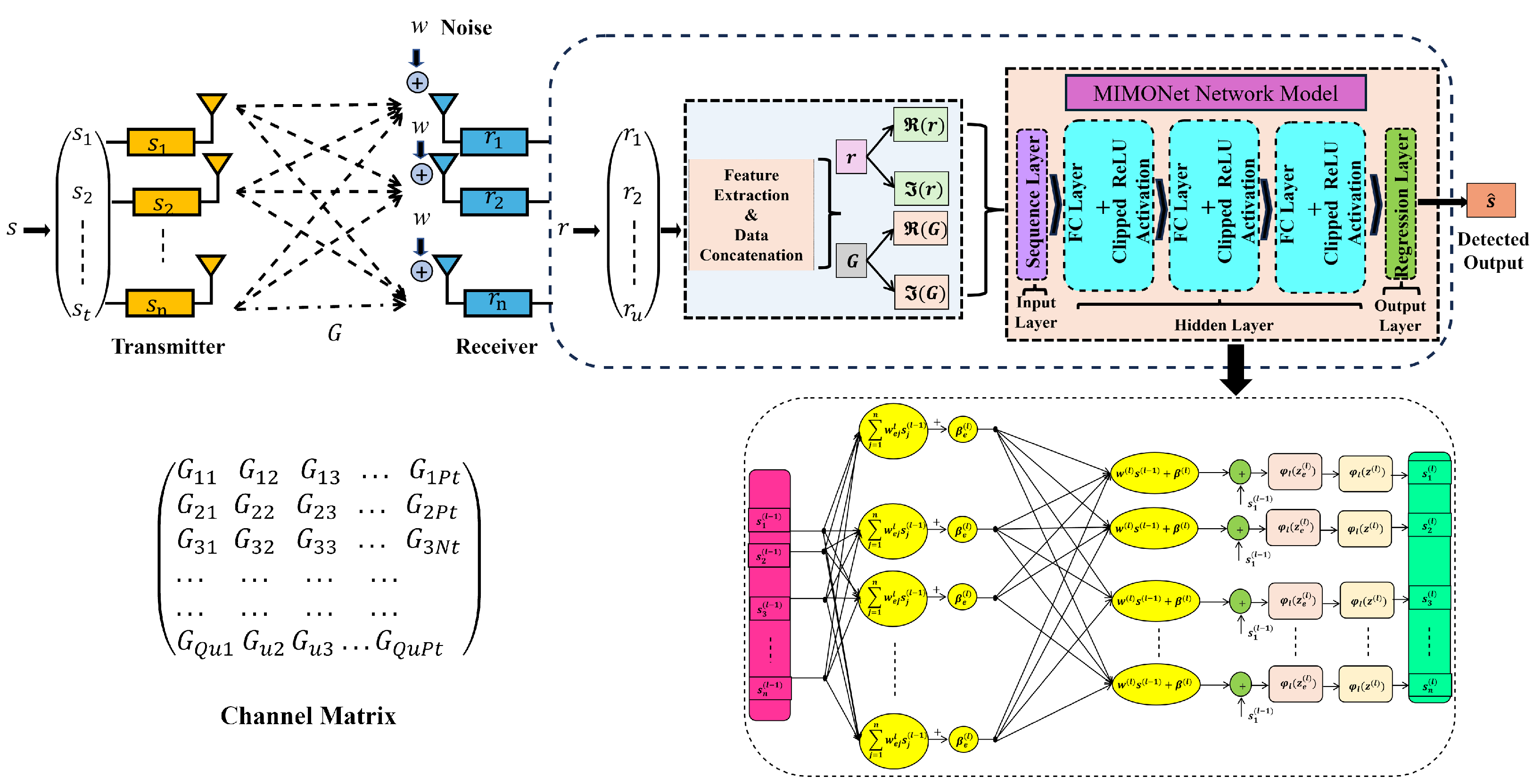
5. MIMONet: A DL-Based MIMO Detector
5.1. MIMONet Network Architecture
- Input Layer: In the input layer, the received signal and channel matrix are processed by first separating their real and imaginary parts:The real and imaginary components of the received signal and channel matrix are concatenated into a feature vector that passes through the network’s hidden layers, which process and learn the patterns present in the data.
- Hidden Layers: Each hidden layer of the MIMONet consists of 128 neurons and employs a fully connected layer along with a clipped ReLU activation function to introduce nonlinearity. The output of the first hidden layer is computed as follows:where and represent the weight matrix and bias vector of the first hidden layer, and is the activation function (clipped ReLU). Similarly, the second and third hidden layers produce the outputs and aswhere are the weight matrices for the second and third hidden layers, are the corresponding bias vectors, and are the activation functions for the second and third hidden layers. These hidden layers allow the network to progressively learn more abstract features of the received signal and channel data.
- Output Layer: The final output layer of the network produces the predicted transmitted symbols . This output is obtained by applying an argmax function to the output of the third hidden layer:Similarly, and represent the weight matrix and bias vector for the output layer, respectively. This operation identifies the most likely transmitted symbol, as predicted by the MIMONet detector.
5.2. MIMONet: Training and Testing
5.2.1. Data Generation
5.2.2. Training
5.2.3. Testing
| Algorithm 1: MIMONet: Deep learning-based MIMO detector |
 |
6. Simulation Setup and Results Discussion
6.1. Results Discussion
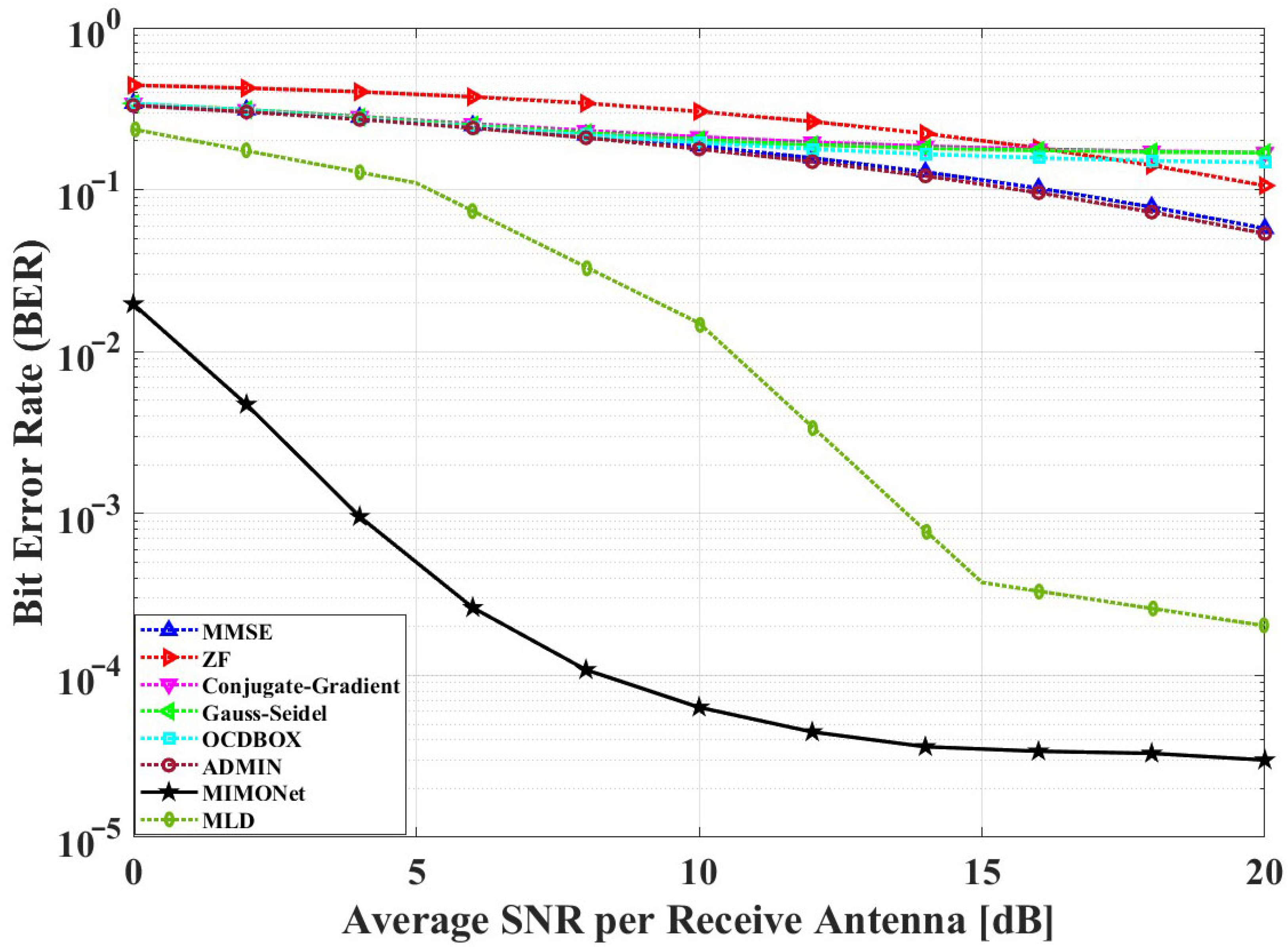
6.1.1. Performance Analysis of MIMONet Detector Against Traditional MIMO Detectors
6.1.2. Performance Analysis of MIMONet Detector Against AI-Based MIMO Detectors
6.1.3. MIMONet Under Diverse Channel Conditions
6.1.4. Training and Validation of MIMONet for 4 × 4 and 8 × 8 MIMO Systems
7. Computational Complexity
Computational Complexity of MIMONet Detector
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO detection techniques: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Yang, S.; Hanzo, L. Fifty years of MIMO detection: The road to large-scale MIMOs. IEEE Commun. Surv. Tutor. 2015, 17, 1941–1988. [Google Scholar] [CrossRef]
- Daha, M.Y.; Rafferty, J.; Ashraf, M.I.; Hadi, M.U. Artificial intelligence-enhanced signal detection technique for beyond fifth generation networks. Comput. Electr. Eng. 2024, 119, 109608. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, C.; Xue, Y.; Xu, S.; You, X. Efficient architecture for soft-output massive MIMO detection with Gauss-Seidel method. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1886–1889. [Google Scholar]
- Yin, B.; Wu, M.; Cavallaro, J.R.; Studer, C. VLSI design of large-scale soft-output MIMO detection using conjugate gradients. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 1498–1501. [Google Scholar]
- Zhang, Z.; Dai, X.; Dong, Y.; Wang, X.; Liu, T. A low-complexity signal detection utilizing AOR iterative method for massive MIMO systems. China Commun. 2017, 14, 269–278. [Google Scholar] [CrossRef]
- Chataut, R.; Akl, R.; Robaei, M. Accelerated and preconditioned refinement of Gauss-Seidel method for uplink signal detection in 5G massive MIMO systems. In Proceedings of the 2020 10th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 6–8 January 2020; pp. 0083–0089. [Google Scholar]
- Ahmad, M.; Sarwar, M.S.; Shin, S.Y. Deep Learning Assisted Channel Estimation for Adaptive Parameter Selection in mMIMO-SEFDM. IEEE Internet Things J. 2025, 12, 1234–1245. [Google Scholar] [CrossRef]
- Gao, J.; Hu, M.; Zhong, C.; Li, G.Y.; Zhang, Z. An attention-aided deep learning framework for massive MIMO channel estimation. IEEE Trans. Wirel. Commun. 2021, 21, 1823–1835. [Google Scholar] [CrossRef]
- Samuel, N.; Diskin, T.; Wiesel, A. Learning to detect. IEEE Trans. Signal Process. 2019, 67, 2554–2564. [Google Scholar] [CrossRef]
- Daha, M.Y.; Ashraf, M.I.; Hadi, M.U. Optimizing signal detection in MIMO systems: AI vs approximate and linear detectors. IEEE Commun. Lett. 2024, 28, 2387–2391. [Google Scholar] [CrossRef]
- Omondi, G.; Olwal, T.O. Variational autoencoder-enhanced DNN-based detection for MIMO systems. e-Prime Adv. Electr. Eng. Electron. Energy 2023, 6, 100335. [Google Scholar] [CrossRef]
- Khurshid, K.; Khan, A.A.; Siddiqui, M.H.; Hadi, M.U.; Rashid, I.; Imran, M. Optimality of Linear MIMO Detection for 5G Systems via 1-Opt Local Search. J. Electr. Eng. Technol. 2021, 16, 1099–1108. [Google Scholar] [CrossRef]
- Daha, M.Y.; Rafferty, J.; Ashraf, M.I.; Hadi, M.U. DM-DETECT–a deep MIMO detector for beyond 5G networks. In Proceedings of the 2023 Second International Conference on Augmented Intelligence and Sustainable Systems (ICAISS), Amman, Jordan, 3–5 April 2023; pp. 1381–1385. [Google Scholar]
- Babu, B.; Daha, M.Y.; Hadi, M.U. Enhancing signal detection in 6G networks through LSTM-based MIMO technology. In Proceedings of the 2024 35th Irish Signals and Systems Conference (ISSC), Cork, Ireland, 11–13 June 2024; pp. 1–6. [Google Scholar]
- Trotobas, B.; Nafkha, A.; Louët, Y. A review to massive MIMO detection algorithms: Theory and implementation. In Advanced Radio Frequency Antennas for Modern Communication and Medical Systems; IntechOpen: London, UK, 2020. [Google Scholar]
- Faisal, M.; Karam, F.W.; Ali, Z.; Bashir, S. Comparative Performance Analysis of Efficient MIMO Detection Approaches. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 8. [Google Scholar] [CrossRef]
- Chaaire, A.; Chakkor, O.; Aytouna, F. A Performance Study of Principals MIMO Signal Detection Algorithms. In Proceedings of the 2020 IEEE 2nd International Conference on Electronics, Control, Optimization and Computer Science (ICECOCS), Kenitra, Morocco, 2–3 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Tong, L.; Sadek, A.K.; Dong, M.; Chen, Z. Adaptive MIMO Detection Using Thresholded Sphere Decoding. IEEE Trans. Wirel. Commun. 2004, 3, 1666–1675. [Google Scholar]
- Apanasenko, N.V.; Burkov, A.A.; Turlikov, A.M. Performance Analysis of ZF and MMSE Algorithms for MIMO Systems. In Proceedings of the 2018 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 26–30 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar]
- Sun, S.; Chen, Y.; Wang, Q.; Lu, J. Sphere Decoding Algorithms for MIMO Detection. IEEE Access 2016, 4, 1560–1573. [Google Scholar]
- Li, Y.; Wang, B.; Yang, L. A Survey on Sphere Decoding Algorithms and Their Applications in MIMO Systems. IEEE Access 2020, 8, 109156–109172. [Google Scholar]
- Wang, Y.; Liu, Q.; Wang, Q.; Wang, J. MMSE-DFE for MIMO Systems With Reduced Complexity. IEEE Trans. Veh. Technol. 2008, 57, 2088–2094. [Google Scholar]
- Bai, L.; Zeng, Q.; Han, R.; Choi, J.; Zhang, W. Deep Learning-Based Low Complexity MIMO Detection via Partial MAP. IEEE Trans. Wirel. Commun. 2024, 24, 2126–2139. [Google Scholar] [CrossRef]
- Muruganathan, S.D.; Khawaja, B.A.; Ooi, B.T.; Poole, P. Low-Complexity MIMO Detection Using Neumann Series Expansion. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4846–4851. [Google Scholar]
- Hassibi, B.; Hochwald, B.M. High-Rate Codes That Are Linear in Space and Time. IEEE Trans. Inf. Theory 2005, 51, 323–342. [Google Scholar]
- Ali, Z.; Faisal, M.; Karam, F.W.; Bashir, S. An Efficient MIMO Detector Based on Adaptive Iterative Methods. IEEE Trans. Wirel. Commun. 2017, 16, 2760–2772. [Google Scholar]
- Li, S.; Zhang, J.-K.; Mu, X. Noncoherent massive space-time block codes for uplink network communications. IEEE Trans. Veh. Technol. 2018, 67, 5013–5027. [Google Scholar] [CrossRef]
- Bucher, S.; Waldschmidt, C. Advanced noncoherent detection in massive MIMO systems via digital beamspace preprocessing. Telecom 2020, 1, 211–227. [Google Scholar] [CrossRef]
- Bucher, S.; Yammine, G.; Fischer, R.F.H.; Waldschmidt, C. A noncoherent massive MIMO system employing beamspace techniques. IEEE Trans. Veh. Technol. 2019, 68, 11052–11063. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Xue, J.; Xu, Z. Learning to Search for MIMO Detection. IEEE Trans. Wirel. Commun. 2020, 19, 7571–7584. [Google Scholar] [CrossRef]
- Albreem, M.A.; Salah, W.; Kumar, A.; Alsharif, M.H.; Rambe, A.H.; Jusoh, M.; Uwaechia, A.N. Low Complexity Linear Detectors for Massive MIMO: A Comparative Study. IEEE Access 2021, 9, 45740–45753. [Google Scholar] [CrossRef]
- Babu, B.; Daha, M.Y.; Ashraf, M.I.; Khurshid, K.; Hadi, M.U. AIDETECT2: A Novel AI-Driven Signal Detection Approach for Beyond 5G and 6G Wireless Networks. Electronics 2024, 13, 3821. [Google Scholar] [CrossRef]
- Yin, B.; Wu, M.; Cavallaro, J.R.; Studer, C. Conjugate Gradient-Based Soft-Output Detection and Precoding in Massive MIMO Systems. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3696–3701. [Google Scholar]
- Wu, M.; Yin, B.; Wang, G.; Dick, C.; Cavallaro, J.R.; Studer, C. Large-Scale MIMO Detection for 3GPP LTE: Algorithms and FPGA Implementations. IEEE J. Sel. Top. Signal Process. 2014, 8, 916–929. [Google Scholar] [CrossRef]
- Shahabuddin, S.; Hautala, I.; Juntti, M.; Studer, C. ADMM-Based Infinity-Norm Detection for Massive MIMO: Algorithm and VLSI Architecture. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 747–759. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Wang, Y. On the Design of Massive MIMO-QAM Detector via ℓ2 Box ADMM Approach. arXiv 2022, arXiv:2208.13122. [Google Scholar]
- He, H.; Wen, C.-K.; Jin, S.; Li, G.Y. A Model-Driven Deep Learning Network for MIMO Detection. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 584–588. [Google Scholar]
- He, H.; Wen, C.-K.; Jin, S.; Li, G.Y. Model-Driven Deep Learning for MIMO Detection. IEEE Trans. Signal Process. 2020, 68, 1702–1715. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Yan, X.; Ouyang, Z. A low-complexity AMP detection algorithm with deep neural network for massive MIMO systems. Digital Commun. Netw. 2024, 10, 1375–1386. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Number of transmitters | 4, 8, 16 |
| Number of receivers | 4, 8, 32 |
| Modulation | QPSK, QAM |
| Constellation size | 4, 16 |
| Data size | 1 Million |
| SNR Range | 0:2:20 dB and 0:5:20 dB |
| Training Function | Adam |
| Number of neurons | 128 |
| Number of hidden layers | 3 |
| Maximum epochs | 2000 |
| Mini Batch Size | 10 |
| Initial learning rate | 0.001 |
| L2-regularization | 0.0001 |
| MIMO Detectors | Computational Complexity |
|---|---|
| MLD [2] | |
| MMSE [12] | |
| ZF [12] | |
| CG [34] | |
| NS [35] | |
| GS [36] | |
| OCDBOX [37] | |
| ADMIN [37] | |
| OAMP-Net [38] | |
| OAMP-Net2 [39] | ( = number of layers) |
| DetNet2 [10] | |
| AMP-DNN [40] | |
| AIDETECT [11] | ( = number of neurons in nth layer) |
| MIMONet |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daha, M.Y.; Sudhakaran, A.; Babu, B.; Hadi, M.U. Enabling Intelligent 6G Communications: A Scalable Deep Learning Framework for MIMO Detection. Telecom 2025, 6, 58. https://doi.org/10.3390/telecom6030058
Daha MY, Sudhakaran A, Babu B, Hadi MU. Enabling Intelligent 6G Communications: A Scalable Deep Learning Framework for MIMO Detection. Telecom. 2025; 6(3):58. https://doi.org/10.3390/telecom6030058
Chicago/Turabian StyleDaha, Muhammad Yunis, Ammu Sudhakaran, Bibin Babu, and Muhammad Usman Hadi. 2025. "Enabling Intelligent 6G Communications: A Scalable Deep Learning Framework for MIMO Detection" Telecom 6, no. 3: 58. https://doi.org/10.3390/telecom6030058
APA StyleDaha, M. Y., Sudhakaran, A., Babu, B., & Hadi, M. U. (2025). Enabling Intelligent 6G Communications: A Scalable Deep Learning Framework for MIMO Detection. Telecom, 6(3), 58. https://doi.org/10.3390/telecom6030058







