Revenue and Efficiency in Spectrum Auctions: A Theoretical and Empirical Assessment of Auction Formats

Abstract

As the electromagnetic spectrum is a limited and valuable resource, auctions have emerged as an effective tool for promoting efficient allocation and generating revenue. This article proposes a theoretical review of the most commonly used auction formats for spectrum auctions, highlighting the primary strengths and weaknesses of each format. Additionally, comparisons are made between the revenue generated by different auction formats and the corresponding countries in North and South America during the 21st century. The conclusion drawn is that the Combinatorial Clock Auction format is the preferred choice, as it consistently leads to more efficient allocation, as measured by the revenue generated from each auction.

1. Introduction

The electromagnetic spectrum is a vital and limited resource that is essential for various communication technologies including radio, television, mobile phones, and satellite-based communications. As the demand for wireless communications continues to grow, the need for efficient allocation of spectrum bandwidth becomes increasingly critical. One of the primary methods for assigning rights globally is through auctions. All frequencies within the electromagnetic spectrum, ranging from low-frequency radio waves to ultra-high frequencies such as gamma rays, are included in the spectrum’s scope [1].

For communication purposes, the most relevant bandwidth ranges from 3 kHz to 300 GHz. Different frequencies exhibit distinct properties: low-frequency waves can cover larger spatial areas and penetrate buildings and solid objects, while higher-frequency waves can transmit more data, albeit over shorter distances [2].

Auctions have become the primary method for allocating spectrum usage rights to mobile operators for the implementation of 3G, 4G, and 5G networks. This trend of employing market-based approaches for spectrum management is expected to persist in 6G, with the design of auctions becoming more complex due to the diverse spectrum bands (low, mid, and high) that will be used, as well as coverage requirements, spectrum trading, and other considerations [3].

Historically, spectrum allocation grants have been managed using various methodologies and auction formats. Some of the mechanisms used throughout history have suffered from inefficiencies, biases, or underutilization of the allocated spectrum. As demand for wireless services continues to grow throughout the world, it is imperative to explore new approaches to maximize efficiency in spectrum allocation.

These auctions are typically conducted by regulatory authorities, such as the Federal Communications Commission (FCC) in the United States, Ofcom in the United Kingdom, and the Agência Nacional de Telecomunicações (Anatel) in Brazil. Several key steps are followed throughout the auction process:

• Planning and Consulting: The authorities identify the spectrum bands to be auctioned and consult with interested parties to determine the auction format and rules.
• The auction project allows the authority to choose from several formats, including Simultaneous Multiple-Round Auctions (SMRAs), Combinatorial Clock Auctions (CCAs), Sealed Bid Auctions, and others. Each format has its own strengths and weaknesses, which the auctioneer must evaluate to achieve the specific goals of the auction process.
• Concession and Payment: Once the dispute has been resolved, the successful bidders are awarded spectrum-specific licenses and are required to make payments to the authorities. The revenue generated from these auctions can be substantial, with some processes yielding billions of dollars.

Auctions within a spectrum context can lead several advantageous outcomes.

• Efficient Allocation: The auction process facilitates the efficient allocation of spectrum to those participants who value it the most, as indicated by their bids, thereby promoting the optimal use of this resource.
• Revenue: Governments, through regulatory agencies, can generate substantial revenue that can subsequently be utilized to fund public services, alleviate deficits, or reduce debt.
• Innovation and Competition: Auction processes can incentivize innovation and competition within the telecommunication resulting in improved services and lower prices for consumers.
• Guarantees and Counterparts: Several key rules may be established during the auction, requiring bidders to provide counterparts if they win. These counterparts may include investments in infrastructure, coverage, availability, and others factors, all aimed at ensuring a desirable outcome and promoting transparency.

Although generally beneficial, auctioneers must take action to address the shortcomings of each structure.

• Protective Competition: Larger market players may possess sufficient resources to outcompete smaller incumbents, potentially leading to a concentration of market share. Regulators must remain vigilant when designing auctions to ensure that monopolistic behaviors or non-competitive strategies are not employed by these players.
• Spectrum Fragmentation: Auctions may result in incumbents owning licenses to fragmented slices of spectrum across different frequency ranges. This fragmentation can complicate network implementation and hinder interoperability.
• Technological and Regulatory Uncertainties: The increasing complexity of available services and technologies makes it particularly challenging to anticipate the needs and obligations of incumbents. Regulators must balance the need for flexibility with the assurance of stability with respect to spectrum rights.

Spectrum auctions are a critical tool for managing a limited and valuable resource. Grounded in game theory and economics, as discussed in works such as [4,5]), auctions can facilitate efficient allocation, generate substantial revenue, and ensure that the advantages of spectrum services are fully realized. This paper evaluates and compares the effectiveness of primary auction structures, analyzing both their theoretical efficiency and their actual revenue outcomes according to country and format.

Section 2 of this document introduces the historical aspects of auctioning and focuses on the structural weaknesses that prompted advancements in new auction formats.

Section 3 provides a theoretical overview of the primary auction formats employed in spectrum auctions, along with the potential challenges that may arise and the most effective solutions currently available.

Section 4 compares three major auction structures in terms of allocation efficiency and provides empirical comparisons of auction performance over the past 24 years. It also examines revenue, efficiency of allocation, and the various types and options implemented by different countries and regulators in North and South America.

Section 5 discusses the conclusions drawn by the authors.

2. Auction Types Overview

Auctions have served as a mechanism for pricing goods and services for over two thousand years. Herodotus documents the existence of auctions in ancient Babylon about 500 BCE as noted in [6]. Perhaps the most renowned auction in history took place in BCE [7], during which the entire Roman Empire was sold. Over the years, various new auction formats have been proposed to enhance procedural efficiency in the buying and selling of items, as well as their allocation.

Amongst the most recognizable formats, the English auction is arguably the most intuitive, making it an ideal first case for evaluation. In this auction structure, bidders continuously increase their offers for the item until only one buyer remains. This process achieves what economists refer to as market efficiency, an optimal state in which the final price reflects the maximum value the buyer is willing to pay for the item. Consequently, the good is assigned to the individual who values it the most [8]. This approach is particularly effective for the goods that are rare or lack a defined market price, such as works of art, antiques, and historical artifacts.

Another common type of auction is the Dutch auction, which prioritizes speed of resolution over maximizing revenue. Also known as the Tulip Auction, this method gained notoriety due to its annual occurrence in the Netherlands. In this process, the seller announces an initial price for their harvest, and if no bids are made, the price is gradually lowered in successive rounds until a buyer expresses interest. This participant then agrees to purchase a specified quantity of tulips at the final price established in the last round of the auction. This auction format is particularly effective for perishable items that require prompt sale, such as fish, cheese, and flowers.

The versatility of the auctioning processes allows their application in a myriad of cases, adapting itself to each specific situation. While English and Dutch auctions are often associated with the sale of luxury items or perishable goods, other formats have been developed to achieve particular objectives, as highlighted by [9]. Each format presents unique challenges that must be addressed according to the auctioneer’s needs.

Should a governing body decide to sell a state-owned company or construct athletic arenas for an international event, there may be necessary to achieve certain standards and elevate their significance beyond merely the price paid. This is exemplified in beauty contest auctions, where a committee evaluates each proposal and selects the one that is most impressive, drawing a clear analogy to that type of contest. In theory, the deciding panel aims to maximize societal utility rather than simply minimizing costs or maximizing revenue.

These examples provide a brief introduction to scenarios in which the proponent has varying goals and interests. Due to the diverse objectives that each agent may possess, several auction formats have been proposed to address these differences while striving to maximize allocation efficiency.

In recent decades, the rapid advancement of telecommunications technologies and the exploration of radio and Internet bandwidth have led to a resurgence of auctions in Economic Theory. Cramton (1998) According to [10], spectrum auctions can generate significant revenue for their respective countries.

Spectrum auctions involve the transfer of rights to explore a specific band of the electromagnetic spectrum within a designated area. Licenses can vary significantly because the spectrum utilized by telecommunication systems exhibits distinct characteristics based on the frequency range. Although lower-frequency waves can travel greater distances, higher-frequency waves enable faster data transfer but have reduced penetrating power and coverage. In addition, deploying two or more signals on the same frequency can lead to data loss and interference with existing equipment. Consequently, a mechanism that allows the seller to transfer exploration rights exclusively to a single entity is needed while still recognizing the potential synergies among the auctioned licenses.

However, the previously cited structures do not account for such synergies. How can a system extract the intrinsic value of a bundle of goods from buyers? How can one capture the synergy between related items while still allowing each to be bid upon individually? Milgrom [11] proposes the Simultaneous Multiple-Round Auction (SMRA) format, which won the Nobel Prize in 2020 and has become the standard for spectrum auctions in the United States since the mid-1990s. Since 2014, countries such as India, Canada, and the United States have also explored a new auction format following SMRA: the Combinatorial Clock Auction (CCA) to auction 5G licenses (for more information, the reader may consult the notice [12] from June 2022, accessed on 20 April 2024).

Brazil has yet to conduct an auction in either format. To date, spectrum auctions in Brazil have utilized the Sealed Bid Auction, a single-round adaptation of the Dutch system in which the highest bidder prevails.

3. Spectrum Auction Structures

The most commonly used auction formats exhibit strengths and weaknesses, which stem from their underlying structure. In this section, we provide a concise overview of the primary auction formats proposed, along with the key issues encountered in auction design.

The definition of the auction process must be clearly established before it can be discussed. According to [13], auctions can be defined by their primary characteristic: the promotion of Walrasian equilibrium, which refers to the balance between supply and demand. The authors further illustrate that the auction process is particularly effective when applied to the buying and selling of items for which there is no well-defined market, such as privatizations, spectrum licenses, and works of art.

During each auction, players are presumed to be selfish and greedy, meaning they are uninterested in the outcomes of bids made by other participants. Each player prefers to win rather than lose. In addition, players are assumed to be straightforward bidders.

Each participant strives to maximize their utility function, which can be expressed through a variety of inputs, including revenue, costs, accessibility, the pairing of auctioned items, market fragmentation, and any other factors that the player (including the auctioneer) may consider valuable.

However, without loss of generality, the efficiency of each auction structure can be assessed by analyzing the prices paid or the bids submitted by each participant, considering all benefits and costs consolidated into a single variable that represents the agent’s payoff (${\pi }_i$). This method has the added advantage of simplifying analysis by reducing it to a single observable variable.

Throughout this section, we review the English auction, Dutch auction and its variants, beauty contest, Vickrey auction, Simultaneous Multiple-Round Auction, and Combinatorial Clock Auction models.

As most structures exhibit similar weaknesses, they are categorized following the presentation of several auctions to enhance readability. The explanations assume either SMRA or CCA structures. As the previous models develop, the applicable solutions are also relevant for earlier structures.

3.1. English Auction

The English auction is the most recognizable format. Intuitively, one thinks of this type of auction as a scenario in which participants compete to purchase a generic item through bidding. Ultimately, the item is awarded to the individual who places the highest bid.

This auction format may or may not include a reserve price, which is the minimum bid value required to initiate the bidding process. The starting price can be set at either $p^0$ = 0 or $p^0$ = X, the representative price in round zero. Participants who wish to continue competing for the auctioned item must increase their bids to surpass those of their opponents.

Let $S_i$ be the action space for each player, and let the Cartesian product of these spaces be denoted by $\mathbb{S}=S_1,\times \cdots \times S_n$.

An element of $S_i$, representing the player’s i bid is denoted by $b_i=[0,\infty ]\in {\mathbb{R}}_{+}$. This represents the player’s action to increase their standing bid such that $b_i^{n+1}=p^n+ϵ$, ($ϵ\in {\mathbb{R}}_{+}$). Should a player decide to abandon the auction, $b_i^n=0$. The Cartesian product of the possible actions (bidding or quitting) is referred to as the strategy space.

Assume $V_1$ is the maximum valuation among all players $(V_1,\dots ,V_j,\dots V_n)$, representing each player’s willingness to pay for the item. The auction continues until $p^n$ > $V_j$. At this point, player J quits the auction. The auction concludes when only one player remains willing to bid. The winning player is denoted by $\widehat{i}$, and the final price is given by $p^{*}$ = $p_{\widehat{i}}$.

The utility function of each player ($U_i$) is defined as the intrinsic value assigned to the object by the player, minus the price paid.

$$U_i=\left\{\begin{array}{cc}{V}_i-p_i,\hfill & \mathrm{if} i=\widehat{i}\hfill \\ 0,\hfill & \mathrm{if} i\ne \widehat{i}\hfill \end{array}\right.$$

(1)

It follows that the payment equals zero for all players, except $\widehat{i}$, which is declared the winner.

3.2. Dutch Auction

The Dutch auction is characterized by distinct rounds and a descending price trend.

Especially practical for perishable items, the initial phase of this structure is characterized with a high reserve price denoted as $p^0=Y$. Participants must decide whether to bid or abstain from the round. If all participants choose to abstain, a new round begins with a reduced price, $p^1<p^0$, until the first player expresses interest in acquiring the auctioned item at the price $p^{*}$, which is announced at the beginning of the nth round.

Descending price auctions can vary in their approach to defining rounds. One, popular in Japan, is the Clock Auction. In this format, rounds progress after a predetermined amount of time, eliminating the need for the auctioneer to announce each round and wait for its conclusion.

Another variant that is popular in spectrum auctions worldwide, including Brazil (2021) and Argentina (2014), is the Sealed Bid variant. This method follows the same logic as the Dutch auction, where each participant submits a sealed bid indicating the price $p^{*}$ they would have announced in a traditional Dutch auction. Once all bids are submitted, they are revealed, and the highest bidder is awarded the contract.

The primary objective of this auction format is to place players in a vulnerable position, as sealed bids prevent them from understanding their opponents’ behavior or pricing ranges. This compels each player to bid $p_i=V_i$. Strategically, this format is equivalent to the English auction.

As highlighted by [13], two auctions with the same players and the same strategic space are said to be strategically equivalent if the expected payoff of each player is identical in both cases.

This is indeed the case with the Sealed Bid auction, where each player’s utility equals ($V_{\widehat{i}}$ − $p_{\widehat{i}}$) for the winner and $U_{i\ne \widehat{i}}=0$ for all others.

The structure reversal allows the auction to close in a single round while transferring the decision process to the players themselves. However, assuming rationality by each player, the bids may be compressed given their expectations of other players’ behavior, resulting in inefficiencies. Each player i can try to evaluate their opponents $V_j$ and try to win the dispute bidding $b_{\widehat{i}}$ = ${\mathbb{E}}_i\left[V_j\right]+ϵ$, $ϵ\in {\mathbb{R}}_{+}$.

This phenomenon occurs due to each player’s incentive to maximize their payoff, that is, attempting to win the auction while expending as little as possible. The difference between the actual price paid and the second-highest bid is known as the “winner’s curse”.

Suppose an auction for a pen where player 1 bids USD 10 while player 2 bids USD 7. The item is awarded to the former, who honors its bid of USD 10. The difference $10-7=3$ equals the curse of the winner incurred by player 1.

3.3. Vickrey Auction or Second Price Auction

Vickrey [8] proposed an auction structure designed to eliminate the winner’s curse as well as underbidding, winning the 1996’s Nobel Prize in Economics.

In general terms, the Vickrey auction can be described as follows. Let the set of players be defined as I = 1, ..., n. The action space is defined within ${\mathbb{R}}_{+}$, that is, bids are strictly nonnegative and there is no upper limit to the possible bid amount. Therefore, the possible bids are given by the Cartesian product $\mathbb{S}$ = {$S_1,\times \cdots \times S_n$}.

Each player’s bid is mapped through $b_i$. The two highest bids are considered when defining the winner and the final price of the auction.

$$b^{\max }=max\{b_1,\dots ,b_n\} \mathrm{and} b^{2\mathrm{nd}}=max\left\{\{b_1,\dots ,b_n\}\setminus \left\{b^{\max }\right\}\right\},$$

(2)

where $b^{max}$ is the maximum among all bid values and $b^{2nd}$ the maximum of the remaining set, excluding $b^{max}$.

In a Vickrey auction, the bids are sealed and unknowable to other parties. The highest bidder is awarded the prize. However, the price is equal to the second highest bid received.

As expounded by [4], supposing the absence of moral risks, collusion, and certain axioms characterizing the preferences of the players, it is possible to represent each player’s preferences $i\in I$ by the following utility function:

$$U_i=\left\{\begin{array}{cc}{V}_i-p^{*},\hfill & \mathrm{if} i=\widehat{i},\hfill \\ 0,\hfill & \mathrm{if} i\ne \widehat{i}.\hfill \end{array}\right.$$

(3)

The utility function allows us to map each player’s payoff:

$$\pi (b_1,\dots ,b_n)=\left\{\begin{array}{cc}{V}_i-b^{2nd},\hfill & \mathrm{if} i=\widehat{i}(b_1,\dots ,b_n),\hfill \\ 0,\hfill & \mathrm{if} i\ne \widehat{i}(b_1,\dots ,b_n).\hfill \end{array}\right.$$

(4)

This specific game structure leads to the conclusion that, in every scenario, each player’s optimal strategy is to bid their true valuation of the item. In other words, each player i has an incentive to bid $b_i=V_i$. This format ensures efficiency and mitigates the curse of the winner.

It may seem counterintuitive to consider the concept of the second price. However, in both continuous- and multiple-round English auctions, where infinitesimally small bid increments are possible, participants will continue to raise their bids by such amounts until the auction concludes. This occurs precisely when the losing bidder withdraws, which corresponds to the exact amount of the second price. Since English and Dutch auctions are strategically equivalent, a Vickrey auction is equally efficient in terms of allocation for all parties involved.

The second-price mechanism was extensively utilized in the early 2000s due to rapid technological advancements and widespread Internet access.

The website eBay successfully negotiated bids of up to USD 200 million monthly, according to [14]. The users were asked to enter the maximum value they were willing to pay for an asset ($V_i$), which remained confidential to all other participants. The website used an algorithm to discreetly place bids, in small increments, up to the maximum bid amount ($b_i=V_i$). The process involved comparing all the values submitted $V_i$, selecting the two highest offers. The highest bid received the award, while the second highest bid determined the final price paid.

The work by Bonanno (2018) illustrates the second-price auction mechanism through a mock oil reserve auction. In this example, bids are made in increments of ten million dollars, and a tie-breaking rule favors Player 2 ($P_2$).

Table 1. Vickrey Auction.

		Player 2
	Bid	$10	$20	$30	$40	$50
Player 1	$10	0	0	0	0	0
	$20	20	0	0	0	0
	$30	20	10	0	0	0
	$40	20	10	0	0	0
	$50	20	10	0	−10	0

Adapted from [4].

presents the payoffs (${\pi }_i$) received by each player. The value of the oil license is USD 30 million.

The first line in the table shows that, in all cases, a bid of USD 10 by $P_1$ is insufficient to win, regardless of $b_2$. In all other cases, should $b_2$ = 10, $P_1$ wins the dispute, while its payoff is calculated as ${\pi }_1$ = $V_1$ − $b_2$. The payoff for Player 1 would result in ${\pi }_1$ = 30 − 10 = 20, regardless of $p_1$. Even if $P_1$ offered USD 50, at the second price $b_2=10$, the second price mechanism would drive the payouts back to 20. However, bidding $p_1=50$ opens Player 1 up to a negative reward, which means that it is not the profit-maximizing strategy.

An analysis of the payoff matrix, through two theorems, concludes that the optimal strategy for each player is to bid precisely $b_i=V_i$, that is, to bid honestly.

3.4. Beauty Contest

In an auction process, maximizing revenue or minimizing costs may not be the most important aspect for the auctioneer. The acquisition of goods and services by the government (from war assets to building hospitals) is commonly approached by a beauty contest auction. Theoretically, the winning project would be the one that better serves the auctioneer’s needs, with the price relevant, albeit secondary.

Suppose a purchase auction for pens where two firms dispute the contract. The products are homogeneous, aside from their duration. Firm 1 offers its product at $p_1$, which is capable of writing for 1 Km. On the other hand, Firm 2 charges $p_2$, while the product lasts for 5 Km. Assume $p_1<p_2<2p_1$.

A cost–benefit analysis immediately shows that Firm 2’s product is a better option. However, in a standard auction, Firm 1 would always be the winner, should price/revenue alone be observed.

The precept of the beauty contest auction is that the auctioneer clearly defines the requested characteristics, weighs each one, and communicates with all parties involved prior to the dispute. Each competitor presents their product, price, and distinctions to be valued and judged by a committee that awards the best offer as the winner.

However, this structure is highly susceptible to information asymmetry between the participants and the auctioneer. The committee may not fully understand the process structure of each firm and product, which creates opportunities for firms to mislead the ruling board. Even if the committee has comprehensive technical knowledge, it may not be beneficial to elaborate on every detail, leading to an excessively stringent procedure.

The subjective nature of committee decisions, combined with information asymmetry, inevitably raises questions about the integrity of the decision-making board.

A report by the OECD indicates that in Spain, as a result of the 3G spectrum allocation, the unsuccessful firm France Telecom challenged the outcome through the judicial system.

In Austria, concerns about the potential for collusion led the regulatory body to distance itself from beauty contests. Investigations were warranted in the Netherlands and Italy due to suspected collusive behavior. In addition, the firms were found to have formed alliances to manipulate the process.

In the observed database, only Chile has held a beauty contest auction in South America or North America in the last 24 years.

3.5. Simultaneous Multiple-Round Auction

First applied in 1994, the Simultaneous Multiple-Round Auction originated from the need for a structured format that would enable the FCC to maximize revenue from the allocation of spectrum band rights (according to [15]).

The primary objective of the auction is to enable players to submit bids for both individual items and combinations of items. After each round, the winning bid is updated, and disclosed to the players, facilitating information sharing and strategic adjustments for all participants. New rounds continue until no additional bids are placed for any individual or combined bids.

This structure aims to achieve market equilibrium (Walrasian tâtonnement, a theoretical auction equilibrium achieved through price fluctuations, using trial and error, until supply and demand are satisfied; although auction prices cannot practically fluctuate downward, a sufficiently small increment would suffice to approach optimal prices), while the primary challenge is mitigating the negative impact of player exposure. This exposure, in turn, reduces bids due to the uncertainty of acquiring all desired items simultaneously.

In the seminal article by Milgrom [11], the author elaborates on the concepts of equilibrium, demonstrating both its existence and convergence in a scenario where licenses are mutually substitutable.

However, spectrum licenses are often heterogeneous and frequently exhibit complementarities. Acquiring a 5G license may be more advantageous for a company that already has the rights to a 4G band. How do we address situations where the combined value of licenses surpasses the individual worth of each license? How can we safeguard the participant who values this combination? This challenge, known as exposure, is prevalent in all auction formats.

3.5.1. Exposure

In the SMRA format, equilibrium is both present and stable (for more information, please refer to the seminal article [11]), under the assumption of mutually substitutive licenses and straightforward bidding. However, if even a single player prefers to combine items, this can disrupt the equilibrium.

Table 2. Exposure.

		Licenses
Player	A	B	AB
1	a	b	a + b + c
2	a + d	b + d	a + b + d

Adapted from [11].

presents a simplified version of this problem.

Let the valuation of $P_1$ for licenses A and B be a and b, respectively. However, the combination AB is valued at $V_1$ = $a+b+c$. In contrast, $P_2$ values each license at $a+d$ and $b+d$, regardless of whether you obtain both licenses or just one. Let ${\displaystyle \frac{c}{2}}$ < d < c.

The auctioneer would prefer to assign both licenses to $P_1$ at prices $a+b+c$, as this allocation achieves the highest efficiency in terms of both distribution and revenue. However, without any guarantee of securing both licenses, $P_1$ is unwilling to bid higher than a for the first item, as doing so would expose him to risk. To outbid $P_2$, the first player must bid $p_a\ge a+d$ and $p_b\ge b+d$. However, at those prices, $P_1$ would prefer to abstain entirely from the auction. Consequently, there is no equilibrium in this structure. The outcome is consistently that $P_2$ wins both licenses separately at prices $a+ϵ$ and $b+ϵ$, (with $ϵ$ representing the smallest possible increment), resulting in inefficiencies.

Although the previous example illustrates that there is a breakdown in equilibrium due to combinatorial preferences, this phenomenon also occurs with items sold individually.

Table 3. The case for an Activity Rule.

	Licenses		Budget
Player	A	B
1	15	30	20
2	10	-	20
3	-	0.9% = 15 0.1% = 5	20

Adapted from [11].

illustrates a scenario in which the fear of exposure causes an auction to stall, as each player’s optimal strategy is to wait for another player to make a move.

Let the players be restricted in their actions as follows: $P_1$ is eligible to bid on both licenses, while $V_{1A}=15$ and $V_{1B}=30$. Player 2 is restricted to license A, and $V_{2A}=10$. Finally, $P_3$ is allowed to bid solely on license B, with varying valuation probabilities. It is assumed that the bidding increments are uniform.

Each player has an incentive to wait for the other players to bid before determining their own actions. Consider $P_2$ as our case study: In a scenario where $J_3$ reveals a preference with a $b_{3B}>$ USD 5, all players immediately recognize that $V_{3B}=15$. Since $V_{1B}>V_{1A}$, it is common knowledge that $b_{1B}=16$. All players’ budgets are standardized at USD 20; therefore, $P_1$ no longer has sufficient budget to outbid $P_2$ for license A, resulting in $b_{2A}=$ USD 5 being adequate to secure the win. Player 2’s payoff is then ${\pi }_2=10-5=5$. Consequently, $P_2$’s optimal strategy is to consistently wait for the other players to bid, to maximize their payoff. This strategy applies equally to all other players.

This example serves as a foundation to illustrate the necessity of an activity rule. By implementing a rule that requires each player to announce their bids each round while increasing the prices, this vulnerability can be effectively mitigated.

Let the minimum bid for a given round be $M{B}^{n+1}=H{B}^n+ϵ(p\vee \widehat{p})$, where $H{B}^n$ represents the highest bid submitted in round n. The second term represents the increase in the price vector, as previously defined by the established rule.

The wait-out game generally lacks equilibrium; however, the introduction of such a rule would force $P_3$ to disclose their preferences, as they have the lowest $V_i$ among all players. Once the threshold for $V_3$ is surpassed, every player will know precisely what to bid in order to obtain their licenses.

Empirical studies, as reported by [11] reveal that even with such a rule in place, players prefer to wait as long as possible to avoid exposure. In an American auction, 3.333 data points were observed, with only 30 (less than 1%) exceeding the minimum required by the activity rule.

3.5.2. Free-Riding

Another issue that may arise in a combinatorial auction is known as free-riding. Allowing combinatorial bids in addition to strictly individual submissions can introduce inefficiencies into the system. If a dispute occurs among more than two players, free-riding may become a significant factor.

Expanding the game structure to allow for combinatorial bids, the game presented in

Table 4. Free-riding.

	Licenses
Player	A	B	AB	Budget
1	4	-	-	3
2	-	4	-	3
3	1 + $ϵ$	$1+ϵ$	$2+ϵ$	2

Adapted from [11].

could proceed as follows: $P_1$ is interested solely in License A, valuing it at USD 4. Player 2 has a symmetrical interest regarding License B. Player 3 is interested in both licenses, with $V_{3A}=V_{3B}$ = $1+ϵ$ and $V_{3AB}$ = $2+ϵ$. Each player is constrained by their budget.

It is clear that the optimal allocation for the auctioneer is to assign licenses A and B to $P_1$ and $P_2$, respectively, with $p_A=p_B=3$. However, each player has an incentive to wait for the subgame between $P_3$ and the other party.

If $P_1$ waits for $b_{2B}=3$ to occur, such a bid would eliminate $P_3$, as the combination AB would no longer be available. Consequently, Player 1 could acquire A for USD 2, increasing ${\pi }_1$. Player 2’s behavior is symmetrical. Solving this game through backward induction reveals that the optimal strategy for both Players 1 and 2 is to adopt a mixed strategy, where the bids are made with a probability ${\displaystyle \frac{2}{3}}$ of bidding and ${\displaystyle \frac{1}{3}}$ of bidding low.

The problem arises when both players adopt the “bid low” strategy. In $({\displaystyle \frac{1}{3}}\times {\displaystyle \frac{1}{3}})={\displaystyle \frac{1}{9}}$ of scenarios, both players choose to bid low in hopes that the other player will remove $P_3$ and will win the auction. If this situation occurs, it will lead $P_3$ winning the auction with $b_{3AB}=2+ϵ$, resulting in an inefficient allocation for all parties involved.

As the free-riding problem is fundamentally a probabilistic error, it can be advantageous for the auctioneer to increase the number of participants in any given auction. One effective method, commonly observed in recent auctions such as FCC-101 and several others, is to implement special rules, such as offering bidding credits for new incumbents. This approach inflates the number of participants, thereby reducing the likelihood that free-riding will have a significant impact.

One solution to completely eliminate the possibility of free-riding is to simultaneously close bidding for all licenses. However, this approach introduces a new problem.

3.5.3. Collusion

In an auction with simultaneous closing of all licenses, players can collude among themselves to skew prices downward.

The simplified structure presented in

Table 5. Collusion.

	Licenses
Player	A	B	Budget
1	10	10	20
2	10	10	20

Adapted from [11].

illustrates the collusion problem. In this example, each player is limited by a budget of USD 20, with symmetrical valuations per license set at $V_i=10$. A tie-breaking rule is in effect, and we employ the simplest method: a coin toss determines which player is awarded item A, while the other item is assigned to the remaining participant. Bids are made in discrete increments of one for the sake of simplicity.

It can be intuitively assumed that equilibrium occurs when both players bid USD 10 on each item, the coin toss takes place, and the game concludes with the payoff for each player being ${\pi }_i=V_i-10=0$. In fact, this is just one of many possible equilibria. Assuming rationality for both players, each player understands that raising their bids would lead to the aforementioned outcome. Consequently, participants can anticipate this and agree to bid USD 1 each. The established rules would require coin tossing, resulting in ${\pi }_1={\pi }_2=V_i-1=9$. Both players, being rational, would have incentives to cooperate in order to maximize their profits.

Individually closing license bids helps prevent collusion through a principle known as the trembling hand. Assume that both players agree to bid USD 1 for License A. A coin toss determines that Player 1 ($P_1$) is the winner, leaving them with a remaining budget of USD 19. When license B is auctioned, $P_1$ has an incentive to breach the agreement by bidding higher for license B, which is valued at USD 10. Player 2 anticipates this behavior and therefore would bid higher on License A from the outset. According to this principle, the price of each license would be at least USD 9 (one increment below $V_i$) due to the implicit threat that each player faces if they attempt to cooperate.

3.6. Generalized Vickrey Auction—Gloves–Clarke Auction

As previously discussed, the second-price auction is considered the most effective format for auctioning individual items. In practice, however, goods often exhibit certain complementarities. This characteristic has prompted some authors to extend the Vickrey auction into a generalized form, which allows for greater flexibility while preserving the core features of second-price auctions, such as preventing collusion and exposure, and ensuring the bidding process remains truthful.

The results of the Gloves–Clarke auction from these attempts successfully achieved most of the proposed goals. However, if several synergistic items are sold simultaneously, the computational burden required to analyze each possibility and combination of revenue becomes prohibitively high. Consequently, this format is beyond the scope of this article; however, it remains tangentially relevant due to its efficiency in resource allocation, serving as a theoretical benchmark against which all other combinatorial auctions can be compared [11,16,17].

In a Generalized Vickrey Auction (GVA), the auctioneer must evaluate all possible combinations. Let L represent a set of licenses and P the set of allocations; thus, P is an indexed subset of L. For any allocation $S\subset P$, the element $S_i$ signifies the set allocated to player i. The rules of a GVA stipulate that each player submits a bid for a nonempty set that is a partition of L. The auctioneer then needs to analyze and compare all submitted bids, ultimately selecting an allocation $S^{*}$ that maximizes efficiency.

In a scenario with L licenses, the total number of possible combinations is $2^L-1$. In the Netherlands, an auction featuring 18 licenses generated over 260,000 combinatorial options to be evaluated. Auctions such as Auction 101, conducted by the FCC in 2019, began with 3072 licenses, while Auction 102, held in the same year, offered 2909 distinct licenses for sale.

Milgrom [11] proposed a mechanism known as Adaptive User Selection Mechanism (AUSM) to help alleviate the computational demands of GVAs when implemented in the SMRA format.

By enabling users to enhance other players’ bids and consolidate them into a single offer, this mechanism expedites the selection process by streamlining the algorithm utilized by the auctioneer.

Table 6. AUSM.

	Licenses
Player	A	B	CD	ABCD
1	-	$ϵ$1	-	20
2	12	$ϵ$2	-	-
3	-	$ϵ$3	10	-

Adapted from [11].

illustrates a scenario in which four licenses are auctioned. The reader may note that, even with such small numbers, the number of combinations that the auctioneer would need to map would be 15, were it not for the AUSM.

Player 1 is interested in the ABCD combination and is not interested in single licenses. Player 2 values A at USD 12, while Player 3 desires CD, valuing it at USD 10. All players have a minimal interest in B but would still prefer to have it rather than not.

In round 1 of this auction, players submit bids as previously described. Player 2, however, notices $P_3$’s bid of USD 10 and realizes that this bid could be elevated to a new combined offer of $b_{\{2,3\}\left\{ACD\right\}}=12+10=22$ since the interests of both $P_2$ and $P_3$ show no conflict. Upon receiving this offer, the auctioneer would then calculate USD 22 − USD 20 = USD 2. Since the combined offer exceeds $b_{\left\{1\right\}\left\{ABCD\right\}}$, the licenses would be redistributed to $P_2$ and $P_3$, while B would be freed.

Some additional rules need to be established to ensure the continuity of the process; however, these are relatively benign in comparison. For a more detailed explanation, the reader can refer to [11].

3.7. Combinatorial Clock Auction

The Simultaneous Multiple-Round Auction was rapidly adopted worldwide, demonstrating significant improvements over its predecessors. However, over time, it became apparent that the auction format lacked a mechanism for players to understand each other’s preferences and valuations. This deficiency led to protracted disputes, as each player attempted to “feel” the others’ preferences by analyzing their previous bids, which were often minimal increments due to concerns about exposure.

This mechanism, known as price discovery, became the primary focus of the next significant advancement in auction theory: the Combinatorial Clock Auction (CCA).

The CCA structure consists of three distinct steps: the first two involve bidding and acceptance, while the third step focuses on the effective allocation of goods to the winners.

The first stage involves the clock mechanism. In each round, the auctioneer announces a price for the goods being auctioned, and players submit the quantities they are willing to purchase at that price. If demand exceeds supply, a new round begins with $p^2>p^1$. Players continue to submit their desired quantities until $p^{*}$ is reached, where supply equals demand. This stage is designed to assist competitors in discovering their peers’ pricing with minimal compromise.

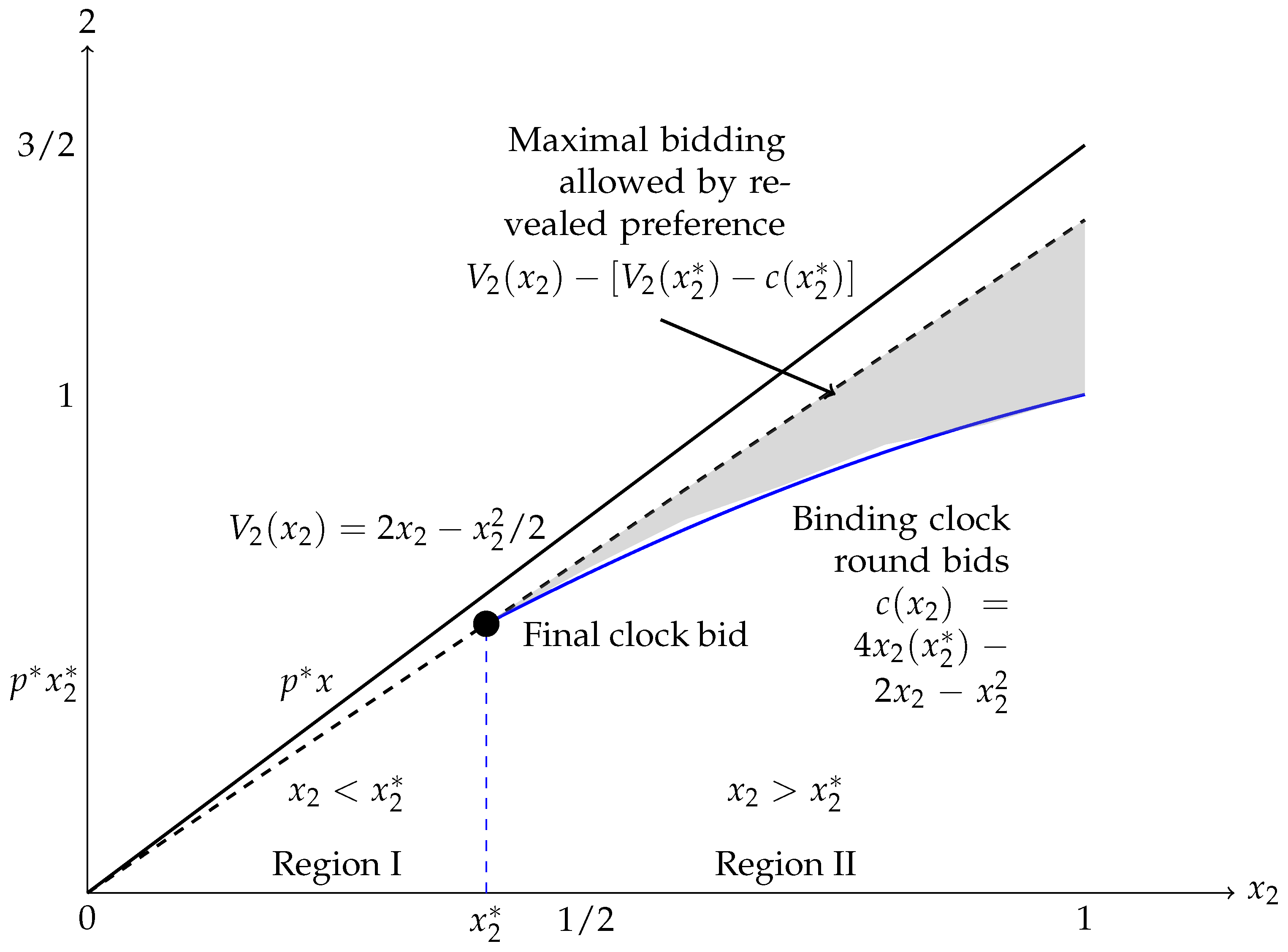
The second stage, as described by [18], consists of sealed offers for the goods. The players can bid for higher values or quantities than those stated in the first stage. The only restriction is that players must adhere to the Generalized Axiom of Revealed Preferences; that is, no player can offer less than what was revealed in the first stage of the auction, while also being bound by an upper limit, as illustrated in Figure 1.

Bids revealed in the first stage of the auction are still regarded as active bids, while bids in the second stage are complementary and also considered active.

According to [19], there are instances in which players can engage in detrimental actions by increasing prices or quantities, indicating that further investigation is necessary to address these behaviors.

The auctioneer assesses all submitted bids from each round, in both stages, determining which resource allocation is most advantageous for all parties, while considering player eligibility.

All bids are treated as all-or-nothing; that is, there is no possibility of arbitrary division within bid blocks. The price paid by each player is determined through the analysis of counterfactual scenarios to derive the Vickrey price. This mechanism encourages players to disclose their $V_i$, bidding honestly, similar to a standard second-price auction.

The third and final stage of the CCA is known as the assignment phase. This stage is introduced to streamline the viable strategies identified in the first and second stages. The central idea is to consider goods as homogeneous whenever possible. For instance, the block 710–715 MHz is equivalent to the block 720–725 MHz.

In a European auction [20], participants had the opportunity to bid on six homogeneous licenses within the 800 MHz spectrum block. During the first two phases, the items were considered identical, with their characteristics disclosed only in the third phase to speed up the process.

Figure 2 was adapted from a presentation to the FCC by Lawerence M. Ausubel and Oleg B. Baranov in February 2013. It illustrates the Combinatorial Clock Auction. Notably, the first CCA occurred the following year.

4. Theoretical Efficiency Comparison Between Combinatorial Auction Formats and Empirical Data

In an article published in the Proceedings of the National Academy of Sciences, ref. [22] proposed a comparison of the SMRA structure (the primary format used by the FCC at that time), the round clock auction, and the Combinatorial Clock Auction.

The authors proposed a comparison using a hypothetical auction of ten items to be sold as individual licenses. Several scenarios were imposed on the experiment to limit potential strategies, such as whether the licenses had synergies or were valid. Participants were incentivized to take the mock auctions seriously through monetary rewards based on their performance.

Another observation was the magnitude of the effects, depending on whether the players possessed market power and the scenarios in which the effort required to displace the current winner was either higher or lower (gain). Figure 3 provides a comparison between CCA and SMRA.

Table 7. Allocative efficiency.

Case	Own	Gain	Auction Type	% Efficiency
1	0.81	Yes	CCA	100, 100, 100
			CRA	78, 79, 78
			SMRA	59
1	0.81	No	CCA	100, 100, 100
			CRA	97, 79
			SMRA	63
1	0.70	Yes	CCA	100, 100, 100, 100
			CRA	100, 100
			SMRA	70
2a	0.80	Yes	CCA	100, 100, 99, 100, 99, 100
			CRA	99, 99, 99, 95, 94, 95, 95
			SMRA	100, 99, 95, 95
2b	0.94	Yes	CCA	100, 100, 100
			CRA	91, 94, 94
			SMRA	100
2b	0.94	Yes	CCA	100, 100, 100
			CRA	95, 95
			SMRA	100
2b	0.80	Yes	CCA	100, 100, 100
			CRA	100, 91
			SMRA	100

Adapted from [22].

compares 55 different auctions conducted by the authors, distinguishing each analyzed scenario.

The authors concluded throughout the paper that the Combinatorial Clock Auction was superior to its peer in producing more efficient results, noting that it consistently achieved allocations close to 100%.

Since the spectrum is a limited resource, managing its allocation is essential. To this end, auctions have been widely adopted to promote efficiency. In many instances, revenue is not the primary determining factor; instead, considerations such as coverage, accessibility, infrastructure, and other aspects are important. In Economic Theory, each agent’s interests can be represented through a utility function which all agents strive to maximize. However, revenue serves as a measurable indicator to assess the success of the auction, allocative efficiency, and participant interest.

Two primary factors contribute to the value of a spectrum license: $\left(a\right)$ the band, measured in MHz, which is typically divided into blocks by regulatory authorities, and $\left(b\right)$ the population served by each license, as most cash flow projections rely on the expected revenue per user (ERPU). Consequently, a useful metric for comparing auction performance is the price/MHz/population (USD/MHz/pop). This metric aligns with analyses found in the international literature, such as [23].

Due to the heterogeneity of the observed auctions, we chose to consider the duration of each license in our study. To achieve this, we divided the USD/MHz/population by the length, in years, of the acquired exploitation rights. Data utilized consisted of auctions from North and South America between 2000 and 2024. These data are publicly accessible and generally available on each nation’s official website.

Figure 4 illustrates the adoption trends by auction type. The rise of the Simultaneous Multiple-Round Auction (SMRA) during the first decade of the millennium can be attributed to its structure, which allows participants to bid on combinations of licenses. This feature is a critical factor in spectrum auctions, as it provides improved security for acquiring paired licenses.

In 2014, the United States implemented its first CCA, which quickly became the dominant format in both the United States and Canada. It is also important to note that the CCA generally achieves higher allocative efficiency, as indicated by the revenue generated per auction type.

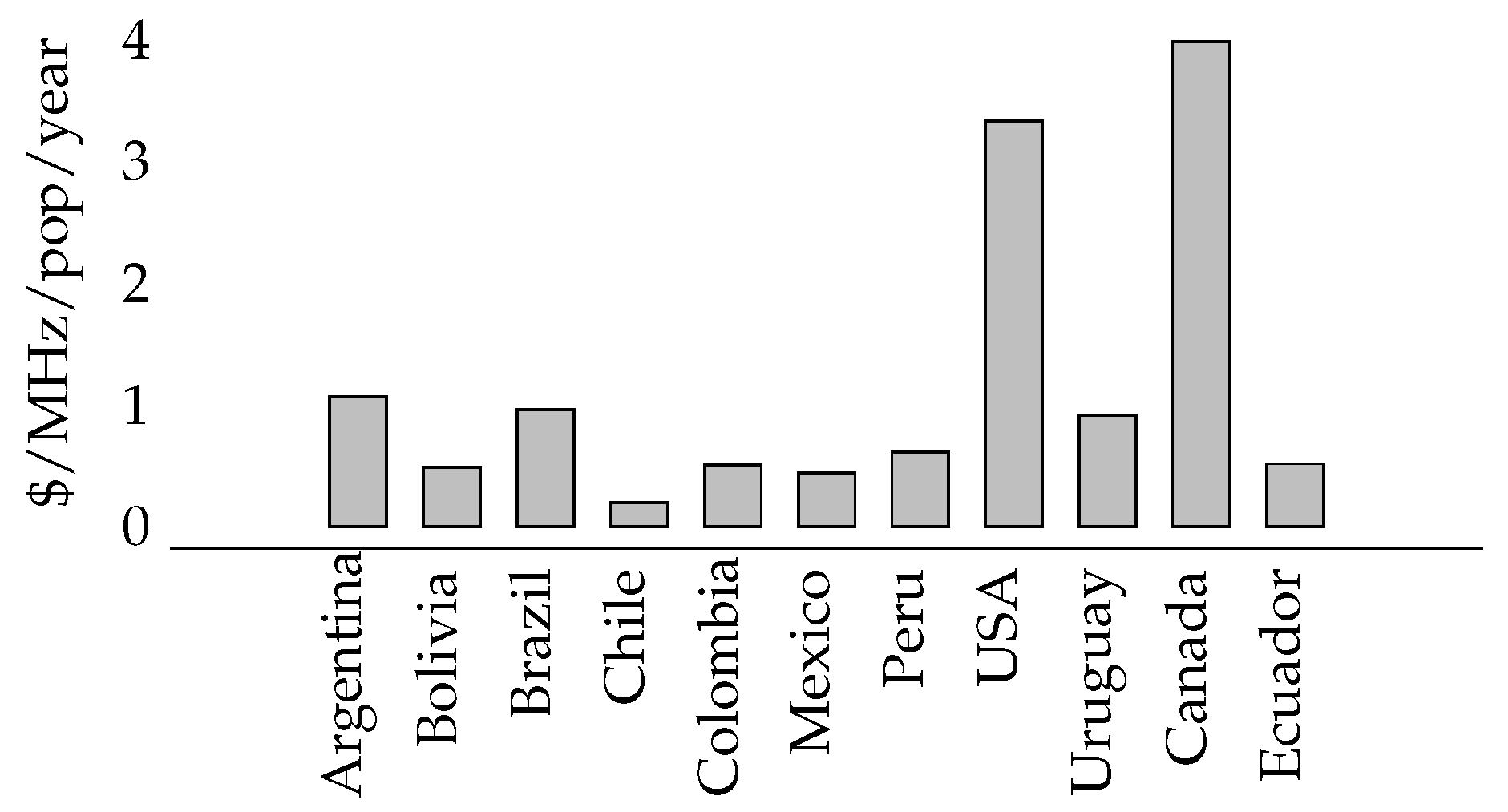
This phenomenon is visible when the revenue per auction is compared, evaluating USD/MHz/population/year as shown in Figure 5.

In 2021, Brazil auctioned national licenses in the 700 MHz, 3.5 GHz, and 26 GHz bands, using a sealed bid format. The Brazilian regulatory agency, Anatel, reported that the revenue generated was USD 5.285 million (values converted via USD/BRL rates of 5.6417, as the average yearly exchange rate). Revenue per band was USD 612 million for the 26 GHz band, with 1200 MHz of spectrum sold. The observed price/MHz/pop/year observed was USD 0.011. The 3.5 GHz band, which consists of 300 MHz of spectrum, generated USD 22,796 million in revenue. Thus, the price/MHz/pop/year was USD 6.2733. Finally, the remaining 20 MHz of the 700 MHz band was sold at USD 14.7406 cents/MHz/pop/year Figure 6.

The values set by the Brazilian authorities were comparable to those observed in the rest of Latin America but significantly lower than those achieved by the United States and Canada, which employed the CCA format for their auctions.

The revenue of each nation can be further analyzed by evaluating the auction format it is using. This is illustrated in Figure 7.

It is important to highlight Canada’s exceptional SMRA performance. This achievement is indicative of the 2008 auction, where 90 MHz of spectrum was sold for nearly USD 4 billion, resulting in USD 13.1071 cents/MHz/pop/year, much higher than any other observed auction. Further research is necessary to comprehend the intricacies involved in such an auction and its remarkable outcomes.

5. Performance in 6G-Specific Scenarios

The 6 GHz band is crucial for regulatory bodies and telecommunications organizations worldwide, serving both existing technologies and future 6G systems. Those networks will integrate frequency bands, including millimeter-wave and terahertz technologies, for enhanced data transmission and connectivity [24].

Regulatory frameworks for spectrum allocation consider factors such as spectrum scarcity and regional compatibility [3]. Managing the 6 GHz band requires balancing licensed and unlicensed spectra. Additionally, 6 GHz auctions must align internationally to prevent interference. The International Telecommunication Union works to harmonize spectrum allocations for the interoperability of the global 6G network [3].

Role of Spectrum Auctions in Allocating These Bands

Spectrum auctions can play a critical role in the allocation of 6G bands by facilitating an efficient and equitable distribution of this valuable resource, necessary to advance next-generation communications. As 6G networks are poised to operate across a broader range of frequencies, including higher frequency bands such as millimeter wave (mmWave), terahertz (THz) and potentially optical spectrum, the need for effective spectrum management becomes paramount [3].

The most successful cases of spectrum auctions used around the world are the SMRA and CCA models, but CCA has been dominant in fashion for its computability characteristics [25]. Although SMRA and CCA have been the state of the art in spectrum auctions in the last decades, advances in secure spectrum auction designs are critical in this area, which demands new approaches to these issues. As 6G capabilities are still an open space for research, development, and applications, the same can be said with respect to spectrum auction design for this technology.

Some possibilities are being developed, but there is no clearance of the full possibilities of 6G or of the most appropriate spectrum action models for this technology. As a brief exposition of the new possibilities in development, we discuss below some of the new and recent approaches concerning auction design focusing on possibilities for 6G technologies. This list is not exhaustive but shows the wide range of improvements that are in view for now.

The cases listed below are the first approaches to this problem. We will see these and possibly completely new models in development in the next few years.

• THEMIS, a secure spectrum auction mechanism, uses cryptographic techniques to address fraud and bid-rigging issues. By keeping bidding values confidential, while computing and revealing auction results, THEMIS ensures a fair and secure auction process, thus enhancing trust in spectrum auctions for 6G band allocation [26].
• Dynamic spectrum access (DSA) is another aspect closely related to spectrum auctions. In this approach, the spectrum bands are dynamically allocated to accommodate the varying demand, reducing underutilization. Auction theory underpins many DSA models, determining bidding strategies and revenue impacts for spectrum owners when multiple bidders compete for access. This dynamic allocation is anticipated to be particularly important for 6G, where wireless service providers may need to flexibly adjust their spectrum usage to meet changing demands [27].
• The Block6Tel scheme integrates the blockchain in the allocation process, facilitating a fairer and more efficient distribution of resources between telecom providers. This method operates in two phases: first, a protocol stack model based on cell-free communication infrastructure is proposed, and then a blockchain-based auction algorithm is executed. Smart contracts also ensure that the allocation process is transparent and trusted by all stakeholders, outperforming traditional static allocation methods in terms of resource utilization, overhead, and fairness [28].
• The ARMOR framework is designed to conduct combinatorial auctions for heterogeneous spectrums while safeguarding bidders’ sensitive information. This is achieved through advanced cryptographic techniques that protect location and valuation data. ARMOR’s objectives are to ensure high levels of customer satisfaction and social welfare while providing verifiable protection against fraudulent payment schemes [29]. Similarly, the PROST framework offers a double-auction mechanism that preserves privacy and improves the efficiency of spectrum allocation while protecting user privacy in online auction settings [30].
• The integration of artificial intelligence (AI) and machine learning (ML) in auction design for the 6G spectrum is essential to managing the expected surge in wireless communication demands. The incorporation of artificial intelligence (AI) in auction design aims primarily to optimize the spectrum allocation process, making it more dynamic and responsive to real-time network demands. Using AI algorithms, spectrum auctions can be designed to predict network usage patterns with more accuracy, ensuring a more effective distribution of this finite resource. AI and ML contribute significantly to creating more efficient 6G networks by enabling intelligent resource management. This integration allows for self-configuration and self-healing capabilities, vital for managing the complexities of 6G wireless networks [31]. In addition to resource optimization, the integration of AI and ML in auction design addresses security concerns associated with the usage of the 6G spectrum. The move towards intelligent network solutions includes robust security measures to protect against adversarial attacks that could compromise network integrity [32].

Spectrum auctions not only facilitate the allocation of spectrum bands necessary for 6G implementation but also ensure that this is done efficiently and securely. They support dynamic resource management by encouraging technological innovation and fair competition, aligning with the broad operational spectrum and the high demands expected for 6G networks.

6. Considerations on a Proposed Auction for Brazilian 6G

Using the review carried out so far and the relationships observed with regard to the practices implemented by the countries that have historically performed above average, we can start structuring a hypothetical auction aimed at the Brazilian telecommunications scenario, allowing its regulator to achieve a better result through competition and mitigation of auction risks.

This study examined a hypothetical auction structure in Brazil. The spectrum bands related to the 700 MHz spectrum are divided into regional licenses of 5 and 10 MHz, exclusively in pairs. We used homogeneous 5 MHz blocks as a mechanism to facilitate price discovery, diverging from the current structure, which consists of 5 and 10 MHz blocks, without loss of generality. Each block was worth one eligibility point. Players had to make deposits in advance with the auctioneer to guarantee the amount eligible for bidding, in accordance with the minimum price set for each block.

The selected structure for modeling was the Combinatorial Clock Auction, proposed by Cramton, carried out in three phases, namely clock, proxy, and assignment.

6.1. Clock Phase

We use the simplified game structure presented in

Table 8. Individual prices ($v_i$) and quantities demanded.

Player	A (USD)	D {A}	B (USD)	D {B}	C (USD)	D {C}	Budget (USD)
1	10	3	6	2	0	0	50
2	8	2	8	2	7	3	50
3	15	5	0	0	4	5	50

to illustrate the process. The quantities offered for each item are limited to four units, except for C, which can be divided into two pairs, namely, two blocks related to the 708–713 range and two blocks related to the 713–718 MHz range. This information is not revealed to the bidders during the clock phase; it is kept by the auctioneer. The bidders only know that C contains four blocks of 5 MHz each. The table illustrates the preferences of the players as follows: A (USD), B (USD), and C (USD) represent the maximum price each player is willing to pay (in monetary units) for each item i, and $D\left\{A\right\},D\left\{B\right\}$, and $D\left\{C\right\}$ represent the maximum amount demanded by each player for each item. Taking the first player as an example, $v_1\left\{A\right\}=10$ and $D_1\left\{A\right\}=3$, which means that Player 1 is willing to demand up to three units of item A, for all $p_A^n\le 10$. All players are subject to the same budget constraint of 50 monetary units.

In the first phase, the generic spectrum blocks are offered at a minimum price $p_i^0$ for each block i set by the auctioneer. Each block represents a license to exploit spectrum within a specific range. The players must decide whether to demand each block, together with the desired quantity, while honoring their bids in case the round results in market clearing. That is, $D_i^n=O_i$, where $D_i^n$ is the total demand in the nth round and $O_i$ is the quantity offered for each block i.

Table 9. First-round bids and budget constraints.

Player	P {A}	P {B}	P {C}	D {A}	D {B}	D {C}	Cost	Cost	Cost	Total
							{A}	{B}	{C}	Cost (USD)
1	3	3	3	3	2	0	9	6	0	15
2	3	3	3	2	2	3	6	6	9	21
3	3	3	3	5	0	5	15	0	15	30

illustrates a scenario in which $p_i^0=3\forall i$. Taking Player 1 as an example in the first row, we can observe that given $p_A^0\le v_1\left\{A\right\}$, the player will demand units for this item, subject to their budget constraint. The same player is interested in demanding up to three units, as represented by $D_1\left\{A\right\}$ in Table 8. The total amount spent on item A is represented in the column Cost {A}, and the sum of expenses for all items is subject to the player’s budget constraint. Thus, Player 1 forms the package ${\{3A,2B\}}_1=15$, which is considered valid as it does not violate their budget.

If the quantity demanded for a block $D_i^n$ exceeds the quantity offered $O_i$, a new round is opened, in which $p_i^1>p_i^0$, where $p_i^1$ is the price of block i in round 1, and this process continues until market clearing for all the blocks offered. The quantities demanded by the players must obey the Relaxed Generalized Axiom of Revealed Preferences (RRP), which means that the quantities must be consistent (the axiom and its mechanisms can be found in [10]) from round to round. An increase in the price of a particular block cannot imply an increase in its demand. For example, if Player 1 demanded x units at price $p_i^n$, they could not demand $x+1$ units at price $p_i^{n+1}>p_i^n$, as this would be contradictory; if they were interested in $x+1$ units, then it should already have been demanded in the previous round. This forces players to behave according to their real demands: if one wishes to be a whale at the end of the process, one must behave like so from the beginning.

The excess demand, in turn, is determined by the number of requested blocks minus the number of offered blocks. In the example of Table 9, excess demand for item {A} is 4 − 10 = −6, indicating excess supply for item {A}. Item {B} shows 4 − 4 = 0, indicating market clearing, while {C} shows a deficit of four units.

In case of excess demand or market clearing for a particular item, its price for the subsequent round is raised according to

Table 10. Table of price increment.

Excess Demand (in Number of Blocks)	Price Increment
<0	0%
0	1%
1	2%
2	3%
3	4%
≥4	5%

. If this increment results in $O_i>D_i$, we return to the previous round price where $O_i\le D_i$. If, for instance, there are three more blocks demanded than offered, then the minimum price for the subsequent round should be set following an a priori rule such as $p_i^{n+1}=1.04\left(p_i^n\right)$, for example. The iterative procedure continues until there is no additional excess demand.

Table 10 illustrates a suggested progression of price increases (the activity rule controls price increases after each-round when there is excess demand) that must be defined a priori by the auctioneer and made broadly known. For simplicity, we applied a different activity rule in each step of the example, as needed for conceptual demonstrations.

The subsequent round of the auction is represented in

Table 11. Forced clearing on market C due to unbalanced activity rule.

Player	P {A}	P {B}	P {C}	D {A}	D {B}	D {C}	Cost	Cost	Cost	Total
							{A}	{B}	{C}	Cost (USD)
1	6	6	6	3	2	0	18	12	0	30
2	6	6	6	2	2	3	12	12	18	42
3	6	6	6	5	0	0	30	0	0	30

. Here, the rule $p_i^{n+1}=2p_i^n$ is used for all items where $D_i^n\le O_i$. The minimum prices are raised from USD 3 to USD 6 for all items, as there is no excess supply in the initial round. This new activity rule shows a clear problem, as explained in Table 8. Player 3 is not willing to pay more than USD 4 for each unit of item {C}. Thus, there is a market imbalance: $O_C>D_C^n$ by one unit. As explained previously, the auctioneer must return to the last-round price where $D_i^n\le O_i$. In this example, the auctioneer is forced to set $P\left\{C\right\}=3$ for all subsequent rounds and consider the market to be “solved”. In other words, we observe that the critical point for item {C}—$v_3\left\{C\right\}=4$—is wasted due to the implementation of an inefficient activity rule.

Item {B}, meanwhile, is not affected by this new activity rule: Players 1 and 2 continue to demand two units each, as the auctioneer does not reveal provisional winners. Players know only that market {B} did not clear in the initial round. Thus, they continue to demand while $P\left\{B\right\}\le v_i\left\{B\right\}$ for all $i=\{1,2\}$.

It is possible for more than one price combination to be considered active at the end of the clock round. This example can be observed in

Table 12. Well-balanced activity rule leading to price discovery

Player	P {A}	P {B}	P {C}	D {A}	D {B}	D {C}	Cost	Cost	Cost	Total
							{A}	{B}	{C}	Cost (USD)
1	6.6	6.6	3	3	0	0	19.8	0	0	19.8
2	6.6	6.6	3	2	2	3	13.2	13.2	9	35.4
3	6.6	6.6	3	5	0	5	33	0	15	48

in the market for product {B}. In this round, we apply the activity rule again, adding 10% to the price of the previous round, except for market {C}, which is considered solved. The demand from Player 1 is altered at this point, as $v_1\left\{B\right\}<P\left\{B\right\}$, resulting in a demand $2=D_B^n<O_B$. Player 2, in turn, continues to demand units of this good. The auctioneer, as previously established, defines $P{\left\{B\right\}}^{n-1}$ according to the last clock round in which $D_B^n\le O_B$, that is, $P\left\{B\right\}=6$ as observed in the previous round $n-1$. The players gain an important advantage at the end of this round: it becomes common knowledge that $6\le \left(P_B^{*}\right)\le 6.6$, where $P_B^{*}$ denotes the critical market clearing price for {B}, allowing them greater flexibility with their budgets if they wish to demand other available goods or greater quantities. The auctioneer notes that, at prices $P{\left\{B\right\}}^n$, Player 2 was still demanding two units of this good and therefore defines a preference for the desirable allocation for this player in the event of a tie, to the detriment of Player 3, who abstained from competing at prices of USD 6.6.

The price increase process continues for n rounds until the last market reaches equilibrium. It should be noted that even if $P\left\{A\right\}>10$, players are not aware of Player 1’s withdrawal. They only know that $D_A^n>O_A$. Further rounds are held until $P\left\{A\right\}=12.5$, at which point Player 3 discontinues their demand due to their budget constraint.

Another mechanism in place during the auction is the eligibility mechanism, which serves as a containment for the “snake in the grass” strategies, through which a player can drastically increase their demand in the final rounds of the process. If a player wishes to be a large demander at the end of the process, it must be a large demander from the start. The auctioneer must announce an Activity Requirement in force for the subsequent n clock rounds. The players demand a single package of interest in each round, composed of one or more blocks (for instance, a package may consist of three units of A and two of B), as prices rise, while being subject to two rules: the Eligibility Activity Rule (ER) and the RRP Axiom. Because the RRP Axiom is more restrictive than the ER and guides strategies toward profit maximization, the Eligibility Rule is automatically enforced in most cases. The rule is kept active as a tool that the auctioneer can use if it is desirable to accelerate the process. In our examples, the participants do not attempt to execute such a strategy.

The Eligibility Activity Rule therefore serves as a competition-building mechanism. Players must remain active, placing package bids that meet a minimum Activity Requirement in each round based on the following indicator:

$$E_i^{n+1}={\displaystyle \frac{(\mathrm{Observed} {\mathrm{Activity})}^n}{(\mathrm{Activity} {\mathrm{Requirement})}^n}},$$

(5)

where $E_i^{n+1}$ is the player’s eligibility in round $n+1$. For example, suppose that Player 1 has $E_1=10$ eligibility points and the auctioneer sets a minimum requirement of 70%. If Player 1 demands a package of eight licenses (provisional winner or not) in round n, then $E_1^{n+1}$ = 8/0.7 = 11.

As a player cannot increase their eligibility, it is set to 10, as previously defined by the player through their initial deposit. On the other hand, if the player demands a package valued at 5, their eligibility is penalized to $E_1^{n+1}$ = 5/0.7 = 7, which then becomes their new maximum demand. This mechanism is introduced to enable players to test the environment and possible combinations without directly committing to purchases that may cause regret. The auctioneer gradually increases the Activity Requirement as the rounds progress. The auction ends only when this requirement reaches 100% and there is market clearing. If the incremental demand per round is sufficiently small, the auctioneer reserves the right to close this phase in advance, as proposed by [25].

The auctioneer must, therefore, supply specific software to the bidders, capable of calculating the restrictions and violations of RPP before allowing the player to submit an offer, as finding the right combinations can be a computationally intensive process. By offering such software, bidders can focus on the aspect that really matters: price discovery.

6.2. Proxy Phase

With the conclusion of the clock phase, in which prices are adjusted until there is balance between supply and demand (or by auctioneer’s decision), the auctioneer identifies the combination of bids that results in the greatest allocative efficiency. As illustrated in

Table 13. Well-balanced activity rule leading to price discovery.

Player	P {A}	P {B}	P {C}	D {A}	D {B}	D {C}	Cost	Cost	Cost	Total
							{A}	{B}	{C}	Cost (USD)
1	11	6	3	0	2	0	0	12	0	12
2	11	6	3	0	2	3	0	12	9	21
3	11	6	3	4	0	2	44	0	6	50

, this combination guarantees the maximum possible efficiency because it is able to sell all available goods. The prices shown in columns $P\left\{A\right\}$, $P\left\{B\right\}$, and $P\left\{C\right\}$ reflect the values found in the initial round, except for item {A}, which only clears the market when $P\left\{A\right\}=12.50$. The previous allocation at $P\left\{A\right\}=11$ still exists, since, when maximizing their payoff, Player 3 demands in some round the bundle $\{4A\times 11,2C\times 3\}=50$. This bundle does not trigger market clearing in market {A}, causing prices to continue to rise iteratively until $P\left\{A\right\}=12.50$. The auctioneer opts for the allocation at $P\left\{A\right\}=11$, submitted in a previous round by Player 3, which is preferable in the auctioneer’s view to the bundle $\{4A\times 12.50\}=50$ because it implies greater dispersion of the available licenses. Then, these are defined as the minimum price for submitting bids requesting specific blocks and allocation preferences. It should be noted that bidders are not required to offer these prices in this round because if there are no distortions in the price discovery, the proxy round does not alter the allocations even if no bidder submits any bids. In our example, there is a distortion caused by the activity rule in the second round, as shown in Table 11.

Bidders now enter a more strategic moment in the auction. Previously, they were competing for generic blocks; now they have the opportunity to define preferences for specific spectrum licenses. The proxy phase introduces a closed-bid mechanism to allow efficient allocation.

During this phase, the bidders learn the specifics of the licenses up for auction. Instead of generic 5 MHz blocks, participants learn that Block C comprises two paired licenses: (708–713 MHz) and (713–718 MHz). This differentiation allows bidders to reveal more granular preferences—especially for incumbent operators who wish to acquire spectrum adjacent to their holdings.

Bids in this phase are placed in closed envelopes and must respect minimum prices established during the clock phase. Bidders may submit additional bids to maximize their synergy. This approach prevents bidders from overpaying, while also allowing efficient price discovery.

To ensure the bids reflect true valuations, Vickrey pricing is used to determine the winners and payments. In cases where combinatorial constraints arise, the Nearest Core Vickrey Price (NCVP) may be used. This guarantees incentives for bidders to submit their true valuations ($v_i$) for their respective blocks or combinations, keeping the spirit of the Vickrey auction pricing and both eliminating the winner’s curse and incentivizing straightforward bidding.

Table 14. Sealed bidding in the proxy phase.

Player	A	${\mathit{Q}}_{\mathit{A}}$	B	${\mathit{Q}}_{\mathit{B}}$	C	${\mathit{Q}}_{\mathit{C}}$	${\mathit{p}}_{\mathit{min}}\left\{\mathit{A}\right\}$	${\mathit{p}}_{\mathit{min}}\left\{\mathit{B}\right\}$	${\mathit{p}}_{\mathit{min}}\left\{\mathit{C}\right\}$
1	10	0	6	2	0	0	11	6	3
2	8	0	8	2	7	3	11	6	3
3	15	4	0	0	3	1	11	6	3

shows the bids that each bidder placed in their closed envelopes for blocks {A}, {B}, and {C}. Q_A, Q_B, and Q_C represent the number of licenses each bidder wins for each block. The minimum prices needed to enable preferred spectrum delivery are represented in the last column for each bidder. Player 2, aware that they cannot suffer the curse of the winner due to Vickrey pricing under NCVP, bids USD 7 for three C licenses, securing preferred delivery due to their highest closed envelope bid and the fact that they were the only bidder when Market C cleared under the activity rule. This same bidder is also rewarded with the preferred delivery for Market B for having placed the highest closed envelope bid and for being the only bidder during market B clearing (Table 12). Finally, for Item {A}, Player 1 prevails, noting that the critical price for this license was set at 11 (Table 13). Upon submitting a package $\{4A\times 11,2C\times 3\}$, they are only able to acquire a single C license, as Player 2 demanded three out of the four available.

Prices and bids from the clock rounds remain active and are incorporated into the bids placed by bidders in the subsequent proxy phase. The auctioneer then selects the combination that maximizes total revenue while respecting the preferences of the bidders.

6.3. Assignment

In the third and final phase, the auctioneer utilizes all combinations of bids submitted by bidders in the two previous phases to identify, in a lexicographically maximized manner, the combination that (i) maximizes revenue; (ii) maximizes spectrum dispersion; (iii) maximizes the number of spectrum licenses assigned (with due consideration for bidders’ preferences); and (iv) in case of a tie, introduces a random draw to break it.

This final allocation is then compared with the submissions of the bidders to allow the calculation of Vickrey payments for each license. In cases where combinatorial constraints arise, the Nearest Core Vickrey Price (NCVP) is used to identify the nearest point in the core if the Vickrey price falls outside the set of core allocations.

In our example, the Vickrey prices for the licenses to be cleared upon transfer are $P\left\{A\right\}=10$, $P\left\{B\right\}=6$, and $P\left\{C\right\}=4$, yielding total revenue of 80 monetary units.

Once payments for each license are determined, their transfer is completed within 90 days in order to avoid leverage and a “new Winity”, aligning with Cramton [25] and acknowledging the risks that stem from delayed payments.

7. Conclusions

Exploring the spectrum emerges as a vital avenue for governments to generate revenue, which can subsequently be allocated to social programs or infrastructure, thus incentivizing a wider population coverage. Selecting the optimal format for auctioning spectrum licenses is essential for the auctioneer to maximize efficiency and revenue. Furthermore, a thorough examination of participants’ strategies may help mitigate the adoption and prevalence of detrimental behaviors during an auction through the implementation of carefully designed regulations. Examples noted in the writing of this article include the activity rule, AUSM, spectrum cap, bidding credits, and coverage obligations, among others.

Throughout this article, we evaluated and compared the performance of the primary auction structures, both in terms of theoretical efficiency and in a real-world comparison of revenues stratified by country and format.

Auctions, including English auctions, sealed bids, and second-price auctions, have been found to be inadequate because they do not consider the complementarities between the auctioned goods.

The Simultaneous Multiple-Round Auction addresses these limitations by allowing the auctioneer to assess and extract the relative value of the license synergies as perceived by the participants. However, it is constrained by the computational power needed to accurately evaluate all offered offers, which hinders the effective price discovery between the parties involved.

Finally, the Combinatorial Clock Auction emerges as an alternative to the Simultaneous Multiple-Round Auction (SMRA), aiming to address this specific issue by incorporating a stage specifically designed to facilitate price discovery. Simultaneously, it offers the auctioneer a broader range of options to consider for resource allocation.

The level of adoption demonstrated by developed economies in North America, along with the higher revenues generated from spectrum auctions, appears to support the theoretical analysis presented by [22], suggesting that the CCA format tends to outperform other formats in terms of allocation efficiency. (It is worth noting that the North American spectrum market is highly competitive, among other factors, which may, in turn, influence prices in the US and Canada.).

Additional studies are necessary to understand the unique characteristics of each country and the specific nuances of each dispute to generate revenue from spectrum licenses. The regulatory frameworks must also be evaluated to determine whether a particular rule has a positive or negative impact, as well as to understand the requirements of each regulatory body when considering spectrum auctions.

A continuous review of the intricacies of the primary auction structures is essential for projecting structural changes and adapting auction formats to meet the needs of the regulatory authorities in each country and their specific objectives.