Research on Task Interleaving Scheduling Method for Space Station Protection Radar with Shifting Constraints
Abstract
1. Introduction
- The integration of time pointer and pulse interleaving algorithms. The time pointer scheduling approach enables the scheduling system to dynamically select and execute the next optimal task based on the current radar’s operating status and task queue conditions, typically prioritizing tasks according to their urgency. The pulse interleaving technique further refines the execution gaps between tasks. By inserting additional tasks during the idle periods between radar transmission and signal reception, it increases the density of task execution, thereby optimizing the overall task execution efficiency without compromising high-priority tasks.
- The introduction of time shifting constraints. By strictly controlling the deviation between the actual execution time and the expected execution time of tasks, the scheduling system can avoid significant deviations in the task execution time and reduce the risk of task failure or performance degradation caused by excessive time shifts. It also enables the scheduling system to allocate radar resources more reasonably, ensuring that tasks aiming at high-threat targets can be prioritized and executed accurately while not ignoring the needs of other tasks.
- Enhancing the on-orbit safety of space stations. The method proposed in this paper augments the radar system’s processing capability in multi-task environments, effectively addressing the complexities of the space environment surrounding space stations. It ensures that, when tracking high-speed, high-threat targets, the deviation between predicted and actual positions remains within a controllable range, thereby improving tracking accuracy and reliability and ultimately bolstering the on-orbit safety of space stations.
2. Composition of Resource Scheduling Module
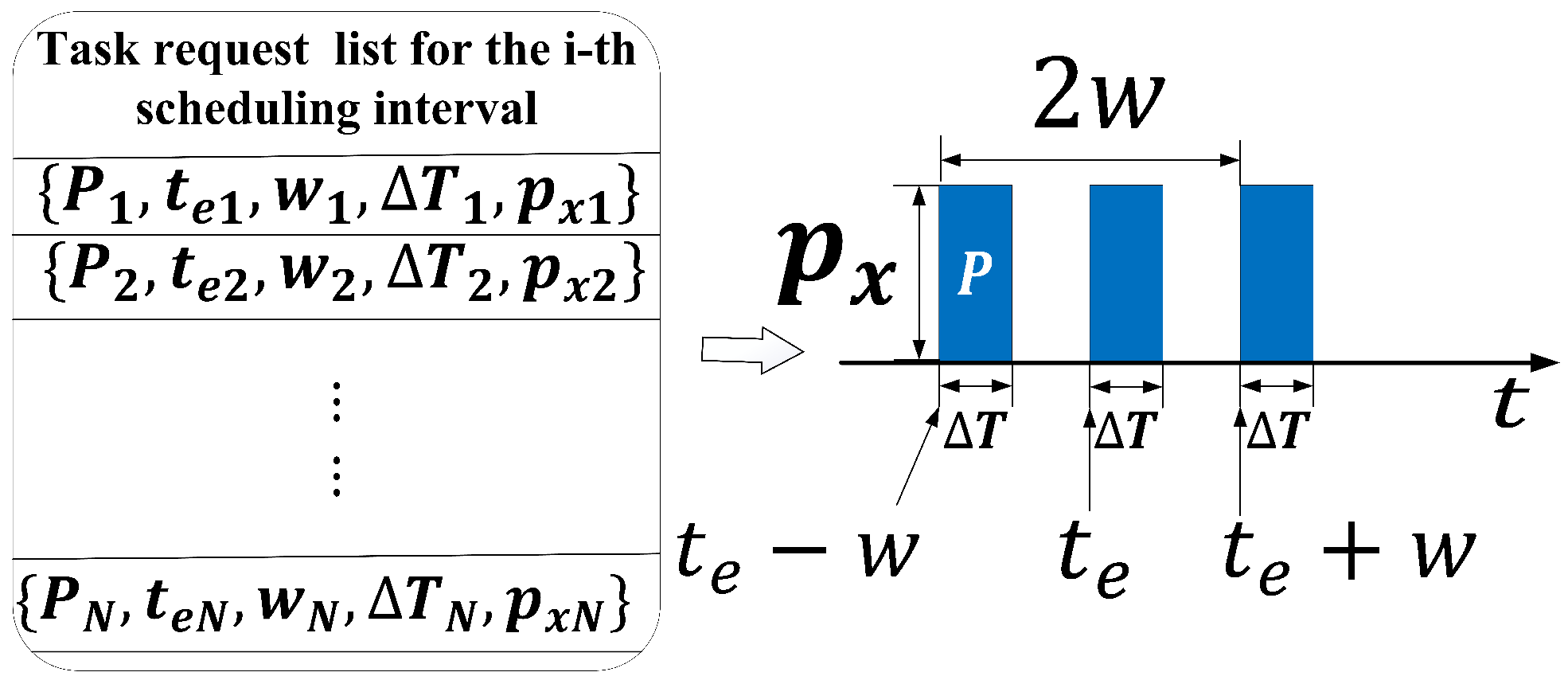
2.1. Task Planning Module
2.2. Priority Assignment Module and Dwell Task Model
2.3. Task Scheduling Module
3. The Scheduling Method Based on Time Shifting Constraints and Pulse Interleaving
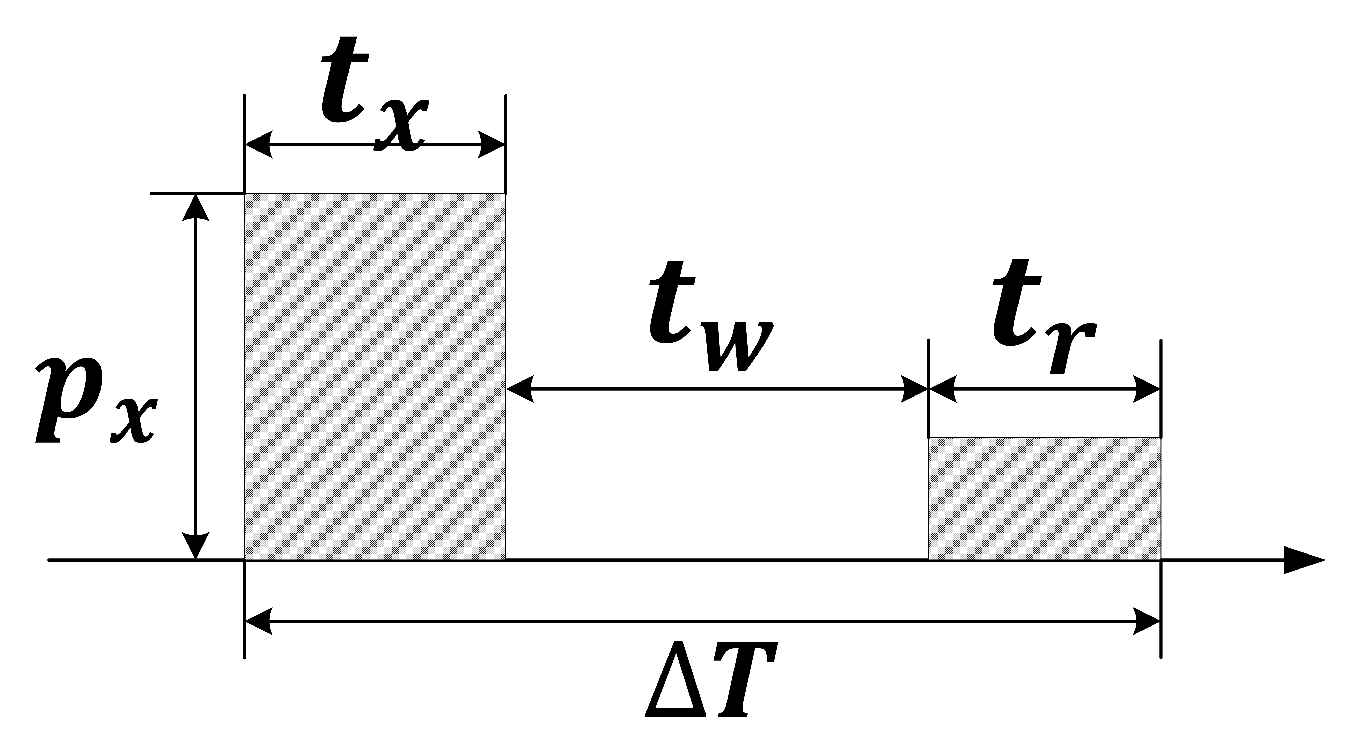
3.1. Pulse Interleaving Technology
- (1)
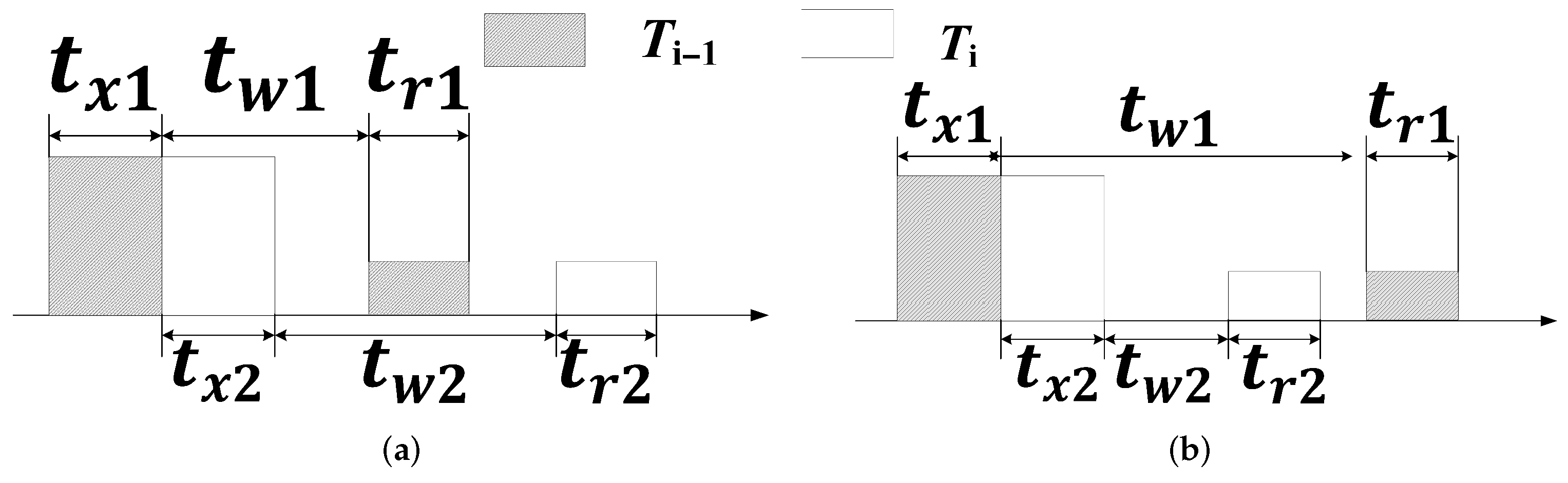
- If the interleaving method shown in Figure 4a is adopted, the parameters of the new task are updated as follows:
- when :
- when :
- (2)
- If the interleaving method shown in Figure 4b is adopted, the parameters of the new task are updated as follows:
- when :
- when :
3.2. The Description of Proposed Methodology
- (1)
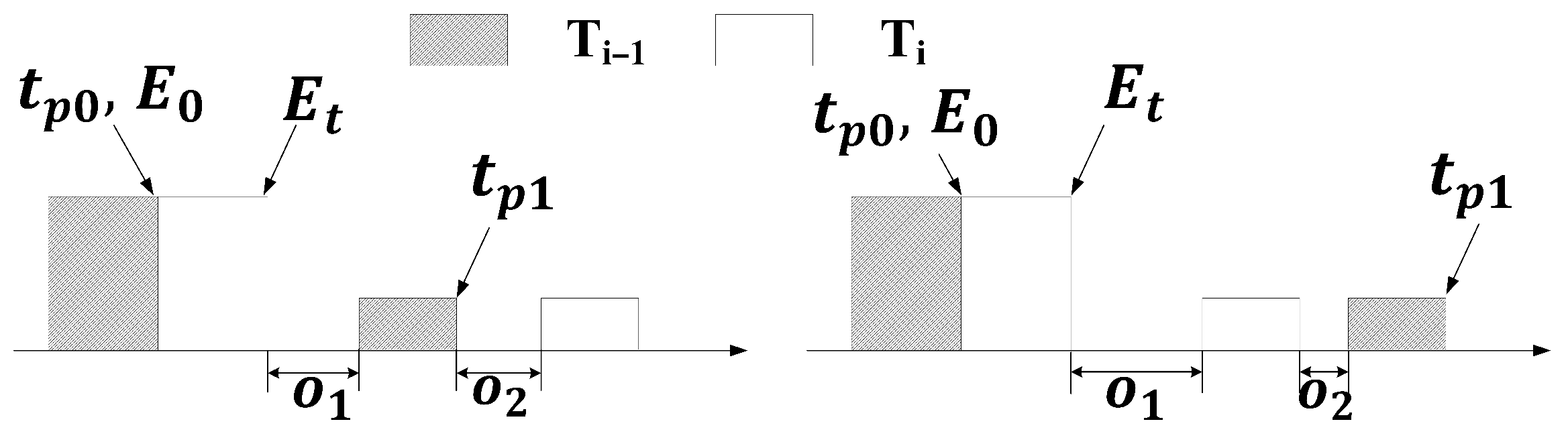
- Scheduling begins. Initializing the time pointers and to point to the start time of the scheduling interval, i.e., = = ; Initialize counter i = 0, system energy , and pulse interleaving identifier . The variable ∈{0,1} is a binary decision variable that takes on the value 1(0) if the current task can be interleaved with the previous task (cannot be interleaved).
- (2)
- Let the task request list within the scheduling interval [,] be denoted as T = [,,…,].
- (3)
- All tasks in T that satisfy the condition + w < are moved to the deletion list. Let the total number of such tasks be M, and update the counter by setting i = i + M.
- (4)
- Find all tasks from T that satisfy + w < , which can be executed at time , to form a task set R = [,,…,], and calculate the priority of tasks in R. The method for calculating priority follows an improved MHPF (Modified Highest Priority First) criterion: Let the work mode priority of each task in set R be denoted as P = [,,…,], the deadlines as = [,,…,], and the threat degrees as = [, ,…, ]. Task i is considered to have a higher priority than task j if > , or if = , > , or if = , = , < .
- (5)
- Select all tasks from the set R that satisfy the shifting constraint given in (18) to form a new set Q = [,,…,]. If Q is empty, meaning that none of the tasks in Q satisfy the shifting constraints of (18), proceed to Step 6; otherwise, proceed to Step 7.
- (6)
- Update time pointers , , and total system energy consumption:when = :otherwise:where l represents the minimum step length for the time pointer to slide; proceed to Step 8.
- (7)
- Find the task with the highest priority from set Q:
- (a)
- If = 0, it indicates that task cannot be interleaved with the previous task. In this case, schedule task at time and move into the execution task queue. If task can be interleaved, then update parameters according to (23); if interleaving is not possible, then update parameters and tp1 according to (24). Based on the type of task , update and , and increment i by 1.
- (b)
- If = 1 and task satisfies the constraints of (3), (4), (7), and (17), then task is moved into the execution task queue, i is incremented by 1, and the parameters are updated according to (8) to (15). If task does not satisfy the constraints, the parameters are updated according to (25) to (28).when , the following applies:In other cases:
- (8)
- Check whether or . If either condition is true, the task scheduling for the current interval is complete. Delete the time pointers, and output the execution queue and deletion queue for this scheduling interval. Otherwise, proceed to Step 3.
4. Simulation and Results
4.1. Scheduling Performance Evaluation Metrics
- (1)
- Scheduling Success Ratio (SSR):represents the number of successfully scheduled tasks, and N denotes the total number of radar tasks requested to be scheduled. The SSR is defined as the proportion of successfully scheduled tasks.
- (2)
- Average time shift ratio (ASTR):represents the time window length of task i, is the expected execution time of task i, and is the actual execution time of task i. The ATSR indicates the timeliness of task scheduling.
- (3)
- Hit value ratio (HVR):represents the number of successfully scheduled tasks, denotes the priority of each successfully scheduled task, N is the total number of radar tasks requested for scheduling, and represents the priority of all tasks requested for scheduling. HVR quantifies the proportion of radar resources (such as time and energy) that successfully contribute to the high-value tasks such as detection, tracking, and engagement of targets.
4.2. Scenario and Parameter Settings
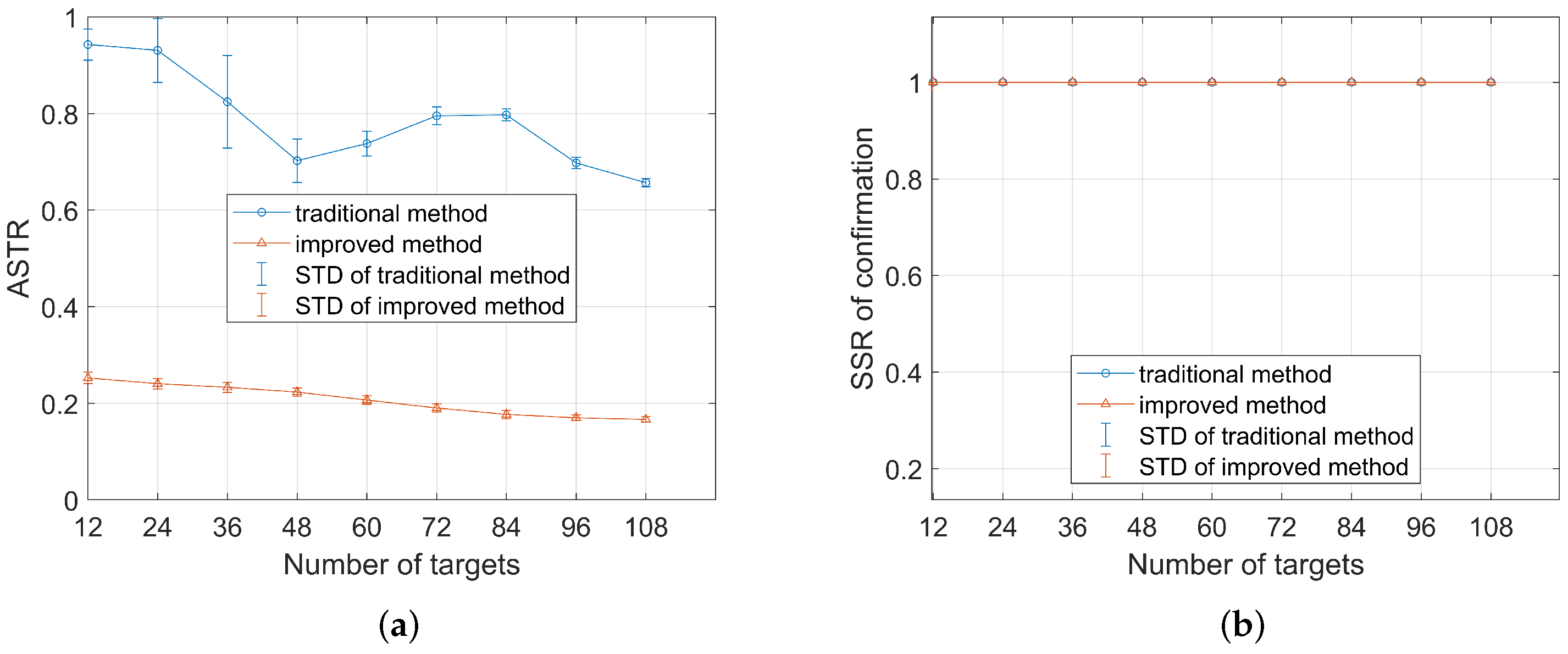
4.3. Simulation Results
5. Discussion and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McDowell, J.C. The low earth orbit satellite population and impacts of the SpaceX Starlink constellation. Astrophys. J. Lett. 2020, 892, L36. [Google Scholar] [CrossRef]
- Muntoni, G.; Montisci, G.; Pisanu, T.; Andronico, P.; Valente, G. Crowded space: A review on radar measurements for space debris monitoring and tracking. Appl. Sci. 2021, 11, 1364. [Google Scholar] [CrossRef]
- Dobritsa, D.; Pashkov, S.; Khristenko, I.F. Protective properties of pleated wire mesh shields for spacecraft protection against meteoroids and space debris. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2021; Volume 2318. [Google Scholar] [CrossRef]
- Buchs, R.; Florin, M.V. Collision Risk from Space Debris: Current Status, Challenges and Response Strategies. 2021. Available online: https://infoscience.epfl.ch/handle/20.500.14299/178442 (accessed on 6 January 2025).
- Murtaza, A.; Pirzada, S.J.H.; Xu, T.; Jianwei, L. Orbital debris threat for space sustainability and way forward. IEEE Access 2020, 8, 61000–61019. [Google Scholar] [CrossRef]
- Kollias, P.; Palmer, R.; Bodine, D.; Adachi, T.; Bluestein, H.; Cho, J.Y.; Griffin, C.; Houser, J.; Kirstetter, P.E.; Kumjian, M.R.; et al. Science applications of phased array radars. Bull. Am. Meteorol. Soc. 2022, 103, E2370–E2390. [Google Scholar] [CrossRef]
- Yang, J.; Lu, X.; Dai, Z.; Yu, W.; Tan, K. A cylindrical phased array radar system for uav detection. In Proceedings of the 2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 9–11 April 2021; pp. 894–898. [Google Scholar] [CrossRef]
- Basha, M.; Ware, N.R. Design for Reliability of Phased Array Radars. In Proceedings of the 2021 6th International Conference for Convergence in Technology (I2CT), Maharashtra, India, 2–4 April 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Gao, T.; Wei, Q.; Wang, P.; Dong, Y.; Jiang, H.; Zhu, B. The development status and trend of airborne multifunctional radar. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Industrial Design (AIID), Guangzhou, China, 28–30 May 2021; pp. 327–330. [Google Scholar] [CrossRef]
- Han, Q.; Zhang, Y.; Yang, Z.; Long, W.; Liang, Z. Antenna array aperture resource management of opportunistic array radar for multiple target tracking. IEEE Access 2020, 8, 228357–228368. [Google Scholar] [CrossRef]
- Cheng, T.; Liu, L.; Li, Z.; Heng, S. Real-Time Dwell Scheduling Based on a Unified Pulse Interleaving Framework for Phased Array Radar. Tsinghua Sci. Technol. 2024, 29, 1540–1553. [Google Scholar] [CrossRef]
- Li, B.; Tian, L.; Chen, D.; Han, Y. A task scheduling algorithm for phased-array radar based on dynamic three-way decision. Sensors 2019, 20, 153. [Google Scholar] [CrossRef]
- Meng, F.; Tian, K. Phased-array radar task scheduling method for hypersonic-glide vehicles. IEEE Access 2020, 8, 221288–221298. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Ge, J.; Zhang, Z.; Zong, B. A hybrid adaptively genetic algorithm for task scheduling problem in the phased array radar. Eur. J. Oper. Res. 2019, 272, 868–878. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, T.; Heng, S. Real-time dwell scheduling algorithm for phased array radar based on a backtracking strategy. IET Radar Sonar Navig. 2023, 17, 261–276. [Google Scholar] [CrossRef]
- Luo, M.; Jiang, B.; Xing, W.g. Networked Radar Mission Planning Algorithm Based on Pulse Interleaving and Cross-Scheduling Interval. J. Phys. Conf. Ser. 2023, 2670, 012027. [Google Scholar] [CrossRef]
- Duan, Y.; Tan, X.S.; Qu, Z.G.; Wang, H. Index for task scheduling in phased array radar. J. Eng. 2019, 2019, 7550–7554. [Google Scholar] [CrossRef]
- Hao, L.; Yang, X.; Hu, S. Task scheduling of improved time shifting based on genetic algorithm for phased array radar. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1655–1660. [Google Scholar] [CrossRef]
- Luo, R.; Huang, S.; Zhao, Y.; Song, Y. Threat Assessment Method of Low Altitude Slow Small (LSS) Targets Based on Information Entropy and AHP. Entropy 2021, 23, 1292. [Google Scholar] [CrossRef]





| Task Type | Priority | Dwell Time | Time Window | Cycle | Transmission Power |
|---|---|---|---|---|---|
| Confirmation | 4 | 4 ms | 60 ms | - | 5.5 kw |
| Precision tracking | 3 | 10 ms | 60 ms | 400 ms | 5 kw |
| General tracking | 2 | 10 ms | 80 ms | 600 ms | 5 kw |
| Search | 1 | 5 ms | 100 ms | - | 3 kw |
| Numbers of Target | SSR of Search | SSR of Track | SSR of Confirmation | ATSR | HVR | SSR of All Tasks |
|---|---|---|---|---|---|---|
| 12 | ||||||
| 24 | ||||||
| 36 | ||||||
| 48 | ||||||
| 60 | ||||||
| 72 | ||||||
| 84 | ||||||
| 96 | ||||||
| 108 |
| Numbers of Target | SSR of Search | SSR of Track | SSR of Confirmation | ATSR | HVR | SSR of All Tasks |
|---|---|---|---|---|---|---|
| 12 | ||||||
| 24 | ||||||
| 36 | ||||||
| 48 | ||||||
| 60 | ||||||
| 72 | ||||||
| 84 | ||||||
| 96 | ||||||
| 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhou, H.; Yang, H.; Hou, J.; Xu, G.; Wang, D. Research on Task Interleaving Scheduling Method for Space Station Protection Radar with Shifting Constraints. Telecom 2025, 6, 49. https://doi.org/10.3390/telecom6030049
Zhang G, Zhou H, Yang H, Hou J, Xu G, Wang D. Research on Task Interleaving Scheduling Method for Space Station Protection Radar with Shifting Constraints. Telecom. 2025; 6(3):49. https://doi.org/10.3390/telecom6030049
Chicago/Turabian StyleZhang, Guiqiang, Haocheng Zhou, Hong Yang, Jiacheng Hou, Guangyuan Xu, and Dawei Wang. 2025. "Research on Task Interleaving Scheduling Method for Space Station Protection Radar with Shifting Constraints" Telecom 6, no. 3: 49. https://doi.org/10.3390/telecom6030049
APA StyleZhang, G., Zhou, H., Yang, H., Hou, J., Xu, G., & Wang, D. (2025). Research on Task Interleaving Scheduling Method for Space Station Protection Radar with Shifting Constraints. Telecom, 6(3), 49. https://doi.org/10.3390/telecom6030049




