Cell-Free Massive MIMO Power Consumption with Serial Front-Hauls
Abstract
1. Introduction
2. System Model and Problem Statement
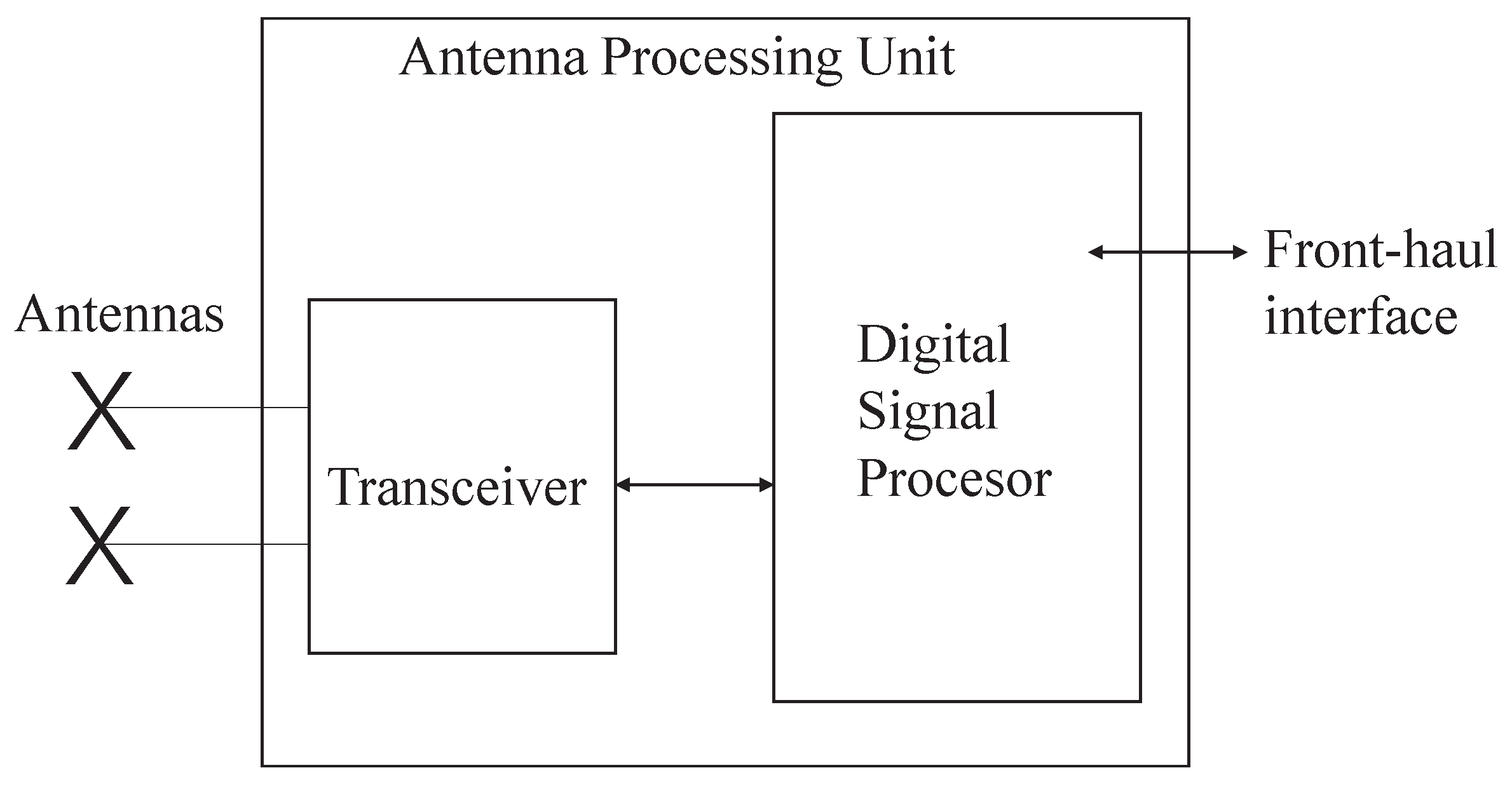
2.1. System Model
2.2. Problem Statement
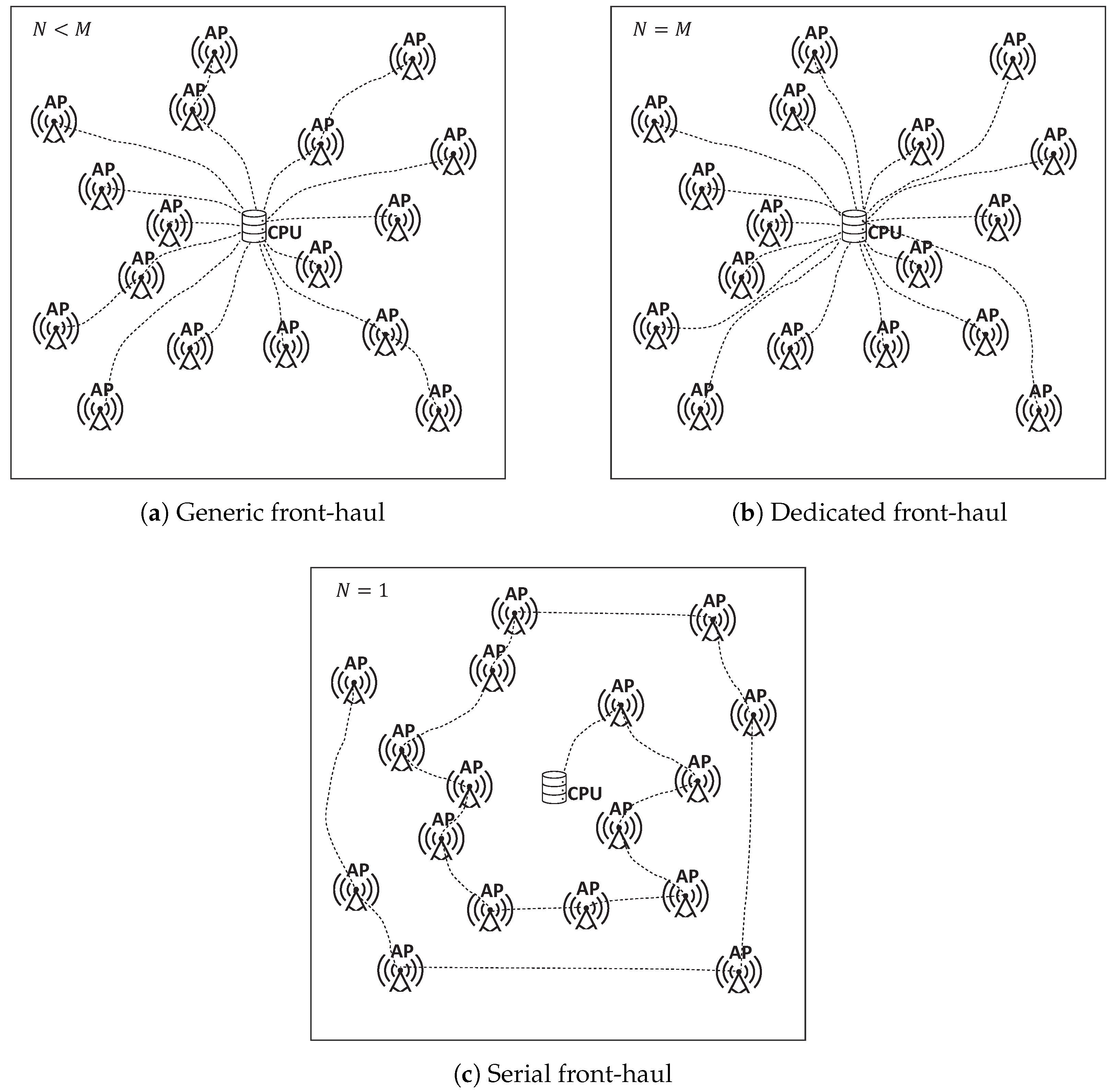
3. Proposed Adaptations of the Model for Serial Distributed Systems
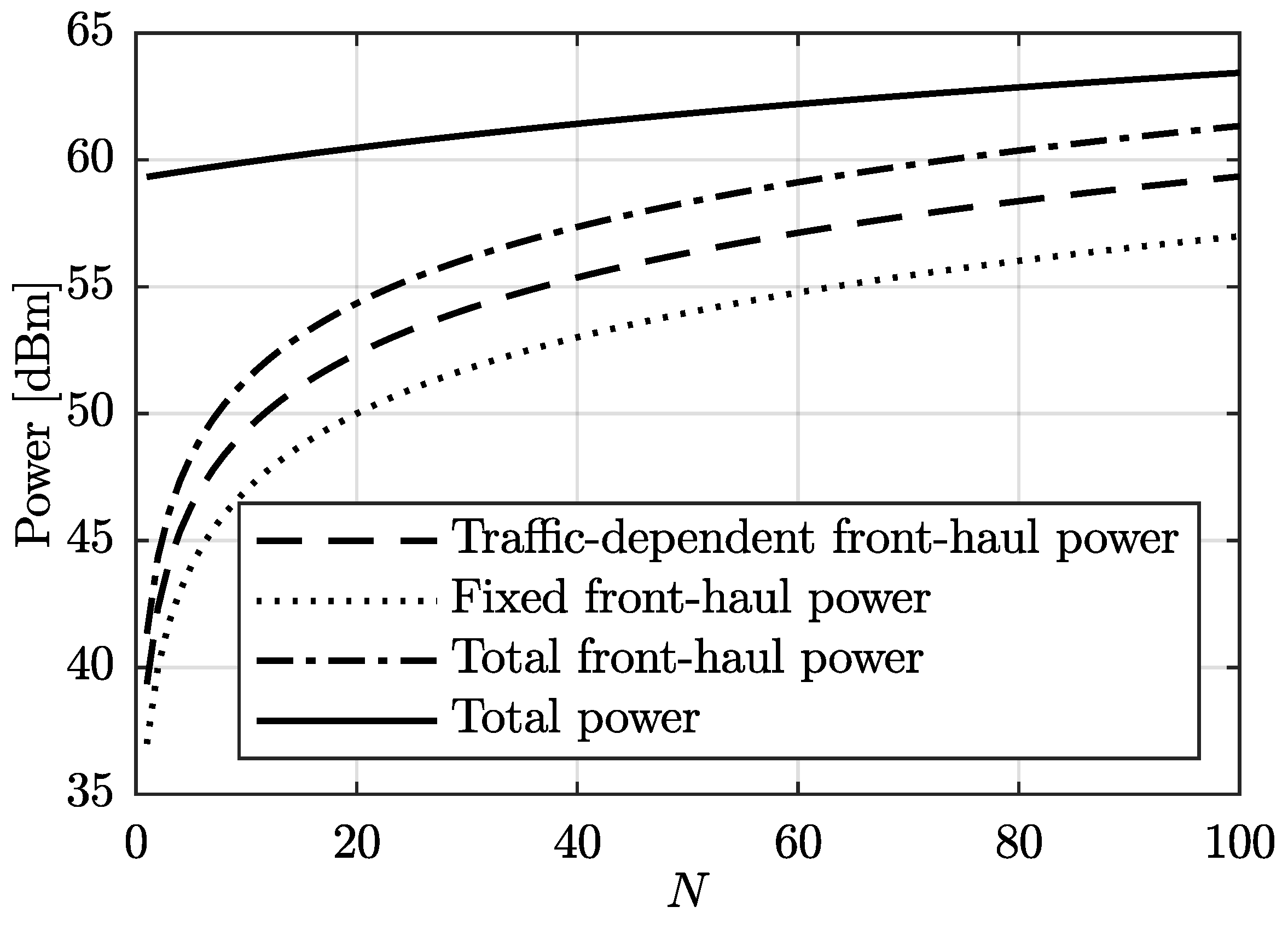
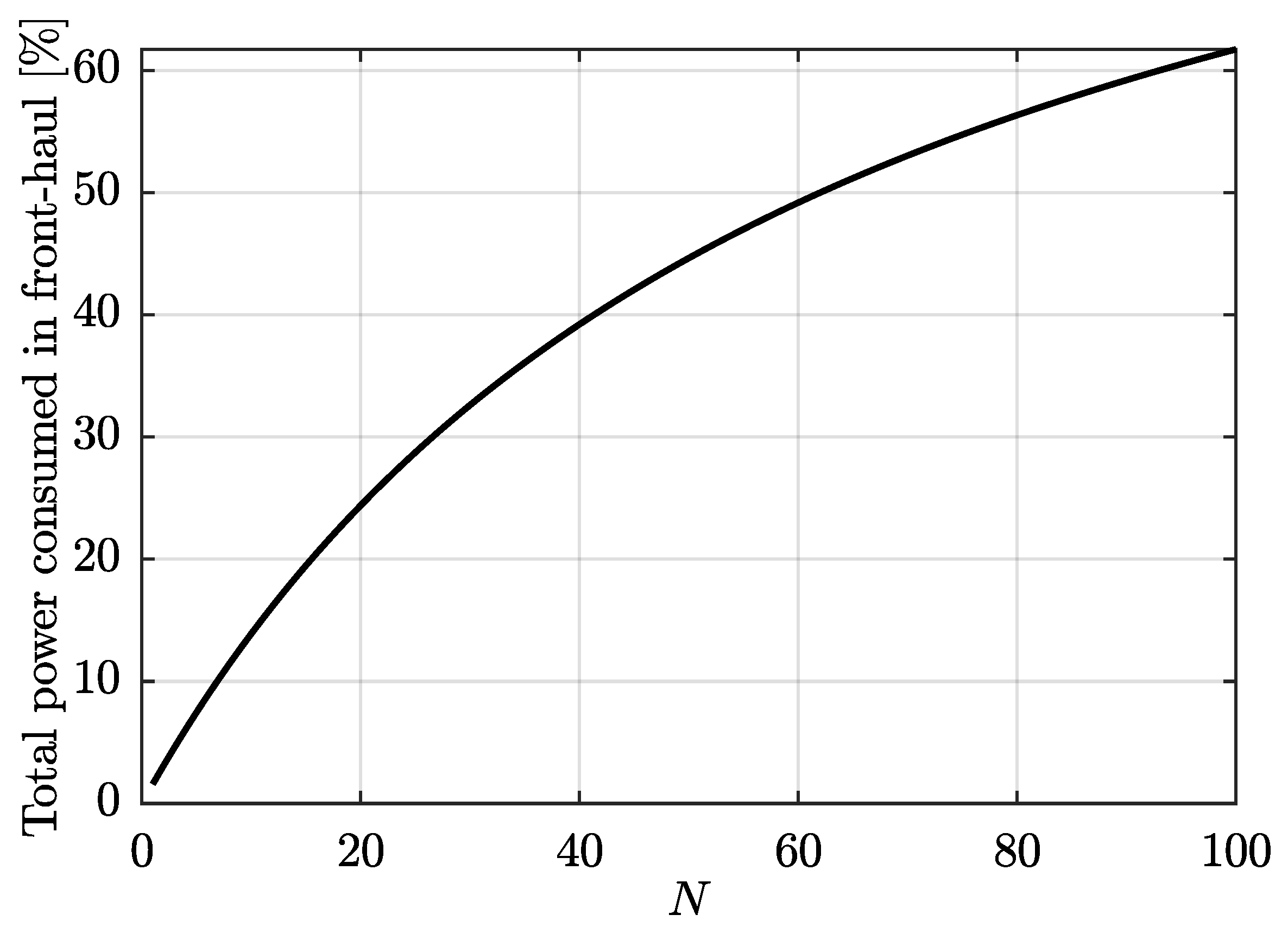
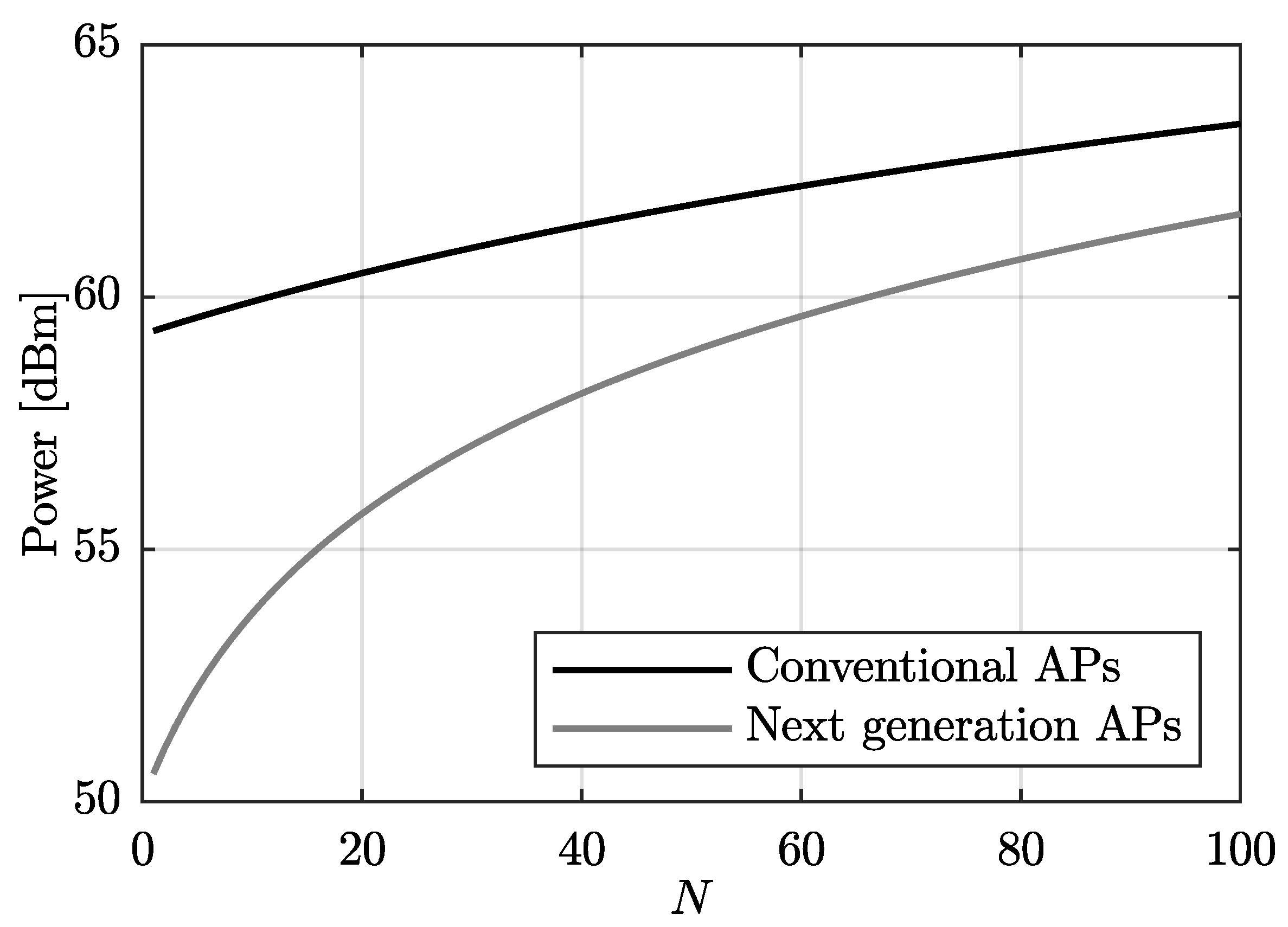
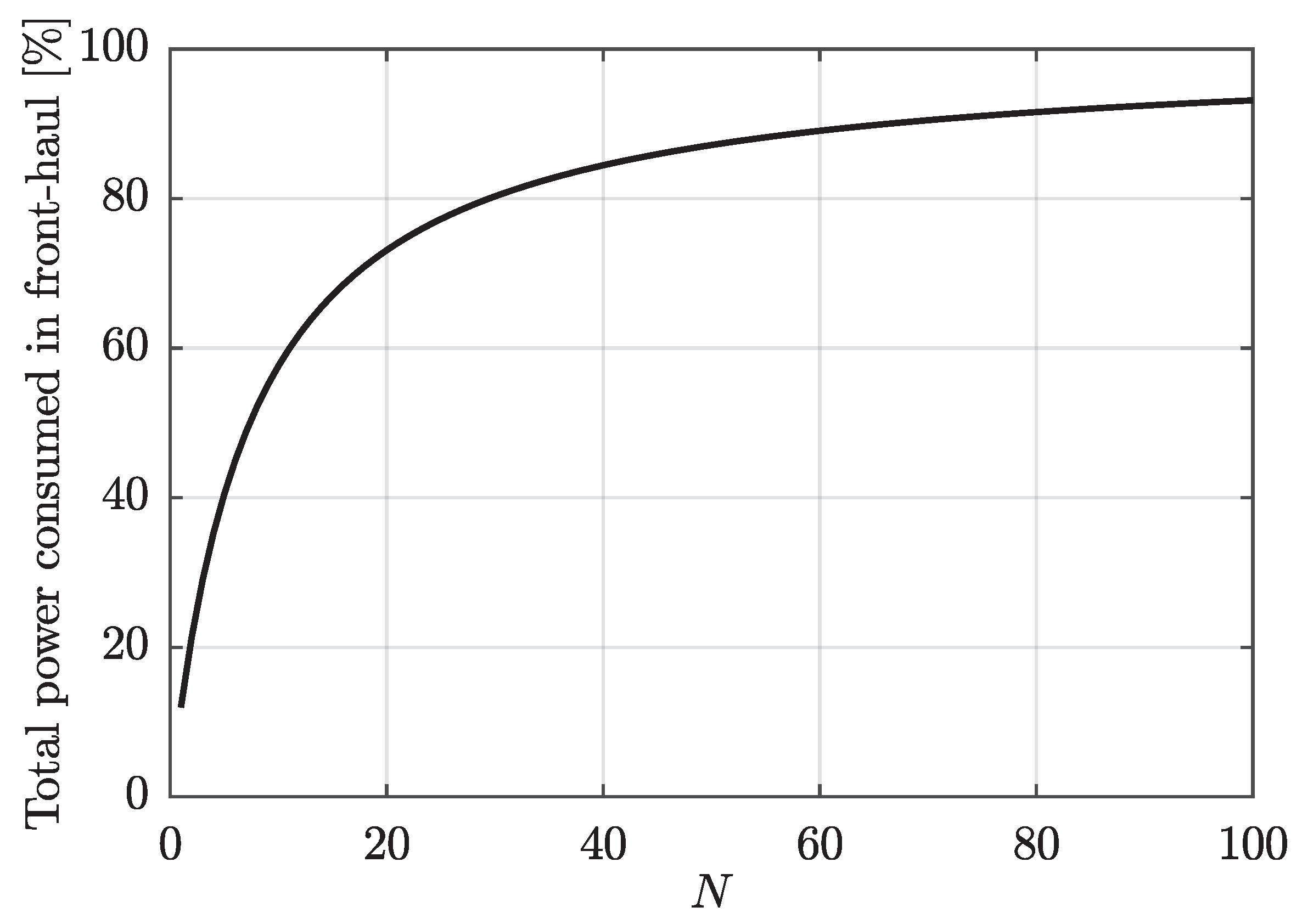
4. Power Consumption Comparison
4.1. Considering Conventional APs
4.2. Considering Next Generation APs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Molisch, A.F. Wireless Communications; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 34. [Google Scholar]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO Versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef]
- Bjornson, E.; der Perre, L.V.; Buzzi, S.; Larsson, E.G. Massive MIMO in Sub-6 GHz and mmWave: Physical, Practical, and Use-Case Differences. IEEE Wirel. Commun. 2019, 26, 100–108. [Google Scholar] [CrossRef]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar] [CrossRef]
- Ngo, H.Q. Cell-Free Massive MIMO. In Encyclopedia of Wireless Networks; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Yang, H.; Rao, B.D. Precoding and Power Optimization in Cell-Free Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2017, 16, 4445–4459. [Google Scholar] [CrossRef]
- Interdonato, G.; Frenger, P.; Larsson, E.G. Scalability Aspects of Cell-Free Massive MIMO. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Tran, L.N.; Duong, T.Q.; Matthaiou, M.; Larsson, E.G. On the Total Energy Efficiency of Cell-Free Massive MIMO. IEEE Trans. Green Commun. Netw. 2018, 2, 25–39. [Google Scholar] [CrossRef]
- Nguyen, L.D.; Duong, T.Q.; Ngo, H.Q.; Tourki, K. Energy Efficiency in Cell-Free Massive MIMO with Zero-Forcing Precoding Design. IEEE Commun. Lett. 2017, 21, 1871–1874. [Google Scholar] [CrossRef]
- Alonzo, M.; Buzzi, S.; Zappone, A.; D’Elia, C. Energy-Efficient Power Control in Cell-Free and User-Centric Massive MIMO at Millimeter Wave. IEEE Trans. Green Commun. Netw. 2019, 3, 651–663. [Google Scholar] [CrossRef]
- Garcia-Morales, J.; Femenias, G.; Riera-Palou, F. Energy-Efficient Access-Point Sleep-Mode Techniques for Cell-Free mmWave Massive MIMO Networks With Non-Uniform Spatial Traffic Density. IEEE Access 2020, 8, 137587–137605. [Google Scholar] [CrossRef]
- Hasabelnaby, M.A.; Chaaban, A. Energy-Efficient Multi-Pair Computation for Intra Cell-Free Massive MIMO Communications. IEEE Wirel. Commun. Lett. 2024, 13, 776–780. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhu, P.; Li, J.; Wang, D.; You, X. Energy Efficiency Enhancement in User-Centric and Cell-Free Millimeter-Wave Massive MIMO Systems With Hybrid Beamforming. IEEE Trans. Veh. Technol. 2024, 73, 5484–5499. [Google Scholar] [CrossRef]
- Ericsson. 2020. Available online: https://www.ericsson.com/en/blog/2019/2/radio-stripes (accessed on 20 July 2024).
- López, O.L.A.; Kumar, D.; Souza, R.D.; Popovski, P.; Tölli, A.; Latva-Aho, M. Massive MIMO With Radio Stripes for Indoor Wireless Energy Transfer. IEEE Trans. Wirel. Commun. 2022, 21, 7088–7104. [Google Scholar] [CrossRef]
- Azarbahram, A.; López, O.L.A.; Popovski, P.; Latva-Aho, M. On the Radio Stripe Deployment for Indoor RF Wireless Power Transfer. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Chiotis, I.; Moustakas, A.L. On the Uplink Performance of Finite-Capacity Radio Stripes. In Proceedings of the 2022 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Athens, Greece, 5–8 September 2022; pp. 118–123. [Google Scholar] [CrossRef]
- Papazafeiropoulos, A.; Ngo, H.Q.; Kourtessis, P.; Chatzinotas, S.; Senior, J.M. Towards Optimal Energy Efficiency in Cell-Free Massive MIMO Systems. IEEE Trans. Green Commun. Netw. 2021, 5, 816–831. [Google Scholar] [CrossRef]
- Bjornson, E.; Sanguinetti, L.; Kountouris, M. Deploying Dense Networks for Maximal Energy Efficiency: Small Cells Meet Massive MIMO. IEEE J. Sel. Areas Commun. 2016, 34, 832–847. [Google Scholar] [CrossRef]
- Dai, B.; Yu, W. Energy Efficiency of Downlink Transmission Strategies for Cloud Radio Access Networks. IEEE J. Sel. Areas Commun. 2016, 34, 1037–1050. [Google Scholar] [CrossRef]
- Fehske, A.J.; Marsch, P.; Fettweis, G.P. Bit per joule efficiency of cooperating base stations in cellular networks. In Proceedings of the 2010 IEEE Globecom Workshops, Miami, FL, USA, 6–10 December 2010; pp. 1406–1411. [Google Scholar]
- Shaik, Z.H.; Björnson, E.; Larsson, E.G. Cell-free massive MIMO with radio stripes and sequential uplink processing. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Hederen, J.; Frenger, P. Improved Antenna Arrangement for Distributed Massive MIMO. U.S. Patent Application No. 16/764,126, 17 December 2020. [Google Scholar]
- Interdonato, G.; Björnson, E.; Ngo, H.Q.; Frenger, P.; Larsson, E.G. Ubiquitous cell-free Massive MIMO communications. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 197. [Google Scholar] [CrossRef]
| Parameters | Value |
|---|---|
| Power amplifier efficiency () | |
| AP maximum transmit power () | W |
| Number of RF chains () | 1 |
| Coherence interval length () | 200 samples |
| Training phase length () | 20 samples |
| Spectral efficiency in downlink () | 86 Mbits/s/Hz |
| Bandwidth (B) | 20 MHz |
| Traffic-dependent power consumption | W/Gbps |
| coefficient (, ) | |
| Fixed front-haul power per link | 5 W |
| in conventional systems () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prado-Alvarez, D.; Inca, S.; Martín-Sacristán, D.; Monserrat, J.F. Cell-Free Massive MIMO Power Consumption with Serial Front-Hauls. Telecom 2024, 5, 1021-1030. https://doi.org/10.3390/telecom5040052
Prado-Alvarez D, Inca S, Martín-Sacristán D, Monserrat JF. Cell-Free Massive MIMO Power Consumption with Serial Front-Hauls. Telecom. 2024; 5(4):1021-1030. https://doi.org/10.3390/telecom5040052
Chicago/Turabian StylePrado-Alvarez, Danaisy, Saúl Inca, David Martín-Sacristán, and Jose F. Monserrat. 2024. "Cell-Free Massive MIMO Power Consumption with Serial Front-Hauls" Telecom 5, no. 4: 1021-1030. https://doi.org/10.3390/telecom5040052
APA StylePrado-Alvarez, D., Inca, S., Martín-Sacristán, D., & Monserrat, J. F. (2024). Cell-Free Massive MIMO Power Consumption with Serial Front-Hauls. Telecom, 5(4), 1021-1030. https://doi.org/10.3390/telecom5040052








