Abstract
The data used during training in any given application space are directly tied to the performance of the system once deployed. While there are many other factors that are attributed to producing high-performance models based on the Neural Scaling Law within Machine Learning, there is no doubt that the data used to train a system provide the foundation from which to build. One of the underlying heuristics used within the Machine Learning space is that having more data leads to better models, but there is no easy answer to the question, “How much data is needed to achieve the desired level of performance?” This work examines a modulation classification problem in the Radio Frequency domain space, attempting to answer the question of how many training data are required to achieve a desired level of performance, but the procedure readily applies to classification problems across modalities. The ultimate goal is to determine an approach that requires the lowest amount of data collection to better inform a more thorough collection effort to achieve the desired performance metric. By focusing on forecasting the performance of the model rather than the loss value, this approach allows for a greater intuitive understanding of data volume requirements. While this approach will require an initial dataset, the goal is to allow for the initial data collection to be orders of magnitude smaller than what is required for delivering a system that achieves the desired performance. An additional benefit of the techniques presented here is that the quality of different datasets can be numerically evaluated and tied together with the quantity of data, and ultimately, the performance of the architecture in the problem domain.
1. Introduction
Machine Learning (ML) is “the capacity of computers to learn and adapt without following explicit instructions, by using algorithms and statistical models to analyze and infer from patterns in data” [1]. No matter the field, ML begins and ends with the data available to use during training. Without relevant data to learn from, ML is effectively a “garbage in, garbage out” system [2]. The application of ML to problems within the Radio Frequency (RF) domain is no exception to this rule, yet within the scope of intentional human-made emissions, data are easier to synthesize than within more prolific domains such as image processing [3]. Due to the readily available tools for developing ML-based algorithms (TensorFlow [4], PyTorch [5], etc.) and this ease of synthesis for establishing comprehensive datasets, there has been an explosion of published work in the field. Adding to the ease of training models, the RF domain has the availability of open-source toolsets for synthesizing RF waveforms such as GNU Radio [6] and Liquid-DSP [7], to name a few. However, going from a purely synthetic environment to a functional application running in the real world has a number of considerations that must be addressed. A brief explanation about the gaps from synthetic data to functional application data is discussed in Section 1.2.
This paper focuses on providing an applied understanding of working with ML in the RF spectrum, with particular regard to understanding the training data in applications that fall in the domain space of Radio Frequency Machine Learning (RFML). To better clarify this, RFML is a subset of ML that overlaps communications, radar, or any other application space that utilizes the RF spectrum in a statistically repeatable manner, where ML algorithms are applied as intelligently close to the digitized samples of the RF spectrum, or the physical layer in the Open Systems Interconnection (OSI) model, as possible [8]. For simplicity within this work, focus will be given to the field of Deep Learning (DL) as the particular subset within ML due to the well-suited nature of DL systems at extracting inference from raw data [9]. Two fundamental questions for developing a DL architecture for a given application are
- What data should be or are available to be used in order to train the system;
- How many data are needed for the current approach to achieve the desired performance level?
These two questions are systematically addressed within this work, providing a blueprint for how they can be answered in general.
The two most common problems in regard to datasets with DL systems are having a large enough quantity of data, and having those data be of a high enough quality, in order to develop a well-generalized model [9]. In fact, answering the question of how many data are needed is a fundamental unknown that relies on the developers’ experience and insight into the problem space. The end results of attempts at answering this question are the common rule of thumb answers of “ten times the feature space” or “as many data as are available”, which is an issue across all domains [10,11,12,13,14,15,16,17,18,19]. The desire to understand how the final performance of a system is linked with the available training dataset size is in the domain of research looking at Neural Scaling Laws (NSLs) [20,21,22,23,24]. The NSLs tie the final loss of a network to the number of parameters in the architecture, training dataset size, and available computing budget [21]. In this work, the number of parameters is fixed and the available compute budget is assumed to be infinite, directly evaluating the loss of the trained network to its available training dataset size; however, the metric of interest is actually the performance of the network rather than its loss. The driving force of this approach allows the network and dataset size to be tied directly to an operational goal, rather than the less intuitive values of loss, which in the problem space used in this work greatly deviates from the typical power-law relationship as the performance reaches a functional limit, let alone the fluctuations seen in the empirical relationships [22].
The work of Chen et al. [25] describes the concept of quality in three ways: Comprehensiveness, Correctness, and Variety.In this work, the primary focus is on understanding the aspect of Variety in terms of the origin of the data, Captured (received spectral samples by a sensor), Synthetic (samples generated from formulae), and Augmented (a mixture of the previous origins), while the other two aspects are more concerned with the information being both present in the dataset as well as being correctly labeled, which is given for the datasets used. More details about the origin of the data are presented in Section 1.2.2, while data quantity and quality are discussed in more detail in Section 2.
The discussion of characteristics inherited in the application of ML is given in Section 1.1, along with the RFML problem of Automatic Modulation Classification (AMC), which is discussed in more detail in Section 1.1.3. The more well-discussed problems and nuisances inherent to the RF spectrum are discussed in Section 1.2. Examining the effects of data quantity, along with the concept of how data quality can be quantified, are presented in Section 2. The problem of estimating the data needs from a minimal set are contrasted to the full availability of data in Section 3 where a combination of two metrics offers a more balanced estimate than either metric alone. Finally, conclusions about how the presented AMC approaches can be well generalized to RFML at large are presented in Section 4.
1.1. Machine Learning Concepts
ML, in the most general form, is the process of creating a function that maps an observable in the form raw data, meta data, and/or extracted features of the data to some more convenient form for an applied task through observations available during training [9].
Therefore, given a training dataset () with N samples, , drawn from an observation space, , where is a subset of the generalized problem space, . The application of ML works to create a particular mapping . The ultimate goal of the learned mapping is to be well generalized so that the mapping can also be applied to the whole with the same performance as within the . A visualization of the relationship between the generalized problem space, , and the observation space from which training data are collected, , is shown in Figure 1a with the training dataset, , shown in Figure 1b.

Figure 1.
(a) A visualization of how the generalized problem space, , encompasses the application space, , as well as all possible data collection methods, . (b) The process of sampling from a collection method, , in order to produce a training dataset, . (c) The sampling of data from the application space to produce an evaluation dataset, , for estimating a trained model’s performance if used within the application space. (d) The training process, , with a given architecture, , and training set, , to produce the parameters, , that can be used for inference with the architecture, . (e) The inference process using a trained model on the evaluation dataset, .
The mapping is learned through a training procedure, , which produces the parameter space, , which defines the behavior of f and is visualized in Figure 1d. Given the focus on DL systems, is a set of weights and biases that are used within the DL architecture, f. Applying the trained network on unseen data, it becomes . For conditions where the unseen data are a sample from , the best performance of this network is expected; however, if comes from some other subset (Figure 1c), the generalization of the trained model is being tested, as shown in Figure 1e.
The DL architecture used in this work, shown in Figure 2, is the architecture that was shown to be well suited to the AMC problem space in the work of West and O’Shea [26]. The regularization added to the network is incorporated from the work of Flowers and Headley for the increased convergence rate [27]. The challenges and discussion within AMC are discussed in further detail in Section 1.2.
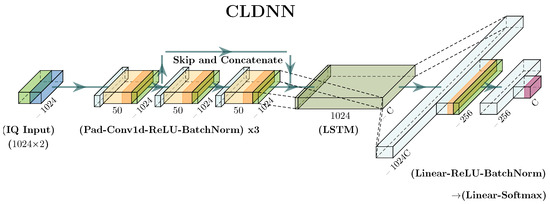
Figure 2.
DL NN image representing the CLDNN architecture used in this work as the DL approach for the 10-class waveform AMC problem space.
A brief overview of concepts utilized in this work with regard to ML is given below. In particular, the concepts of DL and Transfer Learning (TL) are fundamental to the setup and analysis of the crux of this work.
1.1.1. Deep Learning
Goodfellow et al. [9] goes into great detail in developing an understanding of the complexities surrounding DL. A brief explanation is as follows. DL is a subset of ML that makes use of multiple layers of processing that can, in theory, approach the problem with simple computations. The accumulated simple computations allow for solving a complex problem [9]. The DL approach used in this work uses Deep Neural Networks (DNNs), which make use of three sequential layers consisting of convolutional layers, a recurrent Long Short-Term Memory (LSTM) layer, whose hidden size is tied to the dimension of the classification space, and two successive linear layers, before producing the model output. After each convolutional and linear layer that is not the final layer of the network, a Rectified Linear Unit (ReLU) non-linear activation is used followed by the Batch Normalization regularization layer. The final layer is followed by a softmax activation to give the output as an estimate of the probability that the current observation is one of the classes specified during training. A visualization of this architecture is shown in Figure 2 for the 10-class AMC classification problem. In this work, is substituted out for the more general to indicate a particular trained network for simplicity. The estimated probability is then written as , where C is the number of classes in the classification problem. By making a hard decision on the inferred estimate, it provides the decision of the network, .
1.1.2. Transfer Learning
TL is the practice of training a model on one dataset/domain (i.e., source), or otherwise taking a pretrained model, and training with a new dataset/domain (i.e., target) instead of starting from a random initialization [28]. Depending on assumptions between the source and target, the TL application can be categorized as homogeneous, where differences exist in the distributions between source and target, or heterogeneous, where the differences are in the feature space of the problem [28,29]. A valuable discussion for understanding the concepts of homogeneous and heterogeneous within the RFML domain is provided by Wong and Michaels [30]. By explaining the different datasets in use, this works as a change in the dataset’s collected/generated domain. The feature space of the problem can be associated with the intended task the source model is trained on and can be contrasted with the task of the target problem. The two most common types of TL include retraining the classification head, where early layers are frozen during training, preserving feature extraction, or fine-tuning of the whole model [31]. In this work, TL is applied in a homogeneous problem space where the underlying distributions of the data vary, but the generalized problem space is the same between datasets. The subset of TL is notated as Domain Adaptation in [30], and more specifically, an Environment Platform Co-Adaptation. Additionally, wherever the retraining is carried out in this work, the fine-tuning approach is utilized, allowing for adjustments to the feature space, which might not be observable in the source dataset. An important note here is that this work does not evaluate any aspect of TL on the problem space (i.e., the evaluation dataset does not change) but rather makes use of metrics developed for the purpose of TL. Understanding how TL is best used within RFML is beyond the scope of this work.
The study of TL is complex and well explored [28,29,30,31,32,33], and from the effort to understand how to choose an optimal pretrained model for a desired application, the metrics Negative Conditional Entropy (NCE) [32], Log Expected Empirical Prediction (LEEP) [31], and Logarithm of Maximum Evidence (LogME) [33] are repurposed to analyze the relationship between available data quantity during training and system performance for a given evaluation set.
In this paper, the evaluation set has the same labels as the training set, but the distributions are not assumed to be equivalent. Therefore, the evaluation set, , is drawn from an observation space, , which is inherent to the generalized problem space, , visualized in Figure 1a,c. For clarity going forward, due to the shared labels between source and target in this work, the source labels are found through a forward pass of the evaluation set through the network; therefore, the observation’s source label is given by , with the inference given as . The process of extracting the evaluation inference of a trained model is visualized in Figure 1e. By contrast, the target label directly gives by the truth of the observation and can be one-hot encoded to provide . Given the above notation, NCE is given as
where are the empirical distributions found as
The source labels are iterated over with j, while k iterates over the target labels. LEEP is given as
where the empirical conditional probability is given as
The LEEP score, for the combination of the model and evaluation set, is given as the average log of all probabilities of obtaining the correct label in the evaluation set given the empirical probability of the labels provided by the model being tested [31]. LogME is given as
where and are iteratively solved to maximize the evidence, , for a linear transform applied to , which is then averaged over the number of classes, C, and normalized by the number of observations, N, in the evaluation set [33].
In the most general sense, the importance of these metrics is how well correlated, either positively or negatively, the metric is with the desired performance of the network after being retrained on the target dataset. Within this work, the explanation provided by You et al. [33] for using Kendall’s coefficient [34] is utilized as the most significant relationship between performance, and the metric of choice is a shared general monotonicity that allows for a trend in the metric to indicate a trend in performance as well.
1.1.3. Automatic Modulation Classification
The RF problem presented in this work is then the classification of the modulation present in the original transmitted waveform . AMC is then the problem of being able to identify how information (or lack thereof) is being applied to a specific time and frequency slice of the overall spectrum. When coupled with the problem of signal detection, whether a waveform present or not in a time and frequency slice, the problem space is often referred to as Automatic Modulation Recognition; however, in this work, the trained network is determining what is there, rather than the additional task of where is it, so AMC is a better category for the task. While AMC is one of the oldest disciplines within RFML, traditional approaches have relied on expert analysis and feature extraction [35,36,37,38], though over the last three decades, heavier reliance on ML has been used for feature fusion and decision -making [39], as well as direct application to raw waveforms [40,41].
To help understand how data quantity and quality affect the performance of the system, there are three primary datasets used while training, and one unique evaluation set for evaluating the performance of all models that are trained. The four datasets are described in Table 1. Captured data make up the first dataset (), along with the evaluation set () such that the two sets are disjoint (). This dataset was collected at Virginia Tech’s Kentland Farms in 2019 over a four-month window. It consists of narrowband transmissions between two Ettus Research B210s stationed at two setup points, which were approximately 110m and 1km apart in their locations, with the first being line-of-sight and the latter having natural occlusions in between them. Data generation occurred using the out-of-tree module “gr-signal_exciter” [42], producing collections of over 20 waveforms with more than 2.1 million examples per class of 1024 complex-baseband samples with sample separations between any two observations being another 1024 samples apart in time. The second set is a synthetic dataset () that makes the waveforms in their pure form, as shown in (7) using the same setup as with the captured dataset’s transmissions except saved to a file rather than transmitted. To increase the practical usage of the synthetic data, synthetic errors are added to the saved data that can be associated with detection algorithms such as Frequency Offset (FO) and Sample Rate Mismatch (SRM), as well as varying the SNR to indicate different received power levels in the dataset. The second and third datasets make use of a Joint Kernel Density Estimate (KDE) on to mimic the distortions of FO, SRM, and SNR within them to attempt to minimize changing the distributions in the data to any extreme. The third dataset, by contrast with , applies synthetic permutations to observations from , thereby creating an augmented dataset. These permutations are similar, if not identical, to the synthetic errors introduced in the synthetic dataset.

Table 1.
Description of datasets used within this work.
Additionally, in order to observe greater diversity in the application of dataset quality and quantity, the work shows the classification performance of three classification groups given in Table 2. These waveforms are selected for the typical usage in qualifying AMC approaches, with the comparison in between BPSK (Binary Phase-Shift Keying) and QPSK (Quadrature PSK) being considered the simplest problem as BPSK carries information only on the in-phase, or real, component while QPSK makes use of both the in-phase and quadrature (IQ) components of a complex baseband signal. The inclusion of Quadrature Amplitude Modulation (QAM) waveforms with 16 and 64 constellation points in increases the difficulty of classification significantly under the same power constraints, with lower SNR values typically completely obscuring the difference between the two QAM modulations. The final waveform set, , further increases the difficulty by introducing analog waveforms with amplitude and frequency variations, as well as Frequency-Shift Keying (FSK) {BFSK, BGFSK, GMSK}, that prevent typical constellation-based reasoning from being the determining factor.

Table 2.
Three waveform sets used in the work.
1.2. RF Characteristics
In the idealized world where the transceivers are in a physically stationary environment, RF signals can be thought of as processing signals at a complex baseband (BB) with a channel between transmitter and receiver. The transmitter’s waveform is then represented as
where the channel introduces a static set of unknowns: gain (); delay (); and phase shift (), and a time-varying additive noise to the receiver observation, in addition to the transmitter’s modulated baseband signal, however, with the received signal being modeled after perfect synchronization, eliminating the static unknowns with a perfect low pass filter results in the received signal given as
The ratio of power in the signal to that of the noise, or the Signal-to-Noise Ratio (SNR), often expressed in dB (), is then the primary limiting factor explaining the performance of the system, with most commonly assumed to be a circularly symmetric complex Gaussian process.
1.2.1. Real-World Degradation
In practice, the problem becomes vastly more complex as relative motion between transceivers, multiple transceivers, environmental noise, environmental motion, unintended radio emissions from man-made devices, multipath interference, and the imperfect hardware that transmits and receives the waveform are introduced. An introduction to the effects of imperfect hardware is given by Fettweis et al. in [43] by looking at the individual degradations the hardware can add to a system, as well as some mitigation strategies that can be applied; however, it is worth mentioning that these degradations are compounding and time-varying, so while the worst of the effects can be calibrated out, the effects persist and cause a separation from the ideals assumed in (8). For an example of how these degradations affect the ideal, here, the frequency-independent In-phase and Quadrature Imbalance (IQI) of the transceivers result in carrier modulation functions that are ideally expressed as for the transmitter for a carrier frequency and for the receiver as
where is the magnitude ratio imbalance and is the phase difference between the quadrature mixer and the in-phase mixer [43]. The ideal carrier modulators are recovered when the magnitude ratio imbalance is unity, , and the phase difference is zero, . This results in an ideal received signal being changed from the ideal baseband transmitted waveform in (8) into
where the is a function for the addition of IQI when both the transmitter’s and receiver’s parameters are known in the received signal as an additive interference, given as
1.2.2. Understanding RF Data Origin
There are three common sources of data within ML dataset generation [8]. The first is the captured or collected data acquired by using a sensor and recording the data. Under the most intuitive conditions, data collection performed using this approach in the application space provides the highest quality of data for the problem to learn from because all unknown characteristics and sensor degradations will be present in the data [41]. However, when performing the capture of rare events or while in search of other infrequent and uncontrollable events, performing collection events can prove to be difficult to properly label, let alone find. These problems, along with having to procure and sustain the equipment and personnel to perform the collection, often make collection in large quantities impractical and expensive.
Synthetic datasets are therefore the most common and typically orders of magnitude cheaper to procure due to not being bound to waiting on real-world limitations. For example, synthetic generation can occur in parallel for vastly different conditions, with the limitation being computation resources, rather than the sensors and personnel in collection events. The trade-off with synthesis is that significantly more information on the data is necessary in order to properly simulate, which, without the appropriate knowledge, can render models in the field useless [41].
The process of creating an augmented dataset tries to bridge the strengths of captured and the synthetic dataset creation, while covering their weaknesses [8]. By taking captured data and adding synthetic permutations of SNR, FO, and SRM, the augmented dataset can smooth out missing observations from a limited collection event by having a better understanding of the detection characteristics of the sensors in use, while preserving all other real-world degradations native to the application space.
Here, the different origins of data are kept separate from each other to achieve a better understanding of the characteristics of each approach, but the fusion of such datasets should be carried out either by directly combining the datasets or by performing staged learning in practice.
2. Materials and Methods
The work performed in Clark et al. [41] showed that, within the realm of AMC, the quantity of data has a functional relationship to the performance of a trained system given all other variables are constant. Additionally, the work showed that the performance could be found to have a log-linear, or power-law, relation to the quantity of data for lower performance regions, but a log-sigmoidal relationship is more appropriate as the performance reaches a maximum. The process of regressing the relationship between quantity and performance was then suggested as a quantification measure of dataset quality in [44], where different datasets could then be compared across different quantities with the expected accuracy (e.g., dataset A needs X observations, while dataset B needs observations to achieve an accuracy of ), or another metric of performance, taken as the quality ( or in the previous example) of the dataset. The inherent quality of any dataset can be described in three generalized terms: Comprehensiveness, Correctness, and Variety [25]. In this work, the datasets are already examined and confirmed to be Comprehensive, in that all the information being sought is included within the dataset, and Correct, in that the observations for each modulation are correctly identified and labeled. The main concept of quality being examined is then that of Variety or rather that the distributions on the observations within the datasets match, approximate, or deviate from the distributions of the test set, and therefore, only the effect of quality in terms of Variety can be examined in this work.
While these works give an initial understanding of the data quantity and quality that fundamentally drive the process of an ML system, they provide minimal utility when trying to understand how many data are needed in order to achieve ideal performance and therefore reliably plan a data collection campaign. For example, in [44] fourth figure that is looking at the 10-class classification performance, the log-linear fit predicts a performance of 90% accuracy at roughly an order of magnitude less data than the corresponding log-sigmoidal fit, while both fits use the full range of trials available to regress the fit. The results discussed above all depend on some initial good dataset to contrast with, and while this work does not alleviate that requirement, here, we answer the question of how to best use a limited good dataset to forecast how many total data would be needed during training if neither the model nor training approach is modified.
An ideal approach would be to use a metric that is both strongly correlated with the desired performance of the system, such as accuracy, in terms of Kendall’s and has a relationship with data quantity that can be linearly derived from minimal data; however, a metric that reduces the error over that of performance directly regressed with quantity will be sufficient. For this reason, the metrics that have been developed to predict the transferability of a pretrained model onto a new target dataset, discussed in Section 1.1.2, are repurposed to predict data quantity requirements and provide a new metric of quality for a model’s training dataset with regard to the target dataset, which is the evaluation dataset in this work, as shown in Figure 1c.
2.1. Examining the Correlation between Performance and Metrics
The first step is the confirmation that the chosen metrics correlate in a beneficial manner with the performance value of interest, which is classification accuracy in this case. In order to understand whether a metric is well correlated with classification accuracy, the weighted Kendall’s is calculated using the SciPy implementation [45] and found for three datasets (Table 1: ) and compared against three sets of modulation classification sets (Table 2: ). Kendall’s weighted correlations are presented in Table 3 and show high values of correlation for all three metrics in the case of and datasets; however, the correlation for the dataset shows a worse correlation between accuracy and all three metrics. Looking at the performance at the relationships between performance and the proposed metrics in Figure 3 shows that the performance and metrics are tightly clustered, while for and , definite trends are observable. Looking at the performance of the different datasets as a function of quantity used during training in Figure 4 helps to further explain this decrease in correlation in that the performance results of networks trained on are comparably independent of the quantity of data used for the synthetic observations. Therefore, the classification accuracy and metrics extracted from the networks trained on are more akin to noisy point measurements rather than a discernible trend to examine.

Table 3.
Kendall’s weighted correlation across datasets () and waveform sets for Accuracy and (NCE, LEEP, LogME). Strong correlations will have an absolute value near 1, while no discernible correlation will be around 0. Bold values represent the combination of the problem set and metric with the highest correlation with accuracy on the evaluation set.
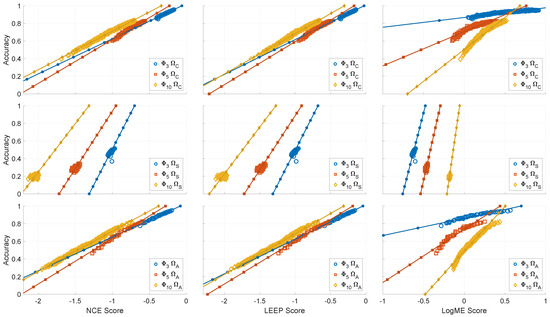
Figure 3.
Visualization of the relationships between the three metrics (Left column: NCE, Middle column: LEEP, Right column: LogME) and the performance metric (Accuracy) of each network when measured on the results of the evaluation set , or the target dataset in TL vernacular. Each dataset used for training is positioned along the rows (Top row: , Middle row: , Bottom row: ).

Figure 4.
Relationship between the quantity of data used from each dataset (Top: , Middle: , Bottom: ) and the accuracy achieved by networks trained on that amount of data.
The main observation is that when there is a discernible trend between performance and data quantity, the correlation of all three metrics is considerably high, and therefore, 5h3y are potential metrics with which to regress the relationship with data quantity in search of a quantity estimator for the total data needed to achieve the desired performance.
2.2. Regression of Quantity and Metrics
With the confidence that the TL metrics discussed above have a positive and significant correlation with the performance of the system when performance increases with regard to the quantity of data used during training, the goal is to now derive the relationship between those metrics and data quantity, with preference being given to the metric that has a better goodness of fit (GoF) with a form of linear regression. In this case, a log-linear regression is used between the metrics and the data quantity. Starting with the accuracy of each network shown in Figure 4, the log-linear fit is able to provide a quality value in terms of the accuracy achievable for a given number of observations per class (OPCs) for the three datasets. Looking at the problem set shows the quality quantification as follows:
- accuracy M OPC
- accuracy M OPC
- accuracy M OPC,
but the quality can just as easily be defined as the OPC needed in order to achieve a given accuracy given the linear fit can be inverted as
- M OPC accuracy
- OPC accuracy
- M OPC accuracy.
However, the log-linear regression between data quantity and accuracy has an undesired effect between the data points and the linear fit, which is that at the ends of the available data, there is increased error relative to the center of the data points. Additionally, because the sign of error is the same at both ends, this suggests that the linear fit between data quantity and accuracy when there are minimal data will severely underestimate the data quantity needed to achieve high-performance systems. For a better look at this issue, Figure 5 examines the residuals for the waveform set across the three dataset types.
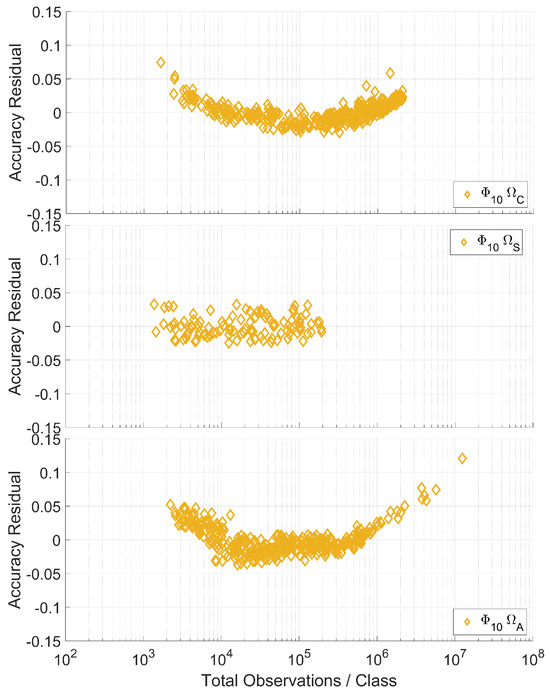
Figure 5.
Residuals between the regressed log-linear fits of the quantity of data available during training and the accuracy of each trained network and the observed accuracy of each network.
This same sign of error at the ends of the available data suggests that a non-log-linear fit would be more appropriate for regressing the relationship between accuracy and data quantity, which is poorly suited to understanding the full relationship as available data become more limited to a narrow subset of the full data range. For example, just looking at a narrow portion of either end, with high or low data quantity, does not provide enough context to predict a good non-linear fit. Therefore, a GoF measure that weights the outer errors more significantly than the errors toward the center of the data range is desired. Additionally, since both edges of the residual are of equal significance and the results are non-uniformly sampled across the observation space, a weighting that balances the weights into histogram bins will be used to normalize equal significance in the edges of the GoF measure. For simplicity, three bins will be used to indicate observations with lower, mid, and high data quantity relative to the log-linear fit. The weights are suggested as
where the middle bin has one-third the weight of the edges, which without it, would have all three regions equally weighted. The division edges between bins are taken as evenly spaced on the log scale between the minimum and maximum data quantities in the set, with being the number of elements in the set, while are the numbers of observations within that bin. Those weights are then normalized such that their sum is unity. The GoF is then taken as the Normalized Root Weighted Mean Squared Error (NRWMSE).
where the quantities () and accuracies () are used to derive the log-linear fit (); however, the accuracies and fit can be swapped out for any other metric and matching fit.
The GoF for the accuracy, NCE, LEEP, and LogME metrics are given in Table 4. A general conclusion is that all three metrics have the potential to provide a better prediction of data quantity needed to achieve high performance; however, considering the correlation presented in Table 3 in addition to these results suggests that NCE will be the most consistent estimate, with LEEP being a close second. LogME, by comparison, offers the most promise with regard to the augmented dataset but has the highest variability among the three metrics examined here. One more unique attribute about the linear regressions of the metrics is that accuracy, NCE, and LEEP all have residuals typically indicating that the true quantity of data that are needed will be underestimated, while LogME’s residuals are inverted, suggesting that that LogME’s regression will overestimate the number of data, giving soft bounds of the required quantity of data being between the estimates of NCE and LogME predictions.

Table 4.
Goodness of fit (GoF) for a log-linear regression between dataset quantity available for training across datasets () and waveform sets () for Accuracy () and NCE, LEEP, LogME. Perfect fit would have a value of 0. Bold values represent the best GoF value for the log-linear regression between the metric and data quantity available during training.
2.3. Predicting the Data Quantity Needed
Now that the metrics have been compared in terms of a regressed log-linear fit with the quantity of data used to train the model, the question is how to determine what value of the metrics will provide the desired performance. Looking back at Figure 3 shows that the metrics and accuracy do not have an easily fit relationship that would map a metric back to accuracy, and in fact, it would only be trading one non-linear regression for another. To overcome this problem, label whitening to acquire near-perfect performance is proposed to act as a quasar that can help map the performance of the metrics with accuracy.
The procedure starts with label smoothing [46] (14) of the truth labels for the evaluation set, followed by a logit transform (15), which, without the label smoothing, would not be a useful approach as infinite values would be returned for the correct class and negative infinity for all other classes.
Label smoothing applied on its own does not affect the value of accuracy, NCE, nor LogME, but it does affect the LEEP score and is dependent on the smoothing factor, , and the number of classes in the classification problem, C. The effect of on the LEEP metric can significantly affect the metric, so is chosen as the minimum value that approaches within the chosen machine precision. The effect of label smoothing and the logit transform allows for the values to now sit at a finite coordinate to which noise can be added to stochastically decrease the accuracy of the system in a controlled manner. The normal distribution is used to whiten the logits, in this case, where the standard deviation of the noise, , can be chosen for the degradation of accuracy, , of the true labels given the number of classes in the problem space and the label smoothing in use.
With the whitened logits the inverse logit, or logistic, transform is applied and balanced such that the sum of any result is unity, .
Figure 6 shows the effects of this procedure on the error and metrics for a given averaged over 1000 iterations and shows a trend that can be maintained with increasing ; however, an important note is that this type of error does not properly reflect the distributions of error that can be expected, so smaller values () of will likely be more appropriate than larger values (). Looking at the residual error, (19), in terms of the dependent variable, , relative to the measured value, , as seen in the top left plot of Figure 6, the minimum average error across the three classes is achieved at , with the average normalized residuals being nearly equal at the extremes ().
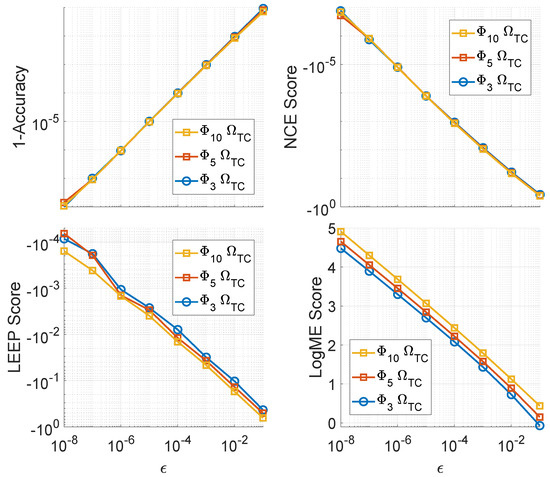
Figure 6.
The change in the values of {Top Left: Accuracy (1-Accuracy, log scale); Top Right: NCE (log scale); Bottom Left: LEEP (log scale); Bottom Right: LogME (linear scale)} as a function of the induced error, , expected to achieve accuracy from the whitening the truth labels of the evaluation set . The results plotted are the average values over 1000 iterations per data point.
At this point, a means for determining the value for each metric has been proposed that will not suffer from the need to have a perfect response that can be used and will help with metrics such as LogME, where the maximum is not immediately known given the iterative solution that is employed to produce the score. These values for a given small can then be used to regress the corresponding metric’s data estimate for achieving such performance. The log-linear regressions for each metric, dataset, and waveform space combinations are shown in Figure 7, while the log-linear regressions for accuracy are shown in Figure 3, and together help to better visualize the GoF results given in Table 4.
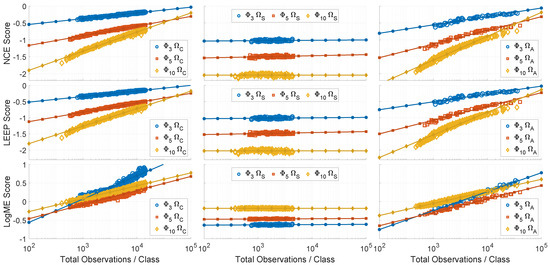
Figure 7.
Relationship between the quantity of data used from each dataset (Left: , Center: , Right: ) and the metric (Top: NCE, Middle: LEEP, Bottom: LogME) achieved by networks trained on that amount of data.
Making use of the whitening procedure above and the log-linear regressions between data quantity and the metric’s score, a prediction of data quantity needed to achieve arbitrarily high performance can then be found. For example, applying an error of to each examined problem space for the metrics and selecting a value averaged over 1000 iterations, the data quantity predictions can be made for each metric, as shown in Table 5, where the predictions are found by inverting the linear fit to estimate the quantity from the predicted metric as
where the value is the logarithm base ten of the quantity estimate for the selected metric Accuracy, NCE, LEEP, LogME], is the metric value found through the whitening procedure, and are the slope and y-intercept, respectively, of the log-linear regression given a base ten logarithm applied.

Table 5.
The performance of Accuracy (), NCE, LEEP, and LogME for the label whitening procedure proposed in Section 2 for a desired error . Additionally, the data quantity needed per metric for the log-linear regression of the metric with the data quantity used during training is provided.
3. Results and Discussion
The prior sections made use of all data points taken in order to establish the best predictions for data quantity with their given metric. As these are estimates that are intended to predict the data quantity needed to achieve high-performance systems through the increase in available data alone, certifying any result in particular is beyond the scope of this work, as the expected predicted quantities will far exceed the available data acquired. Instead, the focus shifts to how having fewer data available during training relatively affects the prediction capability for each metric in comparison to greater quantities of available data.
Due to the performance of the synthetic dataset stagnating, further analysis will ignore this case going forward. For the purpose of finding how well the log-linear regression with each metric is able to predict the data quantity needed, the data quantities provided in Table 5, with preference for a quantity estimate given by the GoF in Table 4, will be used such that the metric that achieved the best GoF will be used as the truth for the problem space. Therefore, predictions of the models making use of will use the LEEP metric’s quantity prediction for and but will make use of the NCE prediction for , while the predictions for will all make use of the LogME metric, and these quantity prediction are summarized in Table 6. The predictions for each metric can be seen in Figure 8, where the top row shows the predictions when using the dataset, while the bottom shows the predictions for the dataset. The columns consist of waveform spaces {,,} from left to right.

Table 6.
Quantity estimates being taken as truth for the combinations of waveform groups, , and training datasets, . The augmented quantities are estimated using the LogME metric regression, while the captured quantities are estimated from either the NCE or LEEP metric based on the GoF in Table 4.
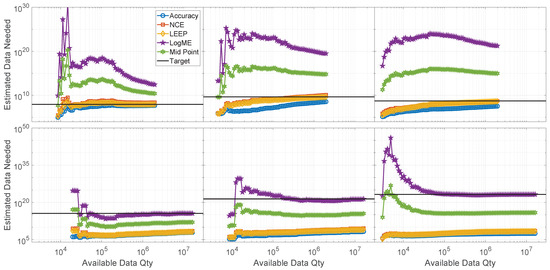
Figure 8.
Quantity predictions based on a limited number of available data used to regress the estimate on the {Top Row: Capture ; Bottom Row: Augmented } datasets when being used to estimate across the {Left: ; Center: ; Right: } waveform space. The lines represent using {Accuracy: circle, NCE: square, LEEP: diamond, LogME: pentagram, Log Scale Midpoint of NCE and LogME: hexagram, Target: none} to predict data quantity needed, while Target is determined in Table 6.
The general understanding given in Figure 8 is that both NCE and LEEP will give a more realistic prediction for data quantity than Accuracy alone, while the prediction given by LogME can serve as an upper bound. Due to the log-linear regression, any deviation can result in orders of magnitude error in terms of either underestimation or overestimation, and since there are not enough data to acquire the metric that produces the best GoF regression, a midpoint estimate is recommended when only minimal data are available. The midpoint estimate seeks to balance the two extremes such that the estimate becomes , such that the midpoint estimate averages the quantity estimates on the log scale rather than the linear.
Returning to Table 6, an important note is understanding how long a sequential collection of data of this kind would take in order to accomplish; that is, for a collection that records at 10kHz, these waveforms from three waveform groups {,,}, a collection of the number of observations implied, would require [1.72, 144.5, 33.4] years to acquire the target observations needed for the predictions and would require [0.989, 82.9, 19.1] terabytes of storage to store them in an uncompressed state. While this could be feasible if the collection was performed in a parallel rather than a sequential collection, the suggestion that should be taken rather than immediately starting a long-term collection is to instead improve the training routine and model architecture to instead allow for this procedure to produce a regression with a more significant slope than the approach used to produce these results.
4. Conclusions
The problem of estimating the number of data needed in order to achieve a high-performing ML model for AMC problems is discussed within this work. Typical approaches in this type of estimate focus on reducing the loss function rather than performance metrics of interest, whereas this provides a direct linking of performance to the available dataset size required to achieve it before performing costly collections and data acquisition. While if large quantities of data are already available, observations per class in the problem presented in this work, a log-scale nonlinear regression between performance and data quantity can help to determine how many more data are needed, which is often not feasible for problems with only a small number of data on hand (i.e., observations per class) due to the potential for the asymptotic bends in performance not being visible, leading to the performance of power-law estimations to significantly underestimating the amount required. The metrics developed for TL in order to choose a model to help linearize, on a log scale, the relation between accuracy predictions and data quantity can be used by utilizing the metrics NCE, LEEP, and LogME. These metrics in turn can help bring a bound to the number of data that would be needed with a current approach and help determine whether a large-scale data collection should take place or if further refinement to the training procedure and model architecture is a better approach given the program’s constraints. Given the tendency for NCE and LEEP metrics to underestimate the numbwe of data needed (to a lesser extent than power-law approaches) and the tendency of LogME to overestimate the number of data, a midpoint approach is proposed, on a log scale, between NCE and LogME to offer a balanced estimate. Given that NCE and LEEP offer similar performance estimates and GoF measures on the collected dataset problems, and LogME is seen to offer a better GoF for the augmented dataset problems, and balancing the two offers a more reasonable measure under data-constrained conditions when performing an estimate.
While this approach shows traction within the RFML problem space of AMC, additional research is still needed in order to understand if these techniques can be more widely applied to other classification problem spaces in ML in general.
Author Contributions
Conceptualization, W.H.C.IV and A.J.M.; methodology, W.H.C.IV; software, W.H.C.IV; validation, W.H.C.IV; formal analysis, W.H.C.IV; investigation, W.H.C.IV; resources, A.J.M.; data curation, W.H.C.IV; writing—original draft preparation, W.H.C.IV; writing—review and editing, W.H.C.IV and A.J.M.; visualization, W.H.C.IV; supervision, A.J.M.; All authors have read and agreed to the published version of the manuscript.
Funding
This research is based upon work supported, in part, by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA). The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of ODNI, IARPA, or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes, notwithstanding any copyright annotation therein.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of a corporate IRAD effort and the authors are unable to distribute.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Oxford University Press. Machine Learning. In Oxford English Dictionary, 3rd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Sanders, H.; Saxe, J. Garbage In, Garbage Out: How Purportedly Great ML Models can be Screwed up by Bad Data; Technical Report; Black Hat: Las Vegas, NV, USA, 2017. [Google Scholar]
- O’Shea, T.; West, N. Radio Machine Learning Dataset Generation with GNU Radio. In Proceedings of the GNU Radio Conference, Boulder, CO, USA, 6 September 2016; Volume 1. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://tensorflow.org (accessed on 7 January 2020).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Glasgow, UK, 2019; pp. 8024–8035. [Google Scholar]
- Blossom, E. GNU Radio: Tools for Exploring the Radio Frequency Spectrum. Linux J. 2004, 2004, 122. [Google Scholar]
- Gaeddart, J. Liquid DSP. Available online: https://liquidsdr.org/ (accessed on 7 January 2020).
- Wong, L.J.; Clark, W.H., IV; Flowers, B.; Buehrer, R.M.; Headley, W.C.; Michaels, A.J. An RFML Ecosystem: Considerations for the Application of Deep Learning to Spectrum Situational Awareness. IEEE Open J. Commun. Soc. 2021, 2, 2243–2264. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 7 January 2020).
- Cengiz, A.B.; McGough, A.S. How much data do I need? A case study on medical data. In Proceedings of the IEEE International Conference on Big Data (BigData), Sorrento, Italy, 15–18 December 2023; pp. 3688–3697. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Zhao, X. How Much Data is Sufficient for Neural Transliteration? In Proceedings of the 2022 International Conference on Asian Language Processing (IALP), Singapore, 27–28 October 2022; pp. 470–475. [Google Scholar] [CrossRef]
- Meyer, B.M.; Depetrillo, P.; Franco, J.; Donahue, N.; Fox, S.R.; O’Leary, A.; Loftness, B.C.; Gurchiek, R.D.; Buckley, M.; Solomon, A.J.; et al. How Much Data Is Enough? A Reliable Methodology to Examine Long-Term Wearable Data Acquisition in Gait and Postural Sway. Sensors 2022, 22, 6982. [Google Scholar] [CrossRef] [PubMed]
- Ng, L.H.X.; Robertson, D.C.; Carley, K.M. Stabilizing a supervised bot detection algorithm: How much data is needed for consistent predictions? Online Soc. Netw. Media 2022, 28, 100198. [Google Scholar] [CrossRef]
- Balcan, M.F.; DeBlasio, D.; Dick, T.; Kingsford, C.; Sandholm, T.; Vitercik, E. How much data is sufficient to learn high-performing algorithms? Generalization guarantees for data-driven algorithm design. In Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing, STOC 2021, New York, NY, USA, 21–25 June 2021; pp. 919–932. [Google Scholar] [CrossRef]
- Estepa, R.; Díaz-Verdejo, J.E.; Estepa, A.; Madinabeitia, G. How Much Training Data is Enough? A Case Study for HTTP Anomaly-Based Intrusion Detection. IEEE Access 2020, 8, 44410–44425. [Google Scholar] [CrossRef]
- Besser, K.L.; Matthiesen, B.; Zappone, A.; Jorswieck, E.A. Deep Learning Based Resource Allocation: How Much Training Data is Needed? In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, D.; Liu, P.; Wang, H.; Beadnall, H.; Kyle, K.; Ly, L.; Cabezas, M.; Zhan, G.; Sullivan, R.; Cai, W.; et al. How Much Data are Enough? Investigating Dataset Requirements for Patch-Based Brain MRI Segmentation Tasks. arXiv 2024, arXiv:2404.03451. [Google Scholar] [CrossRef]
- Mühlenstädt, T.; Frtunikj, J. How much data do you need? Part 2: Predicting DL class specific training dataset sizes. arXiv 2024, arXiv:2403.06311. [Google Scholar] [CrossRef]
- Mahmood, R.; Lucas, J.; Acuna, D.; Li, D.; Philion, J.; Alvarez, J.M.; Yu, Z.; Fidler, S.; Law, M.T. How Much More Data Do I Need? Estimating Requirements for Downstream Tasks. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 275–284. [Google Scholar] [CrossRef]
- Cortes, C.; Jackel, L.D.; Solla, S.; Vapnik, V.; Denker, J. Learning Curves: Asymptotic Values and Rate of Convergence. In Proceedings of the Advances in Neural Information Processing Systems; Cowan, J., Tesauro, G., Alspector, J., Eds.; Morgan-Kaufmann: Denver, CO, USA, 1993; Volume 6. [Google Scholar]
- Kaplan, J.; McCandlish, S.; Henighan, T.; Brown, T.B.; Chess, B.; Child, R.; Gray, S.; Radford, A.; Wu, J.; Amodei, D. Scaling Laws for Neural Language Models. arXiv 2020, arXiv:2001.08361. [Google Scholar]
- Caballero, E.; Gupta, K.; Rish, I.; Krueger, D. Broken Neural Scaling Laws. arXiv 2023, arXiv:2210.14891. [Google Scholar]
- Bahri, Y.; Dyer, E.; Kaplan, J.; Lee, J.; Sharma, U. Explaining neural scaling laws. Proc. Natl. Acad. Sci. USA 2024, 121, e2311878121. [Google Scholar] [CrossRef]
- Bordelon, B.; Atanasov, A.; Pehlevan, C. A Dynamical Model of Neural Scaling Laws. arXiv 2024, arXiv:2402.01092. [Google Scholar]
- Chen, H.; Chen, J.; Ding, J. Data Evaluation and Enhancement for Quality Improvement of Machine Learning. IEEE Trans. Reliab. 2021, 70, 831–847. [Google Scholar] [CrossRef]
- West, N.E.; O’Shea, T. Deep architectures for modulation recognition. In Proceedings of the 2017 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 6–9 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Flowers, B.; Headley, W.C. Adversarial Radio Frequency Machine Learning (RFML) with PyTorch. In Proceedings of the 2019 IEEE Military Communications Conference (MILCOM 2019), Norfolk, VA, USA, 12–14 November 2019. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Wong, L.J.; Michaels, A.J. Transfer Learning for Radio Frequency Machine Learning: A Taxonomy and Survey. Sensors 2022, 22, 1416. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.V.; Hassner, T.; Archambeau, C.; Seeger, M.W. LEEP: A New Measure to Evaluate Transferability of Learned Representations. arXiv 2020, arXiv:2002.12462. [Google Scholar]
- Tran, A.; Nguyen, C.; Hassner, T. Transferability and Hardness of Supervised Classification Tasks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1395–1405. [Google Scholar] [CrossRef]
- You, K.; Liu, Y.; Wang, J.; Long, M. LogME: Practical Assessment of Pre-trained Models for Transfer Learning. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; Volume 139, pp. 12133–12143. [Google Scholar]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Dandawate, A.V.; Giannakis, G.B. Detection and classification of cyclostationary signals via cyclic-HOS: A unified approach. SPIE 1992, 1770, 315–326. [Google Scholar] [CrossRef]
- Swami, A.; Sadler, B. Hierarchical digital modulation classification using cumulants. Commun. IEEE Trans. 2000, 48, 416–429. [Google Scholar] [CrossRef]
- Headley, W.; da Silva, C. Asynchronous Classification of Digital Amplitude-Phase Modulated Signals in Flat-Fading Channels. Commun. IEEE Trans. 2011, 59, 7–12. [Google Scholar] [CrossRef]
- Dobre, O.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. Commun. IET 2007, 1, 137–156. [Google Scholar] [CrossRef]
- Nandi, A.; Azzouz, E. Modulation recognition using artificial neural networks. Signal Process. 1997, 56, 165–175. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional Radio Modulation Recognition Networks. In Proceedings of the Engineering Applications of Neural Networks; Jayne, C., Iliadis, L., Eds.; Springer: Cham, Switzerland, 2016; pp. 213–226. [Google Scholar]
- Clark, W.H., IV; Hauser, S.; Headley, W.C.; Michaels, A.J. Training data augmentation for deep learning radio frequency systems. J. Def. Model. Simul. 2021, 18, 217–237. [Google Scholar] [CrossRef]
- Clark, W.H., IV. Efficient waveform spectrum aggregation for algorithm verification and validation. In Proceedings of the GNU Radio Conference, Boulder, CO, USA, 6 September 2016. [Google Scholar]
- Fettweis, G.; Lohning, M.; Petrovic, D.; Windisch, M.; Zillmann, P.; Rave, W. Dirty RF: A new paradigm. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; Volume 4, pp. 2347–2355. [Google Scholar] [CrossRef]
- Clark, W.H., IV; Michaels, A.J. Quantifying Dataset Quality in Radio Frequency Machine Learning. In Proceedings of the MILCOM 2021 Track 1-Waveforms and Signal Processing (MILCOM 2021 Track 1), San Diego, CA, USA, 29 Novembar–2 December 2021. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.; Kornblith, S.; Hinton, G. When does label smoothing help? In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2024; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).