Optimizing Priority Queuing Systems with Server Reservation and Temporal Blocking for Cognitive Radio Networks
Abstract
1. Introduction
1.1. Motivations
1.2. Contributions
- The study introduces two priority models, non-pre-emptive and pre-emptive, within the M/D/1 framework to address SU starvation in CRNs with a high PU arrival rate.
- The research compares the proposed non-pre-emptive and pre-emptive priority models and an M/D/1 model with PU delay to determine which improves the average total waiting time for PUs and SUs.
- Numerical analysis and Monte Carlo simulations are used to analyze the suggested models’ impact on waiting times in different scenarios, helping to elucidate system dynamics.
- To model real-time systems, the research extends the proposed models to include finite buffer capacity for both PUs and SUs, leading to significant improvements in average total waiting time with non-pre-emptive and pre-emptive priority.
- The suggested models improve average total waiting time for PUs and SUs, providing useful insights for priority-scheme design and optimization in CR networks with high PU arrival rates.
2. Related Work
3. Proposed Framework
Delay by PUs
- (i).
- Scheme 1: M/D/1 with PU delay and non-pre-emptive priority model
- (ii).
- Scheme 2: M/D/1 with PU delay and pre-emptive priority model
| Algorithm 1: Algorithmic workflow of the proposed framework. | |||
| 1. | Initialize system parameters: | ||
| 2. | Initialize system state: | ||
| 3. | Set waiting time of SUs to 0 | ||
| 4. | Set waiting time of PUs to 0 | ||
| 5. | For do | ||
| 6. | Generate random number of arrivals for PUs according to Poisson distribution with rate | ||
| 7. | Generate random number of arrivals for SUs according to Poisson distribution with rate | ||
| 8. | Update the current number of PUs and SUs in the system: | ||
| 9. | If | ||
| 10. | Discard incoming requests | ||
| 11. | End If | ||
| 12. | If | ||
| 13. | Dequeue first user from buffer | ||
| 14. | Update and as per user type | ||
| 15. | Update remaining service time of users in | ||
| 16. | End If | ||
| 17. | Repeat steps 12 to 16 until all users get service | ||
| 18. | End For | ||
| 19. | Calculate total average waiting time and for SUs and PUs | ||
| 20. | Exit | ||
4. Performance Analysis of Proposed Algorithm
4.1. Time Complexity
4.2. Convergence Speed
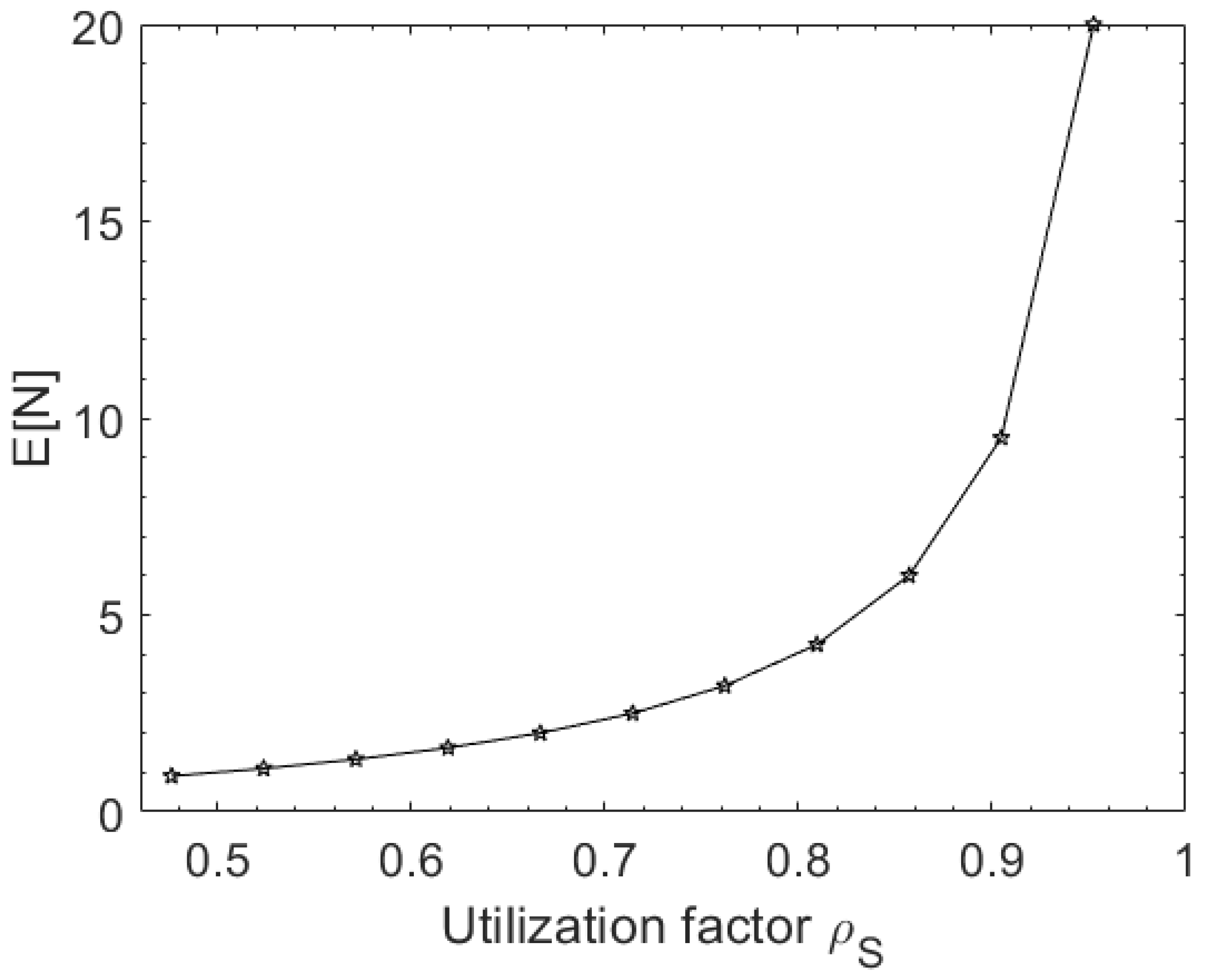
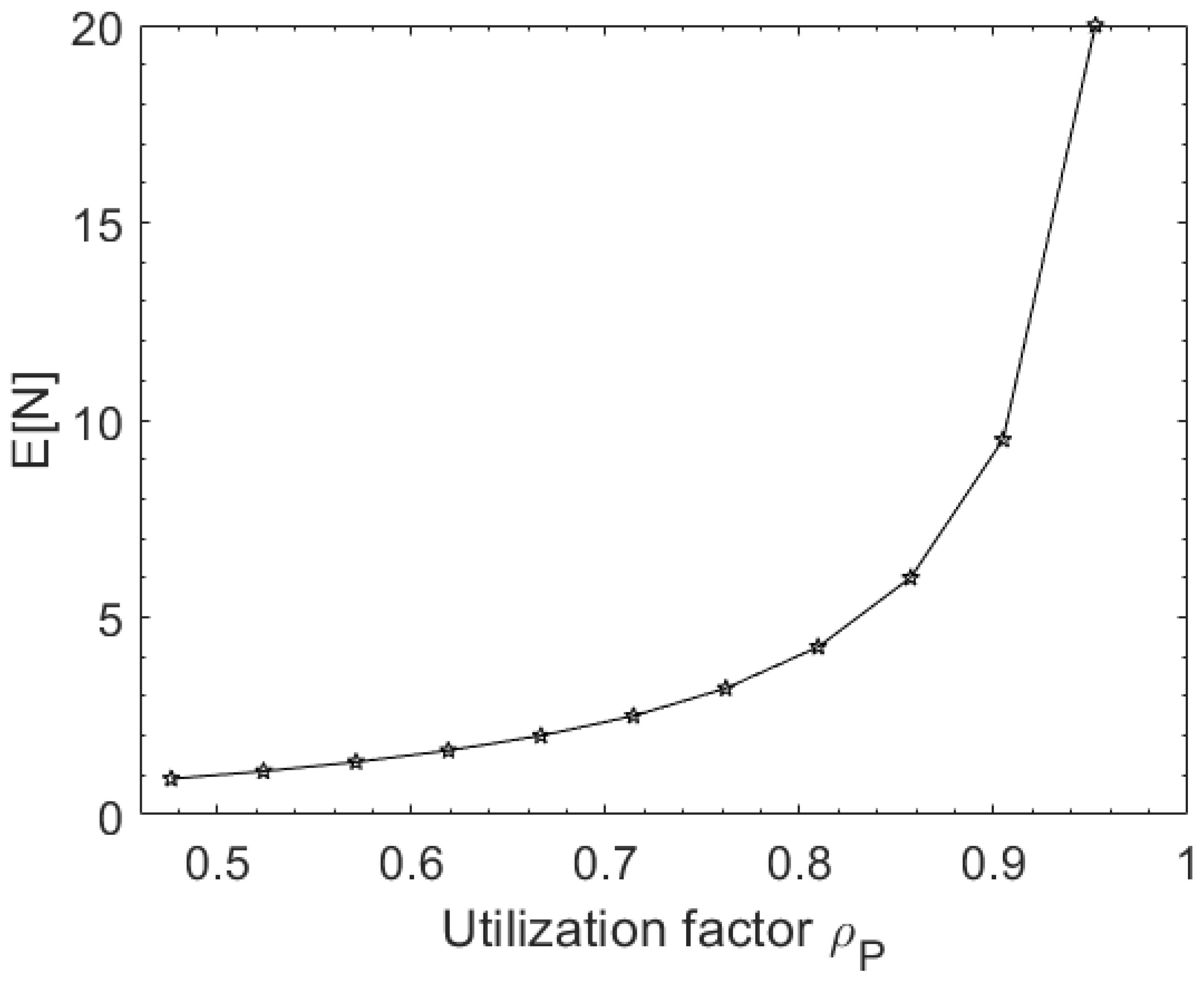
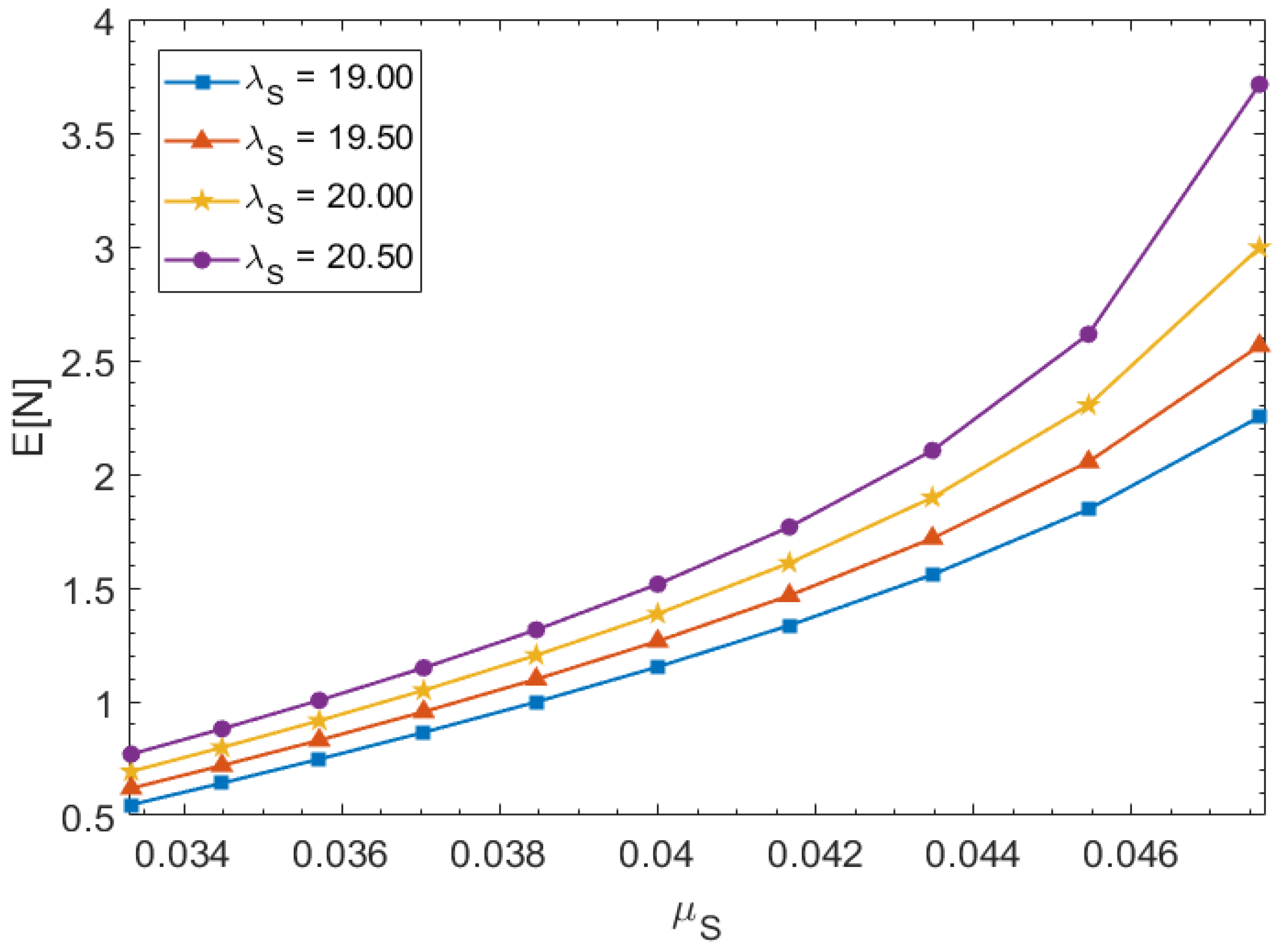
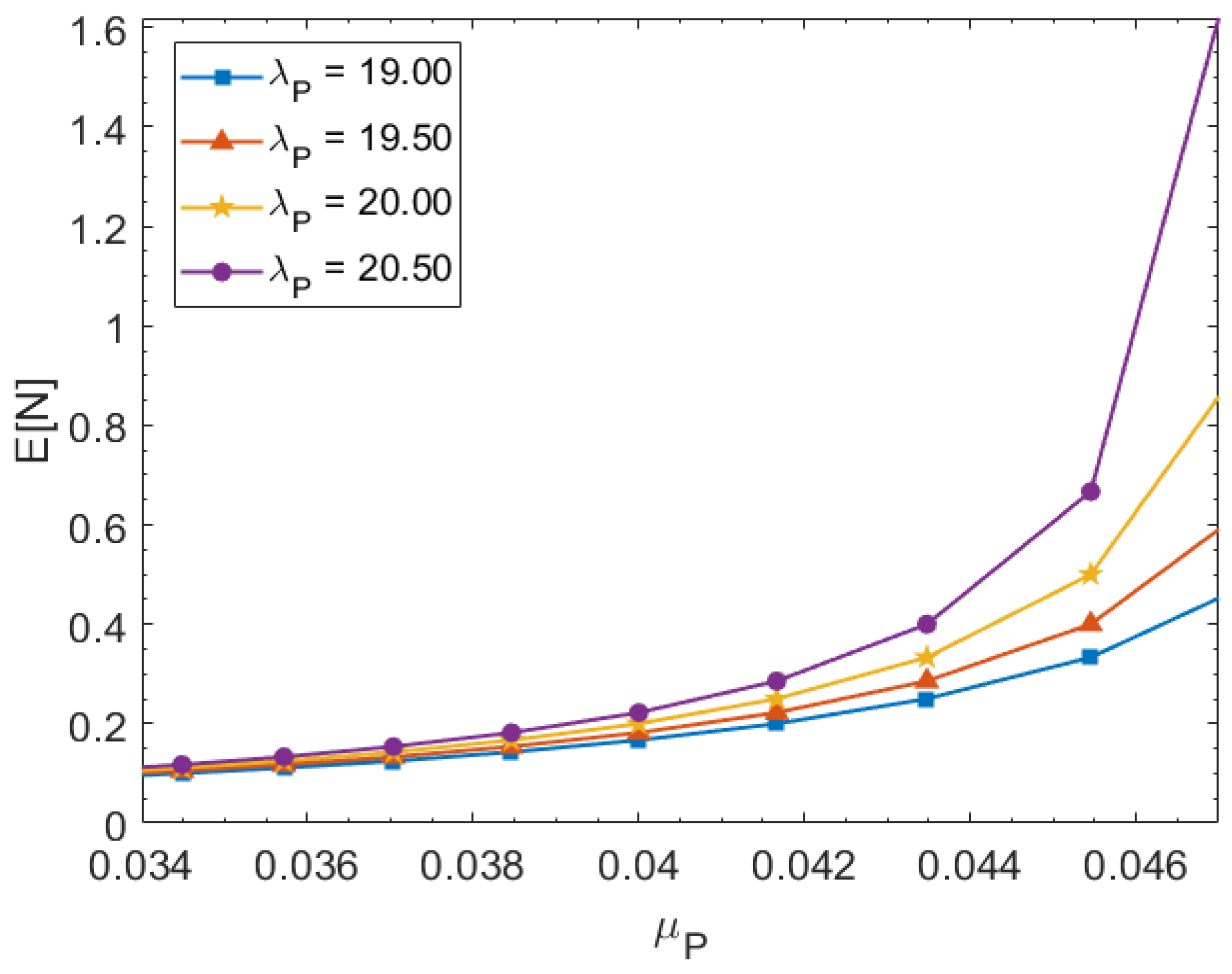
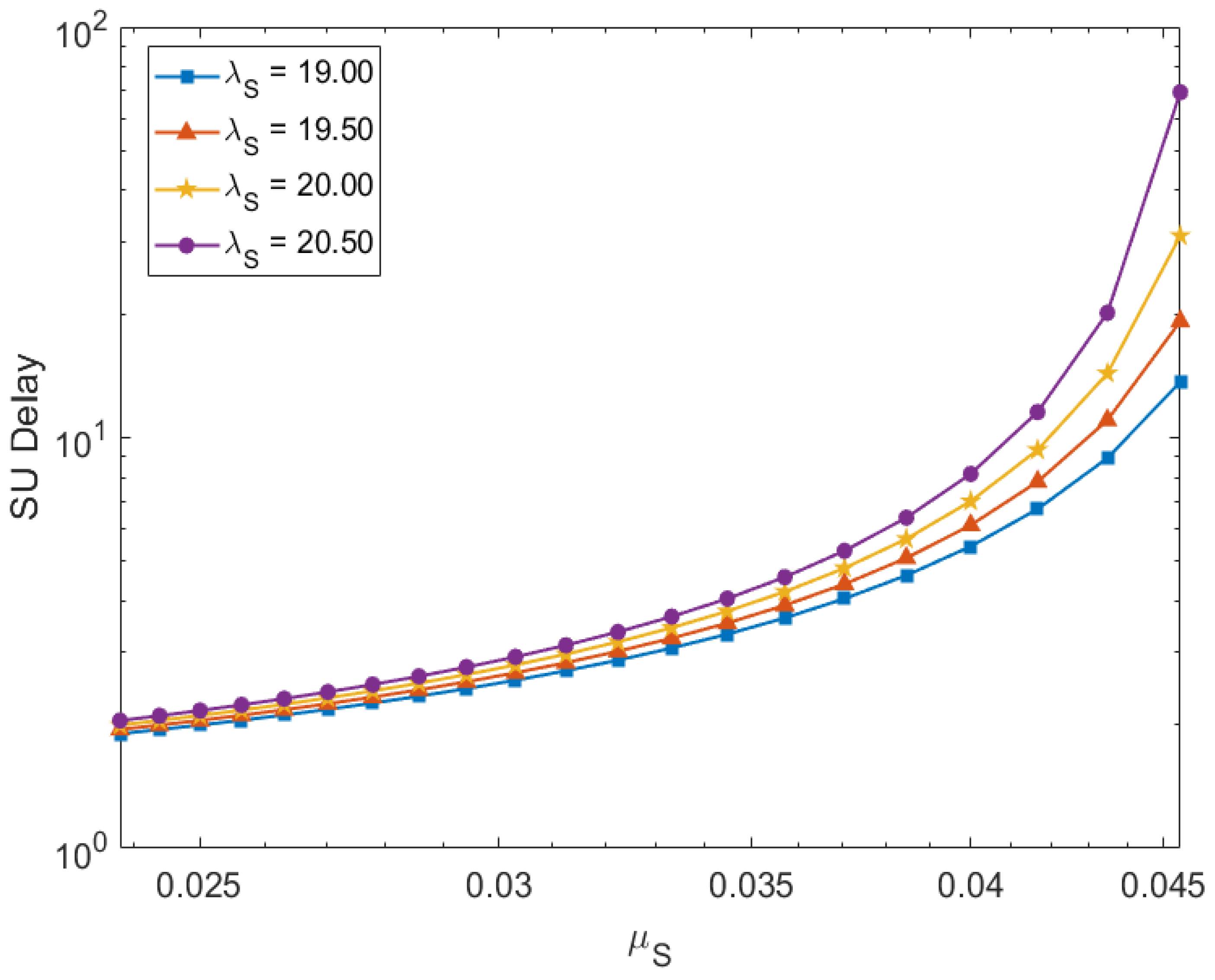
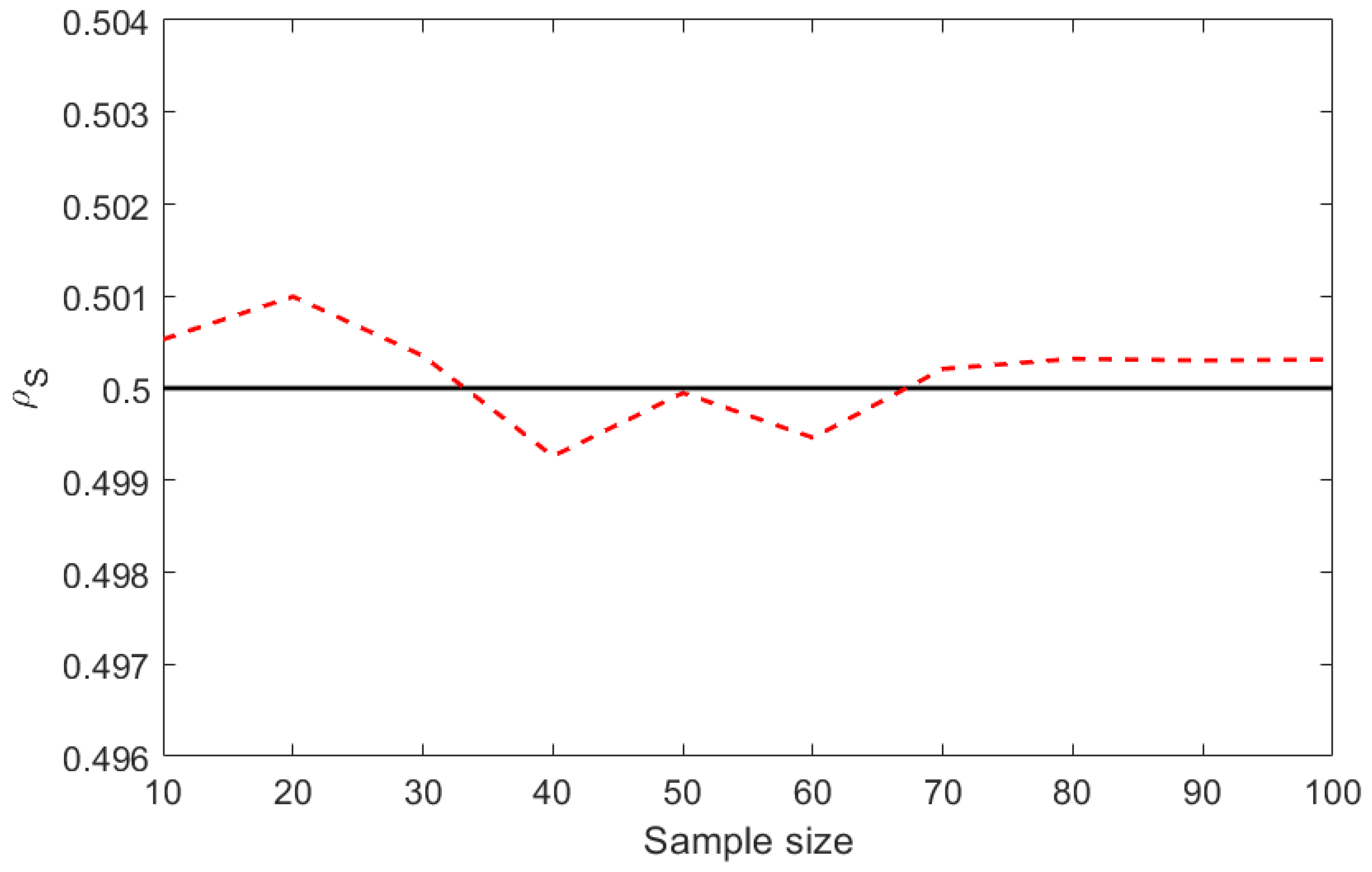
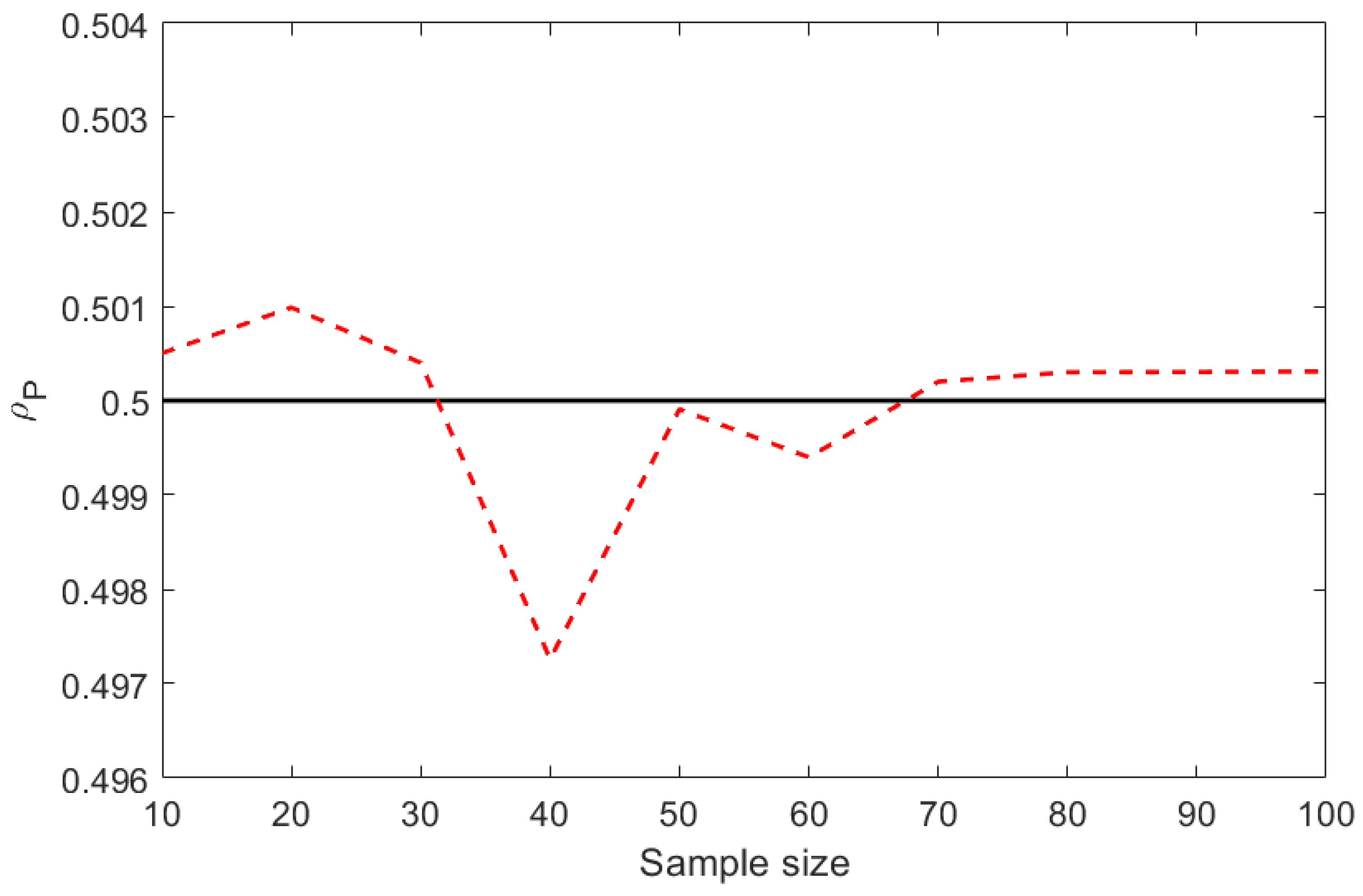
5. Results
6. Comparative Analysis
7. Challenges and Limitations
8. Conclusions and Future Scope
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paluncic, F.; Alfa, A.S.; Maharaj, B.T.; Tsimba, H.M. Queueing models for cognitive radio networks: A survey. IEEE Access 2018, 6, 50801–50823. [Google Scholar] [CrossRef]
- D’Apice, C.; D’Arienzo, M.P.; Dudin, A.; Manzo, R. Admission control in priority queueing system with servers reservation and temporal blocking admission of low priority users. IEEE Access 2023, 11, 44425–44443. [Google Scholar] [CrossRef]
- Mitrany, I.L.; Avi-Itzhak, B. A many-server queue with service interruptions. Oper. Res. 1968, 16, 628–638. [Google Scholar] [CrossRef]
- Falin, G.I. Waiting time in a single-channel queueing system with repeated calls. Mosc. Univ. Comput. Math. Cybern. 1977, 4, 83–87. [Google Scholar]
- Falin, G.I. An M/G/1 system with repeated calls in heavy traffic. Mosc. Univ. Comput. Math. Cybern. 1980, 6, 48–50. [Google Scholar]
- Falin, G.I. On the waiting-time process in a single-line queue with repeated calls. J. Appl. Probab. 1986, 23, 185–192. [Google Scholar] [CrossRef]
- Artalejo, J.R.; Phung-Duc, T. Markovian retrial queues with two way communication. J. Ind. Manag. Optim. 2012, 8, 781–806. [Google Scholar] [CrossRef]
- Salameh, O.; De Turck, K.; Bruneel, H.; Blondia, C.; Wittevrongel, S. Analysis of secondary user performance in cognitive radio networks with reactive spectrum handoff. Telecommun. Syst. 2017, 65, 539–550. [Google Scholar] [CrossRef]
- Gavrilovska, L.; Rakovic, V.; Denkovski, D. From cloud ran to open ran. Wirel. Pers. Commun. 2020, 113, 1523–1539. [Google Scholar] [CrossRef]
- Niknam, S.; Roy, A.; Dhillon, H.S.; Singh, S.; Banerji, R.; Reed, J.H.; Saxena, N.; Yoon, S. Intelligent O-RAN for beyond 5G and 6G wireless networks. arXiv 2020, arXiv:2005.08374. [Google Scholar]
- Shrimali, B.; Bhadka, H.; Patel, H. A fuzzy-based approach to evaluate multi-objective optimization for resource allocation in cloud. Int. J. Adv. Technol. Eng. Exp. 2018, 5, 140–150. [Google Scholar] [CrossRef]
- Goudarzi, S.; Anisi, M.H.; Abdullah, A.H.; Lloret, J.; Soleymani, S.A.; Hassan, W.H. A hybrid intelligent model for network selection in the industrial internet of things. Appl. Soft. Comput. 2019, 74, 529–546. [Google Scholar] [CrossRef]
- Suganthi, N.; Meenakshi, S. Efficient spectrum allocation for secondary users in cognitive radio network using round robin priority algorithm along with reservation channels. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 16715–16728. [Google Scholar] [CrossRef]
- Sun, K.; Liu, Y.; Li, K. Energy harvesting cognitive radio networks with strategic users: A two-class queueing model with retrials. Comput. Commun. 2023, 199, 98–112. [Google Scholar] [CrossRef]
- Krishna Kumar, B.; Navaneetha Krishnan, R.; Sankar, R.; Rukmani, R. Performance analysis of cognitive wireless retrial queueing networks with admission control for secondary users. Qual. Technol. Quant. Manag. 2023, 20, 633–670. [Google Scholar] [CrossRef]
- Zhang, S.; Ni, Z.; Kuang, L.; Jiang, C.; Zhao, X. Traffic Priority-Aware Multi-User Distributed Dynamic Spectrum Access: A Multi-Agent Deep RL Approach. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 1454–1471. [Google Scholar] [CrossRef]
- Winkler, A. Dynamic scheduling of a single-server two-class queue with constant retrial policy. Ann. Oper. Res. 2013, 202, 197–210. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Li, H. A Spectrum Occupancy Model for Primary Users in Cognitive Radio Systems. J. Comput. Commun. 2023, 11, 78–86. [Google Scholar] [CrossRef]
- Dimitriou, I. A queueing model with two classes of retrial customers and paired services. Ann. Oper. Res. 2016, 238, 123–143. [Google Scholar] [CrossRef]
- Kumar, N.; Aryan, P.; Raja, G.L.; Muduli, U.R. Robust Frequency-Shifting Based Control Amid False Data Injection Attacks for Interconnected Power Systems with Communication Delay. IEEE Trans. Ind. Appl. 2024, 60, 3710–3723. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Effectiveness, fairness and social welfare maximization: Service rules for the interrupted secondary users in cognitive radio networks. Ann. Oper. Res. 2023, 323, 247–286. [Google Scholar] [CrossRef]
- Dey, S.; Saha Misra, I. A novel spectrum handoff switching decision scheme for improved performance of secondary users in cognitive radio network. Int. J. Commun. Syst. 2023, 36, e5413. [Google Scholar] [CrossRef]
- Kulshrestha, R.; Singh, A. Transient analysis of energy-saving strategy for cognitive radio networks using G-queue with heterogeneity. Comput. Commun. 2024, 216, 295–306. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, X.B.; Wang, R.; Zhu, J.; Yao, C. Accumulating Priority Queue for Charging of Unmanned Aerial Vehicles in Cognitive Radio Networks. In Proceedings of the 2023 6th International Symposium on Autonomous Systems (ISAS), Nanjing, China, 23–25 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Zhang, J.; Liang, C.L.; Gao, H.X.; Yan, H.; Zhu, H.B. Throughput-delay tradeoff for opportunistic spectrum access in cognitive radio networks. IET Commun. 2023, 17, 2053–2067. [Google Scholar] [CrossRef]
- Mohamed, A.G.; Gamal, M. Stability region characterization of a two-user age of information restricted cognitive radio model. Alex. Eng. J. 2023, 73, 205–215. [Google Scholar] [CrossRef]
- Perveen, A.; Abozariba, R.; Patwary, M.; Aneiba, A. Dynamic traffic forecasting and fuzzy-based optimized admission control in federated 5G-open RAN networks. Neural Comput. Appl. 2023, 35, 23841–23859. [Google Scholar] [CrossRef]
- Phung-Duc, T.; Akutsu, K.; Kawanishi, K.I.; Salameh, O.; Wittevrongel, S. Queueing models for cognitive wireless networks with sensing time of secondary users. Ann. Oper. Res. 2022, 310, 641–660. [Google Scholar] [CrossRef]
- Mahmood, A.; Kareem, A.R.; Nasser, A.R. Design of Elastic Call Admission Control in Tidal Load Scenario for Cloud-based Cellular Networks. Elektron. Elektrotechnika 2022, 28, 85–91. [Google Scholar] [CrossRef]
- Villota-Jacome, W.F.; Rendon OM, C.; da Fonseca, N.L. Admission control for 5G core network slicing based on deep reinforcement learning. IEEE Syst. J. 2022, 16, 4686–4697. [Google Scholar] [CrossRef]
- Luu, Q.T.; Kerboeuf, S.; Kieffer, M. Admission control and resource reservation for prioritized slice requests with guaranteed SLA under uncertainties. IEEE Trans. Netw. Serv. Manag. 2022, 19, 3136–3153. [Google Scholar] [CrossRef]
- Kanellopoulos, D.; Sharma, V.K.; Panagiotakopoulos, T.; Kameas, A. Networking architectures and protocols for IoT applications in smart cities: Recent developments and perspectives. Electronics 2023, 12, 2490. [Google Scholar] [CrossRef]
- Dudin, A.; Dudin, S.; Manzo, R.; Rarità, L. Analysis of multi-server priority queueing system with hysteresis strategy of server reservation and retrials. Mathematics 2022, 10, 3747. [Google Scholar] [CrossRef]
- Tam, P.; Kang, S.; Ros, S.; Kim, S. Enhancing QoS with LSTM-Based Prediction for Congestion-Aware Aggregation Scheduling in Edge Federated Learning. Electronics 2023, 12, 3615. [Google Scholar] [CrossRef]
- Adelabu, M.A.; Imoize, A.L.; Ugwu, M.B. Radio Resource Management of WLAN Hotspot Access Points in Next Generation Wireless Networks. SN Comput. Sci. 2023, 4, 313. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, Q.; Zheng, X.; Liang, W.; Wang, K.I.-K.; Ma, J.; Pan, Y.; Jin, Q. Personalized Federated Learning with Model-Contrastive Learning for Multi-Modal User Modeling in Human-Centric Metaverse. IEEE J. Sel. Areas Commun. 2024, 42, 817–831. [Google Scholar] [CrossRef]


| Authors | Models Used | Contributions | Limitations |
|---|---|---|---|
| Keilson et al. [3] | M/G/1/1 retrial queue | Analysis of system efficiency metrics | Focus on single-class user models |
| Falin [4] | M/G/1/1 retrial queue | Establishes limiting hypothesis for waiting period during heavy traffic | Single-class user models |
| Falin [5] | M/G/1/1 retrial queue | Develops waiting-time distribution of customers in orbit | Single-class user models |
| Falin [6] | M/G/1/1 retrial queue | Calculates average, variance, and probability distribution based on total number of trials | Single-class user models |
| Artalejo and Phung-Duc [7] | Correlated retry queueing architectures | Showcases two-way interaction with two customer classes without disruptions | N/A |
| Salameh et al. [8] | Queueing framework for cognitive radio networks with reactive-decision spectrum handoff | Introduces blocking probability, average number of sensing SUs, and transmission time metrics | Finite orbit size assumption |
| Shrimali et al. [11] | Multi-objective optimization framework for resource allocation in cloud systems | Proposes weighted-sum-based multi-objective optimization framework utilizing fuzzy logic | - |
| Goudarzi et al. [12] | Multi-point algorithm in heterogeneous networks for RAT selection | Introduces combination of techniques for best RAT selection using biogeography-based optimization | Implementation scheme focused on RAT selection probabilities from MDP |
| Proposed framework | Priority-based M/D/1 queue (with preemption and non-preemption) | Effective in mitigating SU spectrum outage in CRNs. Provides insight into priority-based admission of requests. Consideration of real-time system constraints. | Scalability with increasing users and implementation complexity. |
| Symbols | Description |
|---|---|
| Primary users | |
| Secondary users | |
| Users in the system | |
| The system queue of CRN server | |
| Arrival rate of PUs | |
| Arrival rate of SUs | |
| Service rate of PUs | |
| Service rate of SUs | |
| Number of PUs in the system | |
| Number of SUs in the system | |
| Total number of slots in the system | |
| Waiting time of packets in system | |
| Average waiting time in queue for PU delay | |
| Average waiting time in queue for non-preemptive PU delay | |
| Average waiting time in queue for SU delay | |
| Average waiting time in queue for non-preemptive SU delay | |
| Utilization factor for PU delay | |
| Utilization factor for SU delay |
| Parameter | Value |
|---|---|
| Service Rate (μ) | [11.00, 11.20, 11.40, 11.60] requests/sec |
| Arrival Rate () | [19.00, 19.50, 20.00, 20.50] requests/sec |
| Arrival Rate () | [5:10] requests/sec |
| Buffer Capacity | 50 requests |
| Priority Scheme | PU > SU |
| Processing Time (d) | [0, 1, 2] sec/request |
| System Stability | Stable |
| Packet Accumulation | 20 packets |
| Detection Time | 0.1 s |
| Accuracy | 95% |
| Interference Mitigation | Frequency-hopping |
| Performance Metrics | Avg. waiting time: 2 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behera, J.R.; Imoize, A.L.; Singh, S.S.; Tripathy, S.S.; Bebortta, S. Optimizing Priority Queuing Systems with Server Reservation and Temporal Blocking for Cognitive Radio Networks. Telecom 2024, 5, 416-432. https://doi.org/10.3390/telecom5020021
Behera JR, Imoize AL, Singh SS, Tripathy SS, Bebortta S. Optimizing Priority Queuing Systems with Server Reservation and Temporal Blocking for Cognitive Radio Networks. Telecom. 2024; 5(2):416-432. https://doi.org/10.3390/telecom5020021
Chicago/Turabian StyleBehera, Jnana Ranjan, Agbotiname Lucky Imoize, Sudhansu Sekhar Singh, Subhranshu Sekhar Tripathy, and Sujit Bebortta. 2024. "Optimizing Priority Queuing Systems with Server Reservation and Temporal Blocking for Cognitive Radio Networks" Telecom 5, no. 2: 416-432. https://doi.org/10.3390/telecom5020021
APA StyleBehera, J. R., Imoize, A. L., Singh, S. S., Tripathy, S. S., & Bebortta, S. (2024). Optimizing Priority Queuing Systems with Server Reservation and Temporal Blocking for Cognitive Radio Networks. Telecom, 5(2), 416-432. https://doi.org/10.3390/telecom5020021








