Detection of Transmission State of Multiple Wireless Sources: A Statistical Mechanics Approach
Abstract
1. Introduction
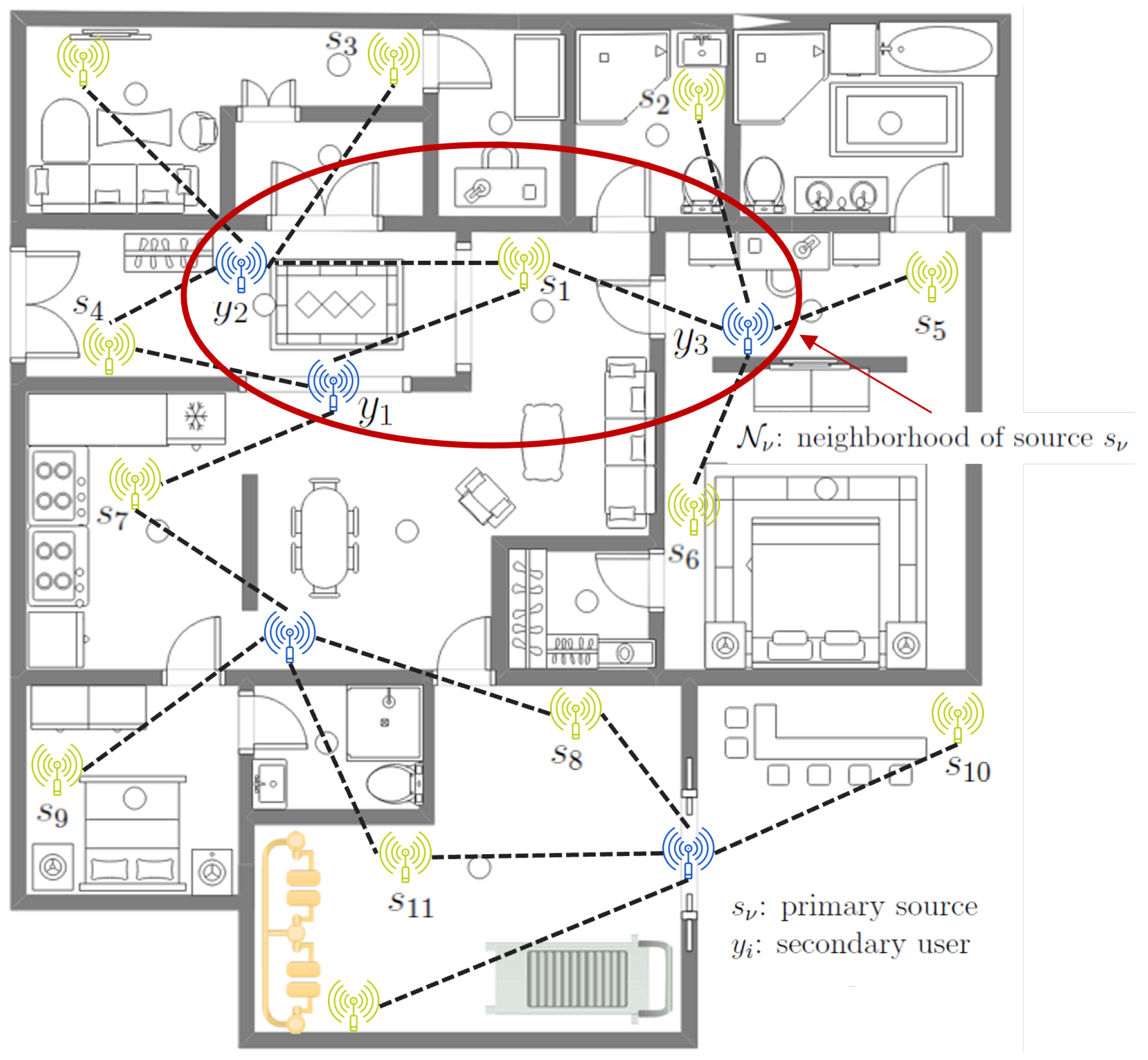
2. System Model
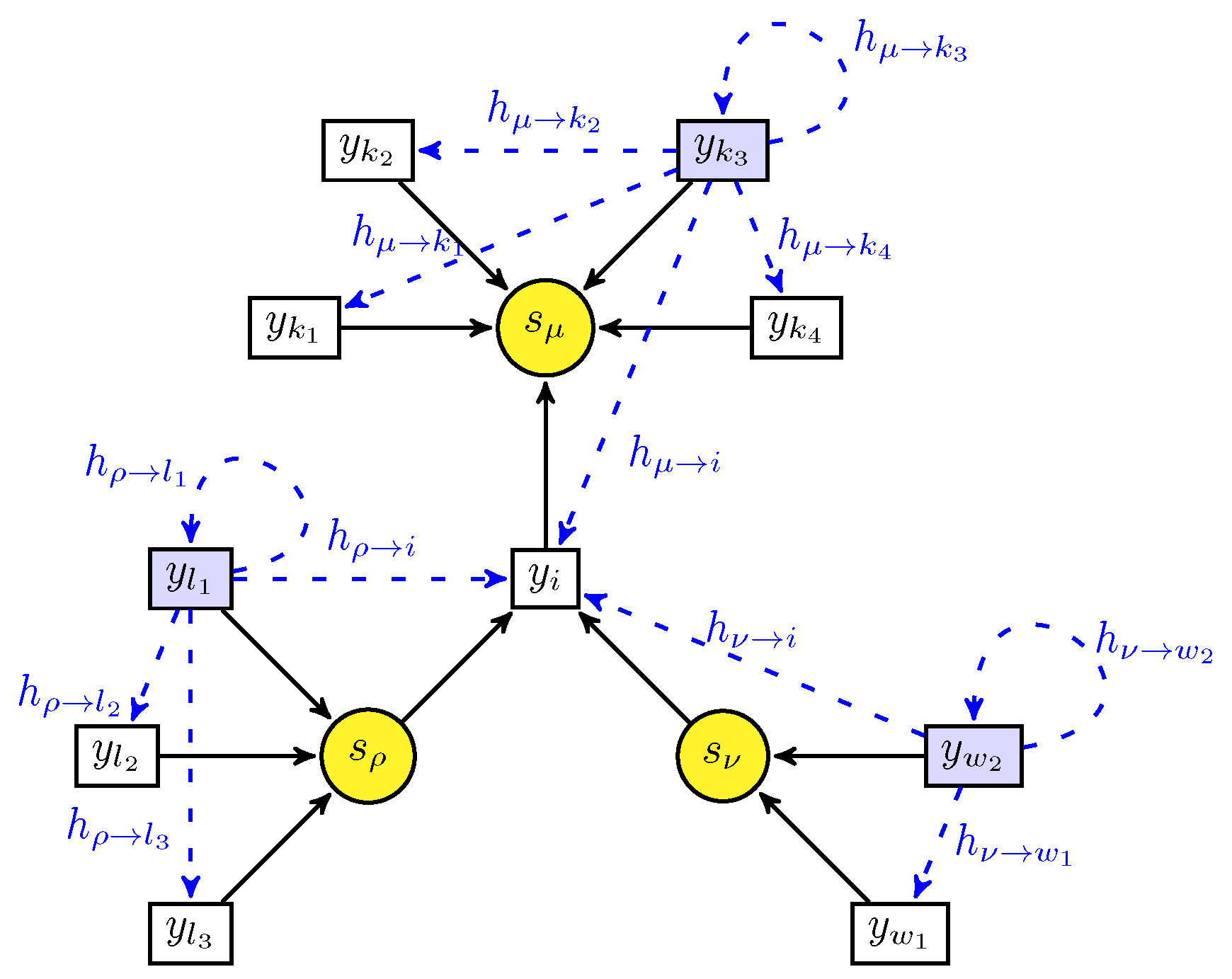
3. The Belief Propagation Algorithm
| Algorithm 1 Message-Passing (Neighborhood Matrix , Prior Distribution ) |
|
4. Connection with Statistical Mechanics
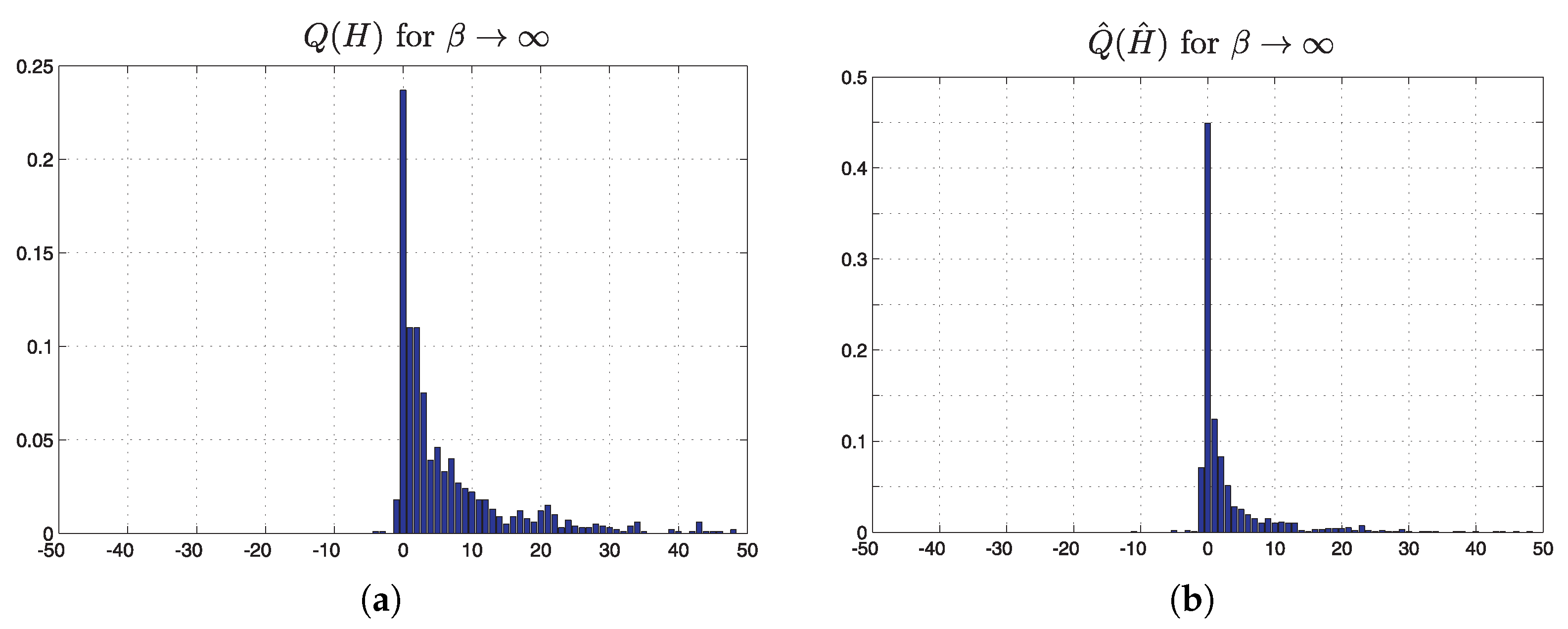
5. Results Using the Replica Approach
| Algorithm 2 Population Dynamics (Graphical Model Ensemble, Resolution K, Number of Iterations I) |
|
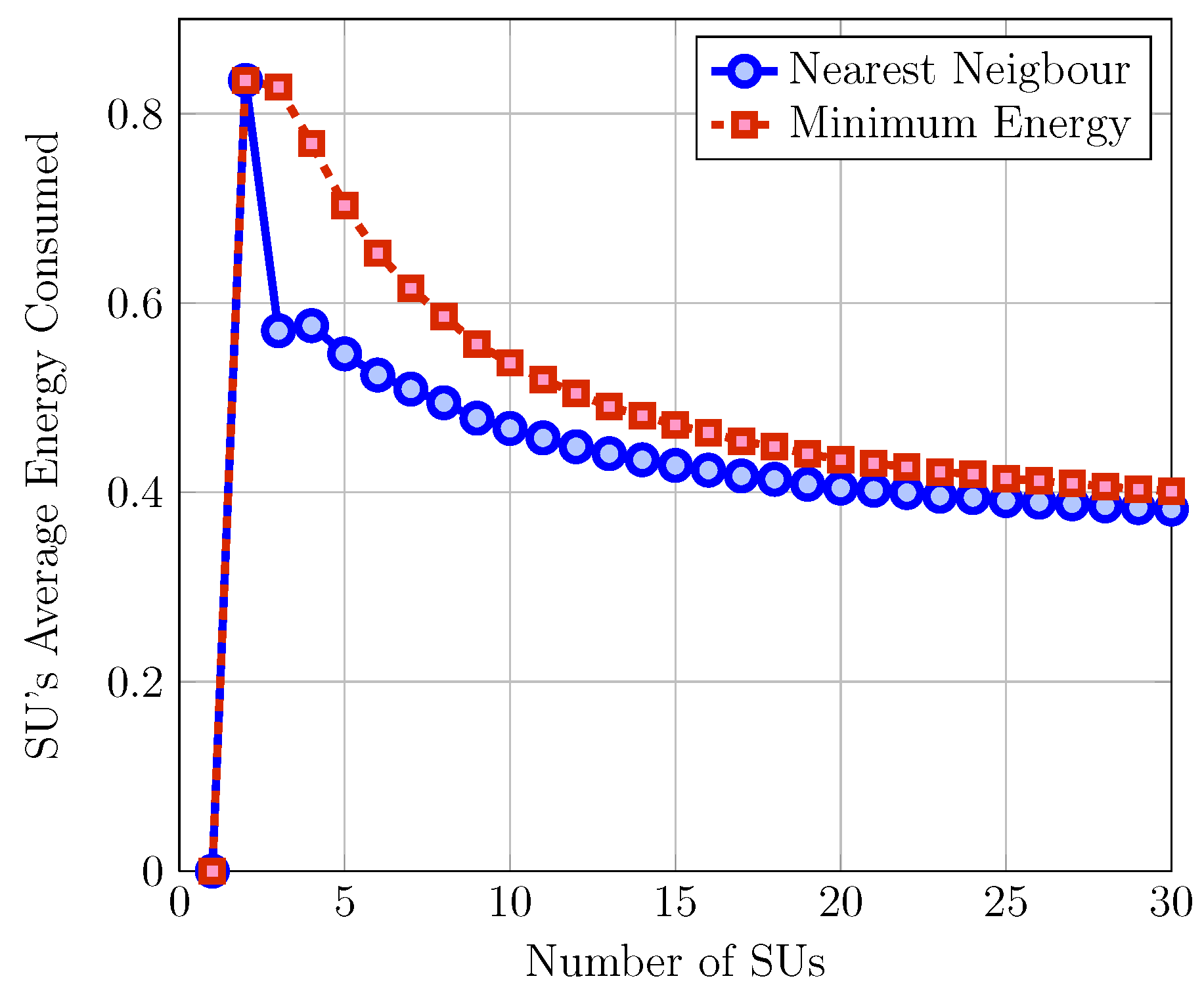
6. Simulation Results
7. Comparison with the Case of Myopic SUs
8. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Network Implementation of the MP Algorithm
Appendix B. The Replica Method
References
- Gharib, A.; Ejaz, W.; Ibnkahla, M. Distributed Spectrum Sensing for IoT Networks: Architecture, Challenges, and Learning. IEEE Internet Things Mag. 2021, 4, 66–73. [Google Scholar]
- Idrees, Z.; Usman, M.; Gelani, H.E.; Zheng, L. Fast and Robust Spectrum Sensing for Cognitive Radio Enabled IoT. IEEE Access 2021, 9, 165996–166007. [Google Scholar]
- Xu, Y.; Gui, G.; Gacanin, H.; Adachi, F. A Survey on Resource Allocation for 5G Heterogeneous Networks: Current Research, Future Trends, and Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 1668–1695. [Google Scholar]
- Li, F.; Lam, K.-Y.; Li, X.; Sheng, Z.; Hua, J.; Wang, L. Advances and Emerging Challenges in Cognitive Internet-of-Things. IEEE Trans. Ind. Inform. 2020, 16, 5489–5496. [Google Scholar]
- Awin, F.A.; Alginahi, Y.M.; Abdel-Raheem, E.; Tepe, K. Technical Issues on Cognitive Radio-Based Internet of Things Systems: A Survey. IEEE Access 2019, 7, 97887–97908. [Google Scholar]
- Rodriguez, A.C.S.; Haider, N.; He, Y.; Dutkiewicz, E. Network Optimisation in 5G Networks: A Radio Environment Map Approach. IEEE Trans. Veh. Technol. 2020, 69, 12043–12057. [Google Scholar]
- Adams, D.C.A.L.; Uher, J. Secondary Spectrum Usage and Signal Detection. In Wireless Coexistence: Standards, Challenges, and Intelligent Solutions; IEEE: Piscataway, NJ, USA, 2021; pp. 115–154. [Google Scholar]
- Maleki, N.; Vosoughi, A.; Rahnavard, N. Distributed Binary Detection Over Fading Channels: Cooperative and Parallel Architectures. IEEE Trans. Veh. Technol. 2016, 65, 1759–1765. [Google Scholar] [CrossRef]
- Huang, Q.; Chung, P.J.; Thompson, J. A nonparametric approach for spectrum sensing using bootstrap techniques. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 851–856. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1988. [Google Scholar]
- Zekavat, R.; Buehrer, R.M. Belief Propagation Techniques for Cooperative Localization in Wireless Sensor Networks. In Handbook of Position Location: Theory, Practice, and Advances; IEEE: Piscataway, NJ, USA, 2019; pp. 967–998. [Google Scholar]
- Murphy, K.P.; Weiss, Y.; Jordan, M.I. Loopy belief propagation for approximate inference: An empirical study. In Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence (UAI’99); Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1999; pp. 467–475. [Google Scholar]
- Sudderth, E.B.; Ihler, A.T.; Isard, M.; Freeman, W.T.; Willsky, A.S. Nonparametric belief propagation. In Commun. ACM 53, 10; Association for Computing Machinery: New York, NY, USA, 2010; pp. 95–103. [Google Scholar]
- Riegler, E.; Kirkelund, G.; Manchon, C.; Badiu, M.; Fleury, B. Merging Belief Propagation and the Mean Field Approximation: A Free Energy Approach. IEEE Trans. Inf. Theory 2013, 59, 588–602. [Google Scholar]
- Cakmak, B.; Winther, O.; Fleury, B. S-AMP: Ap2014 IEEE Information Theory Workshop (ITW 2014) proximate Message Passing for General Matrix Ensembles. In Proceedings of the 2014 IEEE Information Theory Workshop (ITW), Hobart, TAS, Australia, 2–5 November 2014; pp. 192–196. [Google Scholar]
- Rangan, S.; Fletcher, A.; Goyal, V. Asymptotic Analysis of MAP Estimation Via the Replica Method and Applications to Compressed Sensing. IEEE Trans. Inf. Theory 2012, 58, 1902–1923. [Google Scholar]
- Kabashima, Y. A CDMA Multiuser Detection Algorithm on the Basis of Belief Propagation. J. Phys. Math. Gen. 2003, 36, 11111. [Google Scholar] [CrossRef]
- Korada, S.; Montanari, A. Applications of the Lindeberg Principle in Communications and Statistical Learning. IEEE Trans. Inf. Theory 2011, 57, 2440–2450. [Google Scholar]
- Kabashima, Y.; Wadayama, T.; Tanaka, T. Statistical Mechanical Analysis of a Typical Reconstruction Limit of Compressed Sensing. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 1533–1537. [Google Scholar]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing Algorithms for Compressed Sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef]
- Tesfamicael, S.A.; Godana, B.E. Compressed Sensing Performance Analysis via Replica Method Using Bayesian Framework. In Proceedings of the 17th UKSim-AMSS IEEE International Conference on Modelling and Simulation (UKSim), Cambridge, UK, 25–27 March 2015; pp. 281–289. [Google Scholar]
- Mézard, M.; Montanari, A. Information, Physics, and Computation; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Evangelatos, S.; Moustakas, A. Statistical Mechanics Approach for the Detection of Multiple Wireless Sources via a Sensor Network. In Proceedings of the IEEE 12th International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt), Hammamet, Tunisia, 12–16 May 2014; pp. 591–598. [Google Scholar]
- Leon-Garcia, F.; Palomares, J.; Olivares, J. D2R-TED: Data—Domain Reduction Model for Threshold-Based Event Detection in Sensor Networks. Sensors 2018, 18, 3806. [Google Scholar] [CrossRef]
- Abdul-Salaam, G.; Abdullah, A.H.; Anisi, M.H. Energy-Efficient Data Reporting for Navigation in Position-Free Hybrid Wireless Sensor Networks. IEEE Sens. J. 2017, 17, 2289–2297. [Google Scholar] [CrossRef]
- Lewandowski, M.; Płaczek, B. Data Transmission Reduction in Wireless Sensor Network for Spatial Event Detection. Sensors 2021, 21, 7256. [Google Scholar] [CrossRef]
- Cobos, M.; Perez-Solano, J.J.; Felici-Castell, S.; Segura, J.; Navarro, J.M. Cumulative-Sum-Based Localization of Sound Events in Low-Cost Wireless Acoustic Sensor Networks. IEEE/Acm Trans. Audio Speech, Lang. Process. 2014, 22, 1792–1802. [Google Scholar] [CrossRef]
- Miao, J.; Song, X.O. An Enhanced Soft Combination Algorithm Based on CUSUM for Cooperative Spectrum Sensing. In Proceedings of the 2017 IEEE International Conference on Networking and Network Applications (NaNA), Kathmandu, Nepal, 16–19 October 2017; pp. 176–179. [Google Scholar]
- Jain, A.; Sarvepalli, P.; Bhashyam, S.; Kannu, A.P. Algorithms for Change Detection With Sparse Signals. IEEE Trans. Signal Process. 2020, 68, 1331–1345. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, X.; Jin, X.; Zhao, Z.; Zhang, B. A Neuron-Based Kalman Filter with Nonlinear Autoregressive Model. Sensors 2020, 20, 299. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X.; Wang, L. An Adaptive Outlier Detection and Processing Approach Towards Time Series Sensor Data. IEEE Access 2019, 7, 175192–175212. [Google Scholar] [CrossRef]
- Mor, B.; Garhwal, S.; Kumar, A. A Systematic Review of Hidden Markov Models and Their Applications. Arch. Comput. Methods Eng. 2021, 28, 1429–1448. [Google Scholar] [CrossRef]
- Joshi, S.S.; Phoha, V.V. Investigating hidden Markov models capabilities in anomaly detection. In Proceedings of the 43rd Annual Southeast Regional Conference—Volume 1 (ACM-SE 43), Association for Computing Machinery, New York, NY, USA, 18–20 March 2005; pp. 98–103. [Google Scholar]
- Tuğaç, S.; Efe, M. Hidden Markov Model based target detection. In Proceedings of the 13th IEEE International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–7. [Google Scholar]
- Adhikary, A.; Nam, J.; Ahn, J.-Y.; Caire, G. Joint Spatial Division and Multiplexing—the Large-scale Array Regime. IEEE Trans. Inf. Theory 2013, 59, 6441–6463. [Google Scholar] [CrossRef]
- Hata, M. Empirical Formula for Propagation Loss in Land Mobile Radio Services. IEEE Trans. Veh. Technol. 1980, 29, 317–325. [Google Scholar] [CrossRef]
- Bickson, D.; Baron, D.; Ihler, A.; Avissar, H.; Dolev, D. Fault Identification Via Nonparametric Belief Propagation. IEEE Trans. Signal Process. 2011, 59, 2602–2613. [Google Scholar] [CrossRef]
- Franceschetti, M.; Meester, R. Random Networks for Communication; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kirkley, A.; Cantwell, G.T.; Newman, M.E.J. Belief propagation for networks with loops. Sci. Adv. 2021, 7, eabf1211. [Google Scholar] [CrossRef] [PubMed]
- Mézard, M.; Parisi, G.; Virasoro, M.A. Spin Glass Theory and Beyond; World Scientific Publishing Company: Singapore, 1987. [Google Scholar]
- Talagrand, M. Spin Glasses: A Challenge for Mathematicians: Cavity and Mean Field Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Saad, D.; Yeung, C.; Rodolakis, G.; Syrivelis, D.; Koutsopoulos, I.; Tassiulas, L.; Urbanke, R.; Giaccone, P.; Leonardi, E. Physics-inspired Methods for Networking and Communications. IEEE Commun. Mag. 2014, 52, 144–151. [Google Scholar] [CrossRef]
- Guo, D.; Verdu, S. Replica Analysis of Large-system CDMA. In Proceedings of the 2003 IEEE Information Theory Workshop, Paris, France, 31 March–4 April 2003; pp. 22–25. [Google Scholar]
- Sourlas, N. Spin-glass Models as Error-correcting Codes. Nature 1989, 339, 693–695. [Google Scholar] [CrossRef]
- Mukherjee, K.; Gupta, S.; Ray, A.; Wettergren, T.A. Statistical-Mechanics-Inspired Optimization of Sensor Field Configuration for Detection of Mobile Targets. IEEE Trans. Syst. Man Cybern. Part Cybern. 2011, 41, 783–791. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Information Theory, Inference & Learning Algorithms; Cambridge University Press: New York, NY, USA, 2002. [Google Scholar]
- Reeves, G.; Pfister, H.D. The replica-symmetric prediction for compressed sensing with Gaussian matrices is exact. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 665–669. [Google Scholar]
- Decelle, A. An Introduction to Machine Learning: A perspective from Statistical Physics. Phys. Stat. Mech. Its Appl. 2022, 128154. [Google Scholar] [CrossRef]
- Bethe, H.A. Statistical theory of superlattices. Proc. R. Soc. London. Ser. -Math. Phys. Sci. 1935, 150, 552–575. [Google Scholar]
- Guerra, F.; Toninelli, F.L. The Thermodynamic Limit in Mean Field Spin Glass Models. Commun. Math. Phys. 2002, 230, 71–79. [Google Scholar] [CrossRef]
- Raymond, J.; Saad, D. Sparsely Spread CDMA—A Statistical Mechanics-based Analysis. J. Phys. Math. Theor. 2007, 40, 12315. [Google Scholar] [CrossRef]
- Monasson, R. Optimization Problems and Replica Symmetry Breaking in Finite Connectivity Spin Glasses. J. Phys. Math. Gen. 1998, 31, 513. [Google Scholar] [CrossRef]
- Vicente, R.; Saad, D.; Kabashima, Y. Low-density Parity-check Codes—A Statistical Physics Perspective. In ser. Advances in Imaging and Electron Physics; Peter, B.K., Hawkes, W., Mulvey, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 125, pp. 231–353. [Google Scholar]
- Wong, K.Y.M.; Saad, D. Inference and Optimization of Real Edges on Sparse Graphs: A statistical Physics Perspective. Phys. Rev. E 2007, 76, 011115. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Saad, D. Typical Performance of Regular Low-density Parity-check Codes Over General Symmetric Channels. J. Phys. Math. Gen. 2003, 36, 11143. [Google Scholar] [CrossRef]
- Hu, J.; Xie, L.; Zhang, C. Energy-based Multiple Target Localization and Pursuit in Mobile Sensor Networks. IEEE Trans. Instrum. Meas. 2012, 61, 212–220. [Google Scholar] [CrossRef]
- Cetin, M.; Chen, L.; Fisher, J.; Ihler, A.; Moses, R.; Wainwright, M.; Willsky, A. Distributed Fusion in Sensor Networks. IEEE Signal Process. Mag. 2006, 23, 42–55. [Google Scholar] [CrossRef]
- Hubbard, J. Calculation of Partition Functions. Phys. Rev. Lett. 1959, 3, 77–78. [Google Scholar] [CrossRef]
- Bender, C.; Orszag, S. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
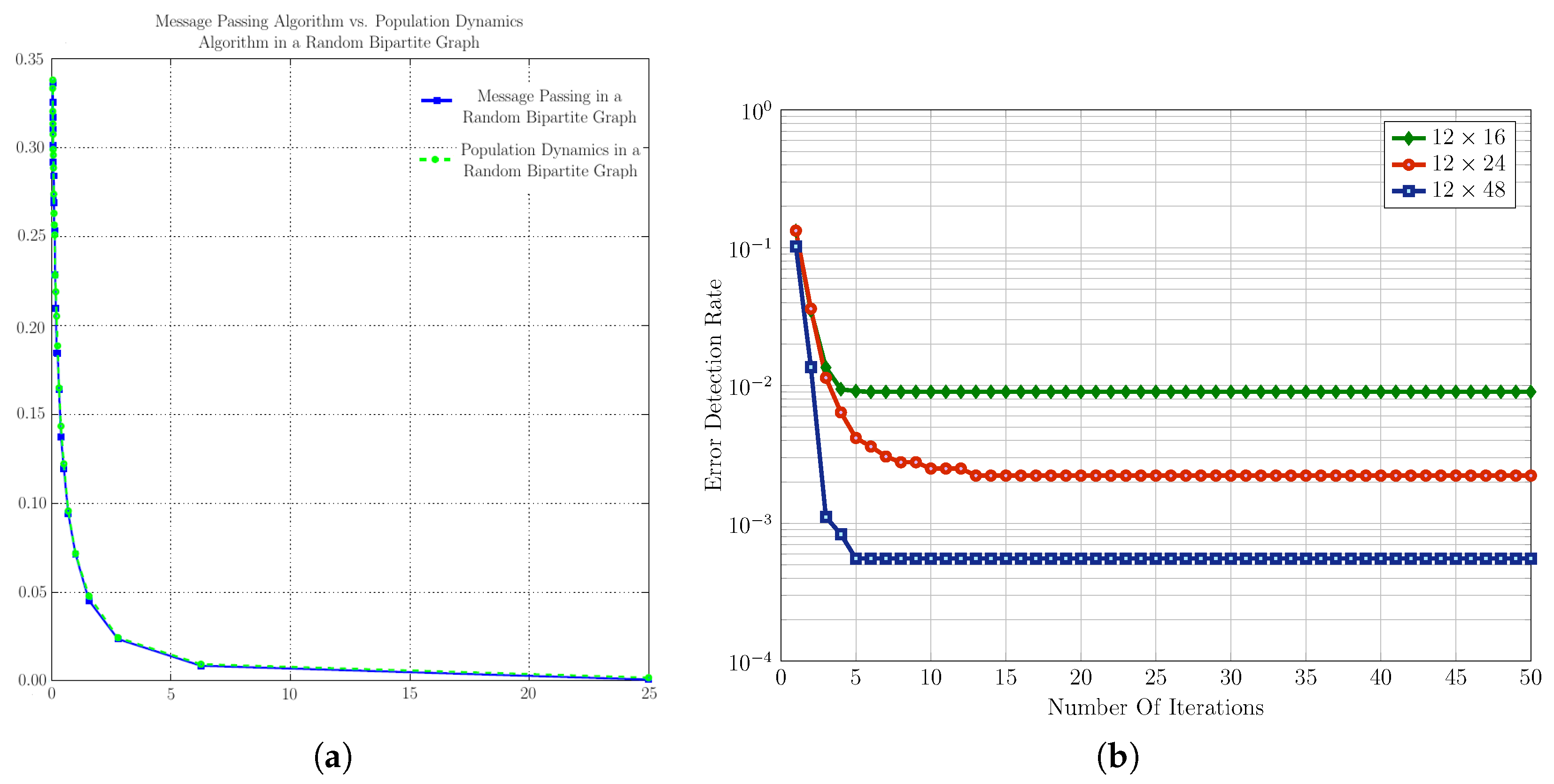
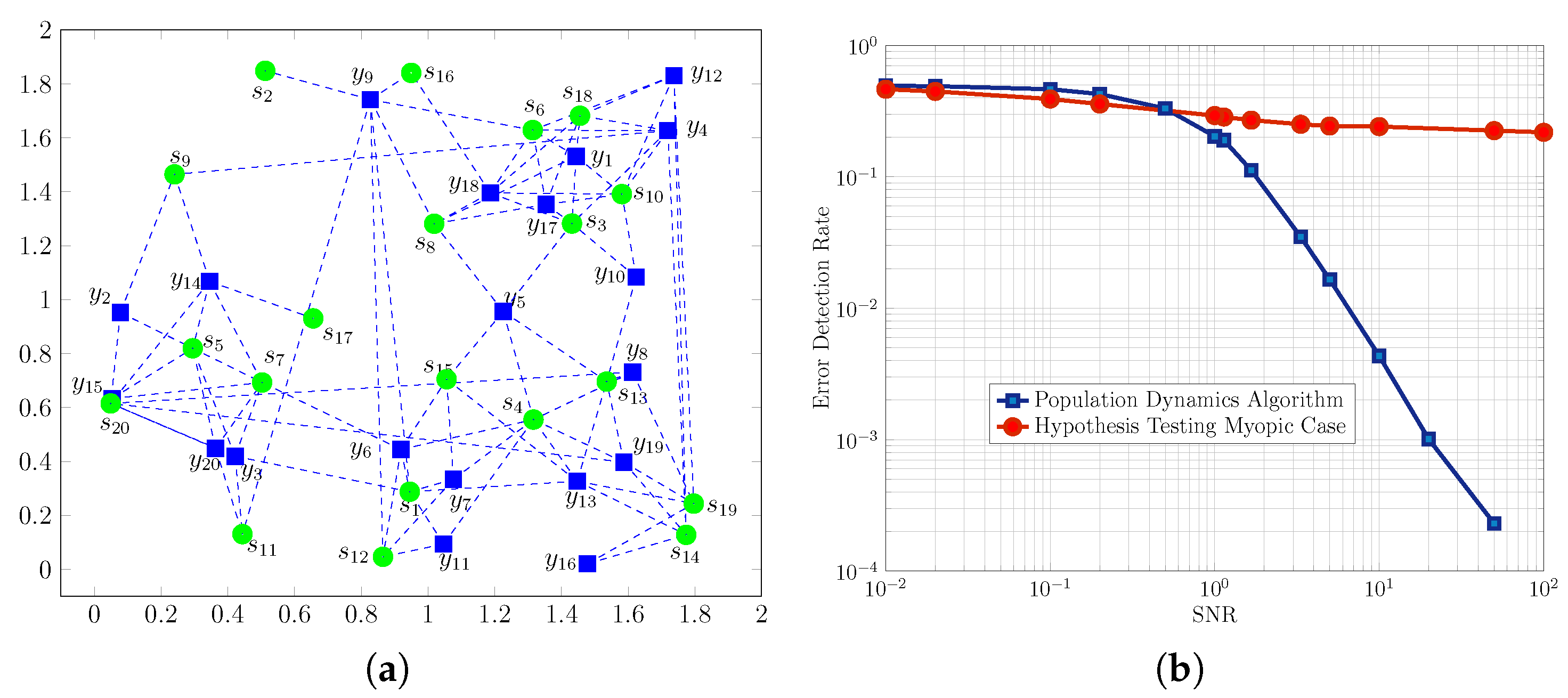
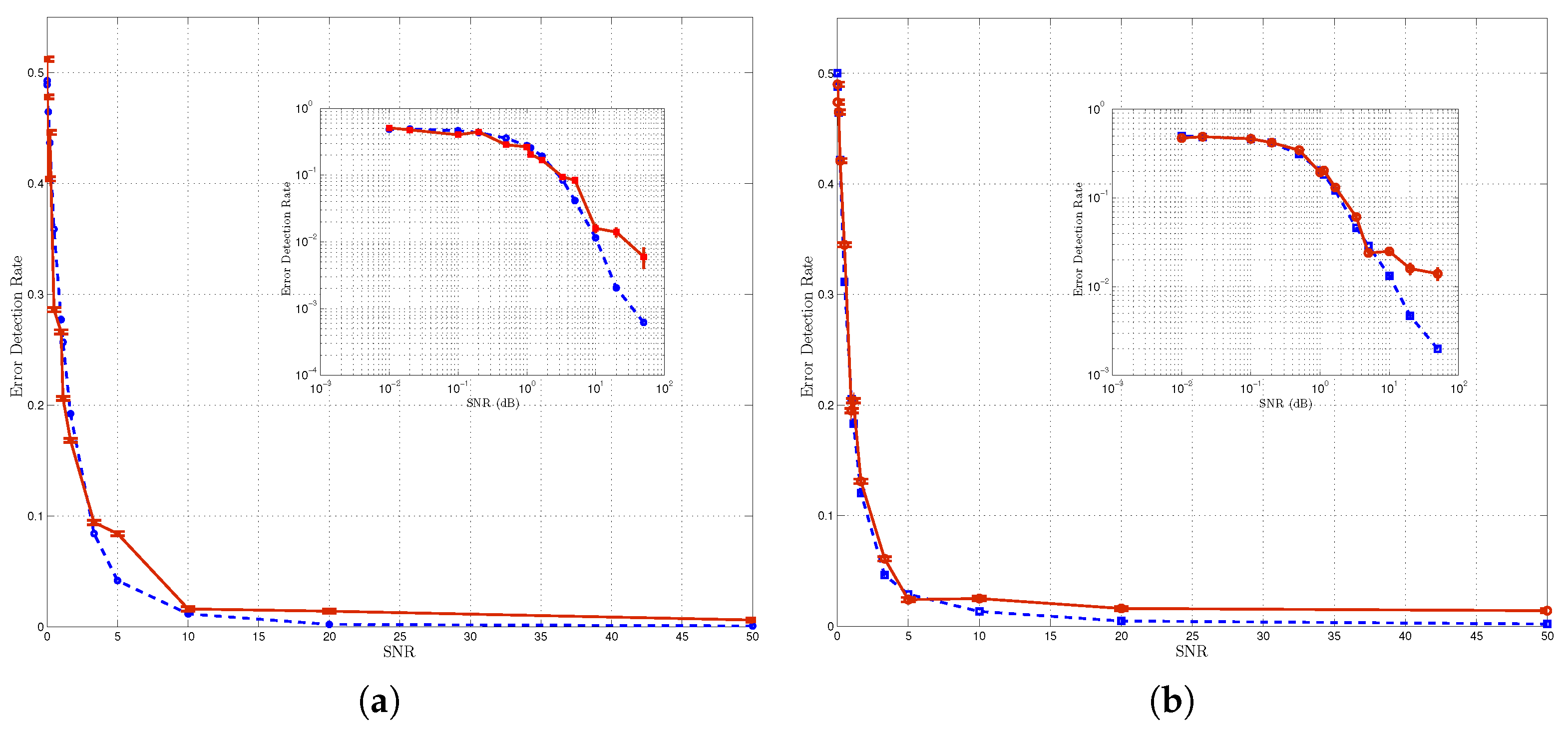
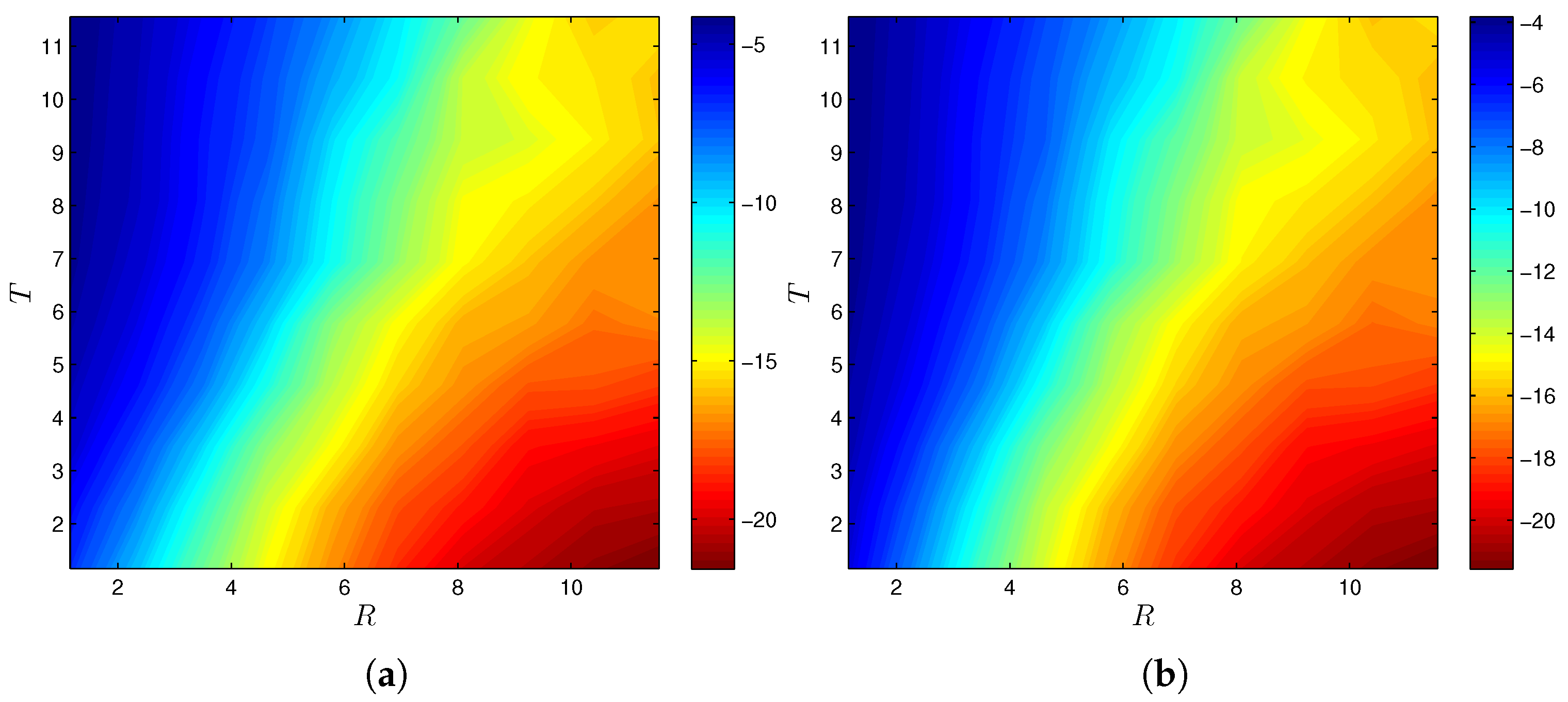
| Thresholding-based methods compare the received signal strength or other relevant parameters with a predefined threshold to infer the emitting state of the primary sources [24,25,26]. In summary, thresholding-based methods offer simplicity and speed but they may lack adaptability and robustness to complex data distributions. Belief propagation, on the other hand, provides adaptability, accuracy, and flexibility but has higher computational complexity and potential convergence challenges. |
| Advantages Compared to the Belief Propagation Algorithm |
|
| Drawbacks Compared to the Belief Propagation Algorithm |
|
| Statistical techniques, such as cumulative sum (CUSUM) or exponentially weighted moving average (EWMA), monitor sensor measurements over time and detect significant changes or deviations from the baseline [27,28,29,30,31]. In summary, statistical techniques are straightforward to implement, provide quick responses to state changes, and are computationally efficient. However, they may struggle to differentiate subtle changes, are prone to false alarms, and lack adaptability to changing environments. On the other hand, belief propagation offers more sophisticated modeling capabilities and can capture contextual information, temporal dependencies, and inter-sensor relationships. It provides higher discriminative power but has higher computational complexity. It may require more computational resources, but it can provide more precise and reliable emitting state detection, especially in complex scenarios. |
| Advantages Compared to the Belief Propagation Algorithm |
|
| Drawbacks Compared to the Belief Propagation Algorithm |
|
| Hidden Markov Models (HMMs), which are widely employed for modeling and detecting the state of sensors, are able to capture the temporal dependencies and transitions between different sensor states. They can infer the most likely sequence of sensor states by analyzing the sequence of observations [32,33,34]. In summary, HMMs excel in capturing temporal dependencies and modeling sequential data, making them suitable for time-series analysis. On the other hand, BP offers flexibility and can be applied to various graphical models, enabling distributed computations and scalable inference. While HMMs assume Markovian processes and have computationally intensive training, BP is more adaptable, but it is sensitive to model structure and may require approximations in loopy graphs. |
| Advantages Compared to the Belief Propagation Algorithm |
|
| Drawbacks Compared to the Belief Propagation Algorithm |
|
| Binary | Bipolar | Transformation |
|---|---|---|
| s.t | s.t |
| Probability | Statistical Mechanics | Statistical Mechanics Terminology |
|---|---|---|
| Energy Functional | ||
| Partition Function | ||
| Gibbs Probability of State s | ||
| Ground State | ||
| Gibbs Free Energy |
| Parameter | Value |
|---|---|
| Path Loss Exponent | |
| Communication Range | |
| Average Density of Sources | |
| Average Density of SUs | |
| Source Activity Probability |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Evangelatos, S.; Moustakas, A.L. Detection of Transmission State of Multiple Wireless Sources: A Statistical Mechanics Approach. Telecom 2023, 4, 649-677. https://doi.org/10.3390/telecom4030029
Evangelatos S, Moustakas AL. Detection of Transmission State of Multiple Wireless Sources: A Statistical Mechanics Approach. Telecom. 2023; 4(3):649-677. https://doi.org/10.3390/telecom4030029
Chicago/Turabian StyleEvangelatos, Spyridon, and Aris L. Moustakas. 2023. "Detection of Transmission State of Multiple Wireless Sources: A Statistical Mechanics Approach" Telecom 4, no. 3: 649-677. https://doi.org/10.3390/telecom4030029
APA StyleEvangelatos, S., & Moustakas, A. L. (2023). Detection of Transmission State of Multiple Wireless Sources: A Statistical Mechanics Approach. Telecom, 4(3), 649-677. https://doi.org/10.3390/telecom4030029






