Abstract
This paper studies the formulation of dark and singular stationary optical solitons that stem from quadratic-cubic and generalized quadratic-cubic forms of nonlinear refractive index coupled with nonlinear chromatic dispersion. The temporal evolution is taken to be of both kinds, namely linear and generalized. The enhanced Kudryashov’s approach enables this retrieval possible.
1. Introduction
The dynamics of soliton propagation through optical fibers and other forms of optical waveguides is a scientifically rich phenomena. Occasionally, it so happens that such an engineering marvel encounters several road blocks. A few of them are soliton radiation and consequently shedding of soliton energy, collision-induced timing jitter, four-wave mixing and many others. Another lesser known and lesser studied detrimental phenomena is the formation of quiescent optical solitons when the chromatic dispersion (CD) is rendered to be nonlinear [1,2,3,4,5,6,7,8,9,10]. This can be triggered from several possible unwanted situations that arise during the course of soliton transmittal across intercontinental distances. These could include rough handling of fibers, twisting and bending of fibers, water pressure from undersea cables, and many others. This would lead to solitons getting stalled during its transmittal. Such a phenomenon is discussed in this paper from a mathematical perspective.
There are two types of nonlinear refractive index structures that are taken into account in this paper. They are quadratic-cubic (QC) and its generalized version that is referred to as generalized QC nonlinearity. The enhanced Kudryashov’s scheme makes the retrieval of the stationary solitons possible. It is dark and singular stationary solitons that are yielded for the model with the two forms of self-phase modulation (SPM) considered in this paper. The temporal evolution is initially considered to be linear and thereafter its generalized version is taken up. The results are derived and exhibited in the rest of the paper. These are penned in detail after a succinct introduction to the model and a quick re-visitation of the integration scheme. To step back in time, the concept of nonlinear CD was introduced by Yan during 2006 that led to the formation of quiescent optical solitons [10]. Thereafter, this concept was further explored for a wide variety of models, which otherwise gave way to mobile solitons, such as the complex Ginzburg–Landau equation, Sasa–Satsuma equation, Lakshmanan–Porsezian–Daniel equation, and many more [11,12,13,14,15]. The current paper revisits the familiar nonlinear Schrödinger’s equation (NLSE) with quadratic-cubic and generalized quadratic-cubic nonlinearities. In this context, for both nonlinear structures, linear temporal evolution as well as generalized temporal evolutions are considered. It must be transparent that the derivation of these quiescent soliton solutions was successful by the aid of direct computer software usage that gave way to implicit forms of quiescent solitons [11,12,13,14,15]. The analytical derivation of such solitons, however, was carried out earlier by the usage of Jacobi’s elliptic function expansion and extended the trial function approach [1,2]. The current paper implements enhanced Kudryashov’s mechanism to recover quiescent solitons to the NLSE.
2. The Enhanced Kudryashov’s Procedure
Consider a governing model
where denotes a wave profile, while t and x depict temporal and spatial variables in sequence.
The relations
condense (1) to
where is the inverse wave width, is the wave variable, and is the wave velocity.
3. Quadratic-Cubic Nonlinearity
The structure of QC nonlinearity was first reported during 1994 [4]. Later, after a long hiatus, this form of SPM was picked up by Fujioka et al. during 2011 [3] and thereafter a deluge of results ensued with such a nonlinearity structure. The current section will derive stationary solitons for QC nonlinearity having nonlinear form of CD.
3.1. Linear Temporal Evolution
In this case, the NLSE shapes up as [3,4]
where purports the wave profile, while x and t stand for the spatial and temporal variables in sequence. The first term signifies the linear temporal evolution, while a comes from the nonlinear CD. Finally, and stem from the SPM, while n arises from the full nonlinearity. It must be noted that, if , we recover the linear CD that yields a mobile soliton.
Equation (2) is the general integration algorithm for real-valued partial differential equations (PDEs). However, Equation (9) is a complex-valued PDE and consequently the phase component of the complex variable is split off so that the real part can be further analyzed as explained in (2). Therefore, model (9) permits the wave form
where depicts the phase constant, and denotes the wave number. Inserting (10) into (9) retrieves the governing equation
Taking simplifies (11) to
By the implementation of the balancing approach in (12), one reduces (4) to
Inserting (13) along with (5) and (6) into (12) provides us with the results:
- Result–1:Putting (14) along with (7) into (13) paves the way for the straddled solitonIf and in (15), the dark and singular solitons stick out asandFigure 1 depicts the plots of dark and singular solitons (16) and (17), respectively. The parameter values chosen are: , and .
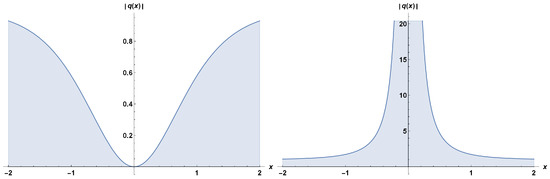 Figure 1. Profiles of stationary dark and singular solitons, respectively.
Figure 1. Profiles of stationary dark and singular solitons, respectively. - Result–2:Putting (18) along with (8) into (13) provides us with the straddled solitonWhen and in (19), one retrieves the dark and singular solitonsandFigure 2 depicts the plots of dark and singular solitons (20) and (21), respectively. The parameter values chosen are: , and .
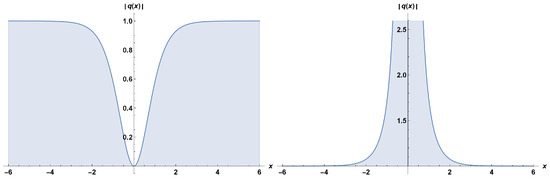 Figure 2. Profiles of stationary dark and singular solitons, respectively.
Figure 2. Profiles of stationary dark and singular solitons, respectively.
3.2. Generalized Temporal Evolution
Thus, the model evolves as
where l stands for the generalized temporal evolution. If , Equation (22) collapses to (9) so that one falls back to the case of linear temporal evolution. Plugging (10) into (22) causes the main equation
Setting condenses (23) to
By the implementation of the balancing scheme in (24), one collapses (4) to
Plugging (25) along with (5) and (6) into (24) provides us with the results:
- Result–1:Inserting (26) along with (7) into (25) reveals the straddled solitonTaking and in (27) secures the dark and singular solitonsandFigure 3 depicts the plots of dark and singular solitons (28) and (29), respectively. The parameter values chosen are: , and .
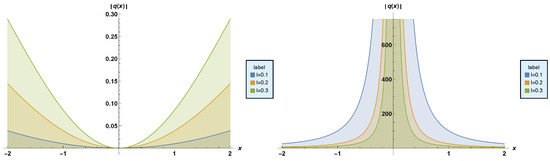 Figure 3. Profiles of stationary dark and singular solitons, respectively.
Figure 3. Profiles of stationary dark and singular solitons, respectively. - Result–2:Putting (30) along with (8) into (25) extracts the straddled solitonSetting and in (31) recovers the dark and singular solitonsandFigure 4 depicts the plots of dark and singular solitons (32) and (33), respectively. The parameter values chosen are: , and .
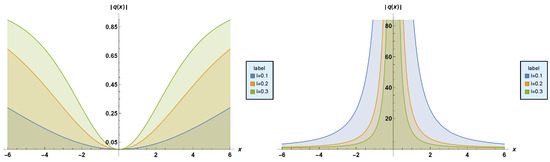 Figure 4. Profiles of stationary dark and singular solitons, respectively.
Figure 4. Profiles of stationary dark and singular solitons, respectively.
4. Generalized Quadratic-Cubic Nonlinearity
This form of nonlinearity was first studied by Triki et al. during 2019 [8]. It was established that, with linear CD, mobile solitons exist. The current section will discuss the formation of stationary solitons when CD is rendered to be nonlinear with linear as well as generalized temporal evolution effects.
4.1. Linear Temporal Evolution
Therefore, the model stands as [8]
Plugging (10) into (34) reveals the strategic equation
Assume . Thus, Equation (35) shapes up as
The relation
collapses Equation (36) to
By the implementation of the balancing algorithm in (38), one simplifies (4) to
Inserting (39) along with (5) and (6) into (38) retrieves the results:
- Result–1:Putting (40) along with (7) into (39) derives the straddled solitonIf and in (41), the dark and singular solitons evolve asandFigure 5 depicts the plots of dark and singular solitons (42) and (43), respectively. The parameter values chosen are: , and .
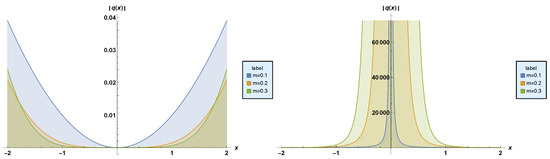 Figure 5. Profiles of stationary dark and singular solitons, respectively.
Figure 5. Profiles of stationary dark and singular solitons, respectively. - Result–2:Inserting (44) along with (8) into (39) secures the straddled solitonWhen and in (45), one acquires dark and singular solitonsandFigure 6 depicts the plots of dark and singular solitons (46) and (47), respectively. The parameter values chosen are: , and .
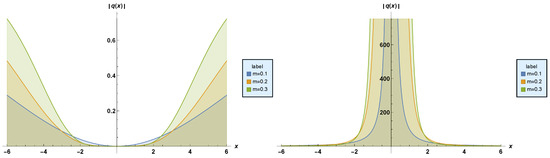 Figure 6. Profiles of stationary dark and singular solitons, respectively.
Figure 6. Profiles of stationary dark and singular solitons, respectively.
4.2. Generalized Temporal Evolution
In this case, Equation (34) reads as
Again, (48) reduces to (34) for , which represents the case with linear temporal evolution. Plugging (10) into (48) paves the way for the fundamental equation
Assume . Thus, Equation (49) changes to
The restriction
collapses Equation (50) to
By the implementation of the balancing procedure in (52), one translates (4) to
Inserting (53) along with (5) and (6) into (52) retrieves the results:
- Result–1:Putting (54) along with (7) into (53) leaves us with the straddled solitonTaking and turns (55) into dark and singular solitonsandFigure 7 depicts the plots of dark and singular solitons (56) and (57), respectively. The parameter values chosen are: , and .
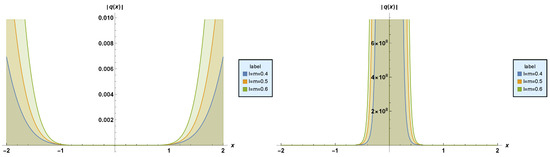 Figure 7. Profiles of stationary dark and singular solitons, respectively.
Figure 7. Profiles of stationary dark and singular solitons, respectively. - Result–2:Substituting (58) along with (8) into (53) provides us with the straddled solitonSetting and condenses (59) to dark and singular solitonsandFigure 8 depicts the plots of dark and singular solitons (60) and (61), respectively. The parameter values chosen are: , and .
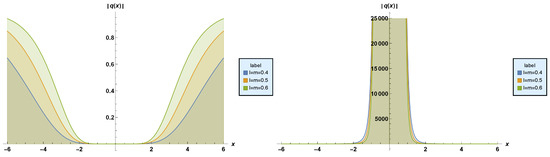 Figure 8. Profiles of stationary dark and singular solitons, respectively.
Figure 8. Profiles of stationary dark and singular solitons, respectively.
5. Conclusions
The current paper revealed stationary singular and dark optical solitons for the model that came with QC and generalized AC nonlinearity. The temporal evolutions were both linear and generalized. There are four forms of the governing model that were studied in this work, which were gradual generalizations of the fundamental model. The first form is the NLSE with the QC form of the nonlinear refractive index as given by [9]. This model for the propagation of optical solitons, with linear CD, was first proposed during 1994 and later studied again during 2011 [3,4]. Subsequently, the model is addressed with generalized temporal evolution and nonlinear CD as given by (22) that gave way to quiescent solitons as well. Thereafter, Equations (9) and (22) are formulated with a generalized form of the QC law of the nonlinear refractive index, which are represented by (34) and (48), respectively. It must be noted that (34) with linear CD was first proposed during 2019 [8]. The enhanced Kudrashov’s scheme has made this retrieval a success. However, it is quite noticeable that the approach has its shortcoming. It failed to recover stationary bright solitons for both forms of SPM.
Later, the method will be implemented to retrieve quiescent solitons that come with triple forms of nonlinearly structured SPM such as polynomial law and triple-power law of nonlinearity. These would be taken up with time, and their results and findings would be later revealed and reported. Some of the lesser known nonlinear media would be later considered. One such form is the saturable form of nonlinearity that yields dissipative solitons. The results of the work thus show the consequential catastrophic effect that nonlinear CD would bring in. The mobile solitons would stall during its transmission along transcontinental and transoceanic distances. Therefore, it is imperative to make sure that such an unwanted feature of nonlinear CD in an optical fiber, or any other forms of waveguides such as optical couplers or PCF or optical metamaterials, must be avoided at all costs. Telecommunication engineers must therefore exercise extreme caution while laying such fiber optic cables underground or under sea. This is therefore a vital component and a vital feature of soliton transmission along intercontinental distances.
Author Contributions
Conceptualization, A.H.A.; methodology, S.K.; software, A.B.; writing—original draft preparation, Y.Y.; writing—review and editing, L.M. and S.M.; project administration, C.I. and H.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the anonymous referees whose comments helped to improve this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ekici, M. Stationary optical solitons with complex Ginzburg–Landau equation having nonlinear chromatic dispersion and Kudryashov’s refractive index structures. Phys. Lett. A 2022, 440, 128146. [Google Scholar] [CrossRef]
- Ekici, M. Stationary optical solitons with Kudryashov’s quintuple power law nonlinearity by extended Jacobi’s elliptic function expansion. J. Nonlinear Opt. Phys. Mater. 2023, 32, 2350008. [Google Scholar] [CrossRef]
- Fujioka, J.; Cortés, E.; Pérez-Pascual, R.; Rodríguez, R.; Espinosa, A.; Malomed, B.A. Chaotic solitons in the quadratic-cubic nonlinear Schrödinger equation under nonlinearity management. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 033120. [Google Scholar] [CrossRef] [PubMed]
- Hayata, K.; Koshiba, M. Prediction of unique solitary-wave polaritons in quadratic-cubic nonlinear dispersive media. JOSA B 1994, 11, 2581–2585. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Stationary solitons of the model with nonlinear chromatic dispersion and arbitrary refractive index. Optik 2022, 259, 168888. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Stationary solitons of the generalized nonlinear Schrödinger equation with nonlinear dispersion and arbitrary refractive index. Appl. Math. Lett. 2022, 128, 107888. [Google Scholar] [CrossRef]
- Sonmezoglu, A. Stationary optical solitons having Kudryashov’s quintuple power law nonlinearity by extended G′/G–expansion. Optik 2022, 253, 168521. [Google Scholar] [CrossRef]
- Triki, H.; Porsezian, K.; Senthilnathan, K.; Nithyanandan, K. Chirped self-similar solitary waves for the generalized nonlinear Schrödinger equation with distributed two-power-law nonlinearities. Phys. Rev. E 2019, 100, 042208. [Google Scholar] [CrossRef] [PubMed]
- Yalçı, A.M.; Ekici, M. Stationary optical solitons with complex Ginzburg–Landau equation having nonlinear chromatic dispersion. Opt. Quantum Electron. 2022, 54, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z. Envelope compactons and solitary patterns. Phys. Lett. A 2006, 355, 212–215. [Google Scholar] [CrossRef]
- Biswas, A.; Khalique, C.M. Stationary solutions for nonlinear dispersive Schrödinger’s equation. Nonlinear Dyn. 2011, 63, 623–626. [Google Scholar] [CrossRef]
- Adem, A.R.; Ntsime, B.P.; Biswas, A.; Asma, M.; Ekici, M.; Moshokoa, S.P.; Alzahrani, A.K.; Belic, M.R. Stationary optical solitons with Sasa–Satsuma equation having nonlinear chromatic dispersion. Phys. Lett. A 2020, 384, 126721. [Google Scholar] [CrossRef]
- Adem, A.R.; Ekici, M.; Biswas, A.; Asma, M.; Zayed, E.M.; Alzahrani, A.K.; Belic, M.R. Stationary optical solitons with nonlinear chromatic dispersion having quadratic-cubic law of refractive index. Phys. Lett. A 2020, 384, 126606. [Google Scholar] [CrossRef]
- Adem, A.R.; Ntsime, B.P.; Biswas, A.; Khan, S.; Alzahrani, A.K.; Belic, M.R. Stationary optical solitons with nonlinear chromatic dispersion for Lakshmanan–Porsezian–Daniel model having Kerr law of nonlinear refractive index. Ukr. J. Phys. Opt. 2021, 22, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Adem, A.R.; Ntsime, B.P.; Biswas, A.; Ekici, M.; Yildirim, Y.; Alshehri, H.M. Implicit quiescent optical solitons with complex Ginzburg–Landau equation having nonlinear chromatic dispersion. J. Optoelectron. Adv. Mater. 2022, 24, 450–462. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).