Adaptive Hierarchical Density-Based Spatial Clustering Algorithm for Streaming Applications
Abstract
:1. Introduction
2. Relevant Work
- The number of Gaussian clusters used to describe pixel history is denoted by k;
- is the weight factor associated with cluster i and time t;
- and are the mean and covariance matrix of i-th Gaussian cluster.
3. Methodology
3.1. Data Preparation
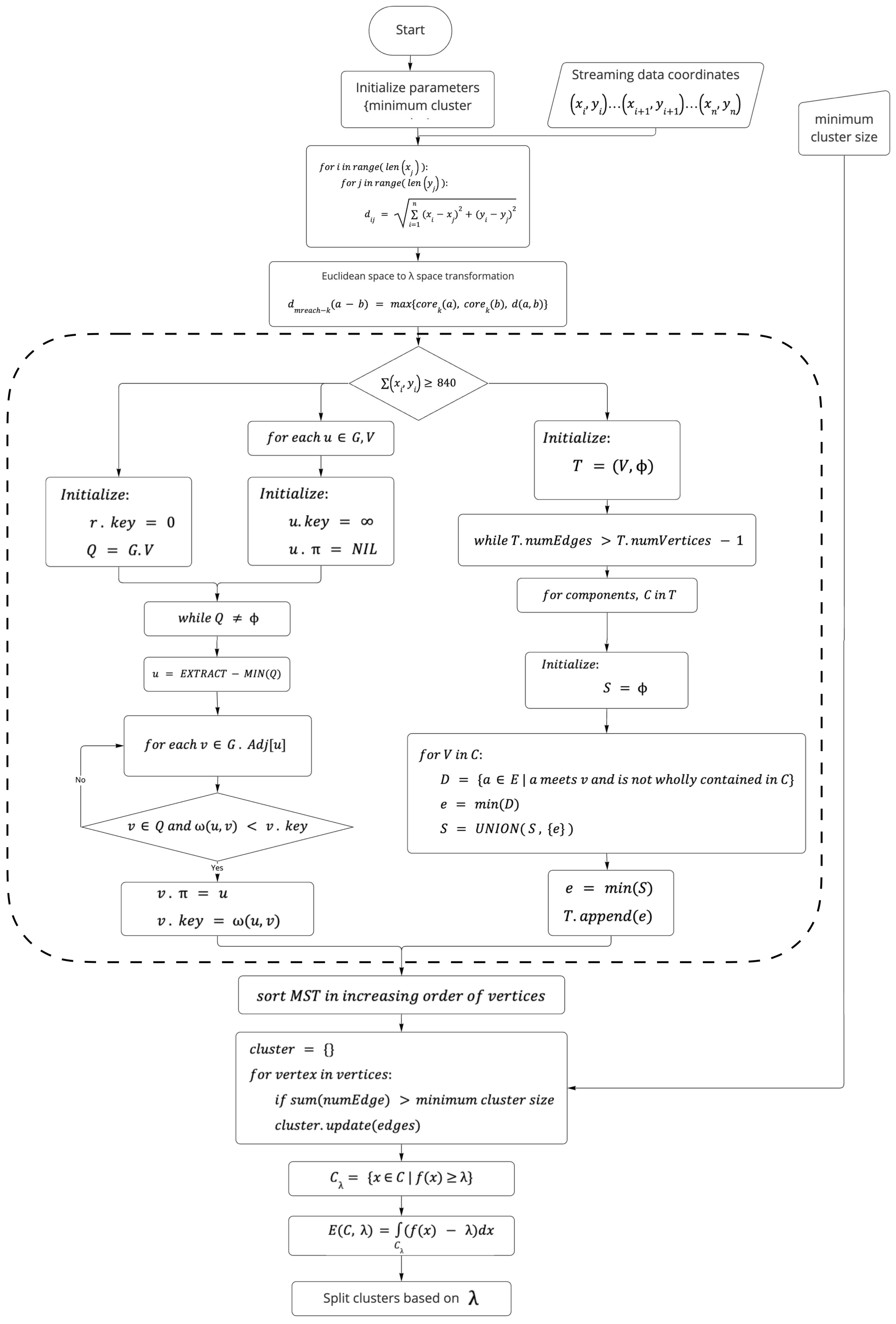
3.2. Adaptive HDBSCAN Implementation
3.3. Pairwise Distance Calculation
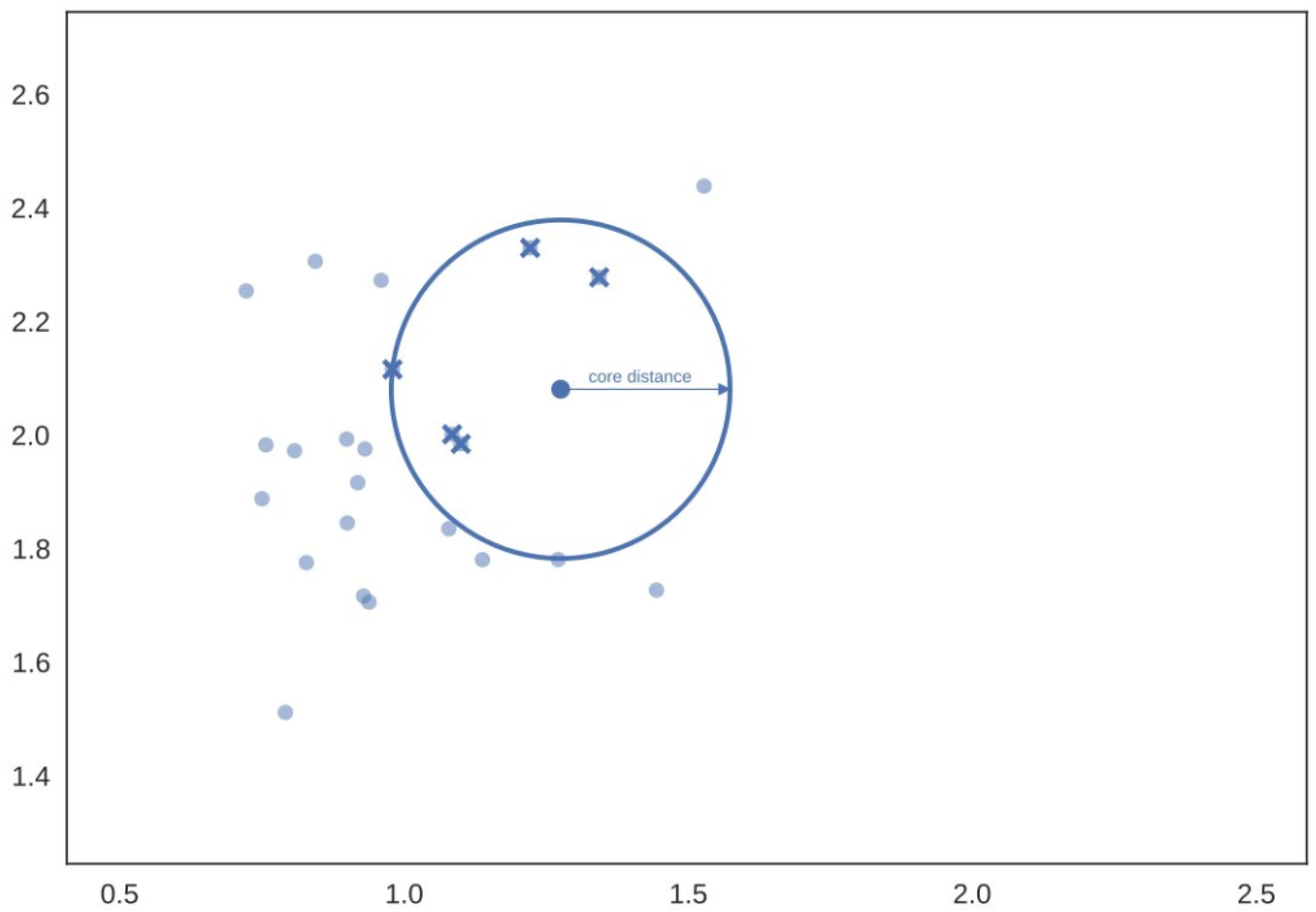
3.4. Euclidean to -Space Transformation
3.5. Determining the Cutoff for Algorithm Selection
3.6. Prim’s Algorithm
3.7. Boruvka’s Algorithm
3.8. Cluster Hierarchy Construction
3.9. Cluster Hierarchy Condensation
3.10. Excess of Mass Calculation
4. Experiment Results and Discussions
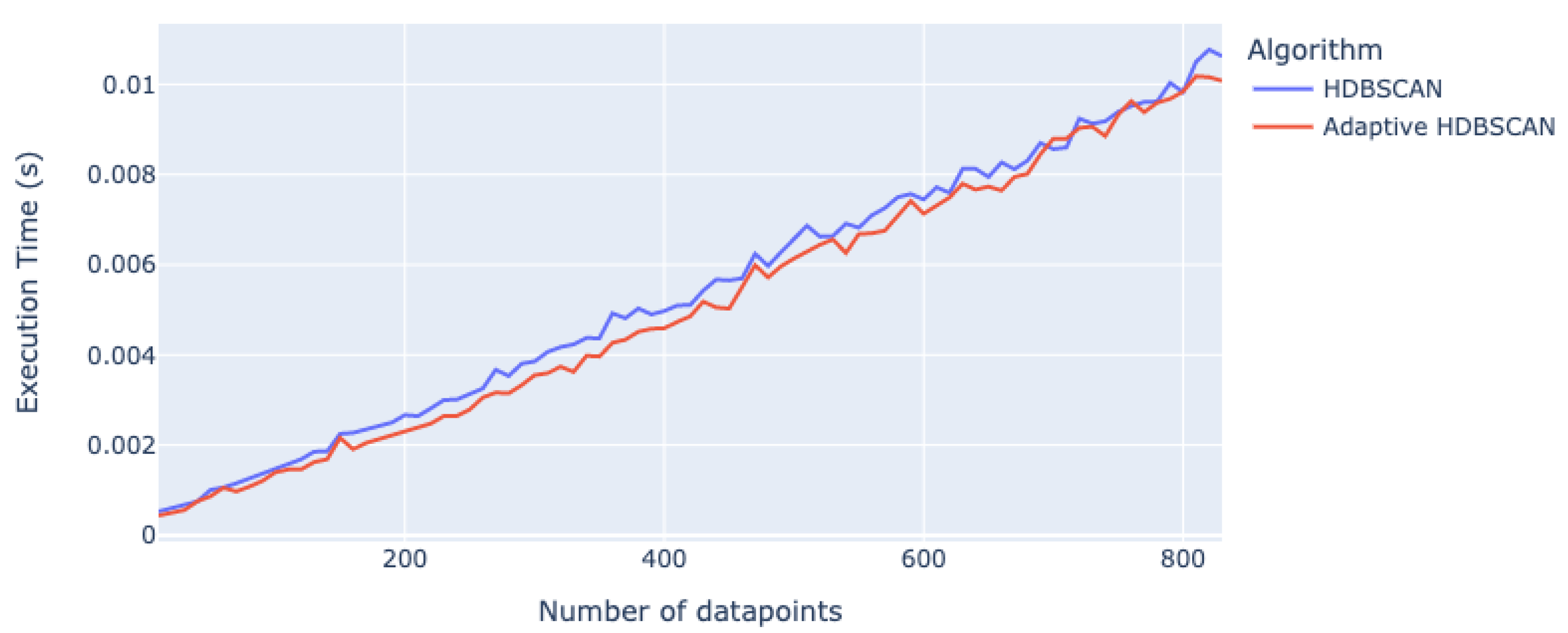
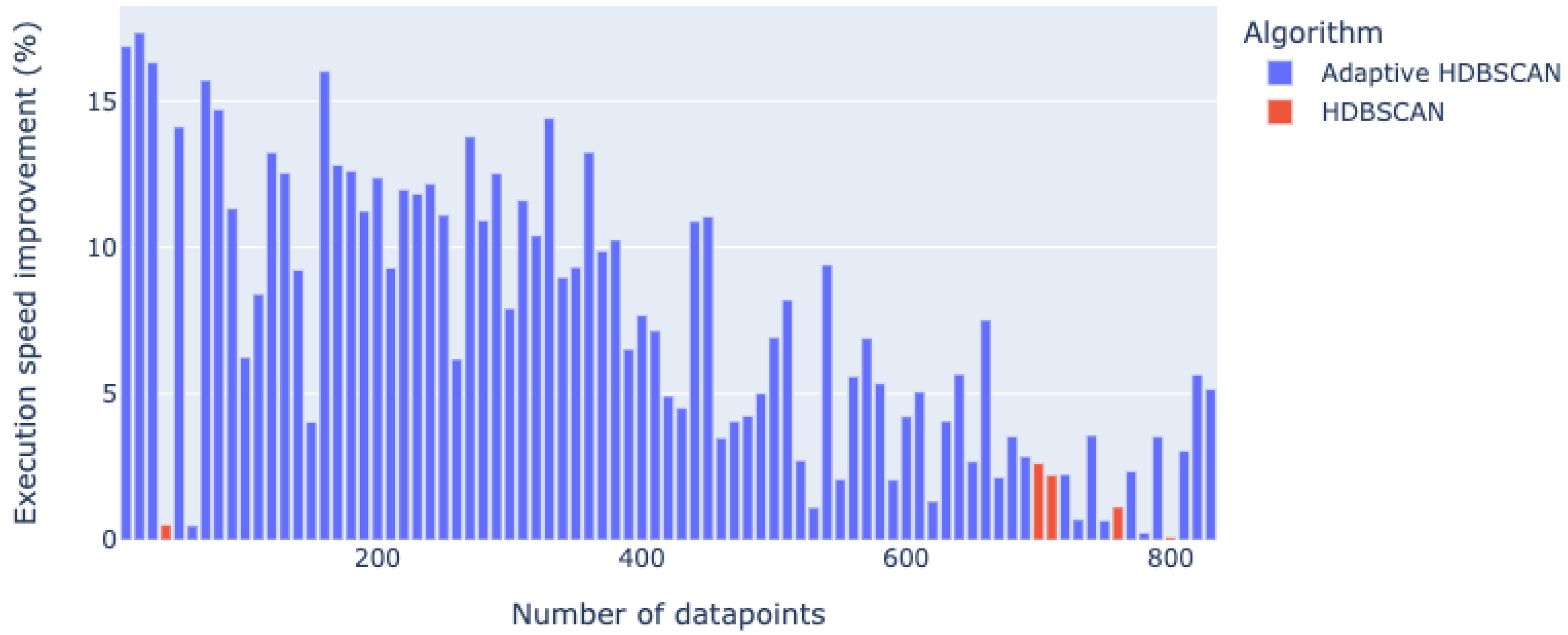
4.1. Experiment Setup to Assess the Execution Time Improvement of Adaptive HDBSCAN
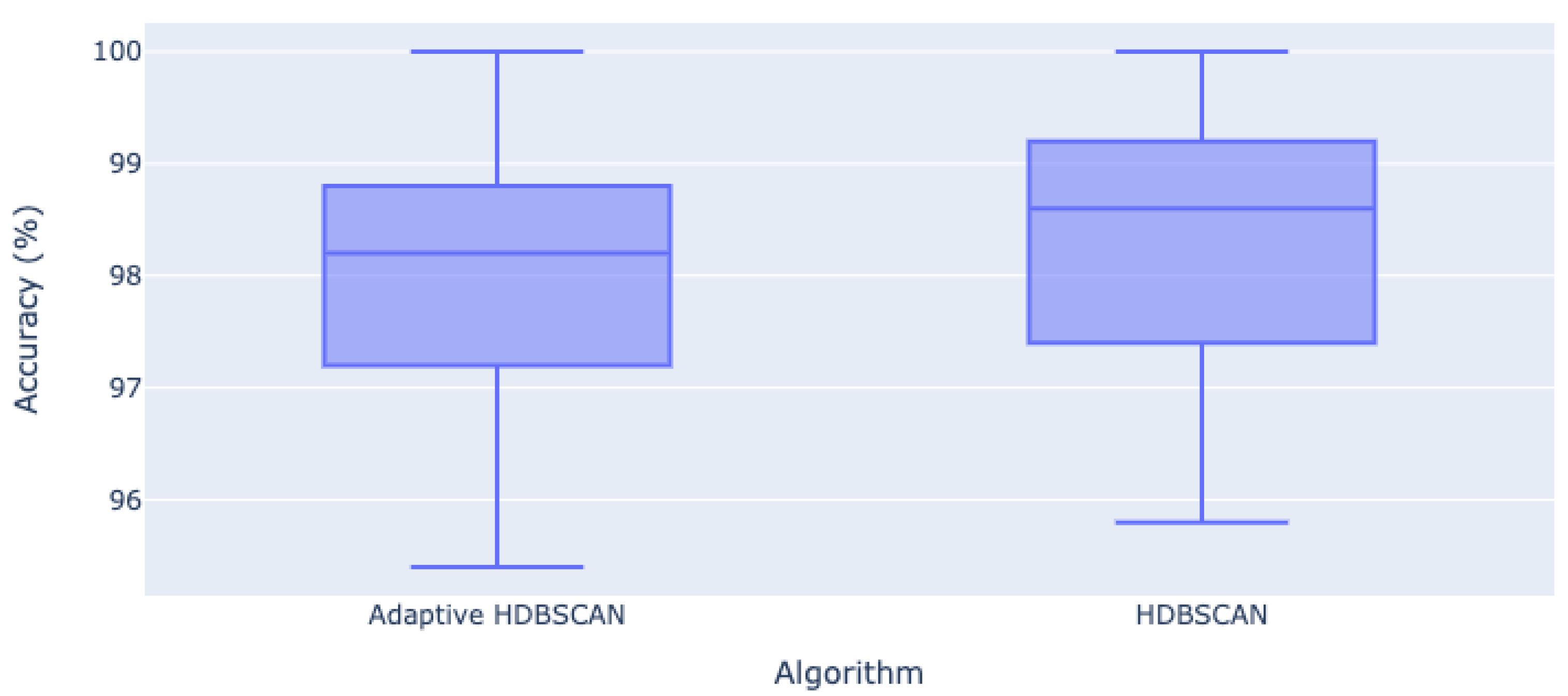
4.2. Experiment Setup to Assess the Accuracy of Clusters Generated by Adaptive HDBSCAN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koh, Y.; Mohan, A.; Wang, G.; Xu, H.; Malik, A.; Lu, Y.; Ebert, D. Improve safety using public network cameras. In Proceedings of the 2016 IEEE Symposium On Technologies For Homeland Security (HST), Waltham, MA, USA, 10–11 May 2016; pp. 1–5. [Google Scholar]
- Molchanov, V.; Vishnyakov, B.; Vizilter, Y.; Vishnyakova, O.; Knyaz, V. Pedestrian detection in video surveillance using fully convolutional YOLO neural network. Autom. Vis. Insp. Mach. Vis. II 2017, 10334, 103340Q. [Google Scholar] [CrossRef]
- Nguyen, M.; Truong, L.; Tran, T.; Chien, C. Artificial intelligence based data processing algorithm for video surveillance to empower industry 3.5. Comput. Ind. Eng. 2020, 148, 106671. [Google Scholar] [CrossRef]
- Campello, R.J.; Moulavi, D.; Zimek, A.; Sander, J. A framework for semi-supervised and unsupervised optimal extraction of clusters from hierarchies. Data Min. Knowl. Discov. 2013, 27, 344–371. [Google Scholar] [CrossRef]
- Collinson, P.A. The application of camera based traffic monitoring systems. In Proceedings of the IEE Seminar on CCTV and Road Surveillance (Ref. No. 1999/126), London, UK, 12 May 1999; pp. 1–8. [Google Scholar]
- Zhang, J.; Chen, X.; Sun, Q. An assessment model of safety production management based on fuzzy comprehensive evaluation method and behavior-based safety. Math. Probl. Eng. 2019, 2019, 4137035. [Google Scholar] [CrossRef] [Green Version]
- Sincan, O.M.; Keles, H.Y.; Tosun, S. Moving object detection and classification in surveillance systems using moving cameras. Commun. Fac. Sci. Univ. Ank. Ser. A2-A3 Phys. Sci. Eng. 2018, 60, 63–82. [Google Scholar]
- Zhou, D.X. Theory of Deep Convolutional Neural Networks: Downsampling. Neural Netw. 2020, 124, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. arXiv 2013, arXiv:1311.2524. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Ren, P.; Wang, L.; Fang, W.; Song, S.; Djahel, S. A novel squeeze YOLO-based real-time people counting approach. Int. J. Bio-Inspired Comput. 2020, 16, 94. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Khaing, H.S.; Thein, T. An Efficient Clustering Algorithm for Moving Object Trajectories. 2014. Available online: https://www.semanticscholar.org/paper/An-Efficient-Clustering-Algorithm-for-Moving-Object-Khaing-Thein/bcfcd76f272d5736a1d48727f809e4b0806a108e (accessed on 2 November 2022).
- Zhang, Z.; Yang, Y.; Tung, A.K.; Papadias, D. Continuous k-Means Monitoring over Moving Objects. IEEE Trans. Knowl. Data Eng. 2008, 20, 1205–1216. [Google Scholar] [CrossRef] [Green Version]
- Campello, R.J.G.B.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates. In Proceedings of the Advances in Knowledge Discovery and Data Mining; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 160–172. [Google Scholar]
- Logan, C.H.A.; Fotopoulou, S. Unsupervised star, galaxy, QSO classification. Astron. Astrophys. 2020, 633, A154. [Google Scholar] [CrossRef]
- Lukacs, E.; King, E. A Property of the Normal Distribution. Ann. Math. Stat. 1954, 25, 389–394. [Google Scholar] [CrossRef]
- Marpaung, F.; Piliang, A. Comparative of prim’s and boruvka’s algorithm to solve minimum spanning tree problems. J. Phys. Conf. Ser. 2020, 1462, 012043. [Google Scholar] [CrossRef]
- Bergantiños, G.; Vidal-Puga, J. The folk solution and Boruvka’s algorithm in minimum cost spanning tree problems. Discret. Appl. Math. 2011, 159, 1279–1283. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J. Accelerated Hierarchical Density Based Clustering. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 33–42. [Google Scholar]
- Rachmawati, D.; Pakpahan, F. Comparative analysis of the Kruskal and Boruvka algorithms in solving minimum spanning tree on complete graph. In Proceedings of the 2020 International Conference On Data Science, Artificial Intelligence, And Business Analytics (DATABIA), Medan, Indonesia, 16–17 July 2020; pp. 55–62. [Google Scholar]


| Number of Data Points | Execution Time (Seconds) | |
|---|---|---|
| HDBSCAN | Adaptive HDBSCAN | |
| 100 | 0.001490 | 0.001397 |
| 200 | 0.002667 | 0.002337 |
| 300 | 0.003855 | 0.003550 |
| 400 | 0.004973 | 0.004591 |
| 500 | 0.006595 | 0.006137 |
| 600 | 0.007446 | 0.007131 |
| 700 | 0.008563 | 0.008794 |
| 800 | 0.009830 | 0.009840 |
| Number of Data Points | Accuracy (%) | |
|---|---|---|
| Adaptive HDBSCAN | HDBSCAN | |
| 100 | 99.6 | 99.8 |
| 200 | 100.0 | 100.0 |
| 300 | 99.2 | 99.6 |
| 400 | 98.6 | 99.2 |
| 500 | 98.6 | 99.0 |
| 600 | 98.4 | 99.0 |
| 700 | 98.8 | 98.8 |
| 800 | 98.4 | 98.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vijayan, D.; Aziz, I. Adaptive Hierarchical Density-Based Spatial Clustering Algorithm for Streaming Applications. Telecom 2023, 4, 1-14. https://doi.org/10.3390/telecom4010001
Vijayan D, Aziz I. Adaptive Hierarchical Density-Based Spatial Clustering Algorithm for Streaming Applications. Telecom. 2023; 4(1):1-14. https://doi.org/10.3390/telecom4010001
Chicago/Turabian StyleVijayan, Darveen, and Izzatdin Aziz. 2023. "Adaptive Hierarchical Density-Based Spatial Clustering Algorithm for Streaming Applications" Telecom 4, no. 1: 1-14. https://doi.org/10.3390/telecom4010001
APA StyleVijayan, D., & Aziz, I. (2023). Adaptive Hierarchical Density-Based Spatial Clustering Algorithm for Streaming Applications. Telecom, 4(1), 1-14. https://doi.org/10.3390/telecom4010001






