Feature Importances: A Tool to Explain Radio Propagation and Reduce Model Complexity
Abstract
1. Introduction
- ○
- Insight into the model’s behavior is gained through the association between the changes in feature importances and the emergence of different radio propagation mechanisms.
- ○
- Simpler and faster models are deployed through a feature selection procedure based on the ranked importances.
2. Propagation Mechanisms According to the Transmitter’s Height
3. Problem Description and Model Used
3.1. Features and the Associated Propagation Mechanisms
3.2. Models Used: XGBoost and Random Forest
3.3. Relative Feature Importances in Tree-Based Models
3.4. Metrics of the Prediction Error
4. Numerical Results
4.1. Path Loss Predictions for Both Models and Transmitter Heights
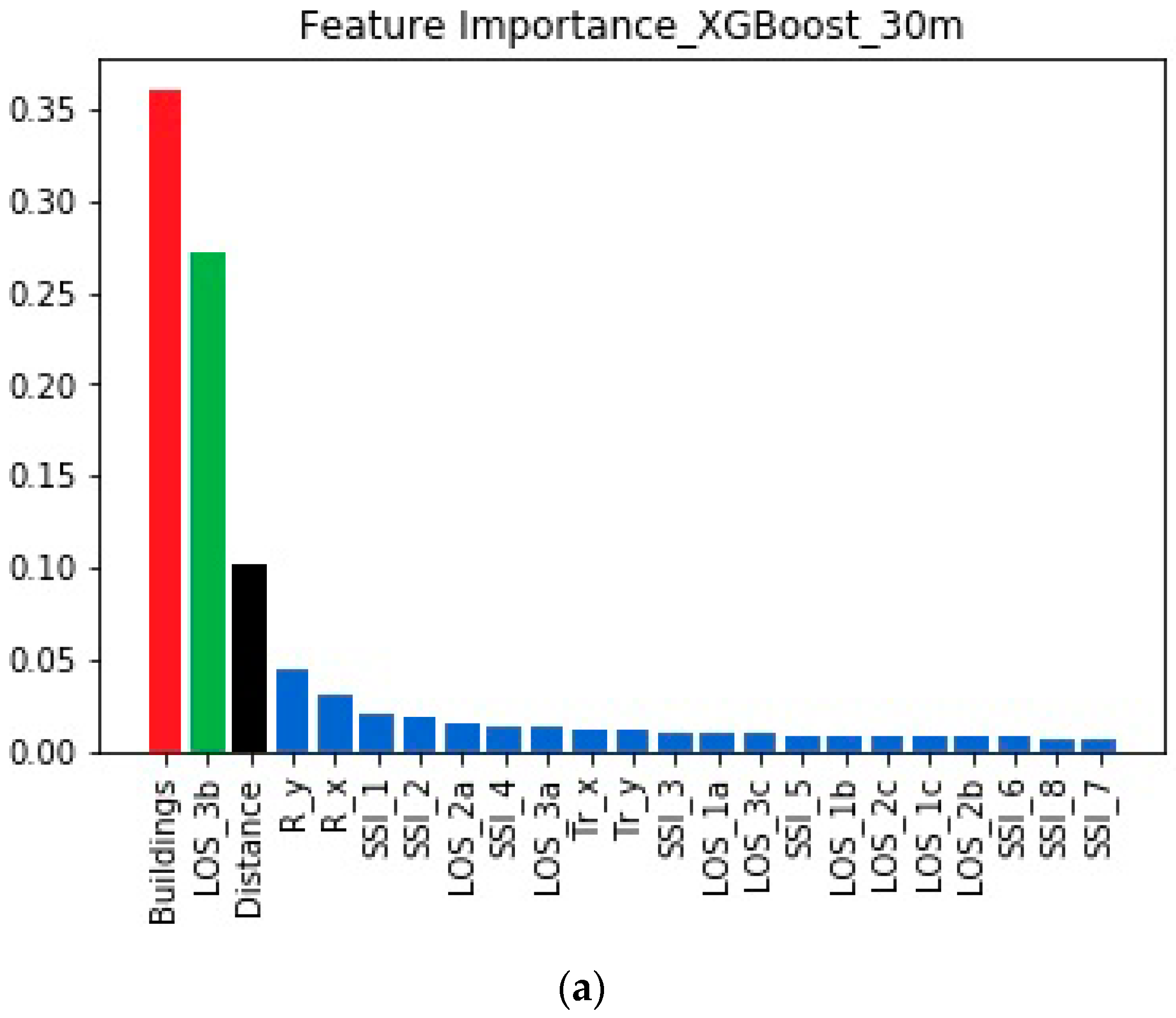
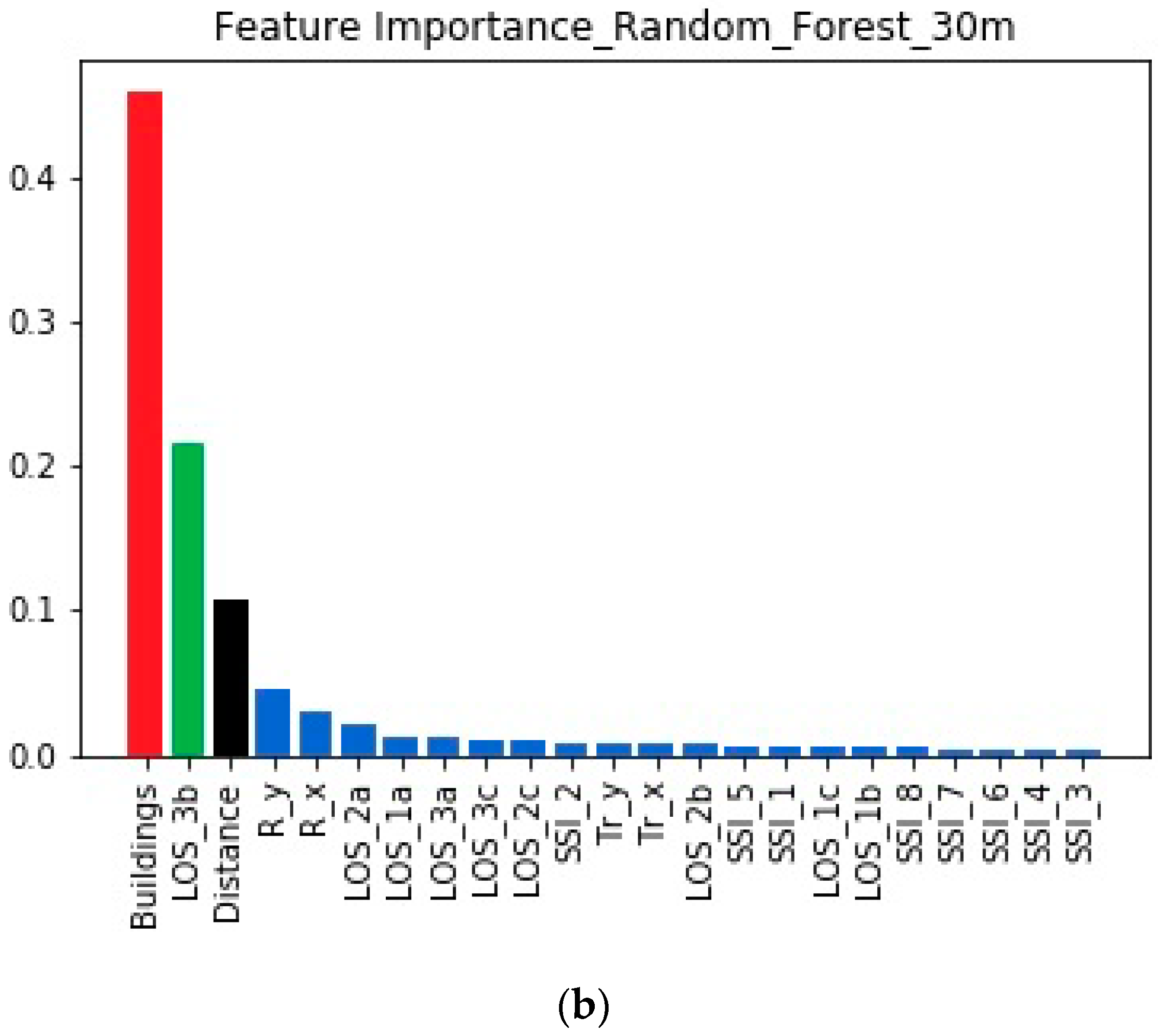
4.2. Feature Importances When the Transmitter is at 30 m
4.3. Feature Importances When the Transmitter is at 35 m
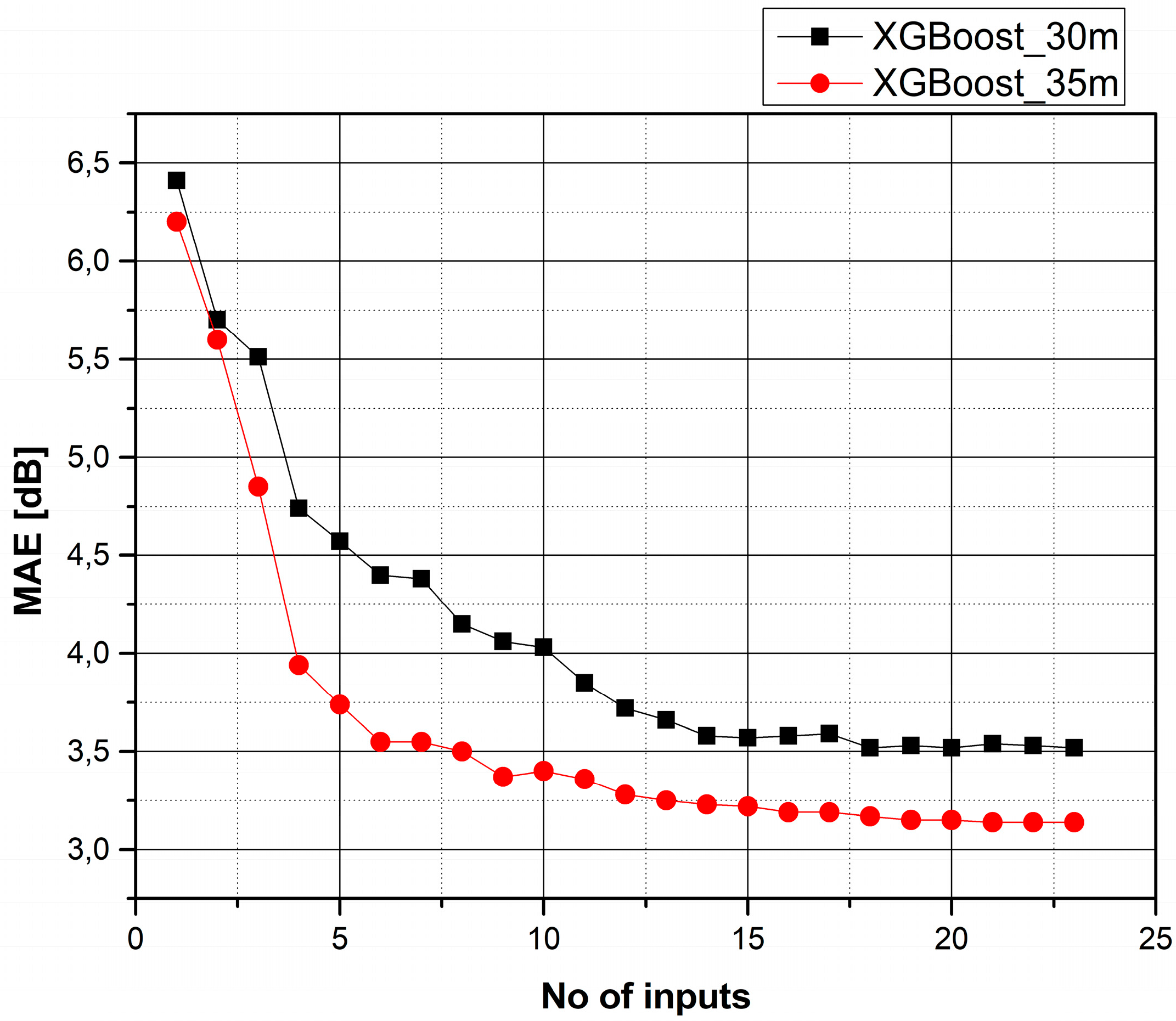
4.4. Gradual Addition of Features with Reverse Order of Importance
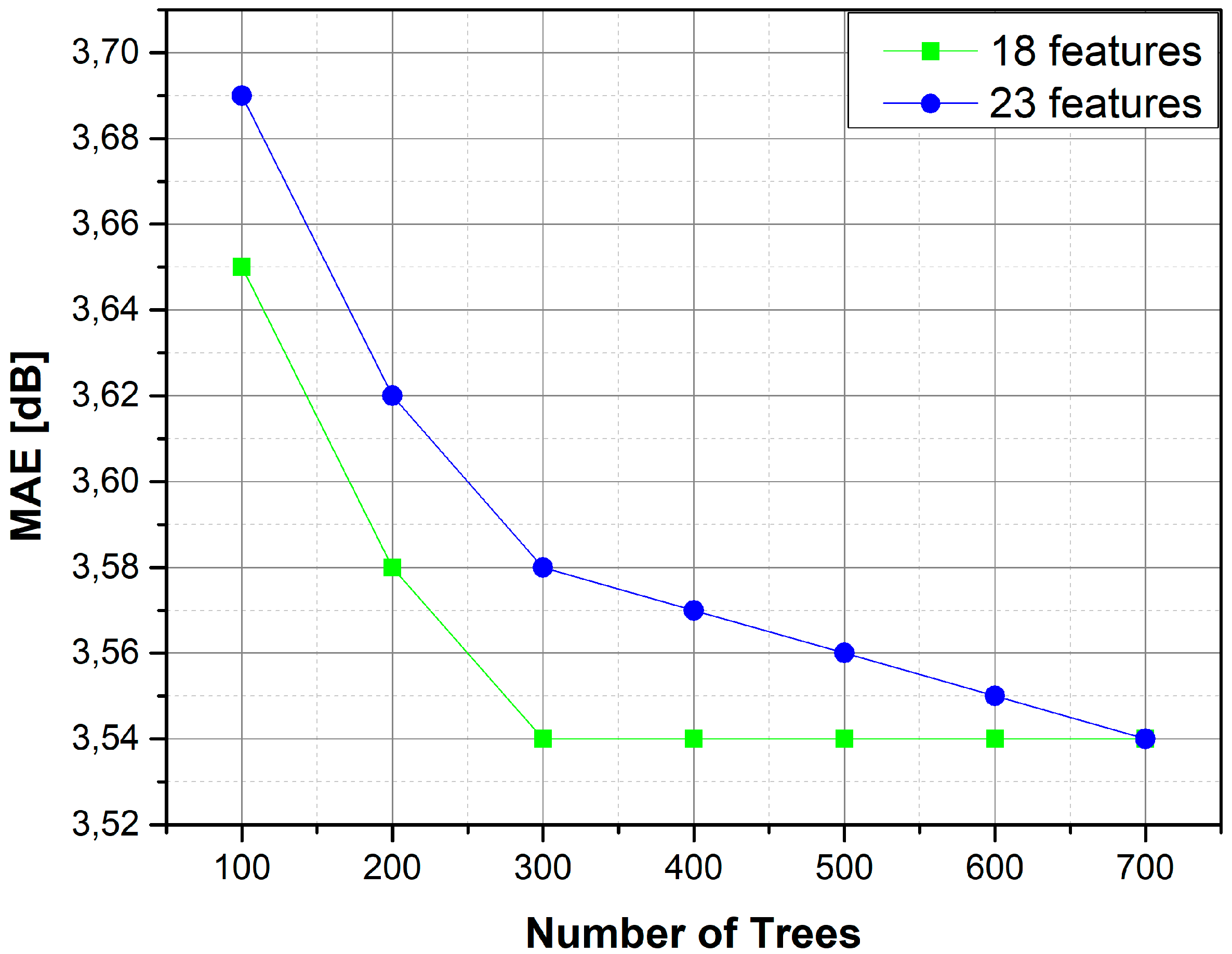
4.5. Model Reduction
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Sotiroudis, S.P.; Siakavara, K.; Sahalos, J.N. A Neural Network Approach to the Prediction of the Propagation Path-loss for Mobile Communications Systems in Urban Environments. PIERS Online 2007, 3, 1175–1179. [Google Scholar] [CrossRef]
- Faruk, N.; Surajudeen-Bakinde, N.T.; Popoola, S.I.; Olawoyin, L.A.; Atayero, A.A.; Abdulkarim, A.; Abdulkarim, A. ANFIS Model for Path Loss Prediction in the GSM and WCDMA Bands in Urban Area. Elektr. J. Electr. Eng. 2019, 18, 1–10. [Google Scholar] [CrossRef][Green Version]
- Sotiroudis, S.P.; Goudos, S.K.; Siakavara, K. Deep learning for radio propagation: Using image-driven regression to estimate path loss in urban areas. ICT Express 2020. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Y.; Yang, G.; He, Z.; Zhang, W. Path Loss Prediction Based on Machine Learning Methods for Aircraft Cabin Environments. IEEE Access 2019, 7, 159251–159261. [Google Scholar] [CrossRef]
- Adeogun, R.O. Calibration of Stochastic Radio Propagation Models Using Machine Learning. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2538–2542. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Goudos, S.K.; Gotsis, K.A.; Siakavara, K.; Sahalos, J.N. Optimal Artificial Neural Network design for propagation path-loss prediction using adaptive evolutionary algorithms. In Proceedings of the 2013 7th European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013; pp. 3795–3799. [Google Scholar]
- Sotiroudis, S.P.; Goudos, S.K.; Gotsis, K.A.; Siakavara, K.; Sahalos, J.N. Application of a Composite Differential Evolution Algorithm in Optimal Neural Network Design for Propagation Path-Loss Prediction in Mobile Communication Systems. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 364–367. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, J.; Yang, G.; He, Z.; Luo, X. Air-to-Air Path Loss Prediction Based on Machine Learning Methods in Urban Environments. Wirel. Commun. Mob. Comput. 2018, 2018, 1–9. Available online: https://www.hindawi.com/journals/wcmc/2018/8489326/ (accessed on 27 July 2020). [CrossRef]
- Zhang, Y.; Wen, J.; Yang, G.; He, Z.; Wang, J. Path Loss Prediction Based on Machine Learning: Principle, Method, and Data Expansion. Appl. Sci. 2019, 9, 1908. [Google Scholar] [CrossRef]
- Goldsmith, A.; Greenstein, L. A measurement-based model for predicting coverage areas of urban microcells. IEEE J. Sel. Areas Commun. 1993, 11, 1013–1023. [Google Scholar] [CrossRef]
- Saunders, S.R. Antennas and Propagation for Wireless Communication Systems; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Maciel, L.R.; Bertoni, H.L.; Xia, H.N. Unified approach to prediction of propagation over buildings for all ranges of base station antenna height. IEEE Trans. Veh. Technol. 1993, 42, 41–45. [Google Scholar] [CrossRef]
- Goncalves, N.; Correia, L.M. A propagation model for urban microcellular systems at the UHF band. IEEE Trans. Veh. Technol. 2000, 49, 1294–1302. [Google Scholar] [CrossRef]
- Popoola, S.I.; Jefia, A.; Atayero, A.A.; Kingsley, O.; Faruk, N.; Oseni, O.F.; Abolade, R.O. Determination of Neural Network Parameters for Path Loss Prediction in Very High Frequency Wireless Channel. IEEE Access 2019, 7, 150462–150483. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Siakavara, K. Mobile radio propagation path loss prediction using Artificial Neural Networks with optimal input information for urban environments. AEU Int. J. Electron. Commun. 2015, 69, 1453–1463. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Goudos, S.K.; Siakavara, K. Neural Networks and Random Forests: A Comparison Regarding Prediction of Propagation Path Loss for NB-IoT Networks. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Goudos, S.K.; Gotsis, K.A.; Siakavara, K.; Sahalos, J.N. Modeling by optimal Artificial Neural Networks the prediction of propagation path loss in urban environments. In Proceedings of the 2013 IEEE-APS Topical Conference on Antennas and Propagation in Wireless Communications (APWC), Torino, Italy, 9–13 September 2013; pp. 599–602. [Google Scholar] [CrossRef]
- Piacentini, M.; Rinaldi, F. Path loss prediction in urban environment using learning machines and dimensionality reduction techniques. Comput. Manag. Sci. 2010, 8, 371–385. [Google Scholar] [CrossRef]
- OpenStreetMap Contributors S. Planet Dump. Available online: https://planet.osm.org (accessed on 27 July 2020).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- EDX Wireless. EDX Wireless Microcell/Indoor Module Reference Manual, Version 7©; EDX Wireless: Eugene, OR, USA, 1996–2011. [Google Scholar]
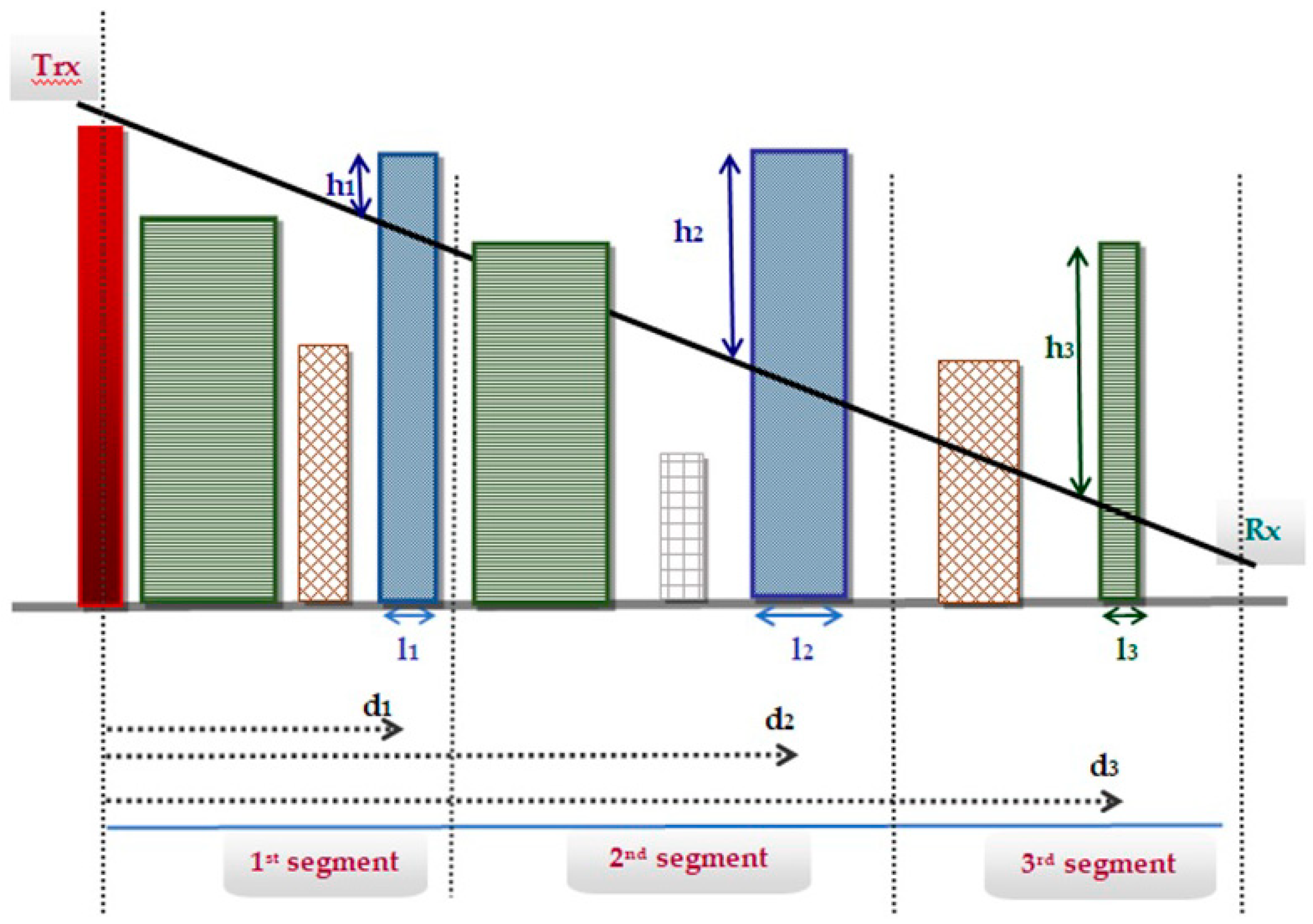
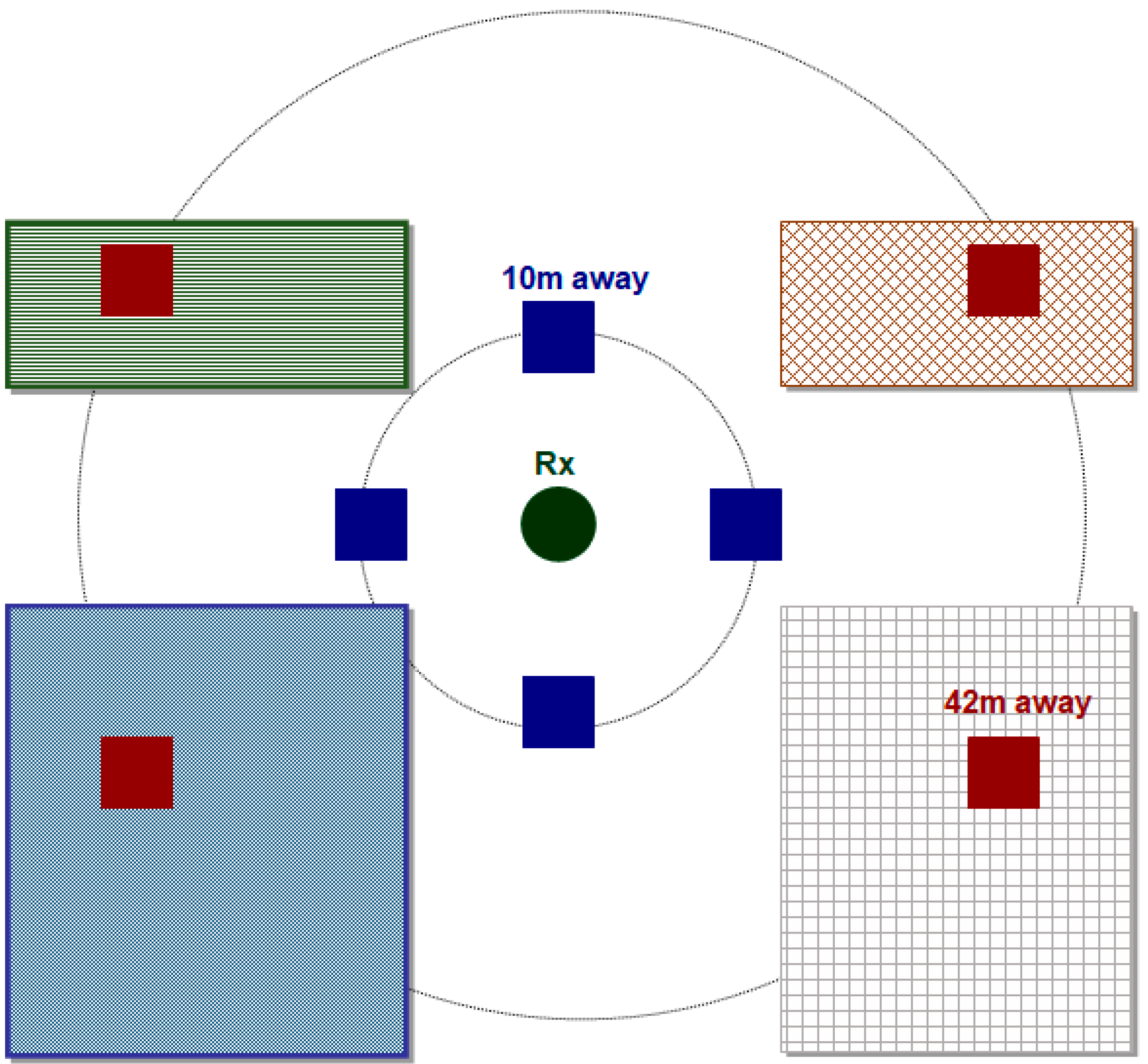


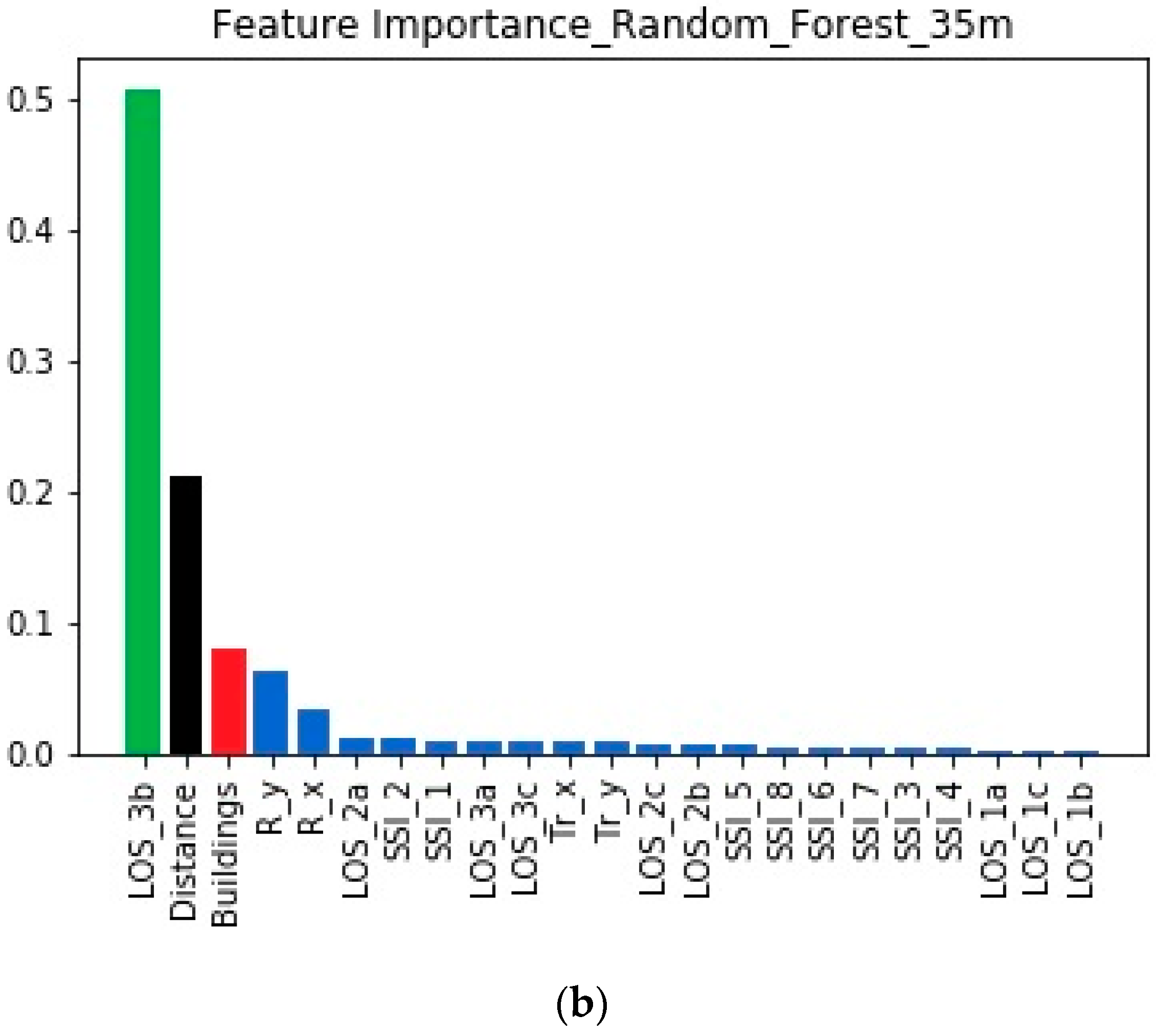
| Number | Name | Description |
|---|---|---|
| 1 | LOS_1a | The distance (h1) of the top of the tallest building of the first segment, from the point at which the building intersects the LOS ray, between Tr and R |
| 2 | LOS_1b | The distance d1 of the tallest building of the first segment from the transmitter |
| 3 | LOS_1c | The length, l1, of the tallest building of the first segment |
| 4 | LOS_2a | The distance (h2) of the top of the tallest building of the second segment, from the point at which the building intersects the LOS ray, between Tr and R |
| 5 | LOS_2b | The distance d2 of the tallest building of the second segment from the transmitter |
| 6 | LOS_2c | The length, l2, of the tallest building of the second segment |
| 7 | LOS_3a | The distance (h3) of the top of the tallest building of the third segment, from the point at which the building intersects the LOS ray, between Tr and R |
| 8 | LOS_3b | The distance d3 of the tallest building of the first segment from the transmitter |
| 9 | LOS_3c | The length, l3, of the tallest building of the third segment |
| 10 | Buildings: | The total number of the buildings which interrupt the LOS path. |
| 11 | SSI_1 | The height of the building (or the existence of a street) 10m right from the receiver |
| 12 | SSI_2 | The height of the building (or the existence of a street) 10 m left from the receiver |
| 13 | SSI_3 | The height of the building (or the existence of a street) 10 m above the receiver |
| 14 | SSI_4 | The height of the building (or the existence of a street) 10 m below the receiver |
| 15 | SSI_5 | The height of the building (or the existence of a street) 10 m left and above the receiver |
| 16 | SSI_6 | The height of the building (or the existence of a street) 10 m left and below the receiver |
| 17 | SSI_7 | The height of the building (or the existence of a street) 10 m right and above the receiver |
| 18 | SSI_8 | The height of the building (or the existence of a street) 10 m right and below the receiver |
| 19 | Tr_x | X_coordinate of the transmitter |
| 20 | Tr_y | Y_coordinate of the transmitter |
| 21 | R_x | X_coordinate of the receiver |
| 22 | R_y | Y_coordinate of the receiver |
| 23 | Distance | The distance between transmitter and receiver in the xy plane |
| Transmitter Height (m) | XGBoost | Random Forest | ||
|---|---|---|---|---|
| MAE (dB) | R2 | MAE (dB) | R2 | |
| 30 | 3.54 | 0.89 | 3.97 | 0.87 |
| 35 | 3.17 | 0.91 | 3.35 | 0.90 |
| Model No | MAE (dB) | Trees | Features | Training Time (s) | Response Time (ms) |
|---|---|---|---|---|---|
| 1 | 3.54 | 700 | 23 | 68.34 | 382.51 |
| 2 | 3.54 | 700 | 18 | 58.46 | 354.79 |
| 3 | 3.54 | 300 | 18 | 32.02 | 147.88 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotiroudis, S.P.; Goudos, S.K.; Siakavara, K. Feature Importances: A Tool to Explain Radio Propagation and Reduce Model Complexity. Telecom 2020, 1, 114-125. https://doi.org/10.3390/telecom1020009
Sotiroudis SP, Goudos SK, Siakavara K. Feature Importances: A Tool to Explain Radio Propagation and Reduce Model Complexity. Telecom. 2020; 1(2):114-125. https://doi.org/10.3390/telecom1020009
Chicago/Turabian StyleSotiroudis, Sotirios P., Sotirios K. Goudos, and Katherine Siakavara. 2020. "Feature Importances: A Tool to Explain Radio Propagation and Reduce Model Complexity" Telecom 1, no. 2: 114-125. https://doi.org/10.3390/telecom1020009
APA StyleSotiroudis, S. P., Goudos, S. K., & Siakavara, K. (2020). Feature Importances: A Tool to Explain Radio Propagation and Reduce Model Complexity. Telecom, 1(2), 114-125. https://doi.org/10.3390/telecom1020009






