Optimal Adaptive Modeling of Hydrogen Polymer Electrolyte Membrane Fuel Cells Based on Meta-Heuristic Algorithms Considering the Membrane Aging Factor
Abstract
:1. Introduction
- A novel adaptive meta-heuristic WHO-based method for PEMFC modeling is proposed.
- A fair comparison of state-of-the-art algorithms dealing with typical PEMFC modeling problems is performed.
- The modeling accuracy and the impact of computational time are used as critical factors for evaluation.
- The robustness of the proposed approach is validated through the implementation of commercial PEMFC devices named 250 W PEMFC, Nedstack-PS6 6 kW, Temasek 1 kW, Ballard-Mark-V 5 kW.
- The accurate adaptive characterization of PEMFC is capable of reflecting dynamic changes in the cell’s performance in accordance with aging behavior.
2. Theoretical Approach
2.1. Description of the PEMFC Model
2.1.1. PEMFC Notion
2.1.2. PEMFC Quasi-Empirical Model
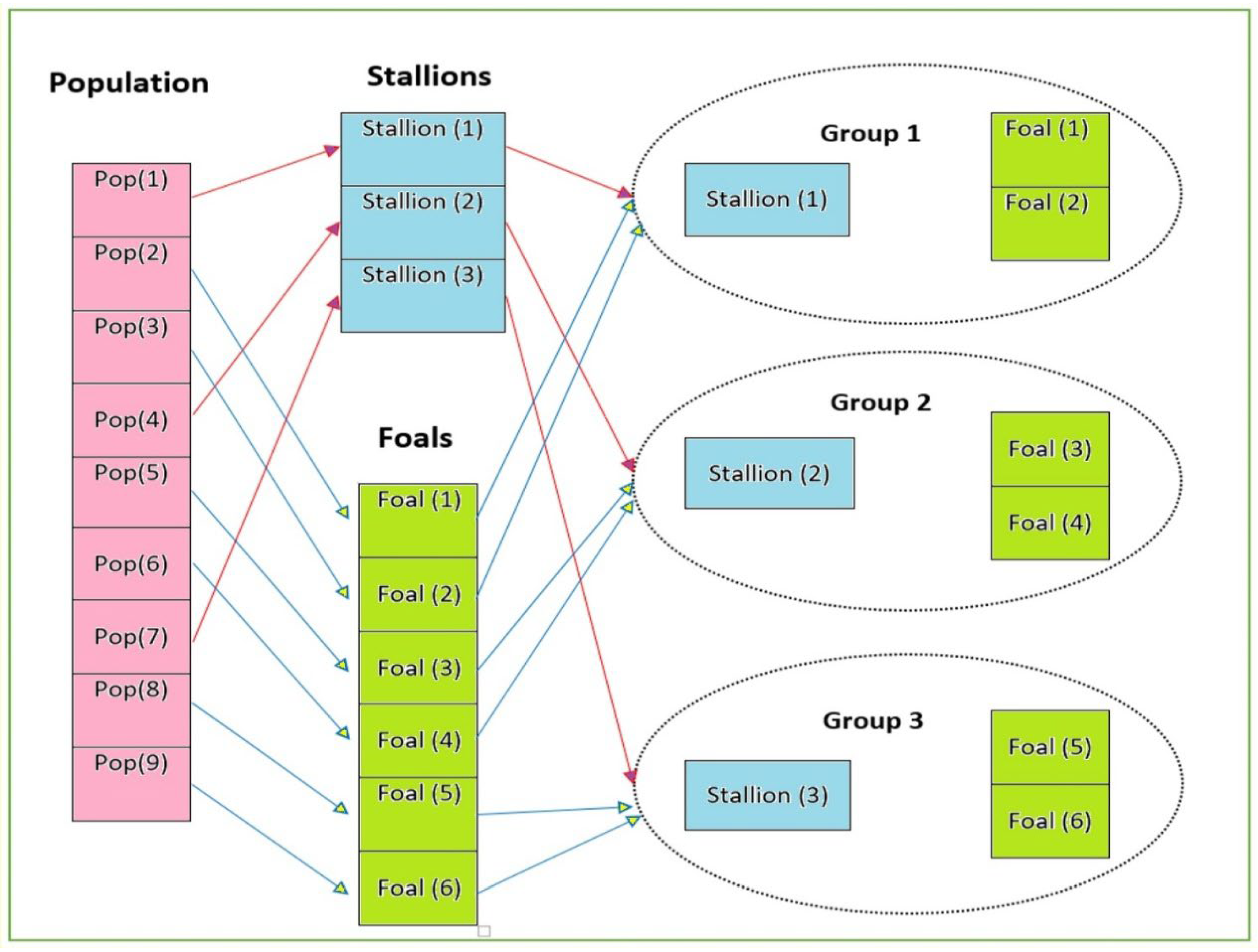
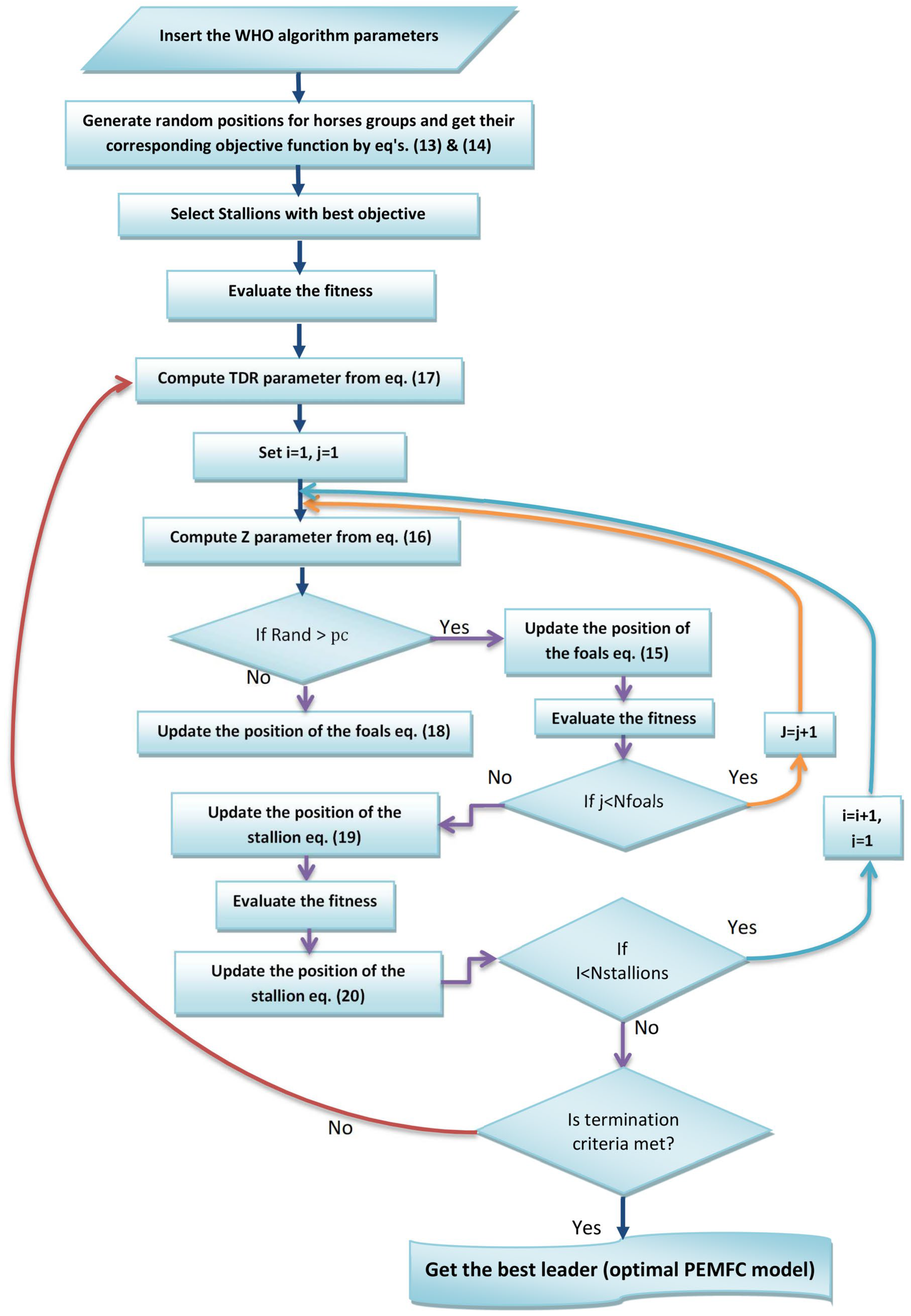
2.2. WHO Algorithm
2.2.1. The WHO Mechanism
- Start with an initial population that simulates horse groups and nominate a leader.
- Simulate grazing and mating behaviors.
- One stallion becomes the leader of the group.
- The group select and replace each new leader with a better leader.
- The best leader is found (the solution).
Starting the Initial Population
The Grazing Simulation Mechanism
The Mating Mechanism
Selecting the Leader Mechanism
2.3. Creating the Objective Function
3. Cases Under Study
- Operating condition (Data set 1): 300/500 kPa (3/5 bar), 353.15 K;
- Operating condition (Data set 2): 100/100 kPa (1/1 bar), 343.15 K;
- Operating condition (Data set 3): 250/300 kPa (2.5/3 bar), 343.15 K;
- Operating condition (Data set 4): 150/150 kPa (1.5/1.5 bar, 343.15 K.
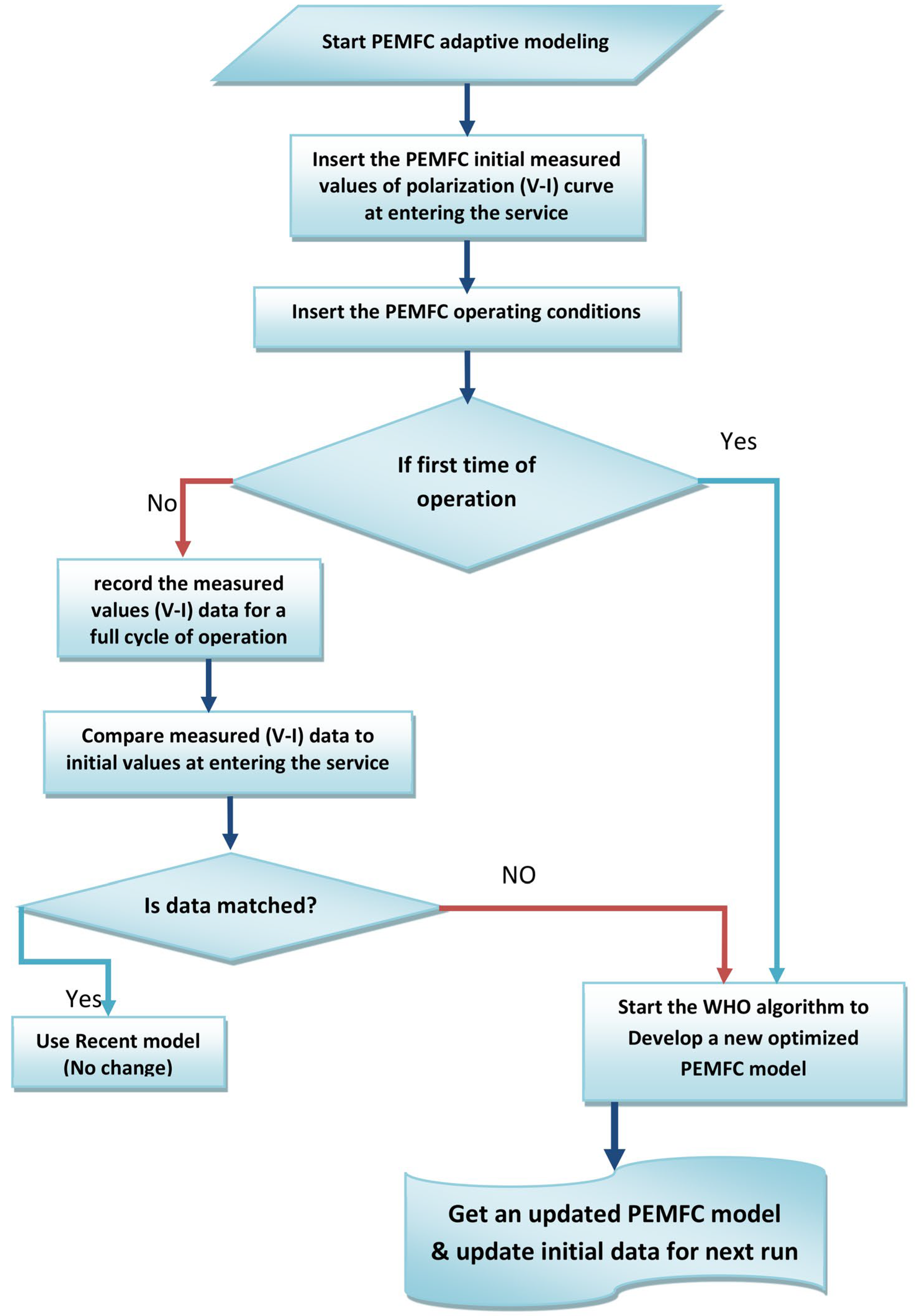
4. Methodology and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barbir, F. PEM Fuel Cells: Theory and Practice, 2nd ed.; Academic Press: Cambridge, MA, USA, 2012; ISBN 9780123877109. [Google Scholar] [CrossRef]
- Kaur, G. PEM Fuel Cells: Fundamentals, Advanced Technologies, and Practical Application, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021; ISBN 9780128237083. [Google Scholar] [CrossRef]
- Xing, Y.; Na, J.; Costa-Castell’o, R. Real-time Adaptive Parameter Estimation for a Polymer Electrolyte Membrane Fuel Cell. IEEE Trans Ind. Inform. 2018, 1551, 6048–6057. [Google Scholar] [CrossRef]
- Dimitrova, Z.; Nader, W.B. PEM fuel cell as an auxiliary power unit for range extended hybrid electric vehicles. Energy 2022, 239, 121933. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Harries, T.J. Performance modeling of the Ballard mark-IV solid polymer electrolyte fuel cell. J. Electrochem. Soc. 1995, 142, 9–15. [Google Scholar] [CrossRef]
- Shang, Z.; Hossain, M.M.; Wycisk, R.; Pintauro, P.N. Poly(phenylene sulfonic acid)-expanded polytetrafluoroethylene composite membrane for low relative humidity operation in hydrogen fuel cells. J. Power Sources 2022, 535, 231375. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Chen, D.; Hu, S.; Xu, X. Thermal-physical modeling and parameter identification method for dynamic model with unmeasurable state in 10-kW scale proton exchange membrane fuel cell system. Energy Convers. Manag. 2023, 276, 116580. [Google Scholar] [CrossRef]
- Fletcher, T.; Thring, R.; Watkinson, M. An Energy Management Strategy to concurrently optimise fuel consumption & PEM fuel cell lifetime in a hybrid vehicle. Int. J. Hydrogen Energy 2016, 41, 21503–21515. [Google Scholar] [CrossRef]
- Zhou, D.; Wu, Y.; Gao, F.; Breaz, E.; Ravey, A.; Miraoui, A. Degradation prediction of pem fuel cell stack based on multiphysical aging model with particle filter approach. IEEE Trans. Ind. Appl. 2017, 53, 4041–4052. [Google Scholar] [CrossRef]
- Singh, R.; Sui, P.; Wong, K.; Kjeang, E.; Knights, S.; Djilali, N. Modeling the effect of chemical membrane degradation on pemfc performance. J. Electrochem. Soc. 2018, 165, 3328–3336. [Google Scholar] [CrossRef]
- Xie, R.; Li, C.; Ma, R.; Xu, L.; Zhou, X. An Explainable Data-Driven Framework for Fuel Cell Aging Prediction Under Dynamic Condition. IEEE Trans. Ind. Electron. 2023, 70, 5960–5970. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, J.; Al-Durra, A.; Muyeen, S.; Zhou, D.; Hua, S. A novel aging prediction method of fuel cell based on empirical mode decomposition and complexity threshold quantitative criterion. J. Power Sources 2023, 574, 233120. [Google Scholar] [CrossRef]
- Xing, Y.; Costa-Castelló, R.; Na, J.; Renaudineau, H. Control-oriented modelling and analysis of a solid oxide fuel cell system. Int. J. Hydrogen Energy 2020, 45, 20659–20672. [Google Scholar] [CrossRef]
- Priya, K.; Rajasekar, N. Application of flower pollination algorithm for enhanced proton exchange membrane fuel cell modelling. Int. J. Hydrogen Energy 2019, 44, 18438–18449. [Google Scholar] [CrossRef]
- Seleem, S.I.; Hasanien, H.M.; El-Fergany, A.A. Equilibrium optimizer for parameter extraction of a fuel cell dynamic model. Renew. Energy 2021, 169, 117–128. [Google Scholar] [CrossRef]
- Turgut, O.E.; Coban, M.T. Optimal proton exchange membrane fuel cell modelling based on hybrid Teaching Learning Based Optimization-Differential Evolution algorithm. Ain Shams Eng. J. 2016, 7, 347–360. [Google Scholar] [CrossRef]
- Jia, J.; Li, Q.; Wang, Y.; Cham, Y.; Han, M. Modeling and dynamic characteristic simulation of a Proton Exchange Membrane Fuel Cell. IEEE Trans. Energy Convers. 2009, 24, 283–291. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. A new heuristic optimization algorithm for modeling of proton exchange membrane fuel cell: Bird mating optimizer. Int. J. Energy Res. 2013, 37, 1196–1204. [Google Scholar] [CrossRef]
- Ali, M.; El-Hameed, M.A.; Farahat, M.A. Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renew. Energy 2017, 111, 455–462. [Google Scholar] [CrossRef]
- Mo, Z.; Zhu, X.; Wei, L.; Cao, G. Parameter optimization for a PEMFC model with a hybrid genetic algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Ohenoja, M.; Leiviska, K. Validation of genetic algorithm results in a fuel cell model. Int. J. Hydrogen Energy 2010, 35, 12618–12625. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, N.; Zhang, L. Circular genetic operators based RNA genetic algorithm for modeling proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 17779–17790. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, N. An adaptive RNA genetic algorithm for modeling of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2013, 38, 219–228. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter identification for proton exchange membrane fuel cell model using particle swarm optimization. Int. J. Hydrogen Energy 2009, 34, 981–989. [Google Scholar] [CrossRef]
- Chakraborty, U.K.; Abbott, T.E.; Das, S.K. PEM fuel cell modeling using differential evolution. Energy 2012, 40, 387–399. [Google Scholar] [CrossRef]
- Gong, W.; Yan, X.; Liu, X.; Cai, Z. Parameter extraction of different fuel cell models with transferred adaptive differential evolution. Energy 2015, 86, 139–151. [Google Scholar] [CrossRef]
- Fathy, A.; Abd Elaziz, M.; Alharbi, A. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. A grouping-based global harmony search algorithm for modeling of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2011, 36, 5047–5053. [Google Scholar] [CrossRef]
- Yang, S.; Wang, N. A novel P system based optimization algorithm for parameter estimation of proton exchange membrane fuel cell model. Int. J. Hydrogen Energy 2012, 37, 8465–8476. [Google Scholar] [CrossRef]
- Rao, R.; Patel, V. Comparative performance of an elitist teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2013, 4, 29–50. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, H.; Li, K. An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int. J. Hydrogen Energy 2014, 39, 3837–3854. [Google Scholar] [CrossRef]
- Guarnieri, M.; Negro, E.; Noto, V.; Alotto, P. A selective hybrid stochastic strategy for fuel-cell multi-parameter identification. J. Power Sources 2016, 332, 249–264. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar] [CrossRef]
- Rao, Y.; Shao, Z.; Ahangarnejad, A.H.; Gholamalizadeh, E.; Sobhanid, B. Shark Smell Optimizer applied to identify the optimal parameters of the proton exchange membrane fuel cell model. Energy Convers. Manag. 2019, 182, 1–8. [Google Scholar] [CrossRef]
- Qin, F.; Liu, P.; Niu, H.; Song, H.; Yousefi, N. Parameter estimation of PEMFC based on Improved Fluid Search Optimization Algorithm. Energy Rep. 2020, 6, 1224–1232. [Google Scholar] [CrossRef]
- Yakout, A.; Hasanien, H.; Kotb, H. Proton Exchange Membrane Fuel Cell Steady State Modeling Using Marine Predator Algorithm Optimizer. Ain Shams Eng. J. 2021, 12, 3765–3774. [Google Scholar] [CrossRef]
- Ali, M.; Mandour, M.; Lotfy, M. Adaptive Estimation of Quasi-Empirical Proton Exchange Membrane Fuel Cell Models Based on Coot Bird Optimizer and Data Accumulation. Sustainability 2023, 15, 9017. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2022, 38 (Suppl.4), 3025–3056. [Google Scholar] [CrossRef]
- Ali, M.; Kamel, S.; Hassan, M.; Tostado-Véliz, M.; Zawbaa, H. An improved wild horse optimization algorithm for reliability based optimal DG planning of radial distribution networks. Energy Rep. 2022, 8, 582–604. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, Y.; Li, J.; Zhu, T.; Zhao, K. A Wild Horse Optimization algorithm with chaotic inertia weights and its application in linear antenna array synthesis. PLoS ONE 2024, 19, e0304971. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.; Taghian, S.; Mirjalili, S.; Faris, H. MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems. Appl. Soft Comput. 2020, 97, 106761. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Zhang, Z. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem. Knowl. Based Syst. 2019, 163, 283–304. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2015, 27, 1053–1073. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2019, 191, 105190. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Matlab (R2020a) Is a Product of the MathWorks. Available online: http://www.mathworks.com (accessed on 10 August 2024).
- IBM SPSS (Version 22) Is a Product of the IBM Corporation. Available online: http://www.ibm.com/analytics/us/en/technology/spss/ (accessed on 2 September 2024).


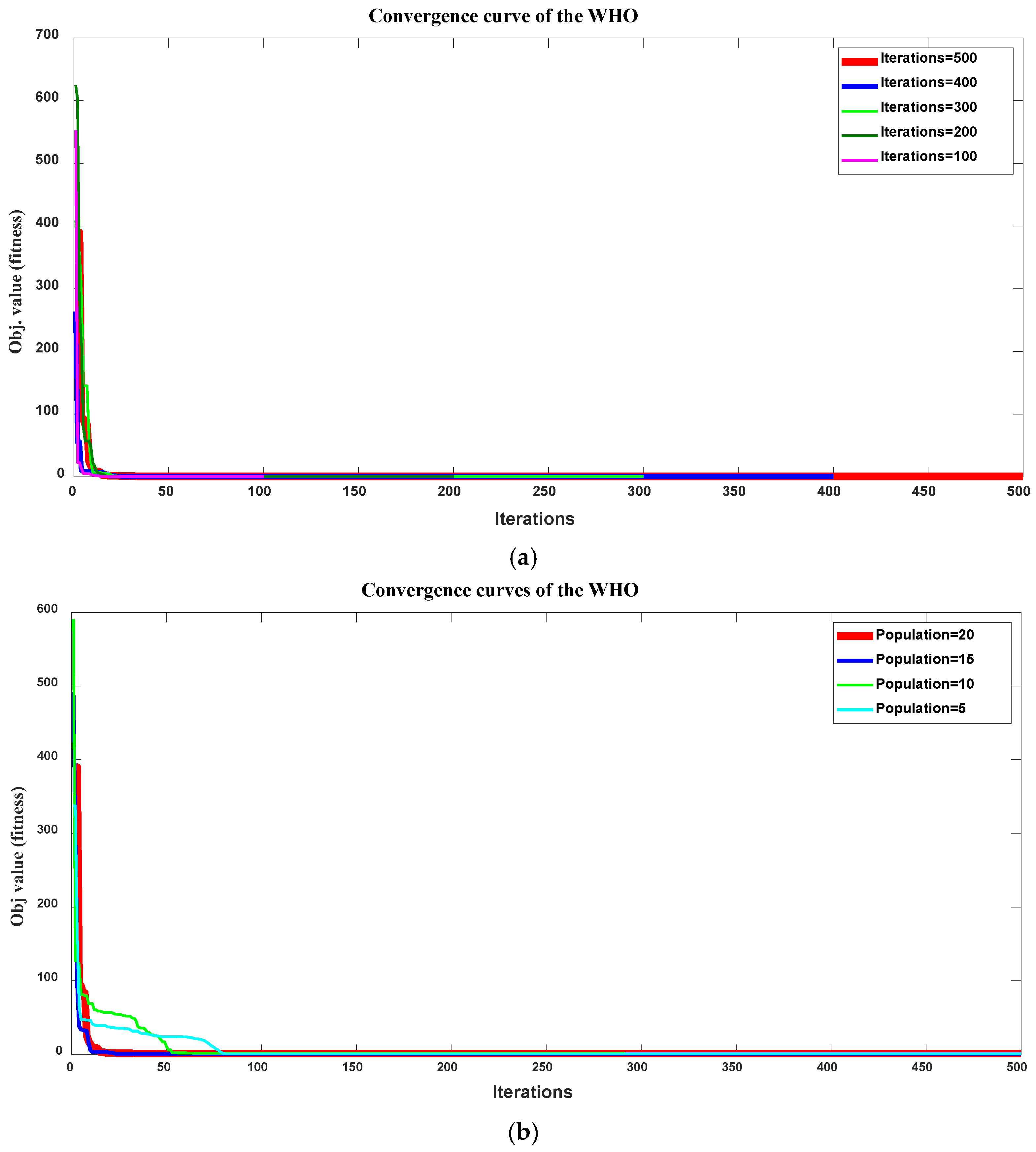


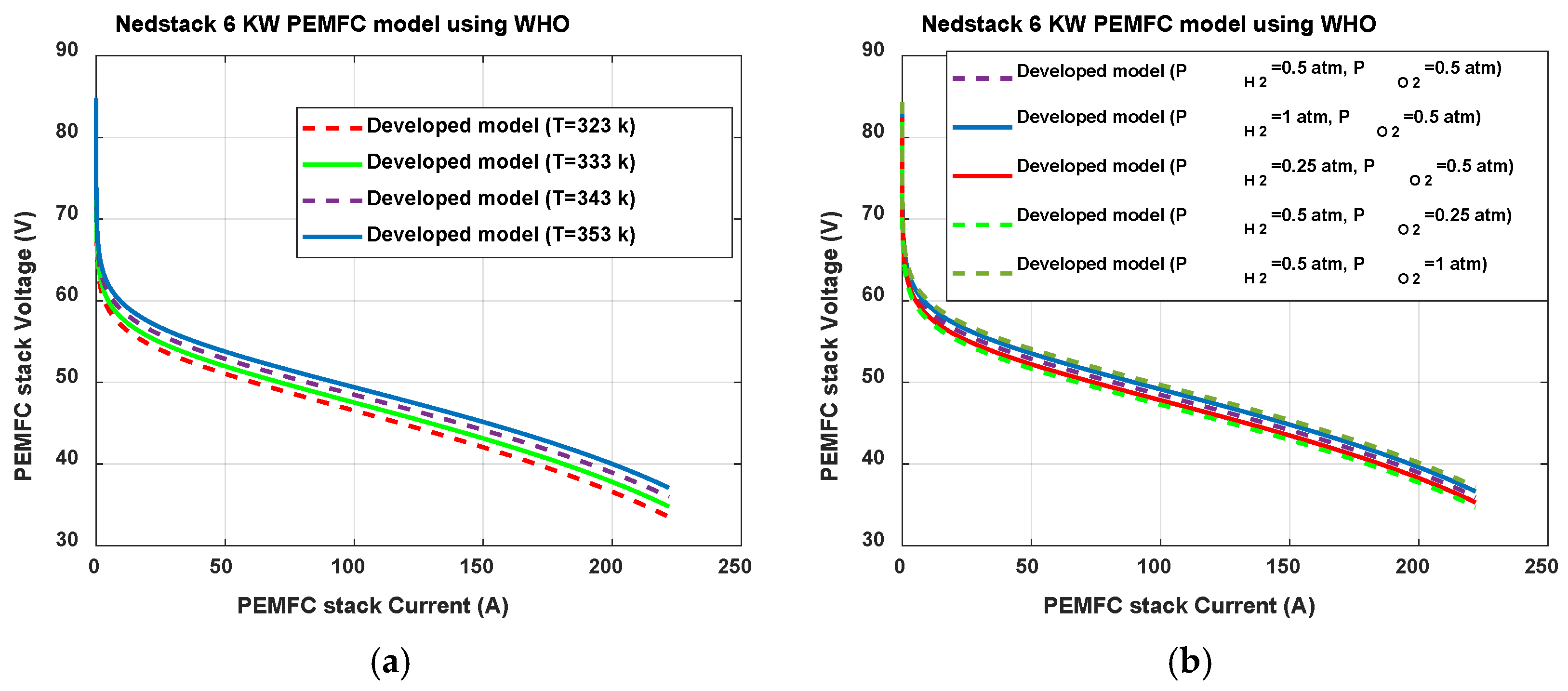
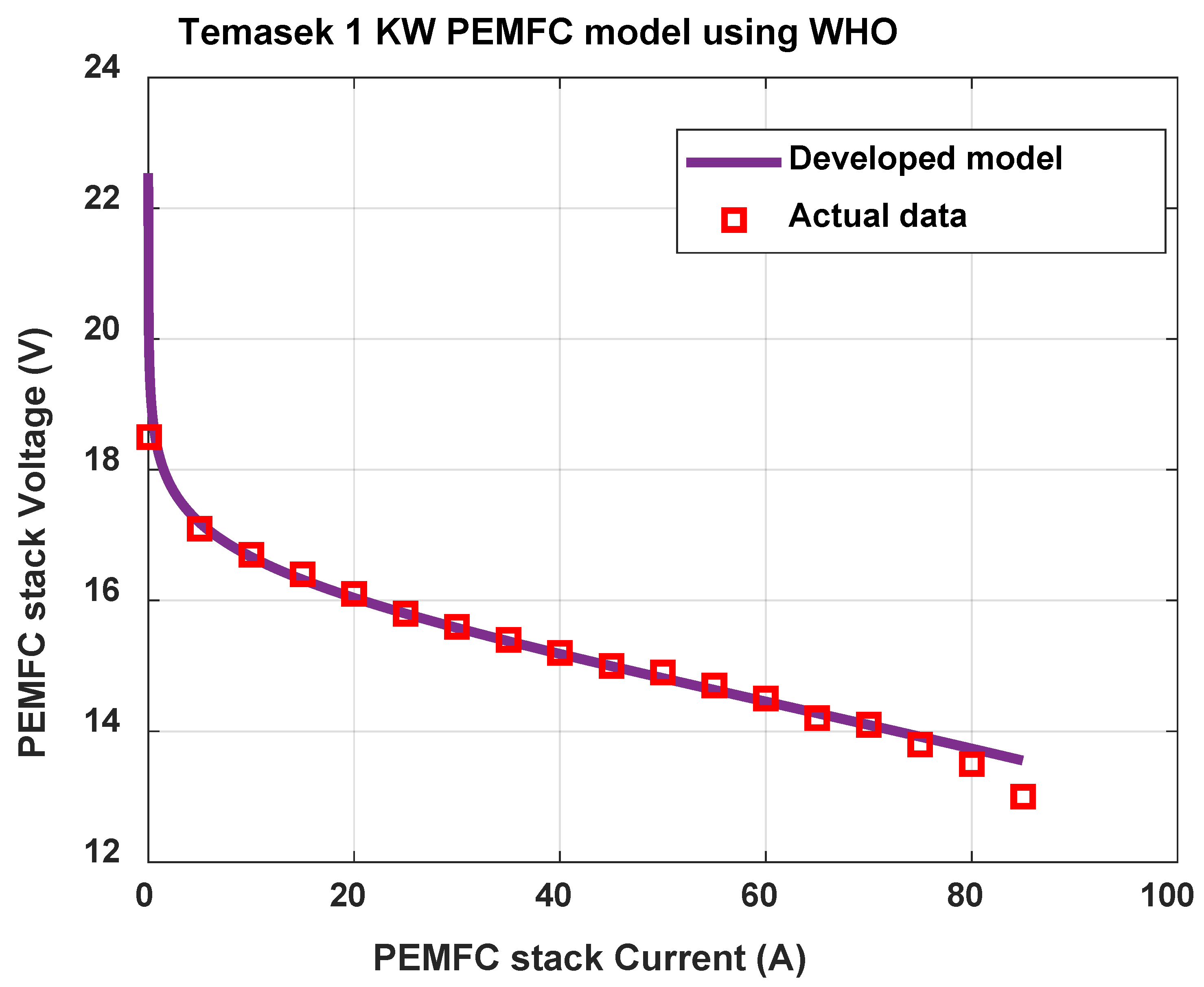


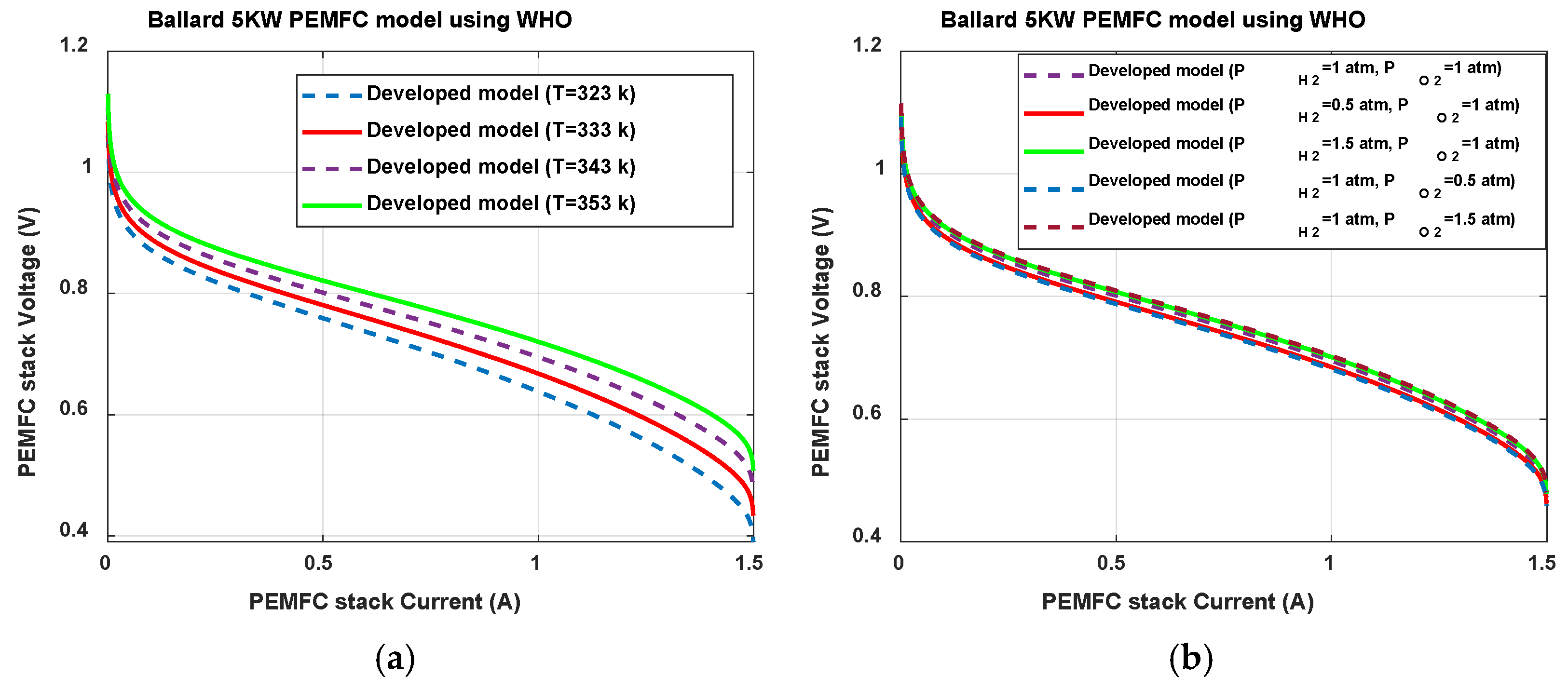
| Model Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Lower boundary | −1.1997 | 0.001 | 3.6 × 10−5 | −2.6 × 10−4 | 10 | 0.0001 | 0.0136 |
| Upper boundary | −0.8532 | 0.005 | 9.8 × 10−5 | −9.54 × 10−5 | 24 | 0.0008 | 0.5 |
| Stack Parameters | Operation Ranges | ||
|---|---|---|---|
| Number of cells in series | 24 | 100–300 kPa (1–3 bar) | |
| Cell’s active area A | ) | 100–500 kPa (1–5 bar) | |
| Nafion 115:5 mil l | 127 × 10−6 m (127 μm) | Stack temperature T | 353.15–343.15 K |
(860 ) | 1 | ||
| Rated power | 1 | ||
| PEMFC Type | Nedstack-PS6 6 kW [15,33] | Temasek 1 kW [19,36] | Ballard-Mark-V 5 kW [19,36] |
|---|---|---|---|
| 65 | 20 | 35 | |
| Cell’s active area ) | 240 × 10−4 ) | 150 × 10−4 ) | 232 × 10−4 m2 () |
| Nafion 115:5 mil l (m) | 178 × 10−6 178 μm | 51 × 10−6 51 μm | 178 × 10−6 178 μm |
| Max current density () | 120 | 150 | 150 |
| Stack temperature T (K) | 343 | 323 | 343 |
| (kPa) | 49.03325–490.3325 | 49.03325 | 98.0665 |
| Oxygen pressure (kPa) | 49.03325–490.3325 | 49.03325 | 98.0665 |
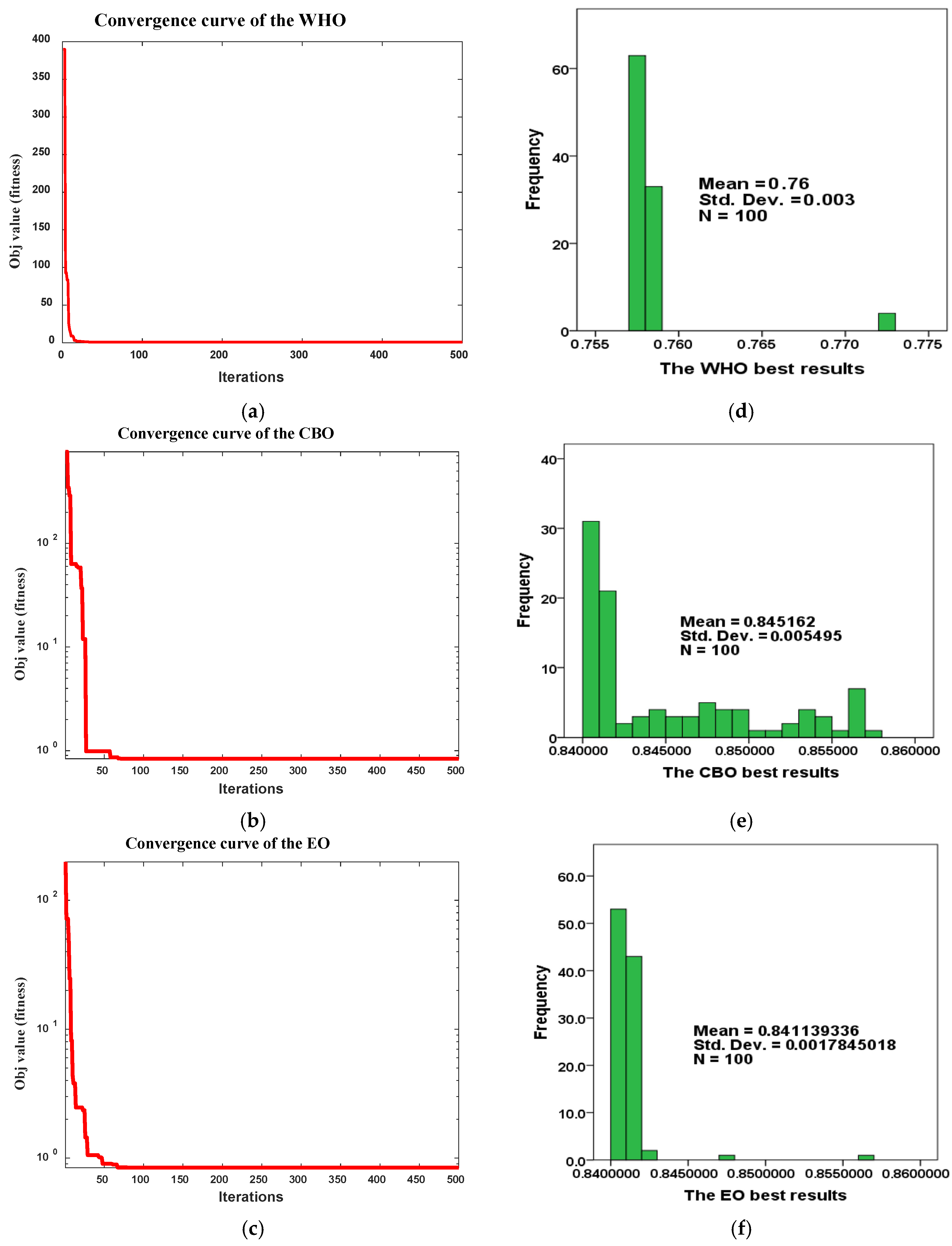
| Method | Fitness (SSE) | Elapsed Time * | |||||||
|---|---|---|---|---|---|---|---|---|---|
| WHO | 0.7579489 | 0.3759676 | −0.9508 | 0.003543705 | 9.80 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| CBO | 0.84042 | 0.38703 | −0.8593 | 0.0032844 | 9.80 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| EO | 0.840419 | 0.42235 | −0.8532 | 0.003267329 | 9.80 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| GOA | 1.0897 | 5.323141 | −1.14622 | 0.00379843 | 8.06 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| MTDE | 1.1531 | 3.804542 | −1.061 | 0.0038525 | 9.80 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| DA | 1.1655 | 33.249382 | −0.8532 | 0.00326576 | 9.80 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| ALO | 1.1659 | 2.75704 | −0.87109 | 0.00303416 | 8.16 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| ASO | 1.3483 | 0.727816 | −1.00738 | 0.00318212 | 6.75 × 10−5 | −9.54 × 10−5 | 23.72 | 0.0005574 | 0.014613 |
| PSO | 1.7193 | 8.954077 | −1.1997 | 0.0042618 | 9.80 × 10−5 | −9.54 × 10−5 | 24 | 0.0001 | 0.0136 |
| VSDE [27] | 1.0526 | Not reported | −1.1921 | 3.199 × 10−3 | 3.79 × 10−5 | 1.870 × 10−4 | 22.81 | 1.202 × 10−4 | 0.02903 |
| TLBO-DE [16] | 7.2776 | Not reported | −0.8532 | 2.6505 × 10−3 | 8.0016 × 10−5 | −1.360 × 10−4 | 15.65 | 1.0000 × 10−4 | 0.0364 |
| QPSO [19] | 7.2776 | Not reported | −0.8569 | 2.5665 × 10−3 | 7.2708 × 10−5 | −1.303 × 10−4 | 13.54 | 3.9173 × 10−4 | 0.0299 |
| ITHS [31] | 7.5798 | Not reported | −0.9228 | 2.7348 × 10−3 | 7.0967 × 10−5 | −1.426 × 10−4 | 16.52 | 1.0091 × 10−4 | 0.0362 |
| Sa-DE [31] | 7.6276 | Not reported | −0.8534 | 2.5846 × 10−3 | 7.5880 × 10−5 | −1.154 × 10−4 | 12.6 | 1.0000 × 10−4 | 0.0329 |
| STLBO [31] | 7.6426 | Not reported | −0.8532 | 2.5843 | 7.6892 × 10−5 | −1.154 × 10−4 | 12.6 | 1.0000 × 10−4 | 0.0329 |
| BIPOA [29] | 7.9416 | Not reported | −0.8016 | 2.6673 × 10−3 | 8.1288 × 10−5 | −1.271 × 10−4 | 13.51 | 0.80 | 0.0324 |
| ARNA-GA [23] | 8.1039 | Not reported | −0.8806 | 2.9450 × 10−3 | 8.4438 × 10−5 | −1.288 × 10−4 | 13.48 | 1.0068 × 10−4 | 0.0316 |
| RGA [21] | 8.4854 | Not reported | −1.1568 | 3.4243 × 10−3 | 6.4161 × 10−5 | −1.154 × 10−4 | 12.89 | 1.4504 × 10−4 | 0.0343 |
| MPSO [19] | 9.7539 | Not reported | −0.9479 | 3.0835 × 10−3 | 7.7990 × 10−5 | −1.880 × 10−4 | 20.76 | 2.8666 × 10−4 | 0.0296 |
| Algorithm | PSO | MTDE | ALO | DA | ASO | GOA | EO | CBO | WHO |
|---|---|---|---|---|---|---|---|---|---|
| Best fitness (min. Obj) | 1.7193 | 1.1531 | 1.1659 | 1.1655 | 1.3483 | 1.0897 | 0.8404196 | 0.84042 | 0.7579489 |
| Stand. Deviation | 0.00509 | 1.99 × 10−15 | 0.008722 | 1.206342 | 2.9229 | 133.37 | 0.0017755 | 0.005467 | 0.002747 |
| Average | 1.72133 | 1.1531 | 1.176198 | 1.390042 | 4.8585 | 87.573 | 0.8411393 | 0.845162 | 0.758657 |
| Median | 1.7199 | 1.1531 | 1.17455 | 1.1773 | 4.1624 | 33.951 | 0.8409335 | 0.841525 | 0.757951 |
| Worst fitness (max. Obj) | 1.7391 | 1.1531 | 1.1937 | 11.7925 | 18.323 | 871.03 | 0.8569407 | 0.85763 | 0.772081 |
| Variance | 2.6 × 10−5 | 4.03 × 10−30 | 7.684 × 10−5 | 2.253582 | 8.6297 | 17,968.8 | 3.184 × 10−5 | 3.019 × 10−5 | 7.62356 × 10−6 |
| Av_time | 8.9540 | 4.14063 | 2.75704 | 33.24938 | 0.7278 | 5.3231 | 0.42235 | 0.387034 | 0.3759676 |
| Comparison | WHO-CBO | WHO-EO | CBO-EO |
|---|---|---|---|
| p-value | 0 | 0 | 0 |
| Positive rank | 0 | 0 | 27 |
| Negative rank | 100 | 100 | 73 |
| Decision | Reject null hypotheses | Reject null hypotheses | Reject null hypotheses |
| Method | Fitness (SSE) | Elapsed Time | |||||||
|---|---|---|---|---|---|---|---|---|---|
| WHO | 1.4957 | 0.3321 | −0.9348 | 2.187 × 10−3 | 4.07 × 10−5 | −1.145 × 10−4 | 10.000 | 1.0 × 10−4 | 0.0727 |
| CBO [37] | 1.5734 | 0.35938 | −1.0945 | 2.881 × 10−3 | 5.66 × 10−5 | −1.162 × 10−4 | 16.287 | 1.01 × 10−4 | 0.1148 |
| VSDE [27] | 2.08849 | Not reported | 1.1212 | 3.348 × 10−3 | 4.67 × 10−5 | 9.54 × 10−5 | 13.000 | 1 × 10−4 | 0.0494 |
| SSO [33] | 2.18067 | Not reported | 0.9719 | 3.348 × 10−3 | 7.91 × 10−5 | 9.543 × 10−5 | 13.000 | 1 × 10−4 | 0.0534 |
| GHO [27] | 2.18586 | Not reported | 1.1997 | 3.55 × 10−3 | 4.61 × 10−5 | 9.54 × 10−5 | 13.009 | 1.01 × 10−4 | 0.0579 |
| VSA [27] | 2.34260 | Not reported | 0.8946 | 3.348 × 10−3 | 9.75 × 10−5 | 9.54 × 10−5 | 13.000 | 1.03 × 10−4 | 0.0429 |
| Approach | Fitness | Elapsed Time | |||||||
|---|---|---|---|---|---|---|---|---|---|
| WHO | 0.1441 | 0.28925 | −1.1603 | 3.13 × 10−3 | 6.03 × 10−5 | −9.54 × 10−5 | 24 | 1 × 10−4 | 0.1821 |
| CBO [37] | 0.15204 | 0.29688 | −0.94212 | 2.842 × 10−3 | 8.70 × 10−5 | −9.54 × 10−5 | 10 | 0.00059487 | 0.1319 |
| FPO [27] | 0.1881 | Not reported | −0.4838 | 1.0 × 10−3 | 2.77 × 10−5 | −7.578 × 10−5 | 11.322 | 1.109 × 10−4 | 0.1287 |
| GWO [19] | 1.6481 | Not reported | −1.0299 | 2.410 × 10−3 | 4.00 × 10−5 | −9.54 × 10−5 | 10.000 | 1.087 × 10−4 | 0.1274 |
| Approach | Fitness | Elapsed Time | |||||||
|---|---|---|---|---|---|---|---|---|---|
| WHO | 0.0006098 | 0.24 | −0.93996 | 3.022 × 10−3 | 9.67 × 10−5 | −1.195 × 10−4 | 12.085 | 0.0008 | 0.0136 |
| CBO [37] | 0.0006159 | 0.25 | −1.1788 | 0.0028743 | 3.64 × 10−5 | −1.195 × 10−4 | 12.08 | 0.0008 | 0.0136 |
| FPO [14] | 0.0006204 | Not reported | −1.0257 | 3.4 × 10−3 | 6.79 × 10−5 | −1.285 × 10−4 | 15.644 | 5.29 × 10−4 | 0.0614 |
| GWO [19] | 0.002067 | Not reported | −1.1827 | 3.708 × 10−3 | 9.36 × 10−5 | −1.192 × 10−4 | 11.76 | 7.87 × 10−4 | 0.0136 |
| IFSO [35] | 0.784 | 3.80 | −1.12 | 3.57 × 10−3 | 8.01 × 10−5 | −1.59 × 10−4 | 22.00 | 1.00 × 10−4 | 0.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.A.; Mandour, M.E.; Lotfy, M.E. Optimal Adaptive Modeling of Hydrogen Polymer Electrolyte Membrane Fuel Cells Based on Meta-Heuristic Algorithms Considering the Membrane Aging Factor. Fuels 2025, 6, 30. https://doi.org/10.3390/fuels6020030
Ali MA, Mandour ME, Lotfy ME. Optimal Adaptive Modeling of Hydrogen Polymer Electrolyte Membrane Fuel Cells Based on Meta-Heuristic Algorithms Considering the Membrane Aging Factor. Fuels. 2025; 6(2):30. https://doi.org/10.3390/fuels6020030
Chicago/Turabian StyleAli, Mohamed Ahmed, Mohey Eldin Mandour, and Mohammed Elsayed Lotfy. 2025. "Optimal Adaptive Modeling of Hydrogen Polymer Electrolyte Membrane Fuel Cells Based on Meta-Heuristic Algorithms Considering the Membrane Aging Factor" Fuels 6, no. 2: 30. https://doi.org/10.3390/fuels6020030
APA StyleAli, M. A., Mandour, M. E., & Lotfy, M. E. (2025). Optimal Adaptive Modeling of Hydrogen Polymer Electrolyte Membrane Fuel Cells Based on Meta-Heuristic Algorithms Considering the Membrane Aging Factor. Fuels, 6(2), 30. https://doi.org/10.3390/fuels6020030







