Abstract
This work provides an extended description of the tools developed in the Wolfram Mathematica environment to characterize proton exchange membrane (PEM) fuel cells. These tools, with their user-friendly interface, facilitate the calculation of the main parameters required to obtain the PEM fuel cell polarization curve, offering a seamless and intuitive experience. Various mathematical models and algorithms are coded to accurately calculate the parameters needed for the polarization curve analysis. This study presents the development and validation of a computational tool designed to simulate the performance of proton exchange membrane (PEM) fuel cells. The tool integrates thermodynamic and electrochemical equations to predict key operational parameters, and was validated using experimental data from a commercial Ballard® PEM fuel cell to ensure its accuracy. The validation process involved comparing the numerical predictions with empirical measurements under various operating conditions. The results demonstrate that the computational tool accurately replicates the performance characteristics observed in the experimental data, confirming its reliability and instilling confidence in its use for simulating PEM fuel cell behavior. This tool offers a valuable resource for optimizing fuel cell design and operation, providing insights into the efficiency, output, and potential areas for improvement. Future work will expand the tool’s capabilities to include degradation mechanisms and long-term performance predictions. This advancement underscores the tool’s potential as a comprehensive solution for academic research and industrial applications in fuel cell technology.
1. Introduction
In this section, the crucial role of accurate and efficient models in the formulation and numerical implementation of proton exchange membrane (PEM) fuel cell models is underscored. PEM fuel cells are a promising, clean, and efficient energy generation technology that find significant application in the aerospace industry. The development of these models is not just important but essential for understanding the behavior of PEM fuel cells and optimizing their design and operation in this specific context.
The numerical implementation of PEM fuel cell models necessitates the development of sophisticated software tools. These advanced tools, with their high computational power and versatility, are capable of simulating fuel cell performance under a wide range of operating conditions and design parameters. They provide comprehensive information on species concentration distribution, current density, and losses throughout the cell, thereby enabling a detailed and comprehensive analysis of the fuel cell’s performance.
The steady-state operation of the PEM fuel cell can be predicted by estimating the voltage of the individual cell, which depends on various operating conditions such as gas concentration, pressures, operating temperatures, and current consumption.
A suite of tools has been developed in the Wolfram Mathematica environment to characterize PEM-FC under different power classes and operating conditions. Wolfram Mathematica was chosen because it offers an integrated platform for symbolic computation within a unified work environment, allowing for the intuitive manipulation of symbols, formulas, and functions. A combination of empirical and experimental loss models provides a good estimate of performance in a short time. Estimating the power output from the fuel cell depends on the cell voltage, which is a function of various parameters such as the partial pressures of oxygen and hydrogen, stack temperature, flow rate, and current output. In the implemented models, another important parameter influencing the assessment of the available power of fuel cells at various pressures and temperatures is the stack voltage, which is a function of activation, ohmic, and concentration losses.
In particular, the suite of tools estimates the major voltage losses through mathematical models of the anode, cathode, and membrane to determine the stack voltage, power, and the required mass flow rate of fuel. Finally, the suite of tools defines the polarization curve (V, I) as a function of current.
In conclusion, the formulation and numerical implementation of PEM fuel cell models are essential and enable simulations, sensitivity analyses, and optimization studies to improve the performance of PEM fuel cells in various applications. The models have been validated through numerous test cases on various types of PEM cells for aerospace applications, such as [1,2].
Several computational models have been developed to simulate PEM fuel cell performance, providing insights into optimization and design improvements.
In this study, the development and validation are presented of a new computational tool using Wolfram Mathematica to simulate the performance of PEM fuel cells. The tool integrates fundamental thermodynamic and electrochemical equations, providing detailed predictions of operational parameters. To ensure accuracy, the tool was validated with experimental data from a 19 kW commercial Ballard® PEM fuel cell (Ballard Power systems Inc., 9000 Glenlyon Parkway Burnaby, BC V5J5J8 Canada). The validation demonstrated a high correlation between the numerical predictions and the manufacturer’s catalogue data, strengthening the reliability and repeatability of the tools.
A key feature of this work is the detailed graphical representation of ohmic losses, concentration, and activation losses in a real-world scenario. This allows for a comprehensive analysis of the factors affecting cell performance. Additionally, this study compares semi-empirical equations from the literature used to estimate these losses, critically evaluating their applicability and accuracy.
The current state of the art in PEM fuel cell modelling involves various approaches, including detailed mechanistic and simplified empirical or semi-empirical models. Bernardi et al. [3] were the first to develop a one-dimensional mechanistic model of PEMFC. Pukrushpan et al. [4] offered detailed insights but these can be computationally intensive. A recent work is that of Wang et al. 2024 [5], which delved into mechanistic models. In contrast, semi-empirical models, like those by Springer et al. [6], Amphlett et al. [7], Kim et al. [8], and Wang et al. 2003 [9], provide a balance between accuracy and computational efficiency, making them suitable for practical applications and real-time simulations.
More recent works concern the applications of PEM fuel cells for automotive use [10,11,12,13], which address the estimation of the minimum consumption and operating cycles of the propulsion system in which the fuel cell is coupled with lithium-ion batteries.
Another line of research concerns applications in the propulsion aeronautical field [14], in which the semi-empirical models for calculating the performance of PEM fuel cells are reviewed with a view to aviation applications. Meanwhile, [15] delved into dynamic characterization models for marine propulsion applications. The authors of [16] addressed the fluid dynamic effects on the performance of fuel cells by carrying out CFD simulations and comparing such data with those of engineering models, while others, such as [17], addressed in detail the problems relating to the management of the supply air.
This study contributes to the state of the art by offering a validated computational tool that provides accurate simulations and facilitates the comparison of different loss estimation methods. This tool is poised to be a valuable resource for researchers aiming to optimize PEM fuel cell design and operation.
2. Software Implementation
The suite of tools was implemented in the Wolfram Mathematica 12.3 environment. Wolfram Mathematica comprises two primary components: the front end and the kernel. The front end manages input, output, and text formatting, while the kernel, operating as a separate application, handles calculations. Initially, a slight delay might be observed due to the kernel activation, but subsequent response times are contingent upon the complexity of calculations processed by the kernel.
Typically, the instructions to be executed are included in a file called Notebook, which can be opened in the front end; the execution of Notebook occurs by using the evaluate menu, which is connected to the kernel.
It consists of three independent codes launched in the same work area. In fact, to run a test case on a fuel cell, the suite’s tools must be uploaded and executed in the following order: first, the tool for assigning input variables, and second, the tool called “Gibbs Standard Nernst Potential Conditions” for computing the Gibbs free energy to determine the standard Nernst potential conditions.
The third tool, called the “Characterization PEM Model”, estimates primary voltage losses, determining stack voltage, power, and the required mass flow rate. The suite plots both the polarization curve and the power curve as a function of the stack current; furthermore, the mass flow rates of hydrogen, oxygen, and produced water are also determined. Finally, the “Characterization PEM Model” generates an output file in txt format, in which all the results are reported. In summary, Figure 1 shows a block diagram and the tool’s operation.

Figure 1.
Schematic block diagram tool.
2.1. Input Data
Before starting the simulation, Table 1 shows the initial variables to be assigned to the tool as input.

Table 1.
Input data tool.
2.2. Gibbs Free Energy
In this section, the second tool is described, which calculates the Gibbs free energy for liquid water, which is necessary to determine the Nernst standard potential conditions.
The Faraday constant and the perfect gas constant are defined in detail. Furthermore, the experimental constants necessary for calculating the enthalpy and entropy variation are defined in [5] and reported in Table 2.

Table 2.
Experimental constants.
The enthalpy variation [18] is as follows:
where T represents the fuel cell temperature.
The entropy variation is as follows:
The quantities ΔH0 and ΔS0 [18] represent the enthalpy and entropy under standard conditions:
where the quantities Δa, Δb, and Δc [18] represent the difference between the values of the products and the reactants, calculated as follows:
The next step is to calculate the Gibbs free energy [18]:
The Nernst standard potential condition E0 is as follows:
where n = 2 is the number of transferred electrons in the electrochemical reaction and F is the Faraday constant.
The Gibbs free energy calculated by the tool at a temperature of 333.15 K is equal to 227.114 kJ/mol.
2.3. Reversible and Irreversible Potential Estimation
In this section, the analytical models implemented in the third code of the suite are presented.
2.3.1. Nerst Equation
The first step consists of calculating the open circuit voltage [19].
The reversible cell voltage refers to the highest voltage achievable by a cell without any overpotentials or irreversibility and the Nernst equation determines it as follows:
The temperature is expressed in Kelvin, and the partial pressures are expressed in atm.
The reactant hydrogen and oxygen partial pressures [20] are obtained as follows:
where pa and pc represent the anode and cathode pressure; ist is the stack current; Am is the membrane area; and is the saturation pressure of water.
The saturation pressure of water is as follows:
where Tc = T − 273.15 [K].
2.3.2. Activation Losses
Activation loss in a proton exchange membrane fuel cell (PEM) refers to the decrease in efficiency in the electro-oxidation of fuel at the anode or the electro-reduction of oxygen at the cathode. This loss is caused by the need to overcome an energy barrier to initiate the electrochemical reactions.
PEM activation loss depends on various factors, including operating temperature, partial pressure of reactants, fuel composition, and the presence of contaminants. To reduce activation loss, efficient catalysts, high-conductivity membrane materials, and cell operating conditions can be optimized.
Two different activation models were implemented by applying the Amphlett and Mann equation [20] and the Tafel equation, respectively. It was considered simpler to generate two versions of the third code of the suite, each characterized by one of the two models.
2.3.3. Amphlett and Mann Equation
If the power value is less than 20 kW, then the Amphlett et al. and Mann et al. [20] equations are used to calculate the activation loss, as follows:
where T is the stack temperature in Kelvin (K), which is nearly equal to cell temperature; i is the drawn current in ampere (A); ) is the concentration of oxygen at the catalyst interface (mol/cm3); and ζn represents the empirical parametric coefficients based on the experimental data, which may vary from one stack to another, or one cell to another, depending on the geometrical design and the materials used in the construction of a PEM fuel cell.
The value of the concentration of oxygen at the catalyst interface ( can be determined based on Henry’s Law:
The values of ζn are determined from the experimental data table developed by Amphlett et al. and Mann [20]:
The cathode hydrogen concentration is equal to:
where R is the ideal gas constant.
2.3.4. Tafel’s Equation
In the case of power up to 40 kW, Tafel’s [6] equation has been implemented to calculate the activation loss:
where the charge transfer coefficient α is set equal to 0.5; the internal current density in = 3 [mA/cm2]; and the exchange current density i0 = 0.1 [mA/cm2]. The quantity i represents the current density:
where ist is the stack current and Am is the membrane active area.
2.3.5. Ohmic Loss
Ohmic losses in a proton exchange membrane (PEM) cell refer to the voltage drop that occurs when an electric current flows through the materials that make up the PEM cell, such as the conductors and the membrane. Ohmic losses are due to the material’s resistance, which increases with the increase in electric current. In PEM, ohmic losses can significantly affect the total cell voltage drop and overall cell efficiency. Ohmic losses can be reduced using low-resistance materials and optimizing the PEM cell geometry.
The ohmic loss [21] is a function of membrane proton conductivity defined as:
The value of the number of water molecules in the structure of the membrane λ is influenced by the membrane fabrication processes, operation time (i.e., time in service), cell relative humidity, and the stoichiometric ratio of the supplied gases. Values of λ are equal to zero for a dry membrane, 14 for a saturated membrane, and 23 for a supersaturated membrane.
The membrane ohmic resistance can be expressed:
where tm is the membrane thickness. Finally, the ohmic loss is as follows:
2.3.6. Concentration Loss
The next step of the tool concerns the calculation of the concentration loss.
PEM concentration loss refers to the situation where protons, instead of crossing the PEM membrane, can diffuse through alternative pathways or be lost due to phenomena such as recombination with electrons or proton loss from the electrolyte. This leads to a decrease in proton concentration in the anodic region, reducing the efficiency of the fuel cell and decreasing energy production.
Various factors, including membrane porosity or wear, defects or structural damage, electrolyte contamination, or inadequate fuel cell humidification, can cause PEM concentration loss.
In this case, the expression used for the concentration loss calculation [22] is as follows:
The value of n is about 8 × 10−3 [cm2/mA].
The diffusion overpotential is directly influenced by the decrease in the concentration of reactant gases and, therefore, is inversely related to the growth rate (n) of by-products generated during the electrochemical reaction in the catalyst layers, flow fields, and across the electrode. Although the specific physical interpretation of the parameters m and n was not provided, Berning et al. [22] discovered in their study that m correlates with electrolyte conductivity, while n relates to the porosity of the gas diffusion layer. Both m and n are associated with water management challenges. When the electrolyte membrane becomes partially dehydrated, its conductivity decreases, which can be represented by the parameter m. Conversely, an excess of liquid water reduces the porosity of the gas diffusion layer, leading to an early onset of mass transport limitations, which can be captured by the parameter n.
The mass transfer coefficient m decreases linearly with cell temperature but it has two dramatically different slopes, as shown by the following expressions:
2.4. Polarization Curve
After calculating the open circuit voltage and the activation, ohmic and concentration losses, the tool determines the effective stack voltage [10], as follows:
where nFC represents the number of cells.
The tool plots the polarization curve as a stack current function, as shown in Figure 2.
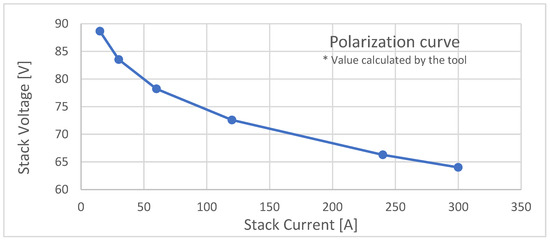
Figure 2.
Polarization curve.
Finally, the tool estimates the power as a function of stack current and stack voltage, as follows:
Similarly to the polarization curve, the tool plots the power curve as a function of stack current, Figure 3.

Figure 3.
Power curve obtained from the tool.
2.5. Mass Flow Rate
The tool for estimating the mass flow rates of hydrogen, oxygen, and water transport in a proton exchange membrane (PEM) fuel cell considers several factors such as molecular weight, number of cells, and stack current.
The expressions of the flow rates expressed in kilograms are the following:
The value for molecular weights is reported in Table 3.

Table 3.
Molecular weight.
2.6. Output Data
The third code of the suite generates a text file with the following outputs, as shown in Table 4:

Table 4.
Output data.
3. Validation and Results
In this section, the test cases to validate the suite of tools for characterizing PEM cells will be reported.
3.1. Ballard 19 kW Validation
Ballard [1] is a renowned global provider of clean energy fuel cell solutions that excel in performance while offering reduced operating costs. They specialize in delivering reliable and cost-effective fuel cell power products, which include motive modules, fuel cell stacks, and backup power systems.
The datasheet fuel cell Ballard 19.4 kW [23] is shown in Table 5.

Table 5.
Ballard 19 kW datasheet.
3.1.1. Losses
This section presents curves representing different types of losses. These include activation, ohmic, and concentration losses, all of which are calculated for the entire stack. Activation losses are calculated using the Amphlett and Mann equation and are represented in Figure 4.
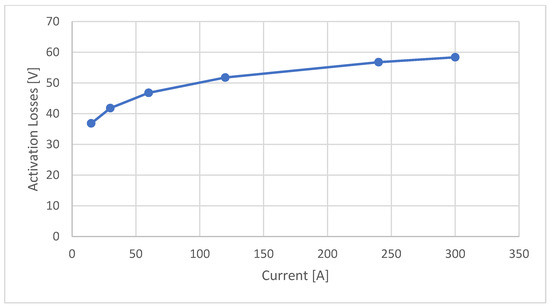
Figure 4.
Ballard 19 kW—activation stack losses diagram.
The activation curve diagram shows that the largest voltage drop, which is 36.84 V, occurs at a current of 15 A. However, for higher current values, the voltage drop continues to increase progressively. For example, at a current of 30 A, the voltage drops amounts to 41.82 V; at 60 A, it reaches 46.79 V; at 120 A, it rises to 51.78 V; at 240 A, it goes up to 56.76 V; and finally, at a current of 300 A, the voltage drop is 58.37 V, as reported in Table 6.

Table 6.
Ballard 19 kW—power and stack voltage percentage error.
Table 6 shows the power and stack errors obtained to vary the stack current.
The results are summarized in Table 7.

Table 7.
Results from the suite of tools on the Ballard 19 kW.
In Figure 5, it can be seen that the ohmic losses increase linearly with the increase in the supplied current stack. The values are reported in Table 6.

Figure 5.
Ballard 19 kW—ohmic stack losses diagram.
Therefore, the concentration losses in Figure 6, having less than a 1% influence, are negligible. The values are shown in Table 6.
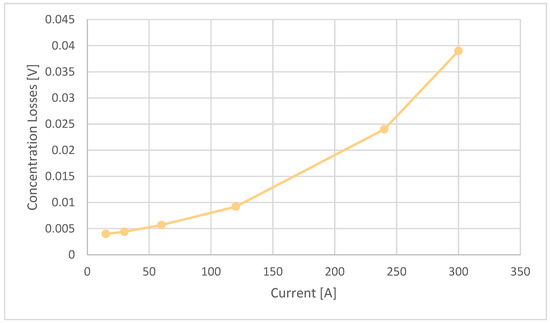
Figure 6.
Ballard 19 kW—concentration stack losses diagram.
In a proton exchange membrane (PEM) fuel cell, the open circuit voltage (OCV) represents the theoretical maximum potential that the cell can provide when no load is applied, meaning when it is not delivering any current. However, in practice, the actual measured voltage is always lower than the ideal theoretical voltage due to various internal losses within the cell, known as activation losses, ohmic losses, and concentration losses.
Figure 7 illustrates the calculated values of individual losses using the PEM tool. By comparing these values, it becomes apparent how each of these losses affects the open circuit voltage, as illustrated in the same graph.
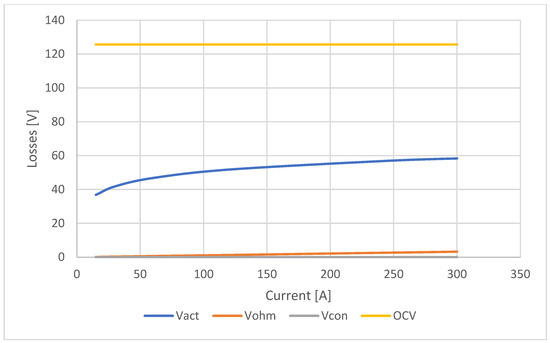
Figure 7.
Ballard 19.4kW—stack losses and open circuit voltage diagram.
The tool calculated the open circuit voltage and the activation, ohmic, and concentration losses for six different current values. As shown in the figure, the open circuit voltage remains constant with varying currents, with a calculated value of approximately 125.67 V. The largest contribution in terms of losses is from the activation loss, which has a minimum value of 36.84 V at a current of 15 A and steadily increases by about 5 V as the current increases, reaching 56.76 V at 240 A. At the maximum current of 300 A, the increase in activation loss is halved, with a value of 58.37 V. The contribution of ohmic loss compared to activation loss is almost negligible; at 15 A, it has a value of 0.16 V and a maximum value of 3.23 V at 300 A. Finally, the concentration loss, as shown in Figure 6, is overlaid on the x-axis and has very small values as the current varies; therefore, its influence on the OCV is negligible.
3.1.2. Polarization Curve and Power Comparison
In the diagram below, Figure 8, the polarization curves are shown as a comparison.
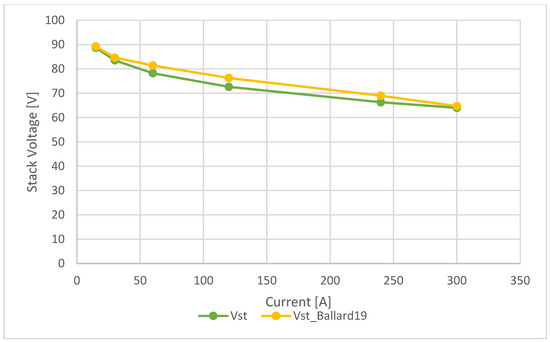
Figure 8.
Ballard 19 kW—polarization curve comparison.
The polarization curve obtained with the tool, indicated in green, has a trend similar to the yellow curve, which indicates the reference values of Ballard 19.4 kW fuel cell. In this case, there are no significant differences. The maximum percentage error of the stack voltage occurs at a stack current of 120 A. Beyond this point, the percentage error decreases as the current increases. The detailed values are shown in Table 6.
The last diagram in Figure 9 shows the comparison between the obtained power, indicated in green, and the declared power, indicated in yellow, for increasing current values. In this case, the obtained curve converges with the datasheet values. A similar behavior described for the polarization curve occurs for the power curve. The maximum percentage error occurs at a current of 120 A. The detailed values are shown in Table 6.
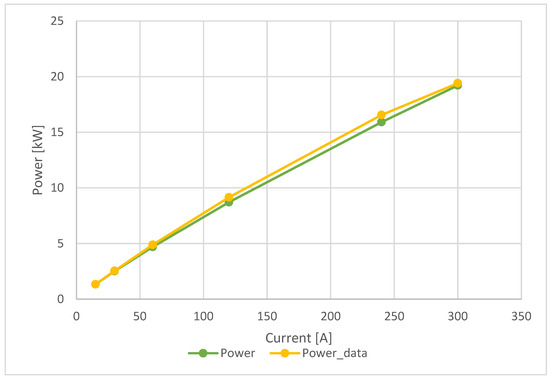
Figure 9.
Ballard 19 kW—power diagram comparison.
3.1.3. Mass Flow Rate
In this section, the calculated values are reported of the mass flow rates of hydrogen and oxygen, the water flow generated, and finally, the total flow that crosses the membrane for Ballard at 19.4 kW. In Figure 10, the mass flow rate trends through the various areas of interest of the fuel cell, which are highlighted with different colors.
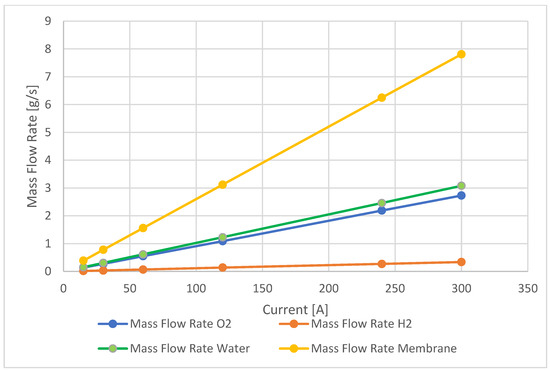
Figure 10.
Ballard 19 kW—mass flow rate diagram.
4. Discussion and Conclusions
In this study, a series of empirical models were meticulously implemented to effectively capture the distinctive behaviors of the 19.4 kW Ballard fuel cell and thoroughly understand its complex performance dynamics. A crucial aspect of this investigation involved estimating the Gibbs free energy by calculating the change in enthalpy and entropy, yielding a value of 227.114 kJ/mol from the tool, this value is also confirmed by the JANAF table [24]. This value is of fundamental importance for estimating the standard Nernst potential, as the standard value of 1.228 V reported in the literature was not applicable in the case examined. Specifically, the calculated value obtained was 1.177 V, which enabled the correct estimation of the open circuit voltage.
Additionally, activation, ohmic, and concentration losses were precisely evaluated as a function of current to construct the polarization curve, whose values are reported in Table 7. This curve was then compared with the one reported in the product’s technical datasheet. From Table 6, the percentage errors between the calculated stack voltage and the values reported in the datasheet, summarized in Table 5, can be deduced. It can be observed that the error is minimal at 15 A with a value of 0.61%, reaches a maximum at a current of 120 A with a value of 4.77%, and then decreases as the current increases, reaching a value of 1.03% at the maximum current of 300 A.
A rigorous comparison was also extended between the calculated power curve derived from the empirical models and the power curve predicted in the technical datasheet. In this case, the trend in percentage error is also similar to that of the stack voltage.
The stack efficiency was also estimated as the current varied, showing that the fuel cell performance is better for currents between 15 and 60 A, while the efficiency for these two values of the range is 70% and 62%, respectively, as reported in Table 7.
The investigation highlighted a limitation in acquiring flow rate data for the Ballard fuel cell, which prevented an in-depth analysis of this specific parameter. However, the final results of this study validated the reliability of the empirical models used, as they closely aligned with the data presented in the technical datasheets. This alignment provided compelling evidence of the models’ intrinsic ability to provide a solid approximation of fuel cell performance. Consequently, this study’s findings underscored the effectiveness of the developed models in accurately characterizing these high-power fuel cells and making comprehensive predictions about their complex behaviors at various current levels. These further insights could lead to improved fuel cell performance and efficiency, thus contributing to the advancement of sustainable energy technologies.
As regards the operating temperature range of the tool, we can say that it has been tested with different fuel cells starting from 1 kW up to 40 kW with a temperature range ranging from 300 K up to 370 K. We report only the test on the 19.4 kW Ballard for which we have more data available for comparison, and above all the data are free to access. In particular, as the temperature increases, the performance of the FC improves to the detriment of the humidification of the membrane and, therefore, the reliability of the system. As regards other data not explicitly defined in the manuscript, we summarize some highlights here. The type of catalyst used in the electrodes is platinum. Regarding the thickness of the gas diffusion layer, we know that increasing or decreasing this geometric parameter changes the distance travelled by the reagents to reach the active zone. One of the future developments on this tool, which we are currently working on, is the introduction of a gas-diffusion-layer model. The typical thickness values of the gas diffusion layer for this type of fuel cell are in the range of 150–300 μm. With these further developments, how this parameter influences the performance and, therefore, the polarization curve of the PEM FC will be highlighted.
Author Contributions
Conceptualization, A.L. and G.D.L.; Data curation, A.L.; formal analysis, A.L.; investigation, A.L.; methodology, A.L. and G.D.L.; project administration, A.L. and G.D.L.; software, A.L.; supervision, G.D.L.; validation, A.L. and G.D.L.; writing—original draft, G.D.L.; writing—review and editing, A.L. and G.D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CIRA in the framework of PRORA, the Italian Aerospace research programme for Greening Aviation studies.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ballard. Available online: https://www.ballard.com/ (accessed on 10 March 2024).
- Fuelcells. Available online: https://www.fuelcellenergy.com/ (accessed on 15 March 2024).
- Bernardi, D.M.; Verbrugge, M.W. Verbrugge, Mathematical model of a gas diffusion electrode bonded to a polymer electrolyte. AIChE J. 1991, 37, 1151–1163. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of Fuel Cell Power Systems, Principles, Modeling, Analysis and Feedback Design, 1st ed.; Springer: London, UK, 2004; 161p. [Google Scholar]
- Wang, T.; Yang, X.; Sun, Z.; Chen, Z. A systematic review of system modeling and control strategy of proton exchange mem-brane fuel cell. Energy Rev. 2024, 3, 100054. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymeric electrolyte fuel cell model. Electrochem. Soc. 1991, 138, 2334. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Rodrigues, A. A model predicting transient responses of proton ex-change membrane fuel cells. J. Power Sources 1996, 61, 183–188. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Srnivasan, S.; Chamberlin, C.E. Modeling of Proton Exchange Membrane Fuel Cell Performance with an Em-pirical Equation. J. Electrochem. Soc. 1995, 142, 2670–2674. [Google Scholar] [CrossRef]
- Wang, L.; Hesar, A.; Zhou, T.; Liu, H. A parametric study of PEM fuel cell performances. Int. J. Hydrogen Energy 2003, 28, 1263–1272. [Google Scholar] [CrossRef]
- Quan, R.; Guo, H.; Li, X.; Zhang, J.; Chang, Y. A real-time energy management strategy for fuel cell vehicle based on Pontryagin’s minimum principle. iScience 2024, 27, 109473. [Google Scholar] [CrossRef] [PubMed]
- Quan, R.; Li, Z.; Liu, P.; Li, Y.; Chang, Y.; Yan, H. Minimum hydrogen consumption-based energy management strategy for hybrid fuel cell unmanned aerial vehicles using direction prediction optimal foraging algorithm. Fuel Cells 2023, 23, 221. [Google Scholar] [CrossRef]
- Ramírez-Cruzado, A.; Ramírez-Peña, B.; Vélez-García, R.; Iranzo, A.; Guerra, J. Experimental Analysis of the Performance and Load Cycling of a Polymer Electrolyte Membrane Fuel Cell. Process 2020, 8, 608. [Google Scholar] [CrossRef]
- Andriyashin, S.N.; Shurov, N.I. Fuel cells as a future of automotive industry: A review of current developments. International Conference on Actual Issues of Mechanical Engineering (AIME 2021). J. Phys. Conf. Ser. 2021, 2061, 12002. [Google Scholar] [CrossRef]
- Donateo, T. Semi-Empirical Models for Stack and Balance of Plant in Closed-Cathode Fuel Cell Systems for Aviation. Energies 2023, 16, 7676. [Google Scholar] [CrossRef]
- Wang, J.; Teng, X.; Zhu, F.; Chen, T.; Chen, H.; Wang, Y. Modeling and simulation of dynamic characteristics of marine PEM fuel cells. J. Phys. Conf. Ser. 2023, 2655, 12010. [Google Scholar] [CrossRef]
- Pham, H.B.; Doan, T.C. Effects of Flow-Field Design on the Performance Characteristic of Proton Exchange Membrane Fuel Cells. Int. J. Sci. Res. Eng. Dev. 2019, 2, 127–130. [Google Scholar]
- Klütsch, J.; Pischinger, S. Systematic Design of Cathode Air Supply Systems for PEM Fuel Cells. Energies 2024, 17, 3534. [Google Scholar] [CrossRef]
- Pourrahmani, H.; Gay, M.; van Herle, J. Electric vehicle charging station using fuel cell technology: Two different scenarios and thermodynamics analysis. Energy Rep. 2021, 7, 6955–6972. [Google Scholar] [CrossRef]
- Ansari, S.; Khalid, M.; Kamal, K.; Ratlamwala, H.T.; Hussain, G.; Alkahtani, M. Modelling and simulation of a proton exchange membrane fuel cell alongside a waste heat recovery system based on the organic Rankine cycle in Matlab/Simulink environment. Sustainability 2021, 13, 1218. [Google Scholar] [CrossRef]
- Amphlett, J.C.; Baumert, R.M.; Mann, R.F.; Peppley, B.A.; Roberge, P.R. Performance modelling of the Ballard Mark IV solid polymer electrolyte fuel cell. J. Electrochem. Soc. 1995, 142, 1. [Google Scholar] [CrossRef]
- Maher, A.R.; Al Bagdadi, S. Modelling of proton exchange membrane fuel cell performance based on semi-empirical equations. Renew. Energy 2005, 30, 1587–1599. [Google Scholar]
- Berning, T.; Djilali, N. Three-dimensional computational analysis of transport phenomena in a PEM fuel cell-A parametric study. J. Power Source 2003, 124, 440–452. [Google Scholar] [CrossRef]
- Ballard FCVelocityTM-9SSL Fuel Cell Stack, Product Specification, D.N. SPC5101531. Available online: https://www.ballard.com/about-ballard/publication_library/product-specification-sheets/fcvelocity-9ssl-spec-sheet (accessed on 15 February 2024).
- JANAF. Table. Available online: https://janaf.nist.gov/tables/H-064.txt (accessed on 15 February 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).