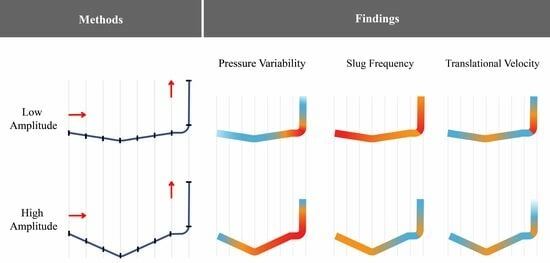
Investigating the Impact of Undulation Amplitude of Unconventional Oil Well Laterals on Transient Multiphase Flow Behavior: Experimental and Numerical Study
Abstract
:1. Introduction
2. Materials and Methods
Methodology
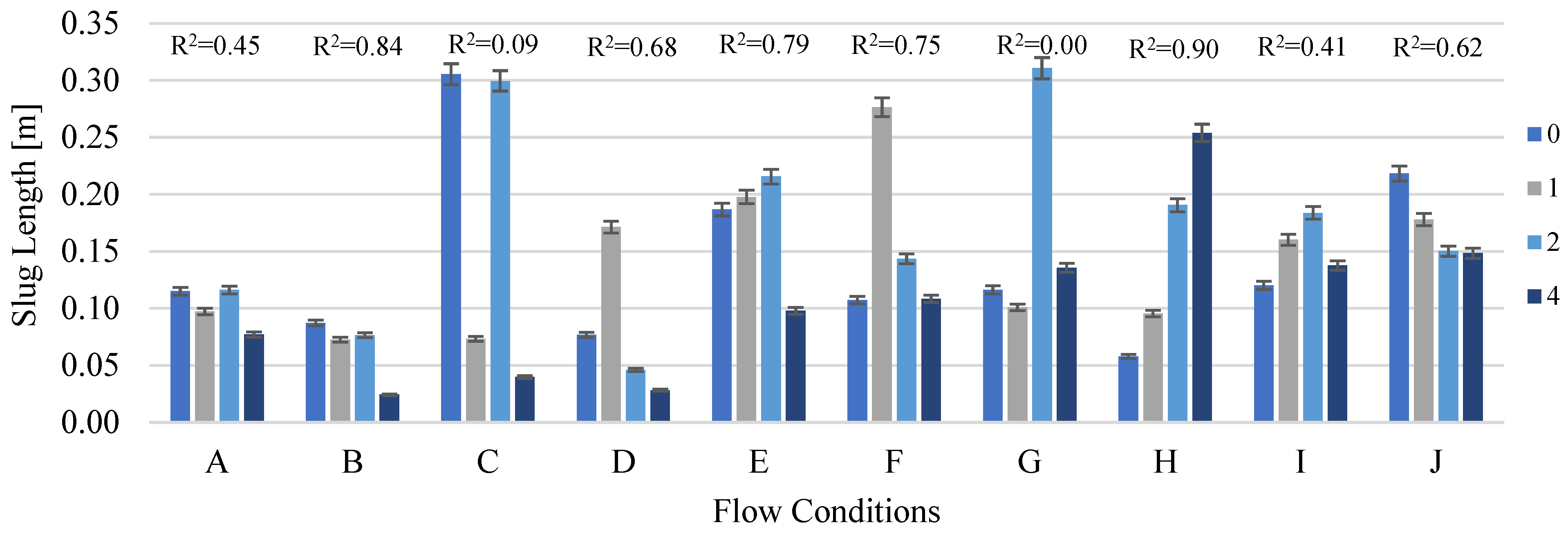
3. Experimental Results
4. Numerical Simulation Results
5. Conclusions
- -
- In general, the slug frequency decreases as the undulation amplitude increases, with a few outlier cases.
- -
- The slug length may either decrease or remain constant with an increasing undulation amplitude, depending on the flow conditions.
- -
- Both higher and lower kinetic energy cases show similar trends except for the translational velocity which is higher for cases of high kinetic energy.
- -
- Horizontal and vertical pressure losses increase with higher undulation amplitudes.
- -
- The variability of pressure at the given location decreases with increased undulation amplitude for cases of high kinetic energy but increases for cases of low energy.
- -
- Slug merging is observed along the lateral section, resulting in a gradual decrease in slug frequency.
- -
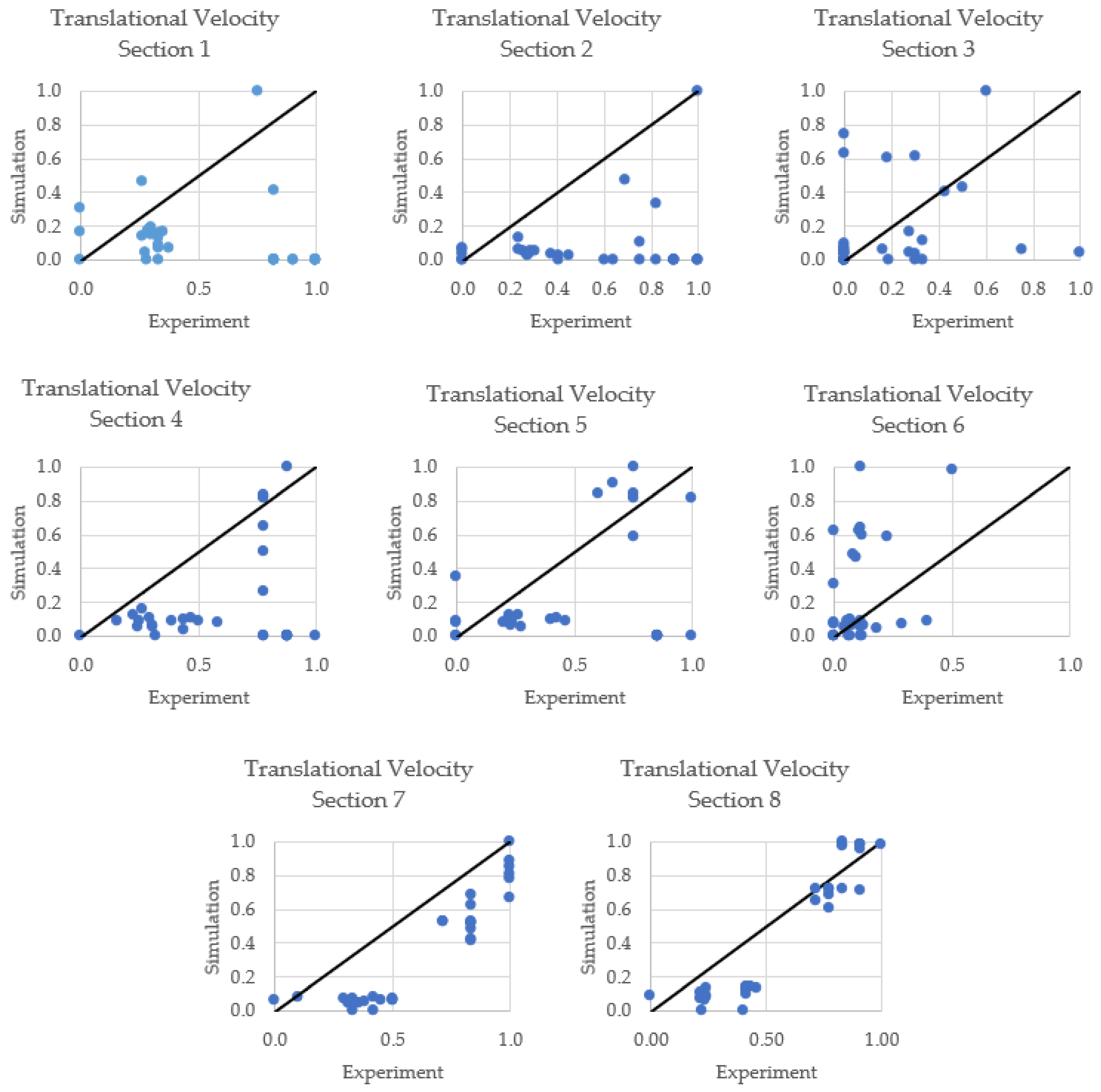
- The numerical simulation predicts lower translational velocities, higher slug lengths, and lower frequencies compared to the experimental results, with no correlation between the two results (experimental and numerical) explaining the importance of the liquid fallback effect in the studied system’s geometry.
- -
- The observed lateral pressure losses are four to five times higher than the numerically obtained pressure losses, likely due to a lack of liquid fallback effect modeling. The lateral section exhibits higher liquid holdup over time in the measured data, as illustrated in Appendix A, Figure A1 and Figure A2.
- -
- The observed vertical pressure losses agree in magnitude and trend with the numerical simulation results.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


| Tag | A | B | C | Measurement Uncertainty |
|---|---|---|---|---|
| HT-M-1 | 23.584 | −17.742 | 2.276 | 5.96 |
| HT-M-2 | 102.720 | −238.930 | 167.100 | 2.64 |
| HT-M-3 | 73.852 | −169.000 | 92.410 | 3.91 |
| HT-M-4 | 42.068 | −52.824 | 1.800 | 9.43 |
| HT-M-5 | 39.419 | −49.680 | 9.689 | 5.18 |
| HT-M-6 | 57.933 | −108.610 | 49.753 | 4.56 |
| HT-M-7 | 12.867 | −8.032 | 2.788 | 7.90 |
| HT-M-8 | 91.940 | −185.090 | 88.557 | 5.62 |
| HT-M-9 | 24.046 | −29.487 | 3.404 | 6.73 |



| Principal Component 1 | Principal Component 2 | Principal Component 3 | Principal Component 4 | |
|---|---|---|---|---|
| Undulation Amplitude | 0.00 | −0.04 | −0.11 | 0.07 |
| Superficial Water Velocity | 0.18 | 0.17 | −0.06 | 0.08 |
| Superficial Air Velocity | 0.21 | −0.03 | −0.04 | −0.03 |
| Gas to Liquid Ratio | 0.04 | −0.36 | 0.04 | −0.19 |
| Translational Velocity VT1 | 0.20 | 0.06 | 0.09 | −0.10 |
| Translational Velocity VT2 | 0.20 | 0.06 | 0.07 | −0.11 |
| Translational Velocity VT3 | 0.03 | −0.02 | 0.33 | 0.33 |
| Translational Velocity VT4 | 0.20 | 0.02 | 0.10 | −0.04 |
| Translational Velocity VT5 | 0.20 | 0.07 | 0.07 | −0.08 |
| Translational Velocity VT6 | 0.06 | −0.11 | 0.24 | 0.40 |
| Translational Velocity VT7 | 0.20 | 0.01 | 0.06 | −0.08 |
| Translational Velocity VT8 | 0.21 | 0.03 | 0.06 | −0.05 |
| Slug Length HT-M-1 | 0.04 | 0.11 | 0.30 | −0.02 |
| Slug Length HT-M-2 | 0.01 | 0.01 | 0.10 | −0.18 |
| Slug Length HT-M-3 | −0.05 | 0.01 | 0.33 | 0.22 |
| Slug Length HT-M-4 | 0.04 | −0.17 | 0.32 | −0.12 |
| Slug Length HT-M-5 | 0.04 | 0.18 | 0.11 | −0.12 |
| Slug Length HT-M-6 | 0.00 | −0.08 | 0.26 | 0.44 |
| Slug Length HT-M-7 | −0.05 | 0.10 | 0.28 | −0.36 |
| Slug Length HT-M-8 | −0.13 | 0.09 | 0.30 | −0.22 |
| Slug Length HT-M-9 | −0.13 | 0.18 | 0.21 | −0.10 |
| Slug Frequency HT-M-1 | 0.17 | 0.13 | 0.03 | 0.18 |
| Slug Frequency HT-M-2 | 0.18 | 0.14 | 0.00 | 0.02 |
| Slug Frequency HT-M-3 | 0.19 | 0.16 | −0.05 | 0.00 |
| Slug Frequency HT-M-4 | 0.17 | 0.14 | −0.08 | 0.02 |
| Slug Frequency HT-M-5 | 0.15 | 0.19 | 0.02 | −0.03 |
| Slug Frequency HT-M-6 | 0.18 | 0.15 | 0.06 | −0.01 |
| Slug Frequency HT-M-7 | 0.12 | 0.28 | 0.09 | −0.07 |
| Slug Frequency HT-M-8 | −0.05 | 0.11 | 0.33 | −0.06 |
| Slug Frequency HT-M-9 | −0.09 | 0.34 | 0.02 | 0.06 |
| Variability PT-M-0 | 0.05 | 0.28 | −0.14 | 0.28 |
| Variability PT-M-1 | 0.20 | −0.13 | 0.02 | 0.02 |
| Variability PT-M-2 | 0.20 | −0.14 | 0.02 | 0.02 |
| Variability PT-M-3 | 0.20 | −0.15 | 0.00 | 0.03 |
| Variability PT-M-4 | 0.20 | −0.15 | 0.00 | 0.02 |
| Variability PT-M-5 | 0.20 | −0.11 | 0.00 | 0.03 |
| Variability PT-M-6 | 0.21 | −0.09 | −0.02 | 0.00 |
| Variability PT-M-7 | 0.21 | −0.08 | −0.03 | −0.02 |
| Variability PT-M-8 | 0.21 | −0.07 | 0.00 | −0.03 |
| Variability PT-M-9 | 0.21 | 0.01 | −0.04 | −0.04 |
| Horizontal Pressure Loss | 0.20 | 0.08 | −0.03 | −0.07 |
| Vertical Pressure Loss | −0.04 | 0.38 | −0.17 | 0.07 |
References
- Khetib, Y.; Ling, K.; Allam, L.; Aoun, A.E. Statistical and Numerical Investigation of the Effect of Wellbore Trajectories in Williston Basin Horizontal Wells and Their Effects on Production Performance. Pet. Petrochem. Eng. J. 2022, 6, 320–335. [Google Scholar] [CrossRef]
- Norris, H.L.; Lee, H. The Use of a Transient Multiphase Simulator to Predict and Suppress Flow Instabilities in a Horizontal Shale Oil Well. SPE 2012, 1009–1019. [Google Scholar] [CrossRef]
- Khetib, Y.; Rasouli, V.; Rabiei, M.; Chellal, H.A.K.; Abes, A.; Bakelli, O.; Aoun, A.E. Modelling Slugging Induced Flow Instabilities and Its Effect on Hydraulic Fractures Integrity in Long Horizontal Wells. In Proceedings of the 56th U.S. Rock Mechanics/Geomechanics Symposium, American Rock Mechanics Association, Santa Fe, NJ, USA, 26–29 June 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Lu, H.; Anifowosh, O.; Xu, L. Understanding the Impact of Production Slugging Behavior on Near-Wellbore Hydraulic Fracture and Formation Integrity. In Proceedings of the SPE International Symposium on Formation Damage Control, OnePetro, Lafayette, LA, USA, 23–24 February 2018; pp. 7–9. [Google Scholar] [CrossRef]
- Khetib, Y. Investigation of Transient Multiphase Flow Performance in Undulating Horizontal Unconventional Wells; University of North Dakota: Grand Forks, ND, USA, 2022. [Google Scholar]
- Khetib, Y.; Aoun, A.E.; Ling, K. Experimental and Numerical Analysis of Toe-Up Trajectory Inclination Angle and Gas Lift Rate Effect on Unconventional Oil Well Performance. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, OnePetro, Denver, CO, USA, 13–15 June 2023; pp. 1–21. [Google Scholar] [CrossRef]
- Zhang, H.; Falcone, G.; Valko, P.P.; Teodoriu, C. Numerical Modeling of Fully-Transient Flow in the Near-Wellbore Region During Liquid Loading in Gas Wells. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Port of Spain, Trinidad and Tobago, 14–15 June 2023; pp. 1–15. [Google Scholar] [CrossRef]
- Tang, H.; Hasan, A.R.; Killough, J.; Hasan, A.R.; Killough, J. Development and Application of a Fully Implicitly Coupled Wellbore/Reservoir Simulator To Characterize the Transient Liquid Loading in Horizontal Gas Wells. SPE J. 2018, 23, 1615–1629. [Google Scholar] [CrossRef]
- Veeken, K.; Hu, B.; Schiferli, W. Gas-Well Liquid-Loading-Field-Data Analysis and Multiphase-Flow Modeling. SPE Prod. Oper. 2010, 25, 275–284. [Google Scholar] [CrossRef]
- Kannan, S.; Nagoo, A.; Lea, J. Understanding Heel Dominant Liquid Loading in Unconventional Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, OnePetro, Calgary, AB, Canada, 30 September–2 October 2019; pp. 1–13. [Google Scholar] [CrossRef]
- Tang, H.; Chai, Z.; He, Y.; Xu, B.; Hasan, A.R.; Killough, J. What Happens after the Onset of Liquid Loading?—An Insight from Coupled Well-Reservoir Simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018; pp. 24–26. [Google Scholar] [CrossRef]
- Jackson, D.F.B.; Virueś, C.J.J.; Sask, D. Investigation of Liquid Loading in Tight Gas Horizontal Wells with a Transient Multiphase Flow Simulator. In Proceedings of the Society of Petroleum Engineers—Canadian Unconventional Resources Conference 2011, CURC 2011, Calgary, AB, Canada, 15–17 November 2011; Volume 3, pp. 2256–2265. [Google Scholar] [CrossRef]
- Adaze, E.; Al-Sarkhi, A.; Badr, H.M.; Elsaadawy, E. Current status of CFD modeling of liquid loading phenomena in gas wells: A literature review. J. Pet. Explor. Prod. Technol. 2019, 9, 1397–1411. [Google Scholar] [CrossRef]
- Tang, H.; Hasan, A.R.; Killough, J. A Fully-Coupled Wellbore-Reservoir Model for Transient Liquid Loading in Horizontal Gas Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017; pp. 1–19. [Google Scholar] [CrossRef]
- Khetib, Y.; Zunez, S. Integrated Pipeline and Wells Transient Behavior of CO2 Injection Operations: Flow Assurance Best Practices. In Proceedings of the PSIG Annual Meeting, OnePetro, San Antonio, TX, USA, 19 May 2023; pp. 1–25. Available online: https://onepetro.org/PSIGAM/proceedings/PSIG23/All-PSIG23/PSIG-2325/520097 (accessed on 22 July 2023).
- Khan, S.; Khulief, Y.A.; Al-Shuhail, A.A. The effect of injection well arrangement on CO2 injection into carbonate petroleum reservoir. Int. J. Glob. Warm. 2018, 14, 462–487. [Google Scholar] [CrossRef]
- Pekot, L.J.; Petit, P.; Adushita, Y.; Saunier, S.; De Silva, R. Simulation of Two-Phase Flow in Carbon Dioxide Injection Wells. In Proceedings of the Society of Petroleum Engineers—Offshore Europe Oil and Gas Conference and Exhibition 2011, OE 2011, Aberdeen, UK, 6–8 September 2011; Volume 1, pp. 94–106. [Google Scholar] [CrossRef]
- Loizzo, M.; Lecampion, B.; Bérard, T.; Harichandran, A.; Jammes, L. Reusing O&G Depleted Reservoirs for CO2 Storage: Pros and Cons. In Proceedings of the Society of Petroleum Engineers—Offshore Europe Oil and Gas Conference and Exhibition 2009, OE 2009, Aberdeen, UK, 8–11 September 2009; Volume 2, pp. 783–792. [Google Scholar] [CrossRef]
- Haigh, M.J. Well Design Differentiators for CO2 Sequestration in Depleted Reservoirs. In Proceedings of the Society of Petroleum Engineers—Offshore Europe Oil and Gas Conference and Exhibition 2009, OE 2009, Aberdeen, UK, 8–11 September 2009; Volume 2, pp. 719–731. [Google Scholar] [CrossRef]
- Cronshaw, M.B.; Bolling, J.D. A Numerical Model of the Non-Isothermal Flow of Carbon Dioxide in Wellbores. In Proceedings of the Society of Petroleum Engineers—SPE California Regional Meeting, CRM 1982, San Francisco, CA, USA, 24–26 March 1982; pp. 173–180. [Google Scholar] [CrossRef]
- Paterson, L.; Lu, M.; Connell, L.D.; Ennis-King, J. Numerical Modeling of Pressure and Temperature Profiles Including Phase Transitions in Carbon Dioxide Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition 2008, Denver, CO, USA, 21–24 September 2008; Volume 4, pp. 2693–2703. [Google Scholar] [CrossRef]
- Tran, N.; Karami, H. Transient Multiphase Analysis of Well Trajectory Effects in Production of Horizontal Unconventional Wells. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium, OnePetro, Oklahoma City, OK, USA, 9 April 2019; pp. 1–13. [Google Scholar] [CrossRef]
- Nair, J.; Pereyra, E.; Sarica, C. Existence and Prediction of Severe Slugging in Toe-Down Horizontal Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, OnePetro, Dallas, TX, USA, 24–26 September 2018; pp. 1–19. [Google Scholar] [CrossRef]
- Pankaj, P.; Patron, K.E.; Lu, H. Artificial Lift Selection and Its Applications for Deep Horizontal Wells in Unconventional Reservoirs. URTeC Tech. 2018, 23–25. [Google Scholar] [CrossRef]
- Dinata, R.; Sarica, C.; Pereyra, E. End of Tubing EOT Placement Effects on the Two-Phase Flow Behavior in Horizontal Wells: Experimental Study. In Proceedings of the SPE Annual Technical Conference and Exhibition, Indianapolis, IN, USA, 23–25 May 2016; pp. 26–28. [Google Scholar] [CrossRef]
- Brito, R.M. Effect of Horizontal Well Trajectory on Two-Phase Gas-Liquid Flow Behavior. Ph.D. Dissertation, The University of Tulsa, Tulsa, OK, USA, 2015. [Google Scholar]
- Brito, R.; Pereyra, E.; Sarica, C. Existence of Severe Slugging in Toe-Up Horizontal Gas Wells. In Proceedings of the Society of Petroleum Engineers—SPE North America Artificial Lift Conference and Exhibition 2016, The Woodlands, TX, USA, 25–27 October 2016; pp. 25–27. [Google Scholar] [CrossRef]
- Brito, R.; Pereyra, E.; Sarica, C. Well trajectory effect on slug flow development. J. Pet. Sci. Eng. 2016, 167, 366–374. Available online: http://onepetro.org/BHRNACMT/proceedings-pdf/BHR16/All-BHR16/BHR-2016-053/1330257/bhr-2016-053.pdf (accessed on 24 June 2021). [CrossRef]
- Tran, N.L.; Orazov, B.; Karami, H. Impacts of Well Geometry and Gas Lift on Flow Dynamic and Production of Unconventional Horizontal Wells. In Proceedings of the SPE Artificial Lift Conference and Exhibition—Americas, Galveston, OnePetro, Galveston, TX, USA, 23–25 August 2022; pp. 1–16. [Google Scholar] [CrossRef]
- Gokcal, B. An Experimental and Theoretical Investigation of Slug Flow for High Oil Viscosity in Horizontal Pipes. Ph.D. Dissertation, University of Tulsa, Tulsa, OK, USA, 2008. [Google Scholar]
- OLGA 2020.2. User Manual. 2020. Available online: https://www.software.slb.com/products/olga (accessed on 15 August 2023).
- Dieck, R.H. Measurement uncertainty models. ISA Trans. 1997, 36, 29–35. [Google Scholar] [CrossRef]
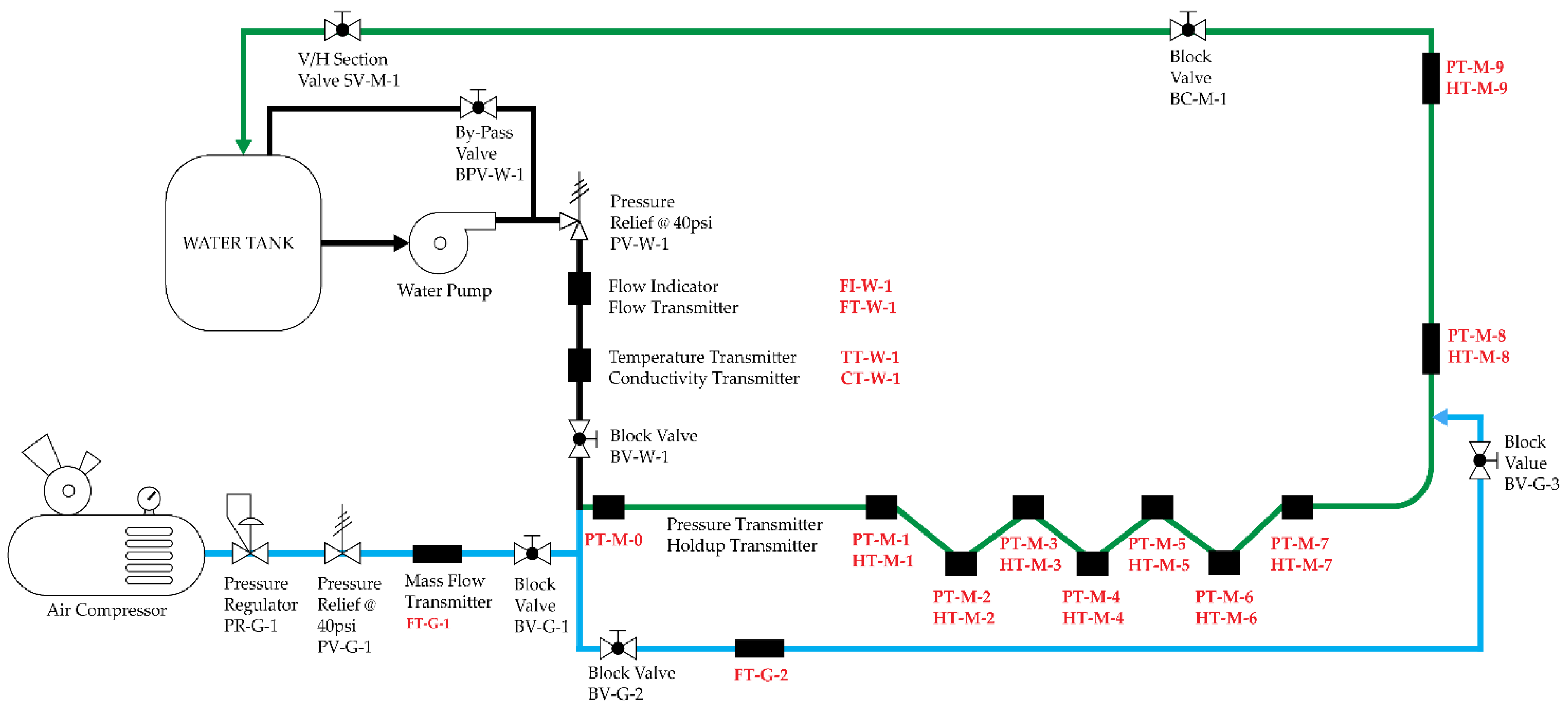
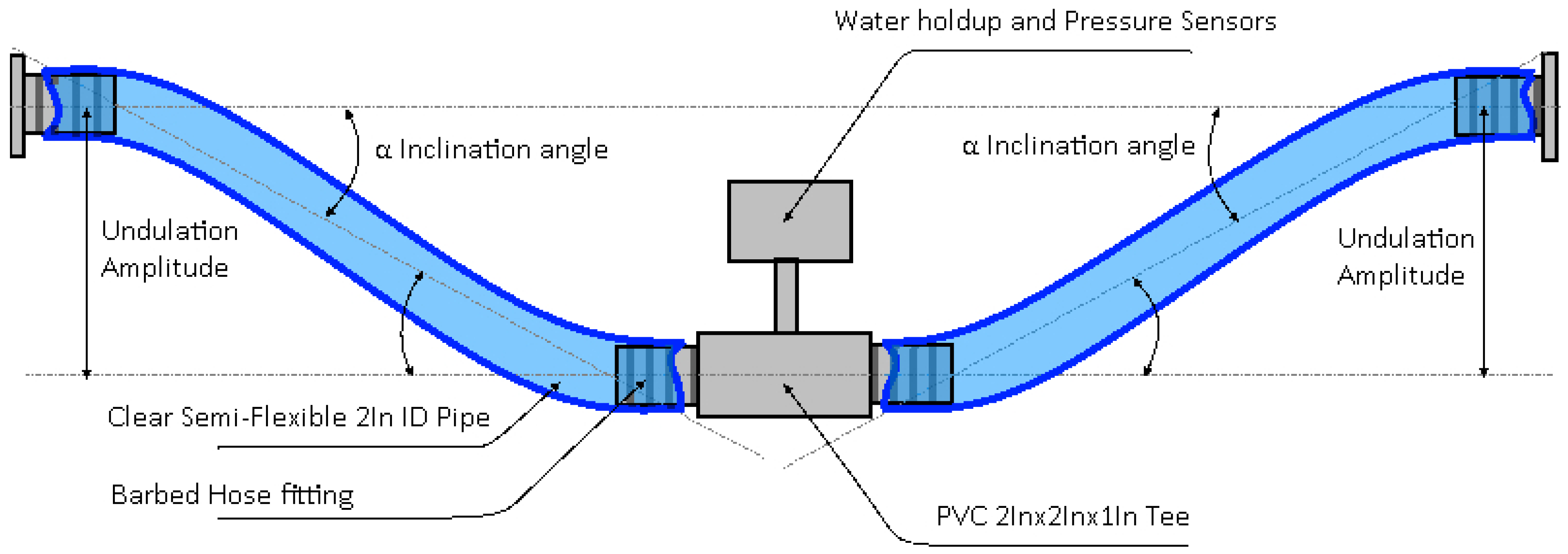




















| Equipment Name | Tag | Model Name | Specifications |
|---|---|---|---|
| Air Compressor | CMP-G-1 | Ingersoll Rand Model 7100 | 15 hp, max pressure 175 psig, 50 CFM |
| Water Pump | PMP-W-1 | Gorman-Rupp Model 3790-95 | 7.5 hp, max pressure 75 psig, max flowrate 157 gpm |
| Liquid Tank | TNK-W-1 | Schutz | 275 gallons |
| High-Speed Camera | CAM-N-1 | Z-CAM E2 | 60 fps, max resolution |
| Pressure Regulator | PR-G-1 | Ingersoll Rand | Range (0 to 160 psig) |
| Heat Exchanger | EX-G-1 | Ingersoll Rand | Flowrate 64 cfm max temperature 140 F, max pressure 203 psig |
| Case | Code | Number of Undulations | Position | Amplitude (cm) ±0.1 cm | Angle (°) ±1° |
|---|---|---|---|---|---|
| 1 | 1U20A | 1 | −20 | 20 | 15.26 |
| 2 | 1U10A | 1 | −10 | 10 | 7.56 |
| 3 | 1U5A | 1 | −5 | 5 | 3.77 |
| 4 | 0U0A | 0 | 0 | 0 | 0.00 |
| Parameter | Flow Conditions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | Unit | |
| Water Flow Rate | 10.0 1 | 10.0 1 | 20.0 1 | 28.0 1 | 20.0 1 | 5.0 1 | 2.5 1 | 2.5 1 | 10.0 1 | 10.0 1 | GPM |
| Water Superficial Velocity | 1.00 1 | 1.02 1 | 2.04 1 | 2.86 1 | 2.04 1 | 0.51 1 | 0.26 1 | 0.26 1 | 1.02 1 | 1.02 1 | ft/s |
| Mass Flow Rate | 0.6 1 | 0.63 1 | 1.26 1 | 1.77 1 | 1.26 1 | 0.32 1 | 0.16 1 | 0.16 1 | 0.63 1 | 0.63 1 | Kg/s |
| Air Flow Rate | 5.0 2 | 10.0 3 | 20.0 3 | 33.0 3 | 10.0 3 | 5.0 2 | 5.0 2 | 2.8 2 | 2.8 2 | 1.1 2 | SCFM |
| Air Superficial Velocity | 3.82 2 | 7.64 3 | 15.28 3 | 25.21 3 | 7.63 3 | 3.83 2 | 3.83 2 | 2.15 2 | 2.15 2 | 0.80 2 | ft/s |
| Mass Flow Rate | 0.003 2 | 0.006 3 | 0.012 3 | 0.020 3 | 0.006 3 | 0.003 2 | 0.003 2 | 0.0017 2 | 0.002 2 | 0.0006 2 | Kg/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khetib, Y.; Ling, K.; Tang, C.; Aoun, A.E.; Fadairo, A.S.; Ouadi, H. Investigating the Impact of Undulation Amplitude of Unconventional Oil Well Laterals on Transient Multiphase Flow Behavior: Experimental and Numerical Study. Fuels 2023, 4, 417-440. https://doi.org/10.3390/fuels4040026
Khetib Y, Ling K, Tang C, Aoun AE, Fadairo AS, Ouadi H. Investigating the Impact of Undulation Amplitude of Unconventional Oil Well Laterals on Transient Multiphase Flow Behavior: Experimental and Numerical Study. Fuels. 2023; 4(4):417-440. https://doi.org/10.3390/fuels4040026
Chicago/Turabian StyleKhetib, Youcef, Kegang Ling, Clement Tang, Ala Eddine Aoun, Adesina Samson Fadairo, and Habib Ouadi. 2023. "Investigating the Impact of Undulation Amplitude of Unconventional Oil Well Laterals on Transient Multiphase Flow Behavior: Experimental and Numerical Study" Fuels 4, no. 4: 417-440. https://doi.org/10.3390/fuels4040026
APA StyleKhetib, Y., Ling, K., Tang, C., Aoun, A. E., Fadairo, A. S., & Ouadi, H. (2023). Investigating the Impact of Undulation Amplitude of Unconventional Oil Well Laterals on Transient Multiphase Flow Behavior: Experimental and Numerical Study. Fuels, 4(4), 417-440. https://doi.org/10.3390/fuels4040026